MetaTrader 5 / Tester
Русский Português
preview
Arithmetic Optimization Algorithm (AOA): From AOA to SOA (Simple Optimization Algorithm)

Arithmetic Optimization Algorithm (AOA): From AOA to SOA (Simple Optimization Algorithm)

MetaTrader 5 — Tester |
344 0
Andrey Dik
Andrey Dik

Contents

  1. Introduction
  2. Implementation of the algorithm
  3. Test results


Introduction

The Arithmetic Optimization Algorithm (AOA) is an original method based on simple arithmetic operations such as addition, subtraction, multiplication and division. Its essence lies in using these basic mathematical principles to find optimal solutions to a variety of problems. AOA was developed by a team of researchers including Laith Abualigah and first introduced in 2021. The algorithm belongs to the class of metaheuristic methods (high-level algorithms) aimed at finding, generating and probabilistically choosing from several heuristics that can provide high-quality solutions in a reasonable time for complex optimization problems where accuracy-based methods may be ineffective or impossible.

This method caught my attention because of its simple and, at the same time, elegant idea of using completely elementary arithmetic operators. The relationship between these basic mathematical operations and metaheuristic approaches creates a synergy that allows solving complex optimization problems. The metaheuristic methods used in AOA include several key principles:

1. Population approach. AOA uses a population of solutions, which allows it to cover a wider space of possible solutions. This helps to avoid local optima and expands the search horizons.

2. Randomness and stochasticity. Incorporating elements of randomness into the search helps algorithms avoid getting stuck in local optima and provides a more complete exploration of the solution space, which increases the probability of finding a global optimum.

3. Balance between exploration and exploitation. Like many other metaheuristic algorithms, AOA strives for a balance between exploring new regions of the solution space and exploiting already known efficient solutions. This is achieved by using arithmetic operations to update the positions of solutions.

Thus, AOA is a striking example of a metaheuristic algorithm that effectively uses the principles of the population approach, randomness, and balancing between exploration and exploitation to solve optimization problems, however we will specifically talk about the efficiency of finding optimal solutions in complex and multidimensional spaces for this algorithm after its implementation and testing.


Implementation of the algorithm

The basic idea of AOA is to use the distributive behavior of arithmetic operators to find optimal solutions. The algorithm is characterized by simple principles, not a very large number of parameters and ease of implementation. The algorithm exploits the distribution characteristics of the four basic arithmetic operators in mathematics, namely: Multiplication (Mε × ε), Division (Dε ÷ ε), Subtraction (Sε − ε) and Addition (Aε + ε). In AOA, the initial population is generated randomly in the range [U; L], where the upper and lower bounds of the search space for the objective function are denoted by U and L, respectively, using the following equation:

x = L + (U − L) × δ, where x represents the population solution, δ is a random variable taking values in the range [0, 1].

At each iteration, the choice of the exploration and exploitation strategy, namely the choice of one of the two groups of operators, either (division; multiplication) or (subtraction; addition) is carried out depending on the result of the MoA (math optimizer accelerated) function, which is, in essence, the calculated value of the probability and changes with each iteration, calculated according to the equation:

MoA(t) = Min + t × (Max − Min) ÷ Maxt, where MoA(t) is the functional result at the t th iteration, t indicates the current iteration, which is in the range from 1 to the maximum number of iterations (Maxt). The minimum possible value of MoA is denoted as Min, while the maximum value is denoted as Max. These are external parameters of the algorithm.

All four arithmetic operator equations use the MoP (math optimizer) factor calculated as follows:

MoP(t) = 1 − (t ÷ Maxt)^(1 ÷ θ), where MoP(t) indicates the value of the MoP function at the t th iteration. θ is a critical parameter that controls the performance of the exploitation over the iterations. In the original work, the authors of the algorithm set it at level 5.

Figure 1 below shows the graphs of MoA and MoP dependence on the current iteration. The graphs show that with each iteration, MoA increases linearly, which means that the probability of choosing a group of operators (subtraction; addition) increases, and the probability of choosing a group of operators (division; multiplication) decreases proportionally. In turn, the MoP ratio decreases non-linearly, thereby reducing the next increment to the current position of agents in the population, which means an increase in the degree of refinement of decisions in the optimization.

MoAandMoP

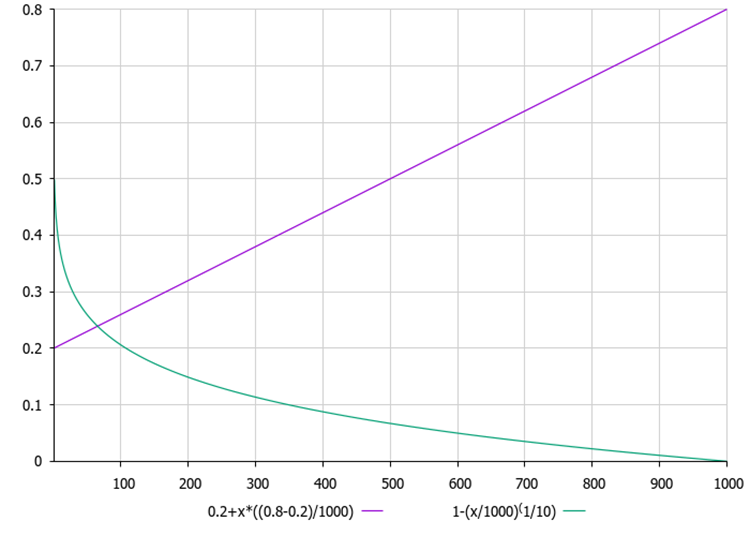
Figure 1. The purple color shows the MoA probability graph, and the green color shows the MoP ratio graph.

Research or global search in AOA is carried out using search strategies based on Division (D) and Multiplication (M) operators if the MoA probability is satisfied, which is formulated as follows, where the following operators are executed with equal probability:

xi,j(t+1) = best(xj) ÷ (MoPr + 𝜖) × ((Uj − Lj) × 𝜇 + Lj), if rand2 < 0.5; 

otherwise:

xi,j(t+1) = best(xj) × (MoPr) × ((Uj − Lj) × 𝜇 + Lj), where xi(t+1) represents the i th solution at the (t+1) th iteration, x(i,j)(t) represents the j th position of the i th individual in the current generation, best(xj) expresses the j th position of the best solution at the moment, ε is a small positive number, the upper and lower limits of the values of the j th position are denoted as Uj and Lj, respectively. The control parameter μ was set to 0.5. 

If the MoA probability is not met, then the exploitation strategy (solution refinement) is performed in AOA. The strategy was developed using the Subtraction (S) or Addition (A) operators. Here μ is also a constant, which is fixed at 0.5 by the authors' intention. 

xi,j(t+1) = best(xj) − (MoPr) × ((Uj − Lj) × 𝜇 + Lj), if rand3 < 0.5 

Otherwise, xi,j(t+1) = best(xj) + (MoPr) × ((Uj − Lj) × 𝜇 + Lj).

In AOA, the parameters 𝜇 and θ are very important as they are involved in balancing the trade-off between exploration and exploitation. Maintaining a well-balanced exploration and exploitation is usually a very challenging task. In the original AOA, the value of 𝜇 was fixed at 0.5 for both exploration and exploitation. However, the θ parameter, which affects the operating efficiency during the iterations, is set to 5. The authors experimented with different values of 𝜇 and θ and found that 𝜇 = 0.5 and θ = 5 most often yielded the best results for unimodal and multimodal test functions in different dimensions. 

Now let's implement the pseudocode of the AOA algorithm:

increase the epoch number by 1

// Starting initialization
IF this is the first launch THEN
    FOR each particle in the population:
        FOR each coordinate:
            set a random position within the allowed range
            bring a position to a discrete value
    mark that initialization is complete
    end function
END IF

// Main optimization process
calculate MoA = minMoA + EpochNumber * ((maxMoA - minMoА) / totalEpochs)
calculate MoP = 1 - (EpochNumber / totalEpochs)^(1/θ)

// Solution space exploration phase
FOR each particle in the population:
    FOR each coordinate:
        generate three random values (rand1, rand2, rand3)
        take the best known value for the coordinate
        
        IF rand1 < MoAc THEN
            IF rand2 > 0.5 THEN
                update position using Division
            OTHERWISE
                update position using Multiplication
            END IF
        OTHERWISE
            IF rand3 > 0.5 THEN
                update position using Subtraction
            OTHERWISE
                update position using Addition
            END IF
        END IF
        
        bring the new position to an acceptable discrete value
        
Update the best solution

Let's move on to writing the code. The C_AO_AOA class is an implementation of the AOA algorithm and is designed to solve optimization problems using a method based on arithmetic operations. Public methods:

1. The SetParams () method sets the values of parameters from the params array. This method allows changing the algorithm parameters after it has been initialized.

2. Init () method:

  • Initializes the algorithm by taking the minimum and maximum search ranges, the search step, and the number of epochs. 
  • Return true if the initialization succeeded, otherwise false.

3. The Moving () method performs the movement of particles in the solution space. This method implements the logic for updating particle positions based on the given parameters and the current state.

4. The Revision() method revises the current positions of particles, updating the best found value of the function and the coordinates of the corresponding particle.

Private fields, class parameters:

  • minT — minimum value of the MoA probability.
  • maxT — maximum value of the MoA probability.
  • θ — parameter that influences the balance of exploration and exploitation.
  • μ — parameter used to control changes in particle positions (movement range).
  • ϵ — small number to prevent division by zero.

Algorithm status info:

  • epochs — total number of epochs that the algorithm will go through.
  • epochNow — current epoch used to track the algorithm progress affects the MoA probability and the MoP ratio.

The C_AO_AOA class implements the main components of the AOA algorithm, including initialization, particle movement, and revision.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AOA () { }
  C_AO_AOA ()
  {
    ao_name = "AOA";
    ao_desc = "Arithmetic Optimization Algorithm";
    ao_link = "https://www.mql5.com/en/articles/16364";

    popSize = 50;   // Population size
    minT    = 0.1;  // Minimum T value
    maxT    = 0.9;  // Maximum T value
    θ       = 10;   // θ parameter
    μ       = 0.01; // μ parameter

    ArrayResize (params, 5); // Resize the parameter array

    // Initialize parameters
    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "minT";    params [1].val = minT;
    params [2].name = "maxT";    params [2].val = maxT;
    params [3].name = "θ";       params [3].val = θ;
    params [4].name = "μ";       params [4].val = μ;
  }

  void SetParams () // Method for setting parameters
  {
    popSize = (int)params [0].val; // Set population size
    minT    = params      [1].val; // Set minimum T
    maxT    = params      [2].val; // Set maximum T
    θ       = params      [3].val; // Set θ
    μ       = params      [4].val; // Set μ
  }

  bool Init (const double &rangeMinP  [], // Minimum search range
             const double &rangeMaxP  [], // Maximum search range
             const double &rangeStepP [], // Search step
             const int     epochsP = 0);  // Number of epochs

  void Moving   (); // Method of moving particles
  void Revision (); // Revision method

  //----------------------------------------------------------------------------
  double minT; // Minimum T value
  double maxT; // Maximum T value
  double θ;    // θ parameter
  double μ;    // μ parameter
  double ϵ;    // Parameter to prevent division by zero

  private: //-------------------------------------------------------------------
  int epochs;    // Total number of epochs
  int epochNow;  // Current epoch
};
//——————————————————————————————————————————————————————————————————————————————

The Init method of the C_AO_AOA class is responsible for initializing the optimization algorithm by setting the parameters of the search range, steps, and the number of epochs during which the optimization will be performed. The method logic:

1. The method first calls StandardInit, which initializes the standard parameters of the algorithm. If this initialization fails, Init immediately terminates execution and returns false.

2. Setting parameters:

  • Sets the total number of epochs based on the passed epochsP parameter.
  • Initializes the current epochNow epoch with 0.
  • Set ϵ (small value to prevent division by zero) to DBL_EPSILON, which is the standard value for representing the smallest positive number that can be represented in the double type.

3. If all steps are completed successfully, the method returns true, which indicates successful initialization of the algorithm.

The Init method is an important part of preparing the algorithm for execution, as it sets the basic parameters that will be used in the optimization. Calling this method will reset all parameters and variables to their original state.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AOA::Init (const double &rangeMinP  [], // Minimum search range
                     const double &rangeMaxP  [], // Maximum search range
                     const double &rangeStepP [], // Search step
                     const int     epochsP = 0)   // Number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; // Initialization of standard parameters

  //----------------------------------------------------------------------------
  epochs   = epochsP;     // Set the total number of epochs
  epochNow = 0;           // Initialize the current epoch
  ϵ        = DBL_EPSILON; // Set ϵ

  return true;            // Return 'true' if initialization was successful
}
//——————————————————————————————————————————————————————————————————————————————

The Moving method is responsible for the movement of particles in the solution space within the AOA algorithm. It implements the basic logic of updating particle positions based on the current state and algorithm parameters. The method logic:

1. Increase epochNow to reflect that a new era of optimization has arrived.

2. Initial random positioning: If no update (revision) has been performed yet, random positions within the given rangeMin and rangeMax ranges are generated for each particle. Each position is then discretized using the SeInDiSp method using the specified step.

3. MoAc and MoPr are calculated based on the current epoch and specified parameters. These values determine the probabilities used to update the particle positions.

4. Research phase. For each particle and each coordinate, the position is updated based on random values and calculated parameters. Positions can be updated using various operators (division and multiplication), as well as probabilistic conditions.

5. After the update, the position is also converted to discrete values using the SeInDiSp method.

//——————————————————————————————————————————————————————————————————————————————
// Particle displacement method
void C_AO_AOA::Moving ()
{
  epochNow++; // Increase the current epoch number

  // Initial random positioning
  if (!revision) // If there has not been a revision yet 
  {
    for (int i = 0; i < popSize; i++) // For each particle
    {
      for (int c = 0; c < coords; c++) // For each coordinate
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);                             // Generate random position
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Convert to discrete values
      }
    }

    revision = true; // Set revision flag
    return;          // Exit the method
  }

  //----------------------------------------------------------------------------
  double MoAc = minT + epochNow * ((maxT - minT) / epochs); // Calculate the MoAc value
  double MoPr = 1.0 - pow (epochNow / epochs, (1.0 / θ));   // Calculate the MoPr value
  double best = 0.0;                                        // Variable to store the best value

  // Research phase using Division (D) and Multiplication (M) operators
  for (int i = 0; i < popSize; i++) // For each particle
  {
    for (int c = 0; c < coords; c++) // For each coordinate
    {
      double rand1 = u.RNDprobab (); // Generate a random value
      double rand2 = u.RNDprobab (); // Generate a random value
      double rand3 = u.RNDprobab (); // Generate a random value

      best = cB [c];                 // Save the current best value

      if (rand1 < MoAc)              // If random value is less than MoAc
      {
        if (rand2 > 0.5)             // If random value is greater than 0.5
        {
          a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Update particle position
        }
        else
        {
          a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
      }
      else // If random value is greater than or equal to MoAc
      {
        if (rand3 > 0.5) // If random value is greater than 0.5
        {
          a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
        else
        {
          a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
      }

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Convert to discrete values
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

The Revision method in the C_AO_AOA class updates information about the best particle in the population. It iterates over all particles, compares their function values with the current best value, and if it finds a better one, updates it and saves the index. Then it copies the coordinates of the best particle into the cB array.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AOA::Revision ()
{
  int ind = -1;                     // Index to store the best particle

  for (int i = 0; i < popSize; i++) // For each particle
  {
    if (a [i].f > fB)               // If the function value is better than the current best one
    {
      fB = a [i].f;                 // Update the best value of the function
      ind = i;                      // Save the index of the best particle
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best particle
}
//——————————————————————————————————————————————————————————————————————————————

The SeInDiSp method of the C_AO_Utilities class limits the In input within the range of [InMin, InMax] with the specified Step.

1. If In is less than or equal to InMin, return InMin.
2. If In is greater than or equal to InMax, return InMax.
3. If Step is equal to 0, return the original value of In.
4. Otherwise, round the value to (In - InMin) / Step and return the adjusted value within the range taking into account the step.

double C_AO_Utilities :: SeInDiSp (double In, double InMin, double InMax, double Step)
{
  if (In <= InMin) return (InMin);
  if (In >= InMax) return (InMax);
  if (Step == 0.0) return (In);
  else return (InMin + Step * (double)MathRound ((In - InMin) / Step));
}


Test results

The AOA algorithm is quite simple, let's look at its performance on test tasks.

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.3914957505847635
25 Hilly's; Func runs: 10000; result: 0.27733670012505607
500 Hilly's; Func runs: 10000; result: 0.2514517003089684
=============================
5 Forest's; Func runs: 10000; result: 0.23495704012464264
25 Forest's; Func runs: 10000; result: 0.1853447250852242
500 Forest's; Func runs: 10000; result: 0.15382470751079919
=============================
5 Megacity's; Func runs: 10000; result: 0.19846153846153847
25 Megacity's; Func runs: 10000; result: 0.11815384615384619
500 Megacity's; Func runs: 10000; result: 0.09475384615384692
=============================
All score: 1.90578 (21.18%)

According to the test results, the algorithm scores only 21.18% out of 100%. This is a very weak result. Unfortunately, it is below the very last one in the current ranking table. Let's try to change the logic of the algorithm to achieve better results. We will make changes step by step and monitor the results.

The logic of the original AOA algorithm involves stochastic search, which consists only of the probabilistic nature of the choice of one of four mathematical operators. Let's add an element of randomness to the μ displacement ratio multiplying it by a random number in the range from 0 to 1.

// Research phase using Division (D) and Multiplication (M) operators
  for (int i = 0; i < popSize; i++) // For each particle
  {
    for (int c = 0; c < coords; c++) // For each coordinate
    {
      double rand1 = u.RNDprobab (); // Generate a random value
      double rand2 = u.RNDprobab (); // Generate a random value
      double rand3 = u.RNDprobab (); // Generate a random value

      best = cB [c];                 // Save the current best value

      μ *= u.RNDfromCI (0, 1);       // Random change of μ

      if (rand1 < MoAc)              // If random value is less than MoAc
      {
        if (rand2 > 0.5)             // If random value is greater than 0.5
        {
          a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Update particle position
        }
        else
        {
          a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
      }
      else // If random value is greater than or equal to MoAc
      {
        if (rand3 > 0.5) // If random value is greater than 0.5
        {
          a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
        else
        {
          a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
      }

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Convert to discrete values
    }
  }

Let's test the algorithm with the same parameters:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.3595591180258857
25 Hilly's; Func runs: 10000; result: 0.2804913285516192
500 Hilly's; Func runs: 10000; result: 0.25204298245610646
=============================
5 Forest's; Func runs: 10000; result: 0.24115834887873383
25 Forest's; Func runs: 10000; result: 0.18034196700384764
500 Forest's; Func runs: 10000; result: 0.15441446106797124
=============================
5 Megacity's; Func runs: 10000; result: 0.18307692307692305
25 Megacity's; Func runs: 10000; result: 0.12400000000000003
500 Megacity's; Func runs: 10000; result: 0.09470769230769309
=============================
All score: 1.86979 (20.78%)

Unfortunately, the result became even worse. Additional steps need to be taken. However, the very fact of adding randomness to a deterministic expression should certainly improve the variability of the search strategy. Let's look closely at the equations of mathematical operators - each of them has the rangeMin [c] term. In essence, the resulting expression in these operators is always centered relative to the minimum boundary of the parameters being optimized. There is no obvious logic to this, so let's remove this element from all equations.

// Research phase using Division (D) and Multiplication (M) operators
for (int i = 0; i < popSize; i++) // For each particle
{
  for (int c = 0; c < coords; c++) // For each coordinate
  {
    double rand1 = u.RNDprobab (); // Generate a random value
    double rand2 = u.RNDprobab (); // Generate a random value
    double rand3 = u.RNDprobab (); // Generate a random value

    best = cB [c];                 // Save the current best value

    μ *= u.RNDfromCI (0, 1);       // Change μ

    if (rand1 < MoAc)              // If random value is less than MoAc
    {
      if (rand2 > 0.5)             // If random value is greater than 0.5
      {
        a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]); // Update particle position
      }
      else
      {
        a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]);     // Update particle position
      }
    }
    else // If random value is greater than or equal to MoAc
    {
      if (rand3 > 0.5) // If random value is greater than 0.5
      {
        a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]);     // Update particle position
      }
      else
      {
        a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]);     // Update particle position
      }
    }

    a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Convert to discrete values
  }
}

Let's perform the test. Below are the results obtained:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.36094646986361645
25 Hilly's; Func runs: 10000; result: 0.28294095623218063
500 Hilly's; Func runs: 10000; result: 0.2524581968477915
=============================
5 Forest's; Func runs: 10000; result: 0.2463208325927641
25 Forest's; Func runs: 10000; result: 0.1772140022690996
500 Forest's; Func runs: 10000; result: 0.15367993432040622
=============================
5 Megacity's; Func runs: 10000; result: 0.1923076923076923
25 Megacity's; Func runs: 10000; result: 0.11938461538461542
500 Megacity's; Func runs: 10000; result: 0.09433846153846229
=============================
All score: 1.87959 (20.88%)

The changes we made did not result in any performance improvements, which is quite strange considering we had already implemented major changes to our search strategy. This may indicate that the strategy itself is flawed and removing individual components does not significantly affect the results.

The search strategy has the MoA component that increases linearly with each iteration (see Fig. 1). Let's try to use this component as a probabilistic choice of one of the coordinates of the best solution and copying it into the current working solution. This should add combinatorial properties to the search strategy by using information exchange through the best solution in the population (in the original version, there is no information exchange between agents).

// Research phase using Division (D) and Multiplication (M) operators
for (int i = 0; i < popSize; i++) // For each particle
{
  for (int c = 0; c < coords; c++) // For each coordinate
  {
    double rand1 = u.RNDprobab (); // Generate a random value
    double rand2 = u.RNDprobab (); // Generate a random value
    double rand3 = u.RNDprobab (); // Generate a random value

    best = cB [c];                 // Save the current best value

    μ *= u.RNDfromCI (0, 1);       // Change μ

    if (rand1 < MoAc)              // If random value is less than MoAc
    {
      if (rand2 > 0.5)             // If random value is greater than 0.5
      {
        a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ); // Update particle position
      }
      else
      {
        a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);     // Update particle position
      }
    }
    else // If random value is greater than or equal to MoAc
    {
      if (rand3 > 0.5) // If random value is greater than 0.5
      {
        a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);     // Update particle position
      }
      else
      {
        a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);     // Update particle position
      }
    }

    if (u.RNDbool () < MoAc) a [i].c [c] = cB [c];                                            // Set to the best value

    a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Convert to discrete values
  }
}

The results obtained after introducing the logic of information exchange through the best solution:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.360814744695913
25 Hilly's; Func runs: 10000; result: 0.28724958448168375
500 Hilly's; Func runs: 10000; result: 0.2523432997811412
=============================
5 Forest's; Func runs: 10000; result: 0.26319762212870146
25 Forest's; Func runs: 10000; result: 0.1796822846691542
500 Forest's; Func runs: 10000; result: 0.1546335398592898
=============================
5 Megacity's; Func runs: 10000; result: 0.18
25 Megacity's; Func runs: 10000; result: 0.12153846153846157
500 Megacity's; Func runs: 10000; result: 0.09373846153846228
=============================
All score: 1.89320 (21.04%)

We see improvements in performance, but so far within the range of the solutions themselves. Now let's add to the same part of the code the probability of generating a random value for a coordinate within the entire acceptable range of optimized parameters, while the coordinate decreases non-linearly according to the MoP equation. 

// Probabilistic update of particle position
if (u.RNDbool () < MoAc) a [i].c [c] = cB [c];                                        // Set to the best value
else
  if (u.RNDbool () < MoPr) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);    // Generate new random position

Let's look at the following results:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.8354927331645667
25 Hilly's; Func runs: 10000; result: 0.3963221867834875
500 Hilly's; Func runs: 10000; result: 0.2526544322311671
=============================
5 Forest's; Func runs: 10000; result: 0.7689954585427405
25 Forest's; Func runs: 10000; result: 0.3144560745800252
500 Forest's; Func runs: 10000; result: 0.15495875390289315
=============================
5 Megacity's; Func runs: 10000; result: 0.6076923076923076
25 Megacity's; Func runs: 10000; result: 0.24646153846153843
500 Megacity's; Func runs: 10000; result: 0.09816923076923163
=============================
All score: 3.67520 (40.84%)

Amazingly, productivity has increased dramatically! This means that we are moving in the right direction. It is worth noting what exactly was added to the AOA logic: at the beginning of optimization, in the first epoch, the probability of copying the coordinates of the global best solution to the current ones is minimal. This is quite logical, since at the initial stage of optimization the strategy is just beginning to explore the search space. At the same time, the probability of generating random solutions within the entire search space at the first iteration is maximum. Throughout all epochs, these probabilities change: the probability of copying the coordinates of the global solution increases, while the probability of generating random solutions, on the contrary, decreases (see Fig. 1).

Since the performance has improved with the changes I made, and it was previously noted that changes in the original logic do not lead to noticeable improvements, it makes sense to completely eliminate all arithmetic operators. Let's test the resulting algorithm on test problems:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8751771961221438
25 Hilly's; Func runs: 10000; result: 0.4645369071659114
500 Hilly's; Func runs: 10000; result: 0.27170038319811357
=============================
5 Forest's; Func runs: 10000; result: 0.8369443889312367
25 Forest's; Func runs: 10000; result: 0.36483865328371257
500 Forest's; Func runs: 10000; result: 0.17097532914778202
=============================
5 Megacity's; Func runs: 10000; result: 0.7046153846153846
25 Megacity's; Func runs: 10000; result: 0.28892307692307695
500 Megacity's; Func runs: 10000; result: 0.10847692307692398
=============================
All score: 4.08619 (45.40%)   

As we can see, the efficiency increased by almost another 5%, which again confirmed the correctness of my reasoning. We got interesting results with the default parameters, however, the changes in logic were so radical that now it is necessary to select the optimal external parameters of the algorithm. An additional bonus to increased productivity was:

  • significant speedup of work, as we got rid of unnecessary generation of random numbers
  • reducing the number of external parameters by one

Let's look at the final results of the obtained algorithm:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.5|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9152036654779877
25 Hilly's; Func runs: 10000; result: 0.46975580956945456
500 Hilly's; Func runs: 10000; result: 0.27088799720164297
=============================
5 Forest's; Func runs: 10000; result: 0.8967497776673259
25 Forest's; Func runs: 10000; result: 0.3740125122006007
500 Forest's; Func runs: 10000; result: 0.16983896751516864
=============================
5 Megacity's; Func runs: 10000; result: 0.6953846153846155
25 Megacity's; Func runs: 10000; result: 0.2803076923076923
500 Megacity's; Func runs: 10000; result: 0.10852307692307792
=============================
All score: 4.18066 (46.45%) 

The obtained result already deserves a place in the rating table, while the final version of the search strategy has completely lost elements of the original logic. So I decided to give this new algorithm a new name - Simple Optimization Algorithm (SOA). Let's look at the entire final code of the SOA algorithm.

#include "#C_AO.mqh"

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_SOA () { }
  C_AO_SOA ()
  {
    ao_name = "SOA";
    ao_desc = "Simple Optimization Algorithm";
    ao_link = "https://www.mql5.com/en/articles/16364";

    popSize = 50;   // Population size
    minT    = 0.1;  // Minimum T value
    maxT    = 0.9;  // Maximum T value
    θ       = 10;   // θ parameter

    ArrayResize (params, 4); // Resize the parameter array

    // Initialize parameters
    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "minT";    params [1].val = minT;
    params [2].name = "maxT";    params [2].val = maxT;
    params [3].name = "θ";       params [3].val = θ;
  }

  void SetParams () // Method for setting parameters
  {
    popSize = (int)params [0].val; // Set population size
    minT    = params      [1].val; // Set minimum T
    maxT    = params      [2].val; // Set maximum T
    θ       = params      [3].val; // Set θ
  }

  bool Init (const double &rangeMinP  [], // Minimum search range
             const double &rangeMaxP  [], // Maximum search range
             const double &rangeStepP [], // Search step
             const int     epochsP = 0);  // Number of epochs

  void Moving   (); // Method of moving particles
  void Revision (); // Revision method

  //----------------------------------------------------------------------------
  double minT; // Minimum T value
  double maxT; // Maximum T value
  double θ;    // θ parameter

  private: //-------------------------------------------------------------------
  int epochs;    // Total number of epochs
  int epochNow;  // Current epoch
  double ϵ;      // Parameter to prevent division by zero
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_SOA::Init (const double &rangeMinP  [], // Minimum search range
                     const double &rangeMaxP  [], // Maximum search range
                     const double &rangeStepP [], // Search step
                     const int     epochsP = 0)   // Number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; // Initialization of standard parameters

  //----------------------------------------------------------------------------
  epochs   = epochsP;     // Set the total number of epochs
  epochNow = 0;           // Initialize the current epoch
  ϵ        = DBL_EPSILON; // Set ϵ

  return true;            // Return 'true' if initialization was successful
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Particle displacement method
void C_AO_SOA::Moving ()
{
  epochNow++; // Increase the current epoch number

  // Initial random positioning
  if (!revision) // If there has not been a revision yet 
  {
    for (int i = 0; i < popSize; i++) // For each particle
    {
      for (int c = 0; c < coords; c++) // For each coordinate
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);                             // Generate random position
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Convert to discrete values
      }
    }

    revision = true; // Set revision flag
    return;          // Exit the method
  }

  //----------------------------------------------------------------------------
  double MoAc = minT + epochNow * ((maxT - minT) / epochs); // Calculate the MoAc value
  double MoPr = 1.0 - pow (epochNow / epochs, (1.0 / θ));   // Calculate the MoPr value
  double best = 0.0;                                        // Variable to store the best value

  // Research phase using Division (D) and Multiplication (M) operators
  for (int i = 0; i < popSize; i++) // For each particle
  {
    for (int c = 0; c < coords; c++) // For each coordinate
    {
      // Probabilistic update of particle position
      if (u.RNDbool () < MoAc) a [i].c [c] = cB [c];                                        // Set to the best value
      else
        if (u.RNDbool () < MoPr) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);    // Generate new random position

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);   // Convert to discrete values
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SOA::Revision ()
{
  int ind = -1;                     // Index to store the best particle

  for (int i = 0; i < popSize; i++) // For each particle
  {
    if (a [i].f > fB)               // If the function value is better than the current best one
    {
      fB = a [i].f;                 // Update the best value of the function
      ind = i;                      // Save the index of the best particle
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best particle
}
//——————————————————————————————————————————————————————————————————————————————

The result is one of the most compact optimization algorithms in terms of code that we have considered previously. The only code that is shorter is the one of RW (RandomWalk) algorithm, which will be discussed in one of the following articles.

Visualizing the performance of search strategies in the solution space speaks volumes. I combined all three tests (Hilly, Forest and Megacity) for the AOA algorithm into one animation, since there are practically no differences in the performance on different types of tasks. Below are separate visualizations of the SOA operation for each of the three test functions.

It is possible to note the work of the new SOA algorithm on problems of small dimensions - a small spread of results, which is a quite rare quality. 

AOA on Hilly, Forest, Megacity

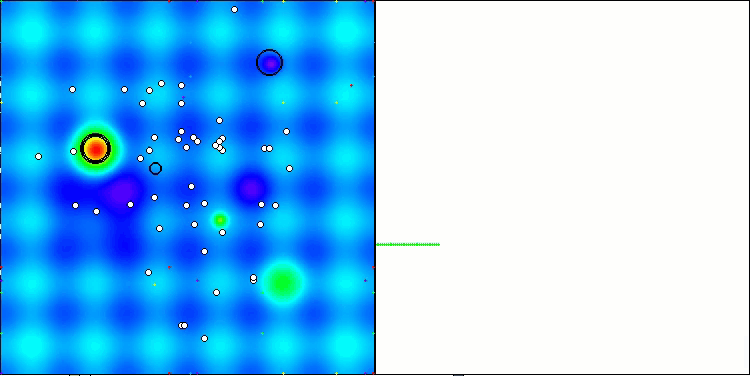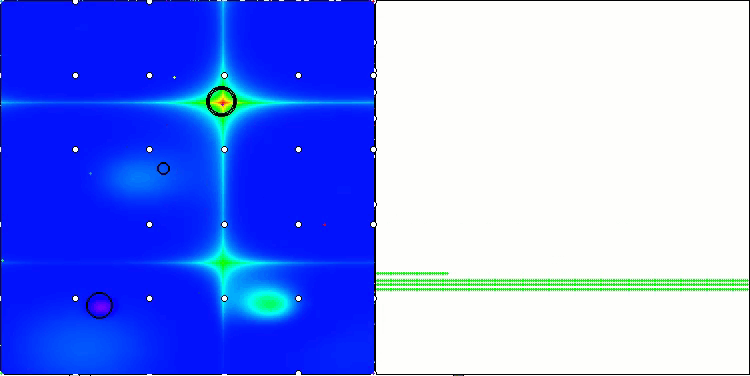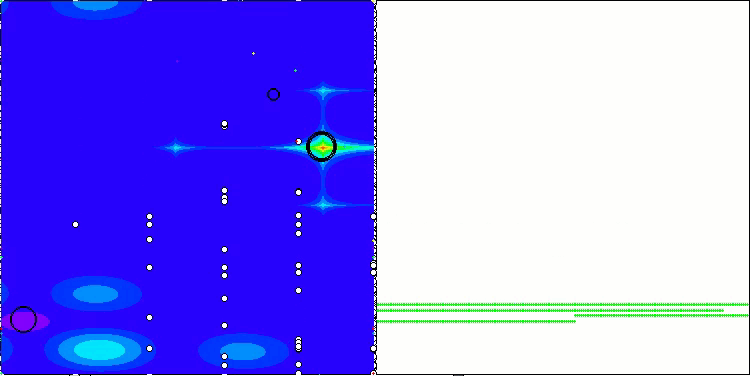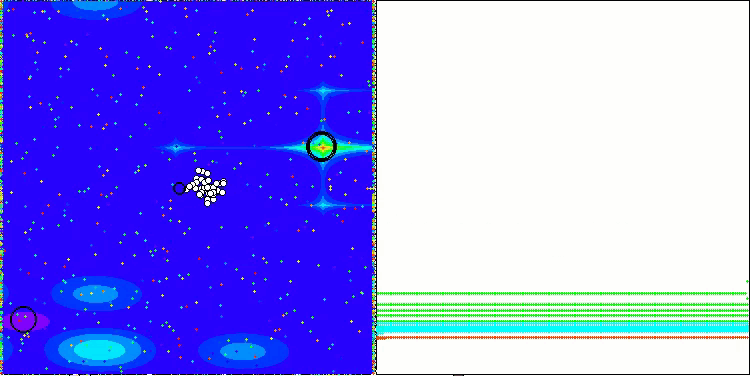
AOA on the Hilly, Forest, Megacity  test functions

Hilly

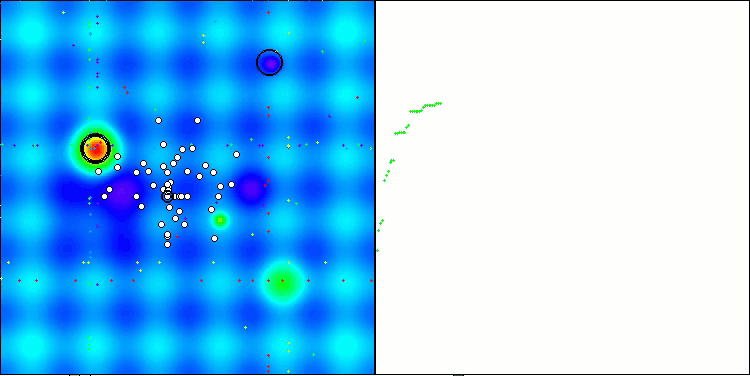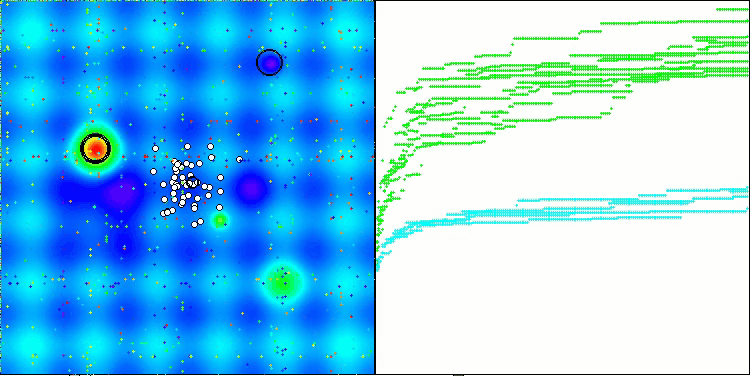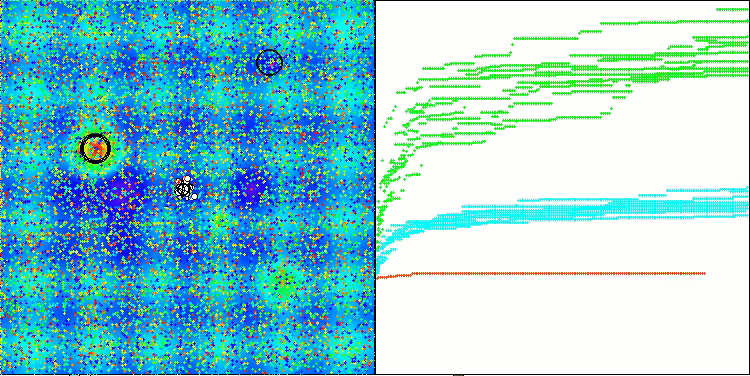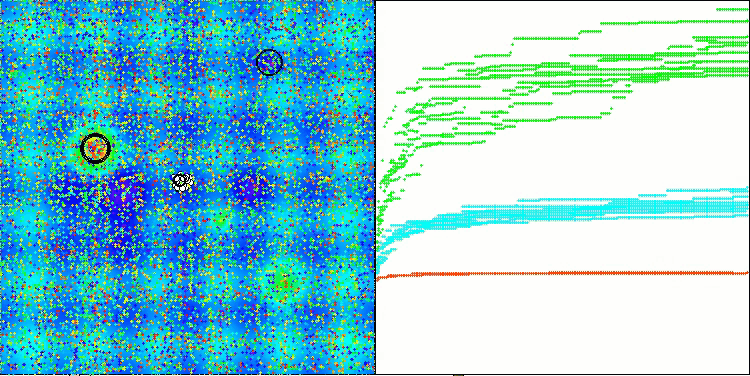
SOA on the Hilly test function

Forest

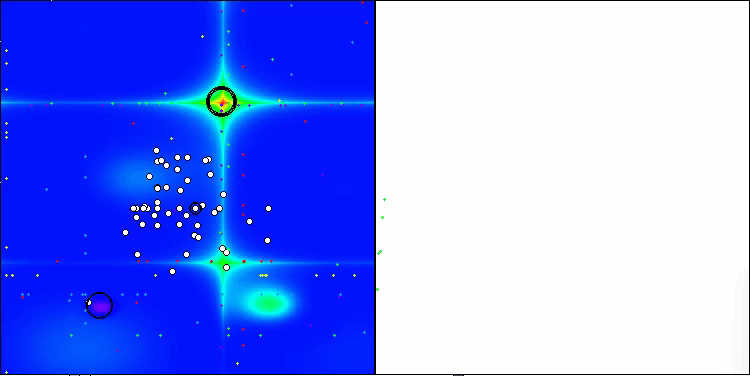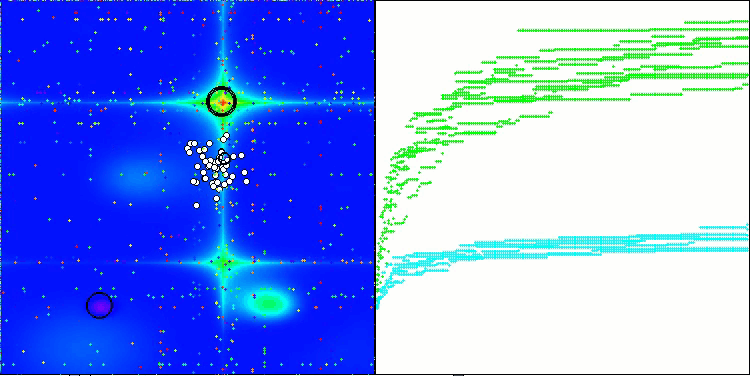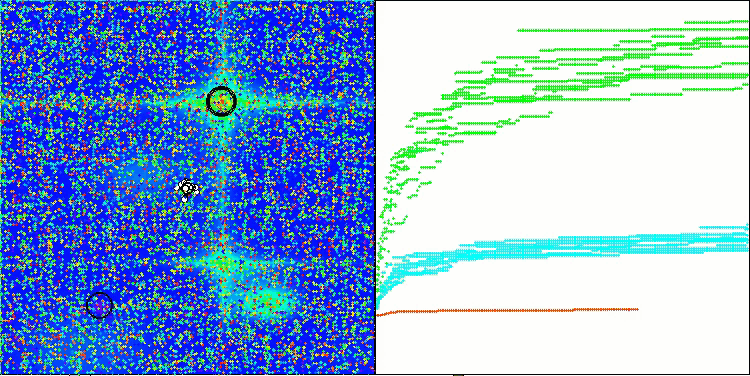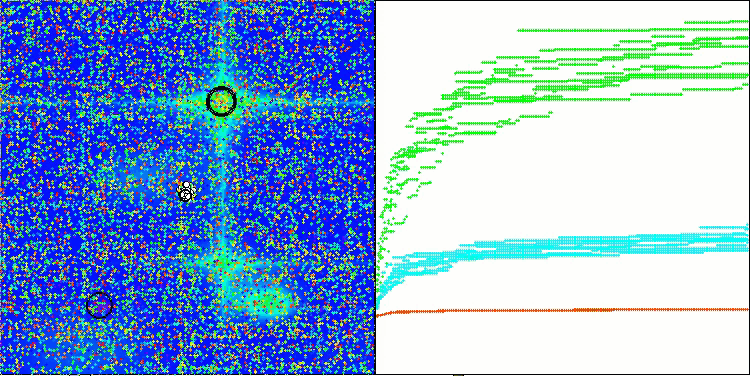
  SOA on the Forest test function

Megacity

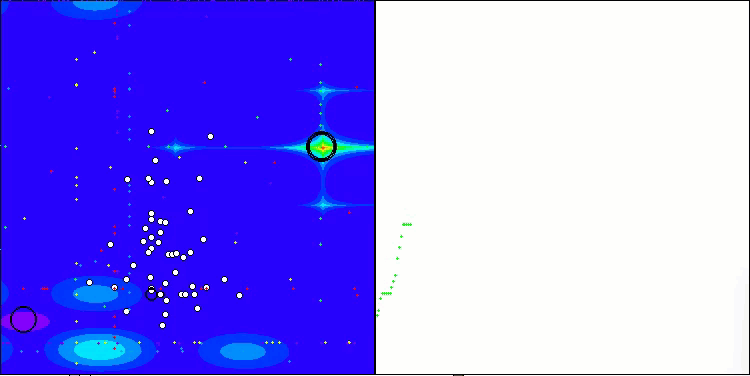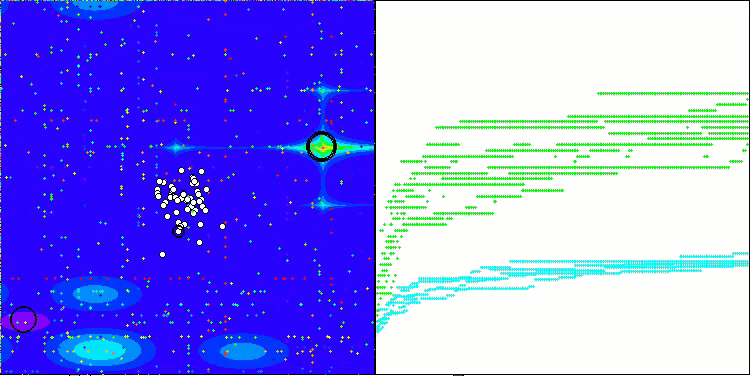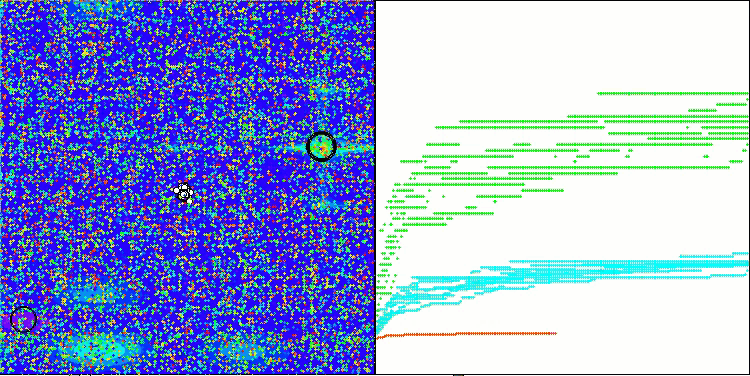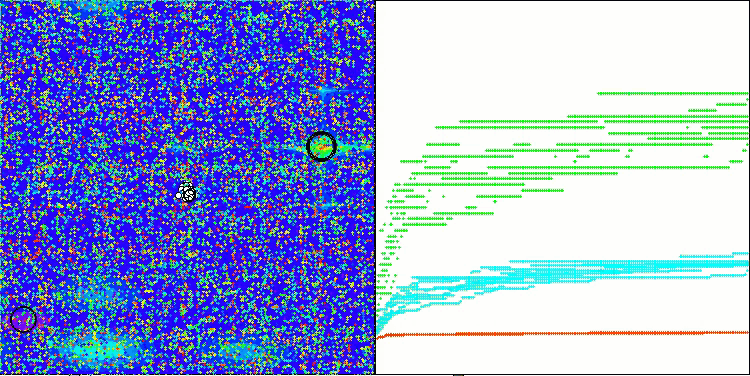
SOA on the Megacity test function


Based on the test results, the original AOA algorithm did not make it into the ranking table, as its result was below 45 th place. The new Simple Optimization Algorithm (SOA) algorithm made it into the ranking and ended up in 29 th place.

# AO Description Hilly Hilly final Forest Forest final Megacity (discrete) Megacity final Final result % of MAX
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
2 CLA code lock algorithm (joo) 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
3 AMOm animal migration ptimization M 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
4 (P+O)ES (P+O) evolution strategies 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
5 CTA comet tail algorithm (joo) 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
6 SDSm stochastic diffusion search M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
7 AAm archery algorithm M 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
8 ESG evolution of social groups (joo) 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
9 SIA simulated isotropic annealing (joo) 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
10 ACS artificial cooperative search 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
11 ASO anarchy society optimization 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
12 AOSm atomic orbital search M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
13 TSEA turtle shell evolution algorithm (joo) 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
14 DE differential evolution 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
15 CRO chemical reaction optimization 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
16 BSA bird swarm algorithm 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
17 HS harmony search 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
18 SSG saplings sowing and growing 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
19 BCOm bacterial chemotaxis optimization M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
20 ABO african buffalo optimization 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
21 (PO)ES (PO) evolution strategies 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
22 TSm tabu search M 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
23 BSO brain storm optimization 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
24 WOAm wale optimization algorithm M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
25 AEFA artificial electric field algorithm 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
26 AEO artificial ecosystem-based optimization algorithm 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
27 ACOm ant colony optimization M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
28 BFO-GA bacterial foraging optimization - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
29 SOA simple optimization algorithm 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
30 ABHA artificial bee hive algorithm 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
31 ACMO atmospheric cloud model optimization 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
32 ASHA artificial showering algorithm 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
33 ASBO adaptive social behavior optimization 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
34 MEC mind evolutionary computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
35 IWO invasive weed optimization 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
36 Micro-AIS micro artificial immune system 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
37 COAm cuckoo optimization algorithm M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
38 SDOm spiral dynamics optimization M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
39 NMm Nelder-Mead method M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
40 FAm firefly algorithm M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
41 GSA gravitational search algorithm 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
42 BFO bacterial foraging optimization 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
43 ABC artificial bee colony 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
44 BA bat algorithm 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
45 AAA algae adaptive algorithm 0.50007 0.32040 0.25525 1.07572 0.37021 0.22284 0.16785 0.76089 0.27846 0.14800 0.09755 0.52402 2.361 26.23


Summary

We have looked in detail at the arithmetic optimization algorithm, the implementation of which turned out to be really simple. However, as sometimes happens, simplicity does not always guarantee high results. The real key to success is super simplicity! I am kidding, of course. The main problems of AOA are the lack of interaction and information exchange between members of the population, which in turn leads to a complete lack of combinatorial qualities in this search strategy.

Another drawback of the algorithm is the lack of variability in its search operators. Although the operators are chosen randomly for each coordinate, this does not allow the algorithm to effectively "hook" on the multidimensional landscape of the search space. However, the AOA algorithm contains rational and logical approaches, such as the MoA and MoP elements changing with each epoch. They became the basis for recreating the algorithm and its evolution into a new, interesting and extremely simple search strategy based on the probabilistic approach of copying information from the best solutions of the population and generating random solutions in the search space.

With each epoch, the randomness in the population's decisions decreases, while the concentration of successful directions increases. This can be compared to the process of building an elegant bridge across a river: in the initial stages of work, various materials and designs are used that may not be suitable for the final result. However, as the project progresses towards completion, the best solutions become more obvious and unnecessary elements are discarded. As a result, the bridge becomes increasingly harmonious and stable, connecting the banks with elegance and strength.

Tab

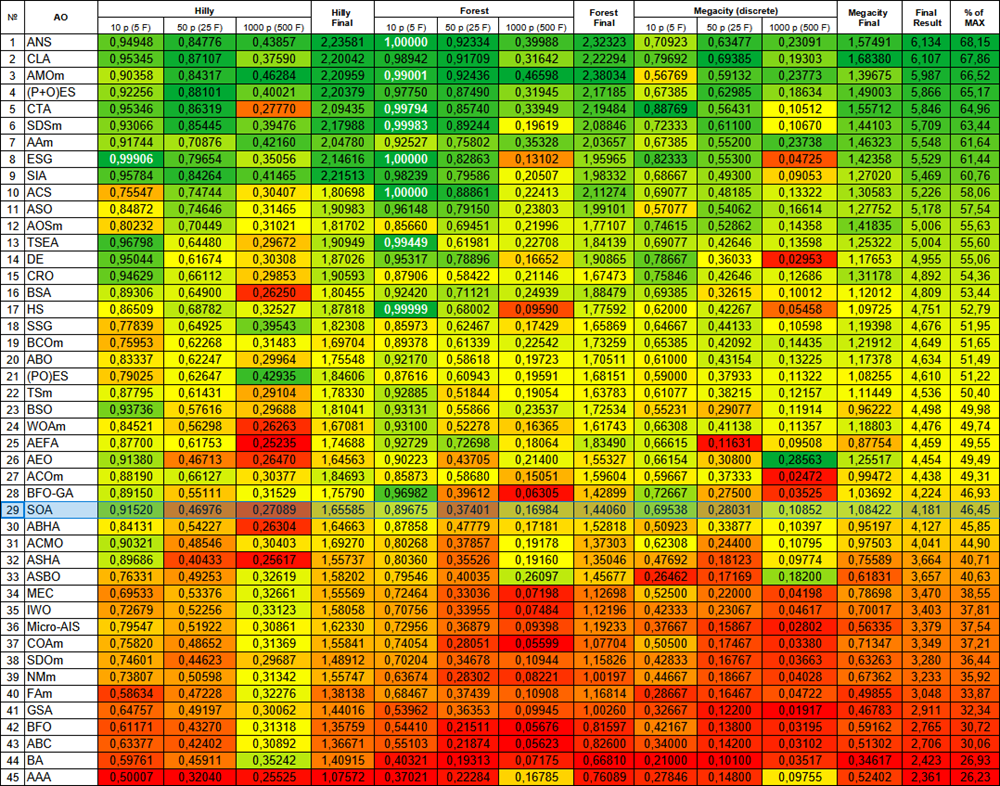
Figure 2. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white

chart

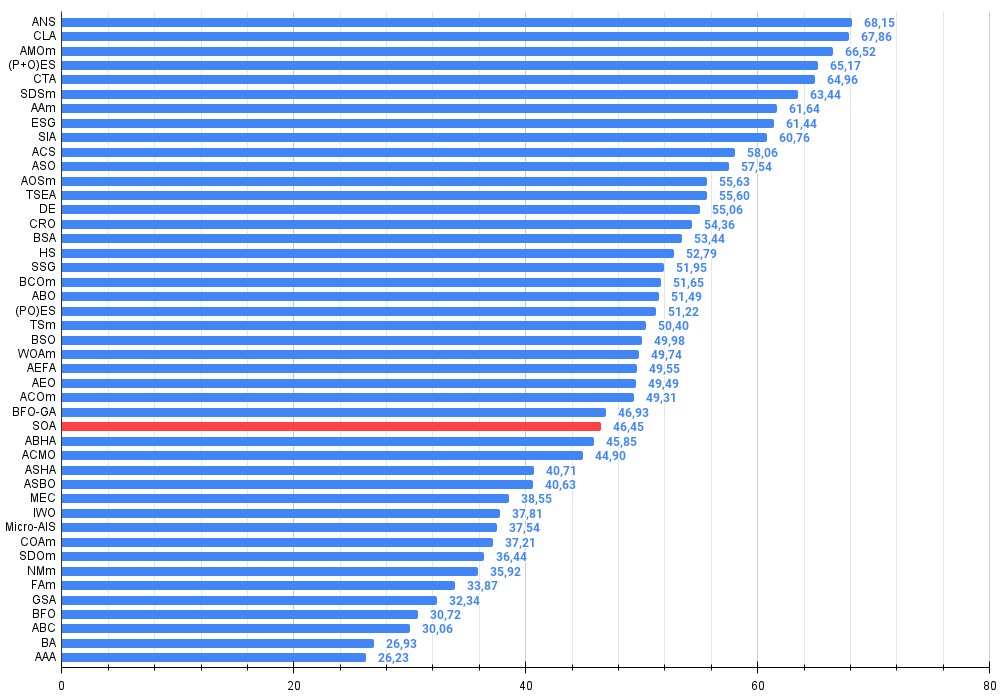
Figure 3. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,

where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)


SOA pros and cons:

Pros:

  1. Small number of external parameters.
  2. Good results on low-dimensional problems, especially discrete ones.
  3. Fast.
  4. Small scatter of results on small-dimensional problems.
  5. Very simple implementation.

Cons:

  1. Low scalability.

The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.

Programs used in the article

# Name Type Description
1 #C_AO.mqh
 Include
 Parent class of population optimization algorithms
2 #C_AO_enum.mqh
 Include
 Enumeration of population optimization algorithms
3 TestFunctions.mqh
 Include
 Library of test functions
4
 TestStandFunctions.mqh
 Include
 Test stand function library
5
 Utilities.mqh
 Include
 Library of auxiliary functions
6
 CalculationTestResults.mqh
 Include
 Script for calculating results in the comparison table
7
 Testing AOs.mq5
 Script The unified test stand for all population optimization algorithms
8
 Simple use of population optimization algorithms.mq5
 Script
A simple example of using population optimization algorithms without visualization
9
 AO_AOA_ArithmeticOptimizationAlgorithm.mqh
 Include AOA algorithm class
10
 AO_SOA_SimpleOptimizationAlgorithm.mqh
 Include
 SOA algorithm class
11
Test_AO_AOA.mq5
 Script AOA test stand
12
 Test_AO_SOA.mq5
 Script
 SOA test stand

Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/16364

Attached files |
Download ZIP
AOA_SOA.zip (141.9 KB)
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.

Other articles by this author

Go to discussion
Neural Networks in Trading: Hyperbolic Latent Diffusion Model (Final Part) Neural Networks in Trading: Hyperbolic Latent Diffusion Model (Final Part)
The use of anisotropic diffusion processes for encoding the initial data in a hyperbolic latent space, as proposed in the HypDIff framework, assists in preserving the topological features of the current market situation and improves the quality of its analysis. In the previous article, we started implementing the proposed approaches using MQL5. Today we will continue the work we started and will bring it to its logical conclusion.
Formulating Dynamic Multi-Pair EA (Part 3): Mean Reversion and Momentum Strategies Formulating Dynamic Multi-Pair EA (Part 3): Mean Reversion and Momentum Strategies
In this article, we will explore the third part of our journey in formulating a Dynamic Multi-Pair Expert Advisor (EA), focusing specifically on integrating Mean Reversion and Momentum trading strategies. We will break down how to detect and act on price deviations from the mean (Z-score), and how to measure momentum across multiple forex pairs to determine trade direction.
Automating Trading Strategies in MQL5 (Part 23): Zone Recovery with Trailing and Basket Logic Automating Trading Strategies in MQL5 (Part 23): Zone Recovery with Trailing and Basket Logic
In this article, we enhance our Zone Recovery System by introducing trailing stops and multi-basket trading capabilities. We explore how the improved architecture uses dynamic trailing stops to lock in profits and a basket management system to handle multiple trade signals efficiently. Through implementation and backtesting, we demonstrate a more robust trading system tailored for adaptive market performance.
From Basic to Intermediate: Union (I) From Basic to Intermediate: Union (I)
In this article we will look at what a union is. Here, through experiments, we will analyze the first constructions in which union can be used. However, what will be shown here is only a core part of a set of concepts and information that will be covered in subsequent articles. The content presented here is intended solely for educational purposes. Under no circumstances should the application be viewed for any purpose other than to learn and master the concepts presented.