取引におけるニューラルネットワーク：Segment Attentionを備えたパラメータ効率重視Transformer (PSformer)

はじめに

多変量時系列予測は、深層学習において重要なタスクであり、気象、エネルギー、異常検知、金融分析などの実用的な応用があります。人工知能の発展により、予測精度向上のための新しいモデル設計が活発化しています。特に、Transformerベースのアーキテクチャは、自然言語処理やコンピュータビジョンで実証された有効性から、大きな注目を集めています。さらに、大規模な事前学習済みTransformerモデルは時系列予測においても高い性能を示しており、モデルのパラメータや学習データを増やすことで予測能力を大幅に向上させられることがわかっています。

一方で、多くの単純な線形モデルは、より複雑なTransformerベースのアーキテクチャに比べても競争力のある結果を達成しています。これらのモデルが時系列予測で成功している理由は、モデルの複雑性が低いため、ノイズや無関係なデータへの過学習のリスクが低いことにあります。限られたデータでも、安定したパターンを効率よく捉えることができます。

長期依存関係のモデリングや複雑な時間的関係の把握に対処するために、PatchTST手法はデータをパッチに分けて局所的特徴を抽出することによって、高い性能を発揮しています。しかし、PatchTSTはチャンネル独立型の構造を使用しており、モデリング効率の改善余地が大きいです。さらに、多変量時系列は時間軸と変数軸が他のデータタイプと大きく異なるという特性を持つため、未開拓の可能性が多く存在します。

深層学習においてモデルの複雑性を減らす方法の1つがパラメータ共有(PS)です。これにより、パラメータ数を大幅に削減しつつ計算効率を向上させることができます。畳み込みネットワークでは、フィルタが空間的な位置にわたって重みを共有し、少ないパラメータで局所特徴量を抽出します。同様にLSTMモデルでは、時間ステップ間で重み行列を共有し、メモリと情報フローを管理します。自然言語処理においても、Transformerでパラメータ共有が拡張され、層間で重みを再利用することで冗長性を減らし、性能を損なわずにモデルサイズを小さくできます。

マルチタスク学習においては、Task-Adaptive Parameter Sharing (TAPS)手法がタスク固有の層を選択的に微調整することで、最大限のパラメータ共有を実現しつつ、タスク固有の調整を最小限に抑えた効率的な学習を可能にします。研究によれば、パラメータ共有はモデルサイズの削減、汎化性能の向上、過学習リスクの低減に寄与することが示されています。

「PSformer:Parameter-efficient Transformer with Segment Attention for Time Series Forecasting」の著者らは、多変量時系列予測向けの革新的なTransformerベースモデルを提案し、パラメータ共有の原則を組み込んでいます。

このモデルでは、2レベルのセグメントベースAttention機構を備えたTransformerエンコーダを導入しています。各エンコーダ層には共有パラメータブロックが含まれており、このブロックには残差接続を持つ3つの全結合層があり、全体のパラメータ数を抑えながらモデル内部の情報交換を維持しています。セグメント内でAttentionを集中させるために、変数ごとの系列を個別のパッチに分割するパッチング手法を適用します。同じ位置にあるパッチを異なる変数でグループ化し、各グループをセグメントとして扱います。これにより、多変量時系列を複数のセグメントに効果的に分割します。

各セグメント内では、Attention機構が局所的な時空間関係を強化し、セグメント間の情報統合が全体の予測精度を向上させます。さらに、過学習を抑制しつつ学習性能を損なわないSAM最適化手法も組み込まれています。長期時系列予測データセットでの大規模実験により、PSformerは高い性能を示し、8つの主要予測ベンチマークのうち6つで最先端モデルを上回る結果を達成しました。

PSformerアルゴリズム

多変量時系列X ∈ RM×LにはM個の変数と長さLのルックバックウィンドウが含まれます。シーケンス長LはN個の重ならないパッチに均等に分割され、各パッチのサイズはPです。そして、M個の変数からのP(i)はi番目のセグメントを形成し、長さCのクロスセクション（ここでC=M×P）を表します。

PSformerの主要な構成要素は、Segment Attention (SegAtt)とパラメータ共有ブロック(PS)です。PSformerエンコーダはモデルの中核として機能し、SegAttモジュールとPSブロックの両方を含みます。PSブロックは、すべてのエンコーダ層に対してパラメータ共有を通じてパラメータを提供します。

他の時系列予測アーキテクチャと同様に、PSformerの著者は分布シフト問題に効果的に対処するためにRevIN手法を使用しています。

セグメントベースの時空間Attention機構(SegAtt)は、同じ位置の異なるチャネルからのパッチを1つのセグメントに統合し、セグメント間の時空間的関係を構築します。具体的には、元の時系列X ∈ RM×Lをまずパッチに分割し(L=P×N)、次に次元MとPを統合してX ∈ R(M×P)×Nに変形します。これによりX ∈ RC×N (C=M×P)が生成され、チャネル間の情報融合が可能になります。

この変換後の空間では、データはReLU活性化関数で分離された2つの同一アーキテクチャのモジュールで処理されます。各モジュールは、パラメータ共有ブロックと既知のSelf-Attention機構を含みます。セグメントに沿った入力Xinの非線形変換によってN次元表現に変換された𝑸uery ∈ RC×N、𝑲ey ∈ RC×N、𝑽alue ∈ RC×Nを計算する一方で、Scaled Dot-product Attentionは主にC次元全体に焦点を分配します。これにより、モデルはチャネル間および時間軸にわたるセグメント間の依存関係を学習できます。

この機構は、Q、K、Vを計算して異なるセグメントからの情報を統合するだけでなく、各セグメント内の局所的な時空間依存関係を捉え、長期的なセグメント間の関係もモデル化します。最終出力はXout ∈ RC×Nであり、Attention処理が完了します。

PSformerは新しいパラメータ共有ブロック（PSブロック）を導入しており、3つの全結合層と残差接続で構成されています。具体的には、学習可能な線形写像Wj ∈ RN×N с j ∈ {1, 2, 3}を使用します。最初の2層の出力は以下のように計算されます。

この構造は、残差接続を持つFeedForwardブロックに類似しています。中間出力𝑿outは3番目の変換の入力として機能します。

全体として、PSブロックは次のように表現できます。

PSブロックの構造は、線形写像の軌跡を保持しつつ非線形変換を可能にします。PSブロック内の3層はそれぞれ異なるパラメータを持ちますが、PSformerエンコーダ内の複数の位置にわたって同一のPSブロック全体が再利用されるため、これらの位置すべてで同じ𝑾Sブロックのパラメータが共通して用いられます。具体的には、PSブロックのパラメータは、各PSformerエンコーダの3つの部分（2つのSegAttモジュールと最終PSブロック）で共有されます。このパラメータ共有戦略により、モデルの表現力を保ちながら総パラメータ数を削減することができます。

2段階のSegAtt機構は、従来のTransformerにおけるFeedForwardブロックと比較できます。ただし、MLPがAttention操作に置き換えられています。入力と出力の間には残差接続が追加され、その結果が最終的なPSブロックに渡されます。

次に次元変換が適用され、𝑿o⁢ut ∈ RM×L、C=M×PおよびL=P×Nが得られます。

PSformerのn層を通過した後、最終的な変換が適用され、出力が予測ホライズンFへと射影されます。

ここで𝑿pred ∈ RM×Fおよび𝑾F ∈ RL×Fは線形写像を表します。

PSformerフレームワークのオリジナルの可視化を以下に示します。

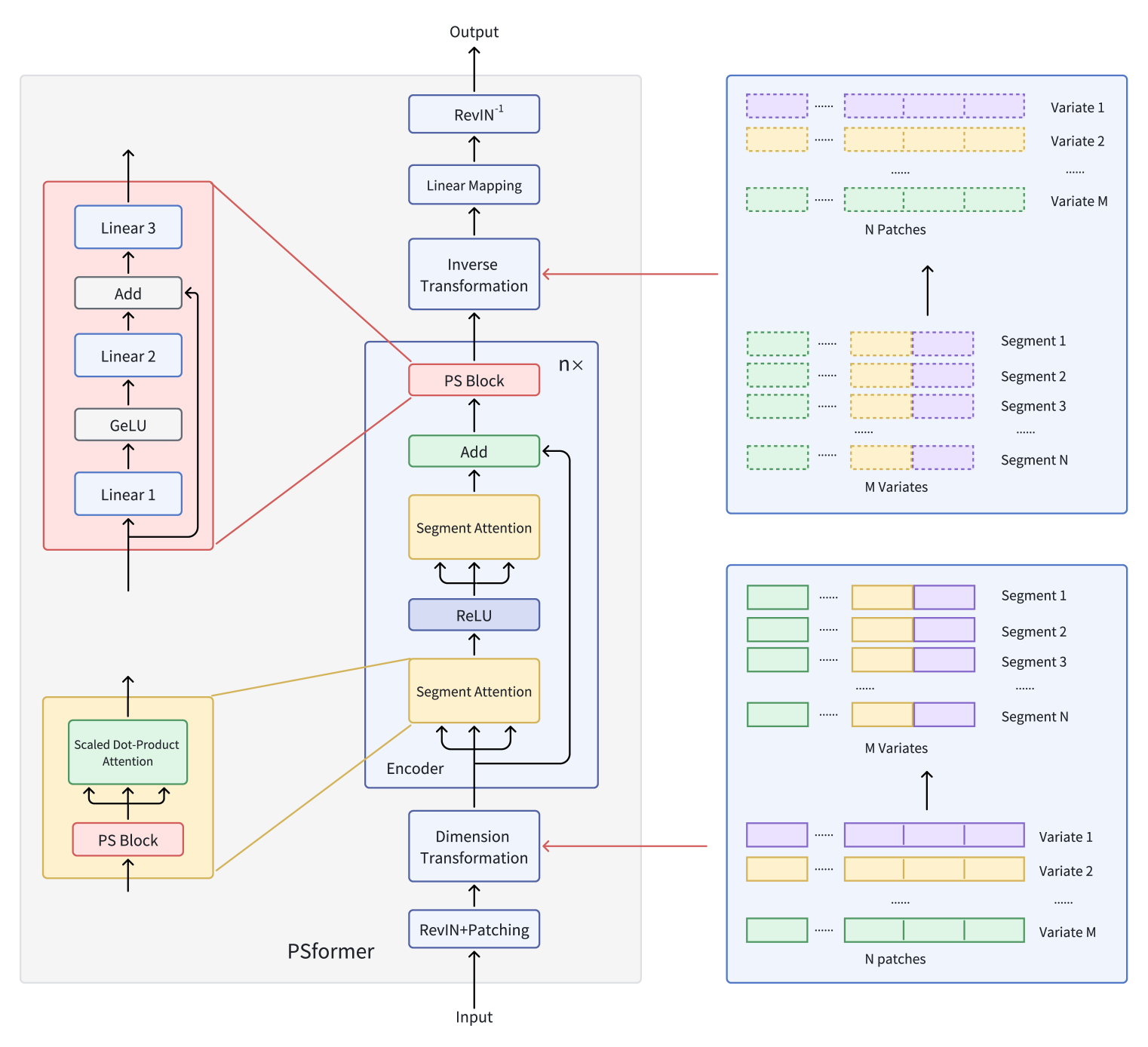
MQL5での実装

PSformerフレームワークの理論面を一通り確認したので、ここからは提案手法に対する私たちのビジョンをMQL5を用いて実装する実務的側面に移ります。特に関心があるのは、パラメータ共有ブロック（PSブロック）を実装するためのアルゴリズムです。

パラメータ共有ブロック

前述のとおり、著者らのオリジナル実装ではPSブロックは3つの全結合層で構成され、そのパラメータが解析されるすべてのセグメントに適用されます。私たちの観点では、ここに難しい点はありません。これまでにも、重ならない解析ウィンドウを持つ畳み込み層を同様の状況で繰り返し用いてきました。本当の課題は別のところ、すなわち複数ブロック間でパラメータを共有するメカニズムにあります。

一方では、同じブロックを単一層内で複数回再利用することは確かに可能です。しかしこの方法には、逆伝播用データを保持する問題が生じます。あるオブジェクトを複数回の順伝播に再利用すると、結果バッファには新しい出力が格納され、以前の順伝播の出力が上書きされてしまいます。典型的なニューラル層のワークフローでは、順伝播と逆伝播を一貫して交互に実行するため、これは問題になりません。各逆伝播の後は、直前の順伝播の結果は不要になり、安全に上書きできるからです。しかしこの交互性が崩れると、正しい逆伝播に必要なデータをすべて保持する問題に直面します。

このような場合、ブロックの最終出力だけでなく、すべての中間値も保存する必要があります。あるいは、それらを再計算しなければならず、これはモデルの計算量を増加させます。さらに、誤差勾配を正しく計算するために、特定のポイントでバッファを同期するメカニズムも必要になります。

明らかに、これらの要件を満たすには、ニューラル層間のデータ交換インターフェイスの変更が必要です。結果として、ライブラリ機能全体により広範な修正を引き起こすことになります。

第2の選択肢は、複数の同一ニューラル層間で、単一のパラメータバッファを本格的に共有する仕組みを確立することです。しかし、このアプローチもまた独自の「隠れた落とし穴」がないわけではありません。

Deep Deterministic Policy Gradientフレームワークを調査した際、私たちはターゲットモデルに対するソフトパラメータ更新のアルゴリズムを実装しました。ただし、更新ごとにパラメータをコピーするのは計算コストが高くなります。理想的には、関連するオブジェクト内のパラメータバッファを共有パラメータ行列に置き換えるのが望ましいです。

ここで、パラメータ行列そのものに加えて、更新時に用いるモメンタムバッファも共有しなければなりません。異なる段階で別々のモメンタムバッファを用いると、パラメータ更新ベクトルが内部層の一方へ偏る可能性があるためです。

さらに重要なポイントがあります。この実装では、逆伝播で用いられるパラメータが、順伝播で用いられたパラメータと異なる場合があります。これは奇異に聞こえるかもしれませんが、パラメータを共有する2つの連続層を例にとって説明します。順伝播では、両層が同じパラメータWを用いて、それぞれ出力O1とO2を生成します。誤差勾配を分配する段階では、それぞれ誤差勾配G1とG2を計算します。したがって、誤差勾配伝播プロセスは正しいです。この時点では、モデルパラメータは不変で、すべての誤差勾配は順伝播時のパラメータWに正しく対応しています。ところが、もし一方の層（例えば第2層）でパラメータを更新してW'にすると、不一致が即座に発生します。誤差勾配は更新後のパラメータに対応していないのです。不一致の勾配をそのまま適用すると、学習過程が歪む可能性があります。

この問題への1つの解決策は、直前の順伝播の出力と対応する誤差勾配に基づいて当該層のターゲット値を決定し、更新後のパラメータで新たに順伝播を実行して、補正された誤差勾配を計算することです。これに聞き覚えがあるとすれば、それは、以前の記事で議論したSAM最適化アルゴリズムに非常に近いアプローチだからです。実際、パラメータ更新を繰り返し順伝播の前に挿入すると、完全なSAM最適化手順が得られます。

まさにこの理由で、PSformerフレームワークの著者らはSAM最適化の使用を推奨しています。これは、勾配とパラメータの不一致リスクを許容できるようにする（勾配がパラメータ更新の前に再計算される）からです。とはいえ、他のシナリオでは、このような不一致が深刻な問題になり得ます。

以上を踏まえ、私たちは第2のアプローチ、つまり、同一層間でパラメータバッファを共有する方式を採用することにしました。

前述のように、元の論文のPSブロックは3つの全結合層を用いていますが、私たちはこれを畳み込み層に置き換えます。したがって、パラメータ共有の実装はCNeuronConvSAMOCL畳み込み層オブジェクトから開始します。

畳み込みのパラメータ共有層では、パラメータバッファとモメンタムバッファへのポインタのみを置き換えます。その他のバッファや内部変数は、パラメータ行列の次元に一致していなければなりません。当然ながら、これはオブジェクトの初期化メソッドに調整を要します。その前に、補助メソッドを2つ用意します。InitBufferLikeとReplaceBufferです。

InitBufferLikeは、与えられた参照バッファに基づいてゼロで初期化された新しいバッファを作成します。アルゴリズムは非常にシンプルです。2つのデータバッファオブジェクトへのポインタを引数に取り、まず参照バッファ(master)ポインタが有効かどうかを確認します。有効な参照ポインタの存在は、その後の処理にとって極めて重要です。このチェックに失敗した場合、メソッドは処理を終了し、falseを返します。

bool CNeuronConvSAMOCL::InitBufferLike(CBufferFloat *&buffer, CBufferFloat *master)
  {
   if(!master)
      return false;

最初のチェックポイントを無事に通過した場合、次に作成されたバッファへのポインタの関連性を確認します。しかし、ここで否定的な結果を得た場合には、単純に新しいオブジェクトのインスタンスを生成します。

   if(!buffer)
     {
      buffer = new CBufferFloat();
      if(!buffer)
         return false;
     }

新しいバッファが正しく作成されたかどうかを確認することを忘れないでください。

次に、必要なサイズのバッファをゼロ値で初期化します。

   if(!buffer.BufferInit(master.Total(), 0))
      return false;

次に、OpenCLコンテキストにそのコピーを作成します。

   if(!buffer.BufferCreate(master.GetOpenCL()))
      return false;
//---
   return true;
  }

その後、メソッドは、操作の論理結果を呼び出し元に返して終了します。

2番目のメソッドReplaceBufferは、指定されたバッファへのポインタを置き換えます。一見すると、単に内部変数オブジェクトにポインタを代入するだけで済むため、わざわざ専用メソッドを用意する必要はないように思えます。しかし、このメソッドの本体では、不要なデータバッファをチェックし、必要に応じて削除します。これにより、RAMとOpenCLコンテキストメモリの両方をより効率的に利用することができます。

void CNeuronConvSAMOCL::ReplaceBuffer(CBufferFloat *&buffer, CBufferFloat *master)
  {
   if(buffer==master)
     return;
   if(!!buffer)
     {
      buffer.BufferFree();
      delete buffer;
     }
//---
   buffer = master;
  }

補助メソッドを作成した後、次に参照インスタンスに基づいた畳み込み層オブジェクトの新しい初期化アルゴリズム(InitPS)の構築に進みます。このメソッドでは、オブジェクトのアーキテクチャを定義する定数群すべてを受け取るのではなく、参照オブジェクトへのポインタのみを受け取る形にします。

bool CNeuronConvSAMOCL::InitPS(CNeuronConvSAMOCL *master)
  {
   if(!master ||
      master.Type() != Type()
     )
      return false;

このメソッドの本体では、まず受け取ったポインタが正しいかどうか、そしてオブジェクトタイプが一致しているかどうかを確認します。

次に、親クラスのメソッド群を一から構築する代わりに、参照オブジェクトから継承されたすべてのパラメータ値を単純に転送します。

   alpha = master.alpha;
   iBatch = master.iBatch;
   t = master.t;
   m_myIndex = master.m_myIndex;
   activation = master.activation;
   optimization = master.optimization;
   iWindow = master.iWindow;
   iStep = master.iStep;
   iWindowOut = master.iWindowOut;
   iVariables = master.iVariables;
   bTrain = master.bTrain;
   fRho = master.fRho;

 次に、参照オブジェクトと同様の結果勾配バッファと誤差勾配バッファを作成します。

   if(!InitBufferLike(Output, master.Output))
      return false;
   if(!!master.getPrevOutput())
      if(!InitBufferLike(PrevOutput, master.getPrevOutput()))
         return false;
   if(!InitBufferLike(Gradient, master.Gradient))
      return false;

その後、まず基本的な全結合層から継承した重みバッファとモーメントバッファにポインターを転送します。

   ReplaceBuffer(Weights, master.Weights);
   ReplaceBuffer(DeltaWeights, master.DeltaWeights);
   ReplaceBuffer(FirstMomentum, master.FirstMomentum);
   ReplaceBuffer(SecondMomentum, master.SecondMomentum);

畳み込み層のパラメータとそのモーメントのバッファに対しても同様の操作を繰り返します。

   ReplaceBuffer(WeightsConv, master.WeightsConv);
   ReplaceBuffer(DeltaWeightsConv, master.DeltaWeightsConv);
   ReplaceBuffer(FirstMomentumConv, master.FirstMomentumConv);
   ReplaceBuffer(SecondMomentumConv, master.SecondMomentumConv);

次に、調整済みパラメータのバッファを作成する必要があります。しかし、特定の条件下では、両方の調整済みパラメータバッファが作成されない場合があります。具体的には、全結合層の調整済みパラメータバッファは、出力接続が存在する場合にのみ作成されます。したがって、まず参照オブジェクト内のこのバッファのサイズを確認します。必要な場合にのみ、該当するバッファを作成します。

   if(master.cWeightsSAM.Total() > 0)
     {
      CBufferFloat *buf = GetPointer(cWeightsSAM);
      if(!InitBufferLike(buf, GetPointer(master.cWeightsSAM)))
         return false;
     }

それ以外の場合は、このバッファをクリアして、メモリ消費を削減します。

   else
     {
      cWeightsSAM.BufferFree();
      cWeightsSAM.Clear();
     }

入力接続の調整済みパラメータバッファは、ぼかし領域係数が0より大きい場合に作成されます。

   if(fRho > 0)
     {
      CBufferFloat *buf = GetPointer(cWeightsSAMConv);
      if(!InitBufferLike(buf, GetPointer(master.cWeightsSAMConv)))
         return false;
     }

それ以外の場合は、このバッファをクリアします。

   else
     {
      cWeightsSAMConv.BufferFree();
      cWeightsSAMConv.Clear();
     }

技術的には、ぼかし係数を使う代わりに、参照オブジェクトの入力接続の調整済みパラメータを格納するバッファのサイズを確認することも可能です。これは、出力接続用の調整済みパラメータバッファでおこなっている処理と同じです。しかし、私たちはぼかし係数が0より大きければ、このバッファは必ず存在することを知っています。そのため、追加のチェックを組み込みます。もしゼロ長のバッファを作成しようとした場合、処理は失敗し、エラーが発生して初期化が停止します。これにより、実行時により深刻な問題が発生するのを防ぐことができます。

初期化メソッドの最後では、すべてのオブジェクトを単一のOpenCLコンテキストに転送し、操作の論理結果を呼び出し元プログラムに返して終了します。

   SetOpenCL(master.OpenCL);
//---
   return true;
  }

畳み込み層オブジェクトの修正が完了した後、次のステップに進みます。ここで、パラメータ共有ブロック（PSブロック）自体を作成します。そのために、新しいオブジェクトCNeuronPSBlockを導入します。理論セクションで述べたように、PSブロックは3つの連続したデータ変換層で構成されます。各層は正方行列のパラメータを持ち、ブロック全体および内部層の入力・出力テンソルの次元が一貫することを保証します。最初の2層の間にはGELU活性化関数が適用されます。2層目の後には、元の入力への残差接続が追加されます。

このアーキテクチャを実装するため、新しいオブジェクトは内部に2つの畳み込み層を含みます。最後の畳み込み層は、クラス自体の構造で直接表現され、畳み込み層クラスから基本機能を継承します。また、学習時にSAM最適化を使用するため、アーキテクチャ内のすべての畳み込み層はSAM対応となります。新しいクラスの構造体は以下のとおりです。

class CNeuronPSBlock :  public CNeuronConvSAMOCL
  {
protected:
   CNeuronConvSAMOCL acConvolution[2];
   CNeuronBaseOCL    cResidual;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronPSBlock(void) {};
                    ~CNeuronPSBlock(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_out, uint units_count, 
                          uint variables, float rho, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   virtual bool      InitPS(CNeuronPSBlock *master);
   //---
   virtual int       Type(void)   const         {  return defNeuronPSBlock;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual CLayerDescription* GetLayerInfo(void);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

構造体から分かるように、新しいオブジェクトは2つの初期化メソッドを宣言しています。これは意図的な設計です。Initは標準の初期化メソッドで、メソッドに渡されるパラメータによってオブジェクトのアーキテクチャが明示的に定義されます。InitPSは畳み込み層クラスの同名メソッドに対応する初期化メソッドで、参照オブジェクトの構造に基づいて新しいオブジェクトを作成します。この過程で、参照オブジェクトからパラメータおよびモメンタムバッファへのポインタがコピーされます。次に、これらのメソッドを構築するアルゴリズムをもう少し詳しく見ていきます。

前述のとおり、Initメソッドはパラメータとして定数群を受け取り、これによりオブジェクトのアーキテクチャを完全に決定できるようになっています。

bool CNeuronPSBlock::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_out, uint units_count,
                          uint variables, float rho,
                          ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronConvSAMOCL::Init(numOutputs, myIndex, open_cl, window, window, window_out,
                               units_count, variables, rho, optimization_type, batch))
      return false;

メソッド本体では、受け取ったすべてのパラメータを親クラスの同名メソッドに即座に転送します。ご存知の通り、親クラスのメソッドには、継承されたオブジェクトに必要なパラメータ検証ポイントと初期化ロジックがすでに含まれています。

また、PSブロック内のすべての畳み込み層は同一の次元を持つため、最初の内部畳み込み層の初期化には、まったく同じパラメータが使用されます。

   if(!acConvolution[0].Init(0, 0, OpenCL, iWindow, iWindow, iWindowOut, units_count,
                             iVariables, fRho, optimization, iBatch))
      return false;
   acConvolution[0].SetActivationFunction(GELU);

次に、GELU活性化関数を追加します。これは、PSformerの著者らの推奨に従ったものです。

ただし、ユーザーがブロック出力のテンソル次元を変更できるようにもしています。そのため、残差接続の後に続く第2の内部畳み込み層を初期化する際には、解析ウィンドウサイズとフィルタ数のパラメータを入れ替えます。これにより、出力の次元が元の入力データの次元に一致することが保証されます。

   if(!acConvolution[1].Init(0, 1, OpenCL, iWindowOut, iWindowOut, iWindow, units_count,
                             iVariables, fRho, optimization, iBatch))
      return false;
   acConvolution[1].SetActivationFunction(None);

ここでは活性化関数は使用しません。

次に、残差接続のデータを保持するための基底ニューラル層を追加します。そのサイズは、第2のネストされた畳み込み層の結果バッファに対応しています。

   if(!cResidual.Init(0, 2, OpenCL, acConvolution[1].Neurons(), optimization, iBatch))
      return false;
   if(!cResidual.SetGradient(acConvolution[1].getGradient(), true))
      return false;
   cResidual.SetActivationFunction(None);

参照インスタンスに基づいてオブジェクトを作成した直後、誤差勾配バッファを置き換えます。この最適化により、逆伝播時のデータコピー回数を削減することができます。

次に、パラメータ共有ブロック用の活性化関数を明示的に無効化し、メソッドを完了させます。最後に、操作の論理結果を呼び出し元に返して終了します。

   SetActivationFunction(None);
//---
   return true;
  }

2つ目の初期化メソッドは、やや簡略化されています。このメソッドは参照オブジェクトへのポインタを受け取り、それを親クラスの同名メソッドに直接渡します。

ここで重要なのは、現在のメソッドでのパラメータ型が親クラスのものと異なるという点です。そのため、渡されるオブジェクトの型を明示的に指定しています。

bool CNeuronPSBlock::InitPS(CNeuronPSBlock *master)
  {
   if(!CNeuronConvSAMOCL::InitPS((CNeuronConvSAMOCL*)master))
      return false;

親クラスのメソッドには、すでに必要なバリデーションチェックや、定数のコピー、新しいバッファの作成、パラメータおよびモメンタムバッファのポインタ保存のロジックが含まれています。

その後、内部の畳み込み層を順に反復処理し、それぞれの初期化メソッドを呼び出し、対応する参照オブジェクトからデータをコピーします。

   for(int i = 0; i < 2; i++)
      if(!acConvolution[i].InitPS(master.acConvolution[i].AsObject()))
         return false;

残差接続層には学習可能なパラメータは含まれず、そのサイズは第2の内部畳み込み層の結果バッファに一致します。したがって、この層の初期化ロジックは、メインの初期化メソッドからそのまま継承されます。

   if(!cResidual.Init(0, 2, OpenCL, acConvolution[1].Neurons(), optimization, iBatch))
      return false;
   if(!cResidual.SetGradient(acConvolution[1].getGradient(), true))
      return false;
   cResidual.SetActivationFunction(None);
//---
   return true;
  }

前述と同様に、誤差勾配バッファへのポインタを置き換えます。

初期化メソッドが完了したら、次に順伝播アルゴリズムに進みます。この部分は比較的簡単です。メソッドは入力データオブジェクトへのポインタを受け取り、それを最初の内部畳み込み層の順伝播メソッドに直接渡します。

bool CNeuronPSBlock::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!acConvolution[0].FeedForward(NeuronOCL))
      return false;

結果は、次の畳み込み層に順番に渡されます。その後、結果の値を元の入力と合計します。合計を残差接続バッファに保存します。

   if(!acConvolution[1].FeedForward(acConvolution[0].AsObject()))
      return false;
   if(!SumAndNormilize(NeuronOCL.getOutput(), acConvolution[1].getOutput(), cResidual.getOutput(),
                                                                       iWindow, true, 0, 0, 0, 1))
      return false;

ここで、オリジナルのPSformerアルゴリズムとはやや異なる処理をおこないます。残差テンソルを最終畳み込み層に渡す前に正規化します。最終畳み込み層の機能は、親クラスから継承されています。

   if(!CNeuronConvSAMOCL::feedForward(cResidual.AsObject()))
      return false;
//---
   return true;
  }

メソッドは、操作の論理結果を呼び出し元に返すことで終了します。

誤差勾配分布メソッドcalcInputGradientsも比較的単純ですが、重要な注意点があります。このメソッドは、誤差勾配を伝播させる対象の元データ層オブジェクトへのポインタを受け取ります。

bool CNeuronPSBlock::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
     return false;

まず、受信したポインタの有効性をチェックします。無効な場合は、それ以上の処理は無意味です。

次に、勾配をすべての畳み込み層に逆順に渡します。

   if(!CNeuronConvSAMOCL::calcInputGradients(cResidual.AsObject()))
      return false;
   if(!acConvolution[0].calcHiddenGradients(acConvolution[1].AsObject()))
      return false;
   if(!NeuronOCL.calcHiddenGradients(acConvolution[0].AsObject()))
      return false;

注意すべき点として、残差接続オブジェクトから第2の内部畳み込み層への明示的な誤差勾配転送はコード化されていません。しかし、前述のデータバッファのポインタ置換により、情報は完全に伝達されます。

畳み込み層パイプラインを通じて誤差勾配を元データ層オブジェクトに返した後、残差接続ブランチからの勾配も加えます。このとき、元データオブジェクトに活性化関数があるかないかによって2つのケースが考えられます。

ここで改めて確認すると、残差接続オブジェクトには活性化関数の導関数による調整をせずに誤差勾配を渡しています。このオブジェクトに対して活性化関数が存在しないことは、明示的に示しています。

したがって、元データオブジェクトに活性化関数が存在しない場合は、2つのバッファの対応する値を単純に加算するだけでよいことになります。

   if(NeuronOCL.Activation() == None)
     {
      if(!SumAndNormilize(NeuronOCL.getGradient(), cResidual.getGradient(), NeuronOCL.getGradient(),
                                                                        iWindow, false, 0, 0, 0, 1))
         return false;
     }

そうでない場合、まず取得した誤差勾配を活性化関数の導関数で調整し、別のバッファに格納します。その後、得られた結果を、元データオブジェクトのバッファに以前から蓄積されていた値と合算します。

   else
     {
      if(!DeActivation(NeuronOCL.getOutput(), cResidual.getGradient(), cResidual.getPrevOutput(), 
                                                                           NeuronOCL.Activation()) ||
         !SumAndNormilize(NeuronOCL.getGradient(), cResidual.getPrevOutput(), NeuronOCL.getGradient(),
                                                                          iWindow, false, 0, 0, 0, 1))
         return false;
     }
//---
   return true;
  }

そしてメソッドを完了します。

最後に、ブロックのパラメータを更新するupdateInputWeightsメソッドについて少し触れておきます。このブロックの処理は非常にシンプルで、親クラスおよび学習可能なパラメータを持つ内部オブジェクトの対応するメソッドを呼び出すだけです。

bool CNeuronPSBlock::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!CNeuronConvSAMOCL::updateInputWeights(cResidual.AsObject()))
      return false;
   if(!acConvolution[1].UpdateInputWeights(acConvolution[0].AsObject()))
      return false;
   if(!acConvolution[0].UpdateInputWeights(NeuronOCL))
      return false;
//---
   return true;
  }

しかし、SAM最適化を使用する場合は、操作順序に厳密な制約があります。SAM最適化では、調整済みパラメータで再度順伝播を実行します。このとき結果バッファが更新されます。これは現在の層のパラメータ更新には問題ありませんが、後続の層のパラメータ更新を混乱させる可能性があります。なぜなら、後続層は前層の順伝播結果を利用しているためです。これを防ぐために、内部オブジェクトを通じてパラメータを逆順で更新する必要があります。こうすることで、各層のパラメータが別の層によって入力バッファが変更される前に調整されることが保証されます。

これで、CNeuronPSBlockパラメータ共有ブロックアルゴリズムの説明は終了です。このクラスとそのメソッドのフルソースコードは、添付ファイルに記載されています。

作業はまだ完了していませんが、記事が長くなったため、ここで短い休憩を取り、次の記事で作業を続けます。

結論

本記事では、PSformerフレームワークについて詳しく解説しました。著者らは、PSformerが時系列予測における高精度と計算リソースの効率的な利用を両立する点を強調しています。PSformerの主要なアーキテクチャ要素には、パラメータ共有ブロック(PS)とセグメントベースの時空間Attention機構(SegAtt)があります。これにより、局所的および大域的な時系列依存関係を効果的にモデル化しつつ、パラメータ数を抑えながら予測精度を維持できます。

実践的なセクションでは、MQL5において提案手法の独自解釈を実装し始めました。作業はまだ完了していません。次回の記事では、開発を継続し、特定のタスクに関連する実データセットでこれらの手法の有効性を評価する予定です。

参照文献

PSformer:Parameter-efficient Transformer with Segment Attention for Time Series Forecasting

この連載の他の記事記事

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	事例収集用EA
2	ResearchRealORL.mq5	EA	Real-ORL法を用いた例収集用のEA
3	Study.mq5	EA	モデル学習用EA
4	StudyEncoder.mq5	EA	エンコーダ学習用EA
5	Test.mq5	EA	モデルテスト用EA
6	Trajectory.mqh	クラスライブラリ	システム状態記述の構造体
7	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
8	NeuroNet.cl	ライブラリ	OpenCLプログラムコードライブラリ