MetaTrader 5 / Probador
English Русский 中文 Deutsch 日本語 Português
preview
Algoritmo de optimización aritmética (AOA): De AOA a SOA (Simple Optimization Algorithm)

Algoritmo de optimización aritmética (AOA): De AOA a SOA (Simple Optimization Algorithm)

MetaTrader 5 — Probador |
270 0
Andrey Dik
Andrey Dik

Contenido

  1. Introducción
  2. Implementación del algoritmo
  3. Resultados de la prueba


Introducción

El algoritmo de optimización aritmética (AOA) es un método original basado en operaciones aritméticas simples como suma, resta, multiplicación y división. Su esencia radica en utilizar estos principios matemáticos básicos para encontrar soluciones óptimas a una variedad de problemas. AOA fue desarrollado por un equipo de investigadores que incluía a Laith Abualigah y se presentó por primera vez en 2021. El algoritmo pertenece a la clase de métodos metaheurísticos (algoritmos de alto nivel) destinados a encontrar, generar y elegir probabilísticamente entre varias heurísticas que puedan proporcionar soluciones de alta calidad en un tiempo razonable para problemas de optimización complejos donde los métodos basados en la precisión pueden ser ineficaces o imposibles.

Este método me llamó la atención por su idea simple y, al mismo tiempo, elegante de utilizar operadores aritméticos completamente elementales. La relación entre estas operaciones matemáticas básicas y los enfoques metaheurísticos crea una sinergia que permite resolver problemas de optimización complejos. Los métodos metaheurísticos utilizados en AOA incluyen varios principios clave:

1. Enfoque poblacional. AOA utiliza una población de soluciones, lo que le permite cubrir un espacio más amplio de posibles soluciones. Esto ayuda a evitar óptimos locales y amplía los horizontes de búsqueda.

2. Aleatoriedad y estocasticidad. La incorporación de elementos de aleatoriedad en la búsqueda ayuda a los algoritmos a evitar quedarse estancados en óptimos locales y proporciona una exploración más completa del espacio de soluciones, lo que aumenta la probabilidad de encontrar un óptimo global.

3. Equilibrio entre exploración y explotación. Al igual que muchos otros algoritmos metaheurísticos, AOA busca un equilibrio entre la exploración de nuevas regiones del espacio de soluciones y la explotación de soluciones eficientes ya conocidas. Esto se logra mediante el uso de operaciones aritméticas para actualizar las posiciones de las soluciones.

Así, AOA es un ejemplo sorprendente de un algoritmo metaheurístico que utiliza eficazmente los principios del enfoque poblacional, la aleatoriedad y el equilibrio entre exploración y explotación para resolver problemas de optimización, sin embargo hablaremos específicamente de la eficiencia de encontrar soluciones óptimas en espacios complejos y multidimensionales para este algoritmo después de su implementación y prueba.


Implementación del algoritmo

La idea básica de AOA es utilizar el comportamiento distributivo de los operadores aritméticos para encontrar soluciones óptimas. El algoritmo se caracteriza por principios simples, un número no muy grande de parámetros y facilidad de implementación. El algoritmo explota las características de distribución de los cuatro operadores aritméticos básicos en matemáticas, a saber: Multiplicación (Mε × ε), División (Dε ÷ ε), Resta (Sε − ε) y Suma (Aε + ε). En AOA, la población inicial se genera aleatoriamente en el rango [U; L], donde los límites superior e inferior del espacio de búsqueda para la función objetivo se denotan por U y L, respectivamente, utilizando la siguiente ecuación:

x = L + (U − L) × δ, donde x representa la solución poblacional, δ es una variable aleatoria que toma valores en el rango [0, 1].

En cada iteración, la elección de la estrategia de exploración y explotación, es decir, la elección de uno de los dos grupos de operadores, ya sea (división; multiplicación) o (resta; suma), se realiza en función del resultado de la función MoA (optimizador matemático acelerado), que es, en esencia, el valor calculado de la probabilidad y cambia con cada iteración, calculada según la ecuación:

MoA(t) = Mín + t × (Máx − Mín) ÷ Maxt, donde MoA(t) es el resultado funcional en la t-ésima iteración, t indica la iteración actual, que está en el rango de 1 al número máximo de iteraciones (Maxt). El valor mínimo posible de MoA se denota como Min, mientras que el valor máximo se denota como Max. Estos son parámetros externos del algoritmo.

Las cuatro ecuaciones de operadores aritméticos utilizan el factor MoP (optimizador matemático) calculado de la siguiente manera:

MoP(t) = 1 − (t÷ Máx.)^(1÷ θ), donde MoP(t) indica el valor de la función MoP en la t-ésima iteración. θ es un parámetro crítico que controla el rendimiento de la explotación a lo largo de las iteraciones. En el trabajo original, los autores del algoritmo lo establecieron en el nivel 5.

La figura 1 a continuación muestra los gráficos de dependencia de MoA y MoP en la iteración actual. Los gráficos muestran que con cada iteración, MoA aumenta linealmente, lo que significa que la probabilidad de elegir un grupo de operadores (resta; suma) aumenta y la probabilidad de elegir un grupo de operadores (división; multiplicación) disminuye proporcionalmente. A su vez, el ratio MoP disminuye de forma no lineal, reduciendo así el siguiente incremento a la posición actual de los agentes en la población, lo que supone un aumento en el grado de refinamiento de las decisiones en la optimización.

MoA y MoP

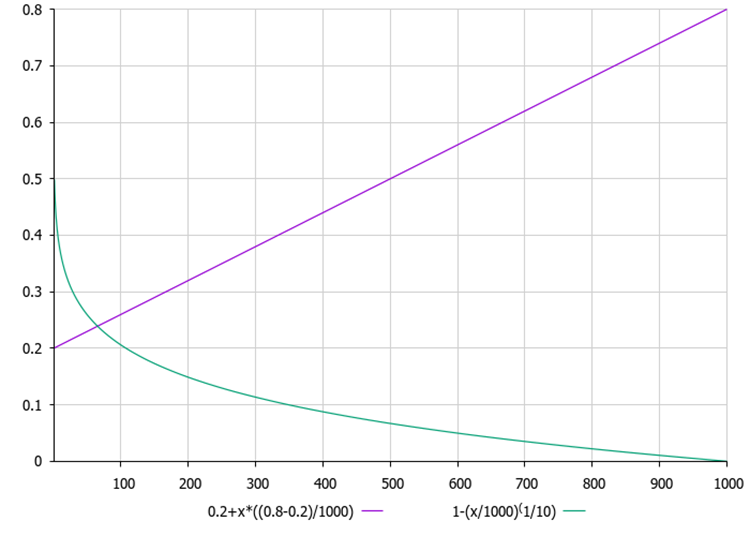
Figura 1. El color púrpura muestra el gráfico de probabilidad de MoA y el color verde muestra el gráfico de relación de MoP.

Investigación o búsqueda global en AOA se lleva a cabo utilizando estrategias de búsqueda basadas en operadores de División (D) y Multiplicación (M) si se satisface la probabilidad MoA, la cual se formula de la siguiente manera, donde los siguientes operadores se ejecutan con igual probabilidad:

xi,j(t+1) = mejor(xj) ÷ (MoPr + 𝜖) × ((Uj − Lj) × 𝜇 + Lj), si rand2 < 0,5; 

de lo contrario:

xi,j(t+1) = mejor(xj) × (MoPr) × ((Uj − Lj) × 𝜇 + Lj), donde xi(t+1) representa la i-ésima solución en la (t+1)-ésima iteración, x(i,j)(t) representa la j-ésima posición del i-ésimo individuo en la generación actual, best(xj) expresa la j-ésima posición de la mejor solución en el momento, ε es un número positivo pequeño, los límites superior e inferior de los valores de la j-ésima posición se denotan como Uj y Lj, respectivamente. El parámetro de control μ se estableció en 0,5. 

Si no se cumple la probabilidad de MoA, entonces estrategia de explotación (refinamiento de la solución) se realiza en AOA. La estrategia se desarrolló utilizando los operadores de Resta (Subtraction, S) o Suma (Addition, A). Aquí μ también es una constante, que se fija en 0,5 por intención de los autores. 

xi,j(t+1) = mejor(xj) − (MoPr) × ((Uj − Lj) × 𝜇 + Lj), si rand3 < 0,5 

De lo contrario,xi,j(t+1) = mejor(xj) + (MoPr) × ((Uj − Lj) × 𝜇 + Lj).

En AOA, los parámetros 𝜇 y θ son muy importantes ya que intervienen en el equilibrio entre exploración y explotación. Mantener un equilibrio adecuado entre exploración y explotación suele ser una tarea muy difícil. En el AOA original, el valor de 𝜇 se fijó en 0,5 tanto para la exploración como para la explotación. Sin embargo, el parámetro θ, que afecta la eficiencia operativa durante las iteraciones, se establece en 5. Los autores experimentaron con diferentes valores de 𝜇 y θ y descubrieron que 𝜇 = 0,5 y θ = 5 producían con mayor frecuencia los mejores resultados para funciones de prueba unimodales y multimodales en diferentes dimensiones. 

Ahora implementemos el pseudocódigo del algoritmo AOA:

Aumentar el número de época en 1.

// Inicialización inicial
SI este es el primer lanzamiento ENTONCES
    PARA cada partícula de la población:
        PARA cada coordenada:
            Establecer una posición aleatoria dentro del rango permitido
            Llevar una posición a un valor discreto
    Marcar que la inicialización se ha completado
    Fin de la función
FIN SI

// Proceso principal de optimización
Calcular MoA = minMoA + Número de época * ((maxMoA - minMoA) / totalEpochs)
Calcular MoP = 1 - (Número de época / Épocas totales)^(1/θ)

// Fase de exploración del espacio de soluciones
PARA cada partícula de la población:
    Para cada coordenada:
        Generar tres valores aleatorios (rand1, rand2, rand3)
        Toma el valor más conocido para la coordenada
        
        SI rand1 < MoAc ENTONCES
            SI rand2 > 0,5 ENTONCES
                Actualizar posición utilizando División
            DE LO CONTRARIO
                Actualizar posición mediante multiplicación
            FIN SI
        DE LO CONTRARIO
            SI rand3 > 0,5 ENTONCES
                Actualizar posición utilizando la sustracción
            DE LO CONTRARIO
                Actualizar posición mediante adición
            FIN SI
        FIN SI
        
        Llevar la nueva posición a un valor discreto aceptable
        
Actualizar la mejor solución

Pasemos a escribir el código. La clase C_AO_AOA es una implementación del algoritmo AOA y está diseñada para resolver problemas de optimización utilizando un método basado en operaciones aritméticas. Métodos públicos:

1. El método SetParams () establece los valores de los parámetros de la matriz params. Este método permite cambiar los parámetros del algoritmo después de que se haya inicializado.

2. Método Init ():

  • Inicializa el algoritmo tomando los rangos de búsqueda mínimo y máximo, el paso de búsqueda y el número de épocas. 
  • Devuelve true si la inicialización se ha realizado correctamente; en caso contrario, devuelve false.

3. El método Moving() realiza el movimiento de las partículas en el espacio de soluciones. Este método implementa la lógica para actualizar las posiciones de las partículas basándose en los parámetros dados y el estado actual.

4. El método Revision() revisa las posiciones actuales de las partículas, actualizando el mejor valor encontrado de la función y las coordenadas de la partícula correspondiente.

Campos privados, parámetros de clase:

  • minT — Valor mínimo de la probabilidad MoA.
  • maxT — Valor máximo de la probabilidad MoA.
  • θ — Parámetro que influye en el equilibrio entre exploración y explotación.
  • μ — Parámetro utilizado para controlar los cambios en las posiciones de las partículas (rango de movimiento).
  • ϵ — Número pequeño para evitar la división por cero.

Información sobre el estado del algoritmo:

  • epochs — Número total de épocas por las que pasará el algoritmo.
  • epochNow — La época actual utilizada para realizar un seguimiento del progreso del algoritmo afecta a la probabilidad MoA y a la relación MoP.

La clase C_AO_AOA implementa los componentes principales del algoritmo AOA, incluyendo la inicialización, el movimiento de partículas y la revisión.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AOA () { }
  C_AO_AOA ()
  {
    ao_name = "AOA";
    ao_desc = "Arithmetic Optimization Algorithm";
    ao_link = "https://www.mql5.com/en/articles/16364";

    popSize = 50;   // Population size
    minT    = 0.1;  // Minimum T value
    maxT    = 0.9;  // Maximum T value
    θ       = 10;   // θ parameter
    μ       = 0.01; // μ parameter

    ArrayResize (params, 5); // Resize the parameter array

    // Initialize parameters
    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "minT";    params [1].val = minT;
    params [2].name = "maxT";    params [2].val = maxT;
    params [3].name = "θ";       params [3].val = θ;
    params [4].name = "μ";       params [4].val = μ;
  }

  void SetParams () // Method for setting parameters
  {
    popSize = (int)params [0].val; // Set population size
    minT    = params      [1].val; // Set minimum T
    maxT    = params      [2].val; // Set maximum T
    θ       = params      [3].val; // Set θ
    μ       = params      [4].val; // Set μ
  }

  bool Init (const double &rangeMinP  [], // Minimum search range
             const double &rangeMaxP  [], // Maximum search range
             const double &rangeStepP [], // Search step
             const int     epochsP = 0);  // Number of epochs

  void Moving   (); // Method of moving particles
  void Revision (); // Revision method

  //----------------------------------------------------------------------------
  double minT; // Minimum T value
  double maxT; // Maximum T value
  double θ;    // θ parameter
  double μ;    // μ parameter
  double ϵ;    // Parameter to prevent division by zero

  private: //-------------------------------------------------------------------
  int epochs;    // Total number of epochs
  int epochNow;  // Current epoch
};
//——————————————————————————————————————————————————————————————————————————————

El método Init de la clase C_AO_AOA se encarga de inicializar el algoritmo de optimización estableciendo los parámetros del rango de búsqueda, los pasos y el número de épocas durante las cuales se llevará a cabo la optimización. La lógica del método:

1. El método primero llama a StandardInit, que inicializa los parámetros estándar del algoritmo. Si esta inicialización falla, Init termina inmediatamente la ejecución y devuelve false.

2. Configuración de parámetros:

  • Establece el número total de épocas basándose en el parámetro epochsP pasado.
  • Inicializa la época actual epochNow con 0.
  • Establezca ϵ (valor pequeño para evitar la división por cero) en DBL_EPSILON, que es el valor estándar para representar el número positivo más pequeño que se puede representar en el tipo double.

3. Si todos los pasos se completan correctamente, el método devuelve true, lo que indica que la inicialización del algoritmo se ha realizado correctamente.

El método Init es una parte importante de la preparación del algoritmo para su ejecución, ya que establece los parámetros básicos que se utilizarán en la optimización. Al llamar a este método, se restablecerán todos los parámetros y variables a su estado original.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AOA::Init (const double &rangeMinP  [], // Minimum search range
                     const double &rangeMaxP  [], // Maximum search range
                     const double &rangeStepP [], // Search step
                     const int     epochsP = 0)   // Number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; // Initialization of standard parameters

  //----------------------------------------------------------------------------
  epochs   = epochsP;     // Set the total number of epochs
  epochNow = 0;           // Initialize the current epoch
  ϵ        = DBL_EPSILON; // Set ϵ

  return true;            // Return 'true' if initialization was successful
}
//——————————————————————————————————————————————————————————————————————————————

El método Moving es responsable del movimiento de las partículas en el espacio de soluciones dentro del algoritmo AOA. Implementa la lógica básica de actualización de las posiciones de las partículas en función del estado actual y los parámetros del algoritmo. La lógica del método:

1. Aumenta epochNow para reflejar que ha llegado una nueva era de optimización.

2. Posicionamiento aleatorio inicial: si aún no se ha realizado ninguna actualización (revisión), se generan posiciones aleatorias dentro de los rangos rangeMin y rangeMax para cada partícula. A continuación, cada posición se discretiza utilizando el método SeInDiSp con el paso especificado.

3. MoAc y MoPr se calculan en función de la época actual y los parámetros especificados. Estos valores determinan las probabilidades utilizadas para actualizar las posiciones de las partículas.

4. Fase de investigación. Para cada partícula y cada coordenada, la posición se actualiza en función de valores aleatorios y parámetros calculados. Las posiciones se pueden actualizar utilizando diversos operadores (división y multiplicación), así como condiciones probabilísticas.

5. Después de la actualización, la posición también se convierte a valores discretos utilizando el método SeInDiSp.

//——————————————————————————————————————————————————————————————————————————————
// Particle displacement method
void C_AO_AOA::Moving ()
{
  epochNow++; // Increase the current epoch number

  // Initial random positioning
  if (!revision) // If there has not been a revision yet 
  {
    for (int i = 0; i < popSize; i++) // For each particle
    {
      for (int c = 0; c < coords; c++) // For each coordinate
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);                             // Generate random position
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Convert to discrete values
      }
    }

    revision = true; // Set revision flag
    return;          // Exit the method
  }

  //----------------------------------------------------------------------------
  double MoAc = minT + epochNow * ((maxT - minT) / epochs); // Calculate the MoAc value
  double MoPr = 1.0 - pow (epochNow / epochs, (1.0 / θ));   // Calculate the MoPr value
  double best = 0.0;                                        // Variable to store the best value

  // Research phase using Division (D) and Multiplication (M) operators
  for (int i = 0; i < popSize; i++) // For each particle
  {
    for (int c = 0; c < coords; c++) // For each coordinate
    {
      double rand1 = u.RNDprobab (); // Generate a random value
      double rand2 = u.RNDprobab (); // Generate a random value
      double rand3 = u.RNDprobab (); // Generate a random value

      best = cB [c];                 // Save the current best value

      if (rand1 < MoAc)              // If random value is less than MoAc
      {
        if (rand2 > 0.5)             // If random value is greater than 0.5
        {
          a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Update particle position
        }
        else
        {
          a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
      }
      else // If random value is greater than or equal to MoAc
      {
        if (rand3 > 0.5) // If random value is greater than 0.5
        {
          a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
        else
        {
          a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
      }

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Convert to discrete values
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método Revision de la clase C_AO_AOA actualiza la información sobre la mejor partícula de la población. Itera sobre todas las partículas, compara sus valores de función con el mejor valor actual y, si encuentra uno mejor, lo actualiza y guarda el índice. A continuación, copia las coordenadas de la mejor partícula en la matriz cB.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AOA::Revision ()
{
  int ind = -1;                     // Index to store the best particle

  for (int i = 0; i < popSize; i++) // For each particle
  {
    if (a [i].f > fB)               // If the function value is better than the current best one
    {
      fB = a [i].f;                 // Update the best value of the function
      ind = i;                      // Save the index of the best particle
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best particle
}
//——————————————————————————————————————————————————————————————————————————————

El método SeInDiSp de la clase C_AO_Utilities limita la entrada In dentro del rango [InMin, InMax] con el Step especificado.

1. Si In es menor o igual que InMin, devuelve InMin.
2. Si In es mayor o igual que InMax, devuelve InMax.
3. Si Step es igual a 0, devuelve el valor original de In.
4. De lo contrario, redondee el valor a (In - InMin) / Paso y devuelva el valor ajustado dentro del rango teniendo en cuenta el paso.

double C_AO_Utilities :: SeInDiSp (double In, double InMin, double InMax, double Step)
{
  if (In <= InMin) return (InMin);
  if (In >= InMax) return (InMax);
  if (Step == 0.0) return (In);
  else return (InMin + Step * (double)MathRound ((In - InMin) / Step));
}


Resultados de la prueba

El algoritmo AOA es bastante sencillo, veamos su rendimiento en tareas de prueba.

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.3914957505847635
25 Hilly's; Func runs: 10000; result: 0.27733670012505607
500 Hilly's; Func runs: 10000; result: 0.2514517003089684
=============================
5 Forest's; Func runs: 10000; result: 0.23495704012464264
25 Forest's; Func runs: 10000; result: 0.1853447250852242
500 Forest's; Func runs: 10000; result: 0.15382470751079919
=============================
5 Megacity's; Func runs: 10000; result: 0.19846153846153847
25 Megacity's; Func runs: 10000; result: 0.11815384615384619
500 Megacity's; Func runs: 10000; result: 0.09475384615384692
=============================
All score: 1.90578 (21.18%)

Según los resultados de la prueba, el algoritmo solo obtiene una puntuación del 21,18 % sobre 100 %. Este es un resultado muy débil. Desafortunadamente, está debajo del último lugar en la tabla de clasificación actual. Intentemos cambiar la lógica del algoritmo para lograr mejores resultados. Haremos cambios paso a paso y monitorearemos los resultados.

La lógica del algoritmo AOA original implica una búsqueda estocástica, que consiste únicamente en la naturaleza probabilística de la elección de uno de cuatro operadores matemáticos. Añadamos un elemento de aleatoriedad a la relación de desplazamiento μ multiplicándola por un número aleatorio en el rango de 0 a 1.

// Research phase using Division (D) and Multiplication (M) operators
  for (int i = 0; i < popSize; i++) // For each particle
  {
    for (int c = 0; c < coords; c++) // For each coordinate
    {
      double rand1 = u.RNDprobab (); // Generate a random value
      double rand2 = u.RNDprobab (); // Generate a random value
      double rand3 = u.RNDprobab (); // Generate a random value

      best = cB [c];                 // Save the current best value

      μ *= u.RNDfromCI (0, 1);       // Random change of μ

      if (rand1 < MoAc)              // If random value is less than MoAc
      {
        if (rand2 > 0.5)             // If random value is greater than 0.5
        {
          a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Update particle position
        }
        else
        {
          a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
      }
      else // If random value is greater than or equal to MoAc
      {
        if (rand3 > 0.5) // If random value is greater than 0.5
        {
          a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
        else
        {
          a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
      }

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Convert to discrete values
    }
  }

Probemos el algoritmo con los mismos parámetros:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.3595591180258857
25 Hilly's; Func runs: 10000; result: 0.2804913285516192
500 Hilly's; Func runs: 10000; result: 0.25204298245610646
=============================
5 Forest's; Func runs: 10000; result: 0.24115834887873383
25 Forest's; Func runs: 10000; result: 0.18034196700384764
500 Forest's; Func runs: 10000; result: 0.15441446106797124
=============================
5 Megacity's; Func runs: 10000; result: 0.18307692307692305
25 Megacity's; Func runs: 10000; result: 0.12400000000000003
500 Megacity's; Func runs: 10000; result: 0.09470769230769309
=============================
All score: 1.86979 (20.78%)

Desafortunadamente, el resultado fue aún peor. Es necesario tomar medidas adicionales. Sin embargo, el mero hecho de añadir aleatoriedad a una expresión determinista ciertamente debería mejorar la variabilidad de la estrategia de búsqueda. Veamos de cerca las ecuaciones de los operadores matemáticos: cada uno de ellos tiene el término rangeMin [c]. En esencia, la expresión resultante de estos operadores siempre está centrada en relación con el límite mínimo de los parámetros que se están optimizando. No hay ninguna lógica evidente en esto, así que vamos a eliminar este elemento de todas las ecuaciones.

// Research phase using Division (D) and Multiplication (M) operators
for (int i = 0; i < popSize; i++) // For each particle
{
  for (int c = 0; c < coords; c++) // For each coordinate
  {
    double rand1 = u.RNDprobab (); // Generate a random value
    double rand2 = u.RNDprobab (); // Generate a random value
    double rand3 = u.RNDprobab (); // Generate a random value

    best = cB [c];                 // Save the current best value

    μ *= u.RNDfromCI (0, 1);       // Change μ

    if (rand1 < MoAc)              // If random value is less than MoAc
    {
      if (rand2 > 0.5)             // If random value is greater than 0.5
      {
        a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]); // Update particle position
      }
      else
      {
        a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]);     // Update particle position
      }
    }
    else // If random value is greater than or equal to MoAc
    {
      if (rand3 > 0.5) // If random value is greater than 0.5
      {
        a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]);     // Update particle position
      }
      else
      {
        a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]);     // Update particle position
      }
    }

    a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Convert to discrete values
  }
}

Realicemos la prueba. A continuación se presentan los resultados obtenidos:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.36094646986361645
25 Hilly's; Func runs: 10000; result: 0.28294095623218063
500 Hilly's; Func runs: 10000; result: 0.2524581968477915
=============================
5 Forest's; Func runs: 10000; result: 0.2463208325927641
25 Forest's; Func runs: 10000; result: 0.1772140022690996
500 Forest's; Func runs: 10000; result: 0.15367993432040622
=============================
5 Megacity's; Func runs: 10000; result: 0.1923076923076923
25 Megacity's; Func runs: 10000; result: 0.11938461538461542
500 Megacity's; Func runs: 10000; result: 0.09433846153846229
=============================
All score: 1.87959 (20.88%)

Los cambios que hicimos no resultaron en ninguna mejora en el rendimiento, lo cual es bastante extraño considerando que ya habíamos implementado cambios importantes en nuestra estrategia de búsqueda. Esto puede indicar que la estrategia en sí es defectuosa y que la eliminación de componentes individuales no afecta significativamente los resultados.

La estrategia de búsqueda tiene el componente MoA que aumenta linealmente con cada iteración (ver Figura 1). Intentemos utilizar este componente como una elección probabilística de una de las coordenadas de la mejor solución y copiándolo en la solución de trabajo actual. Esto debería añadir propiedades combinatorias a la estrategia de búsqueda mediante el intercambio de información a través de la mejor solución de la población (en la versión original, no hay intercambio de información entre los agentes).

// Research phase using Division (D) and Multiplication (M) operators
for (int i = 0; i < popSize; i++) // For each particle
{
  for (int c = 0; c < coords; c++) // For each coordinate
  {
    double rand1 = u.RNDprobab (); // Generate a random value
    double rand2 = u.RNDprobab (); // Generate a random value
    double rand3 = u.RNDprobab (); // Generate a random value

    best = cB [c];                 // Save the current best value

    μ *= u.RNDfromCI (0, 1);       // Change μ

    if (rand1 < MoAc)              // If random value is less than MoAc
    {
      if (rand2 > 0.5)             // If random value is greater than 0.5
      {
        a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ); // Update particle position
      }
      else
      {
        a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);     // Update particle position
      }
    }
    else // If random value is greater than or equal to MoAc
    {
      if (rand3 > 0.5) // If random value is greater than 0.5
      {
        a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);     // Update particle position
      }
      else
      {
        a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);     // Update particle position
      }
    }

    if (u.RNDbool () < MoAc) a [i].c [c] = cB [c];                                            // Set to the best value

    a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Convert to discrete values
  }
}

Los resultados obtenidos tras introducir la lógica de intercambio de información a través de la mejor solución:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.360814744695913
25 Hilly's; Func runs: 10000; result: 0.28724958448168375
500 Hilly's; Func runs: 10000; result: 0.2523432997811412
=============================
5 Forest's; Func runs: 10000; result: 0.26319762212870146
25 Forest's; Func runs: 10000; result: 0.1796822846691542
500 Forest's; Func runs: 10000; result: 0.1546335398592898
=============================
5 Megacity's; Func runs: 10000; result: 0.18
25 Megacity's; Func runs: 10000; result: 0.12153846153846157
500 Megacity's; Func runs: 10000; result: 0.09373846153846228
=============================
All score: 1.89320 (21.04%)

Vemos mejoras en el rendimiento, pero hasta ahora dentro del alcance de las propias soluciones. Ahora agreguemos a la misma parte del código la probabilidad de generar un valor aleatorio para una coordenada dentro de todo el rango aceptable de parámetros optimizados, mientras la coordenada disminuye de forma no lineal según la ecuación MoP. 

// Probabilistic update of particle position
if (u.RNDbool () < MoAc) a [i].c [c] = cB [c];                                        // Set to the best value
else
  if (u.RNDbool () < MoPr) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);    // Generate new random position

Veamos los siguientes resultados:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.8354927331645667
25 Hilly's; Func runs: 10000; result: 0.3963221867834875
500 Hilly's; Func runs: 10000; result: 0.2526544322311671
=============================
5 Forest's; Func runs: 10000; result: 0.7689954585427405
25 Forest's; Func runs: 10000; result: 0.3144560745800252
500 Forest's; Func runs: 10000; result: 0.15495875390289315
=============================
5 Megacity's; Func runs: 10000; result: 0.6076923076923076
25 Megacity's; Func runs: 10000; result: 0.24646153846153843
500 Megacity's; Func runs: 10000; result: 0.09816923076923163
=============================
All score: 3.67520 (40.84%)

¡Sorprendentemente, la productividad ha aumentado drásticamente! Esto significa que estamos avanzando en la dirección correcta. Vale la pena señalar qué se agregó exactamente a la lógica AOA: al comienzo de la optimización, en la primera época, la probabilidad de copiar las coordenadas de la mejor solución global a las actuales es mínima. Esto es bastante lógico, ya que en la etapa inicial de optimización la estrategia apenas comienza a explorar el espacio de búsqueda. Al mismo tiempo, la probabilidad de generar soluciones aleatorias dentro de todo el espacio de búsqueda en la primera iteración es máxima. A lo largo de todas las épocas, estas probabilidades cambian: la probabilidad de copiar las coordenadas de la solución global aumenta, mientras que la probabilidad de generar soluciones aleatorias, por el contrario, disminuye (véase la figura 1).

Dado que el rendimiento ha mejorado con los cambios que realicé, y ya se observó que los cambios en la lógica original no producen mejoras notables, tiene sentido eliminar por completo todos los operadores aritméticos. Probemos el algoritmo resultante en problemas de prueba:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8751771961221438
25 Hilly's; Func runs: 10000; result: 0.4645369071659114
500 Hilly's; Func runs: 10000; result: 0.27170038319811357
=============================
5 Forest's; Func runs: 10000; result: 0.8369443889312367
25 Forest's; Func runs: 10000; result: 0.36483865328371257
500 Forest's; Func runs: 10000; result: 0.17097532914778202
=============================
5 Megacity's; Func runs: 10000; result: 0.7046153846153846
25 Megacity's; Func runs: 10000; result: 0.28892307692307695
500 Megacity's; Func runs: 10000; result: 0.10847692307692398
=============================
All score: 4.08619 (45.40%)   

Como podemos ver, la eficiencia aumentó casi otro 5%, lo que confirmó nuevamente la exactitud de mi razonamiento. Obtuvimos resultados interesantes con los parámetros predeterminados, sin embargo, los cambios en la lógica fueron tan radicales que ahora es necesario seleccionar los parámetros externos óptimos del algoritmo. Un beneficio adicional al aumento de la productividad fue:

  • Aceleración significativa del trabajo, ya que eliminamos la generación innecesaria de números aleatorios
  • reduciendo el número de parámetros externos en uno

Veamos los resultados finales del algoritmo obtenido:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.5|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9152036654779877
25 Hilly's; Func runs: 10000; result: 0.46975580956945456
500 Hilly's; Func runs: 10000; result: 0.27088799720164297
=============================
5 Forest's; Func runs: 10000; result: 0.8967497776673259
25 Forest's; Func runs: 10000; result: 0.3740125122006007
500 Forest's; Func runs: 10000; result: 0.16983896751516864
=============================
5 Megacity's; Func runs: 10000; result: 0.6953846153846155
25 Megacity's; Func runs: 10000; result: 0.2803076923076923
500 Megacity's; Func runs: 10000; result: 0.10852307692307792
=============================
All score: 4.18066 (46.45%) 

El resultado obtenido ya merece un lugar en la tabla de clasificación, mientras que la versión final de la estrategia de búsqueda ha perdido por completo elementos de la lógica original. Así que decidí darle a este nuevo algoritmo un nuevo nombre: Algoritmo de Optimización Simple (Simple Optimization Algorithm, SOA). Veamos el código final completo del algoritmo SOA.

#include "#C_AO.mqh"

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_SOA () { }
  C_AO_SOA ()
  {
    ao_name = "SOA";
    ao_desc = "Simple Optimization Algorithm";
    ao_link = "https://www.mql5.com/en/articles/16364";

    popSize = 50;   // Population size
    minT    = 0.1;  // Minimum T value
    maxT    = 0.9;  // Maximum T value
    θ       = 10;   // θ parameter

    ArrayResize (params, 4); // Resize the parameter array

    // Initialize parameters
    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "minT";    params [1].val = minT;
    params [2].name = "maxT";    params [2].val = maxT;
    params [3].name = "θ";       params [3].val = θ;
  }

  void SetParams () // Method for setting parameters
  {
    popSize = (int)params [0].val; // Set population size
    minT    = params      [1].val; // Set minimum T
    maxT    = params      [2].val; // Set maximum T
    θ       = params      [3].val; // Set θ
  }

  bool Init (const double &rangeMinP  [], // Minimum search range
             const double &rangeMaxP  [], // Maximum search range
             const double &rangeStepP [], // Search step
             const int     epochsP = 0);  // Number of epochs

  void Moving   (); // Method of moving particles
  void Revision (); // Revision method

  //----------------------------------------------------------------------------
  double minT; // Minimum T value
  double maxT; // Maximum T value
  double θ;    // θ parameter

  private: //-------------------------------------------------------------------
  int epochs;    // Total number of epochs
  int epochNow;  // Current epoch
  double ϵ;      // Parameter to prevent division by zero
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_SOA::Init (const double &rangeMinP  [], // Minimum search range
                     const double &rangeMaxP  [], // Maximum search range
                     const double &rangeStepP [], // Search step
                     const int     epochsP = 0)   // Number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; // Initialization of standard parameters

  //----------------------------------------------------------------------------
  epochs   = epochsP;     // Set the total number of epochs
  epochNow = 0;           // Initialize the current epoch
  ϵ        = DBL_EPSILON; // Set ϵ

  return true;            // Return 'true' if initialization was successful
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Particle displacement method
void C_AO_SOA::Moving ()
{
  epochNow++; // Increase the current epoch number

  // Initial random positioning
  if (!revision) // If there has not been a revision yet 
  {
    for (int i = 0; i < popSize; i++) // For each particle
    {
      for (int c = 0; c < coords; c++) // For each coordinate
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);                             // Generate random position
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Convert to discrete values
      }
    }

    revision = true; // Set revision flag
    return;          // Exit the method
  }

  //----------------------------------------------------------------------------
  double MoAc = minT + epochNow * ((maxT - minT) / epochs); // Calculate the MoAc value
  double MoPr = 1.0 - pow (epochNow / epochs, (1.0 / θ));   // Calculate the MoPr value
  double best = 0.0;                                        // Variable to store the best value

  // Research phase using Division (D) and Multiplication (M) operators
  for (int i = 0; i < popSize; i++) // For each particle
  {
    for (int c = 0; c < coords; c++) // For each coordinate
    {
      // Probabilistic update of particle position
      if (u.RNDbool () < MoAc) a [i].c [c] = cB [c];                                        // Set to the best value
      else
        if (u.RNDbool () < MoPr) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);    // Generate new random position

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);   // Convert to discrete values
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SOA::Revision ()
{
  int ind = -1;                     // Index to store the best particle

  for (int i = 0; i < popSize; i++) // For each particle
  {
    if (a [i].f > fB)               // If the function value is better than the current best one
    {
      fB = a [i].f;                 // Update the best value of the function
      ind = i;                      // Save the index of the best particle
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best particle
}
//——————————————————————————————————————————————————————————————————————————————

El resultado es uno de los algoritmos de optimización más compactos en términos de código que hemos considerado anteriormente. El único código que es más corto es el del algoritmo RW (RandomWalk), que se analizará en uno de los siguientes artículos.

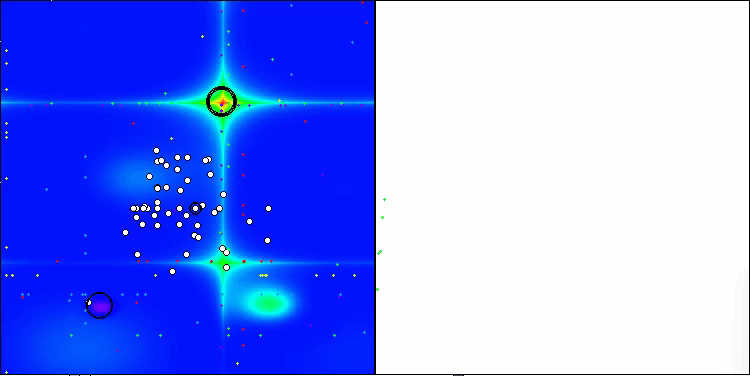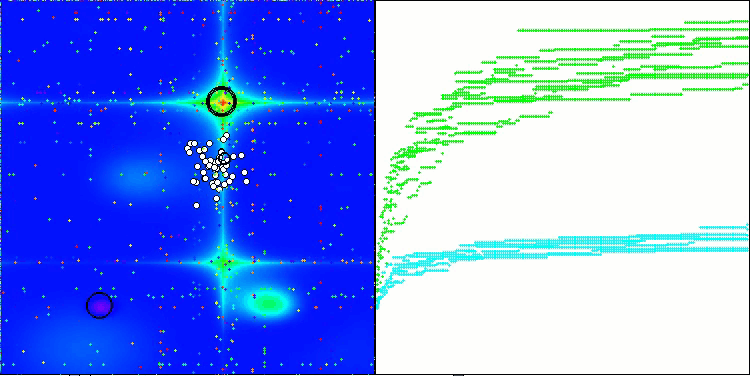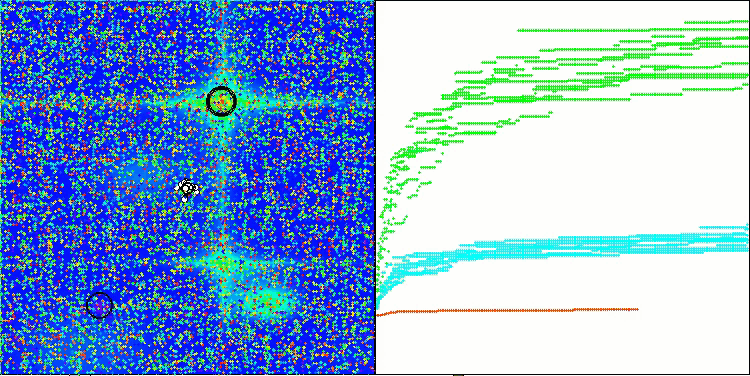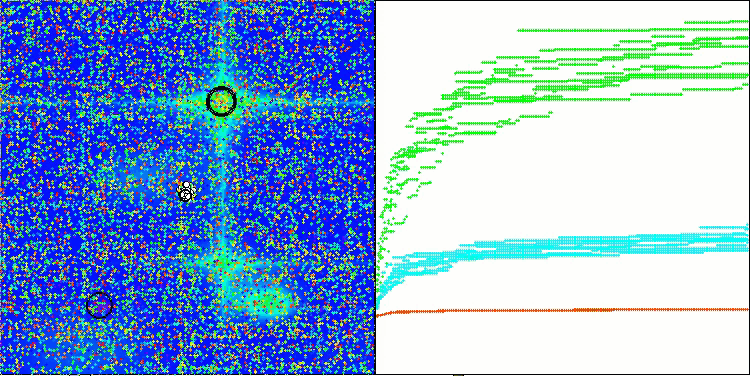
Visualizar el rendimiento de las estrategias de búsqueda en el espacio de soluciones dice mucho. Combiné las tres pruebas (Hilly, Forest y Megacity) para el algoritmo AOA en una animación, ya que prácticamente no hay diferencias en el rendimiento en diferentes tipos de tareas. A continuación se muestran visualizaciones separadas del funcionamiento de SOA para cada una de las tres funciones de prueba.

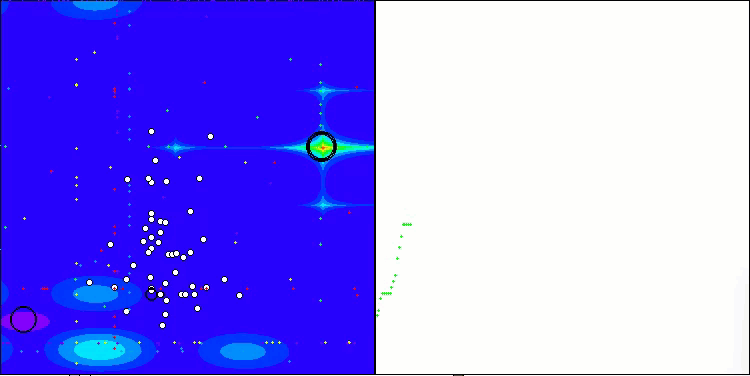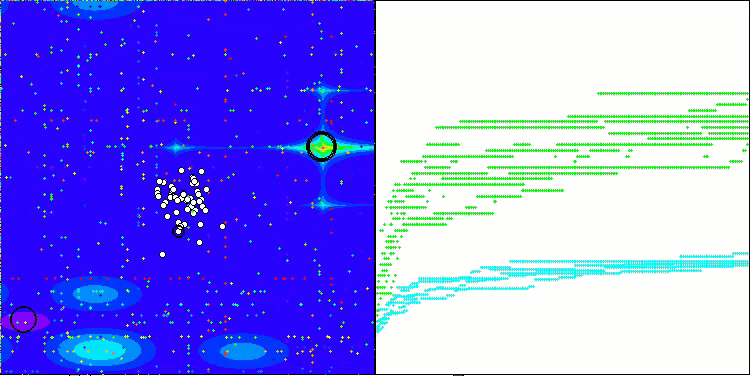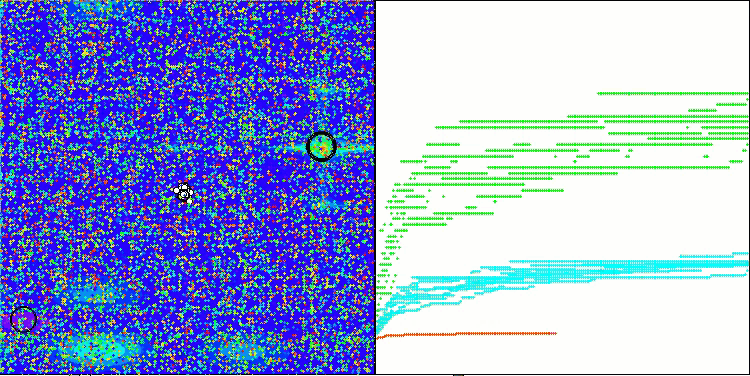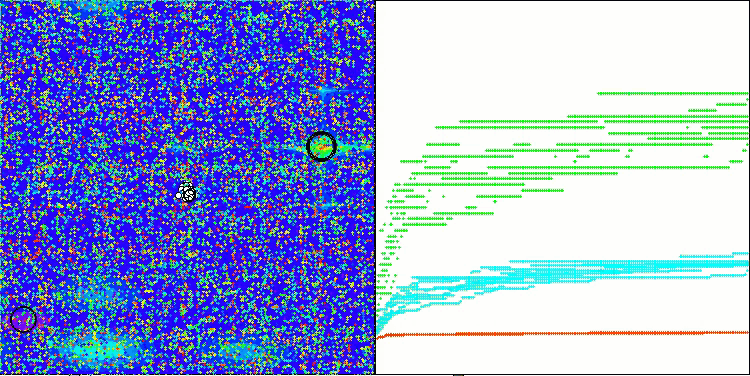
Se puede observar el trabajo del nuevo algoritmo SOA en problemas de pequeñas dimensiones: una pequeña dispersión de resultados, lo que es una cualidad bastante rara. 

AOA en Hilly, Forest, Megacity

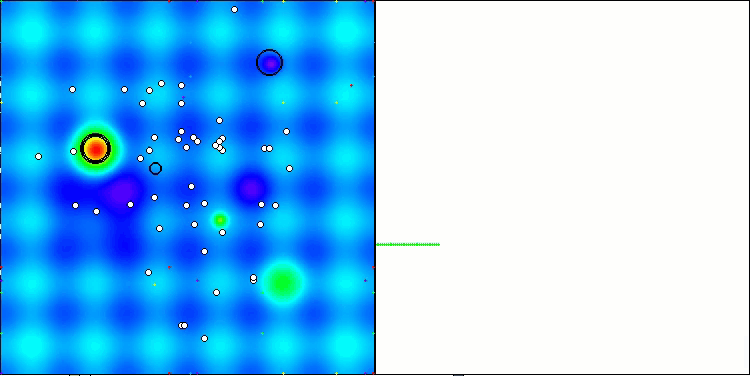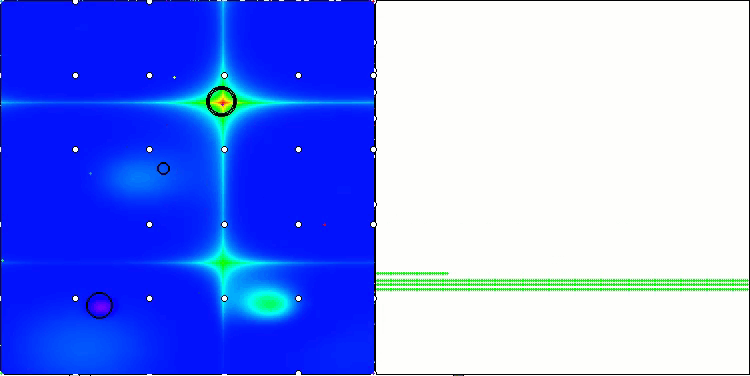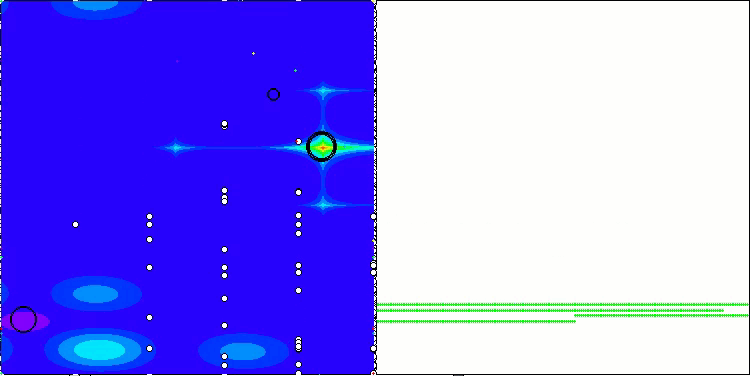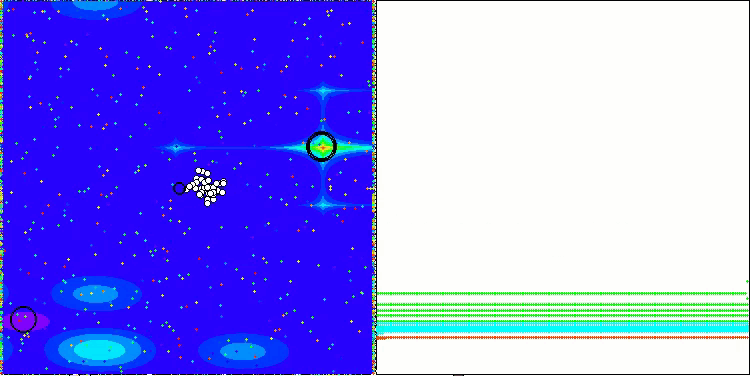
AOA en las funciones de prueba Hilly, Forest, Megacity

Hilly

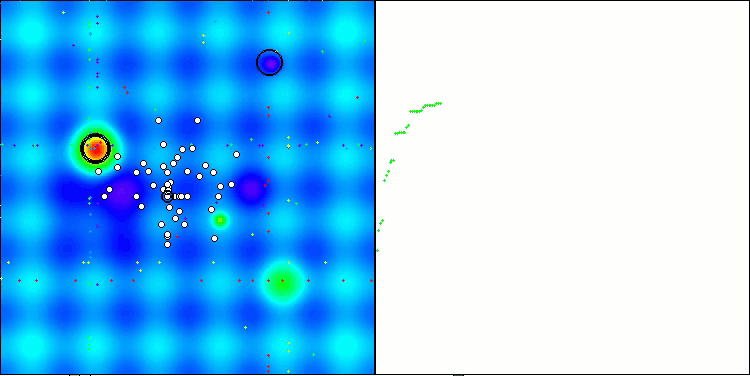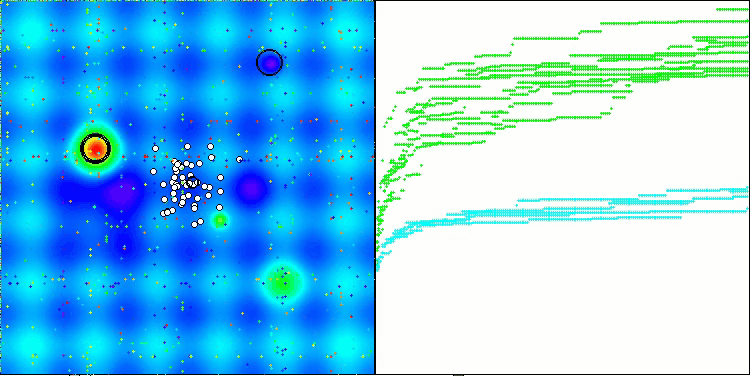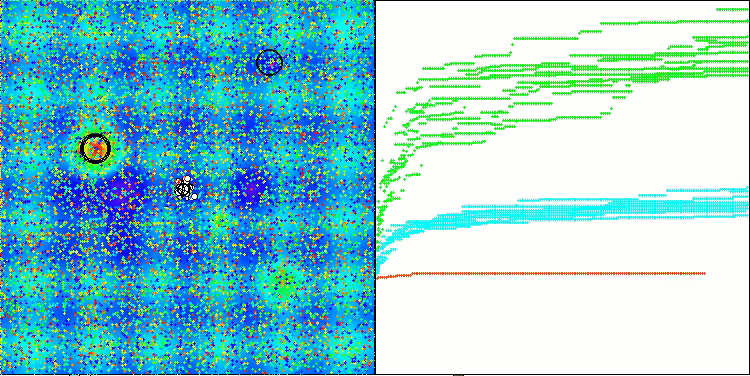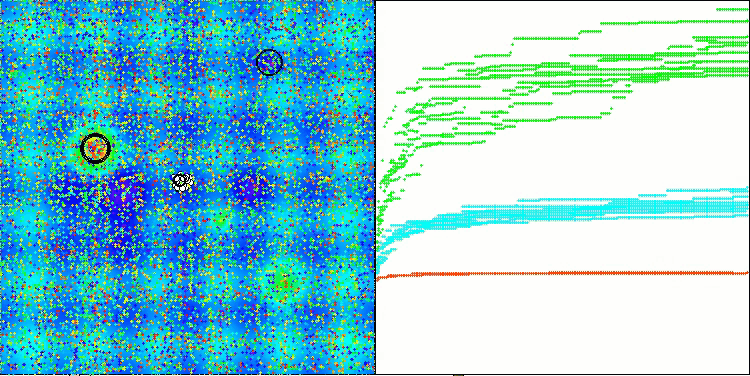
SOA en la función de prueba Hilly

Forest

  SOA en la función de prueba Forest

Megacity

SOA en la función de prueba Megacity


Según los resultados de la prueba, el algoritmo AOA original no logró entrar en la tabla de clasificación, ya que su resultado quedó por debajo del puesto 45. El nuevo algoritmo Simple Optimization Algorithm (SOA) logró entrar en el ranking y terminó en el puesto 29.

# AO Descripción Hilly Hilly final Forest Forest final Megacity (discreto) Megacity final Resultado final % de MÁX
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 ANS búsqueda en todo el vecindario 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
2 CLA algoritmo de bloqueo de código (joo) 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
3 AMOm optimización de la migración animal M 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
4 (P+O)ES estrategias de evolución (P+O) 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
5 CTA algoritmo de cola de cometa (joo) 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
6 SDSm búsqueda de difusión estocástica M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
7 AAm algoritmo de tiro con arco M 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
8 ESG evolución de los grupos sociales (joo) 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
9 SIA recocido isotrópico simulado (joo) 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
10 ACS búsqueda cooperativa artificial 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
11 ASO optimización de la sociedad anárquica 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
12 AOSm búsqueda orbital atómica M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
13 TSEA algoritmo de evolución del caparazón de tortuga (joo) 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
14 DE evolución diferencial 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
15 CRO optimización de reacciones químicas 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
16 BSA algoritmo de enjambre de aves 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
17 HS búsqueda de armonía 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
18 SSG siembra y crecimiento de plantones 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
19 BCOm optimización de la quimiotaxis bacteriana M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
20 ABO optimización del búfalo africano 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
21 (PO)ES (PO) estrategias de evolución 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
22 TSm búsqueda tabú M 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
23 BSO optimización de la lluvia de ideas 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
24 WOAm algoritmo de optimización de wale M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
25 AEFA algoritmo de campo eléctrico artificial 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
26 AEO algoritmo de optimización basado en ecosistemas artificiales 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
27 ACOm optimización de colonias de hormigas M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
28 BFO-GA optimización de la alimentación bacteriana - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
29 SOA algoritmo de optimización simple 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
30 ABHA algoritmo de colmena artificial 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
31 ACMO optimización del modelo de nubes atmosféricas 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
32 ASHA algoritmo de ducha artificial 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
33 ASBO optimización del comportamiento social adaptativo 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
34 MEC computación evolutiva de la mente 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
35 IWO optimización de malezas invasoras 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
36 Micro-AIS microsistema inmunológico artificial 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
37 COAm algoritmo de optimización de cuco M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
38 SDOm Optimización de la dinámica espiral M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
39 NMm método Nelder-Mead M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
40 FAm algoritmo de luciérnaga M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
41 GSA algoritmo de búsqueda gravitacional 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
42 BFO optimización de la búsqueda de alimento bacteriano 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
43 ABC colonia de abejas artificial 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
44 BA algoritmo de murciélago 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
45 AAA algoritmo adaptativo de algas 0.50007 0.32040 0.25525 1.07572 0.37021 0.22284 0.16785 0.76089 0.27846 0.14800 0.09755 0.52402 2.361 26.23


Resumen

Hemos analizado en detalle el algoritmo de optimización aritmética, cuya implementación resultó ser realmente sencilla. Sin embargo, como a veces ocurre, la simplicidad no siempre garantiza buenos resultados. ¡La verdadera clave del éxito es la súper simplicidad! Estoy bromeando, por supuesto. Los principales problemas de AOA son la falta de interacción e intercambio de información entre los miembros de la población, lo que a su vez conduce a una falta total de cualidades combinatorias en esta estrategia de búsqueda.

Otro inconveniente del algoritmo es la falta de variabilidad en sus operadores de búsqueda. Aunque los operadores se eligen aleatoriamente para cada coordenada, esto no permite que el algoritmo se "enganche" efectivamente al paisaje multidimensional del espacio de búsqueda. Sin embargo, el algoritmo AOA contiene enfoques racionales y lógicos, como el cambio de los elementos MoA y MoP con cada época. Se convirtieron en la base para recrear el algoritmo y su evolución hacia una nueva, interesante y extremadamente simple estrategia de búsqueda basada en el enfoque probabilístico de copiar información de las mejores soluciones de la población y generar soluciones aleatorias en el espacio de búsqueda.

Con cada época, la aleatoriedad en las decisiones de la población disminuye, mientras que la concentración de direcciones exitosas aumenta. Esto se puede comparar con el proceso de construcción de un elegante puente sobre un río: en las etapas iniciales del trabajo se utilizan diversos materiales y diseños que pueden no ser adecuados para el resultado final. Sin embargo, a medida que el proyecto avanza hacia su finalización, las mejores soluciones se hacen más obvias y se descartan elementos innecesarios. Como resultado, el puente se vuelve cada vez más armonioso y estable, conectando las orillas con elegancia y fuerza.

Pestaña

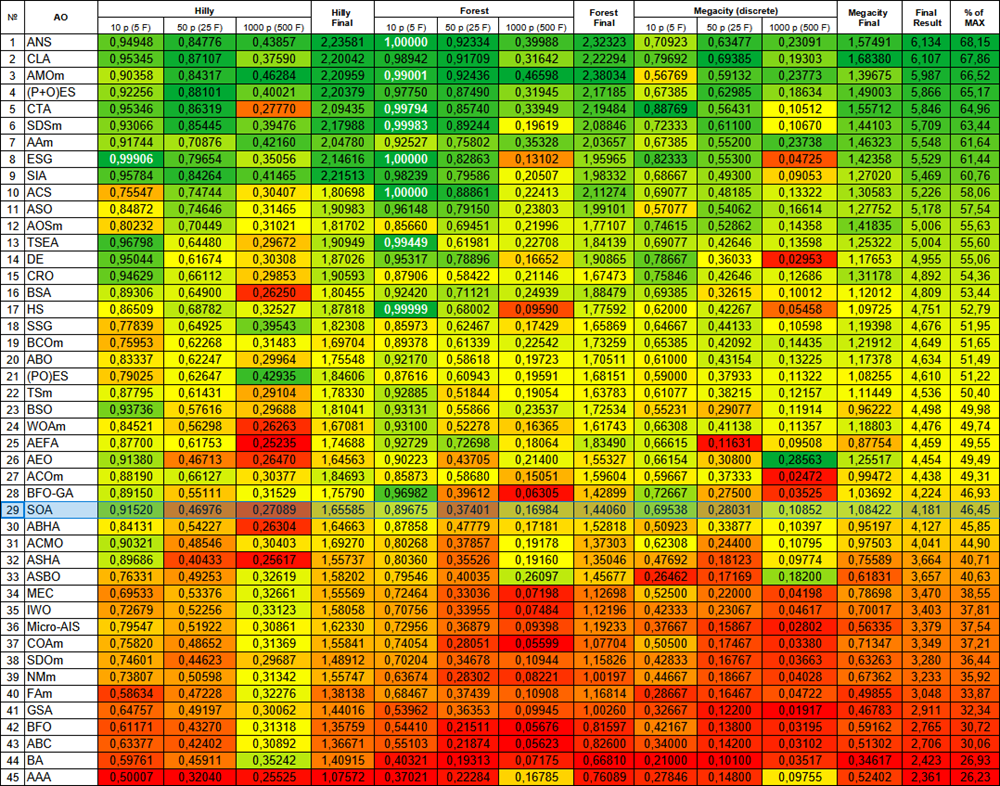
Figura 2. Gradación de color de los algoritmos según las pruebas pertinentes. Los resultados mayores o iguales a 0,99 se resaltan en blanco.

Gráfico

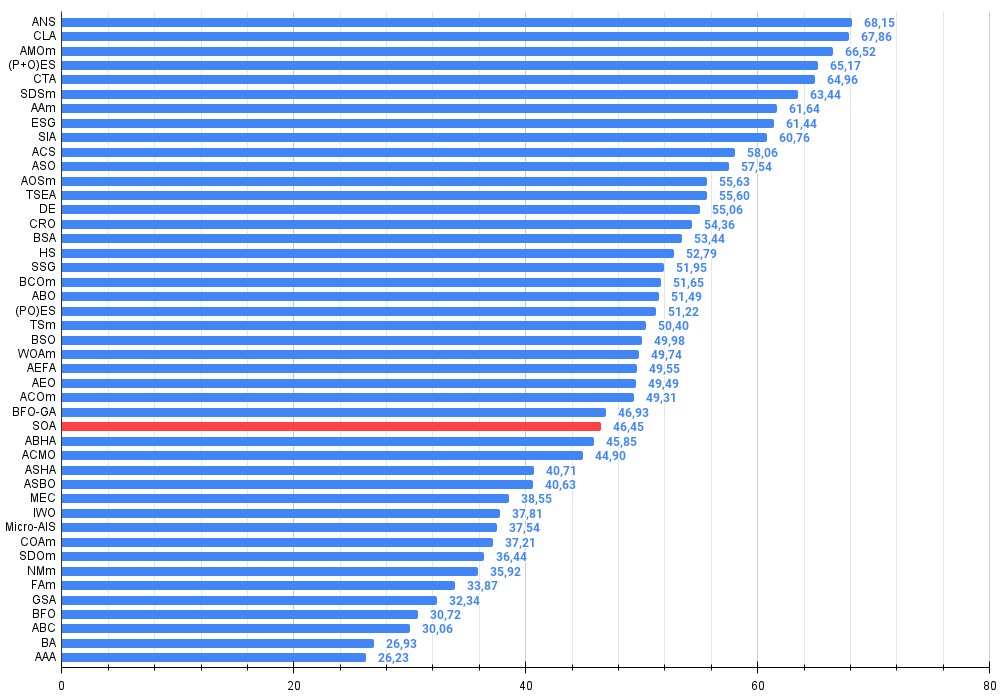
Figura 3. El histograma de los resultados de la prueba del algoritmo (en una escala de 0 a 100, cuanto más, mejor).

Donde 100 es el resultado teórico máximo posible, el archivo incluye un script para calcular la tabla de calificación.


Ventajas y desventajas de SOA:

Ventajas:

  1. Pequeño número de parámetros externos.
  2. Buenos resultados en problemas de baja dimensión, especialmente los discretos.
  3. Rápido.
  4. Pequeña dispersión de resultados en problemas de pequeña dimensión.
  5. Implementación muy sencilla.

Contras:

  1. Baja escalabilidad.

El artículo se acompaña de un archivo con las versiones actuales de los códigos del algoritmo. El autor del artículo no es responsable de la exactitud absoluta en la descripción de los algoritmos canónicos. Se han realizado cambios en muchos de ellos para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos.

Programas utilizados en el artículo

# Nombre Tipo Descripción
1 #C_AO.mqh
 Include
 Clase padre de algoritmos de optimización de población
2 #C_AO_enum.mqh
 Include
 Enumeración de algoritmos de optimización de poblaciones
3 TestFunctions.mqh
 Include
 Biblioteca de funciones de prueba
4
 TestStandFunctions.mqh
 Include
 Biblioteca de funciones del banco de pruebas
5
 Utilities.mqh
 Include
 Biblioteca de funciones auxiliares
6
 CalculationTestResults.mqh
 Include
 Script para calcular resultados en la tabla de comparación
7
 Testing AOs.mq5
 Script El banco de pruebas unificado para todos los algoritmos de optimización de la población
8
 Uso sencillo de algoritmos de optimización de algorithms.mq5
 Script
Un ejemplo sencillo de uso de algoritmos de optimización de población sin visualización
9
 AO_AOA_ArithmeticOptimizationAlgorithm.mqh
 Include Clase de algoritmo AOA
10
 AO_SOA_SimpleOptimizationAlgorithm.mqh
 Include
 Clase de algoritmo SOA
11
Test_AO_AOA.mq5
 Script Banco de pruebas AOA
12
 Test_AO_SOA.mq5
 Script
 Banco de pruebas SOA

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16364

Archivos adjuntos |
Descargar ZIP
AOA_SOA.zip (141.9 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores
MQL5 Wizard techniques you should know (Part 49): Aprendizaje por refuerzo con optimización de políticas proximales MQL5 Wizard techniques you should know (Part 49): Aprendizaje por refuerzo con optimización de políticas proximales
La optimización de políticas proximales es otro algoritmo del aprendizaje por refuerzo que actualiza la política, a menudo en forma de red, en pasos incrementales muy pequeños para garantizar la estabilidad del modelo. Examinamos cómo esto podría ser útil, tal y como hemos hecho en artículos anteriores, en un asesor experto creado mediante un asistente.
Información mutua como criterio para la selección de características paso a paso Información mutua como criterio para la selección de características paso a paso
En este artículo, presentamos una implementación MQL5 de selección de características paso a paso basada en la información mutua entre un conjunto de predictores óptimos y una variable objetivo.
Perspectivas bursátiles a través del volumen: más allá de los gráficos OHLC Perspectivas bursátiles a través del volumen: más allá de los gráficos OHLC
Sistema de negociación algorítmica que combina el análisis de volumen con técnicas de aprendizaje automático, concretamente redes neuronales LSTM. A diferencia de los enfoques tradicionales de negociación, que se centran principalmente en los movimientos de los precios, este sistema hace hincapié en los patrones de volumen y sus derivados para predecir los movimientos del mercado. La metodología incorpora tres componentes principales: análisis de derivadas de volumen (derivadas primera y segunda), predicciones LSTM para patrones de volumen e indicadores técnicos tradicionales.
Desarrollo de un kit de herramientas para el análisis de la acción del precio (Parte 2): Script de comentarios analíticos Desarrollo de un kit de herramientas para el análisis de la acción del precio (Parte 2): Script de comentarios analíticos
En línea con nuestra visión de simplificar la acción del precio, nos complace presentar otra herramienta que puede mejorar significativamente su análisis de mercado y ayudarle a tomar decisiones bien informadas. Esta herramienta muestra indicadores técnicos clave, como los precios del día anterior, los niveles significativos de soporte y resistencia, y el volumen de operaciones, al tiempo que genera automáticamente señales visuales en el gráfico.