学習中にニューロンを活性化する関数：高速収束の鍵は？

はじめに

前回の記事では、単純な多層パーセプトロン(MLP)ニューラルネットワークを取引における近似器（強化学習）として検討しました。その際、活性化関数の特性には特に注目せず、一般的な双曲線正接シグモイドを使用しました。また別の記事では、広く用いられているADAMアルゴリズムの能力について議論し、独立した集団型のグローバル最適化手法であるADAMmに改良しました。

本記事では、ニューラルネットワークをデータ補間（教師あり学習）の観点から考察し、ニューロン活性化関数の特性に焦点を当てます。ニューラルネットワークに組み込まれたADAM最適化アルゴリズム（通常の使用法に従って）を使用し、活性化関数およびその導関数が最適化アルゴリズムの収束速度に与える影響を研究します。

川を想像してください。多くの支流を持つその通常の状態では、水は自由に流れ、複雑な流れや渦を作り出します。しかし、水門や堰のシステムを作り始めたらどうなるでしょうか。水の流れを制御し、適切な方向に導き、流れの強さを調整できるようになります。ニューラルネットワークにおける活性化関数も同様の役割を果たします。どの信号を通すか、どの信号を遅らせるか、あるいは弱めるかを決定するのです。活性化関数がなければ、ニューラルネットワークは単なる線形変換の集合に過ぎません。

活性化関数はニューラルネットワークの動作に動的な性質を加え、データの微妙なニュアンスを捉えることを可能にします。たとえば顔認識タスクでは、活性化関数によって眉のアーチや顎の形状などの小さな特徴を検知できます。適切な活性化関数の選択は、ニューラルネットワークがさまざまなタスクでどのように機能するかに影響します。ある特徴量は学習初期の段階で明確で理解しやすい信号を提供します。別の特徴量はネットワークがより微細なパターンを学習する後期段階で有用です。また、不要な情報を抑制し、重要な特徴量のみを強調する役割を果たすものもあります。

活性化関数の特性を知らなければ、ニューラルネットワークは単純な課題でつまずいたり、重要な詳細を見落としたりし始める可能性があります。活性化関数の主な目的は、ニューラルネットワークに非線形性を導入し、出力値を正規化することです。

本記事の目的は、異なる活性化関数の使用に関連する問題点を明らかにし、誤差を最小化しつつ例点を補間する際のニューラルネットワークの精度に与える影響を検証することです。また、活性化関数が実際に収束速度に影響を与えるのか、それともこれは使用する最適化アルゴリズムの性質によるものなのかを明らかにします。参照アルゴリズムとして、確率的要素を用いた改良版集団ADAMmを使用し、MLPに組み込まれたADAM（従来の使用法）でテストをおこないます。後者は直感的には有利に思えます。なぜなら、活性化関数の導関数を通じて適合度関数の勾配に直接アクセスできるからです。一方、集団型の確率的ADAMmは導関数へのアクセスがなく、最適化問題の表面について全く情報を持たないためです。これらの結果を見て結論を導きます。

本記事は探索的な性格を持ち、物語は実験の順序に沿って進行します。

ADAM内蔵MLPニューラルネットワークの実装

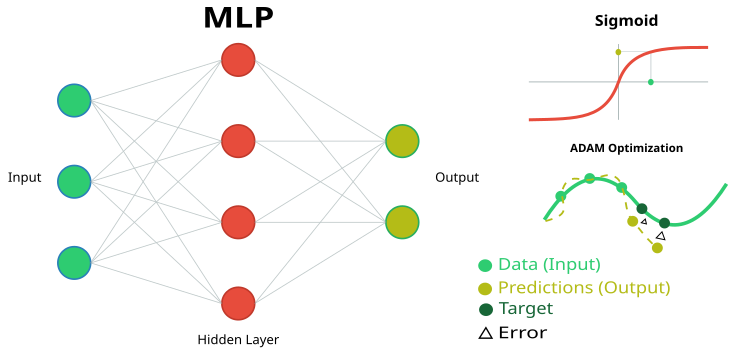
図1：MLPニューラルネットワークとその学習の概略図

本研究をおこなうにあたり、MQL5言語に組み込まれた特殊な行列演算機能を使わずに、単純で透明性の高いMLPニューラルネットワークコードを用意しました。これにより、ニューラルネットワークのロジックで何が起こっているのかを明確に理解でき、特定の結果が何に依存しているのかを把握することが可能になります。

ここでは、内蔵ADAM (Adaptive Moment Estimation)最適化アルゴリズムを備えたMLPを実装します。ニューラルネットワークの実装の一部を表すクラスと構造体を用い、主要な構成要素であるニューロン、ニューロン層、重みを定義します。

1. C_Neuroは、ニューラルネットワークの基本単位であるニューロンを表します。

• C_Neuron()はコンストラクタであり、最適化アルゴリズムで使用する「m」と「v」プロパティの値をゼロに初期化します。
• out：活性化関数を適用した後のニューロンの出力値
• delta：学習中に勾配を計算する際に使用される誤差デルタ
• bias：ニューロン入力に加算されるバイアス値
• mとv：ADAM最適化法で使用するバイアスの一次および二次モーメント

2. S_NeuronLayer構造体は、ニューロンの層を表します。C_Neuron n []は、ニューラルネットワーク層内のニューロン配列です。

ニューロン間の重みを格納する際には、単純な二次元配列ではなく、オブジェクト指向アプローチを使用します。これはC_Weightクラスに基づいており、接続の重み自体だけでなく、ADAMアルゴリズムで使用する一次および二次モーメントといった最適化パラメータも保持します。データ構造は階層的に配置されており、S_WeightsLayerがS_WeightsLayerR構造体の配列を含み、さらにそれぞれがC_Weightオブジェクトの配列を含む形になっています。この構造により、明確なインデックスチェーンを通じてネットワーク内の任意の重みに簡単にアクセスできます。

たとえば、層0の最初のニューロンと次の層の2番目のニューロンの接続重みを参照する場合、表記「wL [0].nOnL [1].nOnR [2].w」を使用します。ここで、最初のインデックスは隣接する層のペアを示し、2番目は左側の層のニューロンを示し、3番目は右側の層のニューロンを示します。

//——————————————————————————————————————————————————————————————————————————————
// Neuron class
class C_Neuron
{
  public:
  C_Neuron ()
  {
    m = 0.0;
    v = 0.0;
  }
  double out;   // Neuron output after the activation function
  double delta; // Error delta
  double bias;  // Bias
  double m;     // First moment of displacement
  double v;     // Second moment of displacement
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Structure of the neuron layer
struct S_NeuronLayer
{
    C_Neuron n []; // neurons in the layer
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Weight class
class C_Weight
{
  public:
  C_Weight ()
  {
    w = 0.0;
    m = 0.0;
    v = 0.0;
  }

  double w; // Weight
  double m; // First moment
  double v; // Second moment
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Weight structure for neurons on the right
struct S_WeightsLayerR
{
    C_Weight nOnR [];
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Weight structure for neurons on the left
struct S_WeightsLayer
{
    S_WeightsLayerR nOnL [];
};
//——————————————————————————————————————————————————————————————————————————————

C_MLPaCクラスは、MLPの基本機能を実装しており、ADAM最適化アルゴリズムを用いた順伝播とバックプロパゲーション（誤差逆伝播）学習をおこなうことができます。その主な機能を以下に示します。

ネットワーク構造

• ネットワークは、入力層 -> 隠れ層 -> 出力層という順次の層で構成されます。
• 各層のニューロンは、次の層のすべてのニューロンと接続されています（全結合ネットワーク）。

主な機能

• Init：与えられた構成でネットワークを作成するメソッド
• ImportWeightsおよびExportWeights：ネットワークの重みを読み込み・保存する関数
• ForwProp：順伝播（入力データに対するネットワークの応答を取得する）
• BackProp：バックプロパゲーションに基づくネットワーク学習メソッド

学習パラメータ（ADAMアルゴリズム）

• alpha (0.001)：ネットワークの学習速度を制御する
• beta1 (0.9)およびbeta2 (0.999)：ネットワークが安定して学習するのを助けるパラメータ
• epsilon (1e-8)：ゼロ除算を防ぐための小さな値

内部コンポーネント

• BackPropは各層のサイズ(layersSize)に関する情報を保持する
• 全ニューロン(nL)およびそれらの間の重み(wL)を含む
• 重みの総数(wC)や層の数(nLC)も追跡する
• actFunc：選択された活性化関数を使用する
  

本質的に、このクラスはニューラルネットワークの「脳」に相当し、入力データを受け取り、ニューロンと重みのシステムを通して処理し、結果を生成し、自らの誤りから学習することで、予測精度を徐々に向上させることができます。

//+-----------------------------------------------------------------------------------------+
//| Multilayer Perceptron (MLP) class                                                       |
//| Implements forward pass through a fully connected neural network and training using the |
//| backpropagation of error by ADAM optimization algorithm                                 |
//| Architecture: Lin -> L1 -> L2 -> ... Ln -> Lout                                         |
//+-----------------------------------------------------------------------------------------+
class C_MLPa
{
  public: //--------------------------------------------------------------------
  ~C_MLPa ()
  {
    delete actFunc;
  }
  C_MLPa ()
  {
    alpha   = 0.001;   // Training speed
    beta1   = 0.9;     // Decay ratio for the first moment
    beta2   = 0.999;   // Decay ratio for the second moment
    epsilon = 1e-8;    // Small constant for numerical stability
  }

  // Network initialization with the given configuration, Returns the total number of weights in the network, or 0 in case of an error
  int    Init          (int &layerConfig [], int actFuncType, int seed);
  bool   ImportWeights (double &weights []);  // Import weights
  bool   ExportWeights (double &weights []);  // Export weights

  // Forward pass through the network
  void   ForwProp (double &inLayer  [],  // input values
                   double &outLayer []); // output layer values

  // Error backpropagation with ADAM optimization algorithm
  void   BackProp (double &errors []);

  // Get the total number of weights in the network
  int    GetWcount () { return wC; }

  // ADAM optimization parameters 
  double alpha;          // Training speed
  double beta1;          // Decay ratio for the first moment
  double beta2;          // Decay ratio for the second moment
  double epsilon;        // Small constant for numerical stability

  int layersSize    [];  // Size of each layer (number of neurons)
  S_NeuronLayer  nL [];  // Layers of neurons, example of access: nLayers [].n [].a
  S_WeightsLayer wL [];  // Layers of weights between layers of neurons, example of access: wLayers [].nOnLeft [].nOnRight [].w

  private: //-------------------------------------------------------------------
  int            wC;       // Total number of weights in the network (including biases)
  int            nLC;      // Total number of neuron layers (including input and output ones)
  int            wLC;      // Total number of weight layers (between neuron layers)
  int            t;        // Iteration counter
  C_Base_ActFunc *actFunc; // Activation functions and their derivatives
};
//——————————————————————————————————————————————————————————————————————————————

Initメソッドは、多層パーセプトロンの構造を初期化します。各層のニューロン数を設定し、活性化関数を選択し、ニューロンの初期重みを生成します。ネットワーク構成の妥当性をチェックし、必要な総重み数を返すか、エラーが発生した場合は0を返します。

パラメータは次のとおりです。

• layerConfig []：各ネットワーク層におけるニューロン数を格納した配列
• actFuncType：ニューラルネットワークで使用する活性化関数の種類（例：シグモイド）
• seed：重みを初期化する際の乱数生成器を初期化するためのシードで、再現可能な結果を得ることができる

動作の流れ

1. 渡されたlayerConfig配列に基づいて層の数を決定します。
2. 層の数が少なくとも2であること、各層に正のニューロン数が含まれていることを確認します。エラーが発生した場合はメッセージを表示して実行を終了します。
3. 層のサイズをlayersSize配列にコピーし、ニューロンおよび重みを格納する配列を初期化します。
4. 層間のニューロンを接続するために必要な総重み数を計算します。
5. さらに、Xavier法を用いて重みを初期化します。これにより、理論的に勾配消失や勾配爆発の問題を回避できます。
6. 渡された活性化関数の種類に応じて、対応する活性化関数オブジェクトを生成します。
7. ADAMアルゴリズムで使用するイテレーションカウンタをゼロに初期化します。
   

//+----------------------------------------------------------------------------+
//| Initialize the network                                                     |
//| layerConfig - array with the number of neurons in each layer               |
//| Returns the total number of weights needed, or 0 in case of an error       |
//+----------------------------------------------------------------------------+
int C_MLPa::Init (int &layerConfig [], int actFuncType, int seed)
{
  nLC = ArraySize (layerConfig);

  if (nLC < 2)
  {
    Print ("Network configuration error! Less than 2 layers!");
    return 0;
  }

  // Check configuration
  for (int i = 0; i < nLC; i++)
  {
    if (layerConfig [i] <= 0)
    {
      Print ("Network configuration error! Layer #" + string (i + 1) + " contains 0 neurons!");
      return 0;
    }
  }

  wLC = nLC - 1;
  ArrayCopy (layersSize, layerConfig, 0, 0, WHOLE_ARRAY);

  // Initialize neuron layers
  ArrayResize (nL, nLC);
  for (int i = 0; i < nLC; i++)
  {
    ArrayResize (nL [i].n, layersSize [i]);
  }

  // Initialize weight layers
  ArrayResize (wL, wLC);
  for (int w = 0; w < wLC; w++)
  {
    ArrayResize (wL [w].nOnL, layersSize [w]);
    for (int n = 0; n < layersSize [w]; n++)
    {
      ArrayResize (wL [w].nOnL [n].nOnR, layersSize [w + 1]);
    }
  }

  // Calculate the total number of weights
  wC = 0;
  for (int i = 0; i < nLC - 1; i++) wC += layersSize [i] * layersSize [i + 1] + layersSize [i + 1];

  // Initialize weights
  double weights [];  ArrayResize (weights, wC);

  srand (seed);
  
  //Xavier: U(-√(6/(n₁+n₂)), √(6/(n₁+n₂)))
  double n = sqrt (6.0 / (layersSize [0] + layersSize [nLC - 1]));
  for (int i = 0; i < wC; i++)
  {
    weights [i] = (2.0 * n) * (rand () / 32767.0) - n;
  }

  ImportWeights (weights);

  switch (actFuncType)
  {
    case eActACON:      actFunc = new C_ActACON      (); break;
    case eActAlgSigm:   actFunc = new C_ActAlgSigm   (); break;
    case eActBentIdent: actFunc = new C_ActBentIdent (); break;
    case eActRatSigm:   actFunc = new C_ActRatSigm   (); break;
    case eActSiLU:      actFunc = new C_ActSiLU      (); break;
    case eActSoftPlus:  actFunc = new C_ActSoftPlus  (); break;
    default:            actFunc = new C_ActTanh      (); break;
  }

  t = 0;
  return wC;
}
//——————————————————————————————————————————————————————————————————————————————

次に、ImportWeightsとExportWeightsの2つのメソッドを見ていきましょう。これらのメソッドは、多層パーセプトロンの重みとバイアスをインポートおよびエクスポートするために設計されています。ImportWeightsは、weights配列からニューラルネットワーク構造に重みとバイアスを読み込む役割を担います。

まず、渡されたweights配列のサイズがwC変数に格納された重みの数と一致するかを確認します。サイズが一致しない場合、メソッドはエラーを示すfalseを返します。

wCNT変数は、weights配列内の現在のインデックスを追跡するために使用されます。
層およびニューロンをループ処理します。

• 最初の層は入力層であり、重みや外側のループは、各層を順に処理します。入力層（インデックス0）は重みやバイアスを持たないため、2層目（インデックス1）から開始します。
• 内側のループは、現在の層の各ニューロンを順に処理します。
• 各ニューロンに対して、biasの値をweights配列から設定し、wCNTカウンタをインクリメントします。
• さらに入れ子のループで、前の層のすべてのニューロンを順に処理し、現在の層のニューロンと前の層のニューロンを接続する重みを設定します。

ExportWeights：このメソッドは、ニューラルネットワーク構造からweights配列へ重みとバイアスをエクスポートする役割を担います。メソッドのロジックはImportWeightsと類似しています。これら両方のメソッドにより、ネットワーククラスに関連して外部プログラムに重みとバイアスを保存することが可能となり、学習済みネットワークを将来使用することや、集団型などの外部最適化アルゴリズムを利用することも可能になります。

//+----------------------------------------------------------------------------+
//| Import network weights and biases                                          |
//+----------------------------------------------------------------------------+
bool C_MLPa::ImportWeights (double &weights [])
{
  if (ArraySize (weights) != wC) return false;

  int wCNT = 0;

  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      nL [ln].n [n].bias = weights [wCNT++];

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        wL [ln - 1].nOnL [w].nOnR [n].w = weights [wCNT++];
      }
    }
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

//+----------------------------------------------------------------------------+
//| Export network weights and biases                                          |
//+----------------------------------------------------------------------------+
bool C_MLPa::ExportWeights (double &weights [])
{
  ArrayResize (weights, wC);

  int wCNT = 0;

  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      weights [wCNT++] = nL [ln].n [n].bias;

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        weights [wCNT++] = wL [ln - 1].nOnL [w].nOnR [n].w;
      }
    }
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

ForwPropメソッド（順伝播）は、多層パーセプトロンの入力層から出力層までの全ての層の値を順に計算します。入力値を受け取り、隠れ層を通して処理し、出力値を生成します。パラメータは次のとおりです。

• inLayer []：ニューラルネットワークの入力値を格納する配列（図1では緑色で示されています）
• outLayer []：処理後に出力層の値が設定される配列（図1では黄色で示されています）
  

メソッドは、入力層ニューロンの活性化値を、inLayer配列から対応するニューロンにコピーすることで初期化します。

隠れ層および出力層の処理：

• 外側のループは、入力層（インデックス0）を除いたすべての層（インデックス1から）を順に反復します。
• 内側のループは、現在の層の各ニューロンを順に処理します。
• 各ニューロンについて、重み付き入力の総和を計算します。
• まず、ニューロンにバイアスを加えます。
• ネストされたループで前の層の全ニューロンを反復し、前の層のニューロンの出力値と対応する重みの積をvalに加えます。
• 総和を計算した後、活性化関数をvalに適用し、その結果を現在の層のニューロンの出力値として格納します。

すべての層を処理した後、最終層（出力層）の出力値をoutLayer配列にコピーします。

//+----------------------------------------------------------------------------+
//| Direct network pass                                                        |
//| Calculate the values of all layers sequentially from input to output       |
//+----------------------------------------------------------------------------+
void C_MLPa::ForwProp (double &inLayer  [],  // input values
                       double &outLayer [])  // output layer values
{
  double val;

  // Set the input layer activation values
  for (int n = 0; n < layersSize [0]; n++)
  {
    nL [0].n [n].out = inLayer [n];
  }

  // Handle hidden and output layers
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      val = nL [ln].n [n].bias;

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        val += nL [ln - 1].n [w].out * wL [ln - 1].nOnL [w].nOnR [n].w;
      }

      nL [ln].n [n].out = actFunc.Activ (val); // Apply activation function
    }
  }

  // Set the output layer values
  for (int n = 0; n < layersSize [nLC - 1]; n++) outLayer [n] = nL [nLC - 1].n [n].out;
}
//——————————————————————————————————————————————————————————————————————————————

BackPropメソッドは、多層パーセプトロンにおけるバックプロパゲーションを実装します。ADAM最適化アルゴリズムを用いて、出力層から入力層に向かってすべての層の重みとバイアスを更新します。動作の流れ

t変数は反復回数を追跡するためにインクリメントされ、ADAMの計算式で使用されます。

全層のデルタ計算

• 外側のループは、出力層から入力層に向かって層を逆順に反復します。
• 内側のループは、現在の層の各ニューロンを順に処理します。
• 現在の層が出力層の場合、デルタは誤差(errors[nCurr])と出力ニューロンの活性化関数の導関数の積として計算されます。
• 隠れ層の場合、デルタは次の層のデルタと対応する重みの積の合計として計算されます。
• その後、デルタを活性化関数の導関数で調整し、その結果をnL[ln].n[nCurr].deltaに格納します。

ADAMを用いたバイアスの更新

• 外側のループは、入力層を除く全層を順に処理します。
• 各ニューロンについて、バイアスのモーメントmとvをbeta1およびbeta2パラメータを用いて更新します。
• その後、補正されたモーメントm_hatとv_hatを計算します。
• 最後に、補正されたモーメントを用いてバイアスを更新します。

ADAMを用いた重みの更新

• 外側のループは、すべての重み層を順に処理します。
• 内側のループは、現在の層および次の層のニューロンを順に処理します。
• 各重みについて勾配を計算し、それを用いてmとvのモーメントを更新します。
• m_hatとv_hatの補正後のモーメントを用いて、重みを更新します。

//+----------------------------------------------------------------------------+
//| Backward network pass                                                      |
//| Update the weights and biases of all layers from output to input           |
//+----------------------------------------------------------------------------+
void C_MLPa::BackProp (double &errors [])
{
  t++;  // Increase the iteration counter

  double delta;     // current neuron delta
  double deltaNext; // delta of the neuron in the next layer connected to the current neuron
  double out;       // neuron value after applying the activation function
  double deriv;     // derivative
  double w;         // weight for connecting the current neuron to the neuron of the next layer

  // 1. Calculating deltas for all layers ----------------------------------------
  for (int ln = nLC - 1; ln > 0; ln--)                  // walk through layers in reverse order from output to input
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)        // iterate through the neurons of the current layer
    {
      if (ln == nLC - 1)
      {
        delta = errors [nCurr] * actFunc.Deriv (nL [ln].n [nCurr].out);
      }
      else
      {
        delta = 0.0;

        // Sum the products of the deltas of the next layer by the corresponding weights
        for (int nNext = 0; nNext < layersSize [ln + 1]; nNext++) // pass the neurons of the next layer in the usual order
        {
          deltaNext = nL [ln + 1].n [nNext].delta;
          w         = wL [ln].nOnL [nCurr].nOnR [nNext].w;
          delta    += deltaNext * w;
        }
      }

      // Delta considering the derivative of the sigmoid
      out   = nL [ln].n [nCurr].out;
      deriv = actFunc.Deriv (out);
      nL [ln].n [nCurr].delta = delta * deriv;
    }
  }

  // 2. Update biases using ADAM ------------------------------
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)
    {
      delta = nL [ln].n [nCurr].delta;

      // Update displacement moments
      nL [ln].n [nCurr].m = beta1 * nL [ln].n [nCurr].m + (1.0 - beta1) * delta;
      nL [ln].n [nCurr].v = beta2 * nL [ln].n [nCurr].v + (1.0 - beta2) * delta * delta;

      // Adjust displacement moments
      double m_hat = nL [ln].n [nCurr].m / (1.0 - pow (beta1, t));
      double v_hat = nL [ln].n [nCurr].v / (1.0 - pow (beta2, t));

      // Update bias
      nL [ln].n [nCurr].bias += alpha * m_hat / (sqrt (v_hat) + epsilon);
    }
  }

  // 3. Update weights using ADAM ---------------------------------
  for (int lw = 0; lw < wLC; lw++)
  {
    for (int nCurr = 0; nCurr < layersSize [lw]; nCurr++)
    {
      for (int nNext = 0; nNext < layersSize [lw + 1]; nNext++)
      {
        deltaNext = nL [lw + 1].n [nNext].delta;
        out       = nL [lw].n [nCurr].out;
        double gradient = deltaNext * out;

        // Update moments for weights
        wL [lw].nOnL [nCurr].nOnR [nNext].m = beta1 * wL [lw].nOnL [nCurr].nOnR [nNext].m + (1.0 - beta1) * gradient;
        wL [lw].nOnL [nCurr].nOnR [nNext].v = beta2 * wL [lw].nOnL [nCurr].nOnR [nNext].v + (1.0 - beta2) * gradient * gradient;

        // Adjust weight moments
        double m_hat = wL [lw].nOnL [nCurr].nOnR [nNext].m / (1.0 - pow (beta1, t));
        double v_hat = wL [lw].nOnL [nCurr].nOnR [nNext].v / (1.0 - pow (beta2, t));

        // Update weight
        wL [lw].nOnL [nCurr].nOnR [nNext].w += alpha * m_hat / (sqrt (v_hat) + epsilon);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

活性化関数を描画するためのスタンド用コード

このスタンドは、ニューラルネットワークで使用されるさまざまな活性化関数の正しい動作をテストし、それらをグラフの形で表示するために設計されています。得られた画像は、後の章でそれらの見た目を視覚的に評価するために使用されます。コード自体はシンプルで、詳細な説明は不要です。

#include <Graphics\Graphic.mqh>
#include <Math\AOs\NeuroNets\MLPa.mqh>

#define SIZE_X 750
#define SIZE_Y 200

//--- input parameters
input E_Act ACT = eActTanh;
input int   CNT = 10000;

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  ObjectDelete (ChartID (), "Test");
  double activ [];
  double deriv [];

  //----------------------------------------------------------------------------
  C_Base_ActFunc *act;
  switch (ACT)
  {
    default:            act = new C_ActTanh      (); break;
    case eActAlgSigm:   act = new C_ActAlgSigm   (); break;
    case eActRatSigm:   act = new C_ActRatSigm   (); break;
    
    case eActSoftPlus:  act = new C_ActSoftPlus  (); break;
    case eActBentIdent: act = new C_ActBentIdent (); break;
    case eActSiLU:      act = new C_ActSiLU      (); break;
    
    case eActACON:      act = new C_ActACON      (); break;
    case eActSnake:     act = new C_ActSnake     (); break;
    case eActSERF:      act = new C_ActSERF      (); break;
  }
  
  //----------------------------------------------------------------------------
  ActFuncTest (act, activ, deriv, CNT, -10, 10);
  
  //----------------------------------------------------------------------------
  CGraphic gr_test;
  gr_test.Create (0, "Test", 0, 0, 20, SIZE_X, SIZE_Y + 20);
  gr_test.YAxis ().Name (act.GetFuncName () + ": Value");
  gr_test.YAxis ().NameSize (13);
  gr_test.HistorySymbolSize (10);
  gr_test.CurveAdd (activ, ColorToARGB (clrRed,  255), CURVE_LINES, "activ");
  gr_test.CurveAdd (deriv, ColorToARGB (clrBlue, 255), CURVE_LINES, "deriv");
  gr_test.CurvePlotAll ();
  gr_test.Redraw (true);
  gr_test.Update ();
  
  //----------------------------------------------------------------------------
  delete act;
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void ActFuncTest (C_Base_ActFunc &act, double &arrayAct [], double &arrayDer [], int testCount, double min, double max)
{
  Print (act.GetFuncName (), " [", min, "; ", max, "]");
  Print (act.Activ (min), " ", act.Activ (0), " ", act.Activ (max));
  Print (act.Deriv (min), " ", act.Deriv (0), " ", act.Deriv (max));

  ArrayResize (arrayAct, testCount);
  ArrayResize (arrayDer, testCount);
  double x    = 0.0;
  double step = (max - min) / testCount;
  
  for (int i = 0; i < testCount; i++)
  {
    x = min + step * i;

    arrayAct [i] = act.Activ (x);
    arrayDer [i] = act.Deriv (x);
  }
}
//——————————————————————————————————————————————————————————————————————————————

活性化関数クラスのコード

ニューラルネットワークでは、さまざまな種類のニューロン活性化関数が使用されています。私は、よく知られている双曲線正接関数(tanh)だけでなく、Snake活性化関数のようなあまり知られていない関数も含め、見た目や特性が非常に似ている関数は除外した上で、いくつかの関数を選定いたしました。これらの活性化関数は、便宜上次の三つのグループに分類することができます。

1. シグモイド関数
2. 非線形スイッチ関数
3. 周期関数

ニューロンの活性化関数を表す基底クラスとしてC_Base_ActFuncを実装します。このクラスには、 活性化を計算するためのActiv関数と、導関数を計算するためのDeriv関数という2つの仮想関数が含まれます。また、GetFuncName()メソッドは、protectedメンバ変数funcNameに格納された活性化関数の名称を返します。このクラスは、具体的な活性化関数を実装するための継承用クラスとして設計されています。活性化関数オブジェクトを生成することで、if文やswitch文を何度も使用する必要がなくなり、計算を高速化することができます。

//——————————————————————————————————————————————————————————————————————————————
// Base class of the neuron activation function
class C_Base_ActFunc
{
  public:
  virtual double Activ (double inp) = 0; // Virtual activation function
  virtual double Deriv (double inp) = 0; // Virtual derivative function
  string         GetFuncName () {return funcName;}
  protected:
  string funcName;
};
//——————————————————————————————————————————————————————————————————————————————

C_ActTanhは、双曲線正接活性化関数およびその導関数を実装し、C_Base_ActFunc基底クラスを継承します。クラスのコンストラクタでは、活性化関数名をfuncName変数にActTanhとして設定します。以下が活性化メソッドです。

• Activ(double x)メソッドは、式「f(x) = 2 / (1 + exp ( − 2  ⋅  (x)) − 1.」を用いて双曲線正接活性化関数の値を計算します。この式により、入力値xは−1から1の範囲に変換されます。

以下が導関数メソッドです。

• Deriv(double x)メソッドは、活性化関数の導関数を計算します。双曲線正接関数の導関数は式「f′(x) = 1 − (f (x)) ^ 2」で表されます。ここで、f(x)は現在の入力値xに対して計算された活性化関数の値です。 この導関数は、入力値に対して関数の値がどの程度変化するか、すなわち関数の変化率を示します。

//——————————————————————————————————————————————————————————————————————————————
// Hyperbolic tangent
class C_ActTanh : public C_Base_ActFunc
{
  public:
  C_ActTanh () {funcName = "ActTanh";}

  double Activ (double x)
  {
    return 2.0 / (1.0 + exp (-2 * (x))) - 1.0;
  }

  double Deriv (double x)
  {
    //1 - (f(x))^2
    double fx = Activ (x);
    return 1.0 - fx * fx;
  }
};
//——————————————————————————————————————————————————————————————————————————————

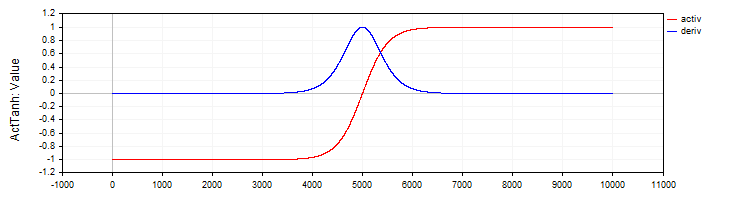
図2：双曲線正接とその導関数

C_ActAlgSigmクラスは、C_ActTanhクラスと同様に、活性化関数として代数的シグモイド関数を実装します。

//——————————————————————————————————————————————————————————————————————————————
// Algebraic sigmoid
class C_ActAlgSigm : public C_Base_ActFunc
{
  public:
  C_ActAlgSigm () {funcName = "ActAlgSigm";}

  double Activ (double x)
  {
    return x / sqrt (1.0 + x * x);
  }

  double Deriv (double x)
  {
    // (1 / sqrt (1 + x * x))^3
    double d = 1.0 / sqrt (1.0 + x * x);
    return d * d * d;
  }
};
//——————————————————————————————————————————————————————————————————————————————

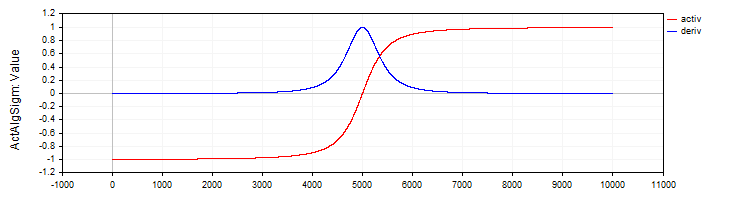
図3：代数的シグモイドとその導関数

C_ActRatSigmクラスは、有理型シグモイド関数を活性化関数として実装し、その計算および導関数を求めるメソッドを備えています。

//——————————————————————————————————————————————————————————————————————————————
// Rational sigmoid
class C_ActRatSigm : public C_Base_ActFunc
{
  public:
  C_ActRatSigm () {funcName = "ActRatSigm";}

  double Activ (double x)
  {
    return x / (1.0 + fabs (x));
  }

  double Deriv (double x)
  {
    //1 / (1 + abs (x))^2
    double d = 1.0 + fabs (x);
    return 1.0 / (d * d);
  }
};
//——————————————————————————————————————————————————————————————————————————————

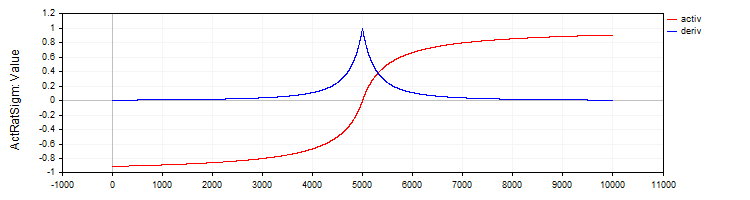
図4：有理型シグモイドとその導関数

C_ActSoftPlusクラスは、Softplus活性化関数とその導関数を実装します。

//——————————————————————————————————————————————————————————————————————————————
// Softplus
class C_ActSoftPlus : public C_Base_ActFunc
{
  public:
  C_ActSoftPlus () {funcName = "ActSoftPlus";}

  double Activ (double x)
  {
    return log (1.0 + exp (x));
  }

  double Deriv (double x)
  {
    return 1.0 / (1.0 + exp (-x));
  }
};
//——————————————————————————————————————————————————————————————————————————————

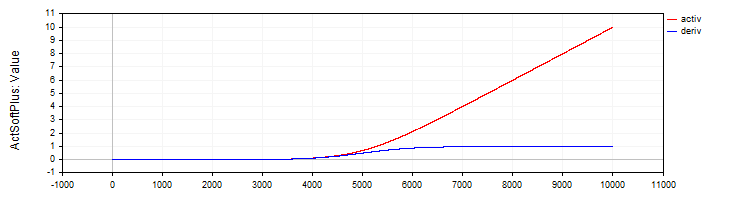
図5：SoftPlus関数とその導関数

C_ActBentIdentクラスは、Bent Identity活性化関数とその導関数を実装します。

//——————————————————————————————————————————————————————————————————————————————
// Bent Identity
class C_ActBentIdent : public C_Base_ActFunc
{
  public:
  C_ActBentIdent () {funcName = "ActBentIdent";}

  double Activ (double x)
  {
    return (sqrt (x * x + 1.0) - 1.0) / 2.0 + x;
  }

  double Deriv (double x)
  {
    return x / (2.0 * sqrt (x * x + 1.0)) + 1.0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

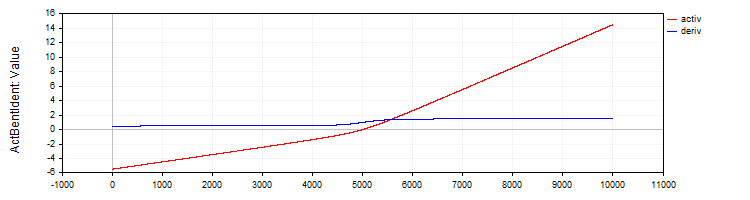
図6：Bent Identity関数とその導関数

C_ActSiLUクラスは、SiLU活性化関数とその導関数の実装を提供します。

//——————————————————————————————————————————————————————————————————————————————
// SiLU (Swish)
class C_ActSiLU : public C_Base_ActFunc
{
  public:
  C_ActSiLU () {funcName = "ActSiLU";}

  double Activ (double x)
  {
    return x / (1.0 + exp (-x));
  }

  double Deriv (double x)
  {
    if (x == 0.0) return 0.5;

    // f(x) + (f(x)*(1 - f(x)))/ x
    double fx = Activ (x);
    return fx + (fx * (1.0 - fx)) / x;
  }
};
//——————————————————————————————————————————————————————————————————————————————

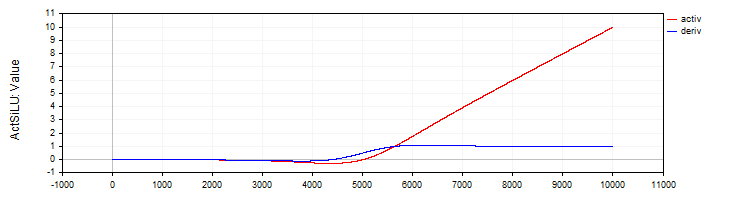
図7：SiLU関数とその導関数

C_ActACONは、ACON活性化関数とその導関数を実装します。

//——————————————————————————————————————————————————————————————————————————————
// ACON
class C_ActACON : public C_Base_ActFunc
{
  public:
  C_ActACON () {funcName = "ActACON";}

  double Activ (double x)
  {
    return (x * cos (x) + sin (x)) / (1.0 + fabs (x));
  }

  double Deriv (double x)
  {
    if (x == 0.0) return 2.0;

    //[2 * cos(x) - x * sin(x)] / [|x| + 1] - x * (sin(x) + x * cos(x)) / [|x| * ((|x| + 1)²)]
    double sinX   = sin  (x);
    double cosX   = cos  (x);
    double fabsX  = fabs (x);
    double fabsXp = fabsX + 1.0;

    // Divide the equation into two parts
    double part1 = (2.0 * cosX - x * sinX) / fabsXp;
    double part2 = -x * (sinX + x * cosX) / (fabsX * fabsXp * fabsXp);
    return part1 + part2;
  }
};
//——————————————————————————————————————————————————————————————————————————————

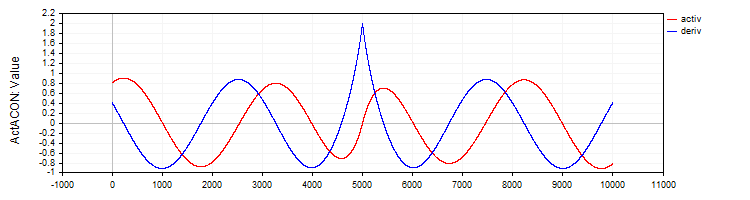
図8：ACON関数とその導関数

C_ActSERFクラスは、SERF活性化関数とその導関数を実装します。

//——————————————————————————————————————————————————————————————————————————————
// SERF (sigmoid-weighted exponential straightening function)
class C_ActSERF : public C_Base_ActFunc
{
  public:
  C_ActSERF ()
  {
    alpha    = 0.5;
    funcName = "ActSERF";
  }

  double Activ (double x)
  {
    double sigmoid = 1.0 / (1.0 + exp (-alpha * x));

    if (x >= 0) return sigmoid * x;
    else return sigmoid * (exp (x) - 1.0);
  }

  double Deriv (double x)
  {
    double sigmoid = 1.0 / (1.0 + exp (-alpha * x));
    double sigmoidDeriv = alpha * sigmoid * (1.0 - sigmoid);
    double e = exp (x);
    if (x >= 0) return sigmoid + x * sigmoidDeriv;
    else return sigmoid * e + (e - 1.0) * sigmoidDeriv;
  }

  private:
  double alpha;
};
//——————————————————————————————————————————————————————————————————————————————

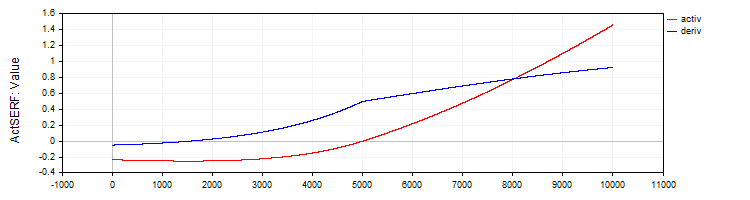
図9：SERF関数とその導関数

C_ActSNAKEクラスは、SNAKE活性化関数とその導関数を実装します。

//——————————————————————————————————————————————————————————————————————————————
// Snake (periodic activation function)
class C_ActSnake : public C_Base_ActFunc
{
  public:
  C_ActSnake ()
  {
    frequency = 1;
    funcName  = "ActSnake";
  }

  double Activ (double x)
  {
    double sinx = sin (frequency * x);
    return x + sinx * sinx;
  }

  double Deriv (double x)
  {
    double fx = frequency * x;
    return 1.0 + 2.0 * sin (fx) * cos (fx) * frequency;
  }

  private:
  double frequency;
};
//——————————————————————————————————————————————————————————————————————————————

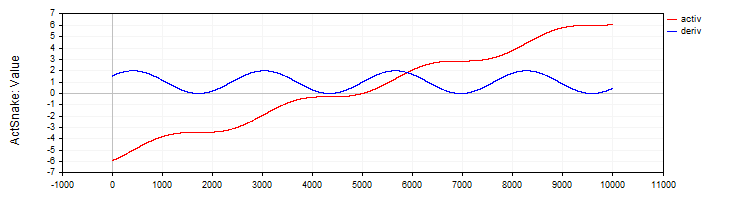
図10：SNAKE関数とその導関数

活性化関数のテスト

ここでは、異なる活性化関数を用いた場合に、MLPネットワークがどのように学習されるかを確認します。活性化関数の複雑さが最適化アルゴリズムに与える影響は、1-1-1構成（1入力・1中間層・1出力）のMLPを用い、単一の学習例（1つの入力値と1つの目標値）で明確に示すことができます。

一見すると、このような単純な課題がなぜ興味深いのか疑問に思われるかもしれません。しかし、ここには重要な方法論上のポイントがあります。単一のデータ点のみを使用することで、活性化関数自体の複雑さおよびその最適化への影響を切り離して検証することが可能になります。大規模なデータセットを用いる場合、学習にはデータの分布、サンプル間の相互依存関係、そしてそれらが活性化関数を通過する際の影響など、多くの要因が関与します。単一の点を用いることにより、これらの外的要因を取り除き、最適化アルゴリズムが特定の活性化関数を扱う難易度にのみ焦点を当てることができます。

注目すべき点は、補間された関数の単一点を通過するニューラルネットワークには、無限に多くの重みの組み合わせが存在し得るということです。これは一見信じがたいかもしれませんが、単純な関係式「in * w + b = out」から導かれます。ここで、inはネットワークの入力、wは重み、bはバイアス、outは出力を表します（1-1構成の場合）。

この構成自体には問題はありませんが、もう1層追加した1-1-1構成にすると、事情が大きく変わります。この場合、最適化アルゴリズムにとって、最も単純な問題でさえ非自明となります。なぜなら、解探索空間が大幅に複雑化し、中間層とその活性化関数を介して、適切な重みの組み合わせを見つけ出す必要があるためです。この複雑さこそが、異なる最適化アルゴリズムが、各種活性化関数のもとでどの程度効率的に重み調整をおこなえるかを評価するうえで有効な基準となります。

以下に、ADAMアルゴリズムの古典的実装および集団型ADAMmによる結果を示します。いずれのアルゴリズムも10,000回の反復を実施しています。集団型アルゴリズムの場合は、集団の存在を考慮しつつ、ニューラルネットワークの総計算回数が同等となるよう調整しました。出力結果には、擬似乱数生成器のシード値（問題のある学習過程を再現するため）、最良の結果を得た反復回数、1000の倍数となるエポック時点での結果が表示されています。

重みの初期化には、ADAMではXavier法による乱数、ADAMmでは[-10, 10]の範囲の乱数を使用しました。複数のシードでテストをおこない、最悪の結果を選定しています。重み探索は、最大反復回数に到達するか、または誤差が0.000001未満に減少する時点で終了しました。

シグモイド活性化関数の結果の表

Tanh	AlgSigm	RatSigm
MLP config:1|1|1, Weights:4, Activation func: eActTanh, Seed:4 -----Integrated ADAM----- 0:0.2415125490594974, 0:0.24151254905949734 0:0.2415125490594974, 1000:0.24987227299268625 0:0.2415125490594974, 2000:0.24999778562849811 0:0.2415125490594974, 3000:0.24999995996010888 0:0.2415125490594974, 4000:0.2499999992693791 0:0.2415125490594974, 5000:0.24999999998663514 0:0.2415125490594974, 6000:0.2499999999997553 0:0.2415125490594974, 7000:0.24999999999999556 0:0.2415125490594974, 8000:0.25 0:0.2415125490594974, 9000:0.25 Best result iteration:0, Err:0.241513 -----Population-based ADAMm----- 0:0.2499999999999871 Best result iteration:883, Err:0.000001	MLP config:1|1|1, Weights:4, Activation func: eActAlgSigm, Seed:4 -----Integrated ADAM----- 0:0.1878131682539310, 0:0.18781316825393096 0:0.1878131682539310, 1000:0.22880505258129305 0:0.1878131682539310, 2000:0.2395439537933131 0:0.1878131682539310, 3000:0.24376284285887292 0:0.1878131682539310, 4000:0.24584964230029535 0:0.1878131682539310, 5000:0.2470364071634453 0:0.1878131682539310, 6000:0.24777681648987268 0:0.1878131682539310, 7000:0.2482702131676117 0:0.1878131682539310, 8000:0.24861563983949608 0:0.1878131682539310, 9000:0.2488669473265396 Best result iteration:0, Err:0.187813 -----Population-based ADAMm----- 0:0.2481251241755712 1000:0.0000009070157679 Best result iteration:1000, Err:0.000001	MLP config:1|1|1, Weights:4, Activation func: eActRatSigm, Seed:4 -----Integrated ADAM----- 0:0.0354471509280691, 0:0.03544715092806905 0:0.0354471509280691, 1000:0.10064226929576263 0:0.0354471509280691, 2000:0.13866170841306655 0:0.0354471509280691, 3000:0.16067944018111643 0:0.0354471509280691, 4000:0.17502946224977484 0:0.0354471509280691, 5000:0.18520767592761297 0:0.0354471509280691, 6000:0.19285431843628092 0:0.0354471509280691, 7000:0.1988366186290051 0:0.0354471509280691, 8000:0.20365853142896836 0:0.0354471509280691, 9000:0.20763502064394074 Best result iteration:0, Err:0.035447 -----Population-based ADAMm----- 0:0.1928944265733889 Best result iteration:688, Err:0.000000

SiLU型活性化関数の結果表

SoftPlus	BentIdent	SiLU
MLP config:1|1|1, Weights:4, Activation func: eActSoftPlus, Seed:2 -----Integrated ADAM----- 0:0.5380138004155748, 0:0.5380138004155747 0:0.5380138004155748, 1000:131.77685264891647 0:0.5380138004155748, 2000:1996.1250363225556 0:0.5380138004155748, 3000:8050.259717531171 0:0.5380138004155748, 4000:20321.169969814575 0:0.5380138004155748, 5000:40601.21872791767 0:0.5380138004155748, 6000:70655.44591598355 0:0.5380138004155748, 7000:112311.81150857621 0:0.5380138004155748, 8000:167489.98562842538 0:0.5380138004155748, 9000:238207.27978678182 Best result iteration:0, Err:0.538014 -----Population-based ADAMm----- 0:18.4801637203493884 778:0.0000022070092175 Best result iteration:1176, Err:0.000001	MLP config:1|1|1, Weights:4, Activation func: eActBentIdent, Seed:4 -----Integrated ADAM----- 0:15.1221330593320857, 0:15.122133059332086 0:15.1221330593320857, 1000:185.646717568436 0:15.1221330593320857, 2000:1003.1026112225994 0:15.1221330593320857, 3000:2955.8393027057205 0:15.1221330593320857, 4000:6429.902382962495 0:15.1221330593320857, 5000:11774.781156010686 0:15.1221330593320857, 6000:19342.379583340015 0:15.1221330593320857, 7000:29501.355075464813 0:15.1221330593320857, 8000:42640.534930000824 0:15.1221330593320857, 9000:59168.850722337185 Best result iteration:0, Err:15.122133 -----Population-based ADAMm----- 0:7818.0964949082390376 Best result iteration:15, Err:0.000001	MLP config:1|1|1, Weights:4, Activation func: eActSiLU, Seed:2 -----Integrated ADAM----- 0:0.0021199944516222, 0:0.0021199944516222444 0:0.0021199944516222, 1000:4.924850697388685 0:0.0021199944516222, 2000:14.827133542234415 0:0.0021199944516222, 3000:28.814259008218087 0:0.0021199944516222, 4000:45.93517121925276 0:0.0021199944516222, 5000:65.82077308420028 0:0.0021199944516222, 6000:88.26782602934948 0:0.0021199944516222, 7000:113.15535264604428 0:0.0021199944516222, 8000:140.41067538093935 0:0.0021199944516222, 9000:169.9878269747845 Best result iteration:0, Err:0.002120 -----Population-based ADAMm----- 0:17.2288020548757288 1000:0.0000030959186317 Best result iteration:1150, Err:0.000001

周期的活性化関数の結果の表

ACON	SERF	Snake
MLP config:1|1|1, Weights:4, Activation func: eActACON, Seed:3 -----Integrated ADAM----- 0:0.8183728267492676, 0:0.8183728267492675 160:0.5853150801288914, 1000:1.2003151947973498 2000:0.0177702331540612, 2000:0.017770233154061187 3000:0.0055801976952827, 3000:0.005580197695282676 4000:0.0023096724537356, 4000:0.002309672453735598 5000:0.0010238849157595, 5000:0.0010238849157594616 6000:0.0004581612824611, 6000:0.0004581612824611273 7000:0.0002019092359805, 7000:0.00020190923598049711 8000:0.0000867118074097, 8000:0.00008671180740972474 9000:0.0000361764073840, 9000:0.00003617640738397845 Best result iteration:9999, Err:0.000015 -----Population-based ADAMm----- 0:1.3784017183806672 Best result iteration:481, Err:0.000000	MLP config:1|1|1, Weights:4, Activation func: eActSERF, Seed:4 -----Integrated ADAM----- 0:0.2415125490594974, 0:0.24151254905949734 0:0.2415125490594974, 1000:0.24987227299268625 0:0.2415125490594974, 2000:0.24999778562849811 0:0.2415125490594974, 3000:0.24999995996010888 0:0.2415125490594974, 4000:0.2499999992693791 0:0.2415125490594974, 5000:0.24999999998663514 0:0.2415125490594974, 6000:0.2499999999997553 0:0.2415125490594974, 7000:0.24999999999999556 0:0.2415125490594974, 8000:0.25 0:0.2415125490594974, 9000:0.25 Best result iteration:0, Err:0.241513 -----Population-based ADAMm----- 0:0.2499999999999871 Best result iteration:883, Err:0.000001	MLP config:1|1|1, Weights:4, Activation func: eActSnake, Seed:4 -----Integrated ADAM----- 0:0.2415125490594974, 0:0.24151254905949734 0:0.2415125490594974, 1000:0.24987227299268625 0:0.2415125490594974, 2000:0.24999778562849811 0:0.2415125490594974, 3000:0.24999995996010888 0:0.2415125490594974, 4000:0.2499999992693791 0:0.2415125490594974, 5000:0.24999999998663514 0:0.2415125490594974, 6000:0.2499999999997553 0:0.2415125490594974, 7000:0.24999999999999556 0:0.2415125490594974, 8000:0.25 0:0.2415125490594974, 9000:0.25 Best result iteration:0, Err:0.241513 -----Population-based ADAMm----- 0:0.2499999999999871 Best result iteration:883, Err:0.000001

ここまでの結果から、古典的な勾配法ADAMと集団型ADAMmにおける活性化関数の複雑さについて、いくつかの予備的な結論を導くことができます。通常のADAMは、活性化関数の勾配に関する直接的な情報を持っています。つまり、最急降下の方向を文字通り知っているにもかかわらず、この一見非常に単純な課題をうまく扱うことができませんでした。ADAMにとって最も単純で扱いやすかった関数はACONでした。この関数に対してのみ、ADAMは一貫して誤差を最小化することができました。一方で、SiLUのような関数はADAMにとって問題となり、誤差が減少しないどころか急激に増加する結果となりました。これは明らかに、ADAMが重みやバイアスに対する境界条件を持たないために、誤った方向に最適化を進めてしまい、重みが増大したことを示しています。その結果、重み値は抑制されることなく自由に発散し、まるで活性化関数の導関数という「風」に吹き飛ばされるかのように振る舞いました。

さらに、層内のニューロン数を増やすとこの問題はより深刻になります。なぜなら、各ニューロンは前の層の出力に対応する重みとの積の総和を入力として受け取るため、その総和が非常に大きくなり、指数関数の計算が正しくおこなえない状況が発生するためです。

一方で、集団型ADAMmにとっては、これらのどの活性化関数も問題とはなりませんでした。すべての関数において安定的に収束し、わずかに1000回を超える反復が必要となった関数もありましたが、全体として一貫した動作を示しました。

活性化関数クラス、MLPおよびADAMの改良

ニューラルネットワーク内で重みが発散してしまう問題を修正するために、活性化関数クラスに変更を加えます。この変更により、各関数の出力範囲（境界）を追跡できるようになり、ニューロンに渡される入力値の総和が過剰に大きくなることを防ぎ、さらに重みおよびバイアス値そのものの範囲を制限できるようになります。

具体的には、基底クラスにGetBoundUpおよびGetBoundLoメソッドを追加します。これらのメソッドは、それぞれ対応する活性化関数の上限値と下限値を取得するためのインターフェースを提供し、他のクラスや関数が許容範囲に関する情報へアクセスできるようにします。

以下に、基底クラスおよび双曲線正接活性化関数クラスに一部変更を加えたコード例を示します。他の活性化関数クラスについても同様に、それぞれの関数特性に応じた境界値を設定して実装します。

//——————————————————————————————————————————————————————————————————————————————
// Base class of the neuron activation function
class C_Base_ActFunc
{
  public:
  double         GetBoundUp  () { return boundUp;}
  double         GetBoundLo  () { return boundLo;}
  protected:
  double boundUp;  // upper bound of the input range
  double boundLo;  // lower bound of the input range
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Hyperbolic tangent
class C_ActTanh : public C_Base_ActFunc
{
  public:
  C_ActTanh ()
  {
    boundUp  =  6.0;
    boundLo  = -6.0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

ニューロンの活性化関数に値を入力する前に、合計値(sum)が指定された境界を超えないようにするための検証処理を、MLPの順伝播メソッドに追加します。この検証によって、合計値が設定された範囲を超えて増加することを防止します。境界値を超えて合計を大きくすることには意味がなく、むしろ非効率です。さらに、この仕組みにより、層内に多数のニューロンを持つネットワーク構成において、合計計算の途中で早期に処理を打ち切ることが可能になります。これにより、計算速度を大幅に向上させることができます。

上限チェック：次のコードスニペットは、合計値が設定された上限を超えていないかを確認する処理を示しています。もし現在の合計値が上限を超えた場合、その値を上限値に固定し、ループの実行を終了します。下限値についても同様の方法でチェックをおこないます。

//+----------------------------------------------------------------------------+
//| Direct network pass                                                        |
//| Calculate the values of all layers sequentially from input to output       |
//+----------------------------------------------------------------------------+
void C_MLPa::ForwProp (double &inLayer  [],  // input values
                       double &outLayer [])  // output layer values
{
  double val;

  // Set the input layer activation values
  for (int n = 0; n < layersSize [0]; n++)
  {
    nL [0].n [n].out = inLayer [n];
  }

  // Handle hidden and output layers
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      val = nL [ln].n [n].bias;

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        val += nL [ln - 1].n [w].out * wL [ln - 1].nOnL [w].nOnR [n].w;

        if (val >  actFunc.GetBoundUp ())
        {
          val =  actFunc.GetBoundUp ();
          break;
        }
        if (val < actFunc.GetBoundLo ())
        {
          val = actFunc.GetBoundLo ();
          break;
        }
      }

      nL [ln].n [n].out = actFunc.Activ (val); // Apply activation function
    }
  }

  // Set the output layer values
  for (int n = 0; n < layersSize [nLC - 1]; n++) outLayer [n] = nL [nLC - 1].n [n].out;
}
//——————————————————————————————————————————————————————————————————————————————

次に、境界の検証コードをバックプロパゲーションメソッドに追加します。これらの追加処理は、与えられた境界から逆の境界へバイアスおよび重みの値を反射させるロジックを実装します。値が許容範囲を外れないようにすることが必要であり、重みやバイアスの制御不能な増減を防ぎます。

単純に境界で値を切り捨てるだけでは、学習が停滞してしまいます。重みが単純に境界に当たってしまい、重みを変更できなくなるためです。まさにそのような状況を防ぐために、値の切り捨てではなく反射を実装しています。これにより、重みやバイアスを調整する際に、「再活性化」や一種の「振動」を与えることが可能になります。

//+----------------------------------------------------------------------------+
//| Backward network pass                                                      |
//| Update the weights and biases of all layers from output to input           |
//+----------------------------------------------------------------------------+
void C_MLPa::BackProp (double &errors [])
{
  t++;  // Increase the iteration counter

  double delta;     // current neuron delta
  double deltaNext; // delta of the neuron in the next layer connected to the current neuron
  double out;       // neuron value after applying the activation function
  double deriv;     // derivative
  double w;         // weight for connecting the current neuron to the neuron of the next layer
  double bias;      // bias

  // 1. Calculating deltas for all layers ----------------------------------------
  for (int ln = nLC - 1; ln > 0; ln--)                  // walk through layers in reverse order from output to input
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)        // iterate through the neurons of the current layer
    {
      if (ln == nLC - 1)
      {
        delta = errors [nCurr] * actFunc.Deriv (nL [ln].n [nCurr].out);
      }
      else
      {
        delta = 0.0;

        // Sum the products of the deltas of the next layer by the corresponding weights
        for (int nNext = 0; nNext < layersSize [ln + 1]; nNext++) // pass the neurons of the next layer in the usual order
        {
          deltaNext = nL [ln + 1].n [nNext].delta;
          w         = wL [ln].nOnL [nCurr].nOnR [nNext].w;
          delta    += deltaNext * w;
        }
      }

      // Delta considering the derivative of the sigmoid
      out   = nL [ln].n [nCurr].out;
      deriv = actFunc.Deriv (out);
      nL [ln].n [nCurr].delta = delta * deriv;
    }
  }

  // 2. Update biases using ADAM ------------------------------
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)
    {
      delta = nL [ln].n [nCurr].delta;

      // Update displacement moments
      nL [ln].n [nCurr].m = beta1 * nL [ln].n [nCurr].m + (1.0 - beta1) * delta;
      nL [ln].n [nCurr].v = beta2 * nL [ln].n [nCurr].v + (1.0 - beta2) * delta * delta;

      // Adjust displacement moments
      double m_hat = nL [ln].n [nCurr].m / (1.0 - pow (beta1, t));
      double v_hat = nL [ln].n [nCurr].v / (1.0 - pow (beta2, t));

      // Update bias
      nL [ln].n [nCurr].bias += alpha * m_hat / (sqrt (v_hat) + epsilon);
      bias = nL [ln].n [nCurr].bias;

      if (bias < actFunc.GetBoundLo ())
      {
        nL [ln].n [nCurr].bias = actFunc.GetBoundUp () - (actFunc.GetBoundLo () - bias);  // reflect from the bottom border 
      }
      else
        if (bias > actFunc.GetBoundUp ())
        {
          nL [ln].n [nCurr].bias = actFunc.GetBoundLo () + (bias - actFunc.GetBoundUp ());  // reflect from the upper border
        }
    }
  }

  // 3. Update weights using ADAM ---------------------------------
  for (int lw = 0; lw < wLC; lw++)
  {
    for (int nCurr = 0; nCurr < layersSize [lw]; nCurr++)
    {
      for (int nNext = 0; nNext < layersSize [lw + 1]; nNext++)
      {
        deltaNext = nL [lw + 1].n [nNext].delta;
        out       = nL [lw].n [nCurr].out;
        double gradient = deltaNext * out;

        // Update moments for weights
        wL [lw].nOnL [nCurr].nOnR [nNext].m = beta1 * wL [lw].nOnL [nCurr].nOnR [nNext].m + (1.0 - beta1) * gradient;
        wL [lw].nOnL [nCurr].nOnR [nNext].v = beta2 * wL [lw].nOnL [nCurr].nOnR [nNext].v + (1.0 - beta2) * gradient * gradient;

        // Adjust weight moments
        double m_hat = wL [lw].nOnL [nCurr].nOnR [nNext].m / (1.0 - pow (beta1, t));
        double v_hat = wL [lw].nOnL [nCurr].nOnR [nNext].v / (1.0 - pow (beta2, t));

        // Update weight
        wL [lw].nOnL [nCurr].nOnR [nNext].w += alpha * m_hat / (sqrt (v_hat) + epsilon);
        w = wL [lw].nOnL [nCurr].nOnR [nNext].w;

        if (w < actFunc.GetBoundLo ())
        {
          wL [lw].nOnL [nCurr].nOnR [nNext].w = actFunc.GetBoundUp () - (actFunc.GetBoundLo () - w);  // reflect from the lower border
        }
        else
          if (w > actFunc.GetBoundUp ())
          {
            wL [lw].nOnL [nCurr].nOnR [nNext].w = actFunc.GetBoundLo () + (w - actFunc.GetBoundUp ());  // reflect from the upper border
          }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

では、先ほどと同じテストを繰り返し、得られた結果を確認します。現在は、重みの発散はなく、学習中に誤差が雪崩のように増大することもありません。

シグモイド活性化関数の結果の表

Tanh	AlgSigm	RatSigm
MLP config:1|1|1, Weights:4, Activation func: eActTanh, Seed:2 -----Integrated ADAM----- 0:0.0169277701441132, 0:0.016927770144113192 0:0.0169277701441132, 1000:0.24726166610109795 0:0.0169277701441132, 2000:0.24996248252671016 0:0.0169277701441132, 3000:0.2499877118017991 0:0.0169277701441132, 4000:0.2260068617570163 0:0.0169277701441132, 5000:2.2499589217599363 0:0.0169277701441132, 6000:2.2499631351033904 0:0.0169277701441132, 7000:2.248459789732414 0:0.0169277701441132, 8000:2.146138260175548 0:0.0169277701441132, 9000:0.15279792149898394 Best result iteration:0, Err:0.016928 -----Population-based ADAMm----- 0:0.2491964938729135 1000:0.0000010386817829 Best result iteration:1050, Err:0.000001	MLP config:1|1|1, Weights:4, Activation func: eActAlgSigm, Seed:2 -----Integrated ADAM----- 0:0.0095411465043040, 0:0.009541146504303972 0:0.0095411465043040, 1000:0.20977102640908893 0:0.0095411465043040, 2000:0.23464558094398064 0:0.0095411465043040, 3000:0.23657904914082925 0:0.0095411465043040, 4000:0.17812555648593617 0:0.0095411465043040, 5000:2.1749975763135927 0:0.0095411465043040, 6000:2.2093668968051166 0:0.0095411465043040, 7000:2.1657244506071813 0:0.0095411465043040, 8000:1.9330415523200173 0:0.0095411465043040, 9000:0.10441382194622865 Best result iteration:0, Err:0.009541 -----Population-based ADAMm----- 0:0.2201830630768654 Best result iteration:750, Err:0.000001	MLP config:1|1|1, Weights:4, Activation func: eActRatSigm, Seed:1 -----Integrated ADAM----- 0:1.2866075458561122, 0:1.2866075458561121 1000:0.2796061866784148, 1000:0.2796061866784148 2000:0.0450819127087337, 2000:0.04508191270873367 3000:0.0200306843648248, 3000:0.020030684364824806 4000:0.0098744349153286, 4000:0.009874434915328582 5000:0.0049448920462547, 5000:0.00494489204625467 6000:0.0024344513388710, 6000:0.00243445133887102 7000:0.0011602603038120, 7000:0.0011602603038120354 8000:0.0005316894732581, 8000:0.0005316894732581081 9000:0.0002339388712666, 9000:0.00023393887126662818 Best result iteration:9999, Err:0.000099 -----Population-based ADAMm----- 0:1.8418367346938778 Best result iteration:645, Err:0.000000

SiLU型活性化関数の結果表

SoftPlus	BentIdent	SiLU
MLP config:1|1|1, Weights:4, Activation func: eActSoftPlus, Seed:2 -----Integrated ADAM----- 0:0.5380138004155748, 0:0.5380138004155747 0:0.5380138004155748, 1000:12.377378915308087 0:0.5380138004155748, 2000:12.377378915308087 3000:0.1996421769021168, 3000:0.19964217690211675 4000:0.1985425345613517, 4000:0.19854253456135168 5000:0.1966512639256550, 5000:0.19665126392565502 6000:0.1933509943676914, 6000:0.1933509943676914 7000:0.1874142582090466, 7000:0.18741425820904659 8000:0.1762132792048514, 8000:0.17621327920485136 9000:0.1538331138702293, 9000:0.15383311387022927 Best result iteration:9999, Err:0.109364 -----Population-based ADAMm----- 0:12.3773789153080873 Best result iteration:677, Err:0.000001	MLP config:1|1|1, Weights:4, Activation func: eActBentIdent, Seed:4 -----Integrated ADAM----- 0:15.1221330593320857, 0:15.122133059332086 0:15.1221330593320857, 1000:25.619316876852988 1922:8.6344718719116980, 2000:8.634471871911698 1922:8.6344718719116980, 3000:8.634471871911698 1922:8.6344718719116980, 4000:8.634471871911698 1922:8.6344718719116980, 5000:8.634471871911698 1922:8.6344718719116980, 6000:8.634471871911698 6652:4.3033564303197833, 7000:8.634471871911698 6652:4.3033564303197833, 8000:8.634471871911698 6652:4.3033564303197833, 9000:7.11489380279475 Best result iteration:9999, Err:3.589207 -----Population-based ADAMm----- 0:25.6193168768529880 Best result iteration:15, Err:0.000001	MLP config:1|1|1, Weights:4, Activation func: eActSiLU, Seed:4 -----Integrated ADAM----- 0:0.6585816582701970, 0:0.658581658270197 0:0.6585816582701970, 1000:5.142928362480306 1393:0.3271208998291733, 2000:0.32712089982917325 1393:0.3271208998291733, 3000:0.32712089982917325 1393:0.3271208998291733, 4000:0.4029355474095988 5000:0.0114993205601383, 5000:0.011499320560138332 6000:0.0003946998191595, 6000:0.00039469981915948605 7000:0.0000686308316624, 7000:0.00006863083166239227 8000:0.0000176901182322, 8000:0.000017690118232197302 9000:0.0000053723044223, 9000:0.000005372304422295116 Best result iteration:9999, Err:0.000002 -----Population-based ADAMm----- 0:19.9499415647445524 1000:0.0000057228950379 Best result iteration:1051, Err:0.000000

周期的活性化関数の結果の表

ACON	SERF	Snake
MLP config:1|1|1, Weights:4, Activation func: eActACON, Seed:3 -----Integrated ADAM----- 0:0.8183728267492676, 0:0.8183728267492675 160:0.5853150801288914, 1000:1.2003151947973498 2000:0.0177702331540612, 2000:0.017770233154061187 3000:0.0055801976952827, 3000:0.005580197695282676 4000:0.0023096724537356, 4000:0.002309672453735598 5000:0.0010238849157595, 5000:0.0010238849157594616 6000:0.0004581612824611, 6000:0.0004581612824611273 7000:0.0002019092359805, 7000:0.00020190923598049711 8000:0.0000867118074097, 8000:0.00008671180740972474 9000:0.0000361764073840, 9000:0.00003617640738397845 Best result iteration:9999, Err:0.000015 -----Population-based ADAMm----- 0:1.3784017183806672 Best result iteration:300, Err:0.000000	MLP config:1|1|1, Weights:4, Activation func: eActSERF, Seed:2 -----Integrated ADAM----- 0:0.0169277701441132, 0:0.016927770144113192 0:0.0169277701441132, 1000:0.24726166610109795 0:0.0169277701441132, 2000:0.24996248252671016 0:0.0169277701441132, 3000:0.2499877118017991 0:0.0169277701441132, 4000:0.2260068617570163 0:0.0169277701441132, 5000:2.2499589217599363 0:0.0169277701441132, 6000:2.2499631351033904 0:0.0169277701441132, 7000:2.248459789732414 0:0.0169277701441132, 8000:2.146138260175548 0:0.0169277701441132, 9000:0.15279792149898394 Best result iteration:0, Err:0.016928 -----Population-based ADAMm----- 0:0.2491964938729135 1000:0.0000010386817829 Best result iteration:1050, Err:0.000001	MLP config:1|1|1, Weights:4, Activation func: eActSnake, Seed:2 -----Integrated ADAM----- 0:0.0169277701441132, 0:0.016927770144113192 0:0.0169277701441132, 1000:0.24726166610109795 0:0.0169277701441132, 2000:0.24996248252671016 0:0.0169277701441132, 3000:0.2499877118017991 0:0.0169277701441132, 4000:0.2260068617570163 0:0.0169277701441132, 5000:2.2499589217599363 0:0.0169277701441132, 6000:2.2499631351033904 0:0.0169277701441132, 7000:2.248459789732414 0:0.0169277701441132, 8000:2.146138260175548 0:0.0169277701441132, 9000:0.15279792149898394 Best result iteration:0, Err:0.016928 -----Population-based ADAMm----- 0:0.2491964938729135 1000:0.0000010386817829 Best result iteration:1050, Err:0.000001

まとめ

では、研究をまとめましょう。実験の趣旨を改めて振り返ります。私たちは、同じ論理に基づく2つの最適化アルゴリズムを用いましたが、根本的に異なる方法で動作します。1つ目（従来のADAM）は、ニューラルネットワーク内部から動作する組み込みのオプティマイザで、活性化関数や内部構造全体に直接アクセスできます。まるで詳細な地図を持ったナビゲータのようです。2つ目（集団型ADAMm）は、ニューラルネットワークを「ブラックボックス」として扱う外部オプティマイザで、内部構造やタスクの詳細情報は持たず、星や大まかな方向を頼りに進む旅行者のようです。

両方のアルゴリズムの対象として同じニューラルネットワークを使用しました。これは非常に重要です。なぜなら、特定の活性化関数で問題が発生した場合、その原因がニューラルネットワーク自体ではなく、最適化アルゴリズムがこれらの関数とどのように相互作用するかにあると確信できるからです。

この実験の構成により、異なる最適化アプローチにおける活性化関数の性能を明確に観察できます。重要なのは、ネットワークの一般化能力や新しいデータでの性能は意図的に考慮していない点です。私たちの目的は、活性化関数と最適化アルゴリズムの相互作用、その互換性および効率を研究することです。

このアプローチにより、外的要因の影響を排除した上で、異なる最適化戦略が異なる活性化関数に対してどのように動作するかを明確に把握できます。実験結果は、時には「盲目的な」外部オプティマイザが、ネットワーク構造の全情報を持つアルゴリズムよりも効率的である場合があることを示しています。

すべての活性化関数において、外部ADAMmは高速かつ安定的に収束し、活性化関数の特性がそれほど重要ではないことを示唆しています。一方で、従来型の組み込みADAMは深刻な問題に直面しました。

次に、各活性化関数における組み込みADAMの挙動を確認し、以下の結論にまとめます。

1. 問題のある関数（停滞または収束が遅い）

• TanH（双曲線正接）
• AlgSigm（代数的シグモイド）
• SERF（シグモイド加重指数直線化）
• Snake（周期関数）

2. 成功したケース（収束）

• RatSigm（有理シグモイド）、シグモイド関数の中で最良
  
• SoftPlus
• BentIdent
  
• SiLU (Swish)、第2グループのベスト
  
• ACON（適応関数）、周期関数の中で最良
  

3. パターン

古典的なシグモイド関数（TanH、AlgSigm）は停滞の問題を示します。より現代的な適応関数（ACON、SiLU）はより良い収束を示します。周期関数の中では、ACONは収束しますが、Snakeは停滞します。

このように、本研究は、重みの制御、活性化関数の境界、学習プロセスを一つの相互接続されたシステムに統合する、ニューラルネットワーク最適化の包括的アプローチを展開します。主な革新は、各活性化関数が自身の境界を定義できるGetBoundUpおよびGetBoundLoメソッドの導入であり、これを用いてネットワークの重みを管理します。この仕組みは、境界に達した際の合計値の早期終了システムと補完的に機能し、大規模ネットワークでの冗長な計算を防ぐだけでなく、活性化関数適用前に値を制御することも可能にします。

特に重要な要素は重み反射メカニズムで、従来のプルーニングや正規化とは異なり、重みが限界に達した際に「揺さぶる」ことで学習の停滞を防ぎます。この解決策により、重大な状況下でも重みを変更可能とし、学習プロセスの連続性を確保します。これらの要素の統合により、学習の柔軟性を損なわずに重みの発散を防ぐ効果的な仕組みが構築され、異なる活性化関数に対応する場合にも重要です。この統合アプローチは、単に重み制御の問題を解決するだけでなく、学習中のニューラルネットワーク構成要素の相互作用理解にも新たな視点を開きます。

本研究は、ADAMがニューラルネットワーク学習に無用であることを示すものではなく、特定の活性化関数に対する挙動に注目しています。おそらく、大規模ニューラルネットワークにおいては（現代的な勾配降下法の類似アルゴリズムを除き）他に代替手段が存在しない可能性があります。これは、ADAM（バックプロパゲーションを用いた現代的最適化アルゴリズムの代表）における効率性の検討や、大規模ネットワークにおける活性化関数の選択がネットワークの一般化能力や新規データでの安定性に与える影響の研究の次の課題となり得ます。

記事で使用されているプログラム

#	名前	種類	詳細
1	#C_AO.mqh	インクルード	集団最適化アルゴリズムの親クラス
2	#C_AO_enum.mqh	インクルード	集団最適化アルゴリズムの列挙
3	MLPa.mqh	スクリプト	ADAMを用いたMLPニューラルネットワーク
4	Tests and Drawing act func.mq5	スクリプト	活性化関数の視覚的な構築のためのスクリプト
5	Test act func in training.mq5	スクリプト	ADAMとADAMmを用いたMLP学習スクリプト