MetaTrader 5 / Tester
English Русский 中文 Español Português
preview
Arithmetischer Optimierungsalgorithmus (AOA): Von AOA zu SOA (Simpler Optimierungsalgorithmus)

Arithmetischer Optimierungsalgorithmus (AOA): Von AOA zu SOA (Simpler Optimierungsalgorithmus)

MetaTrader 5 — Tester |
18 0
Andrey Dik
Andrey Dik

Inhalt

  1. Einführung
  2. Implementierung des Algorithmus
  3. Testergebnisse


Einführung

Der Arithmetische Optimierungsalgorithmus (AOA) ist eine originelle Methode, die auf einfachen arithmetischen Operationen wie Addition, Subtraktion, Multiplikation und Division beruht. Sein Wesen liegt in der Anwendung dieser mathematischen Grundprinzipien, um optimale Lösungen für eine Vielzahl von Problemen zu finden. AOA wurde von einem Forscherteam um Laith Abualigah entwickelt und 2021 erstmals vorgestellt. Der Algorithmus gehört zur Klasse der metaheuristischen Methoden (High-Level-Algorithmen), die darauf abzielen, mehrere Heuristiken zu finden, zu generieren und probabilistisch auszuwählen, die in angemessener Zeit qualitativ hochwertige Lösungen für komplexe Optimierungsprobleme liefern können, bei denen auf Genauigkeit basierende Methoden unwirksam oder unmöglich sind.

Diese Methode erregte meine Aufmerksamkeit wegen ihrer einfachen und gleichzeitig eleganten Idee, völlig elementare arithmetische Operatoren zu verwenden. Die Beziehung zwischen diesen grundlegenden mathematischen Operationen und metaheuristischen Ansätzen schafft eine Synergie, die es ermöglicht, komplexe Optimierungsprobleme zu lösen. Die in AOA verwendeten metaheuristischen Methoden beinhalten mehrere Schlüsselprinzipien:

1. Populationsansatz. AOA verwendet eine Population von Lösungen, wodurch ein größerer Raum möglicher Lösungen abgedeckt werden kann. Dies trägt dazu bei, lokale Optima zu vermeiden und den Suchhorizont zu erweitern.

2. Zufälligkeit und Stochastik. Die Einbeziehung von Zufallselementen in die Suche hilft den Algorithmen, nicht in lokalen Optima stecken zu bleiben, und ermöglicht eine vollständigere Erkundung des Lösungsraums, was die Wahrscheinlichkeit erhöht, ein globales Optimum zu finden.

3. Gleichgewicht zwischen Erkundung und Ausbeutung. Wie viele andere metaheuristische Algorithmen strebt auch AOA nach einem Gleichgewicht zwischen der Erkundung neuer Regionen des Lösungsraums und der Nutzung bereits bekannter effizienter Lösungen. Dies wird durch arithmetische Operationen erreicht, um die Positionen der Lösungen zu aktualisieren.

AOA ist somit ein eindrucksvolles Beispiel für einen metaheuristischen Algorithmus, der die Prinzipien des Populationsansatzes, der Zufälligkeit und des Gleichgewichts zwischen Exploration und Exploitation effektiv zur Lösung von Optimierungsproblemen einsetzt. Wir werden jedoch speziell auf die Effizienz der Suche nach optimalen Lösungen in komplexen und mehrdimensionalen Räumen für diesen Algorithmus eingehen, nachdem wir ihn implementiert und getestet haben.


Implementierung des Algorithmus

Die Grundidee von AOA besteht darin, das Verteilungsverhalten von arithmetischen Operatoren zu nutzen, um optimale Lösungen zu finden. Der Algorithmus zeichnet sich durch einfache Prinzipien, eine nicht sehr große Anzahl von Parametern und einfache Implementierung aus. Der Algorithmus nutzt die Verteilungseigenschaften der vier grundlegenden arithmetischen Operatoren in der Mathematik, nämlich: Multiplikation (Mε × ε), Division (Dε ÷ ε), Subtraktion (Sε - ε) und Addition (Aε + ε). Bei der AOA wird die Ausgangspopulation zufällig im Bereich [U; L] erzeugt, wobei die obere und untere Grenze des Suchraums für die Zielfunktion mit U bzw. L bezeichnet wird, wobei die folgende Gleichung gilt

x = L + (U - L) × δ, wobei x die Populationslösung darstellt und δ eine Zufallsvariable ist, die Werte im Bereich [0, 1] annimmt.

Bei jeder Iteration erfolgt die Wahl der Explorations- und Verwertungsstrategie, d. h. die Wahl einer der beiden Gruppen von Operatoren, entweder (Division; Multiplikation) oder (Subtraktion; Addition), in Abhängigkeit vom Ergebnis der Funktion MoA (Math optimizer Accelerated), die im Wesentlichen der berechnete Wert der Wahrscheinlichkeit ist und sich mit jeder Iteration ändert, berechnet nach der Gleichung:

MoA(t) = Min + t × (Max - Min) ÷ Maxt, wobei MoA(t) das Funktionsergebnis bei der t-ten Iteration ist, t die aktuelle Iteration angibt, die im Bereich von 1 bis zur maximalen Anzahl von Iterationen (Maxt) liegt. Der kleinstmögliche Wert von MoA wird als Min bezeichnet, während der maximale Wert als Max bezeichnet wird. Dies sind externe Parameter des Algorithmus.

Alle vier Gleichungen für arithmetische Operatoren verwenden den MoP-Faktor (math optimizer), der wie folgt berechnet wird:

MoP(t) = 1 − (t ÷ Maxt)^(1 ÷ θ), wobei MoP(t) den Wert der MoP-Funktion bei der t-ten Iteration angibt. θ ist ein kritischer Parameter, der die Leistung der Ausnutzung über die Iterationen steuert. In der ursprünglichen Arbeit setzten die Autoren des Algorithmus diesen Wert auf Stufe 5.

Abbildung 1 unten zeigt die Graphen der MoA- und MoP-Abhängigkeit von der aktuellen Iteration. Die Diagramme zeigen, dass der MoA mit jeder Iteration linear ansteigt, was bedeutet, dass die Wahrscheinlichkeit, eine Gruppe von Operatoren (Subtraktion; Addition) zu wählen, steigt und die Wahrscheinlichkeit, eine Gruppe von Operatoren (Division; Multiplikation) zu wählen, proportional abnimmt. Im Gegenzug nimmt das MoP-Verhältnis nichtlinear ab, wodurch das nächste Inkrement auf die aktuelle Position der Agenten in der Population reduziert wird, was eine Erhöhung des Verfeinerungsgrads der Entscheidungen bei der Optimierung bedeutet.

MoAundMoP

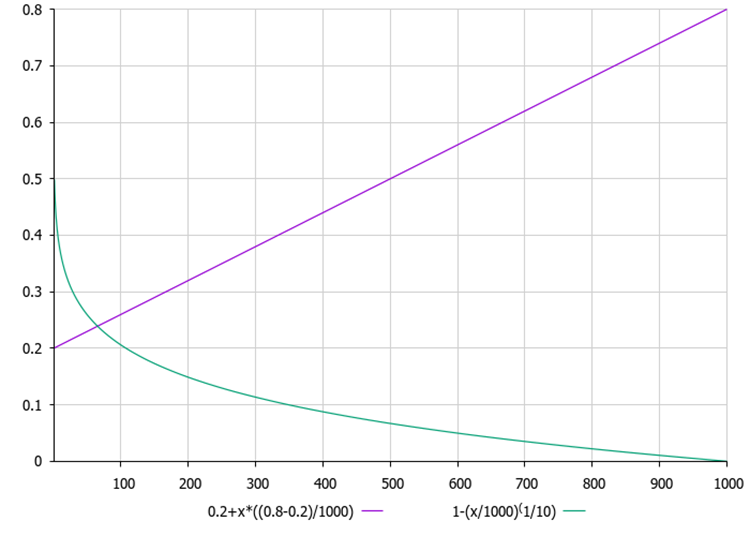
Abbildung 1. Die violette Farbe zeigt die MoA-Wahrscheinlichkeitsgrafik und die grüne Farbe zeigt die MoP-Verhältnisgrafik.

Die Recherche bzw. die globale Suche in AOA erfolgt mit Suchstrategien, die auf den Operatoren Division (D) und Multiplikation (M) basieren, wenn die MoA-Wahrscheinlichkeit erfüllt ist, die wie folgt formuliert ist, wobei die folgenden Operatoren mit gleicher Wahrscheinlichkeit ausgeführt werden:

xi,j(t+1) = best(xj) ÷ (MoPr + 𝜖) × ((Uj − Lj) × 𝜇 + Lj), wenn rand2 < 0.5; 

sonst:

xi,j(t+1) = best(xj) × (MoPr) × ((Uj − Lj) × 𝜇 + Lj), wobei xi(t+1) die i-te Lösung in der (t+1)-ten Iteration darstellt, x(i,j)(t) die j-te Position des i-ten Individuums in der aktuellen Generation darstellt, best(xj) drückt die j-te Position der besten Lösung im Moment aus, ε ist eine kleine positive Zahl, die oberen und unteren Grenzen der Werte der j-ten Position werden als Uj bzw. Lj bezeichnet. Der Kontrollparameter μ wurde auf 0,5 festgelegt. 

Wird die MoA-Wahrscheinlichkeit nicht erfüllt, so wird die Verwertungsstrategie (Lösungsverfeinerung) im AOA durchgeführt. Die Strategie wurde unter Verwendung der Operatoren Subtraktion (S) und Addition (A) entwickelt. Auch hier ist μ eine Konstante, die von den Autoren absichtlich auf 0,5 festgelegt wurde. 

xi,j(t+1) = best(xj) − (MoPr) × ((Uj − Lj) × 𝜇 + Lj), wenn rand3 < 0.5,

sonst xi,j(t+1) = best(xj) + (MoPr) × ((Uj − Lj) × 𝜇 + Lj).

Bei der AOA sind die Parameter 𝜇 und θ sehr wichtig, da sie für die Abwägung zwischen Erkundung und Ausbeutung verantwortlich sind. Die Aufrechterhaltung eines ausgewogenen Verhältnisses zwischen Erkundung und Ausbeutung ist in der Regel eine sehr anspruchsvolle Aufgabe. Im ursprünglichen AOA wurde der Wert von 𝜇 sowohl für die Aufsuchung als auch für die Ausbeutung auf 0,5 festgelegt. Der Parameter θ, der sich auf die Betriebseffizienz während der Iterationen auswirkt, wird jedoch auf 5 gesetzt. Die Autoren experimentierten mit verschiedenen Werten von 𝜇 und θ und fanden heraus, dass 𝜇 = 0,5 und θ = 5 am häufigsten die besten Ergebnisse für unimodale und multimodale Testfunktionen in verschiedenen Dimensionen lieferten. 

Nun wollen wir den Pseudocode des AOA-Algorithmus implementieren:

die Epochenzahl um 1 erhöhen

// Beginn der Initialisierung
WENN dies der erste Start ist DANN
    FÜR jedes Teilchen der Population:
        FÜR jede Koordinate:
            Lege eine zufällige Position innerhalb des zulässigen Bereichs fest.
            Bring eine Position auf einen diskreten Wert.
    Markieren, dass die Initialisierung abgeschlossen ist.
    Ende Funktion
ENDE WENN

// Hauptoptimierungsprozess
Berechne MoA = minMoA + EpochNumber * ((maxMoA - minMoА) / totalEpochs).
Berechne MoP = 1 - (Epochenzahl / Gesamtzahl der Epochen)^(1/θ).

// Phase der Erkundung des Lösungsraums
FÜR jedes Teilchen der Population:
    FÜR jede Koordinate:
        Erzeuge drei Zufallswerte (rand1, rand2, rand3).
        Nimm den besten bekannten Wert für die Koordinate.
        
        WENN rand1 < MoAc DANN
            WENN rand2 > 0.5 DANN
                Aktualisiere die Position durch Division.
            SONST
                Aktualisiere Position durch Multiplikation.
            ENDE WENN
        SONST
            WENN rand3 > 0.5 DANN
                Aktualisiere die Position durch Subtraktion.
            SONST
                Aktualisiere die Position durch Addition.
            ENDE WENN
        ENDE WENN
        
        Bring die neue Position auf einen akzeptablen diskreten Wert.
        
Aktualisiere die beste Lösung.

Kommen wir nun zum Schreiben des Codes. Die Klasse C_AO_AOA ist eine Implementierung des AOA-Algorithmus und dient der Lösung von Optimierungsproblemen mit einer auf arithmetischen Operationen basierenden Methode. Öffentliche Methoden:

1. Die Methode SetParams() setzt die Werte von Parametern aus dem Array params. Diese Methode erlaubt es, die Parameter des Algorithmus zu ändern, nachdem sie initialisiert wurde.

2. Die Methode Init():

  • Initialisiert den Algorithmus, indem sie den minimalen und maximalen Suchbereich, den Suchschritt und die Anzahl der Epochen angibt. 
  • Gibt true zurück, wenn die Initialisierung erfolgreich war, andernfalls false.

3. Die Methode Moving() führt die Bewegung der Partikel im Lösungsraum durch. Diese Methode implementiert die Logik zur Aktualisierung der Partikelpositionen auf der Grundlage der angegebenen Parameter und des aktuellen Zustands.

4. Die Methode Revision() revidiert die aktuellen Positionen der Partikel, wobei der beste gefundene Wert der Funktion und die Koordinaten des entsprechenden Partikels aktualisiert werden.

Private Felder, Klassenparameter:

  • minT - Mindestwert der MoA-Wahrscheinlichkeit.
  • maxT - Höchstwert der MoA-Wahrscheinlichkeit.
  • θ - Parameter, der das Gleichgewicht zwischen Erkundung und Ausbeutung beeinflusst.
  • μ - Parameter zur Kontrolle von Änderungen der Partikelpositionen(Bewegungsbereich).
  • ϵ - kleine Zahl, um eine Division durch Null zu verhindern.

Algorithmus-Status-Info:

  • epochs - Gesamtzahl der Epochen, die der Algorithmus durchlaufen wird.
  • epochNow - die aktuelle Epoche, die zur Verfolgung des Algorithmusfortschritts verwendet wird, wirkt sich auf die MoA-Wahrscheinlichkeit und das MoP-Verhältnis aus.

Die Klasse C_AO_AOA implementiert die Hauptkomponenten des AOA-Algorithmus, einschließlich Initialisierung, Partikelbewegung und Revision.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AOA () { }
  C_AO_AOA ()
  {
    ao_name = "AOA";
    ao_desc = "Arithmetic Optimization Algorithm";
    ao_link = "https://www.mql5.com/de/articles/16364";

    popSize = 50;   // Population size
    minT    = 0.1;  // Minimum T value
    maxT    = 0.9;  // Maximum T value
    θ       = 10;   // θ parameter
    μ       = 0.01; // μ parameter

    ArrayResize (params, 5); // Resize the parameter array

    // Initialize parameters
    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "minT";    params [1].val = minT;
    params [2].name = "maxT";    params [2].val = maxT;
    params [3].name = "θ";       params [3].val = θ;
    params [4].name = "μ";       params [4].val = μ;
  }

  void SetParams () // Method for setting parameters
  {
    popSize = (int)params [0].val; // Set population size
    minT    = params      [1].val; // Set minimum T
    maxT    = params      [2].val; // Set maximum T
    θ       = params      [3].val; // Set θ
    μ       = params      [4].val; // Set μ
  }

  bool Init (const double &rangeMinP  [], // Minimum search range
             const double &rangeMaxP  [], // Maximum search range
             const double &rangeStepP [], // Search step
             const int     epochsP = 0);  // Number of epochs

  void Moving   (); // Method of moving particles
  void Revision (); // Revision method

  //----------------------------------------------------------------------------
  double minT; // Minimum T value
  double maxT; // Maximum T value
  double θ;    // θ parameter
  double μ;    // μ parameter
  double ϵ;    // Parameter to prevent division by zero

  private: //-------------------------------------------------------------------
  int epochs;    // Total number of epochs
  int epochNow;  // Current epoch
};
//——————————————————————————————————————————————————————————————————————————————

Die Methode Init der Klasse C_AO_AOA ist für die Initialisierung des Optimierungsalgorithmus zuständig, indem sie die Parameter für den Suchbereich, die Schritte und die Anzahl der Epochen, in denen die Optimierung durchgeführt wird, festlegt. Die Logik der Methode:

1. Die Methode ruft zunächst StandardInit auf, wodurch die Standardparameter des Algorithmus initialisiert werden. Wenn diese Initialisierung fehlschlägt, bricht Init die Ausführung sofort ab und gibt false zurück.

2. Parameter einstellen:

  • Legt die Gesamtzahl der Epochen auf der Grundlage des übergebenen Parameters epochsP fest.
  • Initialisiert die aktuelle Epoche epochNow mit 0.
  • Wir weisen ϵ (kleiner Wert, um eine Division durch Null zu verhindern) DBL_EPSILON zu, den Standardwert für die Darstellung der kleinsten positiven Zahl, die im Typ double dargestellt werden kann.

3. Wenn alle Schritte erfolgreich abgeschlossen sind, gibt die Methode true zurück, was eine erfolgreiche Initialisierung des Algorithmus anzeigt.

Die Methode Init ist ein wichtiger Teil der Vorbereitung des Algorithmus für die Ausführung, da sie die grundlegenden Parameter festlegt, die bei der Optimierung verwendet werden. Durch den Aufruf dieser Methode werden alle Parameter und Variablen auf ihren ursprünglichen Zustand zurückgesetzt.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AOA::Init (const double &rangeMinP  [], // Minimum search range
                     const double &rangeMaxP  [], // Maximum search range
                     const double &rangeStepP [], // Search step
                     const int     epochsP = 0)   // Number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; // Initialization of standard parameters

  //----------------------------------------------------------------------------
  epochs   = epochsP;     // Set the total number of epochs
  epochNow = 0;           // Initialize the current epoch
  ϵ        = DBL_EPSILON; // Set ϵ

  return true;            // Return 'true' if initialization was successful
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Moving ist für die Bewegung der Partikel im Lösungsraum innerhalb des AOA-Algorithmus verantwortlich. Es implementiert die grundlegende Logik der Aktualisierung der Partikelpositionen auf der Grundlage des aktuellen Zustands und der Algorithmusparameter. Die Logik der Methode:

1. Erhöhe epochNow, um anzuzeigen, dass eine neue Ära der Optimierung angebrochen ist.

2. Erste zufällige Positionierung: Wenn noch keine Aktualisierung (Revision) durchgeführt wurde, werden für jedes Partikel Zufallspositionen innerhalb der angegebenen Bereiche rangeMin und rangeMax erzeugt. Jede Position wird dann mit der Methode SeInDiSp mit dem angegebenen Schritt diskretisiert.

3. MoAc und MoPr werden auf der Grundlage der aktuellen Epoche und der angegebenen Parameter berechnet. Diese Werte bestimmen die Wahrscheinlichkeiten, die zur Aktualisierung der Partikelpositionen verwendet werden.

4. Forschungsphase. Für jedes Partikel und jede Koordinate wird die Position auf der Grundlage von Zufallswerten und berechneten Parametern aktualisiert. Die Positionen können mit verschiedenen Operatoren (Division und Multiplikation) sowie mit probabilistischen Bedingungen aktualisiert werden.

5. Nach der Aktualisierung wird die Position ebenfalls mit der Methode SeInDiSp in diskrete Werte umgewandelt.

//——————————————————————————————————————————————————————————————————————————————
// Particle displacement method
void C_AO_AOA::Moving ()
{
  epochNow++; // Increase the current epoch number

  // Initial random positioning
  if (!revision) // If there has not been a revision yet 
  {
    for (int i = 0; i < popSize; i++) // For each particle
    {
      for (int c = 0; c < coords; c++) // For each coordinate
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);                             // Generate random position
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Convert to discrete values
      }
    }

    revision = true; // Set revision flag
    return;          // Exit the method
  }

  //----------------------------------------------------------------------------
  double MoAc = minT + epochNow * ((maxT - minT) / epochs); // Calculate the MoAc value
  double MoPr = 1.0 - pow (epochNow / epochs, (1.0 / θ));   // Calculate the MoPr value
  double best = 0.0;                                        // Variable to store the best value

  // Research phase using Division (D) and Multiplication (M) operators
  for (int i = 0; i < popSize; i++) // For each particle
  {
    for (int c = 0; c < coords; c++) // For each coordinate
    {
      double rand1 = u.RNDprobab (); // Generate a random value
      double rand2 = u.RNDprobab (); // Generate a random value
      double rand3 = u.RNDprobab (); // Generate a random value

      best = cB [c];                 // Save the current best value

      if (rand1 < MoAc)              // If random value is less than MoAc
      {
        if (rand2 > 0.5)             // If random value is greater than 0.5
        {
          a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Update particle position
        }
        else
        {
          a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
      }
      else // If random value is greater than or equal to MoAc
      {
        if (rand3 > 0.5) // If random value is greater than 0.5
        {
          a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
        else
        {
          a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
      }

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Convert to discrete values
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Revision in der Klasse C_AO_AOA aktualisiert die Informationen über das beste Partikel in der Population. Sie durchläuft alle Partikel, vergleicht ihre Funktionswerte mit dem aktuell besten Wert, aktualisiert ihn, wenn er einen besseren findet, und speichert den Index. Dann kopiert es die Koordinaten des besten Partikels in das Array cB.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AOA::Revision ()
{
  int ind = -1;                     // Index to store the best particle

  for (int i = 0; i < popSize; i++) // For each particle
  {
    if (a [i].f > fB)               // If the function value is better than the current best one
    {
      fB = a [i].f;                 // Update the best value of the function
      ind = i;                      // Save the index of the best particle
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best particle
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode SeInDiSp der Klasse C_AO_Utilities begrenzt den Eingang In auf den Bereich von [InMin, InMax] mit dem angegebenen Step.

1. Wenn In kleiner oder gleich InMin ist, wird InMin zurückgegeben.
2. Wenn In größer oder gleich InMax ist, wird InMax zurückgegeben.
3. Wenn Step gleich 0 ist, wird der ursprüngliche Wert von In zurückgegeben.
4. Andernfalls wird der Wert auf (In - InMin) / Step gerundet und der angepasste Wert innerhalb des Bereichs unter Berücksichtigung des Steps zurückgegeben.

double C_AO_Utilities :: SeInDiSp (double In, double InMin, double InMax, double Step)
{
  if (In <= InMin) return (InMin);
  if (In >= InMax) return (InMax);
  if (Step == 0.0) return (In);
  else return (InMin + Step * (double)MathRound ((In - InMin) / Step));
}


Testergebnisse

Der AOA-Algorithmus ist recht einfach, schauen wir uns seine Leistung bei Testaufgaben an.

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.3914957505847635
25 Hilly's; Func runs: 10000; result: 0.27733670012505607
500 Hilly's; Func runs: 10000; result: 0.2514517003089684
=============================
5 Forest's; Func runs: 10000; result: 0.23495704012464264
25 Forest's; Func runs: 10000; result: 0.1853447250852242
500 Forest's; Func runs: 10000; result: 0.15382470751079919
=============================
5 Megacity's; Func runs: 10000; result: 0.19846153846153847
25 Megacity's; Func runs: 10000; result: 0.11815384615384619
500 Megacity's; Func runs: 10000; result: 0.09475384615384692
=============================
All score: 1.90578 (21.18%)

Den Testergebnissen zufolge erreicht der Algorithmus nur 21,18 % von 100 %. Dies ist ein sehr schwaches Ergebnis. Leider liegt sie in der aktuellen Rangliste auf dem letzten Platz. Wir sollten versuchen, die Logik des Algorithmus zu ändern, um bessere Ergebnisse zu erzielen. Wir werden Schritt für Schritt Änderungen vornehmen und die Ergebnisse überwachen.

Die Logik des ursprünglichen AOA-Algorithmus beinhaltet eine stochastische Suche, die nur aus der probabilistischen Natur der Wahl eines von vier mathematischen Operatoren besteht. Fügen wir dem Verschiebungsverhältnis μ ein Zufallselement hinzu, indem wir es mit einer Zufallszahl aus dem Bereich 0 bis 1 multiplizieren.

// Research phase using Division (D) and Multiplication (M) operators
  for (int i = 0; i < popSize; i++) // For each particle
  {
    for (int c = 0; c < coords; c++) // For each coordinate
    {
      double rand1 = u.RNDprobab (); // Generate a random value
      double rand2 = u.RNDprobab (); // Generate a random value
      double rand3 = u.RNDprobab (); // Generate a random value

      best = cB [c];                 // Save the current best value

      μ *= u.RNDfromCI (0, 1);       // Random change of μ

      if (rand1 < MoAc)              // If random value is less than MoAc
      {
        if (rand2 > 0.5)             // If random value is greater than 0.5
        {
          a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Update particle position
        }
        else
        {
          a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
      }
      else // If random value is greater than or equal to MoAc
      {
        if (rand3 > 0.5) // If random value is greater than 0.5
        {
          a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
        else
        {
          a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
      }

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Convert to discrete values
    }
  }

Testen wir den Algorithmus mit denselben Parametern:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.3595591180258857
25 Hilly's; Func runs: 10000; result: 0.2804913285516192
500 Hilly's; Func runs: 10000; result: 0.25204298245610646
=============================
5 Forest's; Func runs: 10000; result: 0.24115834887873383
25 Forest's; Func runs: 10000; result: 0.18034196700384764
500 Forest's; Func runs: 10000; result: 0.15441446106797124
=============================
5 Megacity's; Func runs: 10000; result: 0.18307692307692305
25 Megacity's; Func runs: 10000; result: 0.12400000000000003
500 Megacity's; Func runs: 10000; result: 0.09470769230769309
=============================
All score: 1.86979 (20.78%)

Leider wurde das Ergebnis noch schlechter. Es müssen zusätzliche Schritte unternommen werden. Allein die Tatsache, dass man einem deterministischen Ausdruck Zufälligkeit hinzufügt, sollte jedoch die Variabilität der Suchstrategie verbessern. Schauen wir uns die Gleichungen der mathematischen Operatoren genauer an - jeder von ihnen hat den Term rangeMin[c]. Im Wesentlichen ist der resultierende Ausdruck in diesen Operatoren immer relativ zur minimalen Grenze der zu optimierenden Parameter zentriert. Es gibt keine offensichtliche Logik dafür, daher sollten wir dieses Element aus allen Gleichungen entfernen.

// Research phase using Division (D) and Multiplication (M) operators
for (int i = 0; i < popSize; i++) // For each particle
{
  for (int c = 0; c < coords; c++) // For each coordinate
  {
    double rand1 = u.RNDprobab (); // Generate a random value
    double rand2 = u.RNDprobab (); // Generate a random value
    double rand3 = u.RNDprobab (); // Generate a random value

    best = cB [c];                 // Save the current best value

    μ *= u.RNDfromCI (0, 1);       // Change μ

    if (rand1 < MoAc)              // If random value is less than MoAc
    {
      if (rand2 > 0.5)             // If random value is greater than 0.5
      {
        a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]); // Update particle position
      }
      else
      {
        a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]);     // Update particle position
      }
    }
    else // If random value is greater than or equal to MoAc
    {
      if (rand3 > 0.5) // If random value is greater than 0.5
      {
        a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]);     // Update particle position
      }
      else
      {
        a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]);     // Update particle position
      }
    }

    a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Convert to discrete values
  }
}

Führen wir den Test durch. Nachstehend sind die Ergebnisse aufgeführt:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.36094646986361645
25 Hilly's; Func runs: 10000; result: 0.28294095623218063
500 Hilly's; Func runs: 10000; result: 0.2524581968477915
=============================
5 Forest's; Func runs: 10000; result: 0.2463208325927641
25 Forest's; Func runs: 10000; result: 0.1772140022690996
500 Forest's; Func runs: 10000; result: 0.15367993432040622
=============================
5 Megacity's; Func runs: 10000; result: 0.1923076923076923
25 Megacity's; Func runs: 10000; result: 0.11938461538461542
500 Megacity's; Func runs: 10000; result: 0.09433846153846229
=============================
All score: 1.87959 (20.88%)

Die von uns vorgenommenen Änderungen hatten keine Leistungsverbesserungen zur Folge, was recht merkwürdig ist, wenn man bedenkt, dass wir bereits größere Änderungen an unserer Suchstrategie vorgenommen hatten. Dies könnte darauf hindeuten, dass die Strategie selbst fehlerhaft ist und das Entfernen einzelner Komponenten die Ergebnisse nicht wesentlich beeinflusst.

Die Suchstrategie hat eine MoA-Komponente, die mit jeder Iteration linear ansteigt (siehe Abb. 1). Versuchen wir, diese Komponente als probabilistische Wahl einer der Koordinaten der besten Lösung zu verwenden und sie in die aktuelle Arbeitslösung zu kopieren. Dies sollte der Suchstrategie kombinatorische Eigenschaften verleihen, indem der Informationsaustausch über die beste Lösung in der Population genutzt wird (in der ursprünglichen Version gibt es keinen Informationsaustausch zwischen den Agenten).

// Research phase using Division (D) and Multiplication (M) operators
for (int i = 0; i < popSize; i++) // For each particle
{
  for (int c = 0; c < coords; c++) // For each coordinate
  {
    double rand1 = u.RNDprobab (); // Generate a random value
    double rand2 = u.RNDprobab (); // Generate a random value
    double rand3 = u.RNDprobab (); // Generate a random value

    best = cB [c];                 // Save the current best value

    μ *= u.RNDfromCI (0, 1);       // Change μ

    if (rand1 < MoAc)              // If random value is less than MoAc
    {
      if (rand2 > 0.5)             // If random value is greater than 0.5
      {
        a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ); // Update particle position
      }
      else
      {
        a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);     // Update particle position
      }
    }
    else // If random value is greater than or equal to MoAc
    {
      if (rand3 > 0.5) // If random value is greater than 0.5
      {
        a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);     // Update particle position
      }
      else
      {
        a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);     // Update particle position
      }
    }

    if (u.RNDbool () < MoAc) a [i].c [c] = cB [c];                                            // Set to the best value

    a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Convert to discrete values
  }
}

Die Ergebnisse, die nach der Einführung der Logik des Informationsaustauschs durch die beste Lösung:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.360814744695913
25 Hilly's; Func runs: 10000; result: 0.28724958448168375
500 Hilly's; Func runs: 10000; result: 0.2523432997811412
=============================
5 Forest's; Func runs: 10000; result: 0.26319762212870146
25 Forest's; Func runs: 10000; result: 0.1796822846691542
500 Forest's; Func runs: 10000; result: 0.1546335398592898
=============================
5 Megacity's; Func runs: 10000; result: 0.18
25 Megacity's; Func runs: 10000; result: 0.12153846153846157
500 Megacity's; Func runs: 10000; result: 0.09373846153846228
=============================
All score: 1.89320 (21.04%)

Wir sehen Leistungsverbesserungen, die sich aber bisher im Rahmen der Lösungen selbst bewegen. Fügen wir nun im gleichen Teil des Codes die Wahrscheinlichkeit hinzu, dass ein Zufallswert für eine Koordinate innerhalb des gesamten akzeptablen Bereichs der optimierten Parameter erzeugt wird, während die Koordinate gemäß der MoP-Gleichung nichtlinear abnimmt. 

// Probabilistic update of particle position
if (u.RNDbool () < MoAc) a [i].c [c] = cB [c];                                        // Set to the best value
else
  if (u.RNDbool () < MoPr) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);    // Generate new random position

Schauen wir uns die folgenden Ergebnisse an:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.8354927331645667
25 Hilly's; Func runs: 10000; result: 0.3963221867834875
500 Hilly's; Func runs: 10000; result: 0.2526544322311671
=============================
5 Forest's; Func runs: 10000; result: 0.7689954585427405
25 Forest's; Func runs: 10000; result: 0.3144560745800252
500 Forest's; Func runs: 10000; result: 0.15495875390289315
=============================
5 Megacity's; Func runs: 10000; result: 0.6076923076923076
25 Megacity's; Func runs: 10000; result: 0.24646153846153843
500 Megacity's; Func runs: 10000; result: 0.09816923076923163
=============================
All score: 3.67520 (40.84%)

Erstaunlicherweise ist die Produktivität drastisch gestiegen! Das bedeutet, dass wir uns in die richtige Richtung bewegen. Es ist erwähnenswert, was genau der AOA-Logik hinzugefügt wurde: Zu Beginn der Optimierung, in der ersten Epoche, ist die Wahrscheinlichkeit, dass die Koordinaten der global besten Lösung in die aktuellen Koordinaten kopiert werden, minimal. Das ist ganz logisch, denn in der Anfangsphase der Optimierung beginnt die Strategie gerade erst, den Suchraum zu erkunden. Gleichzeitig ist die Wahrscheinlichkeit, dass bei der ersten Iteration zufällige Lösungen im gesamten Suchraum entstehen, maximal. Über alle Epochen hinweg ändern sich diese Wahrscheinlichkeiten: Die Wahrscheinlichkeit, die Koordinaten der globalen Lösung zu kopieren, steigt, während die Wahrscheinlichkeit, zufällige Lösungen zu erzeugen, im Gegenteil abnimmt (siehe Abb. 1).

Da sich die Leistung mit den von mir vorgenommenen Änderungen verbessert hat und zuvor festgestellt wurde, dass Änderungen an der ursprünglichen Logik nicht zu spürbaren Verbesserungen führen, ist es sinnvoll, alle arithmetischen Operatoren vollständig zu eliminieren. Testen wir den resultierenden Algorithmus an Testproblemen:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8751771961221438
25 Hilly's; Func runs: 10000; result: 0.4645369071659114
500 Hilly's; Func runs: 10000; result: 0.27170038319811357
=============================
5 Forest's; Func runs: 10000; result: 0.8369443889312367
25 Forest's; Func runs: 10000; result: 0.36483865328371257
500 Forest's; Func runs: 10000; result: 0.17097532914778202
=============================
5 Megacity's; Func runs: 10000; result: 0.7046153846153846
25 Megacity's; Func runs: 10000; result: 0.28892307692307695
500 Megacity's; Func runs: 10000; result: 0.10847692307692398
=============================
All score: 4.08619 (45.40%)   

Wie wir sehen können, stieg die Effizienz um fast weitere 5 %, was wiederum die Richtigkeit meiner Überlegungen bestätigte. Wir haben mit den Standardparametern interessante Ergebnisse erzielt, aber die Änderungen in der Logik waren so radikal, dass es jetzt notwendig ist, die optimalen externen Parameter des Algorithmus zu wählen. Ein zusätzlicher Bonus zur erhöhten Produktivität war:

  • Eine erhebliche Beschleunigung der Arbeit, da wir die unnötige Generierung von Zufallszahlen abgeschafft haben.
  • Die Verringerung der Anzahl der externen Parameter um einen

Schauen wir uns die Endergebnisse des erhaltenen Algorithmus an:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.5|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9152036654779877
25 Hilly's; Func runs: 10000; result: 0.46975580956945456
500 Hilly's; Func runs: 10000; result: 0.27088799720164297
=============================
5 Forest's; Func runs: 10000; result: 0.8967497776673259
25 Forest's; Func runs: 10000; result: 0.3740125122006007
500 Forest's; Func runs: 10000; result: 0.16983896751516864
=============================
5 Megacity's; Func runs: 10000; result: 0.6953846153846155
25 Megacity's; Func runs: 10000; result: 0.2803076923076923
500 Megacity's; Func runs: 10000; result: 0.10852307692307792
=============================
All score: 4.18066 (46.45%) 

Das erzielte Ergebnis verdient bereits einen Platz in der Bewertungstabelle, während in der endgültigen Fassung der Suchstrategie Elemente der ursprünglichen Logik völlig verloren gegangen sind. Daher habe ich beschlossen, diesem neuen Algorithmus einen neuen Namen zu geben - Simple Optimization Algorithm (SOA). Schauen wir uns den gesamten endgültigen Code des SOA-Algorithmus an.

#include "#C_AO.mqh"

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_SOA () { }
  C_AO_SOA ()
  {
    ao_name = "SOA";
    ao_desc = "Simple Optimization Algorithm";
    ao_link = "https://www.mql5.com/de/articles/16364";

    popSize = 50;   // Population size
    minT    = 0.1;  // Minimum T value
    maxT    = 0.9;  // Maximum T value
    θ       = 10;   // θ parameter

    ArrayResize (params, 4); // Resize the parameter array

    // Initialize parameters
    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "minT";    params [1].val = minT;
    params [2].name = "maxT";    params [2].val = maxT;
    params [3].name = "θ";       params [3].val = θ;
  }

  void SetParams () // Method for setting parameters
  {
    popSize = (int)params [0].val; // Set population size
    minT    = params      [1].val; // Set minimum T
    maxT    = params      [2].val; // Set maximum T
    θ       = params      [3].val; // Set θ
  }

  bool Init (const double &rangeMinP  [], // Minimum search range
             const double &rangeMaxP  [], // Maximum search range
             const double &rangeStepP [], // Search step
             const int     epochsP = 0);  // Number of epochs

  void Moving   (); // Method of moving particles
  void Revision (); // Revision method

  //----------------------------------------------------------------------------
  double minT; // Minimum T value
  double maxT; // Maximum T value
  double θ;    // θ parameter

  private: //-------------------------------------------------------------------
  int epochs;    // Total number of epochs
  int epochNow;  // Current epoch
  double ϵ;      // Parameter to prevent division by zero
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_SOA::Init (const double &rangeMinP  [], // Minimum search range
                     const double &rangeMaxP  [], // Maximum search range
                     const double &rangeStepP [], // Search step
                     const int     epochsP = 0)   // Number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; // Initialization of standard parameters

  //----------------------------------------------------------------------------
  epochs   = epochsP;     // Set the total number of epochs
  epochNow = 0;           // Initialize the current epoch
  ϵ        = DBL_EPSILON; // Set ϵ

  return true;            // Return 'true' if initialization was successful
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Particle displacement method
void C_AO_SOA::Moving ()
{
  epochNow++; // Increase the current epoch number

  // Initial random positioning
  if (!revision) // If there has not been a revision yet 
  {
    for (int i = 0; i < popSize; i++) // For each particle
    {
      for (int c = 0; c < coords; c++) // For each coordinate
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);                             // Generate random position
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Convert to discrete values
      }
    }

    revision = true; // Set revision flag
    return;          // Exit the method
  }

  //----------------------------------------------------------------------------
  double MoAc = minT + epochNow * ((maxT - minT) / epochs); // Calculate the MoAc value
  double MoPr = 1.0 - pow (epochNow / epochs, (1.0 / θ));   // Calculate the MoPr value
  double best = 0.0;                                        // Variable to store the best value

  // Research phase using Division (D) and Multiplication (M) operators
  for (int i = 0; i < popSize; i++) // For each particle
  {
    for (int c = 0; c < coords; c++) // For each coordinate
    {
      // Probabilistic update of particle position
      if (u.RNDbool () < MoAc) a [i].c [c] = cB [c];                                        // Set to the best value
      else
        if (u.RNDbool () < MoPr) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);    // Generate new random position

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);   // Convert to discrete values
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SOA::Revision ()
{
  int ind = -1;                     // Index to store the best particle

  for (int i = 0; i < popSize; i++) // For each particle
  {
    if (a [i].f > fB)               // If the function value is better than the current best one
    {
      fB = a [i].f;                 // Update the best value of the function
      ind = i;                      // Save the index of the best particle
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best particle
}
//——————————————————————————————————————————————————————————————————————————————

Das Ergebnis ist einer der kompaktesten Optimierungsalgorithmen in Bezug auf den Code, den wir bisher betrachtet haben. Der einzige Code, der kürzer ist, ist der des RW-Algorithmus (RandomWalk), der in einem der folgenden Artikel behandelt wird.

Die Visualisierung der Leistung von Suchstrategien im Lösungsraum spricht Bände. Ich habe alle drei Tests (Hilly, Forest und Megacity) für den AOA-Algorithmus in einer Animation zusammengefasst, da es praktisch keine Unterschiede in der Leistung bei den verschiedenen Aufgabentypen gibt. Nachfolgend finden Sie separate Visualisierungen des SOA-Betriebs für jede der drei Testfunktionen.

Es ist möglich, die Arbeit des neuen SOA-Algorithmus auf Probleme von kleinen Dimensionen zu bemerken - eine kleine Streuung der Ergebnisse, die eine ziemlich seltene Qualität ist. 

AOA mit Hilly, Forest, Megacity

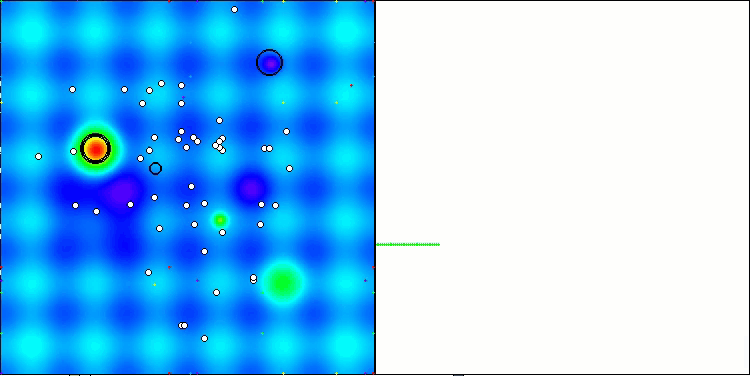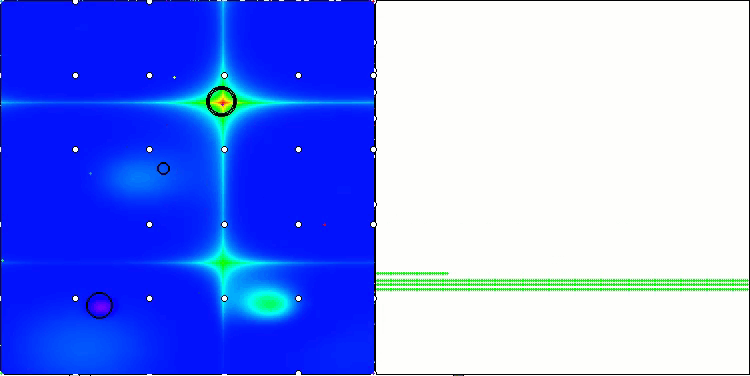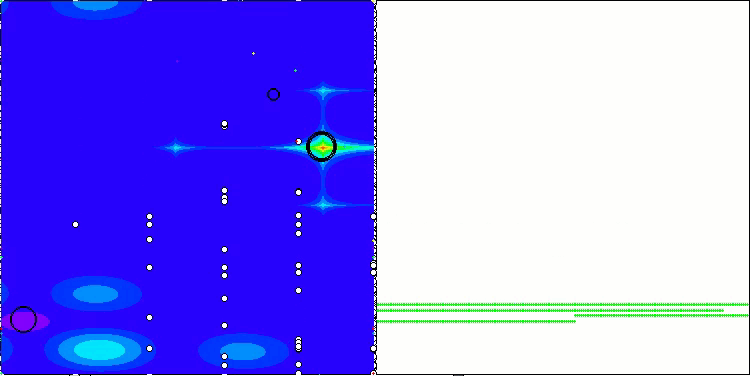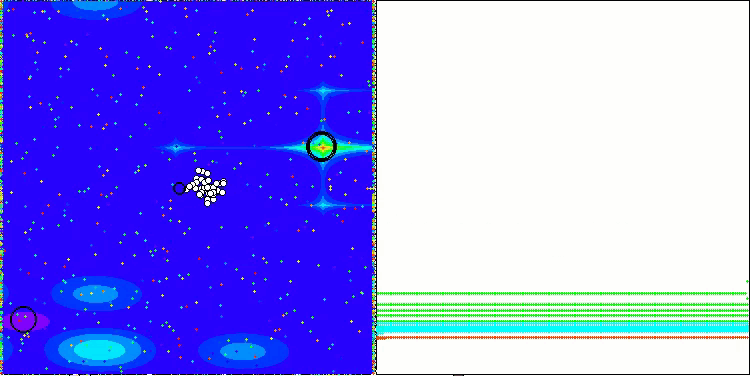
AOA mit den Testfunktionen Hilly, Forest, Megacity 

Hilly

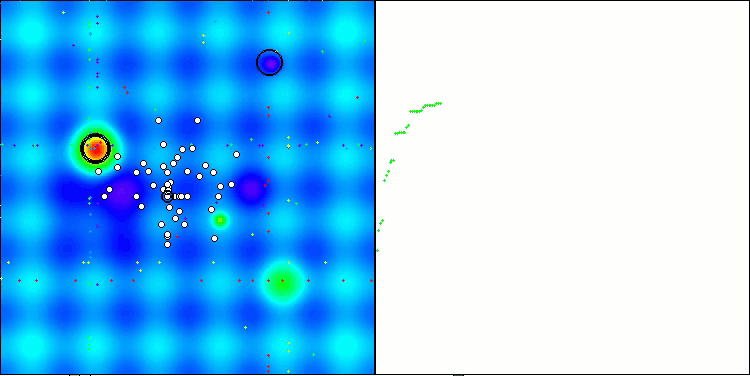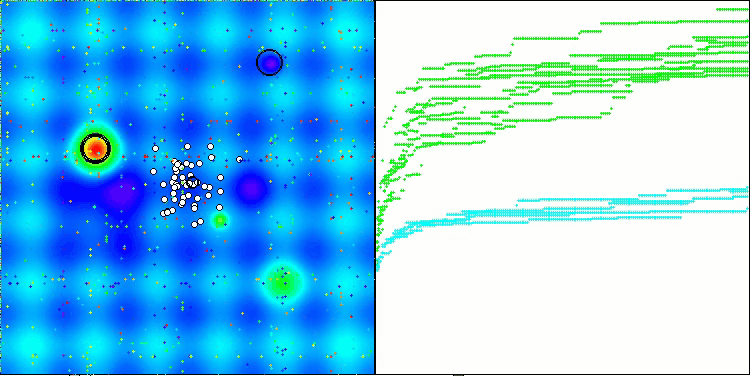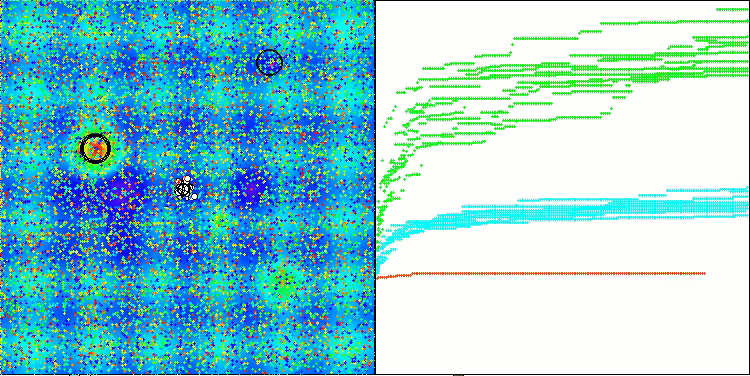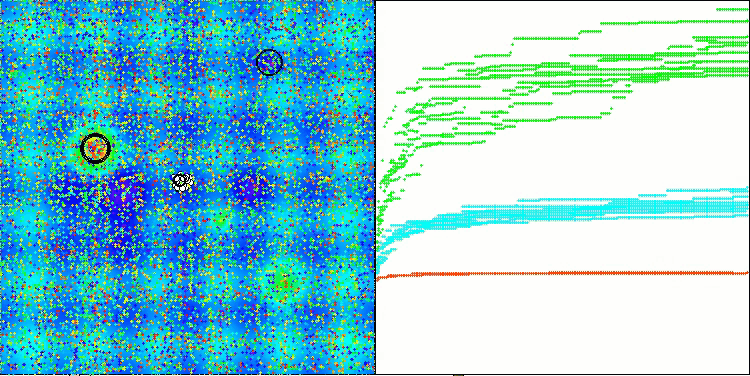
SOA mit der Testfunktion Hilly

Forest

  SOA mit der Testfunktion Forest

Megacity

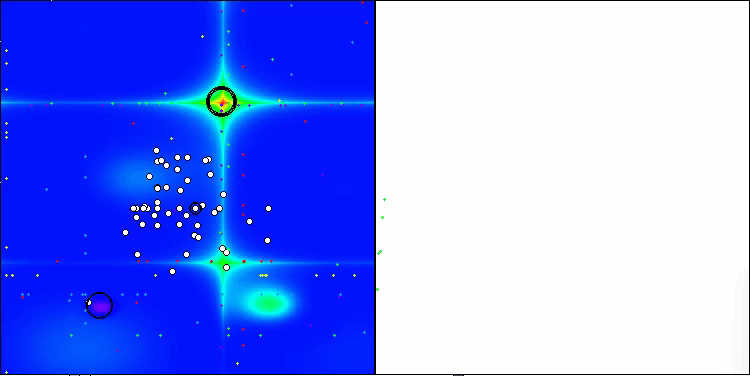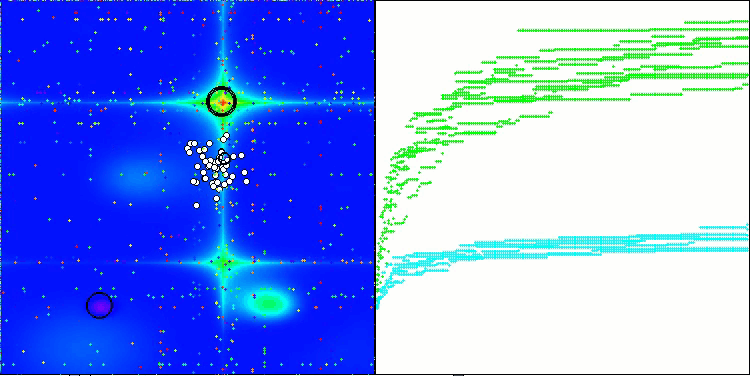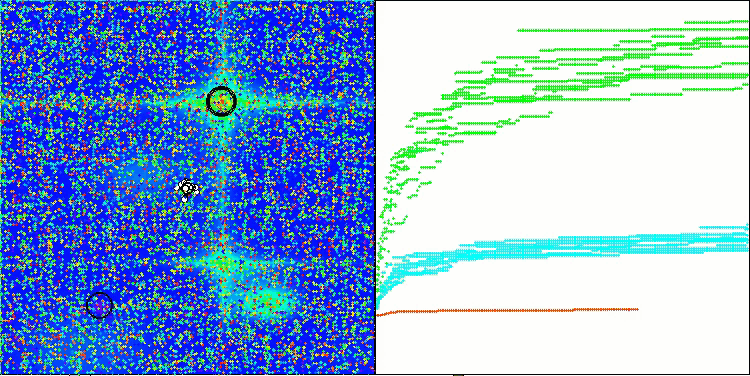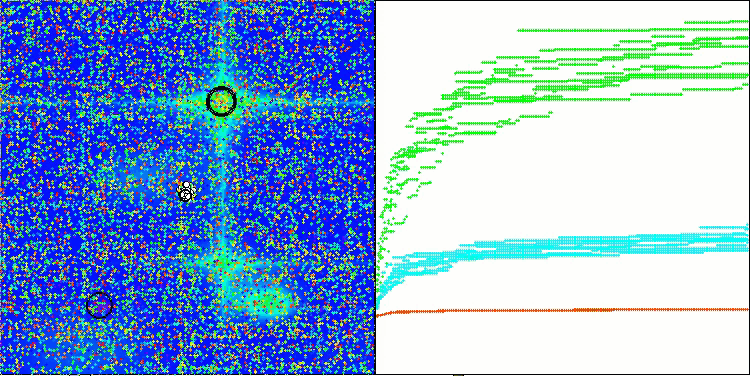
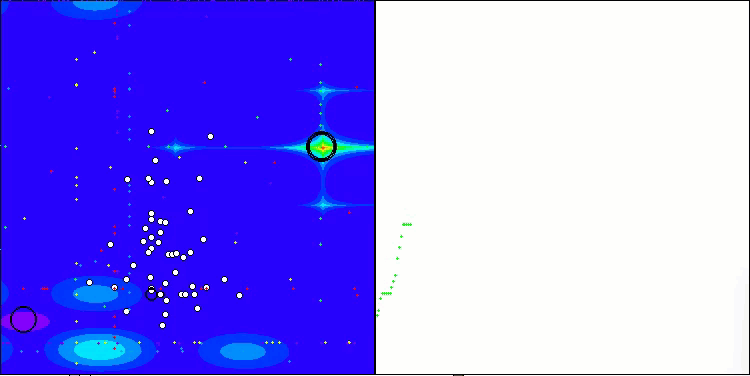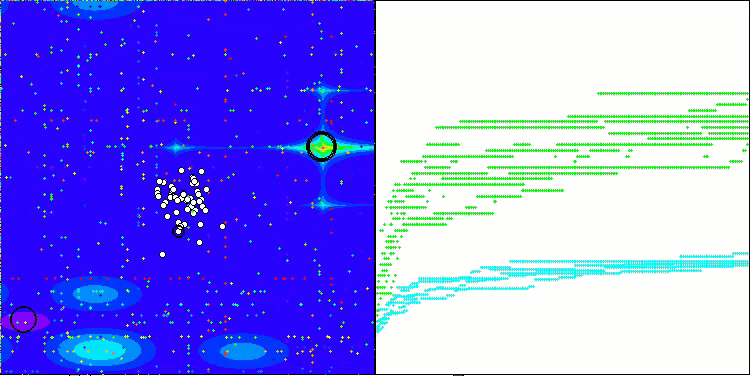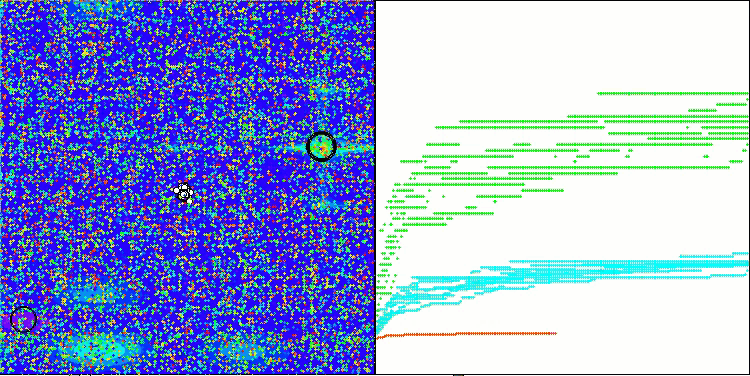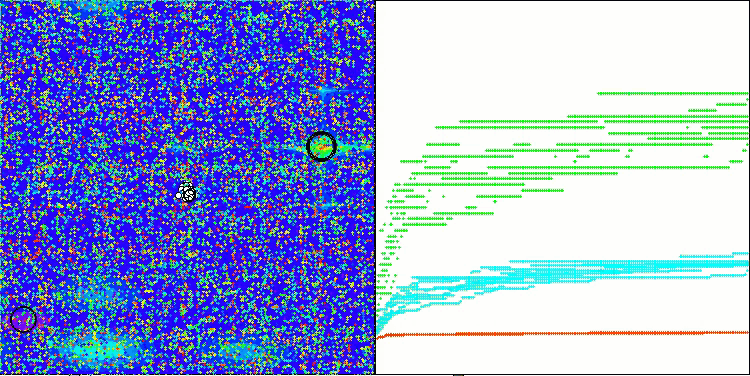
SOA mit der Testfunktion Megacity


Aufgrund der Testergebnisse schaffte es der ursprüngliche AOA-Algorithmus nicht in die Rangliste, da sein Ergebnis unter Platz 45 lag. Der neue Algorithmus Simple Optimization Algorithm (SOA) schaffte es in die Rangliste und landete auf Platz 29.

# AO Beschreibung Hilly Hilly final Forest Forest final Megacity (discrete) Megacity final Final result % of MAX
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 ANS Suche über die gesamte Nachbarschaft 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
2 CLA Code-Sperr-Algorithmus (joo) 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
3 AMOm Optimierung der Tiermigration M 0,90358 0,84317 0,46284 2,20959 0,99001 0,92436 0,46598 2,38034 0,56769 0,59132 0,23773 1,39675 5.987 66,52
4 (P+O)ES (P+O) Entwicklungsstrategien 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
5 CTA Kometenschweif-Algorithmus (joo) 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
6 SDSm stochastische Diffusionssuche M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
7 AAm Algorithmus für das Bogenschießen M 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
8 ESG Entwicklung sozialer Gruppen (joo) 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
9 SIA Simuliertes isotropes Glühen (Joo) 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
10 ACS künstliche, kooperative Suche 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
11 ASO Anarchische Gesellschaftsoptimierung 0,84872 0,74646 0,31465 1,90983 0,96148 0,79150 0,23803 1,99101 0,57077 0,54062 0,16614 1,27752 5.178 57,54
12 AOSm Suche nach atomaren Orbitalen M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
13 TSEA Schildkrötenpanzer-Evolutionsalgorithmus (joo) 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
14 DE differentielle Evolution 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
15 CRO Optimierung chemischer Reaktionen 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
16 BSA Vogelschwarm-Algorithmus 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
17 HS Harmoniesuche 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
18 SSG Setzen, Säen und Wachsen 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
19 BCOm Optimierung mit der bakteriellen Chemotaxis M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
20 ABO Optimierung des afrikanischen Büffels 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
21 (PO)ES (PO) Entwicklungsstrategien 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
22 TSm Tabu-Suche M 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
23 BSO Brainstorming-Optimierung 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
24 WOAm Wal-Optimierungsalgorithmus M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
25 AEFA Algorithmus für künstliche elektrische Felder 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
26 AEO Algorithmus zur Optimierung auf der Grundlage künstlicher Ökosysteme 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
27 ACOm Ameisen-Kolonie-Optimierung M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
28 BFO-GA Optimierung der bakteriellen Futtersuche — ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
29 SOA einfacher Optimierungsalgorithmus 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
30 ABHA Algorithmus für künstliche Bienenstöcke 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
31 ACMO Optimierung atmosphärischer Wolkenmodelle 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
32 ASHA Algorithmus für künstliches Duschen 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
33 ASBO Optimierung des adaptiven Sozialverhaltens 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
34 MEC Evolutionäre Berechnung des Geistes 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
35 IWO Optimierung mit invasiven Unkräutern 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
36 Micro-AIS Künstliches Mikro-Immunsystem 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
37 COAm Kuckuck-Optimierungsalgorithmus M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
38 SDOm Optimierung der Spiraldynamik M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
39 NMm Nelder-Mead-Verfahren M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
40 FAm Firefly-Algorithmus M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
41 GSA Algorithmus für die Schwerkraftsuche 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
42 BFO Optimierung der bakteriellen Futtersuche 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
43 ABC Künstliches Bienenvolk (Artificial Bee Colony, ABC) 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
44 BA Fledermaus-Algorithmus 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
45 AAA Künstlicher Algenalgorithmus (AAA) 0.50007 0.32040 0.25525 1.07572 0.37021 0.22284 0.16785 0.76089 0.27846 0.14800 0.09755 0.52402 2.361 26.23


Zusammenfassung

Wir haben uns ausführlich mit dem arithmetischen Optimierungsalgorithmus beschäftigt, dessen Implementierung sich als sehr einfach herausstellte. Doch wie so oft ist die Einfachheit nicht immer ein Garant für gute Ergebnisse. Der wahre Schlüssel zum Erfolg liegt in der Einfachheit! Ich mache natürlich nur Spaß. Die Hauptprobleme der AOA sind die fehlende Interaktion und der fehlende Informationsaustausch zwischen den Mitgliedern der Population, was wiederum zu einem völligen Mangel an kombinatorischen Qualitäten bei dieser Suchstrategie führt.

Ein weiterer Nachteil des Algorithmus ist die mangelnde Variabilität seiner Suchoperatoren. Obwohl die Operatoren für jede Koordinate nach dem Zufallsprinzip ausgewählt werden, ist es dem Algorithmus dadurch nicht möglich, in der mehrdimensionalen Landschaft des Suchraums effektiv „einzuhaken“. Der AOA-Algorithmus enthält jedoch rationale und logische Ansätze, z. B. dass sich die Elemente MoA und MoP mit jeder Epoche ändern. Sie bildeten die Grundlage für die Neuschöpfung des Algorithmus und seine Weiterentwicklung zu einer neuen, interessanten und äußerst einfachen Suchstrategie, die auf dem probabilistischen Ansatz des Kopierens von Informationen aus den besten Lösungen der Population und der Erzeugung von Zufallslösungen im Suchraum beruht.

Mit jeder Epoche nimmt die Zufälligkeit der Entscheidungen der Population ab, während die Konzentration der erfolgreichen Richtungen zunimmt. Dies ist vergleichbar mit dem Bau einer eleganten Brücke über einen Fluss: In der Anfangsphase der Arbeiten werden verschiedene Materialien und Konstruktionen verwendet, die für das Endergebnis möglicherweise nicht geeignet sind. Je weiter das Projekt jedoch fortschreitet, desto deutlicher werden die besten Lösungen, und unnötige Elemente werden verworfen. Dadurch wird die Brücke immer harmonischer und stabiler und verbindet die Ufer mit Eleganz und Kraft.

Tabelle

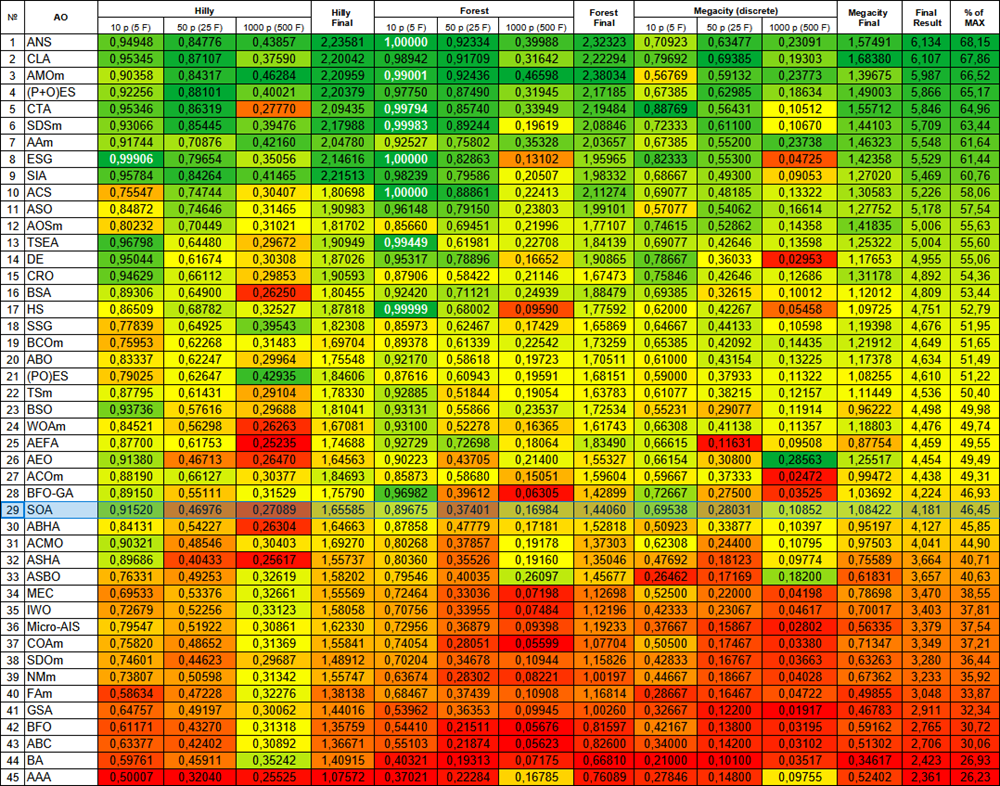
Abbildung 2. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben

Histogramm

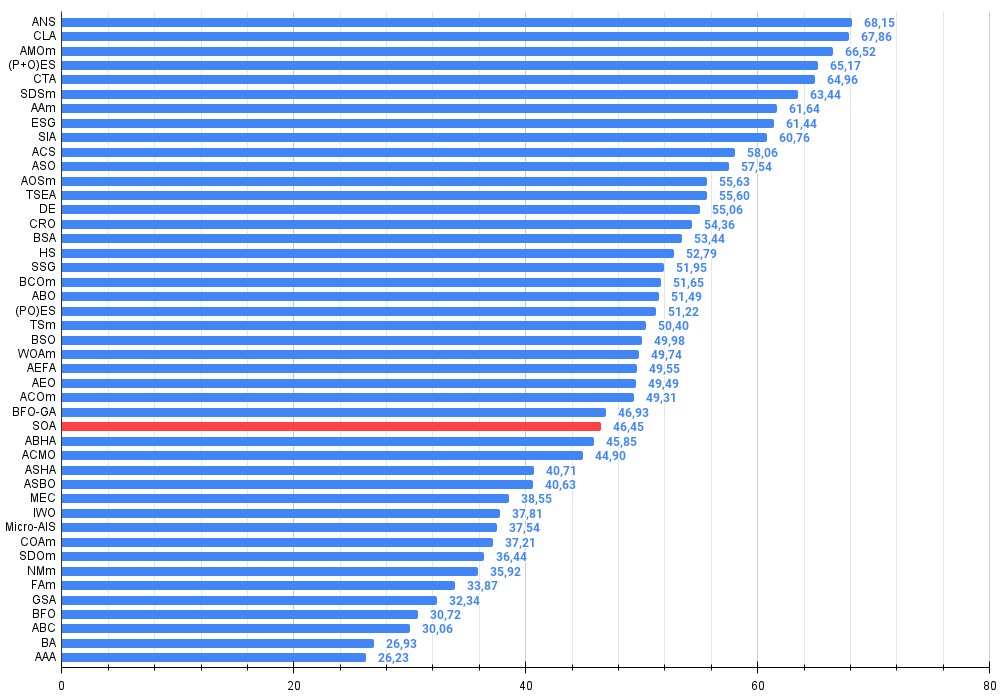
Abbildung 3. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, je mehr, desto besser,

wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Wertungstabelle)


Vor- und Nachteile von SOA:

Vorteile:

  1. Geringe Anzahl von externen Parametern.
  2. Gute Ergebnisse bei niedrigdimensionalen Problemen, insbesondere bei diskreten Problemen.
  3. Schnell.
  4. Geringe Streuung der Ergebnisse bei kleindimensionalen Problemen.
  5. Sehr einfache Umsetzung.

Nachteile

  1. Geringe Skalierbarkeit.

Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.

Programme, die im diesem Artikel verwendet werden

# Name Typ Beschreibung
1 #C_AO.mqh
 Include
 Übergeordnete Klasse von Populationsoptimierungsalgorithmen
2 #C_AO_enum.mqh
 Include
 Aufzählung von Algorithmen zur Populationsoptimierung
3 TestFunctions.mqh
 Include
 Bibliothek mit Testfunktionen
4
 TestStandFunctions.mqh
 Include
 Bibliothek der Testfunktionen
5
 Utilities.mqh
 Include
 Bibliothek der Hilfsfunktionen
6
 CalculationTestResults.mqh
 Include
 Skript zur Berechnung der Ergebnisse in der Vergleichstabelle
7
 Testing AOs.mq5
 Skript Der einheitliche Prüfstand für alle Algorithmen zur Populationsoptimierung
8
 Simple use of population optimization algorithms.mq5
 Skript
Ein einfaches Beispiel für die Verwendung von Algorithmen zur Populationsoptimierung ohne Visualisierung
9
 AO_AOA_ArithmeticOptimizationAlgorithm.mqh
 Include AOA-Algorithmus-Klasse
10
 AO_SOA_SimpleOptimizationAlgorithm.mqh
 Include
 SOA-Algorithmus-Klasse
11
Test_AO_AOA.mq5
 Skript AOA-Test
12
 Test_AO_SOA.mq5
 Skript
 SOA-Test

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16364

Beigefügte Dateien |
ZIP herunterladen
AOA_SOA.zip (141.9 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum
Neuronale Netze im Handel: Hyperbolisches latentes Diffusionsmodell (HypDiff) Neuronale Netze im Handel: Hyperbolisches latentes Diffusionsmodell (HypDiff)
Der Artikel befasst sich mit Methoden zur Kodierung von Ausgangsdaten im hyperbolischen latenten Raum durch anisotrope Diffusionsprozesse. Dies trägt dazu bei, die topologischen Merkmale der aktuellen Marktsituation genauer zu erfassen und die Qualität der Analyse zu verbessern.
Volumetrische neuronale Netzwerkanalyse als Schlüssel zu zukünftigen Trends Volumetrische neuronale Netzwerkanalyse als Schlüssel zu zukünftigen Trends
Der Artikel untersucht die Möglichkeit, die Preisprognose auf der Grundlage der Analyse des Handelsvolumens zu verbessern, indem die Prinzipien der technischen Analyse mit der Architektur des neuronalen Netzes LSTM integriert werden. Besonderes Augenmerk wird auf die Erkennung und Interpretation anomaler Volumina, die Verwendung von Clustern und die Erstellung von Merkmalen auf der Grundlage von Volumina und deren Definition im Rahmen des maschinellen Lernens gelegt.
Nichtlineare Regressionsmodelle an der Börse Nichtlineare Regressionsmodelle an der Börse
Nichtlineare Regressionsmodelle an der Börse: Ist es möglich, die Finanzmärkte vorherzusagen? Betrachten wir die Erstellung eines Modells für die Vorhersage der Preise für EURUSD, und machen zwei Roboter auf der Grundlage - in Python und MQL5.
Schneller Handelsstrategie-Tester in Python mit Numba Schneller Handelsstrategie-Tester in Python mit Numba
Der Artikel implementiert einen schnellen Strategietester für maschinelle Lernmodelle unter Verwendung von Numba. Das ist 50 Mal schneller als der reine Python-Strategie-Tester. Der Autor empfiehlt die Verwendung dieser Bibliothek, um mathematische Berechnungen zu beschleunigen, insbesondere solche, die Schleifen beinhalten.