MetaTrader 5 / Тестер
English 中文 Español Deutsch 日本語 Português
preview
Алгоритм арифметической оптимизации (AOA): Путь от AOA к SOA (Simple Optimization Algorithm)

Алгоритм арифметической оптимизации (AOA): Путь от AOA к SOA (Simple Optimization Algorithm)

MetaTrader 5 — Тестер |
600 0
Andrey Dik
Andrey Dik

Содержание

  1. Введение
  2. Реализация алгоритма
  3. Результаты тестов


Введение

Алгоритм арифметической оптимизации (Arithmetic Optimization Algorithm, AOA) представляет собой оригинальный метод, основанный на простых арифметических операциях, таких как сложение, вычитание, умножение и деление. Его суть заключается в использовании этих базовых математических принципов для поиска оптимальных решений в разнообразных задачах. AOA был разработан командой исследователей, включая Лайита Абулигу и впервые представлен в 2021 году. Этот алгоритм принадлежит к классу метаэвристических методов (высокоуровневых алгоритмов), которые направлены на поиск, генерацию и вероятностный выбор из нескольких эвристик, способных предоставить достаточно качественные решения за разумное время для сложных оптимизационных задач, где точные методы могут оказаться неэффективными или невозможными.

Меня привлек этот метод благодаря своей простой и, в то же время, элегантной идее применения совершенно элементарных арифметических операторов. Взаимосвязь между этими базовыми математическими действиями и метаэвристическими подходами создает взаимодействие, позволяющее решать сложные задачи оптимизации. Методы метаэвристики, применяемые в AOA, включают несколько ключевых принципов:

1. Популяционный подход. AOA использует популяцию решений, что позволяет охватить более широко пространство возможных решений. Это способствует избеганию локальных оптимумов и расширяет горизонты поиска.

2. Случайность и стохастичность. Включение элементов случайности в процесс поиска помогает алгоритмам избегать застревания в локальных оптимумах и обеспечивает более полное исследование пространства решений, что увеличивает вероятность нахождения глобального оптимума.

3. Баланс между исследованием и эксплуатацией. Как и многие другие метаэвристические алгоритмы, AOA стремится к гармонии между исследованием новых областей пространства решений и эксплуатацией уже известных эффективных решений. Это достигается путем применения арифметических операций для обновления позиций решений.

Таким образом, AOA является ярким примером метаэвристического алгоритма, который эффективно использует принципы популяционного подхода, случайности и балансирования между исследованием и эксплуатацией для решения оптимизационных задач, однако конкретно об эффективности находить оптимальные решения в сложных и многомерных пространствах для этого алгоритма мы поговорим после его реализации и тестирования.


Реализация алгоритма

Основная идея AOA заключается в использовании распределительного поведения арифметических операторов для поиска оптимальных решений. Алгоритм характеризуется простыми принципами, не очень большим количеством параметров и легкостью реализации. Алгоритм использует распределительные характеристики четырех основных арифметических операторов в математике, а именно: Умножение (Mε × ε), Деление (Dε ÷ ε), Вычитание (Sε − ε) и Сложение (Aε + ε). В AOA начальная популяция генерируется случайным образом в диапазоне [U; L], где верхние и нижние границы пространства поиска для целевой функции обозначены как U и L соответственно, с использованием следующего уравнения:

x = L + (U − L) × δ, где x представляет собой решение популяции, δ — это случайная переменная, принимающая значения в диапазоне [0, 1].

На каждой итерации выбор стратегии исследования и эксплуатации, а именно выбор одной из двух групп операторов, либо (деления; умножения), либо (вычитания; сложения) осуществляется в зависимости от результата функции MoA (math optimizer accelerated), которая является, по сути, расчетным значением вероятности и изменяется с каждой итерацией, вычисляется согласно уравнению:

MoA(t) = Min + t × (Max − Min) ÷ Maxt, где MoA(t) представляет собой функциональный результат на t-й итерации, t — указывает на текущую итерацию, которая находится в пределах от 1 до максимального числа итераций (Maxt). Минимальное возможное значение MoA обозначается как Min, а максимальное значение — как Max и являются внешними параметрами алгоритма.

Во всех четырех формулах арифметических операторов используется коэффициент MoP (math optimizer), который вычисляется следующим образом:

MoP(t) = 1 − (t ÷ Maxt)^(1 ÷ θ), где MoP(t) указывает значение функции MoP на t-й итерации. θ — это критический параметр,  который контролирует эффективность эксплуатации на протяжении итераций. В исходной работе у авторов алгоритма он установлен на уровне 5.

На рисунке 1 ниже представлены графики зависимости MoA и MoP от текущей итерации. Графики показывают, что с каждой итерации MoA линейно растет, что означает увеличение вероятности выбора группы операторов (вычитания; сложения), а вероятность выбора группы операторов (деления; умножения) пропорционально падает. В свою очередь, коэффициент MoP нелинейно падает, тем самым уменьшая очередное приращение к текущему положению агентов в популяции, что означает увеличение степени уточнения решений в процессе оптимизации.

MoAandMoP

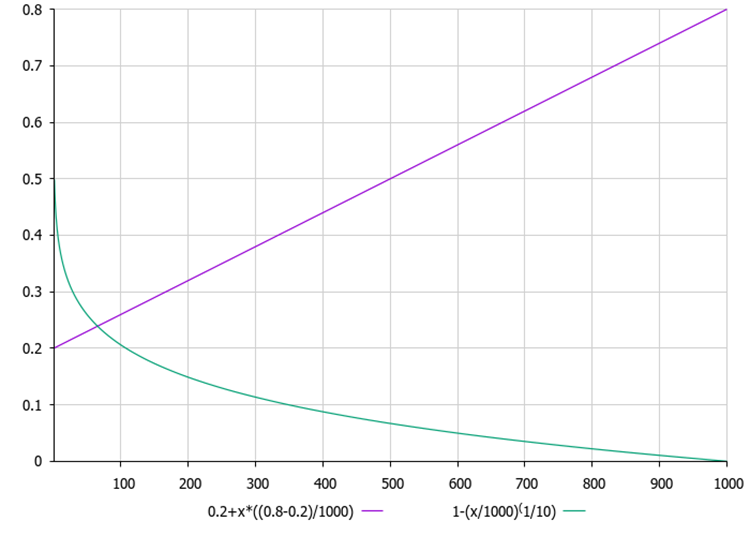
Рисунок 1. Фиолетовым цветом отмечен график вероятности MoA, а зеленым - график коэффициента MoP

Исследование или глобальный поиск в AOA осуществляется с использованием стратегий поиска на основе операторов Деления (D) и Умножения (M), если выполнилась вероятность MoA, что формулируется следующим образом, где с равной вероятностью выполняются следующие операторы:

xi,j(t+1) = best(xj) ÷ (MoPr + 𝜖) × ((Uj − Lj) × 𝜇 + Lj), если rand2 < 0.5; 

в противном случае:

xi,j(t+1) = best(xj) × (MoPr) × ((Uj − Lj) × 𝜇 + Lj), где xi(t+1) представляет собой i-е решение на (t+1)-й итерации, x(i,j)(t) представляет собой j-ю позицию i-го индивидуума в текущем поколении, best(xj) выражает j-ю позицию наилучшего решения на данный момент, ε — это маленькое положительное число, верхние и нижние пределы значений j-й позиции обозначаются как Uj и Lj соответственно. Параметр управления μ был установлен на уровне 0.5. 

Если вероятность MoA не выполнена, то в AOA выполняется стратегия эксплуатации (уточнение решения), которая была разработана с использованием операторов Вычитания (S) или Сложения (A). Здесь μ также является константой, которая фиксирована на уровне 0.5 по замыслу авторов. 

xi,j(t+1) = best(xj) − (MoPr) × ((Uj − Lj) × 𝜇 + Lj), если rand3 < 0.5 

xi,j(t+1) = best(xj) + (MoPr) × ((Uj − Lj) × 𝜇 + Lj), в противном случае.

В AOA параметры 𝜇 и θ являются очень важными, поскольку они участвуют в балансировке компромисса между исследованием и эксплуатацией. Поддержание хорошо сбалансированного исследования и эксплуатации является, как правило, очень сложной задачей. В исходной работе AOA значение 𝜇 было зафиксировано на уровне 0.5 как для исследования, так и для эксплуатации. Однако параметр θ, который влияет на эффективность эксплуатации на протяжении итераций, установлен на уровне 5. Авторы провели эксперименты с различными значениями 𝜇 и θ и обнаружили, что значения 𝜇 = 0.5 и θ = 5 чаще всего давали лучшие результаты для унимодальных и мультимодальных тестовых функций в различных размерностях. 

Теперь напишем псевдокод алгоритма AOA:

увеличить номер эпохи на 1

// Начальная инициализация
ЕСЛИ это первый запуск ТОГДА
    ДЛЯ каждой частицы в популяции:
        ДЛЯ каждой координаты:
            задать случайную позицию в допустимом диапазоне
            привести позицию к дискретному значению
    отметить, что инициализация выполнена
    закончить функцию
КОНЕЦ ЕСЛИ

// Основной процесс оптимизации
вычислить MoA = минMoA + номерЭпохи * ((максMoA - минMoА) / всегоЭпох)
вычислить MoP = 1 - (номерЭпохи / всегоЭпох)^(1/θ)

// Фаза исследования пространства решений
ДЛЯ каждой частицы в популяции:
    ДЛЯ каждой координаты:
        сгенерировать три случайных значения (rand1, rand2, rand3)
        взять лучшее известное значение для этой координаты
        
        ЕСЛИ rand1 < MoAc ТОГДА
            ЕСЛИ rand2 > 0.5 ТОГДА
                обновить позицию используя Деление
            ИНАЧЕ
                обновить позицию используя Умножение
            КОНЕЦ ЕСЛИ
        ИНАЧЕ
            ЕСЛИ rand3 > 0.5 ТОГДА
                обновить позицию используя Вычитание
            ИНАЧЕ
                обновить позицию используя Сложение
            КОНЕЦ ЕСЛИ
        КОНЕЦ ЕСЛИ
        
        привести новую позицию к допустимому дискретному значению
        
Обновить лучшее решение

Переходим к написанию кода. Класс "C_AO_AOA" представляет собой реализацию алгоритма AOA и предназначен для решения задач оптимизации с помощью метода, основанного на арифметических операциях. Публичные методы:

1. Метод "SetParams ()" устанавливает значения параметров из массива "params". Этот метод позволяет изменять параметры алгоритма после его инициализации.

2. Метод "Init ()":

  • Инициализирует алгоритм, принимая на вход минимальный и максимальный диапазоны поиска, шаг поиска и количество эпох. 
  • Возвращает "true", если инициализация прошла успешно, иначе "false".

3. Метод "Moving ()" — выполняет перемещение частиц в пространстве решений. Этот метод реализует логику обновления позиций частиц на основе заданных параметров и текущего состояния.

4. Метод "Revision()" — проводит ревизию текущих позиций частиц, обновляя лучшее найденное значение функции и координаты соответствующей частицы.

Приватные поля, параметры класса:

  • minT  — минимальное значение вероятности MoA.
  • maxT  — максимальное значение вероятности MoA.
  • θ  — параметр, влияющий на баланс исследования и эксплуатации.
  • μ  — параметр, используемый для управления изменениями в позициях частиц (размах перемещения).
  • ϵ — малое число для предотвращения деления на ноль.

Информация о состоянии алгоритма:

  • epochs — общее количество эпох, которые будет проходить алгоритм.
  • epochNow — текущая эпоха, используемая для отслеживания прогресса алгоритма, влияет на вероятность MoA и коэффициент MoP.

Класс "C_AO_AOA" реализует основные компоненты алгоритма AOA, включая инициализацию, перемещение частиц и ревизию.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AOA () { }
  C_AO_AOA ()
  {
    ao_name = "AOA";
    ao_desc = "Arithmetic Optimization Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/16364";

    popSize = 50;   // Размер популяции
    minT    = 0.1;  // Минимальное значение T
    maxT    = 0.9;  // Максимальное значение T
    θ       = 10;   // Параметр θ
    μ       = 0.01; // Параметр μ

    ArrayResize (params, 5); // Изменение размера массива параметров

    // Инициализация параметров
    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "minT";    params [1].val = minT;
    params [2].name = "maxT";    params [2].val = maxT;
    params [3].name = "θ";       params [3].val = θ;
    params [4].name = "μ";       params [4].val = μ;
  }

  void SetParams () // Метод для установки параметров
  {
    popSize = (int)params [0].val; // Установка размера популяции
    minT    = params      [1].val; // Установка минимального T
    maxT    = params      [2].val; // Установка максимального T
    θ       = params      [3].val; // Установка параметра θ
    μ       = params      [4].val; // Установка параметра μ
  }

  bool Init (const double &rangeMinP  [], // Минимальный диапазон поиска
             const double &rangeMaxP  [], // Максимальный диапазон поиска
             const double &rangeStepP [], // Шаг поиска
             const int     epochsP = 0);  // Количество эпох

  void Moving   (); // Метод перемещения частиц
  void Revision (); // Метод ревизии

  //----------------------------------------------------------------------------
  double minT; // Минимальное значение T
  double maxT; // Максимальное значение T
  double θ;    // Параметр θ
  double μ;    // Параметр μ
  double ϵ;    // Параметр для предотвращения деления на ноль

  private: //-------------------------------------------------------------------
  int epochs;    // Общее количество эпох
  int epochNow;  // Текущая эпоха
};
//——————————————————————————————————————————————————————————————————————————————

Метод "Init" класса "C_AO_AOA" отвечает за инициализацию алгоритма оптимизации, устанавливая параметры диапазона поиска, шаги и количество эпох, в течение которых будет выполняться оптимизация. Логика работы метода:

1. Метод сначала вызывает "StandardInit", который инициализирует стандартные параметры алгоритма. Если эта инициализация не удалась, метод "Init" сразу завершает выполнение и возвращает "false".

2. Установка параметров:

  • Устанавливает общее количество эпох "epochs" на основе переданного параметра "epochsP".
  • Инициализирует текущую эпоху "epochNow" значением "0".
  • Устанавливает значение "ϵ" (малое значение для предотвращения деления на ноль) на "DBL_EPSILON", что является стандартным значением для представления наименьшего положительного числа, которое может быть представлено в типе "double".

3. Если все шаги выполнены успешно, метод возвращает "true", что указывает на успешную инициализацию алгоритма.

Метод "Init" является важной частью подготовки алгоритма к выполнению, так как он устанавливает основные параметры, которые будут использоваться в процессе оптимизации. Вызов данного метода приведет к сбросу всех параметров и переменных в исходное состояние.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AOA::Init (const double &rangeMinP  [], // Минимальный диапазон поиска
                     const double &rangeMaxP  [], // Максимальный диапазон поиска
                     const double &rangeStepP [], // Шаг поиска
                     const int     epochsP = 0)   // Количество эпох
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; // Инициализация стандартных параметров

  //----------------------------------------------------------------------------
  epochs   = epochsP;     // Установка общего количества эпох
  epochNow = 0;           // Инициализация текущей эпохи
  ϵ        = DBL_EPSILON; // Установка значения ϵ

  return true;            // Возвращаем true при успешной инициализации
}
//——————————————————————————————————————————————————————————————————————————————

Метод "Moving" отвечает за перемещение частиц в пространстве решений в рамках алгоритма AOA. Он реализует основную логику обновления позиций частиц на основе текущего состояния и параметров алгоритма. Логика работы метода:

1. Увеличивает значение "epochNow", чтобы отразить, что наступила новая эпоха оптимизации.

2. Первоначальное случайное позиционирование: если еще не было выполнено обновление (ревизия), для каждой частицы генерируются случайные позиции в пределах заданных диапазонов  "rangeMin" и "rangeMax". Каждая позиция затем дискретизируется с помощью метода "SeInDiSp" с использованием заданного шага.

3. MoAc и MoPr — вычисляются на основе текущей эпохи и заданных параметров. Эти значения определяют вероятности, которые используются для обновления позиций частиц.

4. Фаза исследования. Для каждой частицы и каждой координаты выполняется обновление позиции на основе случайных значений и вычисленных параметров. Позиции могут быть обновлены с использованием различных операторов (деления и умножения), а также вероятностных условий.

5. После обновления позиция также приводится к дискретным значениям с помощью метода "SeInDiSp".

//——————————————————————————————————————————————————————————————————————————————
// Метод перемещения частиц
void C_AO_AOA::Moving ()
{
  epochNow++; // Увеличиваем номер текущей эпохи

  // Начальное случайное позиционирование
  if (!revision) // Если еще не было ревизии
  {
    for (int i = 0; i < popSize; i++) // Для каждой частицы
    {
      for (int c = 0; c < coords; c++) // Для каждой координаты
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);                             // Генерация случайной позиции
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Приведение к дискретным значениям
      }
    }

    revision = true; // Установка флага ревизии
    return;          // Выход из метода
  }

  //----------------------------------------------------------------------------
  double MoAc = minT + epochNow * ((maxT - minT) / epochs); // Вычисление значения MoAc
  double MoPr = 1.0 - pow (epochNow / epochs, (1.0 / θ));   // Вычисление значения MoPr
  double best = 0.0;                                        // Переменная для хранения лучшего значения

  // Фаза исследования с использованием операторов Деления (D) и Умножения (M)
  for (int i = 0; i < popSize; i++) // Для каждой частицы
  {
    for (int c = 0; c < coords; c++) // Для каждой координаты
    {
      double rand1 = u.RNDprobab (); // Генерация случайного значения
      double rand2 = u.RNDprobab (); // Генерация случайного значения
      double rand3 = u.RNDprobab (); // Генерация случайного значения

      best = cB [c];                 // Сохранение текущего лучшего значения

      if (rand1 < MoAc)              // Если случайное значение меньше MoAc
      {
        if (rand2 > 0.5)             // Если случайное значение больше 0.5
        {
          a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Обновление позиции частицы
        }
        else
        {
          a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Обновление позиции частицы
        }
      }
      else // Если случайное значение больше или равно MoAc
      {
        if (rand3 > 0.5) // Если случайное значение больше 0.5
        {
          a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Обновление позиции частицы
        }
        else
        {
          a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Обновление позиции частицы
        }
      }

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Приведение к дискретным значениям
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Метод "Revision" в классе "C_AO_AOA" обновляет информацию о лучшей частице в популяции. Он перебирает все частицы, сравнивает их значения функции с текущим лучшим значением и, если находит лучшее, обновляет его и сохраняет индекс. Затем копирует координаты лучшей частицы в массив "cB".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AOA::Revision ()
{
  int ind = -1;                     // Индекс для хранения лучшей частицы

  for (int i = 0; i < popSize; i++) // Для каждой частицы
  {
    if (a [i].f > fB)               // Если значение функции лучше, чем текущее лучшее
    {
      fB = a [i].f;                 // Обновление лучшего значения функции
      ind = i;                      // Сохранение индекса лучшей частицы
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Копирование координат лучшей частицы
}
//——————————————————————————————————————————————————————————————————————————————

Метод "SeInDiSp" класса "C_AO_Utilities" ограничивает входное значение "In" в диапазоне [InMin, InMax] с заданным шагом "Step".

1. Если "In" меньше или равно "InMin", возвращает "InMin".
2. Если "In" больше или равно "InMax", возвращает "InMax".
3. Если "Step" равен 0, возвращает исходное значение "In".
4. В противном случае, округляет значение (In - InMin) / Step и возвращает скорректированное значение в пределах диапазона с учетом шага.

double C_AO_Utilities :: SeInDiSp (double In, double InMin, double InMax, double Step)
{
  if (In <= InMin) return (InMin);
  if (In >= InMax) return (InMax);
  if (Step == 0.0) return (In);
  else return (InMin + Step * (double)MathRound ((In - InMin) / Step));
}


Результаты тестов

Алгоритм AOA достаточно простой, посмотрим на его результативность на тестовых задачах.

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.3914957505847635
25 Hilly's; Func runs: 10000; result: 0.27733670012505607
500 Hilly's; Func runs: 10000; result: 0.2514517003089684
=============================
5 Forest's; Func runs: 10000; result: 0.23495704012464264
25 Forest's; Func runs: 10000; result: 0.1853447250852242
500 Forest's; Func runs: 10000; result: 0.15382470751079919
=============================
5 Megacity's; Func runs: 10000; result: 0.19846153846153847
25 Megacity's; Func runs: 10000; result: 0.11815384615384619
500 Megacity's; Func runs: 10000; result: 0.09475384615384692
=============================
All score: 1.90578 (21.18%)

По результатам тестирования алгоритм набирает все лишь 21.18% из 100% возможных. Очень слабый результат, к сожалению, ниже самого последнего в текущей рейтинговой таблице. Попробуем изменить логику алгоритма, чтобы добиться более высоких результатов. Будем производить изменения по шагам и отслеживать результаты.

Логика оригинального алгоритма AOA предусматривает стохастический поиск, который заключается только в вероятностном характере выбора одного из четырех математических операторов. Добавим к коэффициенту смещения μ элемент случайности, помножив его на случайное число в диапазоне от 0 до 1.

// Фаза исследования с использованием операторов Деления (D) и Умножения (M)
  for (int i = 0; i < popSize; i++) // Для каждой частицы
  {
    for (int c = 0; c < coords; c++) // Для каждой координаты
    {
      double rand1 = u.RNDprobab (); // Генерация случайного значения
      double rand2 = u.RNDprobab (); // Генерация случайного значения
      double rand3 = u.RNDprobab (); // Генерация случайного значения

      best = cB [c];                 // Сохранение текущего лучшего значения

      μ *= u.RNDfromCI (0, 1);       // Случайное изменение параметра μ

      if (rand1 < MoAc)              // Если случайное значение меньше MoAc
      {
        if (rand2 > 0.5)             // Если случайное значение больше 0.5
        {
          a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Обновление позиции частицы
        }
        else
        {
          a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Обновление позиции частицы
        }
      }
      else // Если случайное значение больше или равно MoAc
      {
        if (rand3 > 0.5) // Если случайное значение больше 0.5
        {
          a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Обновление позиции частицы
        }
        else
        {
          a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Обновление позиции частицы
        }
      }

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Приведение к дискретным значениям
    }
  }

Протестируем алгоритм с теми же параметрами:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.3595591180258857
25 Hilly's; Func runs: 10000; result: 0.2804913285516192
500 Hilly's; Func runs: 10000; result: 0.25204298245610646
=============================
5 Forest's; Func runs: 10000; result: 0.24115834887873383
25 Forest's; Func runs: 10000; result: 0.18034196700384764
500 Forest's; Func runs: 10000; result: 0.15441446106797124
=============================
5 Megacity's; Func runs: 10000; result: 0.18307692307692305
25 Megacity's; Func runs: 10000; result: 0.12400000000000003
500 Megacity's; Func runs: 10000; result: 0.09470769230769309
=============================
All score: 1.86979 (20.78%)

К сожалению, результат стал еще хуже. Необходимо предпринять дополнительные шаги. Однако сам факт добавления случайности в детерминированное выражение определенно должен улучшить вариативность стратегии поиска. Посмотрим внимательно на формулы математических операторов — в формуле каждого из них присутствует слагаемое "rangeMin [c]". По сути, полученное выражение в этих операторах всегда центрируется относительно минимальной границы оптимизируемых параметров. В этом нет очевидной логики, поэтому удалим этот элемент из всех формул.

// Фаза исследования с использованием операторов Деления (D) и Умножения (M)
for (int i = 0; i < popSize; i++) // Для каждой частицы
{
  for (int c = 0; c < coords; c++) // Для каждой координаты
  {
    double rand1 = u.RNDprobab (); // Генерация случайного значения
    double rand2 = u.RNDprobab (); // Генерация случайного значения
    double rand3 = u.RNDprobab (); // Генерация случайного значения

    best = cB [c];                 // Сохранение текущего лучшего значения

    μ *= u.RNDfromCI (0, 1);       // Изменение параметра μ

    if (rand1 < MoAc)              // Если случайное значение меньше MoAc
    {
      if (rand2 > 0.5)             // Если случайное значение больше 0.5
      {
        a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]); // Обновление позиции частицы
      }
      else
      {
        a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]);     // Обновление позиции частицы
      }
    }
    else // Если случайное значение больше или равно MoAc
    {
      if (rand3 > 0.5) // Если случайное значение больше 0.5
      {
        a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]);     // Обновление позиции частицы
      }
      else
      {
        a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]);     // Обновление позиции частицы
      }
    }

    a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Приведение к дискретным значениям
  }
}

Тестируем. Ниже полученные результаты:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.36094646986361645
25 Hilly's; Func runs: 10000; result: 0.28294095623218063
500 Hilly's; Func runs: 10000; result: 0.2524581968477915
=============================
5 Forest's; Func runs: 10000; result: 0.2463208325927641
25 Forest's; Func runs: 10000; result: 0.1772140022690996
500 Forest's; Func runs: 10000; result: 0.15367993432040622
=============================
5 Megacity's; Func runs: 10000; result: 0.1923076923076923
25 Megacity's; Func runs: 10000; result: 0.11938461538461542
500 Megacity's; Func runs: 10000; result: 0.09433846153846229
=============================
All score: 1.87959 (20.88%)

Внесенные изменения не привели к улучшению производительности, что довольно странно, учитывая, что мы уже реализовали серьезные изменения в стратегии поиска. Это может свидетельствовать о том, что сама стратегия обладает недостатками, и удаление отдельных компонентов не оказывает значительного влияния на результаты.

В стратегии поиска присутствует компонент MoA, который увеличивается линейно с каждой итерацией (см. рисунок 1). Попробуем использовать этот компонент как вероятностный выбор одной из координат самого лучшего решения и копирования в текущее рабочее решение. Это должно добавить комбинаторные свойства в стратегию поиска, используя обмен информацией через лучшее решение в популяции (в авторской версии обмен информацией между агентами отсутствует).

// Фаза исследования с использованием операторов Деления (D) и Умножения (M)
for (int i = 0; i < popSize; i++) // Для каждой частицы
{
  for (int c = 0; c < coords; c++) // Для каждой координаты
  {
    double rand1 = u.RNDprobab (); // Генерация случайного значения
    double rand2 = u.RNDprobab (); // Генерация случайного значения
    double rand3 = u.RNDprobab (); // Генерация случайного значения

    best = cB [c];                 // Сохранение текущего лучшего значения

    μ *= u.RNDfromCI (0, 1);       // Изменение параметра μ

    if (rand1 < MoAc)              // Если случайное значение меньше MoAc
    {
      if (rand2 > 0.5)             // Если случайное значение больше 0.5
      {
        a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ); // Обновление позиции частицы
      }
      else
      {
        a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);     // Обновление позиции частицы
      }
    }
    else // Если случайное значение больше или равно MoAc
    {
      if (rand3 > 0.5) // Если случайное значение больше 0.5
      {
        a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);     // Обновление позиции частицы
      }
      else
      {
        a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);     // Обновление позиции частицы
      }
    }

    if (u.RNDbool () < MoAc) a [i].c [c] = cB [c];                                            // Установка на лучшее значение

    a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Приведение к дискретным значениям
  }
}

Полученные результаты после внесения логики обмена информацией посредством лучшего решения:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.360814744695913
25 Hilly's; Func runs: 10000; result: 0.28724958448168375
500 Hilly's; Func runs: 10000; result: 0.2523432997811412
=============================
5 Forest's; Func runs: 10000; result: 0.26319762212870146
25 Forest's; Func runs: 10000; result: 0.1796822846691542
500 Forest's; Func runs: 10000; result: 0.1546335398592898
=============================
5 Megacity's; Func runs: 10000; result: 0.18
25 Megacity's; Func runs: 10000; result: 0.12153846153846157
500 Megacity's; Func runs: 10000; result: 0.09373846153846228
=============================
All score: 1.89320 (21.04%)

Видим улучшения в производительности, но пока в пределах разброса самих решений. Теперь добавим в туже часть кода вероятность генерации случайного значения для координаты в пределах всего допустимого диапазона оптимизируемых параметров, которая уменьшается нелинейно согласно формуле MoP. 

// Вероятностное обновление позиции частицы
if (u.RNDbool () < MoAc) a [i].c [c] = cB [c];                                        // Установка на лучшее значение
else
  if (u.RNDbool () < MoPr) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);    // Генерация новой случайной позиции

Смотрим следующие результаты:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.8354927331645667
25 Hilly's; Func runs: 10000; result: 0.3963221867834875
500 Hilly's; Func runs: 10000; result: 0.2526544322311671
=============================
5 Forest's; Func runs: 10000; result: 0.7689954585427405
25 Forest's; Func runs: 10000; result: 0.3144560745800252
500 Forest's; Func runs: 10000; result: 0.15495875390289315
=============================
5 Megacity's; Func runs: 10000; result: 0.6076923076923076
25 Megacity's; Func runs: 10000; result: 0.24646153846153843
500 Megacity's; Func runs: 10000; result: 0.09816923076923163
=============================
All score: 3.67520 (40.84%)

Удивительно, производительность резко возросла! Это означает, что мы движемся в правильном направлении. Следует отметить, что именно было добавлено в логику AOA: в начале оптимизации, на первой эпохе, вероятность копирования координат глобального лучшего решения в текущие минимальна. Это вполне логично, поскольку на начальном этапе оптимизации стратегия только начинает исследовать пространство поиска. В то же время вероятность генерации случайных решений в пределах всего пространства поиска на первой итерации максимальна. На протяжении всех эпох эти вероятности изменяются: вероятность копирования координат глобального решения возрастает, тогда как вероятность генерации случайных решений, наоборот, снижается (см. рисунок 1).

Поскольку производительность возросла после внесенных мной изменений, а ранее было замечено, что изменения в авторской логике не приводят к заметным улучшениям, имеет смысл полностью исключить все арифметические операторы. Давайте протестируем полученный алгоритм на тестовых задачах:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8751771961221438
25 Hilly's; Func runs: 10000; result: 0.4645369071659114
500 Hilly's; Func runs: 10000; result: 0.27170038319811357
=============================
5 Forest's; Func runs: 10000; result: 0.8369443889312367
25 Forest's; Func runs: 10000; result: 0.36483865328371257
500 Forest's; Func runs: 10000; result: 0.17097532914778202
=============================
5 Megacity's; Func runs: 10000; result: 0.7046153846153846
25 Megacity's; Func runs: 10000; result: 0.28892307692307695
500 Megacity's; Func runs: 10000; result: 0.10847692307692398
=============================
All score: 4.08619 (45.40%)   

Как видно, результативность возросла еще почти на 5%, что вновь подтвердило правильность моих рассуждений. Мы получили интересные результаты с параметрами по умолчанию, однако, изменения в логику были внесены настолько кардинальные, что теперь необходимо подобрать оптимальные внешние параметры алгоритма. Дополнительным бонусом к увеличению производительности стало:

  • значительное ускорение работы, так как мы избавились от лишних генераций случайных чисел
  • уменьшение количества внешних параметров на один

Посмотрим итоговые результаты полученного алгоритма:

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.5|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9152036654779877
25 Hilly's; Func runs: 10000; result: 0.46975580956945456
500 Hilly's; Func runs: 10000; result: 0.27088799720164297
=============================
5 Forest's; Func runs: 10000; result: 0.8967497776673259
25 Forest's; Func runs: 10000; result: 0.3740125122006007
500 Forest's; Func runs: 10000; result: 0.16983896751516864
=============================
5 Megacity's; Func runs: 10000; result: 0.6953846153846155
25 Megacity's; Func runs: 10000; result: 0.2803076923076923
500 Megacity's; Func runs: 10000; result: 0.10852307692307792
=============================
All score: 4.18066 (46.45%) 

Полученный результат уже заслуживает места в рейтинговой таблице, а итоговая версия стратегии поиска полностью утратила элементы оригинальной логики авторского алгоритма. Поэтому я решил дать этому новому алгоритму и новое название — Простой Алгоритм Оптимизации, или SAO (Simple Optimization Algorithm). Давайте посмотрим на весь итоговый код алгоритма SAO.

#include "#C_AO.mqh"

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_SOA () { }
  C_AO_SOA ()
  {
    ao_name = "SOA";
    ao_desc = "Simple Optimization Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/16364";

    popSize = 50;   // Размер популяции
    minT    = 0.1;  // Минимальное значение T
    maxT    = 0.9;  // Максимальное значение T
    θ       = 10;   // Параметр θ

    ArrayResize (params, 4); // Изменение размера массива параметров

    // Инициализация параметров
    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "minT";    params [1].val = minT;
    params [2].name = "maxT";    params [2].val = maxT;
    params [3].name = "θ";       params [3].val = θ;
  }

  void SetParams () // Метод для установки параметров
  {
    popSize = (int)params [0].val; // Установка размера популяции
    minT    = params      [1].val; // Установка минимального T
    maxT    = params      [2].val; // Установка максимального T
    θ       = params      [3].val; // Установка параметра θ
  }

  bool Init (const double &rangeMinP  [], // Минимальный диапазон поиска
             const double &rangeMaxP  [], // Максимальный диапазон поиска
             const double &rangeStepP [], // Шаг поиска
             const int     epochsP = 0);  // Количество эпох

  void Moving   (); // Метод перемещения частиц
  void Revision (); // Метод ревизии

  //----------------------------------------------------------------------------
  double minT; // Минимальное значение T
  double maxT; // Максимальное значение T
  double θ;    // Параметр θ

  private: //-------------------------------------------------------------------
  int epochs;    // Общее количество эпох
  int epochNow;  // Текущая эпоха
  double ϵ;      // Параметр для предотвращения деления на ноль
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_SOA::Init (const double &rangeMinP  [], // Минимальный диапазон поиска
                     const double &rangeMaxP  [], // Максимальный диапазон поиска
                     const double &rangeStepP [], // Шаг поиска
                     const int     epochsP = 0)   // Количество эпох
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; // Инициализация стандартных параметров

  //----------------------------------------------------------------------------
  epochs   = epochsP;     // Установка общего количества эпох
  epochNow = 0;           // Инициализация текущей эпохи
  ϵ        = DBL_EPSILON; // Установка значения ϵ

  return true;            // Возвращаем true при успешной инициализации
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Метод перемещения частиц
void C_AO_SOA::Moving ()
{
  epochNow++; // Увеличиваем номер текущей эпохи

  // Начальное случайное позиционирование
  if (!revision) // Если еще не было ревизии
  {
    for (int i = 0; i < popSize; i++) // Для каждой частицы
    {
      for (int c = 0; c < coords; c++) // Для каждой координаты
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);                             // Генерация случайной позиции
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Приведение к дискретным значениям
      }
    }

    revision = true; // Установка флага ревизии
    return;          // Выход из метода
  }

  //----------------------------------------------------------------------------
  double MoAc = minT + epochNow * ((maxT - minT) / epochs); // Вычисление значения MoAc
  double MoPr = 1.0 - pow (epochNow / epochs, (1.0 / θ));   // Вычисление значения MoPr
  double best = 0.0;                                        // Переменная для хранения лучшего значения

  // Фаза исследования с использованием операторов Деления (D) и Умножения (M)
  for (int i = 0; i < popSize; i++) // Для каждой частицы
  {
    for (int c = 0; c < coords; c++) // Для каждой координаты
    {
      // Вероятностное обновление позиции частицы
      if (u.RNDbool () < MoAc) a [i].c [c] = cB [c];                                        // Установка на лучшее значение
      else
        if (u.RNDbool () < MoPr) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);    // Генерация новой случайной позиции

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);   // Приведение к дискретным значениям
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SOA::Revision ()
{
  int ind = -1;                     // Индекс для хранения лучшей частицы

  for (int i = 0; i < popSize; i++) // Для каждой частицы
  {
    if (a [i].f > fB)               // Если значение функции лучше, чем текущее лучшее
    {
      fB = a [i].f;                 // Обновление лучшего значения функции
      ind = i;                      // Сохранение индекса лучшей частицы
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Копирование координат лучшей частицы
}
//——————————————————————————————————————————————————————————————————————————————

Получился один из самых компактных по коду алгоритмов оптимизации, которые мы рассматривали ранее. Короче код только алгоритма RW (RandomWalk), который будет рассмотрен в одной из следующих статей.

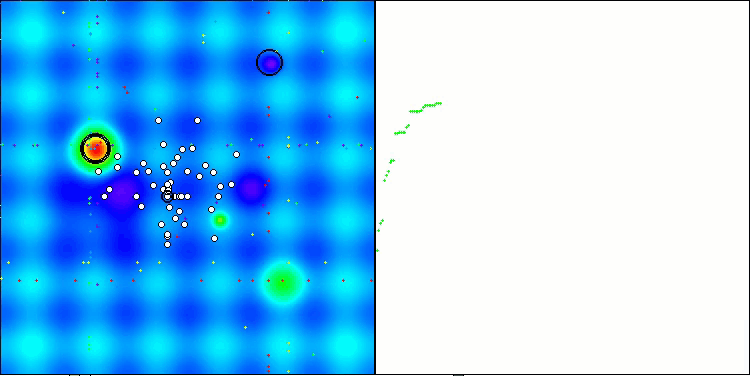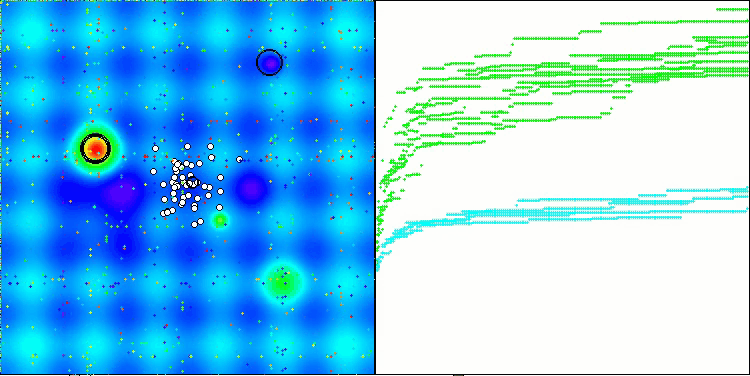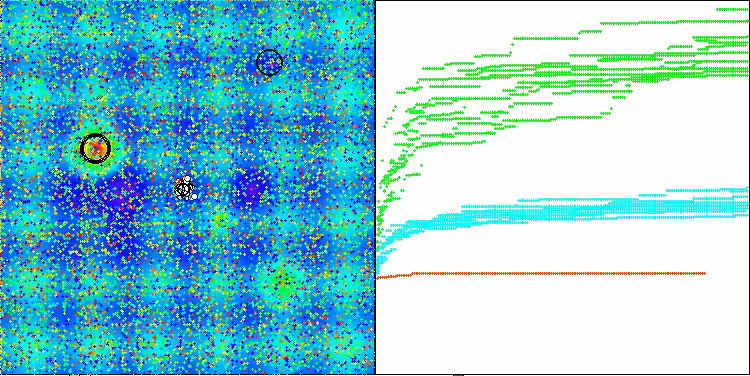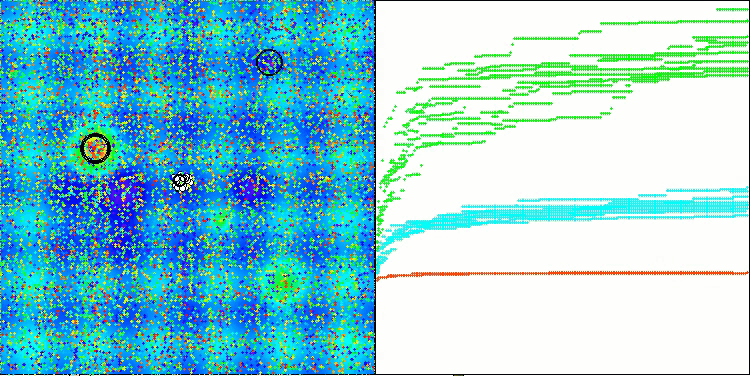
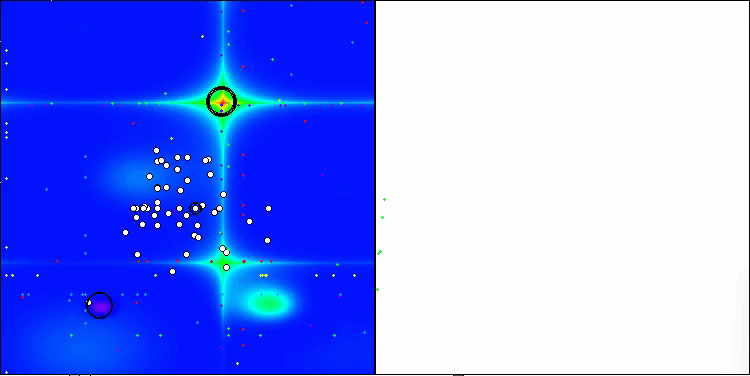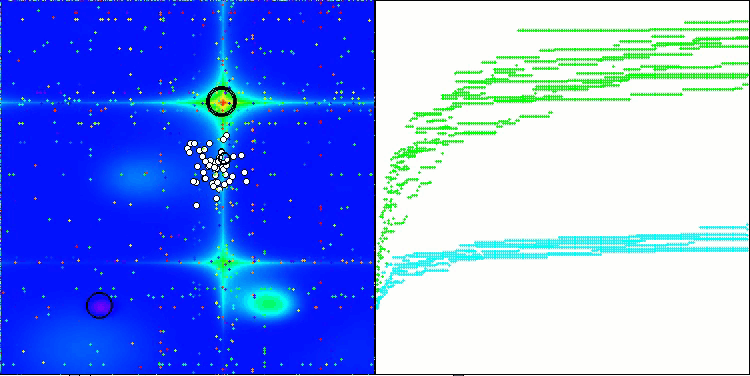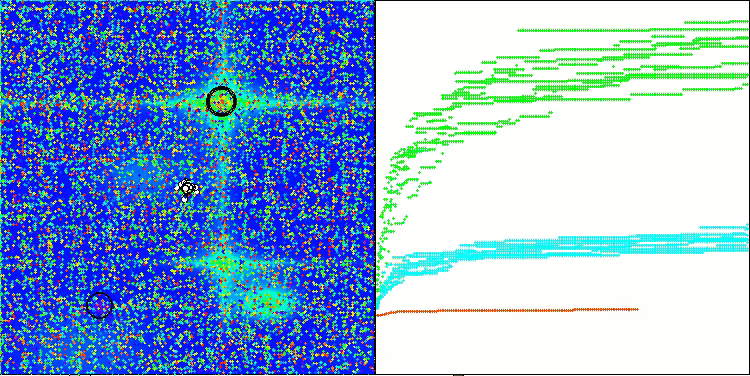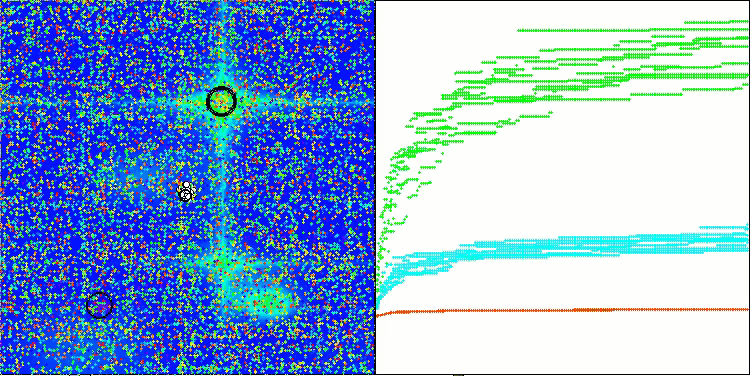
Визуализация работы стратегий поиска в пространстве решений говорит лучше любых слов. Я объединил все три теста (Hilly, Forest и Megacity) для алгоритма AOA в одну анимацию, так как практически не наблюдается никаких отличий в работе на разных типах задач. Ниже представлены отдельные визуализации работы SOA для каждой из трех тестовых функций.

Можно отметить работу нового алгоритма SOA на задачах малых размерностей — небольшой разброс результатов, достаточно редкое качество. 

AOA on Hilly, Forest, Megacity

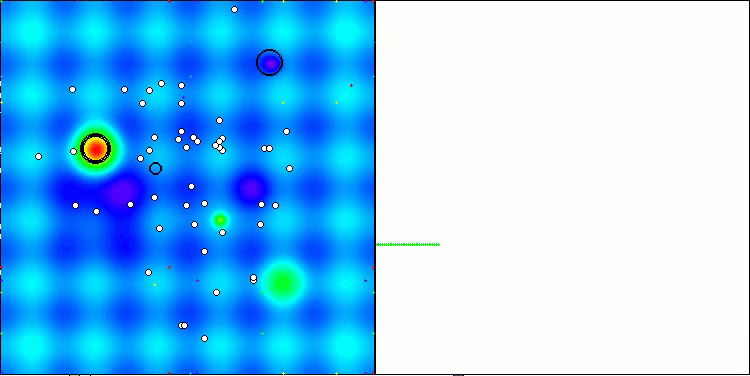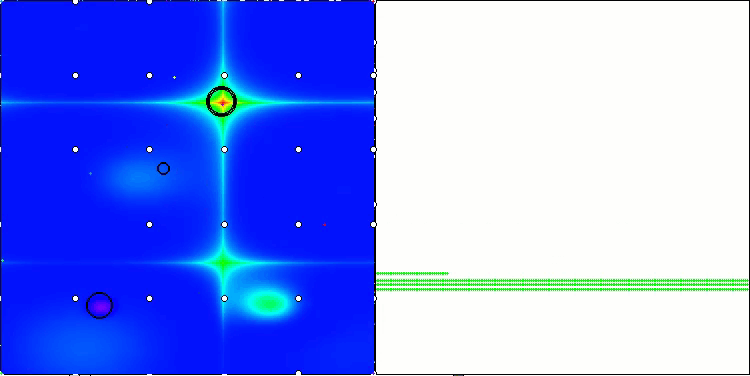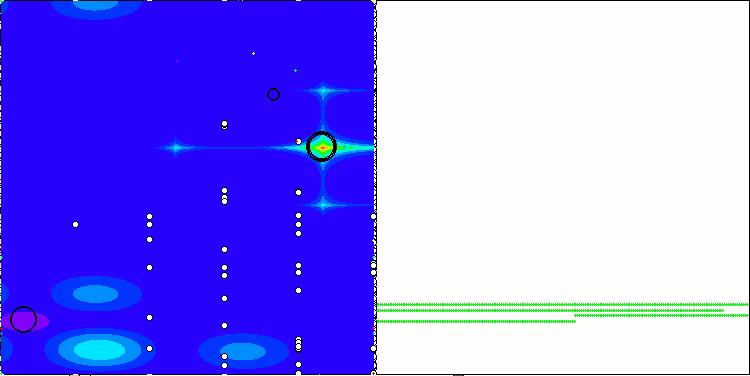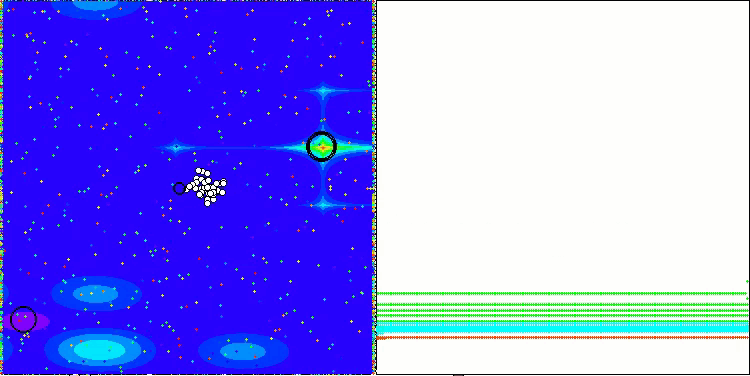
AOA на тестовых функциях Hilly, Forest, Megacity 

Hilly

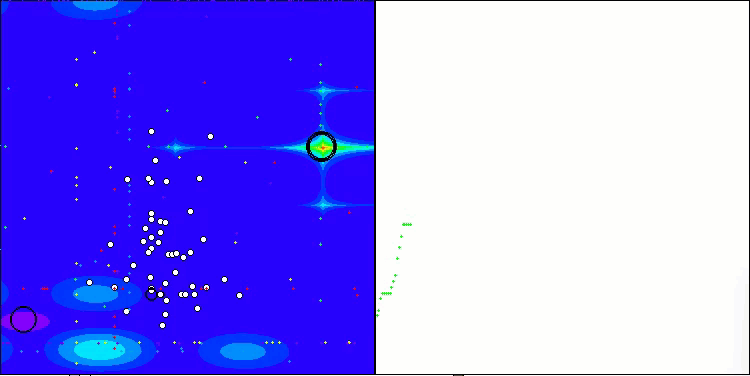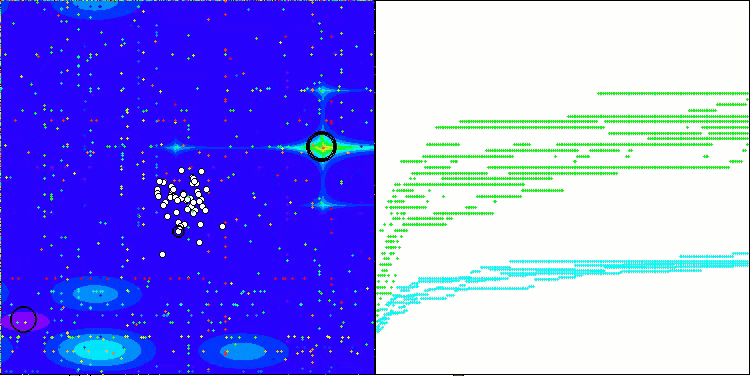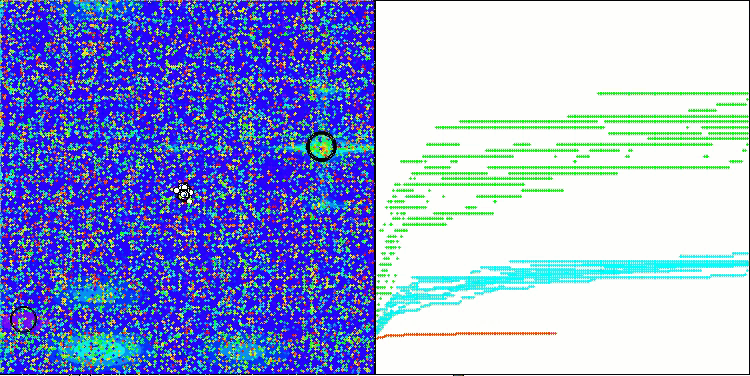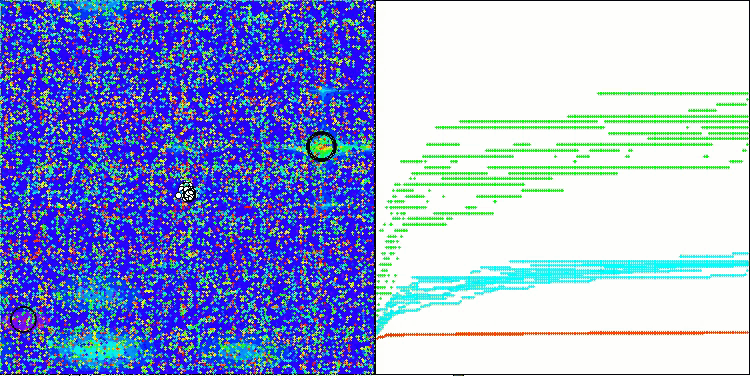
SOA на тестовой функции Hilly

Forest

  SOA на тестовой функции Forest

Megacity

SOA на тестовой функции Megacity


По итогам тестирования оригинальный алгоритм AOA не попал в рейтинговую таблицу, так как его результат оказался ниже 45-го места. Но с другой стороны, новый алгоритм "Простой Алгоритм Оптимизации" (SOA) попал в рейтинг и оказался на 29-м месте.

№ AO Description Hilly Hilly final Forest Forest final Megacity (discrete) Megacity final Final result % of MAX
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 ANS across neighbourhood search 0,94948 0,84776 0,43857 2,23581 1,00000 0,92334 0,39988 2,32323 0,70923 0,63477 0,23091 1,57491 6,134 68,15
2 CLA code lock algorithm (joo) 0,95345 0,87107 0,37590 2,20042 0,98942 0,91709 0,31642 2,22294 0,79692 0,69385 0,19303 1,68380 6,107 67,86
3 AMOm animal migration ptimization M 0,90358 0,84317 0,46284 2,20959 0,99001 0,92436 0,46598 2,38034 0,56769 0,59132 0,23773 1,39675 5,987 66,52
4 (P+O)ES (P+O) evolution strategies 0,92256 0,88101 0,40021 2,20379 0,97750 0,87490 0,31945 2,17185 0,67385 0,62985 0,18634 1,49003 5,866 65,17
5 CTA comet tail algorithm (joo) 0,95346 0,86319 0,27770 2,09435 0,99794 0,85740 0,33949 2,19484 0,88769 0,56431 0,10512 1,55712 5,846 64,96
6 SDSm stochastic diffusion search M 0,93066 0,85445 0,39476 2,17988 0,99983 0,89244 0,19619 2,08846 0,72333 0,61100 0,10670 1,44103 5,709 63,44
7 AAm archery algorithm M 0,91744 0,70876 0,42160 2,04780 0,92527 0,75802 0,35328 2,03657 0,67385 0,55200 0,23738 1,46323 5,548 61,64
8 ESG evolution of social groups (joo) 0,99906 0,79654 0,35056 2,14616 1,00000 0,82863 0,13102 1,95965 0,82333 0,55300 0,04725 1,42358 5,529 61,44
9 SIA simulated isotropic annealing (joo) 0,95784 0,84264 0,41465 2,21513 0,98239 0,79586 0,20507 1,98332 0,68667 0,49300 0,09053 1,27020 5,469 60,76
10 ACS artificial cooperative search 0,75547 0,74744 0,30407 1,80698 1,00000 0,88861 0,22413 2,11274 0,69077 0,48185 0,13322 1,30583 5,226 58,06
11 ASO anarchy society optimization 0,84872 0,74646 0,31465 1,90983 0,96148 0,79150 0,23803 1,99101 0,57077 0,54062 0,16614 1,27752 5,178 57,54
12 AOSm atomic orbital search M 0,80232 0,70449 0,31021 1,81702 0,85660 0,69451 0,21996 1,77107 0,74615 0,52862 0,14358 1,41835 5,006 55,63
13 TSEA turtle shell evolution algorithm (joo) 0,96798 0,64480 0,29672 1,90949 0,99449 0,61981 0,22708 1,84139 0,69077 0,42646 0,13598 1,25322 5,004 55,60
14 DE differential evolution 0,95044 0,61674 0,30308 1,87026 0,95317 0,78896 0,16652 1,90865 0,78667 0,36033 0,02953 1,17653 4,955 55,06
15 CRO chemical reaction optimisation 0,94629 0,66112 0,29853 1,90593 0,87906 0,58422 0,21146 1,67473 0,75846 0,42646 0,12686 1,31178 4,892 54,36
16 BSA bird swarm algorithm 0,89306 0,64900 0,26250 1,80455 0,92420 0,71121 0,24939 1,88479 0,69385 0,32615 0,10012 1,12012 4,809 53,44
17 HS harmony search 0,86509 0,68782 0,32527 1,87818 0,99999 0,68002 0,09590 1,77592 0,62000 0,42267 0,05458 1,09725 4,751 52,79
18 SSG saplings sowing and growing 0,77839 0,64925 0,39543 1,82308 0,85973 0,62467 0,17429 1,65869 0,64667 0,44133 0,10598 1,19398 4,676 51,95
19 BCOm bacterial chemotaxis optimization M 0,75953 0,62268 0,31483 1,69704 0,89378 0,61339 0,22542 1,73259 0,65385 0,42092 0,14435 1,21912 4,649 51,65
20 ABO african buffalo optimization 0,83337 0,62247 0,29964 1,75548 0,92170 0,58618 0,19723 1,70511 0,61000 0,43154 0,13225 1,17378 4,634 51,49
21 (PO)ES (PO) evolution strategies 0,79025 0,62647 0,42935 1,84606 0,87616 0,60943 0,19591 1,68151 0,59000 0,37933 0,11322 1,08255 4,610 51,22
22 TSm tabu search M 0,87795 0,61431 0,29104 1,78330 0,92885 0,51844 0,19054 1,63783 0,61077 0,38215 0,12157 1,11449 4,536 50,40
23 BSO brain storm optimization 0,93736 0,57616 0,29688 1,81041 0,93131 0,55866 0,23537 1,72534 0,55231 0,29077 0,11914 0,96222 4,498 49,98
24 WOAm wale optimization algorithm M 0,84521 0,56298 0,26263 1,67081 0,93100 0,52278 0,16365 1,61743 0,66308 0,41138 0,11357 1,18803 4,476 49,74
25 AEFA artificial electric field algorithm 0,87700 0,61753 0,25235 1,74688 0,92729 0,72698 0,18064 1,83490 0,66615 0,11631 0,09508 0,87754 4,459 49,55
26 AEO artificial ecosystem-based optimization algorithm 0,91380 0,46713 0,26470 1,64563 0,90223 0,43705 0,21400 1,55327 0,66154 0,30800 0,28563 1,25517 4,454 49,49
27 ACOm ant colony optimization M 0,88190 0,66127 0,30377 1,84693 0,85873 0,58680 0,15051 1,59604 0,59667 0,37333 0,02472 0,99472 4,438 49,31
28 BFO-GA bacterial foraging optimization - ga 0,89150 0,55111 0,31529 1,75790 0,96982 0,39612 0,06305 1,42899 0,72667 0,27500 0,03525 1,03692 4,224 46,93
29 SOA simple optimization algorithm 0,91520 0,46976 0,27089 1,65585 0,89675 0,37401 0,16984 1,44060 0,69538 0,28031 0,10852 1,08422 4,181 46,45
30 ABHA artificial bee hive algorithm 0,84131 0,54227 0,26304 1,64663 0,87858 0,47779 0,17181 1,52818 0,50923 0,33877 0,10397 0,95197 4,127 45,85
31 ACMO atmospheric cloud model optimization 0,90321 0,48546 0,30403 1,69270 0,80268 0,37857 0,19178 1,37303 0,62308 0,24400 0,10795 0,97503 4,041 44,90
32 ASHA artificial showering algorithm 0,89686 0,40433 0,25617 1,55737 0,80360 0,35526 0,19160 1,35046 0,47692 0,18123 0,09774 0,75589 3,664 40,71
33 ASBO adaptive social behavior optimization 0,76331 0,49253 0,32619 1,58202 0,79546 0,40035 0,26097 1,45677 0,26462 0,17169 0,18200 0,61831 3,657 40,63
34 MEC mind evolutionary computation 0,69533 0,53376 0,32661 1,55569 0,72464 0,33036 0,07198 1,12698 0,52500 0,22000 0,04198 0,78698 3,470 38,55
35 IWO invasive weed optimization 0,72679 0,52256 0,33123 1,58058 0,70756 0,33955 0,07484 1,12196 0,42333 0,23067 0,04617 0,70017 3,403 37,81
36 Micro-AIS micro artificial immune system 0,79547 0,51922 0,30861 1,62330 0,72956 0,36879 0,09398 1,19233 0,37667 0,15867 0,02802 0,56335 3,379 37,54
37 COAm cuckoo optimization algorithm M 0,75820 0,48652 0,31369 1,55841 0,74054 0,28051 0,05599 1,07704 0,50500 0,17467 0,03380 0,71347 3,349 37,21
38 SDOm spiral dynamics optimization M 0,74601 0,44623 0,29687 1,48912 0,70204 0,34678 0,10944 1,15826 0,42833 0,16767 0,03663 0,63263 3,280 36,44
39 NMm Nelder-Mead method M 0,73807 0,50598 0,31342 1,55747 0,63674 0,28302 0,08221 1,00197 0,44667 0,18667 0,04028 0,67362 3,233 35,92
40 FAm firefly algorithm M 0,58634 0,47228 0,32276 1,38138 0,68467 0,37439 0,10908 1,16814 0,28667 0,16467 0,04722 0,49855 3,048 33,87
41 GSA gravitational search algorithm 0,64757 0,49197 0,30062 1,44016 0,53962 0,36353 0,09945 1,00260 0,32667 0,12200 0,01917 0,46783 2,911 32,34
42 BFO bacterial foraging optimization 0,61171 0,43270 0,31318 1,35759 0,54410 0,21511 0,05676 0,81597 0,42167 0,13800 0,03195 0,59162 2,765 30,72
43 ABC artificial bee colony 0,63377 0,42402 0,30892 1,36671 0,55103 0,21874 0,05623 0,82600 0,34000 0,14200 0,03102 0,51302 2,706 30,06
44 BA bat algorithm 0,59761 0,45911 0,35242 1,40915 0,40321 0,19313 0,07175 0,66810 0,21000 0,10100 0,03517 0,34617 2,423 26,93
45 AAA algae adaptive algorithm 0,50007 0,32040 0,25525 1,07572 0,37021 0,22284 0,16785 0,76089 0,27846 0,14800 0,09755 0,52402 2,361 26,23


Выводы

Итак, мы подробно рассмотрели алгоритм арифметической оптимизации, реализация которого оказалась действительно простой. Однако, как это иногда бывает, простота не всегда гарантирует высокие результаты. Настоящий залог успеха — это суперпростота! Конечно, это шутка. Основные проблемы AOA заключаются в отсутствии взаимодействия и обмена информацией между членами популяции, что, в свою очередь, приводит к полной нехватке комбинаторных качеств в данной стратегии поиска.

Еще один недостаток алгоритма связан с отсутствием вариабельности в его поисковых операторах. Хотя операторы выбираются случайным образом для каждой координаты, это не позволяет алгоритму эффективно "зацепиться" за многомерный ландшафт пространства поиска. Тем не менее в алгоритме AOA присутствуют рациональные и логически обоснованные подходы, такие как изменяемые с каждой эпохой элементы MoA и MoP. Именно они стали основой для пересоздания алгоритма и его эволюции в новую, интересную и чрезвычайно простую стратегию поиска, основанную на вероятностном подходе копирования информации из лучших решений популяции и генерации случайных решений в пространстве поиска.

С каждой эпохой случайность в решениях популяции уменьшается, в то время как концентрация удачных направлений возрастает. Это можно сравнить с процессом строительства изящного моста через реку: на начальных этапах работы используются различные материалы и конструкции, которые могут не подходить для конечного результата. Однако, по мере продвижения к завершению проекта, лучшие решения становятся более очевидными, а ненужные элементы отбрасываются. В результате, мост становится все более гармоничным и устойчивым, соединяя берега с элегантностью и прочностью.

Tab

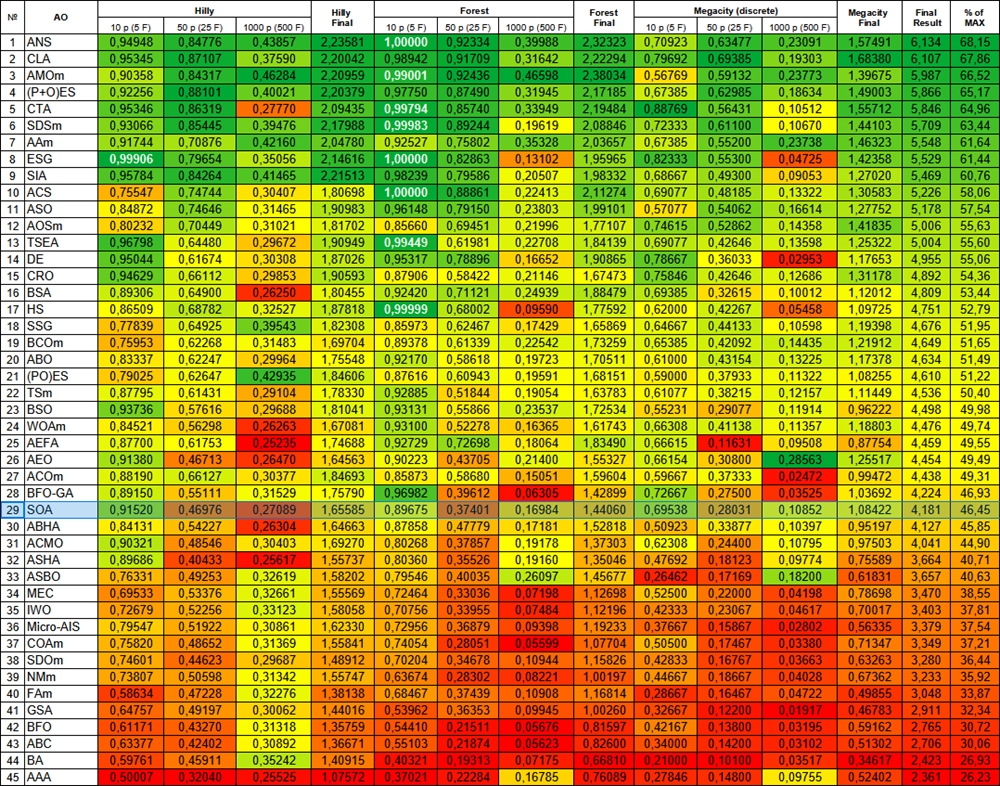
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам. Белым цветом подсвечены результаты больше или равные 0.99

chart

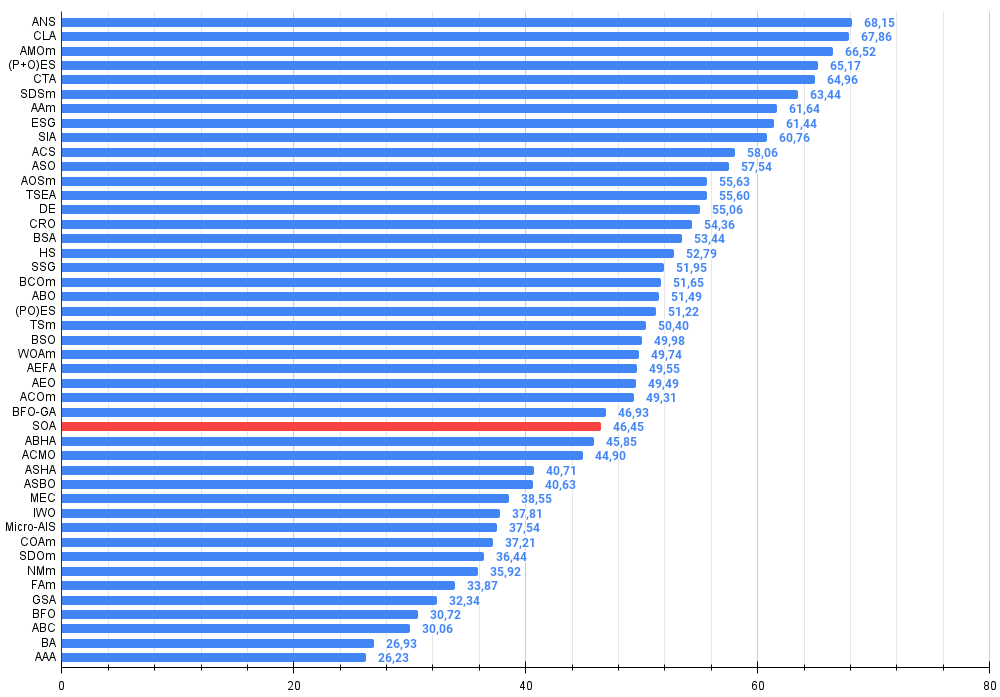
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше,

где 100 - максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)


Плюсы и минусы алгоритма SOA:

Плюсы:

  1. Малое количество внешних параметров.
  2. Неплохие результаты на задачах малой размерности, особенно на дискретных.
  3. Быстрый.
  4. Небольшой разброс результатов на задачах малой размерности.
  5. Очень простая реализация.

Минусы:

  1. Невысокая масштабируемость.

К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.

Программы, используемые в статье

# Имя Тип Описание
1 #C_AO.mqh
 Включаемый файл
 Родительский класс популяционных алгоритмов оптимизации
2 #C_AO_enum.mqh
 Включаемый файл
 Перечисление популяционных алгоритмов оптимизации
3 TestFunctions.mqh
 Включаемый файл
 Библиотека тестовых функций
4
 TestStandFunctions.mqh
 Включаемый файл
 Библиотека функций тестового стенда
5
 Utilities.mqh
 Включаемый файл
 Библиотека вспомогательных функций
6
 CalculationTestResults.mqh
 Включаемый файл
 Скрипт для расчета результатов в сравнительную таблицу
7
 Testing AOs.mq5
 Скрипт Единый испытательный стенд для всех популяционных алгоритмов оптимизации
8
 Simple use of population optimization algorithms.mq5
 Скрипт
Простой пример использования популяционных алгоритмов оптимизации без визуализации
9
 AO_AOA_ArithmeticOptimizationAlgorithm.mqh
 Включаемый файл Класс алгоритма AOA
10
 AO_SOA_SimpleOptimizationAlgorithm.mqh
 Включаемый файл
 Класс алгоритма SOA
11
Test_AO_AOA.mq5
 Скрипт Испытательный стенд для AOA
12
 Test_AO_SOA.mq5
 Скрипт
 Испытательный стенд для SOA
Прикрепленные файлы |
Загрузить ZIP
AOA_SOA.ZIP (139.46 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров
Нейросети в трейдинге: Параметроэффективный Transformer с сегментированным вниманием (Окончание) Нейросети в трейдинге: Параметроэффективный Transformer с сегментированным вниманием (Окончание)
В предыдущей работе мы рассмотрели теоретические аспекты фреймворка PSformer, который включает две основные инновации в архитектуру классического Transformer: механизм совместного использования параметров (Parameter Shared — PS) и внимание к пространственно-временным сегментам (SegAtt). И в данной статье мы продолжаем начатую работу по реализации предложенных подходов средствами MQL5.
Разработка системы репликации (Часть 56): Адаптация модулей Разработка системы репликации (Часть 56): Адаптация модулей
Несмотря на то, что модули уже взаимодействуют друг с другом должным образом, при попытке использовать указатель мыши в сервисе репликации, возникает ошибка. Нам нужно исправить это прежде, чем переходить к следующему этапу. Кроме того, была исправлена проблема в коде индикатора мыши. Таким образом, эта версия наконец-то стала стабильной и правильно доработанной.
Нелинейные регрессионные модели на бирже Нелинейные регрессионные модели на бирже
Нелинейные регрессионные модели на бирже: реально ли прогнозировать финансовые рынки? Попробуем создать моделеь для прогноза цен на евро-доллар, и сделать на ее основе двух роботов - на Python и MQL5.
Применение ассоциативных правил для анализа данных на Форексе Применение ассоциативных правил для анализа данных на Форексе
Как применить предиктивные правила ретейл-аналитики супермаркетов к реальному рынку Форекс? Как связаны покупки печенья, молока и хлеба с транзакциями на бирже? В статье рассматривается инновационный подход к алгоритмическому трейдингу, основанный на применении ассоциативных правил.