汎用MLP近似器に基づくエキスパートアドバイザー

内容

1. はじめに
2. 学習問題への没入
   
3. 汎用近似器
4. 取引EAの一部としてのMLPの実装

はじめに

ニューラルネットワークと聞くと、多くの人は複雑なアルゴリズムや面倒な技術的詳細を思い浮かべます。しかし、ニューラルネットワークの本質は関数の合成に過ぎず、各層は線形変換と非線形活性化関数の組み合わせで構成されています。式で表すと、次のようになります。

F(x) = f2(f1(x))

ここで、f1は第1層の関数、f2は第2層の関数です。

多くの人はニューラルネットワークを非常に複雑で理解が難しいものだと考えますが、ここでは誰でも異なる視点から理解できるよう、簡単な言葉で説明したいと思います。ニューラルネットワークにはさまざまなアーキテクチャがあり、それぞれ特定のタスクを実行するために設計されています。本記事では、最もシンプルな多層パーセプトロン(MLP)に焦点を当てます。MLPは入力情報を非線形関数を通して変換する仕組みです。ネットワークの構造を理解すれば、各ニューロンの活性化関数が非線形変換器として働く分析的な形式で表すことができます。

ネットワークの各層は、複数のニューロンで構成され、情報を多くの非線形変換を通じて処理します。多層パーセプトロンは、近似、分類、外挿といったタスクを実行可能です。パーセプトロンの動作を表す一般式は重みで調整され、さまざまなタスクに適応できるようになっています。

興味深いことに、この近似器は任意の取引システムに組み込むことができます。SGDやADAMといった最適化手法に触れずに考えると、MLPは情報変換器として利用可能です。たとえば、市場状況（フラット、トレンド、過渡状態など）を分析し、その結果に応じて異なる取引戦略を適用することができます。また、インジケーターのデータを取引シグナルに変換するためにもニューラルネットワークを利用できます。

本記事の目的は、ニューラルネットワークを使うことの複雑さに関する神話を払拭し、重み付けや最適化の複雑な詳細を脇に置いたままでも、機械学習の深い知識がなくてもニューラルネットワークに基づく取引EAを作成できることを示すことです。データの収集・準備からモデルの学習、取引戦略への統合まで、EA作成のプロセスをステップごとに解説していきます。

学習問題への没入

学習には大きく分けて3つのタイプがあります。本記事では、市場データ分析に応用する際のこれらの学習タイプのニュアンスに注目します。紹介するアプローチは、これらの学習タイプの欠点を考慮に入れることを目的としています。

教師あり学習：モデルはラベル付きデータで学習し、例に基づいて予測をおこないます。目的関数は、予測値と目標値の誤差を最小化すること（例：平均二乗誤差MSE）です。しかし、この方法にはいくつかの欠点があります。高品質なラベル付きデータを大量に必要とするため、時系列データの文脈では大きな課題となります。手書き文字認識や画像内容認識のように、明確で信頼できる学習用例がある場合、学習はスムーズに進みます。ニューラルネットワークは、まさに学習させた内容を認識するようになります。

しかし、時系列の場合は状況が異なります。データにラベルを付けても、その信頼性や妥当性を確信できる形でラベル付けするのは極めて困難です。実際には、ネットワークは「私たちが仮定したこと」を学習する傾向があり、必ずしも対象プロセスにとって関連のある内容を学習するとは限りません。多くの研究者は、教師あり学習の成功には「良質な」ラベルが必要であると強調していますが、時系列データの文脈ではその質を事前に判断することは難しいのです。

その結果、「過学習」のような主観的な評価が出てきます。また、便宜的に『ノイズ』という概念が導入され、過学習したネットワークはパターンではなくノイズを記憶してしまう可能性があるとされます。時系列分析においては「ノイズ」や「過学習」の明確な定義や定量化は存在せず、非常に主観的です。したがって、時系列データに教師あり学習を適用する場合、多くのニュアンスを考慮する必要があり、それがモデルの新規データへの安定性に大きく影響します。

教師なし学習：モデル自身がラベルなしデータの中から隠れた構造を探索します。目的関数は手法により異なります。結果の品質を評価するのが難しく、明確な検証マーカーがないため、データに明確な構造がなければ有用なパターンを見つけられないことがあります。また、実際に見つかった構造が対象プロセスに直接関連しているかどうかも不明です。

従来、教師なし学習に分類される手法には、K-means、自己組織化写像(SOM)などがあります。これらの手法はそれぞれ特定の目的関数を用いて学習します。

いくつかの例を考えてみましょう。

• K平均法：各点とクラスタ中心との距離の二乗和（クラスタ内分散）を最小化
• 主成分分析(PCA)：データを新しい軸（主成分）に射影した際の分散を最大化
• 決定木(DT)：エントロピー、ジニ係数、分散などを最小化
  

強化学習：目的関数は総報酬です。エージェント（プログラムやロボットなど）が環境と相互作用しながら意思決定を学習します。行動に応じて報酬やペナルティを受け取り、経験から学習して総報酬を最大化することを目標とします。

学習の過程にはランダム性があるため、結果が不安定になることがあります。そのため、モデルの挙動を予測することが難しく、また明確な報酬や罰則の体系が存在しない問題には必ずしも適していないため、学習が効果的でなくなる場合があります。強化学習には、実践的な課題が数多く存在します。その一つは、ADAMなどのニューラルネットワーク学習アルゴリズムを利用する際に、強化学習の目的関数を適切に表現することの難しさです。これは、目的関数の値を[-1;1]に近い範囲に正規化する必要があるためです。その過程では、ニューロンにおける活性化関数の導関数を計算し、誤差をネットワークに逆伝播させて重みを調整しなければなりません。そうすることで「重みの爆発」や、それによってニューラルネットワークの学習が停止してしまうような現象を避けることができます。

これまでに、従来の学習形態の分類について見てきました。ご覧のとおり、それらはいずれも何らかの目的関数の最小化または最大化に基づいています。したがって、それらの主な違いはただ一つ、すなわち「教師」が存在するかどうかです。教師が存在しない場合、学習の種類の区別は、最適化すべき目的関数の特性に依存することになります。

このように、私の考えでは学習形態の分類は次のように表現できます。すなわち、目標値が存在する教師あり学習（目標に対する予測誤差の最小化）と、目標値が存在しない教師なし学習です。教師なし学習の下位分類は、データの性質に基づく目的関数（距離や密度など）、システムの性能（利益や生産性などの統合指標）、分布（生成モデルの場合）、その他の評価基準によって決まります。

汎用近似器

私が提案するアプローチは、第二のタイプ、すなわち教師なし学習に属します。この方法では、ニューラルネットワークに正しい取引方法を「教える」ことや、どこでポジションを開くか閉じるかを指示することはおこないません。なぜなら、私たち自身がこれらの質問に対する答えを知らないからです。代わりに、ネットワーク自身に取引の意思決定をさせ、私たちの役割は、その取引全体の成果を評価することです。

この場合、評価関数を正規化したり、「重みの爆発」や「収束停止」といった問題を心配したりする必要はありません。なぜなら、このアプローチにはそれらの問題が存在しないからです。ニューラルネットワークを最適化アルゴリズムから論理的に分離し、入力データをトレーダーのスキルを反映する新しい情報の形に変換するというタスクのみを与えます。基本的には、時系列のパターンや利益を出すための取引方法を理解することなく、単に一つの情報形式を別の情報形式に変換しているだけです。

この役割には、MLP（多層パーセプトロン）などのニューラルネットワークが理想的であることが、汎用近似定理によって確認されています。この定理は、ニューラルネットワークが任意の連続関数を近似できることを示しています。ここでいう「連続関数」とは、分析対象の時系列において発生するプロセスを意味します。このアプローチにより、「ノイズ」や「過学習」といった人工的で主観的な概念に頼る必要がなくなります。これらは定量的な価値を持たない概念です。

この方法の動作をイメージするには、図1をご覧ください。MLPには現在の市場データに関連する情報（OHLCバーの価格や指標値など）を入力し、出力としてすぐに使える取引シグナルを得ます。取引銘柄の履歴を通して学習をおこなった後、目的関数を計算することができます。目的関数とは、取引結果の総合的評価（あるいは複合的評価）のことであり、外部の最適化アルゴリズムを用いてネットワークの重みを調整し、ニューラルネットワークの取引結果の質を示す目的関数を最大化します。

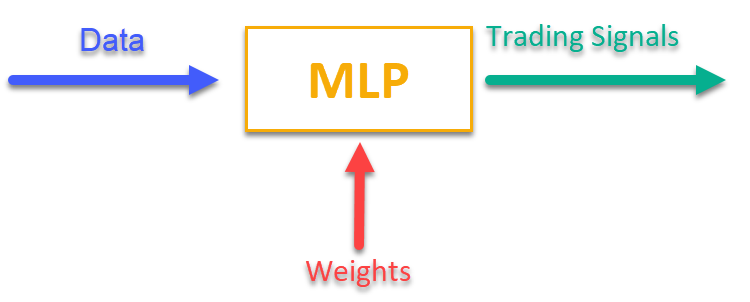
図1：一つの情報形式から別の情報形式への変換

取引EAの一部としてのMLPの実装

まず、MLPクラスを作成し、その後クラスをEAに組み込みます。記事にはネットワークのアーキテクチャが異なる多くの実装例がありますが、ここでは私のバージョンのMLPを示します。これは正真正銘のニューラルネットワークであり、オプティマイザは含まれていません。

MLPを実装するC_MLPクラスを宣言します。主な特徴は以下の通りです。

1. Init：初期化をおこない、必要な層の数や各層のニューロン数に応じてネットワークを設定し、ネットワーク内の総重み数を返します。

2. ANN：入力層から出力層までの順伝播をおこなうメソッドです。入力データと重みを受け取り、ネットワークの出力値を計算します（図1参照）。

3. GetWcount：ネットワーク内の総重み数を返します。

4. LayerCalc：ネットワークの各層の計算をおこないます。

内部要素

• layers：ニューロンの値を格納します。
• weightsCNT：ネットワーク内の総重み数です。
• layersCNT：ネットワークの総層数です。

このクラスを用いることで、任意の数の隠れ層と、それぞれの層に任意の数のニューロンを持つMLPニューラルネットワークを作成することができます。

//+----------------------------------------------------------------------------+
//| Multilayer Perceptron (MLP) class                                          |
//| Implement a forward pass through a fully connected neural network          |
//| Architecture: Lin -> L1 -> L2 -> ... Ln -> Lout                            |
//+----------------------------------------------------------------------------+
class C_MLP
{
  public: //--------------------------------------------------------------------

  // Initialize the network with the given configuration
  // Return the total number of weights in the network, or 0 in case of an error
  int Init (int &layerConfig []);

  // Calculate the values of all layers sequentially from input to output
  void ANN (double &inLayer  [],  // input values
            double &weights  [],  // network weights (including biases)
            double &outLayer []); // output layer values

  // Get the total number of weights in the network
  int GetWcount () { return weightsCNT; }

  int layerConf []; // Network configuration - number of neurons in each layer

  private: //-------------------------------------------------------------------
  // Structure for storing the neural network layer
  struct S_Layer
  {
      double l [];     // Neuron values
  };

  S_Layer layers [];    // Array of all network layers
  int     weightsCNT;   // Total number of weights in the network (including biases)
  int     layersCNT;    // Total number of layers (including input and output ones)
  int     cnt_W;        // Current index in the weights array when traversing the network
  double  temp;         // Temporary variable to store the sum of the weighted inputs

  // Calculate values of one layer of the network
  void LayerCalc (double   &inLayer  [], // values of neurons of the previous layer
                  double   &weights  [], // array of weights and biases of the entire network
                  double   &outLayer [], // array for writing values of the current layer
                  const int inSize,      // number of neurons in the input layer
                  const int outSize);    // outSize  - number of neurons in the output layer
};

MLPは、与えられた層構成で初期化されます。主な手順は以下の通りです。

1. 構成の確認

• ネットワークが少なくとも2層（入力層と出力層）を持っていることを確認します。
• 各層に少なくとも1つのニューロンがあることを確認します。条件を満たさない場合は、エラーメッセージが表示され、関数は0を返します。

2. 各層の構成を保存し、layerconf配列へのアクセスを高速化します。

3. 層の配列の作成：各層のニューロンを格納するためのメモリを確保します。

4. 重みの計算：各ニューロンのバイアスを含め、ネットワーク内の総重み数を計算します。

関数は、総重み数を返すか、エラーの場合は0を返します。

//+----------------------------------------------------------------------------+
//| Initialize the network                                                     |
//| layerConfig - array with the number of neurons in each layer               |
//| Returns the total number of weights needed, or 0 in case of an error       |
//+----------------------------------------------------------------------------+
int C_MLP::Init (int &layerConfig [])
{
  // Check that the network has at least 2 layers (input and output)
  layersCNT = ArraySize (layerConfig);
  if (layersCNT < 2)
  {
    Print ("Error Net config! Layers less than 2!");
    return 0;
  }

  // Check that each layer has at least 1 neuron
  for (int i = 0; i < layersCNT; i++)
  {
    if (layerConfig [i] <= 0)
    {
      Print ("Error Net config! Layer No." + string (i + 1) + " contains 0 neurons!");
      return 0;
    }
  }

  // Save network configuration
  ArrayCopy (layerConf, layerConfig, 0, 0, WHOLE_ARRAY);

  // Create an array of layers
  ArrayResize (layers, layersCNT);

  // Allocate memory for neurons of each layer
  for (int i = 0; i < layersCNT; i++)
  {
    ArrayResize (layers [i].l, layerConfig [i]);
  }

  // Calculate the total number of weights in the network
  weightsCNT = 0;
  for (int i = 0; i < layersCNT - 1; i++)
  {
    // For each neuron of the next layer we need:
    // - one bias value
    // - weights for connections with all neurons of the current layer
    weightsCNT += layerConf [i] * layerConf [i + 1] + layerConf [i + 1];
  }

  return weightsCNT;
}

LayerCalcメソッドは、ニューラルネットワークの単一層に対して計算をおこない、活性化関数として双曲線正接を使用します。主な手順は以下の通りです。

1. 入力および出力パラメータ

• inLayer []：前の層からの入力値を格納する配列です。
• weights []：リンクの重みおよびバイアスを含む配列です。
• outLayer []：現在の層の出力値を格納する配列です。
• inSize：入力層のニューロン数です。
• outSize：出力層のニューロン数です。

2. 出力層の各ニューロンについて次の処理をおこないます。

• バイアス値で初期化します。
• 重み付き入力値を加算します（各入力値に対応する重みを掛けます）。
• ニューロンに対する活性化関数の値を計算します。

3. 活性化関数の適用

• 双曲線正接を使用して、値を-1から1の範囲に非線形変換します。
• 結果をoutLayer []出力配列に書き込みます。

//+----------------------------------------------------------------------------+
//| Calculate values of one layer of the network                               |
//| Implement the equation: y = tanh(bias + w1*x1 + w2*x2 + ... + wn*xn)       |
//+----------------------------------------------------------------------------+
void C_MLP::LayerCalc (double    &inLayer  [],
                       double    &weights  [],
                       double    &outLayer [],
                       const int  inSize,
                       const int  outSize)
{
  // Calculate the value for each neuron in the output layer
  for (int i = 0; i < outSize; i++)
  {
    // Start with the bias value for the current neuron
    temp = weights [cnt_W];
    cnt_W++;

    // Add weighted inputs from each neuron in the previous layer
    for (int u = 0; u < inSize; u++)
    {
      temp += inLayer [u] * weights [cnt_W];
      cnt_W++;
    }

    // Apply the "hyperbolic tangent" activation function
    // f(x) = 2/(1 + e^(-x)) - 1
    // Range of values f(x): [-1, 1]
    outLayer [i] = 2.0 / (1.0 + exp (-temp)) - 1.0;
  }
}

人工ニューラルネットワークの動作は、入力層から出力層まで、すべての層の値を順番に計算することで実現します。 

1. 入力および出力パラメータ

• inLayer []：ニューラルネットワークに入力される値を格納する配列です。
• weights []：ニューロン間の接続の重みおよびバイアスを含む配列です。
• outLayer []：ニューラルネットワークの最終層の出力値を格納する配列です。

2. 重みカウンタのリセット：現在の重み配列内の位置を追跡するcnt_W変数を計算開始前に0にリセットします。

3. 入力データのコピー：inLayerからの入力データをArrayCopy関数を使ってネットワークの最初の層にコピーします。

4. 層ごとのループ処理

• すべての層に対してループをおこないます。
• 各層について、LayerCalc関数を呼び出し、前の層の出力値、重み、層のサイズを基に現在の層の値を計算します。

5. すべての層の計算が完了した後、最終層の出力値をArrayCopy関数を使ってoutLayerにコピーします。

//+----------------------------------------------------------------------------+
//| Calculate the values of all layers sequentially from input to output       |
//+----------------------------------------------------------------------------+
void C_MLP::ANN (double &inLayer  [],  // input values
                 double &weights  [],  // network weights (including biases)
                 double &outLayer [])  // output layer values
{
  // Reset the weight counter before starting the pass
  cnt_W = 0;

  // Copy the input data to the first layer of the network
  ArrayCopy (layers [0].l, inLayer, 0, 0, WHOLE_ARRAY);

  // Calculate the values of each layer sequentially
  for (int i = 0; i < layersCNT - 1; i++)
  {
    LayerCalc (layers    [i].l,     // output of the previous layer
               weights,             // network weights (including bias)
               layers    [i + 1].l, // next layer
               layerConf [i],       // size of current layer
               layerConf [i + 1]);  // size of the next layer
  }

  // Copy the values of the last layer to the output array
  ArrayCopy (outLayer, layers [layersCNT - 1].l, 0, 0, WHOLE_ARRAY);
}

MLPニューラルネットワークを用いた機械学習に基づく自動取引戦略のアドバイザーを作成する時が来ました。

1. 取引操作、取引銘柄情報の処理、数学関数、多層パーセプトロン（MLP）、および最適化アルゴリズムのライブラリを接続します。

2. 取引パラメータとしては、ポジションの取引量や取引開始・終了時間を設定します。学習パラメータとしては、オプティマイザの選択、ニューラルネットワークの構造、分析するバーの数、学習用の履歴深さ、モデルの有効期間、シグナル閾値を設定します。

3. ユーティリティやニューラルネットワークのクラスオブジェクト、入力データ、重み、最後の学習時間を格納する変数を宣言します。

#include "#Symbol.mqh"
#include <Math\AOs\Utilities.mqh>
#include <Math\AOs\NeuroNets\MLP.mqh>
#include <Math\AOs\PopulationAO\#C_AO_enum.mqh>

//------------------------------------------------------------------------------
input group    "---Trade parameters-------------------";
input double   Lot_P              = 0.01;   // Position volume
input int      StartTradeH_P      = 3;      // Trading start time
input int      EndTradeH_P        = 12;     // Trading end time

input group    "---Training parameters----------------";
input E_AO     OptimizerSelect_P  = AO_CLA; // Select optimizer
input int      NumbTestFuncRuns_P = 5000;   // Total number of function runs
input string   MLPstructure_P     = "1|1";  // Hidden layers, <4|6|2> - three hidden layers
input int      BarsAnalysis_P     = 3;      // Number of bars to analyze
input int      DepthHistoryBars_P = 10000;  // History depth for training in bars 
input int      RetrainingPeriod_P = 12;     // Duration in hours of the model's relevance
input double   SigThr_P           = 0.5;    // Signal threshold

//------------------------------------------------------------------------------
C_AO_Utilities U;
C_MLP          NN;
int            InpSigNumber;
int            WeightsNumber;
double         Inputs  [];
double         Weights [];
double         Outs    [1];
datetime       LastTrainingTime = 0;

C_Symbol       S;
C_NewBar       B;
int            HandleS;
int            HandleR;

私は、ニューラルネットワークに渡すデータとして最初に思いついたものを選びました。それは、OHLCバーの価格（設定ではデフォルトで現在のバーの前の3本のバー）と、これらのバーにおけるRSIおよびストキャスティクス指標の値です。OnInit関数は、ニューラルネットワークを使用した取引ストラテジーを初期化します。 

1. インジケーターの初期化：RSIおよびストキャスティクスのオブジェクトを作成します。

2. BarsAnalysis_P入力パラメータに基づいてネットワークの入力シグナルの数を計算します。

3. ニューラルネットワーク構造の設定：ネットワーク構成を示す入力パラメータ文字列を分割し、層数やニューロン数の妥当性をチェックします。入力文字列パラメータはネットワークの隠れ層の数と各層のニューロン数を指定します。デフォルトでは「1|1」となっており、これはネットワークに2つの隠れ層があり、それぞれの層に1つのニューロンがあることを意味します。

4. ニューラルネットワークの初期化：ネットワークを初期化するメソッドを呼び出し、重みおよび入力データ用の配列を作成します。

5. 情報の出力：層数やネットワークパラメータに関するデータを出力します。

6. 初期化成功ステータスの返却：

正常に初期化されたことを示すステータスを返します。

//——————————————————————————————————————————————————————————————————————————————
int OnInit ()
{
  //----------------------------------------------------------------------------
  // Initializing indicators: Stochastic and RSI
  HandleS = iStochastic (_Symbol, PERIOD_CURRENT, 5, 3, 3, MODE_EMA, STO_LOWHIGH);
  HandleR = iRSI        (_Symbol, PERIOD_CURRENT, 14, PRICE_TYPICAL);

  // Calculate the number of inputs to the neural network based on the number of bars to analyze
  InpSigNumber = BarsAnalysis_P * 2 + BarsAnalysis_P * 4;

  // Display information about the number of inputs
  Print ("Number of network logins  : ", InpSigNumber);

  //----------------------------------------------------------------------------
  // Initialize the structure of the multilayer MLP
  string sepResult [];
  int layersNumb = StringSplit (MLPstructure_P, StringGetCharacter ("|", 0), sepResult);

  // Check if the number of hidden layers is greater than 0
  if (layersNumb < 1)
  {
    Print ("Network configuration error, hidden layers < 1...");
    return INIT_FAILED; // Return initialization error
  }

  // Increase the number of layers by 2 (input and output)
  layersNumb += 2;

  // Initialize array for neural network configuration
  int nnConf [];
  ArrayResize (nnConf, layersNumb);

  // Set the number of inputs and outputs in the network configuration
  nnConf [0] = InpSigNumber;   // Input layer
  nnConf [layersNumb - 1] = 1; // Output layer

  // Filling the hidden layers configuration
  for (int i = 1; i < layersNumb - 1; i++)
  {
    nnConf [i] = (int)StringToInteger (sepResult [i - 1]); // Convert a string value to an integer

    // Check that the number of neurons in a layer is greater than 0
    if (nnConf [i] < 1)
    {
      Print ("Network configuration error, in layer ", i, " <= 0 neurons...");
      return INIT_FAILED; // Return initialization error
    }
  }

  // Initialize the neural network and get the number of weights
  WeightsNumber = NN.Init (nnConf);
  if (WeightsNumber <= 0)
  {
    Print ("Error initializing MLP network...");
    return INIT_FAILED; // Return initialization error
  }

  // Resize the input array and weights
  ArrayResize (Inputs,  InpSigNumber);
  ArrayResize (Weights, WeightsNumber);

  // Initialize weights with random values in the range [-1, 1] (for debugging)
  for (int i = 0; i < WeightsNumber; i++)
      Weights [i] = 2 * (rand () / 32767.0) - 1;

  // Output network configuration information
  Print ("Number of all layers     : ", layersNumb);
  Print ("Number of network parameters: ", WeightsNumber);

  //----------------------------------------------------------------------------
  // Initialize the trade and bar classes
  S.Init (_Symbol);
  B.Init (_Symbol, PERIOD_CURRENT);

  return (INIT_SUCCEEDED); // Return successful initialization result
}
//——————————————————————————————————————————————————————————————————————————————

取引ストラテジーの主要なロジックはOnTick関数で実装されています。戦略はシンプルです。出力層ニューロンのシグナルがパラメータで指定された閾値を超えた場合、そのシグナルは買い/売り方向に対応すると解釈されます。さらに、もしポジションがなく、かつ現在の時間が取引可能であれば、ポジションを開きます。ポジションは、ニューラルネットワークが逆のシグナルを受け取った場合、または取引可能時間が終了した場合に強制的に閉じられます。戦略の主な手順を以下に列挙します。

1. 新しい学習の必要性の確認：前回の学習から十分な時間が経過していれば、ニューラルネットワークの学習を開始します。エラーが発生した場合は、メッセージを表示します。

2. 新しいバーの確認：現在のティックが新しいバーの始まりでない場合、関数の実行を終了します。

3. データの取得：価格データ（始値、終値、高値、安値）および指標値（RSIとストキャスティクス）を取得します。

4. データの正規化：取得した銘柄の価格データの最大値と最小値を求め、すべてのデータを-1から1の範囲に正規化します。

5. 予測：正規化されたデータをニューラルネットワークに入力し、出力シグナルを生成します。

6. 取引シグナルの生成：出力データに基づき、買い(1)または売り(-1)のシグナルを生成します。

7. ポジション管理：現在のポジションがシグナルと矛盾していれば閉じます。新規ポジションを開くシグナルが許可された時間に合致する場合はポジションを開きます。それ以外の場合、ポジションがあれば閉じます。

このように、OnTickのロジックは、自動取引の完全なサイクルを実装しています。学習、データ取得、正規化、予測、ポジション管理が含まれています。

//——————————————————————————————————————————————————————————————————————————————
void OnTick ()
{
  // Check if the neural network needs to be retrained
  if (TimeCurrent () - LastTrainingTime >= RetrainingPeriod_P * 3600)
  {
    // Start the neural network training
    if (Training ()) LastTrainingTime = TimeCurrent (); // Update last training time
    else             Print ("Training error...");      // Display an error message

    return; // Complete function execution
  }

  //----------------------------------------------------------------------------
  // Check if the current tick is the start of a new bar
  if (!B.IsNewBar ()) return;

  //----------------------------------------------------------------------------
  // Declare arrays to store price and indicator data
  MqlRates rates [];
  double   rsi   [];
  double   sto   [];

  // Get price data
  if (CopyRates (_Symbol, PERIOD_CURRENT, 1, BarsAnalysis_P, rates) != BarsAnalysis_P) return;

  // Get Stochastic values
  if (CopyBuffer (HandleS, 0, 1, BarsAnalysis_P, sto) != BarsAnalysis_P) return;
  // Get RSI values
  if (CopyBuffer (HandleR, 0, 1, BarsAnalysis_P, rsi) != BarsAnalysis_P) return;

  // Initialize variables to normalize data
  int wCNT   = 0;
  double max = -DBL_MAX; // Initial value for maximum
  double min =  DBL_MAX; // Initial value for minimum

  // Find the maximum and minimum among high and low
  for (int b = 0; b < BarsAnalysis_P; b++)
  {
    if (rates [b].high > max) max = rates [b].high; // Update the maximum
    if (rates [b].low  < min) min = rates [b].low;  // Update the minimum
  }

  // Normalization of input data for neural network
  for (int b = 0; b < BarsAnalysis_P; b++)
  {
    Inputs [wCNT] = U.Scale (rates [b].high,  min, max, -1, 1); wCNT++; // Normalizing high
    Inputs [wCNT] = U.Scale (rates [b].low,   min, max, -1, 1); wCNT++; // Normalizing low
    Inputs [wCNT] = U.Scale (rates [b].open,  min, max, -1, 1); wCNT++; // Normalizing open
    Inputs [wCNT] = U.Scale (rates [b].close, min, max, -1, 1); wCNT++; // Normalizing close

    Inputs [wCNT] = U.Scale (sto   [b],       0,   100, -1, 1); wCNT++; // Normalizing Stochastic
    Inputs [wCNT] = U.Scale (rsi   [b],       0,   100, -1, 1); wCNT++; // Normalizing RSI
  }

  // Convert data from Inputs to Outs
  NN.ANN (Inputs, Weights, Outs);

  //----------------------------------------------------------------------------
  // Generate a trading signal based on the output of a neural network
  int signal = 0;
  if (Outs [0] >  SigThr_P) signal =  1; // Buy signal
  if (Outs [0] < -SigThr_P) signal = -1; // Sell signal

  // Get the type of open position
  int posType = S.GetPosType ();
  S.GetTick ();

  if ((posType == 1 && signal == -1) || (posType == -1 && signal == 1))
  {
    if (!S.PosClose ("", ORDER_FILLING_FOK) != 0) posType = 0;
    else return;
  }

  MqlDateTime time;
  TimeToStruct (TimeCurrent (), time);

  // Check the allowed time for trading
  if (time.hour >= StartTradeH_P && time.hour < EndTradeH_P)
  {
    // Open a new position depending on the signal
    if (posType == 0 && signal != 0) S.PosOpen (signal, Lot_P, "", ORDER_FILLING_FOK, 0, 0.0, 0.0, 1);
  }
  else
  {
    if (posType != 0) S.PosClose ("", ORDER_FILLING_FOK);
  }
}
//——————————————————————————————————————————————————————————————————————————————

次に、ニューラルネットワークを過去データで学習させる手順を見てみましょう。

1. データの取得：過去の価格データを、RSIおよびストキャスティクスインジケーターの値とともに読み込みます。

2. 取引時間の定義：どのバーが許可された取引時間に含まれるかを示す配列を作成します。

3. 最適化パラメータの設定：最適化の境界値およびパラメータのステップを初期化します。

4. 最適化アルゴリズムの選択：最適化アルゴリズムを定義し、集団サイズを指定します。

5. ニューラルネットワーク重み最適化のメインループ 

• 集団の各解について、目的関数の値を計算し、その品質を評価します。
• 評価結果に基づいて、解集団が更新されます。

6. 結果の出力：アルゴリズム名、最良結果を出力し、最良パラメータを重み配列にコピーします。

7. 最適化アルゴリズムオブジェクトが使用していたメモリを解放します。

この関数は、過去のデータに基づいてニューラルネットワークを学習させ、最良のパラメータを見つける処理を実行します。

//——————————————————————————————————————————————————————————————————————————————
bool Training ()
{
  MqlRates rates [];
  double   rsi   [];
  double   sto   [];

  int bars = CopyRates (_Symbol, PERIOD_CURRENT, 1, DepthHistoryBars_P, rates);
  Print ("Training on history of ", bars, " bars");
  if (CopyBuffer (HandleS, 0, 1, DepthHistoryBars_P, sto) != bars) return false;
  if (CopyBuffer (HandleR, 0, 1, DepthHistoryBars_P, rsi) != bars) return false;

  MqlDateTime time;
  bool truTradeTime []; ArrayResize (truTradeTime, bars); ArrayInitialize (truTradeTime, false);
  for (int i = 0; i < bars; i++)
  {
    TimeToStruct (rates [i].time, time);
    if (time.hour >= StartTradeH_P && time.hour < EndTradeH_P) truTradeTime [i] = true;
  }

  //----------------------------------------------------------------------------
  int popSize          = 50;                           // Population size for optimization algorithm
  int epochCount       = NumbTestFuncRuns_P / popSize; // Total number of epochs (iterations) for optimization

  double rangeMin [], rangeMax [], rangeStep [];       // Arrays for storing the parameters' boundaries and steps

  ArrayResize (rangeMin,  WeightsNumber);              // Resize 'min' borders array
  ArrayResize (rangeMax,  WeightsNumber);              // Resize 'max' borders array
  ArrayResize (rangeStep, WeightsNumber);              // Resize the steps array

  for (int i = 0; i < WeightsNumber; i++)
  {
    rangeMax  [i] =  5.0;
    rangeMin  [i] = -5.0;
    rangeStep [i] = 0.01;
  }

  //----------------------------------------------------------------------------
  C_AO *ao = SelectAO (OptimizerSelect_P);             // Select an optimization algorithm

  ao.params [0].val = popSize;                         // Assigning population size....
  ao.SetParams ();                                     //... (optional, then default population size will be used)

  ao.Init (rangeMin, rangeMax, rangeStep, epochCount); // Initialize the algorithm with given boundaries and number of epochs

  // Main loop by number of epochs
  for (int epochCNT = 1; epochCNT <= epochCount; epochCNT++)
  {
    ao.Moving ();                                      // Execute one epoch of the optimization algorithm

    // Calculate the value of the objective function for each solution in the population
    for (int set = 0; set < ArraySize (ao.a); set++)
    {
      ao.a [set].f = TargetFunction (ao.a [set].c, rates, rsi, sto, truTradeTime); //FF.CalcFunc (ao.a [set].c); //ObjectiveFunction (ao.a [set].c); // Apply the objective function to each solution
    }

    ao.Revision ();                                    // Update the population based on the results of the objective function
  }

  //----------------------------------------------------------------------------
  // Output the algorithm name, best result and number of function runs
  Print (ao.GetName (), ", best result: ", ao.fB);
  ArrayCopy (Weights, ao.cB);
  delete ao;                                           // Release the memory occupied by the algorithm object

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

ニューラルネットワークを用いた取引ストラテジーの効率を評価する目的関数を実装します。

1. 変数の初期化：利益、損失、取引回数、その他のパラメータを追跡するための変数を設定します。

2. 過去データの処理：ループで過去データを順に確認し、現在のバーでポジションを開くことが許可されているかどうかをチェックします。

3. データの正規化：各バーについて、価格データ（高値、安値、始値、終値）および指標（RSIとストキャスティクス）を正規化し、ニューラルネットワークに入力できる形にします。

4. シグナル予測：正規化されたデータをニューラルネットワークに入力し、取引シグナル（買いまたは売り）を生成します。

5. OnTickにおける取引ストラテジーに従って、仮想ポジションを管理します。

6. 結果の計算：関数の最後で、総利益/損失の比率を計算し、取引回数を掛け、買いと売りの不均衡に対する減衰係数を考慮します。

この関数は、ニューラルネットワークが生成したシグナルに基づいて利益や損失を分析することで取引ストラテジーの効率を評価し、その品質を数値で返します。本質的には、この関数は取引EAの現在位置から過去の履歴を1回通して実行する処理をおこなっています。

//——————————————————————————————————————————————————————————————————————————————
double TargetFunction (double &weights [], MqlRates &rates [], double &rsi [], double &sto [], bool &truTradeTime [])
{
  int bars = ArraySize (rates);

  // Initialize variables to normalize data
  int    wCNT       = 0;
  double max        = 0.0;
  double min        = 0.0;
  int    signal     = 0;
  double profit     = 0.0;
  double allProfit  = 0.0;
  double allLoss    = 0.0;
  int    dealsNumb  = 0;
  int    sells      = 0;
  int    buys       = 0;
  int    posType    = 0;
  double posOpPrice = 0.0;
  double posClPrice = 0.0;

  // Run through history
  for (int h = BarsAnalysis_P; h < bars - 1; h++)
  {
    if (!truTradeTime [h])
    {
      if (posType != 0)
      {
        posClPrice = rates [h].open;
        profit = (posClPrice - posOpPrice) * signal - 0.00003;

        if (profit > 0.0) allProfit += profit;
        else              allLoss   += -profit;

        if (posType == 1) buys++;
        else              sells++;

        allProfit += profit;
        posType = 0;
      }

      continue;
    }

    max  = -DBL_MAX; // Initial value for maximum
    min  =  DBL_MAX; // Initial value for minimum

    // Find the maximum and minimum among high and low
    for (int b = 1; b <= BarsAnalysis_P; b++)
    {
      if (rates [h - b].high > max) max = rates [h - b].high; // Update maximum
      if (rates [h - b].low  < min) min = rates [h - b].low;  // Update minimum
    }

    // Normalization of input data for neural network
    wCNT = 0;
    for (int b = BarsAnalysis_P; b >= 1; b--)
    {
      Inputs [wCNT] = U.Scale (rates [h - b].high,  min, max, -1, 1); wCNT++; // Normalizing high
      Inputs [wCNT] = U.Scale (rates [h - b].low,   min, max, -1, 1); wCNT++; // Normalizing low
      Inputs [wCNT] = U.Scale (rates [h - b].open,  min, max, -1, 1); wCNT++; // Normalizing open
      Inputs [wCNT] = U.Scale (rates [h - b].close, min, max, -1, 1); wCNT++; // Normalizing close

      Inputs [wCNT] = U.Scale (sto   [h - b],       0,   100, -1, 1); wCNT++; // Normalizing Stochastic
      Inputs [wCNT] = U.Scale (rsi   [h - b],       0,   100, -1, 1); wCNT++; // Normalizing RSI
    }

    // Convert data from Inputs to Outs
    NN.ANN (Inputs, weights, Outs);

    //----------------------------------------------------------------------------
    // Generate a trading signal based on the output of a neural network
    signal = 0;
    if (Outs [0] >  SigThr_P) signal =  1; // Buy signal
    if (Outs [0] < -SigThr_P) signal = -1; // Sell signal

    if ((posType == 1 && signal == -1) || (posType == -1 && signal == 1))
    {
      posClPrice = rates [h].open;
      profit = (posClPrice - posOpPrice) * signal - 0.00003;

      if (profit > 0.0) allProfit += profit;
      else              allLoss   += -profit;

      if (posType == 1) buys++;
      else              sells++;

      allProfit += profit;
      posType = 0;
    }

    if (posType == 0 && signal != 0)
    {
      posType = signal;
      posOpPrice = rates [h].open;
    }
  }

  dealsNumb = buys + sells;

  double ko = 1.0;
  if (sells == 0 || buys == 0) return -DBL_MAX;
  if (sells / buys > 1.5 || buys / sells > 1.5) ko = 0.001;

  return (allProfit / (allLoss + DBL_EPSILON)) * dealsNumb;
}
//——————————————————————————————————————————————————————————————————————————————

図2は、MLPベースのEAを用いてニューラルネットワークに未知の新しいデータで取引した際の取引結果の残高のグラフを示しています。入力データは、正規化されたOHLC価格値に加え、指定されたバー数に基づいて計算されたRSIおよびストキャスティクス指標です。EAはニューラルネットワークが最新の状態である限り取引を続けます。最新でない場合は、ネットワークを学習させてから取引を再開します。したがって、図2に示されている結果は、OOS（サンプル外）データに対するパフォーマンスを反映しています。

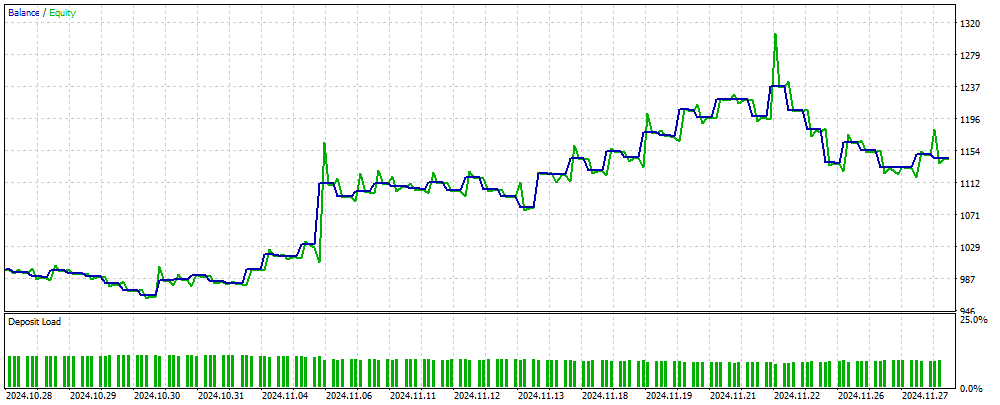
図2：MLPに馴染みのないデータに対するEA操作の結果

まとめ

本記事では、取引EAでニューラルネットワークを使用するための、簡単で分かりやすい方法を紹介しています。この方法は幅広いトレーダーに適しており、機械学習の分野における深い知識を必要としません。この手法では、目的関数の値を正規化してニューラルネットワークに誤差として入力する必要がなく、「重みの爆発」を防ぐための方法も不要です。さらに、「収束停止」という問題も解決され、結果を視覚的に確認しながら直感的に学習を進めることができます。

ただし、このEAには取引操作をおこなう際に必要なチェック機能が備わっておらず、情報提供のみを目的としたものです。

記事で使用されているプログラム

#	名前	種類	詳細
1	#C_AO.mqh	インクルード	集団最適化アルゴリズムの親クラス
2	#C_AO_enum.mqh	インクルード	集団最適化アルゴリズムの列挙
3	Utilities.mqh	インクルード	補助関数のライブラリ
4	#Symbol.mqh	インクルード	取引と補助機能のライブラリ
5	ANN EA.mq5	EA	MLPニューラルネットワークに基づくEA