Algoritmo de optimización del billar — Billiards Optimization Algorithm (BOA)

Contenido

1. Introducción
2. Implementación del algoritmo
3. Resultados de las pruebas

Introducción

En el mundo de los algoritmos de optimización, donde la precisión matemática se une a la inspiración del mundo real, nacen planteamientos de una originalidad asombrosa. Uno de estos métodos es el Algoritmo de Optimización del Billar (BOA), que extrae de la mecánica del clásico juego del billar ideas para las estrategias de búsqueda.

Imagine una mesa de billar en la que cada tronera es una solución potencial, mientras que las bolas son los buscadores de esas soluciones moviéndose por el espacio de posibilidades. Al igual que un jugador de billar experimentado calcula la trayectoria de una bola para golpear con precisión en la tronera, el BOA orienta sus decisiones hacia los mejores resultados posibles mediante un proceso iterativo de búsqueda y perfeccionamiento. Este algoritmo, desarrollado por los investigadores Hadi Givi y Marie Hubalowska en 2023, demuestra un enfoque interesante e inusual para resolver problemas de optimización.

En este artículo, nos sumergiremos en el marco conceptual del BOA, exploraremos su modelo matemático y analizaremos su eficacia en la resolución de problemas multimodales. El algoritmo, que combina la sencillez del concepto con la precisión matemática, descubre nuevos horizontes en el campo de la optimización computacional y representa una valiosa adición al arsenal de métodos modernos de optimización.

Implementación del algoritmo

El BOA es un método de optimización inspirado en el juego del billar. Su esencia es la siguiente: imagine que está buscando la mejor solución a algún problema, lo que, en la terminología del billar, sería como intentar meter la bola en la tronera. Hay 8 troneras en la mesa de billar, además de muchas bolas. Al principio del algoritmo, se crea un grupo de soluciones aleatorias (población). Estas decisiones serían las bolas en una mesa de billar. Para cada solución, se calcula el valor de la función objetivo para determinar su calidad.

En cada iteración del algoritmo, las ocho mejores soluciones de la población se convierten en "troneras" (objetivos a los que aspirar). Las demás soluciones se tratan como bolas que deben dirigirse a estas troneras. Para cada bola (solución), se selecciona al azar una de las troneras (mejores soluciones). A continuación, se calcula una nueva posición de la bola, es decir, una nueva solución que se mueve en la dirección de la tronera seleccionada. Si la nueva posición de la bola da un mejor valor de la función objetivo, la bola se moverá a la nueva posición, y si no, se quedará donde está.

Matemáticamente sería así:

X_new = X + rnd [0.0; 1.0] × (P - I × X)

donde:

• X_new — nueva posición de la bola,
• X — posición actual de la bola,
• P — posición de la tronera (o de la bola que debe golpear la bola actual),
• I —a selección aleatoria de los números 1 ó 2.

El proceso se repite muchas veces y, finalmente, las bolas (soluciones) deberían acercarse a la solución óptima del problema.

La ventaja del BOA puede ser que teóricamente debería equilibrar bien (por un simple factor en la fórmula) entre la búsqueda global y la búsqueda local. Esto se logra mediante un coeficiente aleatorio "I" que posibilita o bien el "alcance corto" de la bola (refinando las soluciones cerca de los puntos buenos) o un "alcance largo" de la misma (explorando diferentes regiones del espacio de soluciones).

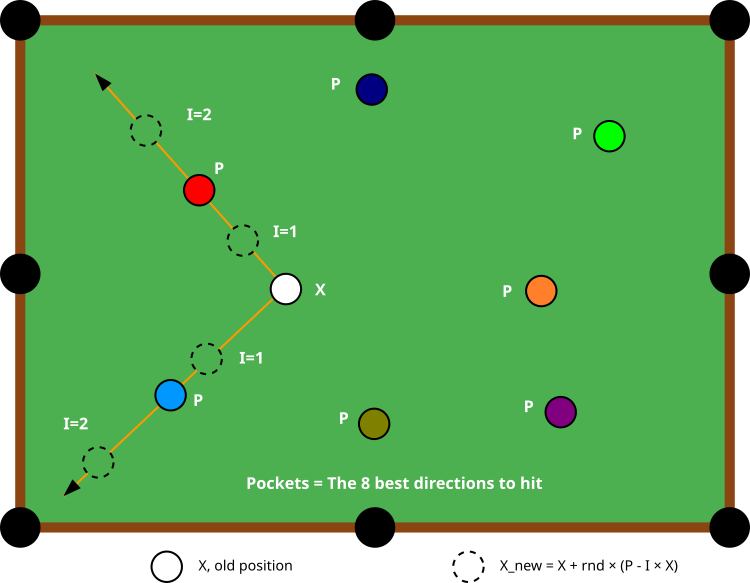
Figura 1. Esquema del algoritmo BOA

La figura 1 ilustra esquemáticamente el principio de funcionamiento del algoritmo BOA. El elemento central, una bola blanca etiquetada con una "X", representa la posición actual del agente en el espacio de búsqueda de soluciones. Alrededor de esta bola hay bolas de colores marcadas con una "P": estas son "bolsas" o "troneras" que representan las 8 mejores soluciones encontradas hasta el momento. El esquema demuestra cómo el agente (bola blanca) puede actualizar su posición moviéndose hacia diferentes troneras, es decir, para cada paso, el agente selecciona aleatoriamente una de las ocho troneras como dirección de movimiento objetivo.

Las líneas naranjas con flechas muestran las posibles trayectorias del movimiento del agente hacia diferentes troneras (en este caso, roja, azul). Los círculos punteados indican las posiciones intermedias que puede adoptar el agente al desplazarse, en función del valor de "I" (1 ó 2). El valor de "I" modifica la "fuerza de impacto" y la naturaleza del movimiento: con I=1 la posición se desplaza hacia la tronera seleccionada, mientras que con I=2 el agente puede realizar movimientos más bruscos, lo que favorece la exploración de una parte más amplia del espacio de soluciones.

Una vez hemos comprendido completamente cómo funciona el algoritmo, podemos comenzar a escribir el pseudocódigo del BOA.

Inicialización
    Determinamos el número de bolas (popSize) y de troneras (numPockets).
    Creamos una población de bolas (agentes).
    Establecemos un espacio de búsqueda con límites mínimo y máximo.

Algoritmo básico
Primera fase: Inicialización primaria (solo se ejecuta una vez)
    Para cada bola de la población:
        Colocamos aleatoriamente las bolas en el espacio de búsqueda.
        Mantenemos su posición inicial.
        Fijamos los valores iniciales de la función de ajuste en los valores mínimos.

Segunda fase: Desplazamiento de las bolas
    Para cada bola de la población:
        Para cada coordenada de la bola:
            Elegimos una tronera al azar (una de las mejores soluciones de numPockets).
            Actualizamos la posición de la bola utilizando la fórmula: X_new = X + rnd [0.0; 1.0] × (P - I × X)
            Comprobamos que la nueva posición se mantiene dentro de los límites permitidos.

Tercera fase: Actualización de las mejores soluciones
    Para cada bola:
        Si el valor de la función de aptitud de la bola es mejor que el mejor valor global, actualizamos el mejor global.
        Si el valor de la función de aptitud de la bola es mejor que su propio mejor, actualizamos su mejor valor.
    Luego clasificamos las bolas según sus mejores valores de función de aptitud.
        Los primeros numPockets de los agentes tras la clasificación se convierten en las troneras de la siguiente iteración.

Después repetimos los pasos "Desplazamiento de las bolas" y "Actualización de las mejores soluciones" hasta que se alcance la condición de parada (por ejemplo, el número máximo de iteraciones).

Vamos a escribir ahora el código del algoritmo. La clase "C_AO_BOA" deriva de la clase "C_AO" (la clase básica de los algoritmos de optimización basados en poblaciones) e implementa el algoritmo de optimización BOA. Veamos sus elementos clave:

Constructor C_AO_BOA () - inicializa los valores de las variables de instancia:

• popSize - se establece en 50, indica el número de bolas (agentes) en el algoritmo.
• numPockets - se establece en 8, forma el número de troneras de la mesa de billar.
• El tamaño del array "params" se modifica, y luego se añaden dos parámetros (popSize y numPockets) al array "params".

Métodos:

• SetParams () - este método es responsable de establecer los parámetros del array "params" de nuevo a las variables locales "popSize" y "numPockets".
• Init () - este método de inicialización configura los valores mínimo y máximo y los pasos para la búsqueda, y establece el número de épocas.
• Moving () - es responsable del desplazamiento de las bolas en el algoritmo.
• Revisión () - realiza la comprobación y revisión de las posiciones/decisiones de los agentes.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BOA () { }
  C_AO_BOA ()
  {
    ao_name = "BOA";
    ao_desc = "Billiards Optimization Algorithm";
    ao_link = "https://www.mql5.com/es/articles/17325";

    popSize    = 50;  // number of balls (agents)
    numPockets = 8;   // number of pockets on a billiard table

    ArrayResize (params, 2);

    params [0].name = "popSize";    params [0].val = popSize;
    params [1].name = "numPockets"; params [1].val = numPockets;
  }

  void SetParams ()
  {
    popSize    = (int)params [0].val;
    numPockets = (int)params [1].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum values
             const double &rangeMaxP  [],  // maximum values
             const double &rangeStepP [],  // step change
             const int     epochsP = 0);   // number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int numPockets;       // number of pockets (best solutions)

  private: //-------------------------------------------------------------------
};
//——————————————————————————————————————————————————————————————————————————————

El método "Init" de la clase "C_AO_BOA" se encarga de inicializar el algoritmo BOA. Luego se llama a la función "StandardInit ()" al principio del método, transmitiéndole los arrays de valores mínimo y máximo y los pasos. Esta función es responsable de ejecutar las acciones generales y las inicializaciones que deben realizarse para todas las clases derivadas de los algoritmos de optimización (incluida la configuración inicial de rangos), así como de preparar los agentes de búsqueda básicos en el algoritmo. Si "StandardInit ()" retorna "false" (inicialización fallida), el método "Init" también devolverá "false". Si tiene éxito, el método retornará "true".

//——————————————————————————————————————————————————————————————————————————————
//--- Initialization
bool C_AO_BOA::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

El método Moving implementa el paso principal del algoritmo BOA y controla el movimiento de los agentes (bolas), en el espacio de soluciones. En primer lugar, se comprueba la condición "if (!revision)" para determinar si el método se llama por primera vez. Si "revision=false", deberemos inicializar las posiciones de los agentes. Para ello, se ejecuta un ciclo sobre todos los agentes definidos como "popSize", dentro del cual se ejecuta un ciclo anidado sobre las coordenadas que especifican los parámetros de decisión de cada agente.

En la etapa de generación de la posición inicial, se selecciona un valor aleatorio para cada coordenada del agente dentro de un rango dado, mientras que la función u.SeInDiSp () lleva el valor a un valor válido dado el paso. La posición inicial del agente se almacena en a[p].cB[c] como la mejor solución individual de la bola (en la primera iteración, la solución inicial es igual a la mejor solución conocida), y tras establecer "revision=true", el método finaliza la ejecución, lo que impide que se reinicialicen los valores.

En la segunda iteración y en las siguientes, se ejecuta un ciclo en todos los agentes que deben ser desplazados. Durante el proceso de actualización de coordenadas, se ejecutan ciclos anidados sobre todos los agentes y sus coordenadas, en los que se selecciona aleatoriamente una de las mejores troneras disponibles para actualizar la posición actual del agente. La posición se actualiza partiendo de la posición anterior, a la que se añade un cambio aleatorio basado en la posición de la tronera seleccionada. La función u.RNDprobab () devuelve un número aleatorio en el rango [0,0; 1,0] para añadir ruido aleatorio, mientras que la función u.RNDintInRange (1, 2) tiene un valor aleatorio de 1 o 2 multiplicado por la posición del agente.

Una vez actualizada la posición, esta se corrige para llevar el valor actualizado al rango indicado, considerando los valores mínimo y máximo, así como el paso de cambio.

//——————————————————————————————————————————————————————————————————————————————
//--- The main step of the algorithm
void C_AO_BOA::Moving ()
{
  //----------------------------------------------------------------------------
  // Initial initialization
  if (!revision)
  {
    for (int p = 0; p < popSize; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [p].c  [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [p].c  [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        a [p].cB [c] = a [p].c [c];  // Save the initial position
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      int pocketID = u.RNDminusOne (numPockets);

      a [p].c [c] = a [p].cB [c] + u.RNDprobab () * (a [pocketID].cB [c] - u.RNDintInRange (1, 2) * a [p].cB [c]);
      a [p].c [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "Revision" se encarga de actualizar la mejor solución global en el algoritmo BOA, y también actualiza las mejores soluciones individuales de las bolas. Al final del método, las bolas se clasifican según sus mejores soluciones individuales.

//——————————————————————————————————————————————————————————————————————————————
//--- Update the best solution taking into account greedy selection and the probability of making worse decisions
void C_AO_BOA::Revision ()
{
  int bestIND = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      bestIND = i;
    }

    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  if (bestIND != -1) ArrayCopy (cB, a [bestIND].c, 0, 0, WHOLE_ARRAY);

  S_AO_Agent aT []; ArrayResize (aT, popSize);
  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

Resultados de las pruebas

Veamos ahora cómo funciona el algoritmo BOA:

BOA|Billiards Optimization Algorithm|50.0|8.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.63960620766331
25 Hilly's; Func runs: 10000; result: 0.3277725645995603
500 Hilly's; Func runs: 10000; result: 0.2514878043770147
=============================
5 Forest's; Func runs: 10000; result: 0.3885662762060409
25 Forest's; Func runs: 10000; result: 0.1955657530616877
500 Forest's; Func runs: 10000; result: 0.15336230733273673
=============================
5 Megacity's; Func runs: 10000; result: 0.5415384615384615
25 Megacity's; Func runs: 10000; result: 0.19046153846153846
500 Megacity's; Func runs: 10000; result: 0.10530769230769324
=============================
All score: 2.79367 (31.04%)

Como podemos ver, el rendimiento del algoritmo es bastante flojo y no entra en nuestra tabla de clasificación, así que hemos decidido analizarlo con más detenimiento y se me han ocurrido algunas ideas para hacerlo funcionar. Veamos de nuevo la fórmula para desplazar las bolas:

X_new = X + rnd [0.0; 1.0] × (P - I × X)

En esta fórmula, el factor "I" se aplica al valor de la coordenada actual de la bola, lo cual posee un oscuro significado físico, ya que en realidad el escalado se aplica al valor absoluto de la coordenada. La acción natural parece ser sacar este coeficiente del paréntesis para proporcionar una escala a la diferencia entre el valor de la "tronera" y el de la coordenada de la bola. Entonces la notación resultante describe efectivamente el significado físico, o bien la bola no llegará a la tronera o volará por encima de ella. Esta variabilidad será proporcionada por el factor de ruido adicional de un número aleatorio en el rango [0,0, 1,0].

Como resultado, obtendremos la fórmula para el desplazamiento de las bolas:

X_new = X + rnd [0.0; 1.0] × (P -X) × I

Así pues, a continuación mostramos el código completo de la versión modificada del método Moving (), mostrando la línea comentada con la fórmula de los autores y a continuación con nuestra versión de la fórmula.

//——————————————————————————————————————————————————————————————————————————————
//--- The main step of the algorithm
void C_AO_BOA::Moving ()
{
  //----------------------------------------------------------------------------
  // Initial initialization
  if (!revision)
  {
    for (int p = 0; p < popSize; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [p].c  [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [p].c  [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        a [p].cB [c] = a [p].c [c];  // Save the initial position as the best individual solution 
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      int pocketID = u.RNDminusOne (numPockets);

      //a [p].c [c] = a [p].cB [c] + u.RNDprobab () * (a [pocketID].cB [c] - u.RNDintInRange (1, 2) * a [p].cB [c]);
      a [p].c [c] = a [p].cB [c] + u.RNDprobab () * (a [pocketID].cB [c] - a [p].cB [c]) * u.RNDintInRange (1, 2);
      a [p].c [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Ahora, tras los cambios realizados, veamos cómo se comporta el algoritmo con los parámetros con los que la versión de los autores mostró sus mejores resultados:

BOA|Billiards Optimization Algorithm|50.0|8.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8727603657603271
25 Hilly's; Func runs: 10000; result: 0.7117647027521633
500 Hilly's; Func runs: 10000; result: 0.25339119302510993
=============================
5 Forest's; Func runs: 10000; result: 0.9228482722678735
25 Forest's; Func runs: 10000; result: 0.7601448268715335
500 Forest's; Func runs: 10000; result: 0.3498925749480034
=============================
5 Megacity's; Func runs: 10000; result: 0.6184615384615385
25 Megacity's; Func runs: 10000; result: 0.45876923076923076
500 Megacity's; Func runs: 10000; result: 0.14586153846153965
=============================
All score: 5.09389 (56.60%)

Haciendo algunos experimentos más, hemos conseguido parámetros con los que se obtienen resultados aún mejores:

BOA|Billiards Optimization Algorithm|50.0|25.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.957565927297626
25 Hilly's; Func runs: 10000; result: 0.8259872884790693
500 Hilly's; Func runs: 10000; result: 0.2523458952211869
=============================
5 Forest's; Func runs: 10000; result: 0.9999999999999929
25 Forest's; Func runs: 10000; result: 0.900362056289584
500 Forest's; Func runs: 10000; result: 0.305018130407844
=============================
5 Megacity's; Func runs: 10000; result: 0.7353846153846153
25 Megacity's; Func runs: 10000; result: 0.5252307692307692
500 Megacity's; Func runs: 10000; result: 0.09563076923077005
=============================
All score: 5.59753 (62.19%)

Echemos un vistazo a la visualización del rendimiento del algoritmo BOA en las funciones de prueba. No existe un comportamiento característico en el espacio de búsqueda; los movimientos de las "bolas" parecen caóticos. Resulta especialmente llamativo que el algoritmo tenga éxito en problemas de dimensionalidades pequeñas y medianas, pero surjan problemas de convergencia en problemas de grande dimensionalidad. Esto resulta especialmente notable en la función Hilly suave, donde el rendimiento es incluso peor que en la Megacity discreta, que es extremadamente rara en comparación con otros algoritmos poblacionales. También debemos considerar la tendencia del algoritmo a quedarse atascado en mínimos locales cuando resuelve problemas de pequeña dimensionalidad.

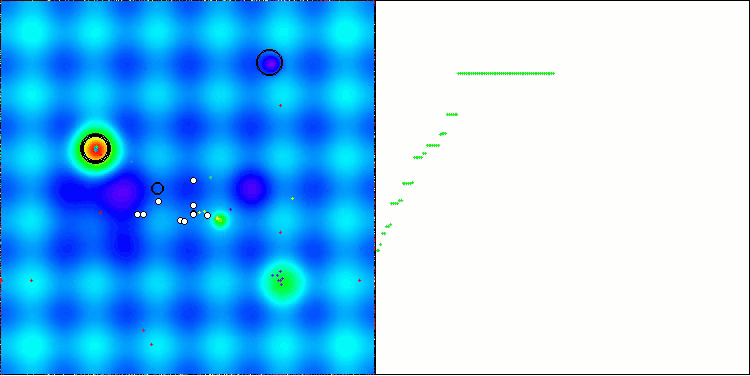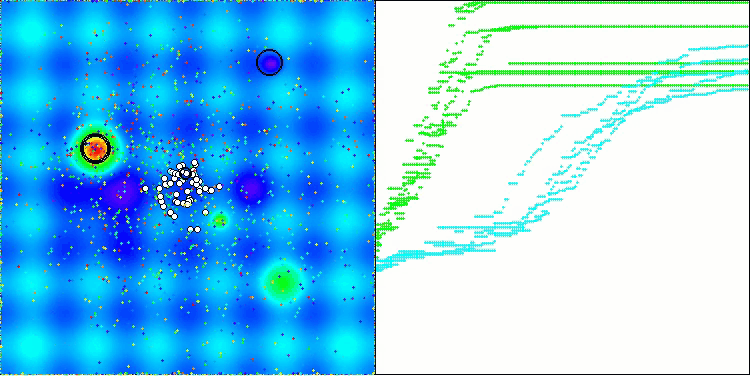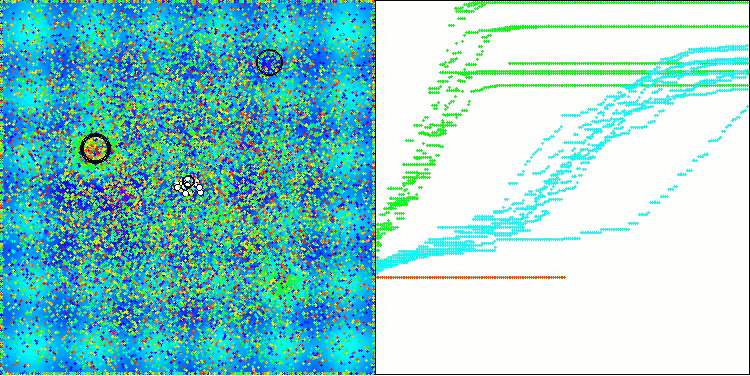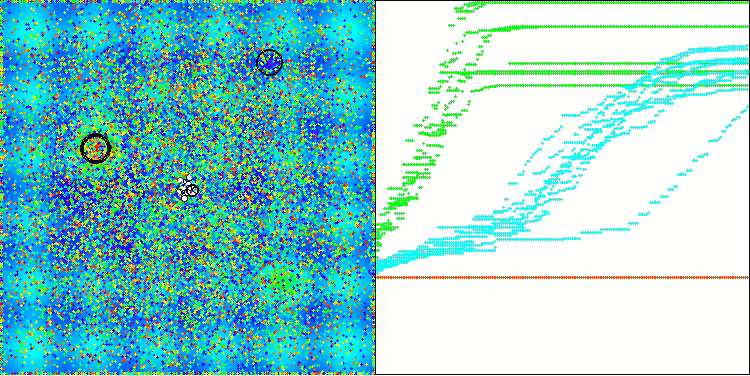
BOA en la función de prueba Hilly

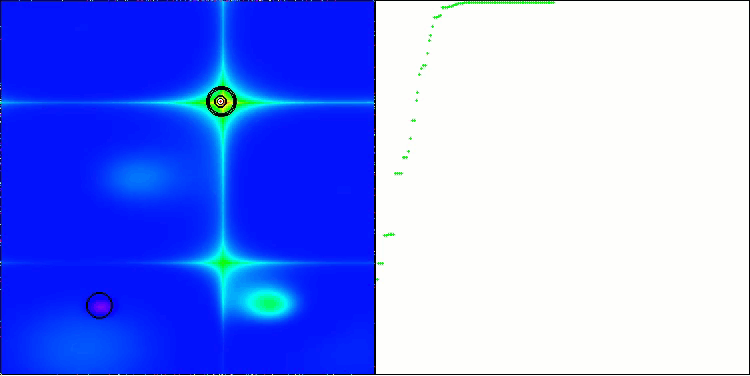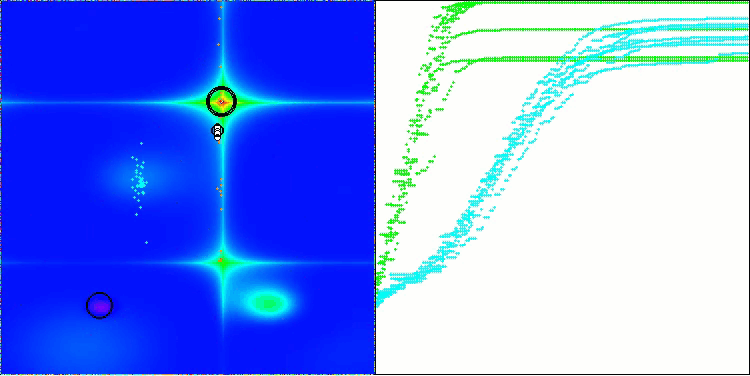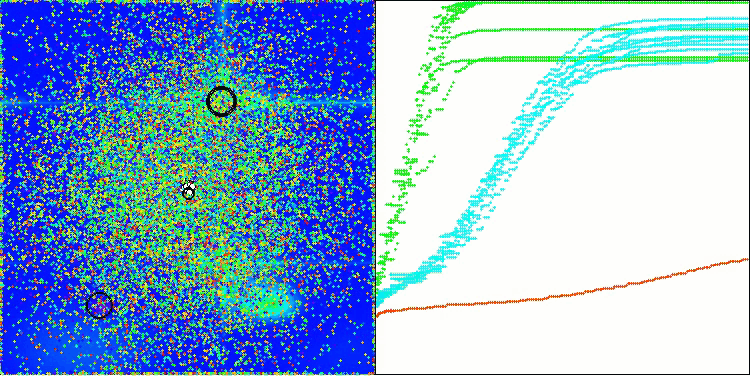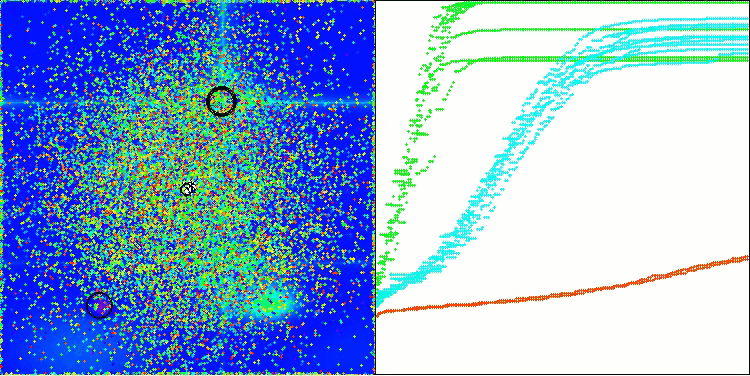
BOA en la función de prueba Forest

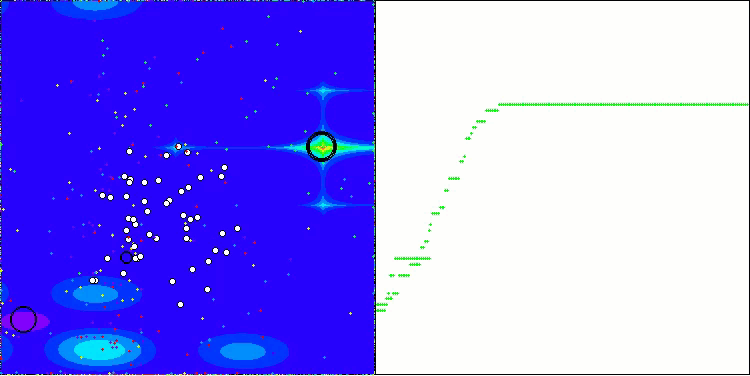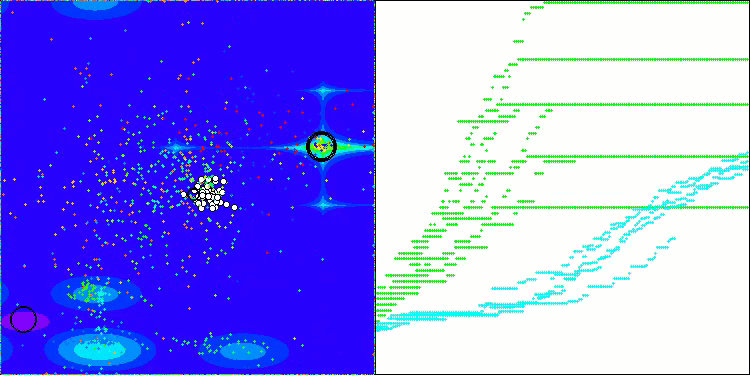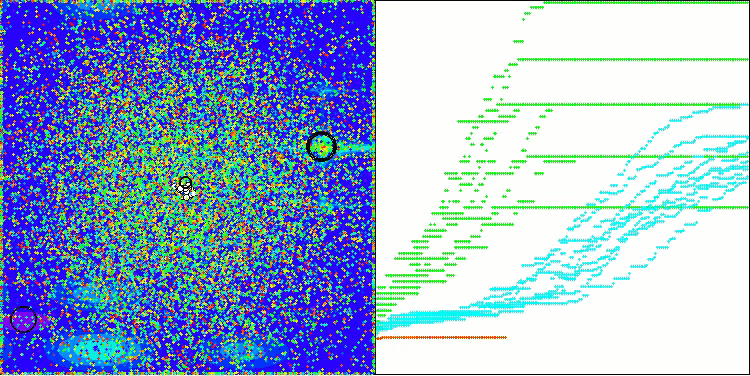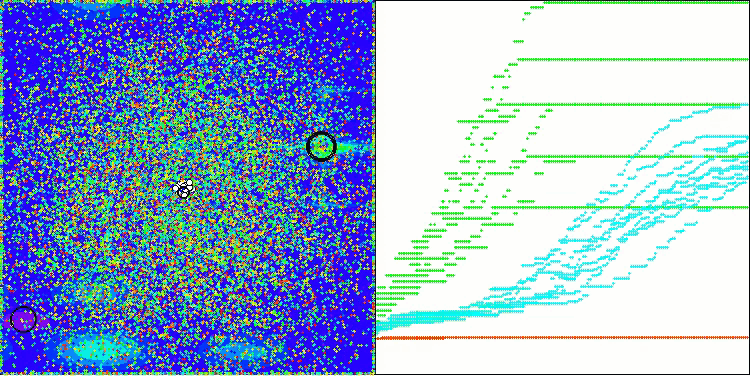
BOA en la función de prueba Megacity

Ahora resumiremos la prueba y veremos los resultados. Incluso teniendo graves defectos, el algoritmo ha ocupado un puesto bastante alto, el 8 en la clasificación de los mejores algoritmos de optimización.

#	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% de MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	code lock algorithm (joo)	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	animal migration optimization M	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O) evolution strategies	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	comet tail algorithm (joo)	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	TETA	time evolution travel algorithm (joo)	0.91362	0.82349	0.31990	2.05701	0.97096	0.89532	0.29324	2.15952	0.73462	0.68569	0.16021	1.58052	5.797	64.41
7	SDSm	stochastic diffusion search M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
8	BOAm	billiards optimization algorithm M	0.95757	0.82599	0.25235	2.03590	1.00000	0.90036	0.30502	2.20538	0.73538	0.52523	0.09563	1.35625	5.598	62.19
9	AAm	archery algorithm M	0.91744	0.70876	0.42160	2.04780	0.92527	0.75802	0.35328	2.03657	0.67385	0.55200	0.23738	1.46323	5.548	61.64
10	ESG	evolution of social groups (joo)	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
11	SIA	simulated isotropic annealing (joo)	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
12	ACS	artificial cooperative search	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
13	DA	dialectical algorithm	0.86183	0.70033	0.33724	1.89940	0.98163	0.72772	0.28718	1.99653	0.70308	0.45292	0.16367	1.31967	5.216	57.95
14	BHAm	black hole algorithm M	0.75236	0.76675	0.34583	1.86493	0.93593	0.80152	0.27177	2.00923	0.65077	0.51646	0.15472	1.32195	5.196	57.73
15	ASO	anarchy society optimization	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
16	RFO	royal flush optimization (joo)	0.83361	0.73742	0.34629	1.91733	0.89424	0.73824	0.24098	1.87346	0.63154	0.50292	0.16421	1.29867	5.089	56.55
17	AOSm	búsqueda de orbitales atómicos M	0.80232	0.70449	0.31021	1.81702	0.85660	0.69451	0.21996	1.77107	0.74615	0.52862	0.14358	1.41835	5.006	55.63
18	TSEA	turtle shell evolution algorithm (joo)	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
19	DE	differential evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
20	CRO	chemical reaction optimization	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
21	BIO	blood inheritance optimization (joo)	0.81568	0.65336	0.30877	1.77781	0.89937	0.65319	0.21760	1.77016	0.67846	0.47631	0.13902	1.29378	4.842	53.80
22	BSA	bird swarm algorithm	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
23	HS	harmony search	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
24	SSG	saplings sowing and growing	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
25	BCOm	bacterial chemotaxis optimization M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
26	ABO	african buffalo optimization	0.83337	0.62247	0.29964	1.75548	0.92170	0.58618	0.19723	1.70511	0.61000	0.43154	0.13225	1.17378	4.634	51.49
27	(PO)ES	(PO) evolution strategies	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
28	TSm	tabu search M	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
29	BSO	brain storm optimization	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
30	WOAm	wale optimization algorithm M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
31	AEFA	artificial electric field algorithm	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
32	AEO	artificial ecosystem-based optimization algorithm	0.91380	0.46713	0.26470	1.64563	0.90223	0.43705	0.21400	1.55327	0.66154	0.30800	0.28563	1.25517	4.454	49.49
33	ACOm	ant colony optimization M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
34	BFO-GA	bacterial foraging optimization - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
35	SOA	simple optimization algorithm	0.91520	0.46976	0.27089	1.65585	0.89675	0.37401	0.16984	1.44060	0.69538	0.28031	0.10852	1.08422	4.181	46.45
36	ABH	artificial bee hive algorithm	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
37	ACMO	atmospheric cloud model optimization	0.90321	0.48546	0.30403	1.69270	0.80268	0.37857	0.19178	1.37303	0.62308	0.24400	0.10795	0.97503	4.041	44.90
38	ADAMm	adaptive moment estimation M	0.88635	0.44766	0.26613	1.60014	0.84497	0.38493	0.16889	1.39880	0.66154	0.27046	0.10594	1.03794	4.037	44.85
39	CGO	chaos game optimization	0.57256	0.37158	0.32018	1.26432	0.61176	0.61931	0.62161	1.85267	0.37538	0.21923	0.19028	0.78490	3.902	43.35
40	ATAm	artificial tribe algorithm M	0.71771	0.55304	0.25235	1.52310	0.82491	0.55904	0.20473	1.58867	0.44000	0.18615	0.09411	0.72026	3.832	42.58
41	ASHA	artificial showering algorithm	0.89686	0.40433	0.25617	1.55737	0.80360	0.35526	0.19160	1.35046	0.47692	0.18123	0.09774	0.75589	3.664	40.71
42	ASBO	adaptive social behavior optimization	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
43	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
44	CSA	circle search algorithm	0.66560	0.45317	0.29126	1.41003	0.68797	0.41397	0.20525	1.30719	0.37538	0.23631	0.10646	0.71815	3.435	38.17
45	IWO	invasive weed optimization	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
	R.W.	random walk	0.48754	0.32159	0.25781	1.06694	0.37554	0.21944	0.15877	0.75375	0.27969	0.14917	0.09847	0.52734	2.348	26.09

Conclusiones

El algoritmo modificado de optimización del billar (BOAm) ha mostrado resultados interesantes en las funciones de prueba. El análisis de los datos presentados muestra que el algoritmo alcanza el mejor rendimiento en problemas de dimensionalidad pequeña y mediana, obteniendo valores máximos en las pruebas Hilly (0,957), Forest (0,999) y Megacity (0,735) al alcanzar las 10.000 iteraciones. Esto indica su gran eficacia a la hora de encontrar soluciones óptimas para problemas de complejidad moderada. Sin embargo, el rendimiento disminuye sustancialmente cuando aumenta la dimensionalidad del problema, como puede verse en los resultados de los escenarios con 1.000 variables, en los que el rendimiento desciende a 0,252, 0,305 y 0,095 respectivamente.

Cabe destacar la notable mejora de rendimiento de la versión modificada del algoritmo, que obtiene un 62,19% de la máxima puntuación posible, el doble que la versión original (31,04%). Esta impresionante mejora se ha conseguido cambiando solo una línea de código relativa a la fórmula de actualización de la posición de las bolas.

La simplicidad del algoritmo supone al mismo tiempo su ventaja y su limitación: es intuitivo, fácil de aplicar y se basa en un elegante concepto de juego de billar, pero puede requerir modificaciones adicionales para tratar eficazmente problemas de gran dimensionalidad. En general, simplemente por encontrarse entre los diez primeros algoritmos de la tabla de clasificación, el BOAm representa un enfoque metaheurístico prometedor con un buen equilibrio entre exploración y explotación del espacio de soluciones.

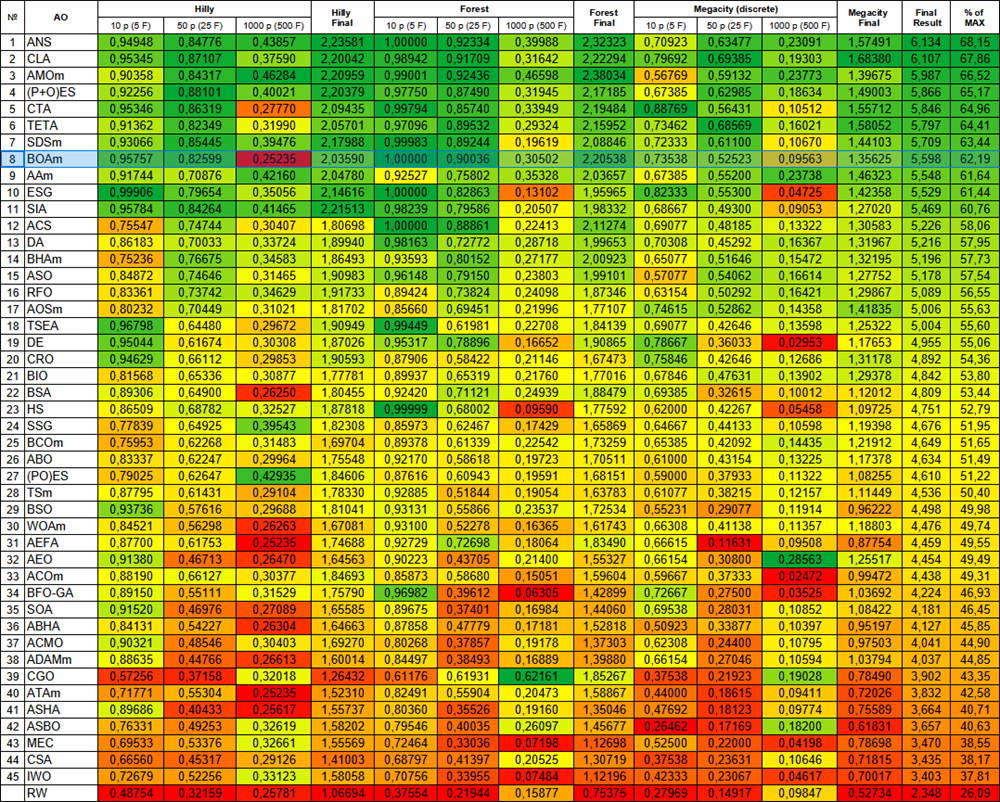
Figura 2. Clasificación por colores de los algoritmos según las pruebas respectivas

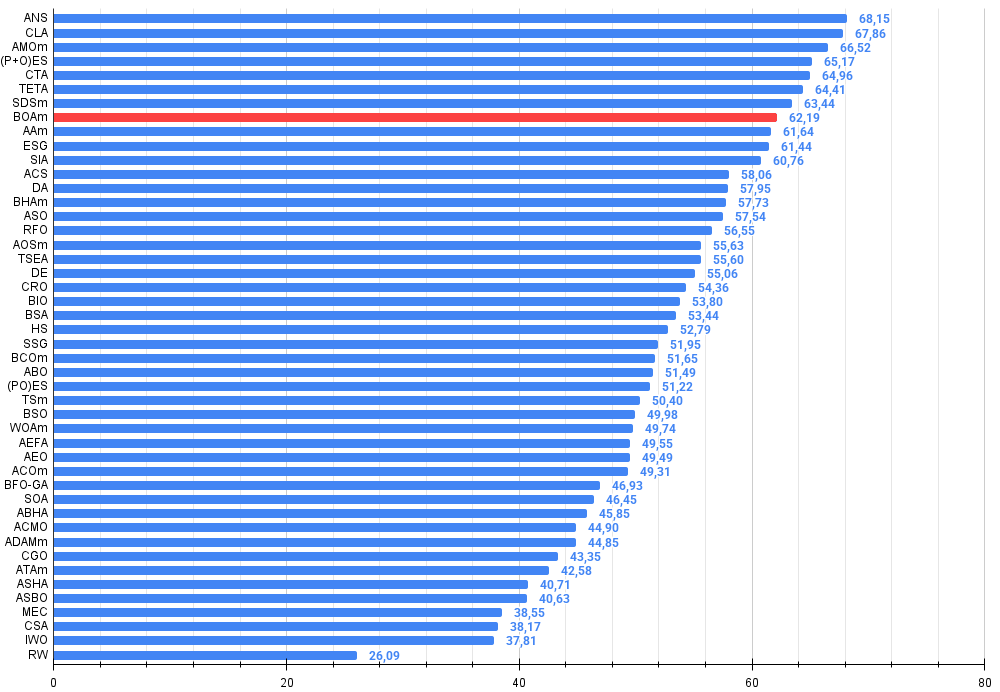
Figura 3. Histograma de los resultados de las pruebas de algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de puntuación está en el archivo)

Ventajas e inconvenientes del algoritmo BOA:

Ventajas:

1. Tiene muy pocos parámetros externos.
2. Implementación sencilla.
   
3. Rinde bien en tareas pequeñas y medianas.
4. Excelentes resultados en problemas con extremos "agudos" (como la función Forest).
   

Desventajas:

1. Se atasca en extremos locales en problemas de baja dimensionalidad.
   
2. Velocidad de convergencia y precisión muy bajas en problemas "suaves" (como la función Hilly) de alta dimensionalidad.

Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	#C_AO.mqh	Archivo de inclusión	Clase padre de algoritmos de población optimizaciones
2	#C_AO_enum.mqh	Archivo de inclusión	Enumeración de los algoritmos de optimización basados en la población
3	TestFunctions.mqh	Archivo de inclusión	Biblioteca de funciones de prueba
4	TestStandFunctions.mqh	Archivo de inclusión	Biblioteca de funciones del banco de pruebas
5	Utilities.mqh	Archivo de inclusión	Biblioteca de funciones auxiliares
6	CalculationTestResults.mqh	Archivo de inclusión	Script para calcular los resultados en una tabla comparativa
7	Testing AOs.mq5	Script	Banco de pruebas único para todos los algoritmos de optimización basados en la población
8	Simple use of population optimization algorithms.mq5	Script	Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización
9	Test_AO_BOAm.mq5	Script	Banco de pruebas para BOAm