Algoritmo de cola de cometa (Comet Tail Algorithm, CTA)

Contenido:

1.Introducción
2.Aplicación del algoritmo
3.Resultados de las pruebas

1. Introducción

En el mundo de la astronomía, los cometas siempre han resultado de especial interés para científicos e investigadores. Estos singulares objetos espaciales, formados principalmente por hielo, polvo y gases, suponen una importante fuente de información sobre los procesos que tienen lugar en el espacio exterior. Uno de las partes más notables e impresionantes de los cometas es su cola, que se forma cuando el cometa se acerca al Sol.

El Sol desempeña un papel clave en la formación de la cola del cometa: su radiación y el viento solar hacen que el material de la superficie del cometa se evapore y descomponga. Este proceso provoca la formación de la cola del cometa, una región de polvo, gases y partículas ionizadas que el viento solar y la fuerza gravitatoria del Sol alejan del cometa.

En este artículo analizaremos el algoritmo de optimización de autor CTA (Comet Tail Algorithm), inspirado en este singular fenómeno astronómico. El algoritmo CTA usa el concepto del movimiento de los cometas y sus colas para encontrar soluciones óptimas en problemas de optimización. Así, estudiaremos con detalle el movimiento del cometa y su cola, así como el papel del Sol en estos procesos. También discutiremos cómo se aplican estos conceptos al algoritmo CTA para encontrar soluciones óptimas de forma eficiente.

Los cometas son pequeños cuerpos del sistema solar que comienzan a vaporizarse y liberar gases al aproximarse al Sol. Este proceso se denomina sublimación. Los cometas suelen tener órbitas muy elípticas y periodos orbitales muy variados, desde unos pocos años hasta varios millones de años.

El movimiento del cometa y de su cola se relaciona estrechamente con la influencia del Sol. El calor del Sol hace que el hielo del cometa se convierta en gases, provocando el agrandamiento de la coma (la envoltura de gas que rodea el núcleo del cometa). La presión de la radiación solar y las partículas solares de alta velocidad (viento solar) pueden arrastrar el polvo y el gas de la coma lejos del Sol, generando a veces una cola larga y brillante. Además, la radiación solar y el viento solar ionizan los gases de la cola del cometa, haciendo que brille.

En el contexto del algoritmo CTA, podemos pensar en cada solución como partículas de la cola de un cometa moviéndose por un espacio de soluciones. El núcleo del cometa supondrá la mejor solución, mientras que las partículas de la cola serán soluciones derivadas que se alejarán del núcleo. Esta representación permitirá al algoritmo "investigar" el espacio de soluciones y adaptarse a sus características.

2. Aplicación del algoritmo

Veamos más de cerca el movimiento del cometa y su cola, que son elementos clave en este algoritmo, además del papel del Sol en estos procesos.

Movimiento de los cometas:

• El cometa se desplaza en una órbita elíptica alrededor del Sol.
• Cuando un cometa se acerca al Sol, comienza a emitir gas y polvo, formando la cola del cometa.
• El movimiento del cometa viene determinado por la atracción gravitatoria del Sol, así como por la repulsión del viento solar y la radiación solar.
• El cometa se desplaza siguiendo su propia órbita, mientras que su cola siempre apunta en dirección opuesta al Sol.

Movimiento de la cola del cometa:

• La cola de gas del cometa está formada por gases ionizados que serán "expulsados" del núcleo del cometa por el viento solar.
• El viento solar es una corriente de partículas cargadas que proceden del Sol. Dicha corriente "repele" la cola de gas del cometa, dirigiéndola en dirección opuesta al Sol.
• La cola de polvo de un cometa está formada por partículas de mayor tamaño que son "repelidas" del núcleo del cometa por la radiación solar.
• La radiación solar ejerce presión sobre las partículas de polvo, desviándolas ligeramente de la dirección de movimiento del cometa, y formando una cola de polvo curvada.

Papel del Sol:

• El Sol es el objeto central en torno al cual gira la órbita de un cometa.
• La atracción gravitatoria del Sol define el movimiento del cometa a lo largo de una órbita elíptica.
• El viento solar y la radiación solar "esculpen" a la cola del cometa dirigiéndola en dirección opuesta al Sol.

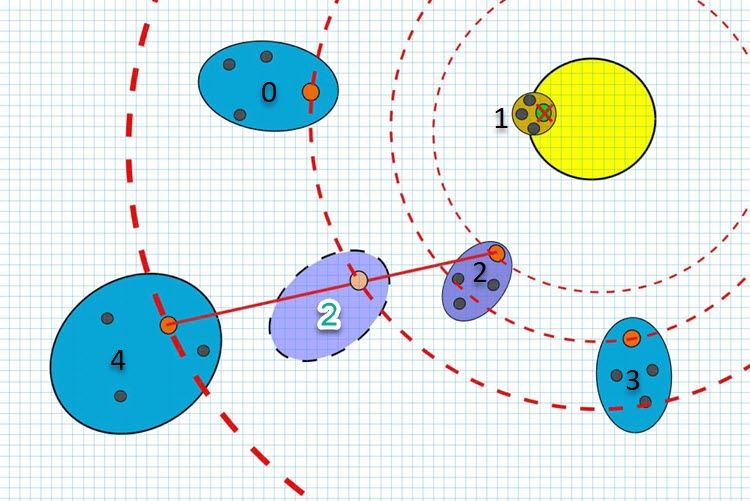
Figura 1. Forma y tamaño de los cometas en el contexto del algoritmo CTA según la distancia hasta la estrella (mejor solución global).

La figura 1 ilustra las propiedades de los cometas en el algoritmo. Cada cometa tiene un número único que se corresponde con su índice en el array. La figura muestra las órbitas condicionales de los cometas respecto a una estrella. Al aumentar la distancia desde la estrella, la cola del cometa se alarga y adquiere una forma cercana a la esférica. En este caso, además, la nube de partículas de la cola estará menos desplazada respecto al núcleo del cometa. Cuanto más cerca se encuentre el cometa de la estrella, menor será el área de probabilidad de la cola y más alargada se volverá.

El cometa número 1 se ha acercado demasiado a la luminaria y se ha vaporizado. No obstante, en el algoritmo, la destrucción del cometa no se produce realmente. En su lugar, sigue actuando la formación de una nube de cola con un centro correspondiente al centro de la estrella. Esto significa que cuanto más pequeña sea la nube de cola, más intenso será el refinamiento de la solución en la región del cometa. Y a la inversa, cuanto mayor sea el tamaño de la cola, más intensa será la exploración del espacio de búsqueda. En este caso, los ejes elípticos de todos los cometas se dirigen siempre lejos de la estrella, es decir, lejos de la mejor solución global actual.

La lógica del algoritmo permite ajustar los coeficientes de expansión de las nubes de cometas tanto hacia la expansión con la distancia desde la estrella como hacia la reducción. También se puede ajustar el grado de aplanamiento de las elipses en función del radio de la órbita del cometa. Incluso es posible dirigir la cola del cometa no hacia el lado opuesto de la estrella, sino hacia ella (si así se desea).

La figura 1 también muestra el momento de la migración condicional del cometa número 2 a una nueva órbita (número 2 enmarcado). Esto ocurre durante el intercambio de la materia de los núcleos de los dos cometas. En la figura, el cometa 2 toma prestada la materia del cometa 4. Si se encuentra una solución mejor durante el intercambio de sustancias entre cometas, el cometa correspondiente cuya formación de sustancias se estaba produciendo en ese momento, se desplazará a una nueva órbita.

El tamaño de la cola del cometa y su desplazamiento respecto al núcleo según la distancia hasta la estrella pueden calcularse convencionalmente según una ley lineal. En este caso, la distancia máxima igual a 1 se corresponde con el rango de valores mínimo y máximo en la correspondiente coordenada optimizada del problema. Este enfoque nos permitirá describir de forma sencilla e ilustrativa la variación de los parámetros de la cola del cometa en función de la distancia hasta la estrella.

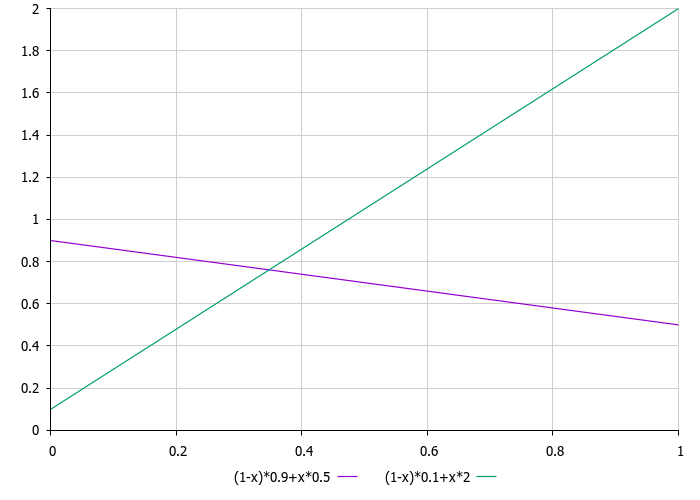
Figura 2. Gráficos de dependencia de los coeficientes de desplazamiento de la cola del cometa (púrpura) y del tamaño de la cola (verde) según la distancia hasta la estrella.

Así pues, hemos elaborado las leyes del cambio de la forma y el tamaño de la nube de partículas para los cometas, por lo que podemos resumir las conclusiones sobre las posibles propiedades del algoritmo. Las principales propiedades del algoritmo inspirado en la cola del cometa, teniendo en cuenta la dirección de la cola desde el Sol (óptimo global) y buscando no solo la mejor región, sino también en la región de soluciones menos óptimas, pueden ser las siguientes:

1. Evaporación y evolución de las soluciones. El algoritmo puede usar un proceso de evaporación y evolución de soluciones, en el que se pueden explorar tanto las mejores regiones como las regiones de soluciones menos óptimas.
2. Multiplicidad de variaciones. El algoritmo puede tratar de generar múltiples soluciones que reflejen diferentes niveles de optimalidad, de manera similar a la diversidad de composición en la cola de un cometa.
3. Adaptabilidad a factores externos. Como un cometa reacciona a la influencia del Sol, el algoritmo puede adaptarse a los cambios del entorno o de la función objetivo.
4. Búsqueda de un óptimo global. La dirección de la cola desde el Sol puede simbolizar la tendencia del algoritmo a buscar un óptimo global, pero también a considerar soluciones menos óptimas para evitar la convergencia prematura a óptimos locales.

Vamos a escribir un esbozo del algoritmo en forma de pseudocódigo:

1. Creamos núcleos de cometas al azar.
2. A partir de los núcleos de los cometas, creamos sus colas, es decir, partículas con una distribución normal con un núcleo en el centro.
3. Calculamos la adaptabilidad de las partículas del cometa.
4. Actualizamos la solución global.
5. Designamos la mejor de las partículas del cometa correspondiente como su núcleo.
6. Para cada coordenada de partícula de cometa, realizamos lo siguiente:
   Con una probabilidad de 0,6 ejecutamos o bien:
      La creación de partículas con una distribución normal con un núcleo de cometa en el centro.
   O bien:
      La creación de una partícula de cometa usando las coordenadas de los núcleos de dos cometas elegidos al azar.
7. Actualizamos la solución global.
8. Designamos la mejor de las partículas del cometa correspondiente como su núcleo.
9. Repetimos desde el punto 6 hasta que se cumpla el criterio de parada.

Para el algoritmo CTA no necesitamos escribir una estructura específica para describir los cometas y sus partículas; nos bastará con la estructura básica del agente utilizada para intercambiar soluciones entre el algoritmo y el programa ejecutor. Recordemos cómo es esta estructura.

La estructura "S_AO_Agent" contiene dos campos:

• c[] - array que almacena las coordenadas del agente en el espacio de soluciones.
• f - valor de aptitud (fitness) del agente que se utiliza para evaluar la calidad de la solución.
  

En el contexto del algoritmo CTA, describiremos tanto los cometas en sí como las partículas de sus colas usando esta estructura.

//——————————————————————————————————————————————————————————————————————————————
struct S_AO_Agent
{
    double c []; //coordinates
    double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

Ahora definiremos la clase "C_AO_CTA", que es descendiente de la clase "C_AO".

• C_AO_CTA () - el constructor inicializa un objeto de la clase con los valores por defecto. También establece algunos parámetros del algoritmo, como el tamaño de la población "popSize", el número de cometas "cometsNumb", el coeficiente de longitud de la cola "tailLengthKo", los coeficientes de desplazamiento máximo y mínimo "maxShiftCoef" y "minShiftCoef", así como los coeficientes máximo y mínimo de tamaño "maxSizeCoef" y "minSizeCoef".
• SetParams() establece los parámetros del algoritmo basándose en los valores del array "params".
• Init() - inicializa el algoritmo con los rangos de búsqueda y el número de épocas especificados.
• Métodos "Moving()", "Revision()": estos métodos implementan la lógica básica del algoritmo.
  

El campo "comets[]" es un array de objetos de tipo "S_AO_Agent" que representa los cometas en el algoritmo.

Los campos privados "tailLength[]", "maxSpaceDistance[]", "partNumber" se usan para el funcionamiento interno del algoritmo.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_CTA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_CTA () { }

  C_AO_CTA ()
  {
    ao_name = "CTA";
    ao_desc = "Comet Tail Algorithm";
    ao_link = "https://www.mql5.com/es/articles/14841";

    popSize      = 50;   //population size
    cometsNumb   = 5;    //number of comets
    tailLengthKo = 0.2;  //tail length coefficient
    maxShiftCoef = 0.9;
    minShiftCoef = 0.5;
    maxSizeCoef  = 0.1;
    minSizeCoef  = 1.5;

    ArrayResize (params, 7);

    params [0].name = "popSize";       params [0].val = popSize;
    params [1].name = "cometsNumb";    params [1].val = cometsNumb;
    params [2].name = "tailLengthKo";  params [2].val = tailLengthKo;
    params [3].name = "maxShiftCoef";  params [3].val = maxShiftCoef;
    params [4].name = "minShiftCoef";  params [4].val = minShiftCoef;
    params [5].name = "maxSizeCoef";   params [5].val = maxSizeCoef;
    params [6].name = "minSizeCoef";   params [6].val = minSizeCoef;
  }

  void SetParams ()
  {
    popSize      = (int)params [0].val;
    cometsNumb   = (int)params [1].val;
    tailLengthKo = params      [2].val;
    maxShiftCoef = params      [3].val;
    minShiftCoef = params      [4].val;
    maxSizeCoef  = params      [5].val;
    minSizeCoef  = params      [6].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  int    cometsNumb;    //number of comets
  double tailLengthKo;  //tail length coefficient
  double maxShiftCoef;  //maximum shift coefficient
  double minShiftCoef;  //minimum shift coefficient
  double maxSizeCoef;   //maximum size coefficient
  double minSizeCoef;   //minimum size coefficient

  S_AO_Agent comets [];

  private: //-------------------------------------------------------------------
  int    epochs;
  int    epochNow;
  double tailLength       [];
  double maxSpaceDistance []; //maximum distance in space
  int    partNumber; //number of particles
};
//——————————————————————————————————————————————————————————————————————————————

Ahora definiremos el método "Init" en la clase "C_AO_CTA". Este método inicializa el algoritmo con los rangos de búsqueda y el número de épocas especificados. Descripción de cada paso:

1. "if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;" - este código llama al método "StandardInit" con los rangos de búsqueda dados. Si "StandardInit" retorna "false", el método "Init" también retornará directamente "false".

2. "ArrayResize (comets, cometsNumb);" - redimensiona el array "comets" según el número de cometas.

3. Dentro del ciclo for, para cada cometa se inicializan sus coordenadas y el valor de la función de aptitud.

4. "ArrayResize (tailLength, coords); ArrayResize (maxSpaceDistance, coords);" - se cambia el tamaño de los arrays "tailLength" y "maxSpaceDistance" en función del número de coordenadas.

5. Dentro del siguiente ciclo "for", se calculan para cada coordenada la distancia máxima en el espacio y la longitud de la cola.

6. "partNumber = popSize / cometsNumb;" - se calcula el número de partículas en la cola de cada cometa.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_CTA::Init (const double &rangeMinP [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;

  ArrayResize (comets, cometsNumb);
  for (int i = 0; i < cometsNumb; i++)
  {
    ArrayResize (comets [i].c, coords);
    comets [i].f = -DBL_MAX;
  }

  ArrayResize (tailLength,       coords);
  ArrayResize (maxSpaceDistance, coords);

  for (int i = 0; i < coords; i++)
  {
    maxSpaceDistance [i] = rangeMax [i] - rangeMin [i];
    tailLength       [i] = maxSpaceDistance [i] * tailLengthKo;
  }

  partNumber = popSize / cometsNumb;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

La formación de partículas en las colas de cometa se produce en el método "Moving()" de la clase "C_AO_CTA". Los pasos básicos del método serían:

1. La función comienza incrementando el contador "epochNow" e inicializando las variables locales "cnt", "min", y "max".
2. Si "revision" es igual a "false", las coordenadas del cometa se inicializarán dentro de los rangos especificados "rangeMin" y "rangeMax". A continuación, se crearán partículas (agentes) alrededor de cada cometa utilizando una distribución gaussiana dentro de un rango definido por la longitud de cola "tailLength".
3. Si "revision" es igual a "true", se actualizará la posición de las partículas (agentes). Para cada partícula, se calculan los coeficientes "coefTail" y "coefSize", que determinarán el desplazamiento y el tamaño de la cola del cometa según la distancia hasta el punto central "cB". Estos coeficientes se usan para determinar la nueva posición de la partícula dentro del intervalo limitado por la longitud de la cola.
4. Si la probabilidad "u.RNDprobab()" es inferior a 0,6, la nueva posición de la partícula se calculará utilizando una distribución gaussiana. En caso contrario, la nueva posición de la partícula se calcula como una combinación lineal de las coordenadas de los núcleos de otros dos cometas elegidos al azar.
5. En todos los casos, las nuevas coordenadas de las partículas se limitan a los rangos "rangeMin" y "rangeMax" y se discretizan con un paso "rangeStep".

La idea general de este método consiste en modelar el movimiento y el comportamiento de los cometas en un algoritmo CTA donde las partículas (agentes) representan la cola del cometa, mientras que sus coordenadas y el tamaño de la cola dependen de la distancia hasta la mejor solución global (el Sol).

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CTA::Moving ()
{
  epochNow++;
  int    cnt = 0;
  double min = 0.0;
  double max = 0.0;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < cometsNumb; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        comets [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        comets [i].c [c] = u.SeInDiSp  (comets [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    for (int i = 0; i < cometsNumb; i++)
    {
      for (int p = 0; p < partNumber; p++)
      {
        for (int c = 0; c < coords; c++)
        {
          min = comets [i].c [c] - tailLength [c] * 0.5; if (min < rangeMin [c]) min = rangeMin [c];
          max = comets [i].c [c] + tailLength [c] * 0.5; if (max > rangeMax [c]) max = rangeMax [c];

          a [cnt].c [c] = u.GaussDistribution (comets [i].c [c], min, max, 1);
          a [cnt].c [c] = u.SeInDiSp  (a [cnt].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }

        cnt++;
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  cnt             = 0;
  double coefTail = 0.0;
  double coefSize = 0.0;

  for (int i = 0; i < cometsNumb; i++)
  {
    for (int p = 0; p < partNumber; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        if (u.RNDprobab () < 0.6)
        {
          coefTail = fabs (comets [i].c [c] - cB [c]) / maxSpaceDistance [c];
          coefSize = coefTail;

          //(1-x)*0.9+x*0.5
          coefTail = (1 - coefTail) * maxShiftCoef + coefTail * minShiftCoef;

          //(1-x)*0.1+x*0.9
          coefSize = (1 - coefSize) * maxSizeCoef + coefSize * minSizeCoef;

          if (cB [c] * Dir > comets [i].c [c] * Dir)
          {
            min = comets [i].c [c] - tailLength [c] * coefTail         * coefSize;
            max = comets [i].c [c] + tailLength [c] * (1.0 - coefTail) * coefSize;
          }
          if (cB [c] * Dir < comets [i].c [c] * Dir)
          {
            min = comets [i].c [c] - tailLength [c] * (1.0 - coefTail) * coefSize;
            max = comets [i].c [c] + tailLength [c] * (coefTail)*coefSize;
          }
          if (cB [c] == comets [i].c [c])
          {
            min = comets [i].c [c] - tailLength [c] * 0.1;
            max = comets [i].c [c] + tailLength [c] * 0.1;
          }

          if (min < rangeMin [c]) min = rangeMin [c];
          if (max > rangeMax [c]) max = rangeMax [c];

          a [cnt].c [c] = u.GaussDistribution (comets [i].c [c], min, max, Power);
          a [cnt].c [c] = u.SeInDiSp  (a [cnt].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }
        else
        {
          int    r   = 0;
          int    r1  = 0;
          int    r2  = 0;

          do
          {
            r = u.RNDminusOne (cometsNumb);
            r1 = r;
          }
          while (r1 == i);

          do
          {
            r = u.RNDminusOne (cometsNumb);
            r2 = r;
          }
          while (r2 == i || r2 == r1);

          a [cnt].c [c] = comets [r1].c [c] + 0.1 * (comets [r2].c [c] - comets [i].c [c]) * u.RNDprobab();
          a [cnt].c [c] = u.SeInDiSp (a [cnt].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }

      cnt++;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

A continuación, implementamos el método "Revision()" de la clase "C_AO_CTA", que se encargará de revisar la posición de los cometas en el Comet Tail Algorithm (CTA).

Los pasos básicos del método serían:

1. Encontramos la mejor solución en una población:

• El método itera todas las soluciones de la población "popSize" y encuentra la solución con el mejor valor de la función objetivo "fB".
• Si se encuentra la mejor solución, su posición "a[ind].c" se copiará en el vector "cB" que almacena la mejor solución conocida.

2. Actualización de la posición del cometa:

• El método itera todos los cometas "cometsNumb" y para cada cometa busca la mejor solución entre las partículas asociadas a ese cometa "partNumber".
• Si se encuentra la mejor solución para un cometa, la posición de ese cometa "comets[i].c" se actualizará a la posición de la mejor solución encontrada "a[ind].c".

Este método implementa un paso importante en el algoritmo CTA, en el que se revisan las posiciones de los cometas usando como base las mejores soluciones encontradas en sus colas. Esto permite dirigir su búsqueda a zonas con valores más altos de la función objetivo.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CTA::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //set a new kernel------------------------------------------------------------
  int cnt = 0;

  for (int i = 0; i < cometsNumb; i++)
  {
    ind = -1;

    for (int p = 0; p < partNumber;  p++)
    {
      if (a [cnt].f > comets [i].f)
      {
        comets [i].f = a [cnt].f;
        ind = cnt;
      }

      cnt++;
    }

    if (ind != -1) ArrayCopy (comets [i].c, a [ind].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Resultados de las pruebas

Impresión de los resultados del algoritmo de cola de cometa CTA:

CTA|Comet Tail Algorithm|80.0|40.0|4.0|-1.0|0.2|1.0|0.5|0.1|15.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9534613588697962
25 Hilly's; Func runs: 10000; result: 0.863192334000326
500 Hilly's; Func runs: 10000; result: 0.27769783965091077
=============================
5 Forest's; Func runs: 10000; result: 0.997942251272262
25 Forest's; Func runs: 10000; result: 0.857403562283056
500 Forest's; Func runs: 10000; result: 0.33949224947400775
=============================
5 Megacity's; Func runs: 10000; result: 0.8876923076923078
25 Megacity's; Func runs: 10000; result: 0.5643076923076924
500 Megacity's; Func runs: 10000; result: 0.10512307692307787
=============================
All score: 5.84631 (64.96%)

Basándonos en las pruebas realizadas, podemos extraer las siguientes conclusiones sobre el rendimiento del algoritmo de optimización CTA (Comet Tail Algorithm):

La puntuación global del algoritmo es de 5,84631, lo cual corresponde al 64,96% de la puntuación máxima posible. Esto indica el excelente rendimiento del algoritmo CTA.

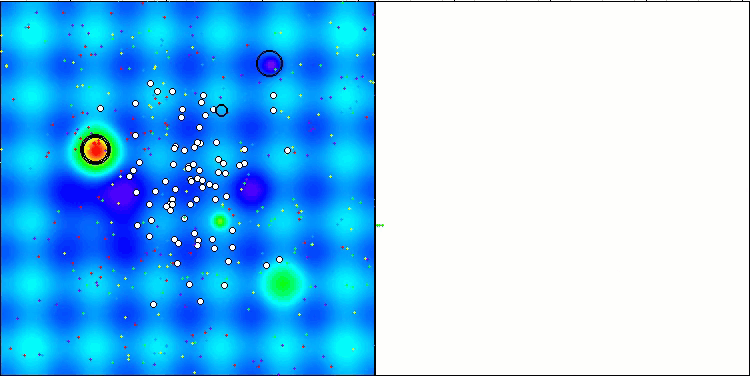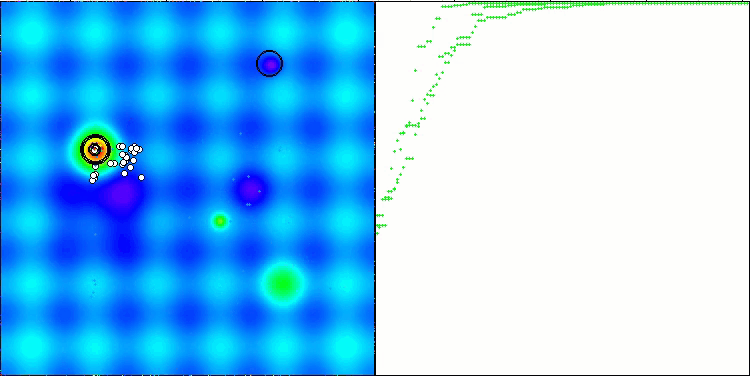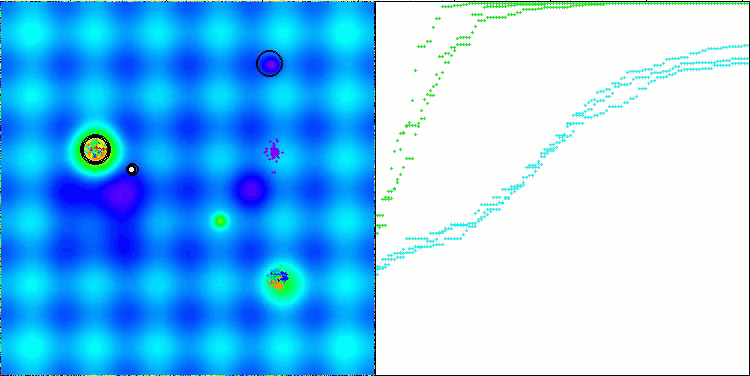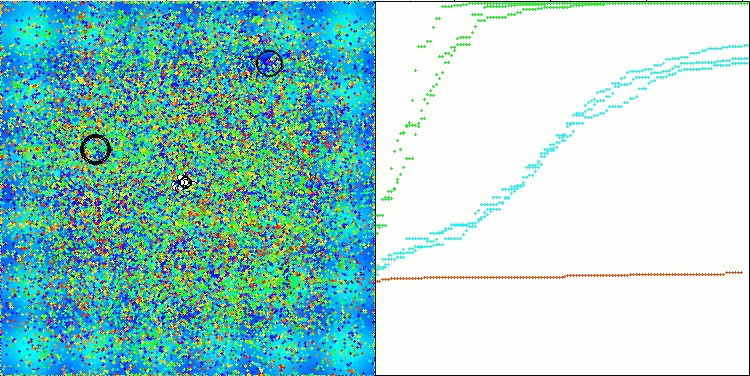
  CTA en la función de prueba Hilly.

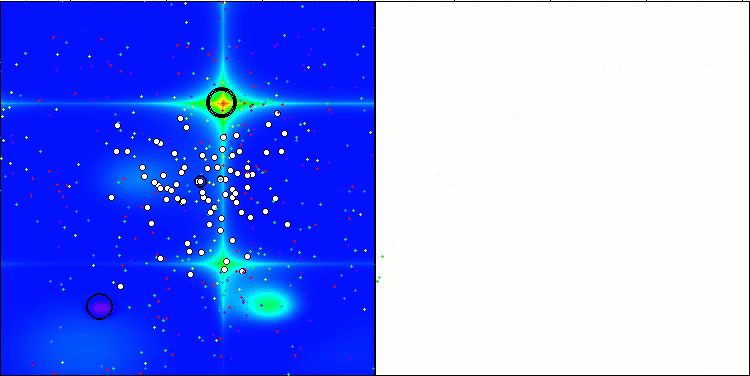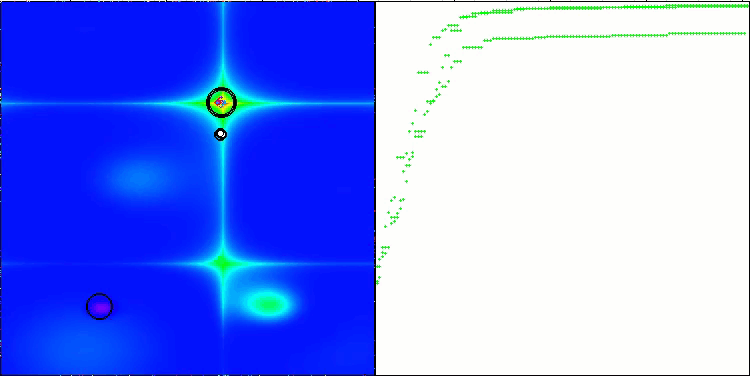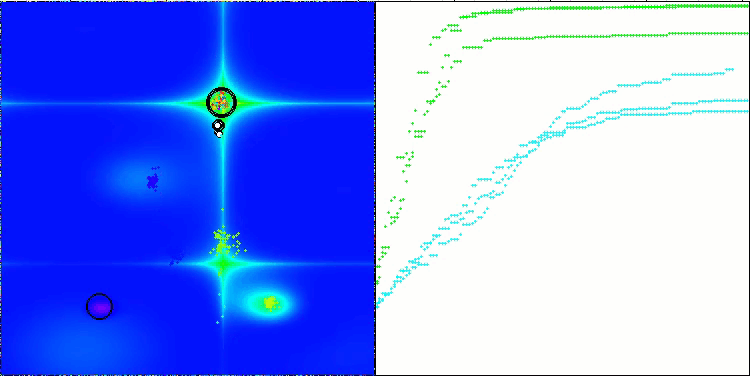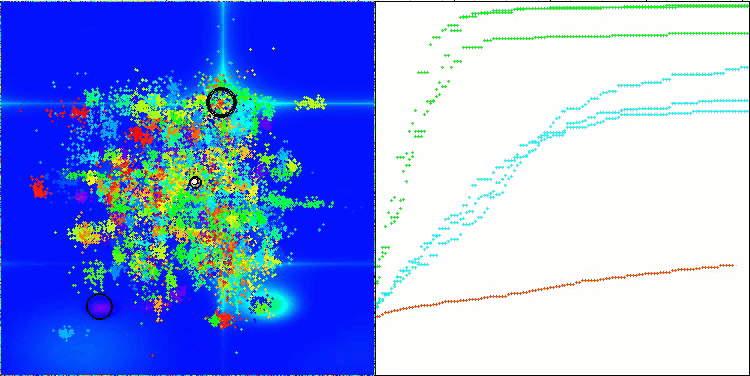
  CTA en la función de prueba Forest.

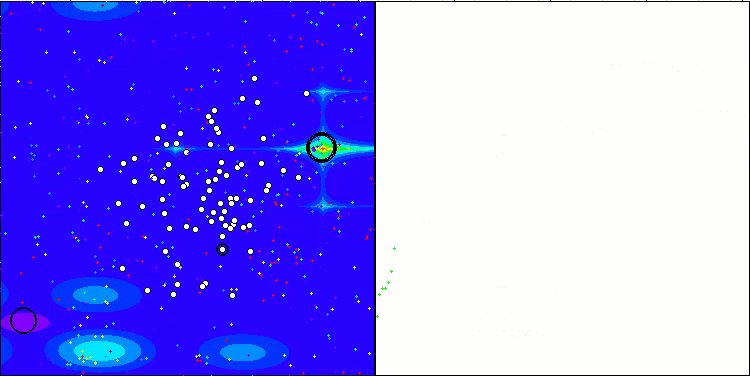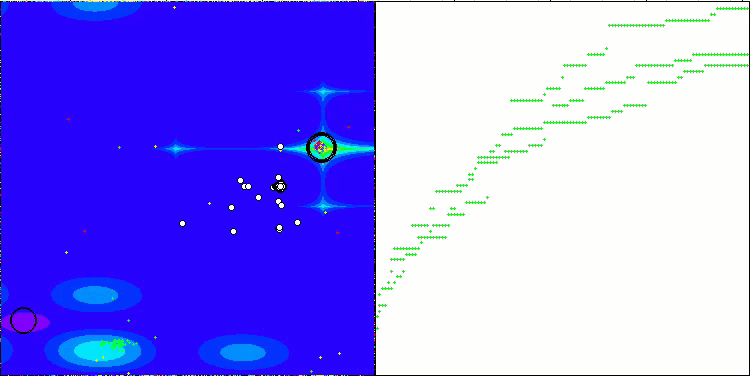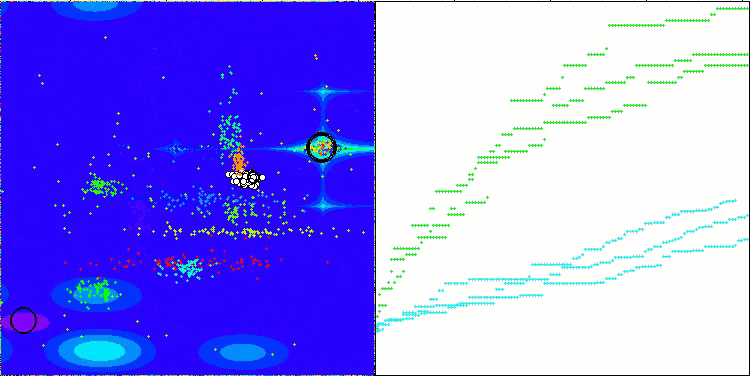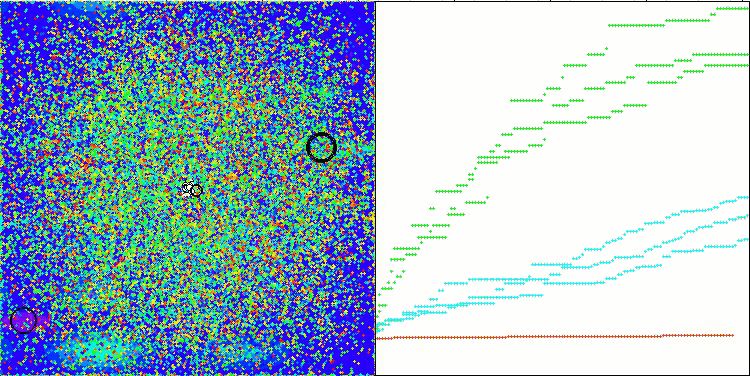
  CTA en la función de prueba Megacity.

Según los resultados de las pruebas, el algoritmo CTA ocupa un meritorio tercer puesto en la tabla de clasificación.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% de MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	BGA	binary genetic algorithm	0,99992	0,99484	0,50483	2,49959	1,00000	0,99975	0,32054	2,32029	0,90667	0,96400	0,23035	2,10102	6,921	76,90
2	(P+O)ES	(P+O) evolution strategies	0,99934	0,91895	0,56297	2,48127	1,00000	0,93522	0,39179	2,32701	0,83167	0,64433	0,21155	1,68755	6,496	72,18
3	CTA	comet tail algorithm	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
4	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
5	ESG	evolution of social groups	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
6	SIA	simulated isotropic annealing	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
7	TSEA	turtle shell evolution algorithm	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
8	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
9	BSA	bird swarm algorithm	0,90857	0,73661	0,25767	1,90285	0,90437	0,81619	0,16401	1,88457	0,61692	0,54154	0,10951	1,26797	5,055	56,17
10	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
11	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
12	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
13	BSO	brain storm optimization	0,91301	0,56222	0,30047	1,77570	0,97162	0,57162	0,23449	1,77772	0,60462	0,27138	0,12011	0,99611	4,550	50,55
14	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
15	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
16	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
17	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
18	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
19	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
20	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
21	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
22	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
23	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
24	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
25	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72
26	ABC	artificial bee colony	0,63377	0,42402	0,30892	1,36671	0,55103	0,21874	0,05623	0,82600	0,34000	0,14200	0,03102	0,51302	2,706	30,06
27	BA	bat algorithm	0,59761	0,45911	0,35242	1,40915	0,40321	0,19313	0,07175	0,66810	0,21000	0,10100	0,03517	0,34617	2,423	26,93
28	SA	simulated annealing	0,55787	0,42177	0,31549	1,29513	0,34998	0,15259	0,05023	0,55280	0,31167	0,10033	0,02883	0,44083	2,289	25,43
29	IWDm	intelligent water drops M	0,54501	0,37897	0,30124	1,22522	0,46104	0,14704	0,04369	0,65177	0,25833	0,09700	0,02308	0,37842	2,255	25,06
30	PSO	particle swarm Optimization	0,59726	0,36923	0,29928	1,26577	0,37237	0,16324	0,07010	0,60572	0,25667	0,08000	0,02157	0,35823	2,230	24,77
31	Boids	boids algorithm	0,43340	0,30581	0,25425	0,99346	0,35718	0,20160	0,15708	0,71586	0,27846	0,14277	0,09834	0,51957	2,229	24,77
32	MA	monkey algorithm	0,59107	0,42681	0,31816	1,33604	0,31138	0,14069	0,06612	0,51819	0,22833	0,08567	0,02790	0,34190	2,196	24,40
33	SFL	shuffled frog-leaping	0,53925	0,35816	0,29809	1,19551	0,37141	0,11427	0,04051	0,52618	0,27167	0,08667	0,02402	0,38235	2,104	23,38
34	FSS	fish school search	0,55669	0,39992	0,31172	1,26833	0,31009	0,11889	0,04569	0,47467	0,21167	0,07633	0,02488	0,31288	2,056	22,84
35	RND	random	0,52033	0,36068	0,30133	1,18234	0,31335	0,11787	0,04354	0,47476	0,25333	0,07933	0,02382	0,35648	2,014	22,37
36	GWO	grey wolf optimizer	0,59169	0,36561	0,29595	1,25326	0,24499	0,09047	0,03612	0,37158	0,27667	0,08567	0,02170	0,38403	2,009	22,32
37	CSS	charged system search	0,44252	0,35454	0,35201	1,14907	0,24140	0,11345	0,06814	0,42299	0,18333	0,06300	0,02322	0,26955	1,842	20,46
38	EM	electroMagnetism-like algorithm	0,46250	0,34594	0,32285	1,13129	0,21245	0,09783	0,10057	0,41085	0,15667	0,06033	0,02712	0,24412	1,786	19,85

Conclusiones

El algoritmo CTA analizado se basa en el concepto de movimiento del cometa y presenta una serie de características que contradicen las leyes físicas y la evolución del cometa. La influencia de estas características en los resultados finales del algoritmo debería considerarse con más detalle.

Una de las contradicciones es la dirección de la cola del cometa. En el algoritmo CTA, el uso de la dirección de la cola hacia la estrella (Dir_P = -1) suele mejorar sustancialmente su rendimiento. Sin embargo, usar la dirección de la cola desde la estrella también mejora la capacidad del algoritmo para explorar el espacio. Los entusiastas de los métodos de optimización pueden considerar el uso del coeficiente dinámico de la dirección de la cola según la época actual, si así lo desean. Cabe destacar que la dirección de la cola desde la estrella ofrece una mejor convergencia en problemas de baja dimensionalidad, mientras que la dirección hacia la estrella resulta más eficiente en problemas de alta dimensionalidad.

Otra contradicción sería el tamaño de la cola del cometa. En el algoritmo CTA, se descubrió que cambiar dinámicamente el tamaño de la cola incrementándolo con el aumento de la distancia hasta la estrella mejora la eficiencia del algoritmo. Esto contradice las leyes de la física, porque en realidad el tamaño de la cola de un cometa aumenta a medida que se acerca al Sol. No obstante, este cambio dinámico en el tamaño de la cola nos permite ampliar la exploración del espacio de soluciones alrededor del núcleo del cometa a regiones distantes de la solución global, lo cual aumenta las posibilidades de detectar soluciones prometedoras y reduce la probabilidad de quedarse atascado en extremos locales. La cola del cometa disminuye a medida que se acerca a la estrella, lo cual aumenta la intensidad del refinamiento de la solución.

El algoritmo CTA también implica el intercambio de información entre cometas, de manera similar a lo que ocurre en la naturaleza cuando los cometas capturan partículas dejadas por otros cometas. Se trata de una característica adicional del algoritmo para explorar el espacio de soluciones. Se ha intentado usar métodos para aumentar la diversidad de la población modelando las emisiones coronales de materia estelar y explotando las propiedades combinatorias del algoritmo tomando prestadas las coordenadas de algunos cometas de otros.

El algoritmo CTA es un nuevo e interesante enfoque de optimización que explota el concepto de movimiento de cometa. El algoritmo demuestra una buena convergencia en varios tipos de funciones (tanto suaves como discretas), es muy sencillo de implementar (la estructura del algoritmo es muy simple, lo cual simplifica su implementación de software), no requiere recursos computacionales significativos (ya que no utiliza la clasificación de soluciones y no utiliza cálculos de distancia entre todas las soluciones, lo cual nos permite aplicarlo a una amplia gama de problemas), demuestra una pequeña dispersión de resultados en funciones discretas (estabilidad y reproducibilidad de los resultados cuando se trabaja con funciones discretas), y no requiere recursos computacionales significativos (ya que no usa la clasificación de soluciones y no utiliza cálculos de distancia entre todas las soluciones, lo cual permite aplicarlo a una amplia gama de problemas).

En general, las peculiaridades del algoritmo CTA residen en el equilibrio dinámico entre la exploración del espacio de soluciones y el refinamiento del óptimo global encontrado.

Así, el algoritmo de la CTA usa una serie de simplificaciones y suposiciones que no son totalmente coherentes con las leyes físicas del movimiento de los cometas. Sin embargo, estas desviaciones de la realidad nos permiten mejorar la eficacia del algoritmo en la resolución de problemas de optimización, manteniendo al mismo tiempo la sencillez de la aplicación.

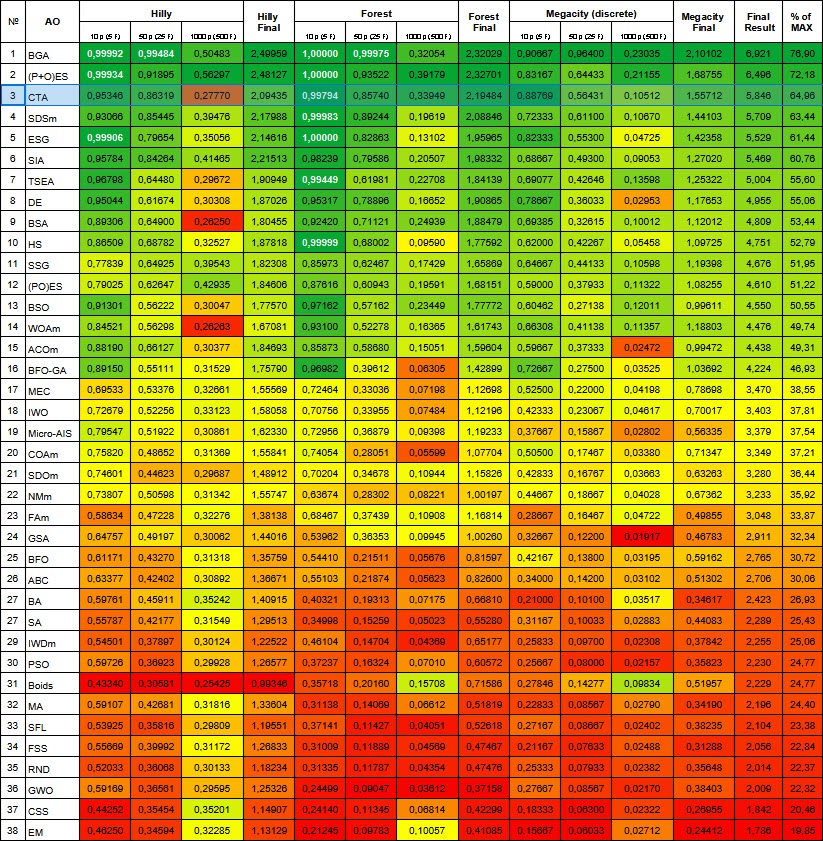
Figura 3. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0,99 aparecen resaltados en blanco.

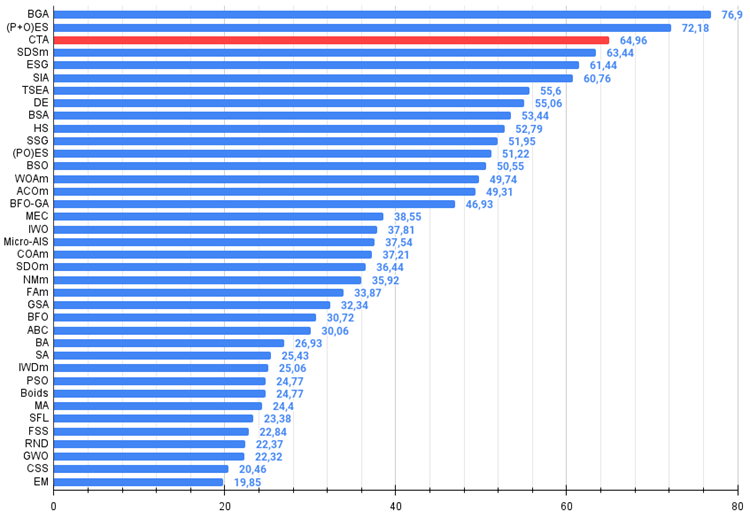
Figura 4. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor),

donde 100 es el máximo resultado teórico posible; hay un script para calcular la tabla de puntuación en el archivo).

Ventajas y desventajas del algoritmo de cola de cometa (CTA):

Ventajas:

1. Buena convergencia en varios tipos de funciones.
2. Implementación sencilla.
3. Resulta poco exigente en cuanto a recursos informáticos.
4. Pequeña dispersión de resultados sobre funciones discretas.
   

Desventajas:

1. Muchos parámetros externos.
   
2. Malos resultados en funciones suaves de alta dimensionalidad.

Códigos fuente

Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/es/code/49355