Algoritmo de Otimização de Bilhar — Billiards Optimization Algorithm (BOA)

Conteúdo

1. Introdução
2. Implementação do algoritmo
3. Resultados dos testes

Introdução

No universo dos algoritmos de otimização, em que a precisão matemática encontra a inspiração no mundo real, surgem abordagens impressionantes pela engenhosidade. Um exemplo é o algoritmo de otimização de bilhar (Billiards Optimization Algorithm, BOA), que utiliza a mecânica do jogo clássico de bilhar como estratégia de busca.

Imagine uma mesa de bilhar em que cada caçapa representa uma solução potencial e as bolas, os buscadores dessas soluções, movendo-se pelo espaço de possibilidades. Assim como um jogador experiente calcula a trajetória da bola para acertar a caçapa, o BOA conduz suas soluções rumo aos melhores resultados por meio de um processo iterativo de busca e refinamento. Desenvolvido pelos pesquisadores Hadi Givi e Mari Hubalovska em 2023, esse algoritmo apresenta uma abordagem interessante e incomum para resolver problemas de otimização.

Neste artigo, vamos explorar a base conceitual do BOA, vamos examinar seu modelo matemático e analisar sua eficácia na resolução de problemas multimodais. O algoritmo combina simplicidade de ideia e precisão matemática, abrindo novos horizontes no campo da otimização computacional e representando uma adição valiosa ao arsenal de métodos modernos de otimização.

Implementação do algoritmo

O algoritmo BOA é um método de otimização inspirado nesse jogo. Sua essência é a seguinte: imagine que você está em busca da melhor solução para um problema; na linguagem do bilhar, seria como tentar encaçapar uma bola. Em uma mesa de bilhar, existem oito caçapas, além de várias bolas. No início da execução do algoritmo, é criada uma população de soluções aleatórias. Essas soluções funcionam como as bolas na mesa de bilhar. Para cada solução, calcula-se o valor da função objetivo, a fim de determinar sua qualidade.

A cada iteração, as oito melhores soluções da população se tornam as "caçapas" (os alvos a serem alcançados). As demais soluções são consideradas como bolas que devem ser direcionadas para essas caçapas. Para cada solução, uma das caçapas é escolhida aleatoriamente. Em seguida, calcula-se a nova posição da bola — uma nova solução —, movendo-a na direção da caçapa escolhida. Se a nova posição resultar em um valor melhor para a função objetivo, a bola é movida para essa posição; caso contrário, ela permanece onde está.

Matematicamente, isso pode ser representado da seguinte forma:

X_new = X + rnd [0.0; 1.0] × (P - I × X)

onde:

• X_new — nova posição da bola,
• X — posição atual da bola,
• P — posição da caçapa (ou bola que deve ser atingida pela bola atual),
• I — escolha aleatória entre os números 1 ou 2.

O processo se repete várias vezes e, no final, as bolas (soluções) devem se aproximar da solução ótima do problema.

A vantagem do BOA é que ele consegue equilibrar, apenas com um único coeficiente na fórmula, a busca global e a busca local. Isso ocorre graças ao coeficiente aleatório "I", que garante tanto o "curto alcance" (refinamento das soluções próximas a boas regiões) quanto o "excesso de alcance" (exploração de diferentes áreas do espaço de soluções).

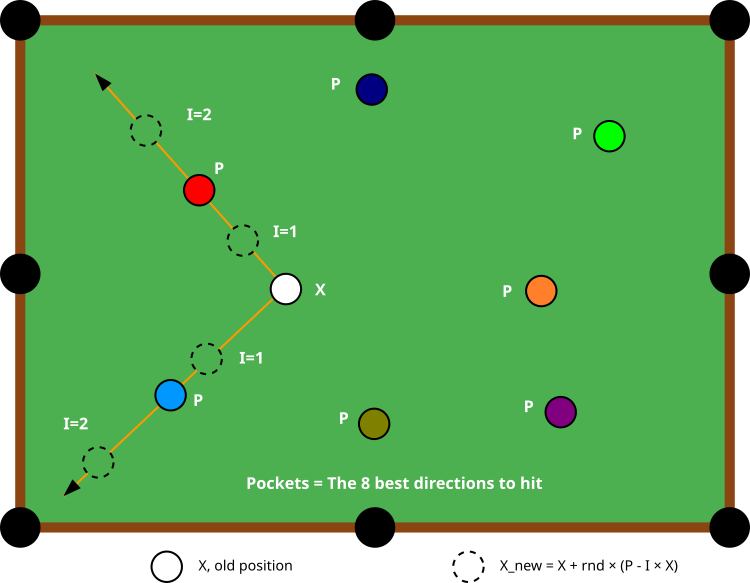
Figura 1. Esquema de funcionamento do algoritmo BOA

A figura 1 representa esquematicamente o princípio de funcionamento do algoritmo BOA. O elemento central — a bola branca marcada com "X" — representa a posição atual do agente no espaço de busca de soluções. Ao redor dessa bola, estão dispostas bolas coloridas com a marcação "P": são os "bolsos" ou "caçapas", que correspondem às oito melhores soluções encontradas até o momento. O diagrama mostra como o agente (bola branca) pode atualizar sua posição ao se mover em direção a diferentes caçapas. Em cada passo, o agente escolhe aleatoriamente uma das oito caçapas como direção-alvo de movimento.

As linhas laranjas com setas mostram as possíveis trajetórias do movimento do agente em direção a diferentes caçapas (neste caso, as vermelha e azul clara). Os círculos tracejados indicam as posições intermediárias que o agente pode assumir durante o movimento, dependendo do valor de "I" (1 ou 2). O valor de "I" altera a "força da tacada" e o estilo do movimento. Quando I=1, a posição se desloca em direção à caçapa escolhida. Quando I=2, o agente pode executar movimentos mais bruscos, o que favorece a exploração de uma maior parte do espaço de soluções.

Agora que compreendemos totalmente como o algoritmo funciona, vamos à escrita do pseudocódigo do BOA.

Inicialização
    Definimos a quantidade de bolas (popSize) e caçapas (numPockets).
    Criamos a população de bolas (agentes).
    Estabelecemos o espaço de busca com limites mínimos e máximos.

Algoritmo principal
Primeira etapa: Inicialização inicial (executada apenas uma vez)
    Para cada bola da população:
        Posicionamos aleatoriamente as bolas no espaço de busca.
        Salvamos sua posição inicial.
        Definimos os valores iniciais da função de adaptabilidade como mínimos.

Segunda etapa: Movimento das bolas
    Para cada bola da população:
        Para cada coordenada da bola:
            Escolhemos aleatoriamente uma caçapa (uma das numPockets melhores soluções).
            Atualizamos a posição da bola pela fórmula: X_new = X + rnd [0.0; 1.0] × (P - I × X)
            Verificamos se a nova posição permanece dentro dos limites permitidos.

Terceira etapa: Atualização das melhores soluções
    Para cada bola:
        Se o valor da função de adaptabilidade da bola for melhor que o melhor global, atualizamos o melhor global.
        Se o valor da função de adaptabilidade da bola for melhor que o seu próprio melhor, atualizamos o seu melhor.
    Ordenamos as bolas de acordo com seus melhores valores da função de adaptabilidade.
        Os primeiros numPockets agentes após a ordenação se tornam as caçapas para a próxima iteração.

Repetimos as etapas "Movimento das bolas" e "Atualização das melhores soluções" até que seja atingida a condição de parada (por exemplo, número máximo de iterações).

Passamos agora à escrita do código do algoritmo. A classe "C\_AO\_BOA" é derivada da classe "C\_AO" (classe base de algoritmos populacionais de otimização) e implementa o algoritmo de otimização BOA. Vamos analisar seus elementos principais:

O construtor C\_AO\_BOA () inicializa os valores das variáveis de instância:

• popSize é definido como 50, representando a quantidade de bolas (agentes) no algoritmo.
• numPockets é definido como 8, representando o número de caçapas na mesa de bilhar.
• O tamanho do array "params" é alterado, e dois parâmetros (popSize e numPockets) são adicionados ao array "params".

Métodos:

• SetParams () — responsável por definir os parâmetros do array "params" de volta para as variáveis locais "popSize" e "numPockets".
• Init () — método de inicialização que configura valores mínimos, máximos e passos de busca, além de definir o número de épocas.
• Moving () — responsável pelo movimento das bolas no algoritmo.
• Revision () — executa a verificação e revisão das posições/soluções dos agentes.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BOA () { }
  C_AO_BOA ()
  {
    ao_name = "BOA";
    ao_desc = "Billiards Optimization Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/17325";

    popSize    = 50;  // число шаров (агентов)
    numPockets = 8;   // число карманов на бильярдном столе

    ArrayResize (params, 2);

    params [0].name = "popSize";    params [0].val = popSize;
    params [1].name = "numPockets"; params [1].val = numPockets;
  }

  void SetParams ()
  {
    popSize    = (int)params [0].val;
    numPockets = (int)params [1].val;
  }

  bool Init (const double &rangeMinP  [],  // минимальные значения
             const double &rangeMaxP  [],  // максимальные значения
             const double &rangeStepP [],  // шаг изменения
             const int     epochsP = 0);   // количество эпох

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int numPockets;       // число карманов (лучших решений)

  private: //-------------------------------------------------------------------
};
//——————————————————————————————————————————————————————————————————————————————

O método "Init" da classe "C_AO_BOA" é responsável pela inicialização do algoritmo BOA. No início desse método, é chamada a função "StandardInit()", passando-se os arrays de valores mínimos e máximos, além dos passos. Essa função é responsável por realizar ações e inicializações comuns a todas as classes derivadas de algoritmos de otimização (incluindo a configuração inicial dos intervalos) e por preparar os agentes básicos de busca no algoritmo. Se "StandardInit()" retornar "false" (inicialização mal-sucedida), o método "Init" também retornará "false". Caso tudo ocorra corretamente, o método retorna "true".

//——————————————————————————————————————————————————————————————————————————————
//--- Инициализация
bool C_AO_BOA::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

O método "Moving" implementa a etapa principal do algoritmo BOA e controla o movimento dos agentes (bolas) no espaço de soluções. Primeiro, é verificada a condição "if (!revision)", que permite determinar se o método está sendo chamado pela primeira vez. Se "revision=false", é necessário inicializar as posições dos agentes. Para isso, é executado um laço sobre todos os agentes definidos como "popSize", dentro do qual ocorre um laço aninhado sobre as coordenadas que definem os parâmetros de solução de cada agente.

Na fase de geração das posições iniciais, um valor aleatório para cada coordenada do agente é escolhido dentro do intervalo definido, e a função u.SeInDiSp () ajusta o valor para o permitido, considerando o passo. A posição inicial do agente é salva em a[p].cB[c] como a melhor solução individual da bola (na primeira iteração, a solução inicial é equivalente à melhor conhecida), e após definir "revision=true" o método finaliza a execução, o que evita a reinicialização dos valores.

Na segunda e nas iterações seguintes, é iniciado o laço sobre todos os agentes para realizar o movimento. Durante a atualização das coordenadas, são executados laços aninhados sobre todos os agentes e suas coordenadas, onde uma das melhores caçapas disponíveis é escolhida aleatoriamente para atualizar a posição atual do agente. A posição é atualizada a partir da posição anterior, à qual é somada uma variação aleatória baseada na posição da caçapa escolhida. A função u.RNDprobab () retorna um número aleatório no intervalo [0.0; 1.0], para adicionar ruído aleatório, enquanto a função u.RNDintInRange (1, 2) fornece o valor 1 ou 2, que é multiplicado pela posição do agente.

Após a atualização da posição, é feita uma correção para ajustar o valor atualizado ao intervalo definido, considerando limites mínimos e máximos, bem como o passo de alteração.

//——————————————————————————————————————————————————————————————————————————————
//--- Основной шаг алгоритма
void C_AO_BOA::Moving ()
{
  //----------------------------------------------------------------------------
  // Начальная инициализация
  if (!revision)
  {
    for (int p = 0; p < popSize; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [p].c  [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [p].c  [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        a [p].cB [c] = a [p].c [c];  // Сохраняем начальную позицию
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      int pocketID = u.RNDminusOne (numPockets);

      a [p].c [c] = a [p].cB [c] + u.RNDprobab () * (a [pocketID].cB [c] - u.RNDintInRange (1, 2) * a [p].cB [c]);
      a [p].c [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "Revision" é responsável pela atualização da melhor solução global no algoritmo BOA, além de atualizar as melhores soluções individuais das bolas. Ao final do método, ocorre a ordenação das bolas de acordo com suas melhores soluções individuais.

//——————————————————————————————————————————————————————————————————————————————
//--- Обновление лучшего решения с учетом жадного выбора и вероятности принятия худших решений
void C_AO_BOA::Revision ()
{
  int bestIND = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      bestIND = i;
    }

    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  if (bestIND != -1) ArrayCopy (cB, a [bestIND].c, 0, 0, WHOLE_ARRAY);

  S_AO_Agent aT []; ArrayResize (aT, popSize);
  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

Resultados dos testes

Agora vejamos como funciona o algoritmo BOA:

BOA|Billiards Optimization Algorithm|50.0|8.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.63960620766331
25 Hilly's; Func runs: 10000; result: 0.3277725645995603
500 Hilly's; Func runs: 10000; result: 0.2514878043770147
=============================
5 Forest's; Func runs: 10000; result: 0.3885662762060409
25 Forest's; Func runs: 10000; result: 0.1955657530616877
500 Forest's; Func runs: 10000; result: 0.15336230733273673
=============================
5 Megacity's; Func runs: 10000; result: 0.5415384615384615
25 Megacity's; Func runs: 10000; result: 0.19046153846153846
500 Megacity's; Func runs: 10000; result: 0.10530769230769324
=============================
All score: 2.79367 (31.04%)

Como é possível perceber, o desempenho do algoritmo é bastante fraco, e ele não entra na nossa tabela de classificação. Por isso decidi revisar o algoritmo com mais atenção — tive algumas ideias de como fazê-lo funcionar. Vamos observar novamente a fórmula de movimento das bolas:

X_new = X + rnd [0.0; 1.0] × (P - I × X)

Nessa fórmula, o coeficiente "I" é aplicado ao valor da coordenada atual da bola, o que não tem um significado físico claro, já que, na prática, o escalonamento é aplicado ao valor absoluto da coordenada. A ação mais natural parece ser retirar esse coeficiente dos parênteses, para que ele escale a diferença entre a "caçapa" e o valor da coordenada da bola. Assim, a nova expressão descreve um sentido físico real: ou a bola não alcança a caçapa, ou passa dela, sendo essa variabilidade garantida pelo fator de ruído do número aleatório no intervalo [0.0, 1.0].

No final, obtemos a fórmula de movimento das bolas:

X_new = X + rnd [0.0; 1.0] × (P - X) × I

Portanto, abaixo apresento o código completo da versão modificada do método Moving (), no qual aparece a linha comentada com a fórmula dos autores e, em seguida, a minha versão da fórmula.

//——————————————————————————————————————————————————————————————————————————————
//--- Основной шаг алгоритма
void C_AO_BOA::Moving ()
{
  //----------------------------------------------------------------------------
  // Начальная инициализация
  if (!revision)
  {
    for (int p = 0; p < popSize; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [p].c  [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [p].c  [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        a [p].cB [c] = a [p].c [c];  // Сохраняем начальную позицию как лучшее индивидуальное решение
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      int pocketID = u.RNDminusOne (numPockets);

      //a [p].c [c] = a [p].cB [c] + u.RNDprobab () * (a [pocketID].cB [c] - u.RNDintInRange (1, 2) * a [p].cB [c]);
      a [p].c [c] = a [p].cB [c] + u.RNDprobab () * (a [pocketID].cB [c] - a [p].cB [c]) * u.RNDintInRange (1, 2);
      a [p].c [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Agora, após as alterações realizadas, vejamos como o algoritmo funciona com os parâmetros que, na versão dos autores, mostravam os melhores resultados:

BOA|Billiards Optimization Algorithm|50.0|8.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8727603657603271
25 Hilly's; Func runs: 10000; result: 0.7117647027521633
500 Hilly's; Func runs: 10000; result: 0.25339119302510993
=============================
5 Forest's; Func runs: 10000; result: 0.9228482722678735
25 Forest's; Func runs: 10000; result: 0.7601448268715335
500 Forest's; Func runs: 10000; result: 0.3498925749480034
=============================
5 Megacity's; Func runs: 10000; result: 0.6184615384615385
25 Megacity's; Func runs: 10000; result: 0.45876923076923076
500 Megacity's; Func runs: 10000; result: 0.14586153846153965
=============================
All score: 5.09389 (56.60%)

Realizando mais alguns experimentos, encontrei parâmetros que permitem obter resultados ainda melhores:

BOA|Billiards Optimization Algorithm|50.0|25.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.957565927297626
25 Hilly's; Func runs: 10000; result: 0.8259872884790693
500 Hilly's; Func runs: 10000; result: 0.2523458952211869
=============================
5 Forest's; Func runs: 10000; result: 0.9999999999999929
25 Forest's; Func runs: 10000; result: 0.900362056289584
500 Forest's; Func runs: 10000; result: 0.305018130407844
=============================
5 Megacity's; Func runs: 10000; result: 0.7353846153846153
25 Megacity's; Func runs: 10000; result: 0.5252307692307692
500 Megacity's; Func runs: 10000; result: 0.09563076923077005
=============================
All score: 5.59753 (62.19%)

Vamos analisar a visualização do funcionamento do algoritmo BOA em funções de teste. No espaço de busca não se observa nenhum comportamento particular; os movimentos das "bolas" parecem caóticos. Chama especialmente a atenção o fato de que o algoritmo lida bem com problemas de baixa e média dimensionalidade, mas em problemas de alta dimensionalidade surgem dificuldades de convergência. Isso fica especialmente evidente na função suave Hilly, onde o desempenho é até pior do que na função discreta Megacity, o que é um fenômeno raro em comparação com outros algoritmos populacionais. Também vale destacar a tendência do algoritmo a ficar preso em mínimos locais ao resolver problemas de baixa dimensionalidade.

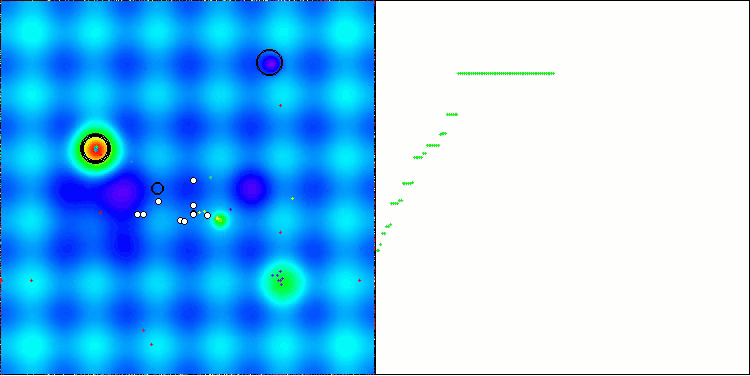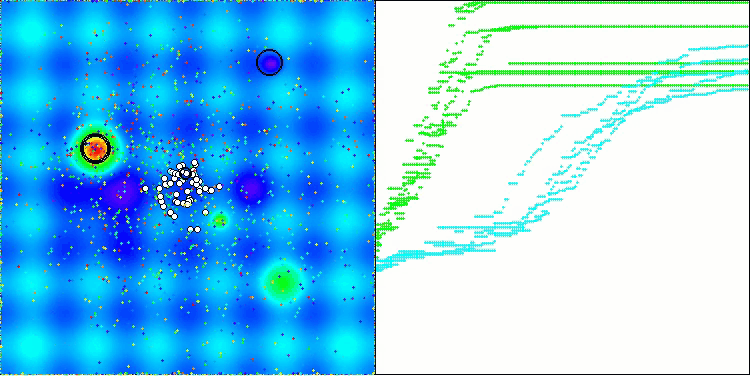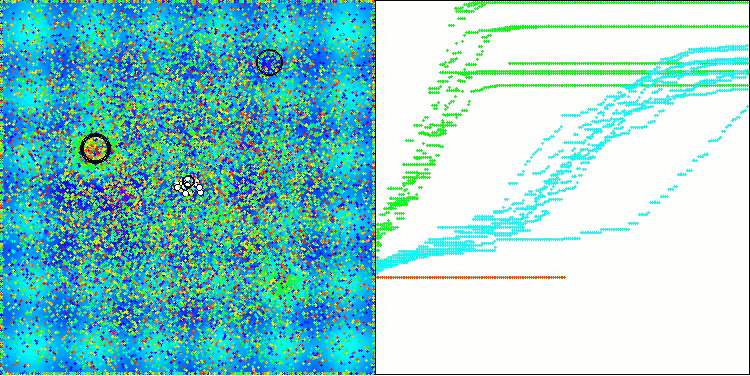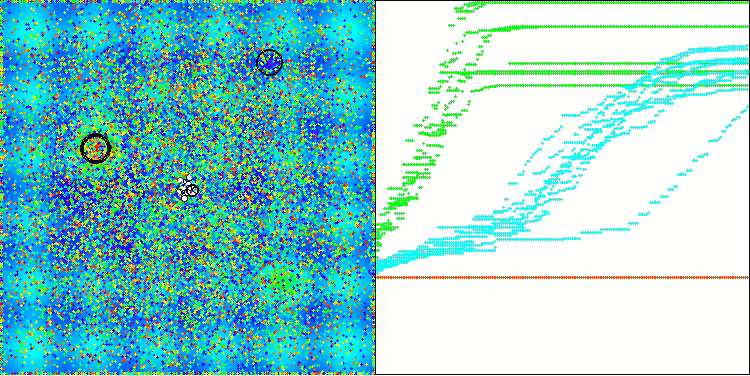
BOA na função de teste Hilly

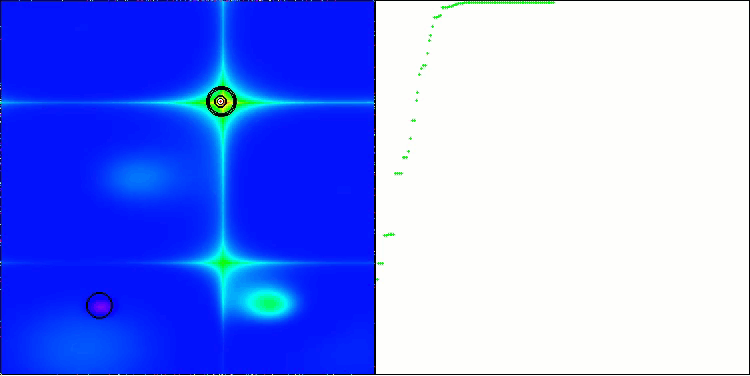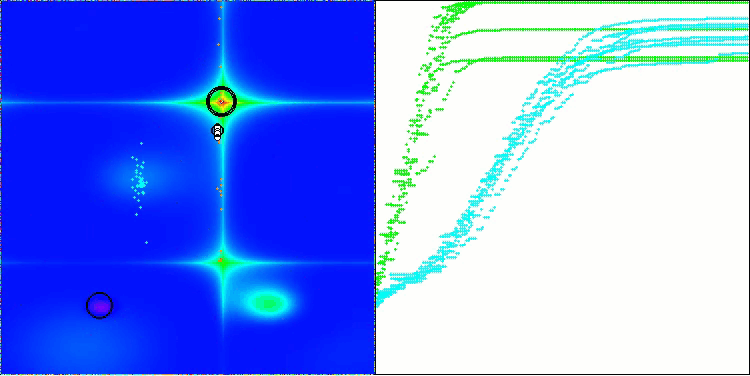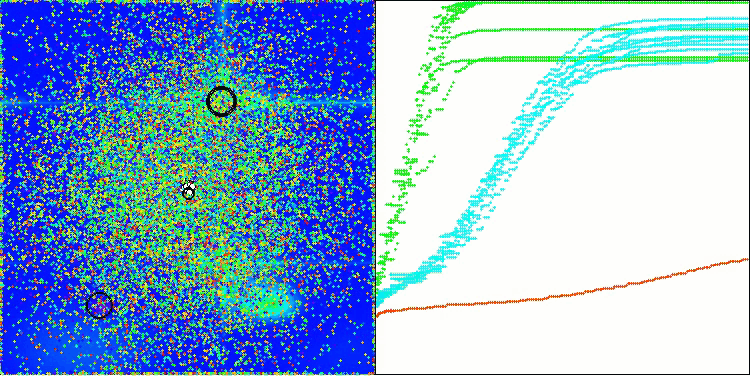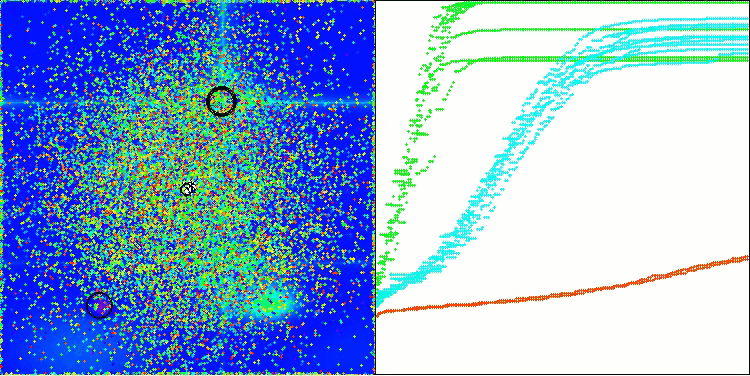
BOA na função de teste Forest

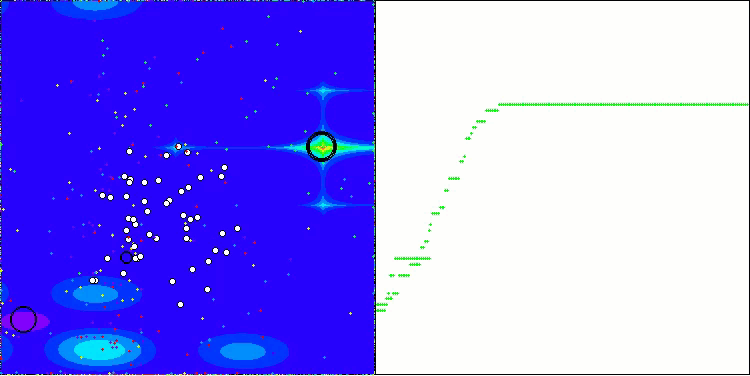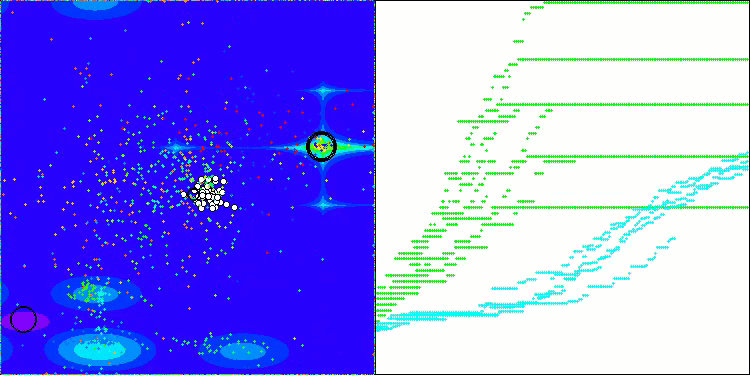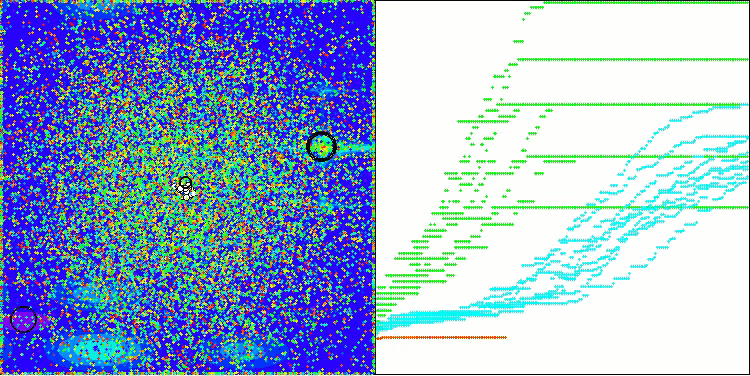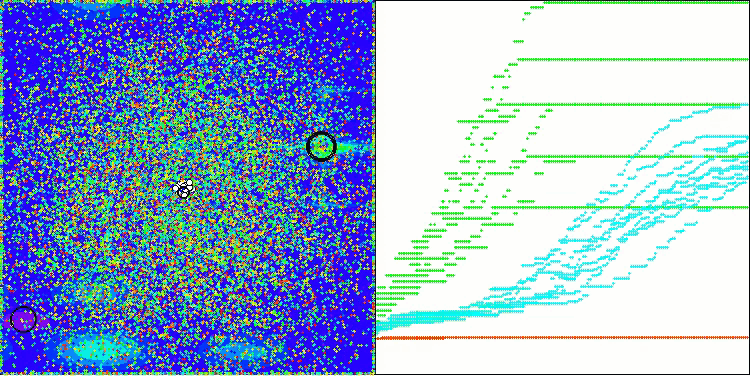
BOA na função de teste Megacity

Façamos agora um balanço dos testes e vejamos a performance. O algoritmo ficou relativamente bem posicionado — em 8º lugar no ranking dos melhores algoritmos de otimização, ainda que com limitações sérias.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
2	CLA	code lock algorithm (joo)	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	AMOm	animal migration ptimization M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5,987	66,52
4	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
5	CTA	comet tail algorithm (joo)	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
6	TETA	time evolution travel algorithm (joo)	0,91362	0,82349	0,31990	2,05701	0,97096	0,89532	0,29324	2,15952	0,73462	0,68569	0,16021	1,58052	5,797	64,41
7	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
8	BOAm	billiards optimization algorithm M	0,95757	0,82599	0,25235	2,03590	1,00000	0,90036	0,30502	2,20538	0,73538	0,52523	0,09563	1,35625	5,598	62,19
9	AAm	archery algorithm M	0,91744	0,70876	0,42160	2,04780	0,92527	0,75802	0,35328	2,03657	0,67385	0,55200	0,23738	1,46323	5,548	61,64
10	ESG	evolution of social groups (joo)	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
11	SIA	simulated isotropic annealing (joo)	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
12	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
13	DA	dialectical algorithm	0,86183	0,70033	0,33724	1,89940	0,98163	0,72772	0,28718	1,99653	0,70308	0,45292	0,16367	1,31967	5,216	57,95
14	BHAm	black hole algorithm M	0,75236	0,76675	0,34583	1,86493	0,93593	0,80152	0,27177	2,00923	0,65077	0,51646	0,15472	1,32195	5,196	57,73
15	ASO	anarchy society optimization	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5,178	57,54
16	RFO	royal flush optimization (joo)	0,83361	0,73742	0,34629	1,91733	0,89424	0,73824	0,24098	1,87346	0,63154	0,50292	0,16421	1,29867	5,089	56,55
17	AOSm	atomic orbital search M	0,80232	0,70449	0,31021	1,81702	0,85660	0,69451	0,21996	1,77107	0,74615	0,52862	0,14358	1,41835	5,006	55,63
18	TSEA	turtle shell evolution algorithm (joo)	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
19	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
20	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
21	BIO	blood inheritance optimization (joo)	0,81568	0,65336	0,30877	1,77781	0,89937	0,65319	0,21760	1,77016	0,67846	0,47631	0,13902	1,29378	4,842	53,80
22	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
23	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
24	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
25	BCOm	bacterial chemotaxis optimization M	0,75953	0,62268	0,31483	1,69704	0,89378	0,61339	0,22542	1,73259	0,65385	0,42092	0,14435	1,21912	4,649	51,65
26	ABO	african buffalo optimization	0,83337	0,62247	0,29964	1,75548	0,92170	0,58618	0,19723	1,70511	0,61000	0,43154	0,13225	1,17378	4,634	51,49
27	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
28	TSm	tabu search M	0,87795	0,61431	0,29104	1,78330	0,92885	0,51844	0,19054	1,63783	0,61077	0,38215	0,12157	1,11449	4,536	50,40
29	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
30	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
31	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
32	AEO	artificial ecosystem-based optimization algorithm	0,91380	0,46713	0,26470	1,64563	0,90223	0,43705	0,21400	1,55327	0,66154	0,30800	0,28563	1,25517	4,454	49,49
33	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
34	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
35	SOA	simple optimization algorithm	0,91520	0,46976	0,27089	1,65585	0,89675	0,37401	0,16984	1,44060	0,69538	0,28031	0,10852	1,08422	4,181	46,45
36	ABHA	artificial bee hive algorithm	0,84131	0,54227	0,26304	1,64663	0,87858	0,47779	0,17181	1,52818	0,50923	0,33877	0,10397	0,95197	4,127	45,85
37	ACMO	atmospheric cloud model optimization	0,90321	0,48546	0,30403	1,69270	0,80268	0,37857	0,19178	1,37303	0,62308	0,24400	0,10795	0,97503	4,041	44,90
38	ADAMm	adaptive moment estimation M	0,88635	0,44766	0,26613	1,60014	0,84497	0,38493	0,16889	1,39880	0,66154	0,27046	0,10594	1,03794	4,037	44,85
39	CGO	chaos game optimization	0,57256	0,37158	0,32018	1,26432	0,61176	0,61931	0,62161	1,85267	0,37538	0,21923	0,19028	0,78490	3,902	43,35
40	ATAm	artificial tribe algorithm M	0,71771	0,55304	0,25235	1,52310	0,82491	0,55904	0,20473	1,58867	0,44000	0,18615	0,09411	0,72026	3,832	42,58
41	ASHA	artificial showering algorithm	0,89686	0,40433	0,25617	1,55737	0,80360	0,35526	0,19160	1,35046	0,47692	0,18123	0,09774	0,75589	3,664	40,71
42	ASBO	adaptive social behavior optimization	0,76331	0,49253	0,32619	1,58202	0,79546	0,40035	0,26097	1,45677	0,26462	0,17169	0,18200	0,61831	3,657	40,63
43	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
44	CSA	circle search algorithm	0,66560	0,45317	0,29126	1,41003	0,68797	0,41397	0,20525	1,30719	0,37538	0,23631	0,10646	0,71815	3,435	38,17
45	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
	RW	random walk	0,48754	0,32159	0,25781	1,06694	0,37554	0,21944	0,15877	0,75375	0,27969	0,14917	0,09847	0,52734	2,348	26,09

Conclusões e considerações finais

O algoritmo de otimização de bilhar modificado (BOAm) apresentou resultados interessantes nas funções de teste. A análise dos dados mostra que o algoritmo alcança os melhores índices em problemas de baixa e média dimensionalidade, obtendo valores máximos nos testes Hilly (0.957), Forest (0.999) e Megacity (0.735), ao atingir 10 000 iterações. Isso confirma sua alta eficiência na busca de soluções ótimas para problemas de complexidade moderada. Entretanto, o desempenho cai consideravelmente quando a dimensionalidade do problema aumenta, como demonstrado nos cenários com 1000 variáveis, onde os resultados caem para 0.252, 0.305 e 0.095, respectivamente.

É especialmente importante destacar a melhoria significativa de desempenho na versão modificada do algoritmo, que atinge 62.19% do resultado máximo possível, o que é o dobro da versão original, que obteve 31.04%. Essa melhoria impressionante foi alcançada apenas com a alteração de uma única linha de código, referente à fórmula de atualização da posição das bolas.

A simplicidade do algoritmo é ao mesmo tempo sua vantagem e sua limitação — ele é intuitivo, de fácil implementação e baseado em uma concepção elegante inspirada no jogo de bilhar, mas pode exigir modificações adicionais para operar de forma eficiente em problemas de alta dimensionalidade. No geral, ao figurar entre os dez primeiros algoritmos na tabela de classificação, o BOAm representa uma abordagem meta-heurística promissora, com um bom equilíbrio entre diversificação e intensificação do espaço de soluções.

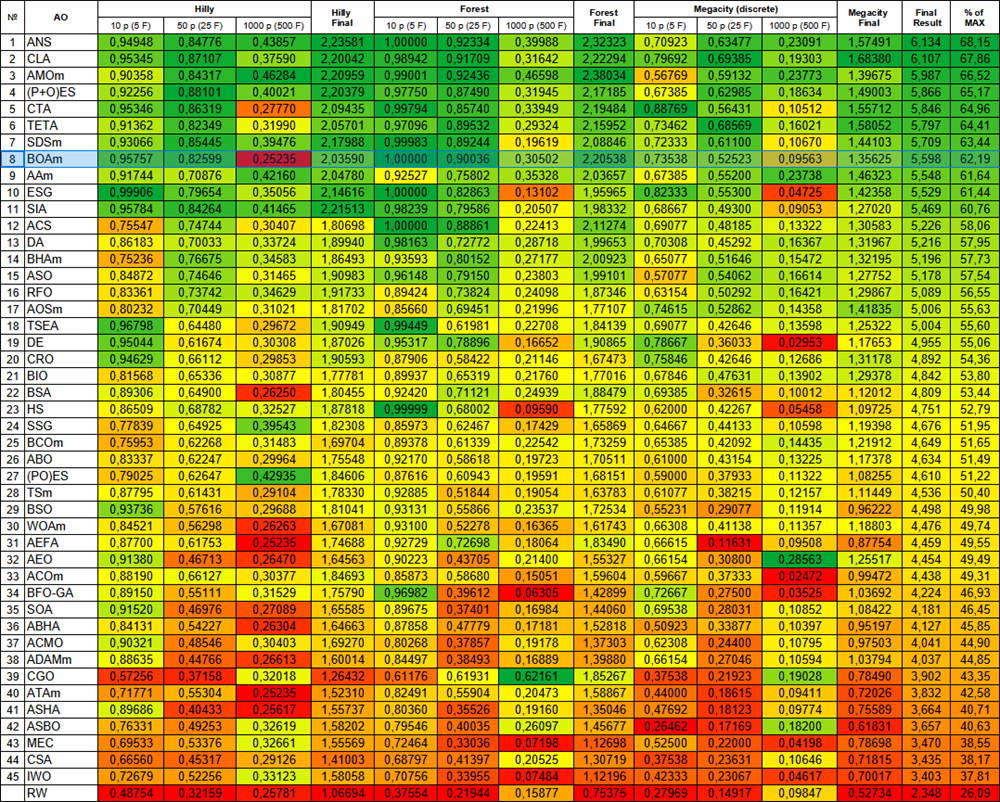
Figura 2. Graduação de cores dos algoritmos de acordo com os testes correspondentes

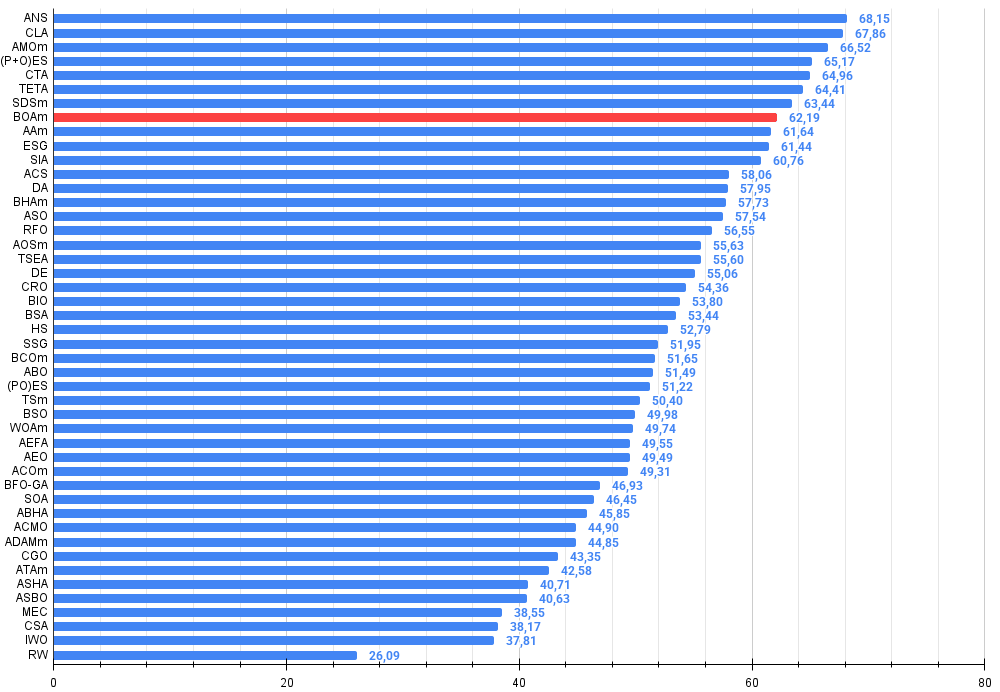
Figura 3. Histograma dos resultados dos testes dos algoritmos (na escala de 0 a 100, quanto maior, melhor, onde 100 — valor máximo teórico possível, no arquivo compactado está o script para cálculo da tabela comparativa)

Prós e contras do algoritmo BOA:

Prós:

1. Muito poucos parâmetros externos.
2. Implementação simples.
   
3. Bom desempenho em problemas de baixa e média dimensionalidade.
4. Excelentes resultados em problemas com extremos "agudos" (como a função Forest).
   

Contras:

1. Tende a ficar preso em extremos locais em problemas de baixa dimensionalidade.
   
2. Velocidade e precisão de convergência muito baixas em problemas "suaves" (como a função Hilly) de alta dimensionalidade.

Ao artigo está anexado um arquivo compactado com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela exatidão absoluta na descrição dos algoritmos canônicos, já que muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e considerações apresentadas nos artigos são baseadas nos resultados dos experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	C_AO.mqh	Arquivo incluído	Classe pai dos algoritmos populacionais de otimização
2	C_AO_enum.mqh	Arquivo incluído	Enumeração de algoritmos populacionais de otimização
3	TestFunctions.mqh	Arquivo incluído	Biblioteca de funções de teste
4	TestStandFunctions.mqh	Arquivo incluído	Biblioteca de funções do ambiente de testes
5	Utilities.mqh	Arquivo incluído	Biblioteca de funções auxiliares
6	CalculationTestResults.mqh	Arquivo incluído	Script para cálculo de resultados na tabela comparativa
7	Testing AOs.mq5	Script	Ambiente unificado de testes para todos os algoritmos populacionais de otimização
8	Simple use of population optimization algorithms.mq5	Script	Exemplo simples de uso de algoritmos populacionais de otimização sem visualização
9	Test_AO_BOAm.mq5	Script	Ambiente de testes para o BOAm