Algoritmos de optimización de la población: Algoritmo de recocido isotrópico simulado (Simulated Isotropic Annealing, SIA). Parte II
413
0
Contenido:
1. Introducción
2. Descripción del algoritmo
3. Resultados de las pruebas
1. Introducción
En la primera parte de este trabajo, consideramos la versión canónica del algoritmo de Recocido Simulado (SA). El algoritmo se basa en tres conceptos principales: la aplicación de la aleatoriedad, la toma de peores decisiones y la disminución gradual de la probabilidad de tomar peores decisiones. El uso de la aleatoriedad nos permite explorar distintas regiones del espacio de búsqueda y evitar quedarnos atascados en óptimos locales. La aplicación de soluciones peores con cierta probabilidad permite al algoritmo "saltar" temporalmente de los óptimos locales y buscar soluciones mejores en otros lugares del espacio de búsqueda, lo cual le permite explorar primero el espacio de búsqueda de forma más amplia y centrarse después en mejorar la solución.
La idea que subyace al algoritmo SA se basa en la analogía con el proceso de recocido de metales. El metal calentado se enfría gradualmente, lo cual provoca un cambio en su estructura. Del mismo modo, el algoritmo de recocido simulado comienza con una temperatura alta (alta probabilidad de tomar la peor decisión) y reduce gradualmente la temperatura (disminuye la probabilidad de tomar la peor decisión), lo que presumiblemente debería ayudar al algoritmo a converger hacia la solución óptima.
El algoritmo comienza con una solución inicial, que puede ser aleatoria o derivada de iteraciones anteriores. A continuación, se aplican operaciones de cambio de estado de la solución, que pueden ser aleatorias o controladas, para conseguir un nuevo estado, aunque sea peor que el actual. La probabilidad de tomar una decisión peor viene determinada por la función de "enfriamiento" que disminuye la probabilidad de tomar una decisión peor con el tiempo.
Se usan varias fórmulas sencillas para describir el proceso de recocido simulado. La fórmula para calcular el cambio en la energía nos permite determinar la diferencia en los valores de la función de aptitud en dos iteraciones consecutivas. La fórmula para calcular la probabilidad de tomar una peor decisión determina la probabilidad de adoptar un nuevo estado dada la diferencia de energía y la temperatura actual.
Los parámetros importantes que hay que ajustar al utilizar el algoritmo de recocido simulado son la temperatura inicial y el factor de enfriamiento. El ajuste de estos parámetros puede tener un impacto significativo en el rendimiento y la calidad de la solución, y supone uno de los puntos débiles del algoritmo, por la dificultad que supone seleccionar los parámetros debido a lo poco evidente de su influencia en el rendimiento. Además, ambos parámetros se influyen mutuamente: el aumento de la temperatura puede ser sustituido casi por igual por la disminución del factor de reducción de la temperatura.
En la primera parte del artículo, identificaremos los principales problemas del algoritmo:
- La parametrización: los parámetros del algoritmo SA, como la temperatura inicial y el coeficiente de enfriamiento, pueden afectar significativamente a su rendimiento y eficacia. Ajustar estos parámetros puede suponer un reto, por lo que será necesario experimentar para alcanzar los valores óptimos.
- El problema del atascamiento en extremos locales: se pueden utilizar diferentes estrategias para superar este problema, como seleccionar la distribución más adecuada de la variable aleatoria al generar nuevas soluciones en combinación con las herramientas disponibles de la estrategia del algoritmo, así como considerar posibles soluciones para aumentar las posibilidades combinatorias.
- La mejora de la velocidad de convergencia: para acelerar la convergencia, se pueden aplicar modificaciones a la función de enfriamiento para reducir más rápidamente la temperatura del sistema (o con una forma diferente de función de enfriamiento). También es posible revisar en el algoritmo los métodos de selección del siguiente estado que consideran la información sobre los estados recorridos anteriormente.
- La mejora de la eficacia del algoritmo SA con un gran número de variables: se trata de uno de los problemas más difíciles para la gran mayoría de algoritmos, ya que a medida que aumenta el número de variables, la complejidad del espacio de búsqueda crece mucho más rápido de lo que pueden explicar las técnicas especiales de las estrategias de búsqueda.
Uno de los principales problemas de los espacios multidimensionales es la explosión combinatoria de las posibles combinaciones de variables. A medida que aumenta el número de variables, el número de estados posibles del sistema a explorar aumenta exponencialmente. Y esto hace que los algoritmos de optimización se enfrenten al problema de la complejidad espacial.
La complejidad espacial implica que el tamaño del espacio de búsqueda crece exponencialmente a medida que aumenta el número de variables. Por ejemplo, si tenemos 10 variables, cada una de las cuales puede tomar 10 valores, entonces el número total de combinaciones posibles será de 10^10, lo cual equivale a 10 mil millones, y ello a pesar de que solo disponemos de 10 mil intentos (el número de ejecuciones de la función de aptitud). Encontrar la solución óptima entre tantas combinaciones se convierte así en una tarea extremadamente difícil. Atención aparte merece el hecho de que en nuestras pruebas optimizamos los parámetros de las funciones con un paso 0. Esto supone unas condiciones extremadamente difíciles para los algoritmos, y aquellos de ellos que rindan satisfactoriamente en problemas de prueba tan complejos tendrán casi garantizado un mejor rendimiento en problemas menos complejos (si se da una igualdad de otras condiciones) del mundo real.
2. Descripción del algoritmo
El algoritmo de recocido simulado es tan sencillo que resulta realmente difícil imaginar cómo podría mejorarse aún más. Es como convertir un vaso de agua en un vino encantador, como un hechizo. Y realmente, qué se puede mejorar si la generación de nuevos valores está uniformemente distribuida, y la idea de tomar una decisión peor va completamente en contra de la lógica habitual de la construcción de algoritmos de optimización.
Para comparar de forma clara los resultados experimentales posteriores con el resultado de referencia inicial del algoritmo de recocido simulado (SA) original, presentamos aquí una impresión de los resultados del artículo anterior:
=============================
5 Rastrigin's; Func runs 10000 result: 65.78409729002105
Score: 0.81510
25 Rastrigin's; Func runs 10000 result: 52.25447043222567
Score: 0.64746
500 Rastrigin's; Func runs 10000 result: 40.40159931988021
Score: 0.50060
=============================
5 Forest's; Func runs 10000 result: 0.5814827554067439
Score: 0.32892
25 Forest's; Func runs 10000 result: 0.23156336186841173
Score: 0.13098
500 Forest's; Func runs 10000 result: 0.06760002887601002
Score: 0.03824
=============================
5 Megacity's; Func runs 10000 result: 2.92
Score: 0.24333
25 Megacity's; Func runs 10000 result: 1.256
Score: 0.10467
500 Megacity's; Func runs 10000 result: 0.33840000000000003
Score: 0.02820
=============================
All score: 2.83750
Bien, vamos allá. Intentaremos mejorar los resultados sustituyendo la distribución uniforme de las variables aleatorias por una distribución normal al generar nuevos estados del sistema.
Utilizaremos la clase del algoritmo de recocido simulado como base para el nuevo algoritmo SIA, por lo que no ofreceremos una descripción de los métodos y funcionalidad de esta clase, ya que todo ha sido presentado en la primera parte del artículo.
A continuación, podemos utilizar el método de la función inversa para generar un número aleatorio con distribución normal. Supongamos que queremos generar un número "x" con una distribución normal, mu (media) y sigma (desviación típica). Entonces podremos utilizar la siguiente fórmula:
x = z0 * sigma + mu
donde:- z0 - lo calculamos según la fórmula:
z0 = sqrt (-2 * log (u1)) * cos(2 * Pi * u2)
donde:-
u1* - número aleatorio en el rango (0.0;1.0] (aquí min no está incluido en el rango)
-
u2** - número aleatorio en el rango [0.0;1.0]
- * y ** son dos números aleatorios independientes con distribución uniforme
En el artículo anterior, añadimos un parámetro de coeficiente de difusión al algoritmo SA que limitaba la región de generación de números aleatorios. Precisamente en esta área tendremos que generar números aleatorios.
Vamos a escribir un método de la clase C_AO_SIA, simulando la difusión - "Diffusion". El método generará un número aleatorio con una distribución normal de hasta dos desviaciones típicas. Fuera de estos límites, envolveremos los valores "hacia dentro" sin perder la forma de la distribución (se tratará con más detalle en próximos artículos).
Conociendo el valor de la desviación estándar (sigma), podremos convertir este rango de valores a nuestro rango deseado que simula la difusión, esto lo haremos utilizando la función de escala "Scale".
//—————————————————————————————————————————————————————————————————————————————— double C_AO_SIA::Diffusion (const double value, const double rMin, const double rMax, const double step) { double logN = 0.0; double u1 = RNDfromCI (0.0, 1.0); double u2 = RNDfromCI (0.0, 1.0); logN = u1 <= 0.0 ? 0.000000000000001 : u1; double z0 = sqrt (-2 * log (logN))* cos (2 * M_PI * u2); double sigma = 2.0;//Sigma > 8.583864105157389 ? 8.583864105157389 : Sigma; if (z0 >= sigma) z0 = RNDfromCI (0.0, sigma); if (z0 <= -sigma) z0 = RNDfromCI (-sigma, 0.0); double dist = d * (rMax - rMin); if (z0 >= 0.0) return Scale (z0, 0.0, sigma, value, value + dist, false); else return Scale (z0, -sigma, 0.0, value - dist, value, false); } //——————————————————————————————————————————————————————————————————————————————
En el método "Moving", usaremos el método "Diffusion" de la siguiente manera:
for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = Diffusion (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } }Tras realizar las pruebas con los cambios efectuados (hemos sustituido la distribución uniforme por una distribución normal) hemos obtenido los resultados que verá a continuación:
=============================
5 Rastrigin's; Func runs 10000 result: 60.999013617749895
Score: 0.75581
25 Rastrigin's; Func runs 10000 result: 47.993562806349246
Score: 0.59467
500 Rastrigin's; Func runs 10000 result: 40.00575378955945
Score: 0.49569
=============================
5 Forest's; Func runs 10000 result: 0.41673083215719087
Score: 0.23572
25 Forest's; Func runs 10000 result: 0.16700842421505407
Score: 0.09447
500 Forest's; Func runs 10000 result: 0.049538421252065555
Score: 0.02802
=============================
5 Megacity's; Func runs 10000 result: 2.7600000000000002
Score: 0.23000
25 Megacity's; Func runs 10000 result: 0.9039999999999999
Score: 0.07533
500 Megacity's; Func runs 10000 result: 0.28
Score: 0.02333
=============================
All score: 2.53305
Al cambiar la distribución de una variable aleatoria en un algoritmo de recocido simulado, al igual que en cualquier otro algoritmo, resulta inevitable que influya en su funcionamiento y sus resultados. La formulación original del algoritmo usa una distribución uniforme para generar pasos aleatorios de exploración del espacio de soluciones. Esta distribución ofrece probabilidades iguales para todos los pasos posibles.
Al sustituir la distribución uniforme por una distribución normal, las propiedades probabilísticas del algoritmo cambian. Las distribuciones normales tienen un pico alrededor de la media y disminuyen a medida que nos alejamos de la media. Esto significa que los pasos aleatorios generados usando una distribución normal se agruparán en torno al valor medio, mientras que los pasos alejados de la media resultarán poco probables, en nuestro caso, el "valor medio" del valor de la coordenada original que queremos mejorar.
Este cambio en la distribución obviamente conduce a pasos menos diversos en la exploración del espacio de soluciones. El algoritmo parece más localizado y menos capaz de explorar regiones más distantes o menos probables del espacio de soluciones.
Las pruebas presentadas anteriormente muestran que, en este caso, el uso de la distribución normal ha provocado un deterioro leve pero estadísticamente significativo de los resultados finales en comparación con una variable aleatoria distribuida uniformemente (como se refleja en la primera parte del artículo). Estos resultados se han obtenido utilizando dos desviaciones típicas, mientras que el aumento del valor de sigma (desviación típica) conlleva un mayor deterioro de los resultados, estadísticamente significativo.
De ahí que concluyamos que, en este caso concreto, cambiar la forma de la distribución por una más aguda empeorará los resultados.
Ahora que nos hemos dado cuenta de que "afinar" la forma de la distribución en el algoritmo original no resulta útil, veamos otro enfoque. Vamos a suponer que en el algoritmo original, las moléculas del metal -y podemos decir cristales enteros dentro de la zona de difusión- carecen de la capacidad de intercambiar energía para distribuirla uniformemente por todo el metal. En tal caso, podemos proponer lo siguiente: permitir que los cristales intercambien moléculas en el proceso de intercambio de energía.
Este proceso de intercambio de moléculas entre cristales con energías diferentes permitirá transferir las coordenadas entre agentes. De esta forma, las moléculas se convertirán en una especie de portadores de energía, capaces de suavizar la distribución de energía en todo el metal. Como resultado de esta interacción entre la red cristalina y las moléculas, la energía se distribuirá de forma más uniforme, lo cual dará lugar a una configuración del sistema más estable y óptima. Es decir, intentaremos aumentar la isotropía en la estructura metálica.
La isotropía es una propiedad de un objeto o sistema que permite conservar las mismas características o propiedades en todas las direcciones. En términos más sencillos: un objeto o sistema es isótropo si tiene el mismo aspecto y se comporta igual en cualquier dirección. Así pues, la isotropía implica que no existe una dirección u orientación preferente y que el objeto o sistema se considera igual u homogéneo en todas las direcciones.
Para conseguir una alineación simulada de las propiedades del metal en todas las direcciones (una mayor isotropía) tendremos que introducir cambios en el método Moving.
La lógica del código es la siguiente: primero se itera sobre cada elemento de la población "popSize" y cada coordenada "coords":
- luego se genera un número entero aleatorio "r" en el rango de 0 a "popSize" utilizando la función RNDfromCI, seleccionando así aleatoriamente un agente en la población
- después se comprueba la siguiente condición: si el valor de aptitud del agente seleccionado es mayor que el valor de aptitud del agente que se está cambiando, entonces copiaremos la coordenada del mejor, de lo contrario la coordenada del agente no cambiará
- a continuación se genera un número aleatorio "rnd" en el intervalo [-0,1;0,1] utilizando la función RNDfromCI
- después se actualiza el valor de la coordenada añadiéndole el producto de "rnd", (rangeMax[c] - rangeMin[c]) y "d", es decir, añadimos un incremento aleatorio en el rango de difusión
- la coordenada recibida se verifica usando la función SeInDiSp para comprobar que se encuentra dentro del rango permitido y con la separación requerida.
int r = 0; double rnd = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { r = (int)RNDfromCI (0, popSize); if (r >= popSize) r = popSize - 1; if (a [r].fPrev > a [i].fPrev) { a [i].c [c] = a [r].cPrev [c]; } else { a [i].c [c] = a [i].cPrev [c]; } rnd = RNDfromCI (-0.1, 0.1); a [i].c [c] = a [i].c [c] + rnd * (rangeMax [c] - rangeMin [c]) * d; a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } }
Resultados del recocido usando los mismos parámetros con distribución uniforme y con isotropía añadida:
C_AO_SIA:50:1000.0:0.1:0.1
=============================
5 Rastrigin's; Func runs 10000 result: 80.52391137534615
Score: 0.99774
25 Rastrigin's; Func runs 10000 result: 77.70887543197314
Score: 0.96286
500 Rastrigin's; Func runs 10000 result: 57.43358792423487
Score: 0.71163
=============================
5 Forest's; Func runs 10000 result: 1.5720970326889474
Score: 0.88926
25 Forest's; Func runs 10000 result: 1.0118351454323513
Score: 0.57234
500 Forest's; Func runs 10000 result: 0.3391169587652742
Score: 0.19182
=============================
5 Megacity's; Func runs 10000 result: 6.76
Score: 0.56333
25 Megacity's; Func runs 10000 result: 5.263999999999999
Score: 0.43867
500 Megacity's; Func runs 10000 result: 1.4908
Score: 0.12423
=============================
All score: 5.45188
El uso de un proceso de mejora de la isotropía en el que se intercambian moléculas entre cristales con energías diferentes, ha permitido mejorar notablemente los resultados del algoritmo; ahora nos encontramos ante un verdadero salto de calidad.
Conclusiones que pueden extraerse del proceso descrito:
- La transferencia de coordenadas entre agentes: el intercambio de moléculas entre cristales con energías diferentes permite transferir información sobre las coordenadas entre los agentes del algoritmo. Esto contribuye a una búsqueda más eficaz y rápida de una solución óptima, pues la información sobre las soluciones positivas se transmite a otros agentes
- El suavizado de la distribución de energía: el proceso de intercambio de moléculas entre cristales con energías diferentes permite suavizar la distribución de energía en todo el volumen del metal. Y esto significa que la energía se distribuirá de forma más uniforme, lo que ayudará a evitar los mínimos locales y a conseguir una configuración del sistema más estable y óptima.
Ahora, después de mejorar significativamente los resultados añadiendo la isotropía, vamos a intentar agregar de nuevo la distribución normal (primero realizaremos la operación de mejora de la isotropía y añadiremos el incremento de la distribución normal a los valores obtenidos).
Resultados del recocido con adición de aumento de isotropía + distribución normal:
C_AO_SIA:50:1000.0:0.1:0.05
=============================
5 Rastrigin's; Func runs 10000 result: 78.39172420614801
Score: 0.97132
25 Rastrigin's; Func runs 10000 result: 66.41980717898778
Score: 0.82298
500 Rastrigin's; Func runs 10000 result: 47.62039509425823
Score: 0.59004
=============================
5 Forest's; Func runs 10000 result: 1.243327107341557
Score: 0.70329
25 Forest's; Func runs 10000 result: 0.7588262864735575
Score: 0.42923
500 Forest's; Func runs 10000 result: 0.13750740782669305
Score: 0.07778
=============================
5 Megacity's; Func runs 10000 result: 6.8
Score: 0.56667
25 Megacity's; Func runs 10000 result: 2.776
Score: 0.23133
500 Megacity's; Func runs 10000 result: 0.46959999999999996
Score: 0.03913
=============================
All score: 4.43177
Los resultados se han deteriorado sustancialmente.
La hipótesis consistía en que, si la simple generación de incrementos con una distribución normal en el algoritmo de simulación del recocido no aportaba ninguna mejora, entonces ¿quizás, tras aplicar el incremento de isotropía, el incremento con una distribución normal daría el efecto esperado? No se han cumplido las expectativas. Esto tiene una explicación: tras aplicar la mejora de isotropía, la distribución aún uniforme posibilita una exploración más uniforme del espacio de soluciones, lo cual permite al algoritmo explorar distintas regiones sin fuertes distorsiones en las preferencias. El intento de mejorar las coordenadas disponibles usando una distribución normal no ha tenido éxito, y esto limita una exploración más amplia de las áreas del algoritmo.
Vamos a realizar un último experimento para sacar finalmente conclusiones a favor de una distribución uniforme de los incrementos de la variable aleatoria tras aplicar el aumento de isotropía. Intentaremos investigar de forma aún más precisa la proximidad de las coordenadas conocidas, para ello utilizaremos la distribución cuadrática. Si una variable aleatoria con una distribución uniforme se eleva al segundo grado, la distribución resultante se llamará distribución de la variable aleatoria al cuadrado o distribución cuadrática.
Resultados del algoritmo de recocido simulado con los mismos parámetros con aumento de isotropía añadido + distribución cuadrática aguda:
C_AO_SIA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result: 70.23675927985173
Score: 0.87027
25 Rastrigin's; Func runs 10000 result: 56.86176837508631
Score: 0.70455
500 Rastrigin's; Func runs 10000 result: 43.100825665204596
Score: 0.53404
=============================
5 Forest's; Func runs 10000 result: 0.9361317757226002
Score: 0.52952
25 Forest's; Func runs 10000 result: 0.25320813586138297
Score: 0.14323
500 Forest's; Func runs 10000 result: 0.0570263375476293
Score: 0.03226
=============================
5 Megacity's; Func runs 10000 result: 4.2
Score: 0.35000
25 Megacity's; Func runs 10000 result: 1.296
Score: 0.10800
500 Megacity's; Func runs 10000 result: 0.2976
Score: 0.02480
=============================
All score: 3.29667
Ahora, vamos a deshacernos de una desventaja más del algoritmo de recocido simulado: la dificultad para seleccionar los ajustes y combinar la temperatura y el factor de reducción de la misma, ya que ambos parámetros se influyen mutuamente. Para vincular ambos parámetros, combinaremos la función de reducción de la temperatura y la función probabilística de tomar las peores decisiones. Aplicaremos la función arcocoseno hiperbólico:
(1 - delta) * (acosh (-(x^3 - 3))) / 1,765
donde:
- delta - diferencia normalizada en el intervalo [0,0;1,0] de los valores de la función de adaptación en las dos últimas iteraciones.
- x - pasos normalizados de las épocas del algoritmo
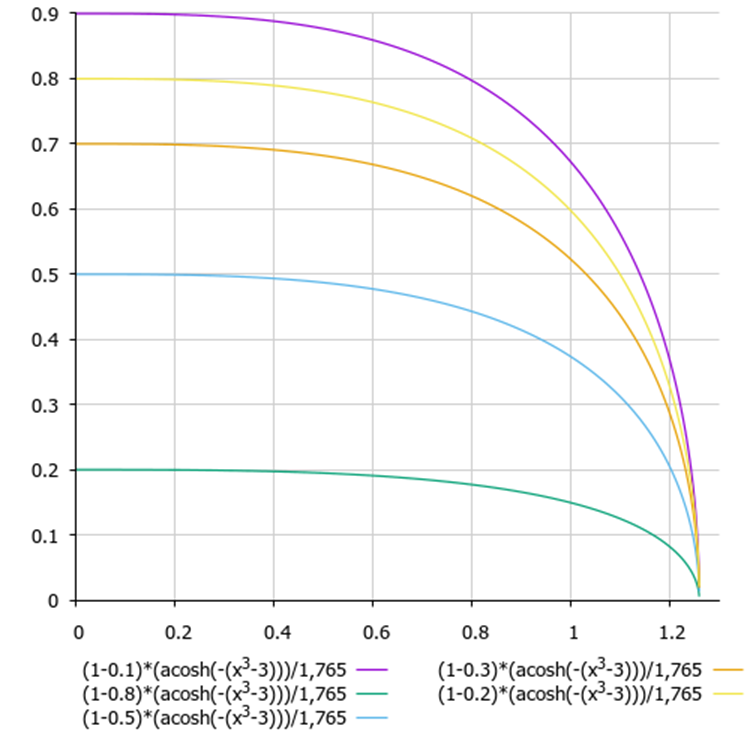
Figura 1. Gráfico de dependencia de la toma de la peor decisión respecto a la diferencia de energía y el número de la época actual (y - diferencia de energía, x - épocas).
3. Resultados de las pruebas
Impresión del rendimiento de la versión final del algoritmo de recocido isotrópico simulado (SIA) en el banco de pruebas:
C_AO_SIA:100:0.01:0.1
=============================
5 Rastrigin's; Func runs 10000 result: 80.49732910930824
Score: 0.99741
25 Rastrigin's; Func runs 10000 result: 78.48411039606445
Score: 0.97246
500 Rastrigin's; Func runs 10000 result: 56.26829697982381
Score: 0.69720
=============================
5 Forest's; Func runs 10000 result: 1.6491133508905373
Score: 0.93282
25 Forest's; Func runs 10000 result: 1.3608802086313785
Score: 0.76978
500 Forest's; Func runs 10000 result: 0.31584037846210056
Score: 0.17866
=============================
5 Megacity's; Func runs 10000 result: 8.6
Score: 0.71667
25 Megacity's; Func runs 10000 result: 6.152
Score: 0.51267
500 Megacity's; Func runs 10000 result: 1.0544
Score: 0.08787
=============================
All score: 5.86552
Impresionantes resultados, con un parámetro menos si se fija.
La visualización del rendimiento del algoritmo muestra una clara separación en grupos aparte de agentes, con todos los extremos locales significativos cubiertos. La imagen se parece a la cristalización real del metal en solidificación. Observe la excelente convergencia en todas las pruebas, incluso (lo que es importante) con muchas variables.
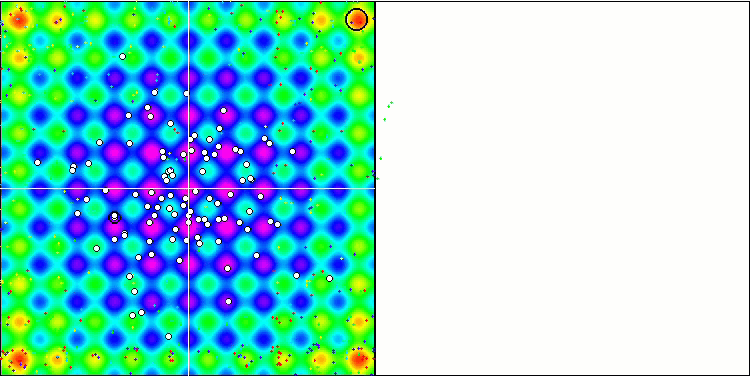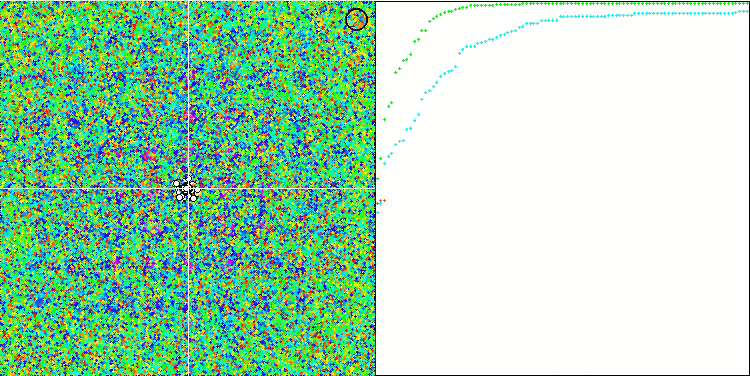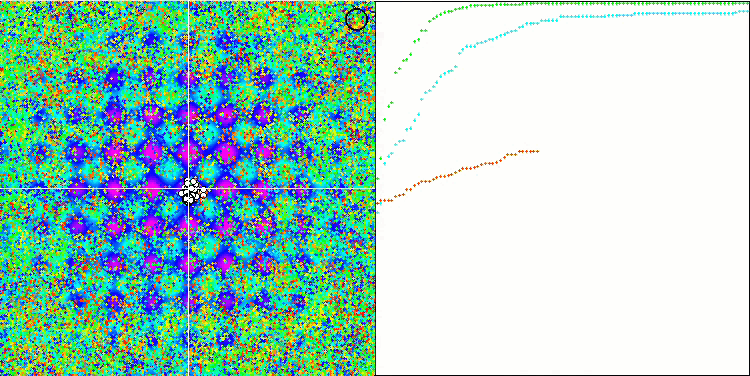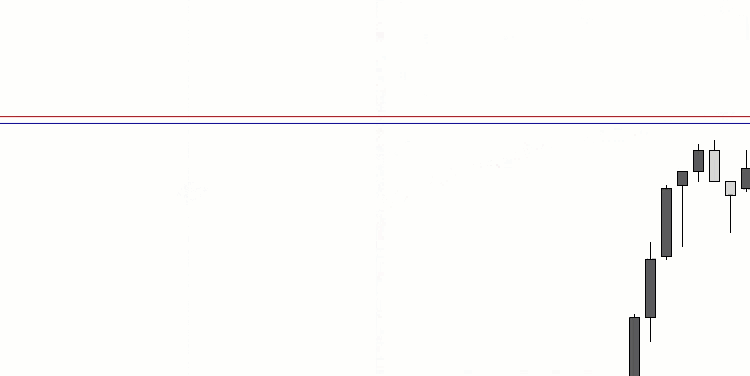
SIA sobre la función de prueba Rastrigin.
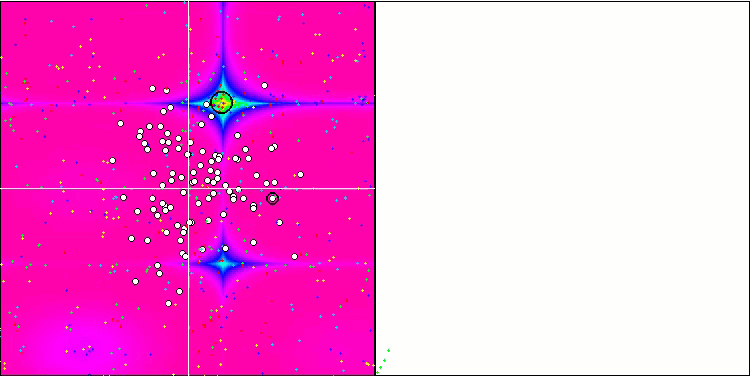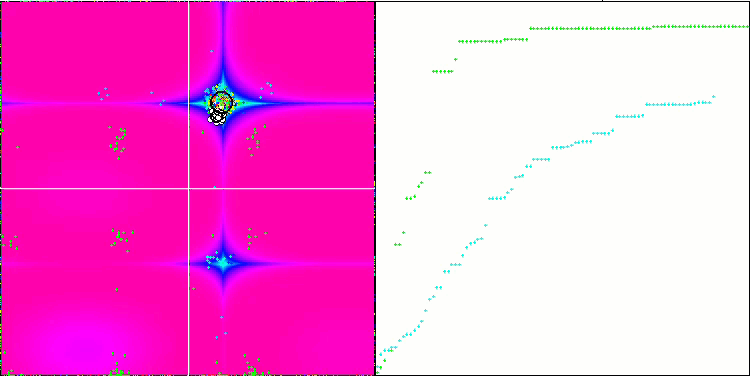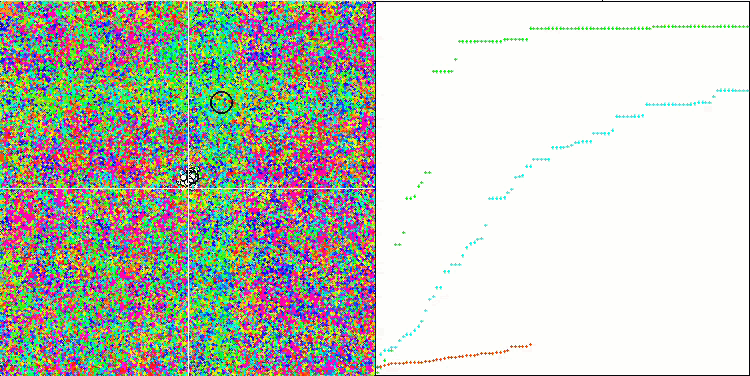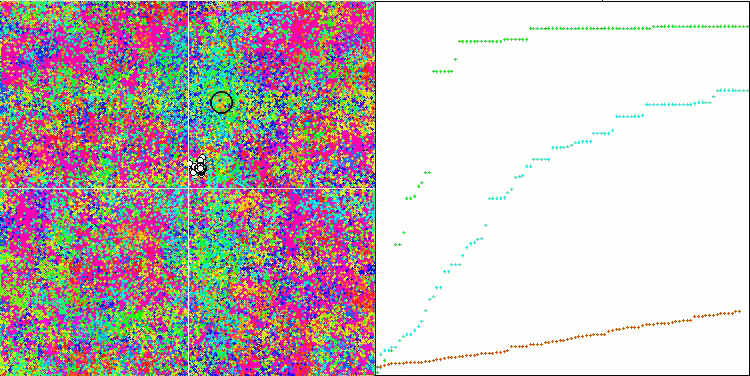
SIA en la función de prueba Forest.
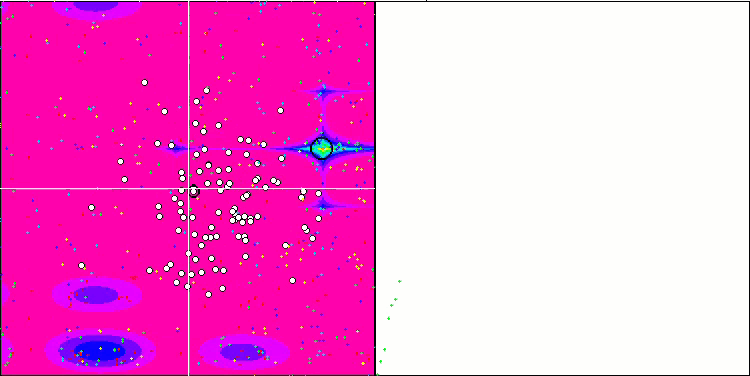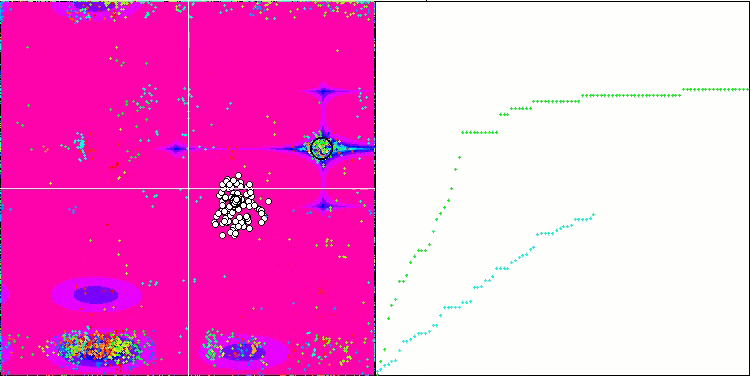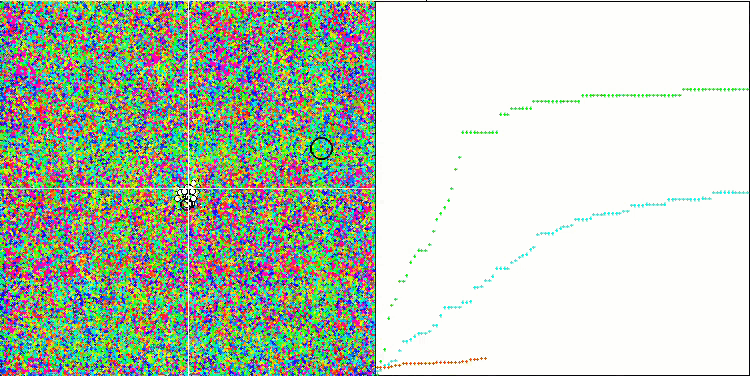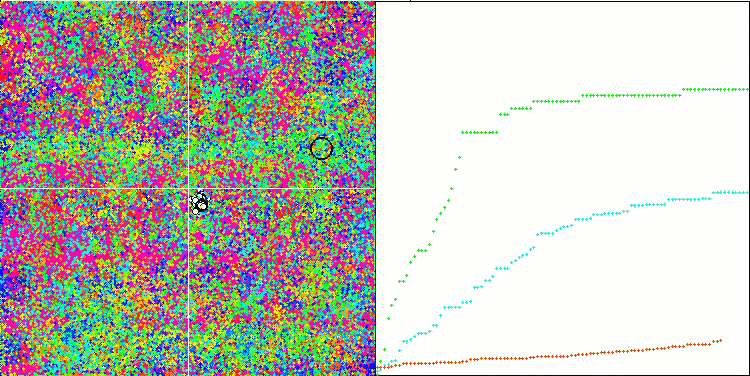
SIA en la función de prueba Megacity.
El nuevo algoritmo de simulación de recocido isotrópico (SIA, 2023), ha quedado segundo en la tabla de clasificación, arrebatando al mismo tiempo el liderazgo a SDSm en las dos pruebas más duras (en Forest agudo y Megacity discreta con 1000 variables).
| № | AO | Description | Rastrigin | Rastrigin final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | |||||||
| 1 | SDSm | stochastic diffusion search M | 0,99809 | 1,00000 | 0,69149 | 2,68958 | 0,99265 | 1,00000 | 0,84982 | 2,84247 | 1,00000 | 1,00000 | 0,79920 | 2,79920 | 100,000 |
| 2 | SIA | simulated isotropic annealing | 0,99236 | 0,93642 | 0,69858 | 2,62736 | 0,88760 | 0,64655 | 1,00000 | 2,53416 | 0,58695 | 0,74342 | 1,00000 | 2,33038 | 89,524 |
| 3 | SSG | saplings sowing and growing | 1,00000 | 0,92761 | 0,51630 | 2,44391 | 0,72120 | 0,65201 | 0,71181 | 2,08502 | 0,54782 | 0,61841 | 0,79538 | 1,96161 | 77,027 |
| 4 | DE | differential evolution | 0,98295 | 0,89236 | 0,51375 | 2,38906 | 1,00000 | 0,84602 | 0,55672 | 2,40274 | 0,90000 | 0,52237 | 0,09615 | 1,51852 | 74,777 |
| 5 | HS | harmony search | 0,99676 | 0,88385 | 0,44686 | 2,32747 | 0,99148 | 0,68242 | 0,31893 | 1,99283 | 0,71739 | 0,71842 | 0,33037 | 1,76618 | 71,983 |
| 6 | IWO | invasive weed optimization | 0,95828 | 0,62227 | 0,27647 | 1,85703 | 0,70170 | 0,31972 | 0,22616 | 1,24758 | 0,57391 | 0,30527 | 0,26478 | 1,14395 | 49,045 |
| 7 | ACOm | ant colony optimization M | 0,34611 | 0,16683 | 0,15808 | 0,67103 | 0,86147 | 0,68980 | 0,55067 | 2,10194 | 0,71739 | 0,63947 | 0,04459 | 1,40145 | 48,119 |
| 8 | MEC | mind evolutionary computation | 0,99270 | 0,47345 | 0,21148 | 1,67763 | 0,60244 | 0,28046 | 0,18122 | 1,06412 | 0,66957 | 0,30000 | 0,20815 | 1,17772 | 44,937 |
| 9 | SDOm | spiral dynamics optimization M | 0,69840 | 0,52988 | 0,33168 | 1,55996 | 0,59818 | 0,38766 | 0,31953 | 1,30537 | 0,35653 | 0,15262 | 0,20653 | 0,71568 | 40,713 |
| 10 | NMm | Nelder-Mead method M | 0,88433 | 0,48306 | 0,45945 | 1,82685 | 0,46155 | 0,24379 | 0,18613 | 0,89148 | 0,46088 | 0,25658 | 0,13435 | 0,85180 | 40,577 |
| 11 | COAm | cuckoo optimization algorithm M | 0,92400 | 0,43407 | 0,24120 | 1,59927 | 0,57881 | 0,23477 | 0,11764 | 0,93121 | 0,52174 | 0,24079 | 0,13587 | 0,89840 | 38,814 |
| 12 | FAm | firefly algorithm M | 0,59825 | 0,31520 | 0,15893 | 1,07239 | 0,50637 | 0,29178 | 0,35441 | 1,15256 | 0,24783 | 0,20526 | 0,28044 | 0,73352 | 32,943 |
| 13 | ABC | artificial bee colony | 0,78170 | 0,30347 | 0,19313 | 1,27829 | 0,53379 | 0,14799 | 0,09498 | 0,77676 | 0,40435 | 0,19474 | 0,11076 | 0,70985 | 30,528 |
| 14 | BA | bat algorithm | 0,40526 | 0,59145 | 0,78330 | 1,78002 | 0,20664 | 0,12056 | 0,18499 | 0,51219 | 0,21305 | 0,07632 | 0,13816 | 0,42754 | 29,964 |
| 15 | CSS | charged system search | 0,56605 | 0,68683 | 1,00000 | 2,25289 | 0,13961 | 0,01853 | 0,11590 | 0,27404 | 0,07392 | 0,00000 | 0,02769 | 0,10161 | 28,825 |
| 16 | GSA | gravitational search algorithm | 0,70167 | 0,41944 | 0,00000 | 1,12111 | 0,31390 | 0,25120 | 0,23635 | 0,80145 | 0,42609 | 0,25525 | 0,00000 | 0,68134 | 28,518 |
| 17 | BFO | bacterial foraging optimization | 0,67203 | 0,28721 | 0,10957 | 1,06881 | 0,39364 | 0,18364 | 0,14700 | 0,72428 | 0,37392 | 0,24211 | 0,15058 | 0,76660 | 27,966 |
| 18 | EM | electroMagnetism-like algorithm | 0,12235 | 0,42928 | 0,92752 | 1,47915 | 0,00000 | 0,02413 | 0,24828 | 0,27240 | 0,00000 | 0,00527 | 0,08689 | 0,09216 | 19,030 |
| 19 | SFL | shuffled frog-leaping | 0,40072 | 0,22021 | 0,24624 | 0,86717 | 0,19981 | 0,02861 | 0,01888 | 0,24729 | 0,19565 | 0,04474 | 0,05280 | 0,29320 | 13,588 |
| 20 | SA | simulated annealing | 0,36938 | 0,21640 | 0,10018 | 0,68595 | 0,20341 | 0,07832 | 0,07964 | 0,36137 | 0,16956 | 0,08422 | 0,08307 | 0,33685 | 13,295 |
| 21 | MA | monkey algorithm | 0,33192 | 0,31029 | 0,13582 | 0,77804 | 0,09927 | 0,05443 | 0,06358 | 0,21729 | 0,15652 | 0,03553 | 0,08527 | 0,27731 | 11,903 |
| 22 | FSS | fish school search | 0,46812 | 0,23502 | 0,10483 | 0,80798 | 0,12730 | 0,03458 | 0,04638 | 0,20827 | 0,12175 | 0,03947 | 0,06588 | 0,22710 | 11,537 |
| 23 | IWDm | intelligent water drops M | 0,26459 | 0,13013 | 0,07500 | 0,46972 | 0,28358 | 0,05445 | 0,04345 | 0,38148 | 0,22609 | 0,05659 | 0,04039 | 0,32307 | 10,675 |
| 24 | PSO | particle swarm optimisation | 0,20449 | 0,07607 | 0,06641 | 0,34696 | 0,18734 | 0,07233 | 0,15473 | 0,41440 | 0,16956 | 0,04737 | 0,01556 | 0,23250 | 8,423 |
| 25 | RND | random | 0,16826 | 0,09038 | 0,07438 | 0,33302 | 0,13381 | 0,03318 | 0,03356 | 0,20055 | 0,12175 | 0,03290 | 0,03915 | 0,19380 | 5,097 |
| 26 | GWO | grey wolf optimizer | 0,00000 | 0,00000 | 0,02093 | 0,02093 | 0,06514 | 0,00000 | 0,00000 | 0,06514 | 0,23478 | 0,05789 | 0,02034 | 0,31301 | 1,000 |
Conclusiones
A partir de los experimentos realizados y los resultados analizados, podemos extraer las siguientes conclusiones:
- El nuevo algoritmo de recocido isotrópico simulado (SIA) muestra resultados impresionantes en la optimización de funciones con múltiples variables, y esto indica la eficacia del algoritmo para encontrar soluciones óptimas en espacios de alta dimensionalidad.
- El algoritmo funciona especialmente bien con funciones que poseen características nítidas y discretas. Esto puede deberse al hecho de que SIA nos permite explorar uniformemente el espacio de soluciones y encontrar puntos óptimos, incluso en dominios complejos e irregulares.
- En general, el nuevo algoritmo SIA supone una potente herramienta de optimización. Gracias a la acertada combinación de estrategias de búsqueda, el algoritmo presenta propiedades cualitativamente nuevas y demuestra una gran eficacia a la hora de buscar soluciones óptimas.
El nuevo algoritmo SIA solo tiene dos parámetros, la temperatura y el coeficiente de difusión, además del tamaño de la población, en lugar de tres como ocurría en el SA. Además, el parámetro de temperatura resulta ahora muy fácil de entender, se expresa en partes de alguna temperatura abstracta y por defecto es 0,01.
Basándonos en la investigación realizada y en el análisis de los resultados, podemos recomendar con confianza el algoritmo SIA para su uso en el entrenamiento de redes neuronales, en tareas comerciales con muchos parámetros y en problemas combinatorios complejos.
Figura 2. Gradación por colores de los algoritmos según sus respectivas pruebas.
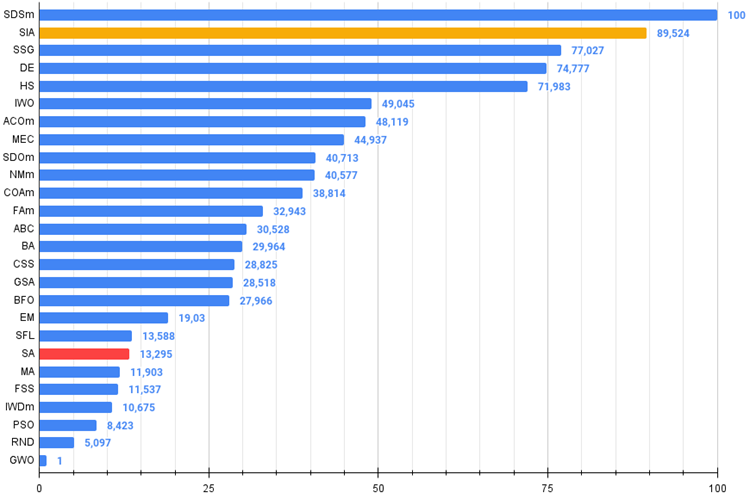
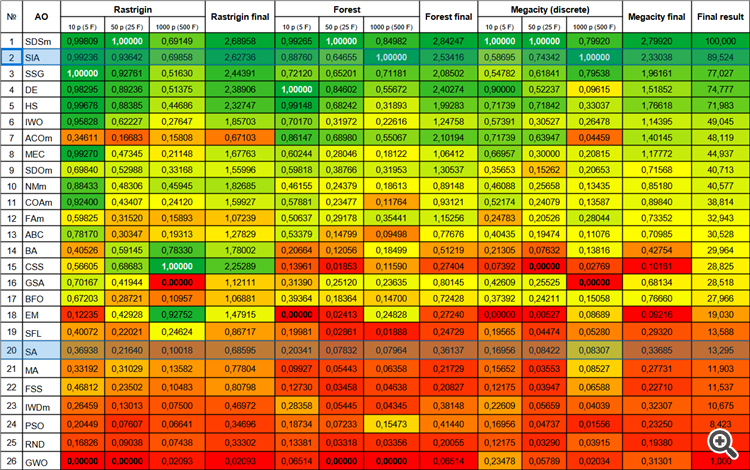
Figura 3. Histograma de los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor,
en el archivo hay un script para calcular la tabla de clasificación según la metodología de este artículo).
Ventajas e inconvenientes del algoritmo de recocido isotrópico simulado (SIA):
- Número mínimo de parámetros externos.
- Alta eficiencia en una gran variedad de tareas.
- Bajo gasto de recursos informáticos.
- Facilidad de aplicación del algoritmo.
- Resistencia a atascarse.
- Buenos resultados en funciones discretas tanto suaves como complejas.
- Alta convergencia.
- No se han detectado.
Adjuntamos al artículo un archivo con las versiones reales actualizadas de los códigos de los algoritmos descritos en los artículos anteriores. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/13870
Aprendizaje automático y Data Science (Parte 16): Una nueva mirada a los árboles de decisión
Asesor Experto Grid-Hedge Modificado en MQL5 (Parte I): Creamos un sencillo asesor de cobertura
Cómo ganar dinero ejecutando encargos en el servicio "Freelance"
Paradigmas de programación (Parte 1): Enfoque procedimental para el desarrollo de un asesor basado en la dinámica de precios
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso