
Búsqueda con restricciones — Tabu Search (TS).
Contenido
Introducción
El algoritmo funciona de la forma siguiente: comienza seleccionando una solución inicial y, a continuación, investiga las opciones vecinas, dando preferencia a las que mejoran el resultado actual. Para evitar volver a soluciones fallidas que ya se han explorado, se utiliza una lista tabú, una estructura que recoge los movimientos "prohibidos". Esto evita procesos cíclicos y permite explorar el espacio de búsqueda de manera más eficiente. Por ejemplo, en el problema de la mochila, el algoritmo puede añadir o eliminar elementos alternativamente en un intento de maximizar su valor, evitando al mismo tiempo volver a combinaciones analizadas anteriormente.
La base de la búsqueda tabú es la memoria adaptativa, que no solo evita volver a soluciones ya encontradas, sino que también gestiona el proceso de búsqueda considerando los pasos anteriores. Otros investigadores, como Manuel Laguna y Rafael Martí, han trabajado posteriormente en el desarrollo de este algoritmo, ampliando enormemente su aplicación en campos que abarcan desde la planificación de la producción hasta el análisis financiero y las telecomunicaciones. La búsqueda tabú sigue siendo una herramienta relevante para resolver problemas combinatorios complejos que requieren análisis profundos y cálculos complejos.
La búsqueda tabú es, por tanto, un excelente ejemplo de cómo las ideas innovadoras pueden transformar las técnicas de optimización de la búsqueda, abriendo nuevas oportunidades en la ciencia y la ingeniería. Aunque el algoritmo se desarrolló originalmente para resolver problemas combinatorios específicos como el problema del viajante de comercio y el problema de la mochila, en el artículo se analiza una modificación del algoritmo clásico que permite resolver problemas de optimización más generales, incluidos problemas en el espacio de búsqueda continua.
Implementación del algoritmo
Hoy analizaremos las fórmulas generales y los mecanismos utilizados en el algoritmo de búsqueda tabú para resolver problemas de optimización combinatoria (la versión clásica del algoritmo):
1. Formulación general del problema de optimización:
- Optimización f (x) - función objetivo.
- x ∈ X, donde X es el conjunto de restricciones sobre el vector de variables x.
2. Vecindad de las soluciones:
- N (x) - conjunto de soluciones alcanzables desde la solución actual x con un único "movimiento".
- N* (x) - vecindad modificada que considera el historial de búsqueda (memoria a corto y largo plazo).
3. Memoria a corto plazo:
- Seguimiento de los atributos (características de las decisiones) que han cambiado en el pasado reciente.
- Prohibición de visitar soluciones que contengan atributos "tabú-activos".
4. Memoria a largo plazo:
- Recuento de las frecuencias de cambio/presencia de atributos en las soluciones visitadas.
- Uso de estas frecuencias para gestionar la diversificación de las búsquedas.
5. Intensificación:
- Selección del mejor movimiento de una vecindad modificada N* (x).
- Regreso a las zonas prometedoras del espacio de soluciones.
6. Diversificación:
- Selección de movimientos que introducen nuevos atributos no encontrados anteriormente.
- Búsqueda de direcciones en una zona distinta de las ya investigadas.
7. Fluctuaciones estratégicas:
- Modificación de las reglas de selección de movimientos al acercarse al "nivel crítico".
- Transición a través de este nivel seguida de un retorno.
8. Encadenamiento de trayectorias:
- Generación de trayectorias que conecten soluciones de referencia de alta calidad.
- Selección de movimientos que acerquen lo más posible la solución actual a las soluciones guía.
Para los problemas de optimización, omitiremos el punto 8 y nos centraremos en la idea principal del algoritmo, intentando implementar una modificación de la búsqueda tabú, manteniendo los puntos 1-7 en la medida de lo posible. El algoritmo original trabaja con soluciones discretas intentando encontrar la trayectoria más corta entre nodos. Para adaptarlo a problemas en un espacio de búsqueda continuo, deberemos discretizar de algún modo las regiones admisibles para cada parámetro optimizado. El problema es que no podemos etiquetar todas las soluciones posibles, ya que el número de etiquetas sería colosal, lo cual haría casi imposible una solución.
En lugar de una lista tabú, introduciremos los conceptos de "lista blanca" y "lista negra" para cada parámetro, dividiendo sus rangos en sectores (un número determinado de sectores para cada parámetro a optimizar). De esta forma, podremos añadir una "etiqueta" a la lista blanca cuando una solución tenga éxito y una etiqueta a la lista negra si la solución no ha mejorado con respecto al paso anterior. Los sectores con soluciones prometedoras acumularán etiquetas, lo cual permitirá explorar más a fondo la zona y perfeccionar la solución. No obstante, un sector exitoso también puede contener soluciones muy poco exitosas, en cuyo caso el etiquetado de ese sector se incluirá en la lista negra. Esto significa que un mismo sector puede contener etiquetas incluidas tanto en la lista blanca como en la negra.
La selección de sectores para generar la siguiente solución deberá hacerse con una probabilidad proporcional al número de etiquetas de la lista blanca. Tras generar una nueva solución, cotejaremos el sector correspondiente con la lista negra y calcularemos una probabilidad proporcional a las etiquetas de la lista negra como fracción de la suma con las etiquetas de la lista blanca. Si se cumple la probabilidad, elegiremos otro sector al azar.
Así, dadas las características superficiales de la función optimizada, el algoritmo genera dinámicamente probabilidades para explorar todas las regiones disponibles en el espacio de búsqueda sin detenerse en ningún sector concreto. Aunque el algoritmo acabe cerca de la solución óptima global, no puede mejorar los resultados de manera indefinida. Esto, a su vez, provocará un aumento de las etiquetas en la lista negra de ese sector, cual obligará al algoritmo a cambiar de sector y seguir buscando en otras zonas del hiperespacio.
Tal y como está concebido, dicho enfoque permitirá diversificar el perfeccionamiento de las soluciones encontradas y realizar una amplia investigación de los problemas. Esto también debería minimizar el número de parámetros externos del algoritmo, confiriéndole propiedades de autoadaptación a la función del problema investigado.
Vamos a destacar los puntos principales de la idea de una realización modificada de la búsqueda tabú clásica:
1. Discretización. La división del espacio de búsqueda en sectores permite explorar zonas con mayor eficacia.
2. Listas blancas y listas negras. Las soluciones acertadas y fallidas se registran por separado, lo cual permite un seguimiento dinámico de las perspectivas de los sectores.
3. Exploración dinámica. El algoritmo genera probabilidades para explorar todas las zonas disponibles, evitando quedarse atascado en sectores ineficientes.
4. Adaptabilidad. El algoritmo reacciona a la acumulación de etiquetas en la lista negra, lo cual le hace cambiar la dirección de su búsqueda y garantizar la diversificación.
Así, nuestra versión del algoritmo combina elementos de búsqueda con restricciones (búsqueda tabú) y algoritmos evolutivos. El algoritmo usa un mecanismo de memoria en forma de listas blancas y negras para guiar la búsqueda hacia regiones prometedoras del espacio de soluciones y evitar las regiones que han conducido al empeoramiento de la solución.
Para mayor claridad, vamos a representar esquemáticamente las listas blancas y negras de los sectores para cada una de las coordenadas. Como ejemplo, tomaremos tres coordenadas, cada una de ellas dividida en 4 sectores. Las listas blancas y negras se registrarán por separado para cada coordenada.
Por ejemplo, para la coordenada "0" en el sector "3)" tendremos cinco "marcas" en la lista blanca, que será el número más alto entre todos los sectores de esta coordenada. Y esto significa que en la siguiente iteración se seleccionará el sector con mayor probabilidad. Sin embargo, el mismo sector tiene seis "marcas" en la lista negra, lo cual aumentará la probabilidad de que sea sustituido al generar una nueva solución, a pesar de ser considerado el más prometedor. Así, puede darse la situación de que un sector con menor potencial tenga menos probabilidades de ser sustituido por otro a la hora de seleccionar los sectores (esto no resulta evidente a primera vista).
Como podemos ver, se da un reequilibrio constante de las probabilidades a medida que se explora el espacio de búsqueda, lo cual permite considerar características superficiales. Este rumbo parece muy prometedor, ya que depende poco de los parámetros externos del algoritmo, lo cual hace que resulte verdaderamente autoadaptativo.
0: |0)____VVV_____|1)____VV______|2)_____V______|3)____VVVVV____| 1: |0)_____VV_____|1)_____V______|2)____VVV_____|3)_____VVV_____| 2: |0)______V_____|1)____VVV_____|2)_____V______|3)_____VVV_____| 0: |0)_____ХХХ____|1)_____ХХ_____|2)_____XX_____|3)____XXXXXX___| 1: |0)______X_____|1)_____XXX____|2)____XXXXX___|3)______X______| 2: |0)_____XX_____|1)_____XXXX___|2)______X_____|3)____XXXXX____|
Ahora podemos componer el pseudocódigo de una versión modificada del algoritmo, que denotaremos como TSm:
1. Inicialización de la población:
Para cada agente de la población:
Establecemos coordenadas aleatorias dentro del rango especificado.
Establecemos el valor inicial de la aptitud anterior como el valor mínimo posible.
2. Ciclo principal del algoritmo:
Hasta que se alcance la condición de finalización, repetimos:
a) Si se trata de la primera iteración:
Realizamos la inicialización inicial de la población.
b) En caso contrario:
Generamos nuevas coordenadas para los agentes:
Para cada agente y cada coordenada:
Con cierta probabilidad copiamos la coordenada de la mejor solución conocida.
De lo contrario:
Seleccionamos un sector de la lista blanca del agente.
Generamos una nueva coordenada en este sector.
Si el sector seleccionado está en la lista negra, seleccionamos un sector aleatorio y generamos una coordenada en él.
Comprobamos que la nueva coordenada no supere el rango aceptable.
c) Evaluamos la aptitud de cada agente con las nuevas coordenadas.
d) Actualizamos las listas negras y blancas:
Para cada agente:
Comparamos la idoneidad actual con la anterior.
Si la idoneidad ha mejorado, aumentamos el contador en la lista blanca del sector correspondiente.
Si empeora, aumentamos el contador de la lista negra.
Mantenemos la idoneidad actual como la idoneidad previa para la siguiente iteración.
e) Actualizamos la mejor solución encontrada si se encuentra un agente con mejor aptitud.
3. Al final del ciclo, retornamos la mejor solución encontrada.
Ahora vamos a escribir el código. Primero describiremos dos estructuras: "S_TSmSector" y "S_TSmAgent"; se utilizan para trabajar con los sectores y los agentes en la estrategia de búsqueda.
1. S_TSmSector - la estructura contiene un array de enteros "sector []", que almacenará las "marcas" para el sector correspondiente (es esencialmente un array de contadores).
2. S_TSmAgent - esta estructura es más compleja, describe el agente de búsqueda en el algoritmo, e incluye:
- blacklist [] - array de listas negras por sectores para cada coordenada.
- whitelist [] - array de listas blancas por sector para cada coordenada.
- fPrev - la variable almacena el valor de aptitud anterior del agente.
El método "Init" inicializa una instancia "S_TSmAgent". Parámetros:
- coords - número de coordenadas.
- sectorsPerCord - número de sectores por cada coordenada.
Lógica:
1. Redimensiona los arrays "blacklist" y "whitelist" al número de coordenadas.
2. Inicialización de cada sector del ciclo por todas las coordenadas:
- Cambiamos el tamaño del array "sector" para la lista negra de la coordenada actual.
- Lo mismo ocurre con la lista blanca.
- Inicializamos todos los elementos de las listas blanca y negra con ceros (son contadores que se incrementarán en uno más adelante).
3. La inicialización "fPrev" establece el valor "fPrev" en "-DBL_MAX", que representa el valor mínimo posible. Se usa para indicar que el agente aún no se ha adaptado.
El código crea una estructura de agentes que puede gestionar las listas negras y blancas para sectores de diferentes dimensiones del espacio de búsqueda donde es necesario llevar un registro de los sectores permitidos y denegados para los agentes visitantes.
//—————————————————————————————————————————————————————————————————————————————— struct S_TSmSector { int sector []; }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— struct S_TSmAgent { S_TSmSector blacklist []; //black list by sectors of each coordinate S_TSmSector whitelist []; //white list by sectors of each coordinate double fPrev; //previous fitness void Init (int coords, int sectorsPerCord) { ArrayResize (blacklist, coords); ArrayResize (whitelist, coords); for (int i = 0; i < coords; i++) { ArrayResize (blacklist [i].sector, sectorsPerCord); ArrayResize (whitelist [i].sector, sectorsPerCord); ArrayInitialize (blacklist [i].sector, 0); ArrayInitialize (whitelist [i].sector, 0); } fPrev = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Describamos la clase "C_AO_TSm", que hereda de la clase básica "C_AO".
1. El constructor establece los valores iniciales de las variables:
- popSize - (tamaño de la población) igual a 50.
- sectorsPerCoord - (número de sectores por coordenada) igual a 100.
- bestProbab - (probabilidad de elegir la mejor solución) igual a 0,8.
- Crea e inicializa un array "params" con tres parámetros que se corresponden con las variables anteriores.
2. El método "SetParams" retorna los valores de los parámetros del array "params" a las variables de clase correspondientes.
3. El método "Init" inicializa el algoritmo con los rangos y pasos de búsqueda especificados.
4. El método Moving () se encarga de desplazar los agentes en el espacio de búsqueda, mientras que el método Revision () realiza la comprobación y actualización de las soluciones actuales utilizando la lógica de búsqueda tabú.
5. Miembros de la clase:
- S_Agent agents [] - array de agentes representan la resolución de problemas en el proceso de búsqueda.
6. Métodos privados:
- InitialisePopulation () - método para inicializar una población de agentes.
- UpdateLists () - método para actualizar las listas negras y blancas del sector para los agentes.
- GenerateNewCoordinates () - método para generar nuevas coordenadas durante el proceso de búsqueda.
- GetSectorIndex () - método para obtener el índice del sector basado en la coordenada y la dimensionalidad.
- ChooseSectorFromWhiteList () - método para seleccionar un sector de una lista blanca para un agente y dimensionalidad dados.
- GenerarCoordenadaEnSector () - método para generar una coordenada en un sector dado.
- IsInBlackList () - método para comprobar la ejecución de la probabilidad de seleccionar otro sector con influencia en la selección de listas blancas y negras.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_TSm : public C_AO { public: //-------------------------------------------------------------------- C_AO_TSm () { ao_name = "TSm"; ao_desc = "Tabu Search M"; ao_link = "https://www.mql5.com/en/articles/15654"; popSize = 50; sectorsPerCoord = 100; bestProbab = 0.8; ArrayResize (params, 3); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "sectorsPerCoord"; params [1].val = sectorsPerCoord; params [2].name = "bestProbab"; params [2].val = bestProbab; } void SetParams () { popSize = (int)params [0].val; sectorsPerCoord = (int)params [1].val; bestProbab = params [2].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); void Moving (); void Revision (); //---------------------------------------------------------------------------- int sectorsPerCoord; double bestProbab; S_TSmAgent agents []; private: //------------------------------------------------------------------- void InitializePopulation (); void UpdateLists (); void GenerateNewCoordinates (); int GetSectorIndex (double coord, int dimension); int ChooseSectorFromWhiteList (int agentIndex, int dimension); double GenerateCoordInSector (int sectorIndex, int dimension); bool IsInBlackList (int agentIndex, int dimension, int sectorIndex); }; //——————————————————————————————————————————————————————————————————————————————
Vamos a analizar el método "Init" de la clase "C_AO_TSm", que se encarga de inicializar el algoritmo de búsqueda tabú. Lo desglosaremos por elementos:
1. El método llama primero a "StandardInit", transmitiéndole los arrays de los valores mínimo y máximo y los pasos. Se trata de una inicialización estándar que establece los parámetros del algoritmo. A continuación, tiene lugar el redimensionamiento del array "agents" según el valor "popSize", se determina el número de agentes de la población. Luego se ejecuta un ciclo que itera cada agente del array "agents". Para cada agente, se llama al método "Init", que inicializa sus parámetros, como las coordenadas "coords" y el número de sectores por coordenada "sectorsPerCoord".
2. Si todos los pasos de inicialización se han realizado correctamente, el método retornará "true", indicando que el algoritmo se ha inicializado correctamente.
El método "Init" es clave para preparar el algoritmo de búsqueda tabú para su funcionamiento. Establece los rangos de búsqueda, inicializa el conjunto de agentes y prepara estos para seguir buscando soluciones. Si se produce un error en cualquier etapa de la inicialización, el método terminará su ejecución y retornará "false".
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_TSm::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (agents, popSize); for (int i = 0; i < popSize; i++) agents [i].Init (coords, sectorsPerCoord); return true; } //——————————————————————————————————————————————————————————————————————————————
Veamos ahora el método "Moving" de la clase "C_AO_TSm". Lógica del método:
- if (!revision) - aquí se comprueba la variable lógica "revision". Si es "false" (es decir, aún no se ha realizado ninguna inicialización), se ejecutará el siguiente bloque de código.
- InitializePopulation () - se encarga de inicializar la población de agentes.
En la segunda y siguientes iteraciones del algoritmo, se llama al método "GenerateNewCoordinates ()", que genera nuevas coordenadas (nuevas soluciones) para los agentes durante la búsqueda.
El métodoMoving controla el proceso de desplazamiento de los agentes en el algoritmo de búsqueda tabú. Primero comprueba si se ha efectuado la inicialización de la población. Si no se ha efectuado, inicializará la población; de lo contrario, el método generará nuevas coordenadas para los agentes.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSm::Moving () { //---------------------------------------------------------------------------- if (!revision) { InitializePopulation (); revision = true; return; } //---------------------------------------------------------------------------- GenerateNewCoordinates (); } //——————————————————————————————————————————————————————————————————————————————
El método "Revision" se encarga de actualizar la mejor solución actual en el proceso de búsqueda tabú. Itera todas las soluciones de la población, compara sus puntuaciones con el mejor valor actual y, si encuentra una solución mejor, actualizará las variables correspondientes. Al final del método, se actualizan la lista blanca y la lista negra, necesarias para la ejecución posterior del algoritmo.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSm::Revision () { //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c); } } //---------------------------------------------------------------------------- UpdateLists (); } //——————————————————————————————————————————————————————————————————————————————
El siguiente método "InitializePopulation" se encarga de inicializar la población de agentes de búsqueda tabú. Genera valores aleatorios para cada coordenada del agente dentro de los rangos dados, y establece un valor inicial para la valoración previa de cada agente. Esto es necesario para las iteraciones posteriores del algoritmo, en las que se estimarán y actualizarán las soluciones.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSm::InitializePopulation () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } agents [i].fPrev = -DBL_MAX; } } //——————————————————————————————————————————————————————————————————————————————
A continuación se ejecuta el método "UpdateLists" de la clase "C_AO_TSm". Lógica del método:
- El ciclo exterior itera todos los agentes de la población, donde "popSize" es el tamaño de la población.
- El ciclo interior itera todas las coordenadas de cada agente.
- Para cada coordenada "c" del agente "a [i]", se calcula el índice del sector usando el método "GetSectorIndex". Esto es necesario para clasificar los valores en sectores específicos para su posterior análisis.
- Si la puntuación actual de un agente "a[i].f" es superior a su puntuación anterior "agentes[i].fPrev", significará que el agente ha mejorado su decisión. En este caso, se incrementará el contador en la lista blanca "whitelist" del sector correspondiente.
- Si la puntuación actual es inferior a la anterior, significará que el agente ha empeorado su decisión y el contador en la lista negra "blacklist" del sector correspondiente aumentará.
- Una vez procesadas todas las coordenadas de un agente, su puntuación anterior se actualizará a la puntuación actual para poder compararla con el nuevo valor en la siguiente iteración.
El método "UpdateLists" se encarga de actualizar las listas (blancas y negras) de cada agente de la población según su puntuación actual y anterior. Esto permite al algoritmo de búsqueda tabú llevar un registro de los sectores que han tenido éxito (lista blanca) y de los que no (lista negra). Así, el método ayuda a gestionar mejor la búsqueda de soluciones evitando revisitar regiones ineficientes del espacio de soluciones.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSm::UpdateLists () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { int sectorIndex = GetSectorIndex (a [i].c [c], c); if (a [i].f > agents [i].fPrev) { agents [i].whitelist [c].sector [sectorIndex]++; } else if (a [i].f < agents [i].fPrev) { agents [i].blacklist [c].sector [sectorIndex]++; } } agents [i].fPrev = a [i].f; } } //——————————————————————————————————————————————————————————————————————————————
Ahora analizaremos el método "GenerateNewCoordinates" de la clase "C_AO_TSm". Lógica del método:
- El ciclo exterior itera todos los agentes de la población, donde "popSize" es el tamaño de la población.
- El ciclo interior itera todas las coordenadas de cada agente.
- En primer lugar, se comprueba la probabilidad usando el método "RNDprobab". Si se cumple la probabilidad, el agente obtendrá la coordenada de la mejor solución global "cB [c]".
- Si no se cumple la probabilidad, se seleccionará un sector de la lista blanca mediante el método "ChooseSectorFromWhiteList ()".
- A continuación, se genera una nueva coordenada en ese sector usando el método "GenerateCoordInSector ()".
- Si el sector seleccionado está en la lista negra, se seleccionará aleatoriamente un nuevo sector utilizando "u.RNDminusOne ()" y se generará una nueva coordenada en él.
- Comprueba si la nueva coordenada se encuentra dentro de los límites especificados y tiene el paso requerido.
El método "GenerateNewCoordinates" se encarga de generar nuevas coordenadas para cada agente de la población. Usa un enfoque probabilístico para elegir entre las mejores coordenadas conocidas, además de la generación aleatoria en sectores basados en listas blancas y listas negras. El método también garantiza la exactitud de las coordenadas comprobando su correspondencia con los límites dados.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSm::GenerateNewCoordinates () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { if (u.RNDprobab () < bestProbab) { a [i].c [c] = cB [c]; } else { int sectorIndex = ChooseSectorFromWhiteList (i, c); double newCoord = GenerateCoordInSector (sectorIndex, c); if (IsInBlackList (i, c, sectorIndex)) { sectorIndex = u.RNDminusOne (sectorsPerCoord); newCoord = GenerateCoordInSector (sectorIndex, c); } newCoord = u.SeInDiSp (newCoord, rangeMin [c], rangeMax [c], rangeStep [c]); a [i].c [c] = newCoord; } } } } //——————————————————————————————————————————————————————————————————————————————
Ahora analizaremos el código de la función "GetSectorIndex", que determina el índice de sector para una coordenada dada en una dimensión especificada. Función lógica:
- Si el valor máximo y mínimo del rango para una medición determinada son iguales, significará que el rango no tiene longitud. En este caso, la función retornará inmediatamente 0 porque no hay forma de dividir el rango en sectores.
- A continuación, se calcula la longitud de un sector "sL", que se obtiene dividiendo la longitud del rango por el número de sectores "sectorsPerCoord".
- El índice sectorial "ind" se calcula usando una fórmula que determina a qué sector pertenece una determinada coordenada. En primer lugar, se resta de la coordenada el valor mínimo del sector, luego el resultado se divide por la longitud del sector y el valor resultante se redondea al entero inferior más próximo.
- Si la coordenada es igual al valor máximo del rango, la función retornará el índice del último sector.
- Las comprobaciones posteriores garantizarán que el índice no esté fuera de los límites. Si el índice es mayor o igual que el número de sectores, se retornará el último sector. Si el índice es inferior a 0, se retornará 0.
//—————————————————————————————————————————————————————————————————————————————— int C_AO_TSm::GetSectorIndex (double coord, int dimension) { if (rangeMax [dimension] == rangeMin [dimension]) return 0; double sL = (rangeMax [dimension] - rangeMin [dimension]) / sectorsPerCoord; int ind = (int)MathFloor ((coord - rangeMin [dimension]) / sL); // Special handling for max value if (coord == rangeMax [dimension]) return sectorsPerCoord - 1; if (ind >= sectorsPerCoord) return sectorsPerCoord - 1; if (ind < 0) return 0; return ind; } //——————————————————————————————————————————————————————————————————————————————
Ahora pasaremos al método "ChooseSectorFromWhiteList", que selecciona un sector de una "lista blanca" de sectores para un agente y una dimensión determinados. El método retorna el índice del sector seleccionado. Lógica de funcionamiento del método:
- La variable "totalCount" se inicializa con cero. Se usa para contar el número total de "marcas" en los sectores de la lista blanca.
- Si "totalCount" es igual a cero, significará que los sectores aún no contienen "marcas" y todos los sectores son iguales. En este caso, el método seleccionará un sector al azar de entre todos los sectores disponibles y lo retornará.
- Acto seguido, se realiza un recuento acumulativo del número de "marcas" en un ciclo. Si el valor aleatorio "randomValue" es menor o igual que el valor acumulado actual, el método retornará el índice del sector actual "s". Esto le permitirá seleccionar un sector de forma proporcional a su peso en la lista blanca.
El método "ChooseSectorFromWhiteList" permite seleccionar un sector de una lista blanca para un agente basándose en una distribución de probabilidad que imita la selección de una ruleta.
//—————————————————————————————————————————————————————————————————————————————— int C_AO_TSm::ChooseSectorFromWhiteList (int agentIndex, int dimension) { int totalCount = 0; for (int s = 0; s < sectorsPerCoord; s++) { totalCount += agents [agentIndex].whitelist [dimension].sector [s]; } if (totalCount == 0) { int randomSector = u.RNDminusOne (sectorsPerCoord); return randomSector; } int randomValue = u.RNDminusOne (totalCount); int cumulativeCount = 0; for (int s = 0; s < sectorsPerCoord; s++) { cumulativeCount += agents [agentIndex].whitelist [dimension].sector [s]; if (randomValue <= cumulativeCount) { return s; } } return sectorsPerCoord - 1; } //——————————————————————————————————————————————————————————————————————————————
Vamos a analizar el método "GenerateCoordInSector", que genera una coordenada aleatoria en un sector dado para una dimensión dada. Lógica de funcionamiento del método:
- Calcula el tamaño del sector para la dimensión indicada.
- sectorStart se calcula como el valor mínimo del rango para esta dimensión más un desplazamiento igual al índice del sector multiplicado por el tamaño del sector. "sectorEnd" se define como "sectorStart" más "sectorSize". Esto definirá los límites del sector.
- A continuación, se llama la función "RNDfromCI", que genera un valor aleatorio entre "sectorStart" y "sectorEnd". Este valor representa la coordenada generada dentro del sector indicado.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_TSm::GenerateCoordInSector (int sectorIndex, int dimension) { double sectorSize = (rangeMax [dimension] - rangeMin [dimension]) / sectorsPerCoord; double sectorStart = rangeMin [dimension] + sectorIndex * sectorSize; double sectorEnd = sectorStart + sectorSize; double newCoord = u.RNDfromCI (sectorStart, sectorEnd); return newCoord; } //——————————————————————————————————————————————————————————————————————————————
Por último, desglosaremos el método "IsInBlackList", que comprueba si un agente está en la "lista negra" para un sector y dimensión determinados. Parámetros:
- agentIndex - índice del agente para el que se realiza la comprobación.
- dimension - índice de dimensión.
- sectorIndex - índice del sector que se está comprobando.
El método retornará "true" si el agente está en la lista negra y la probabilidad de cambio de sector se cumple considerando los "logros" del sector según la lista blanca.
- "blackCount" y "whiteCount" obtienen el número de registros en las listas negra y blanca respectivamente para el agente, la dimensión y el sector especificados.
- El número total de registros "totalCount" se calcula como la suma de los registros blancos y negros.
- Si el número total de registros es igual a cero, el método retornará directamente "false", lo cual significará que el agente no puede estar en la lista negra ya que no hay registros negros ni blancos.
- A continuación, se calcula la probabilidad de que este sector se considere en la lista negra. Esto se hace dividiendo el número de registros negros por el número total de registros.
- El método "RNDprobab ()" genera un número aleatorio entre 0 y 1. Si este número aleatorio es menor que la probabilidad calculada de la lista negra "blackProbability", el método retornará "true".
El método "IsInBlackList" considera tanto los registros negros como blancos para determinar la probabilidad de que un sector esté en la lista negra y haya que cambiarlo. Cuanto mayor sea el número de registros en la lista negra en comparación con los registros en la lista blanca, mayor será la probabilidad de cambiar posteriormente el sector por otro aleatorio.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_TSm::IsInBlackList (int agentIndex, int dimension, int sectorIndex) { int blackCount = agents [agentIndex].blacklist [dimension].sector [sectorIndex]; int whiteCount = agents [agentIndex].whitelist [dimension].sector [sectorIndex]; int totalCount = blackCount + whiteCount; if (totalCount == 0) return false; double blackProbability = (double)blackCount / totalCount; return u.RNDprobab () < blackProbability; } //——————————————————————————————————————————————————————————————————————————————
Resultados de las pruebas
Impresión del rendimiento del algoritmo TSm en las funciones de prueba:
TSm|Tabu Search M|50.0|100.0|0.8|
=============================
5 Hilly's; Func runs: 10000; result: 0.8779456463913048
25 Hilly's; Func runs: 10000; result: 0.6143121517195806
500 Hilly's; Func runs: 10000; result: 0.2910412462428753
=============================
5 Forest's; Func runs: 10000; result: 0.9288481105123887
25 Forest's; Func runs: 10000; result: 0.5184350456698835
500 Forest's; Func runs: 10000; result: 0.19054478009120634
=============================
5 Megacity's; Func runs: 10000; result: 0.6107692307692308
25 Megacity's; Func runs: 10000; result: 0.3821538461538462
500 Megacity's; Func runs: 10000; result: 0.1215692307692319
=============================
All score: 4.53562 (50.40%)
Podemos notar que el algoritmo TSm funciona bastante bien, con resultados decentes tanto en la impresión del trabajo sobre las funciones de prueba como en la visualización. Obviamente, existe una dispersión en las funciones con pequeña dimensionalidad, pero como usted habrá notado, muchos algoritmos están sujetos a este fenómeno. Observamos una buena capacidad del algoritmo para resaltar la mayoría de las regiones superficiales significativas de la función estudiada.
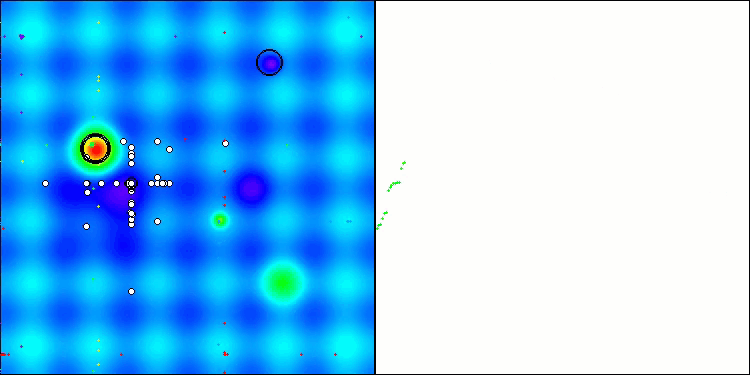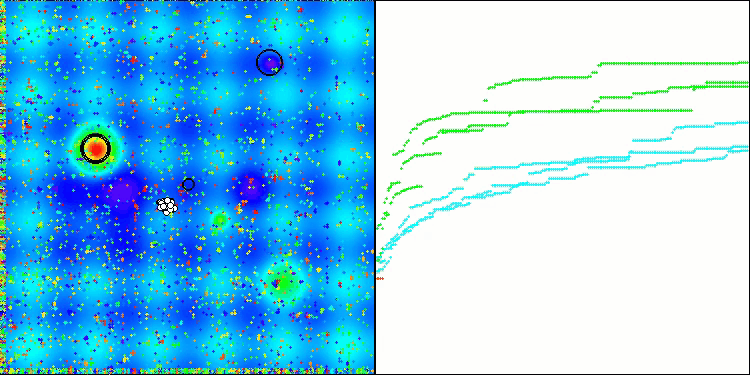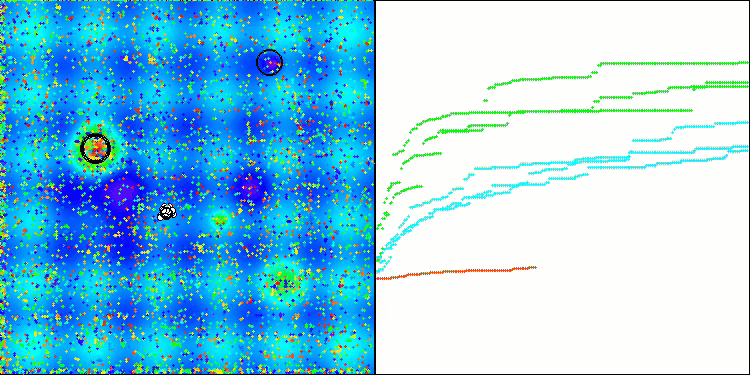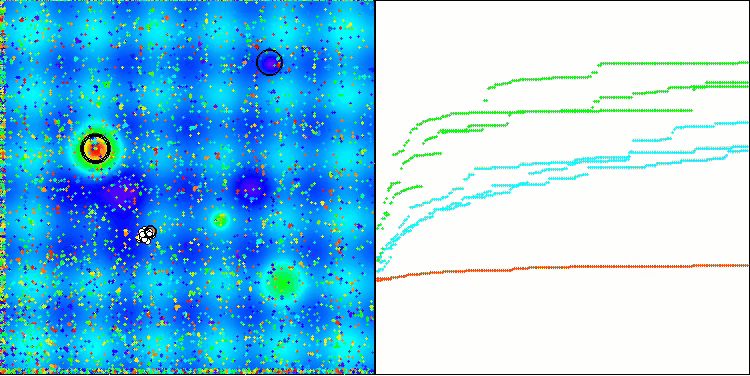
TSm en la función de prueba Hilly
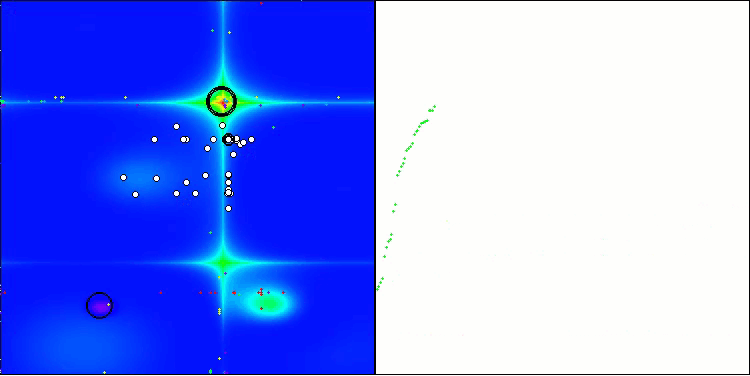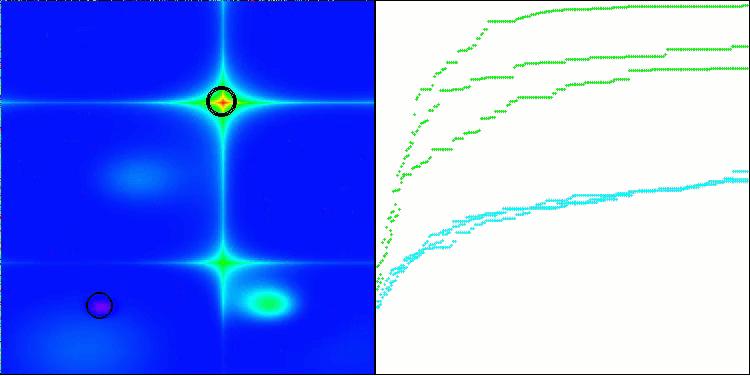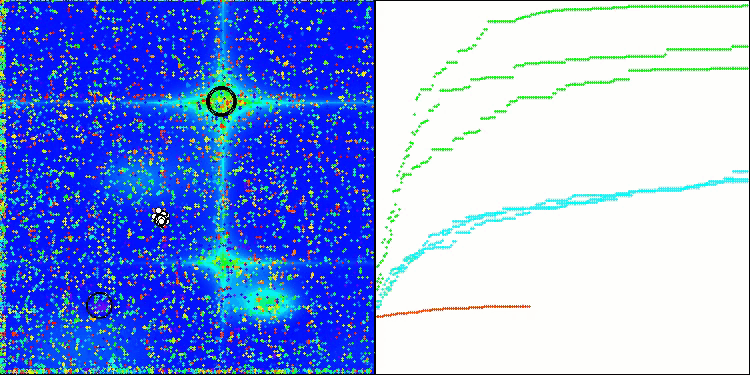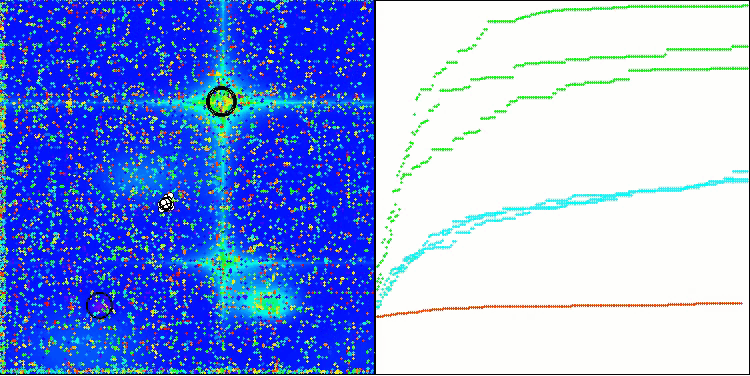
TSm en la función de prueba Forest
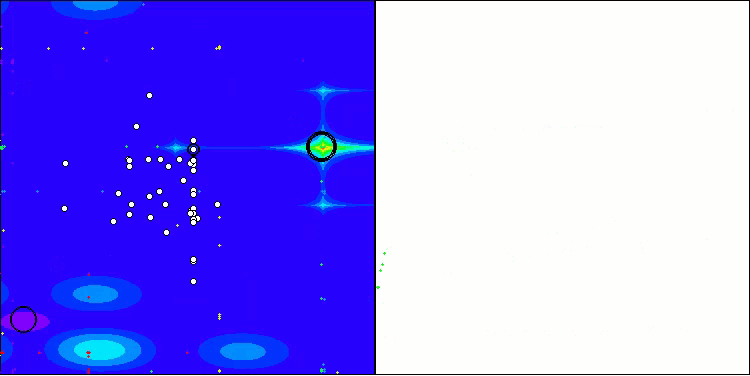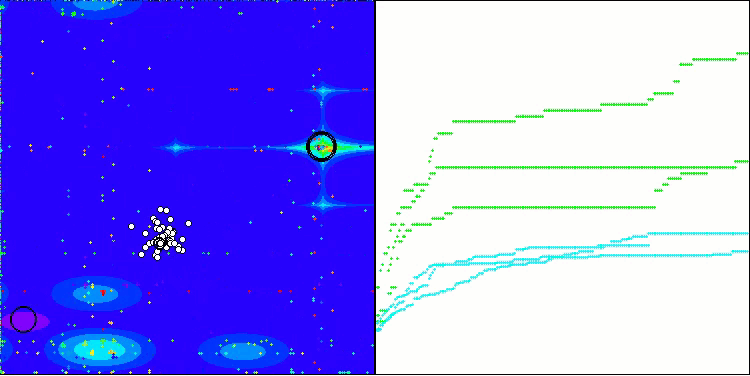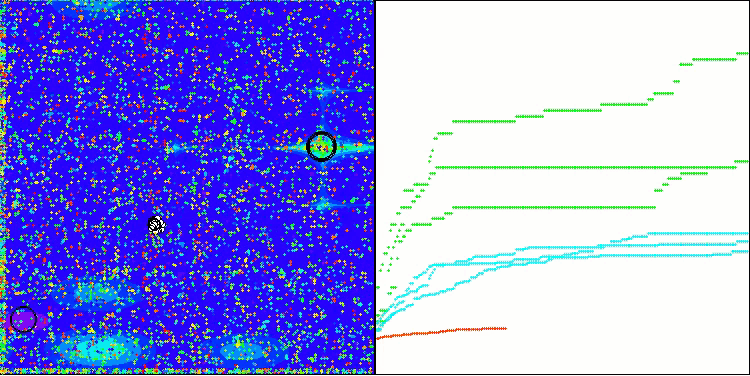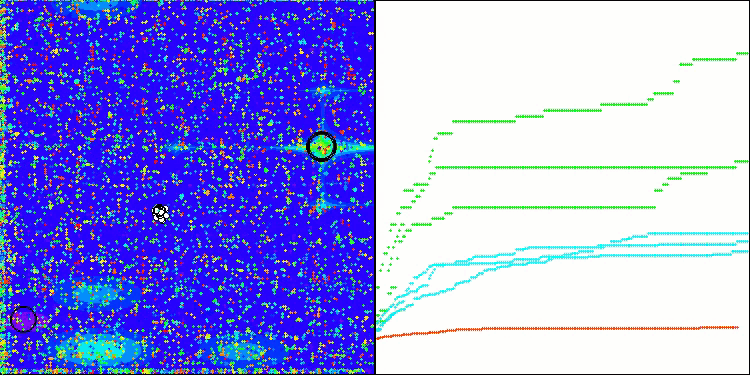
TSm en la función de prueba Megacity
Según los resultados de la prueba, el algoritmo TSm ocupa el puesto 18 en la tabla de clasificación de algoritmos de optimización, lo cual supone un resultado superior a la media.
№ | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration optimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | ESG | evolution of social groups | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 8 | SIA | simulated isotropic annealing | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 9 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 10 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 11 | TSEA | turtle shell evolution algorithm | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 12 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 13 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 14 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 15 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 16 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 17 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 18 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 19 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 20 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 21 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 22 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 23 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 24 | ABH | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4.127 | 45,85 |
| 25 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3.657 | 40,63 |
| 26 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 27 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 28 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 29 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 30 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 31 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 32 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 33 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 34 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 35 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 36 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 37 | AAA | algae adaptive algorithm | 0,50007 | 0,32040 | 0,25525 | 1,07572 | 0,37021 | 0,22284 | 0,16785 | 0,76089 | 0,27846 | 0,14800 | 0,09755 | 0,52402 | 2,361 | 26,23 |
| 38 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 39 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
| 40 | PSO | particle swarm Optimization | 0,59726 | 0,36923 | 0,29928 | 1,26577 | 0,37237 | 0,16324 | 0,07010 | 0,60572 | 0,25667 | 0,08000 | 0,02157 | 0,35823 | 2,230 | 24,77 |
| 41 | Boids | boids algorithm | 0,43340 | 0,30581 | 0,25425 | 0,99346 | 0,35718 | 0,20160 | 0,15708 | 0,71586 | 0,27846 | 0,14277 | 0,09834 | 0,51957 | 2,229 | 24,77 |
| 42 | MA | monkey algorithm | 0,59107 | 0,42681 | 0,31816 | 1,33604 | 0,31138 | 0,14069 | 0,06612 | 0,51819 | 0,22833 | 0,08567 | 0,02790 | 0,34190 | 2,196 | 24,40 |
| 43 | SFL | shuffled frog-leaping | 0,53925 | 0,35816 | 0,29809 | 1,19551 | 0,37141 | 0,11427 | 0,04051 | 0,52618 | 0,27167 | 0,08667 | 0,02402 | 0,38235 | 2,104 | 23,38 |
| 44 | FSS | fish school search | 0,55669 | 0,39992 | 0,31172 | 1,26833 | 0,31009 | 0,11889 | 0,04569 | 0,47467 | 0,21167 | 0,07633 | 0,02488 | 0,31288 | 2,056 | 22,84 |
| 45 | RND | random | 0,52033 | 0,36068 | 0,30133 | 1,18234 | 0,31335 | 0,11787 | 0,04354 | 0,47476 | 0,25333 | 0,07933 | 0,02382 | 0,35648 | 2,014 | 22,37 |
Conclusiones
Considerando los resultados del algoritmo en funciones de prueba de diferente dimensionalidad podemos notar que para el algoritmo resulta más difícil lidiar con problemas de gran dimensionalidad en la función suave "Hilly". En el resto de las pruebas, el algoritmo muestra resultados buenos y estables.
Esta modificación propuesta del conocido algoritmo Tabu Search, a diferencia de la versión original, puede utilizarse en cualquier problema general de optimización en espacios de búsqueda continuos, incluyendo tanto problemas suaves como discretos. El algoritmo puede servir de idea potente que usar como base en otros algoritmos. Para mejorar la precisión de la convergencia, podemos utilizar las técnicas empleadas en los algoritmos comentados anteriormente, pero en esta fase presentamos la modificación "tal cual".
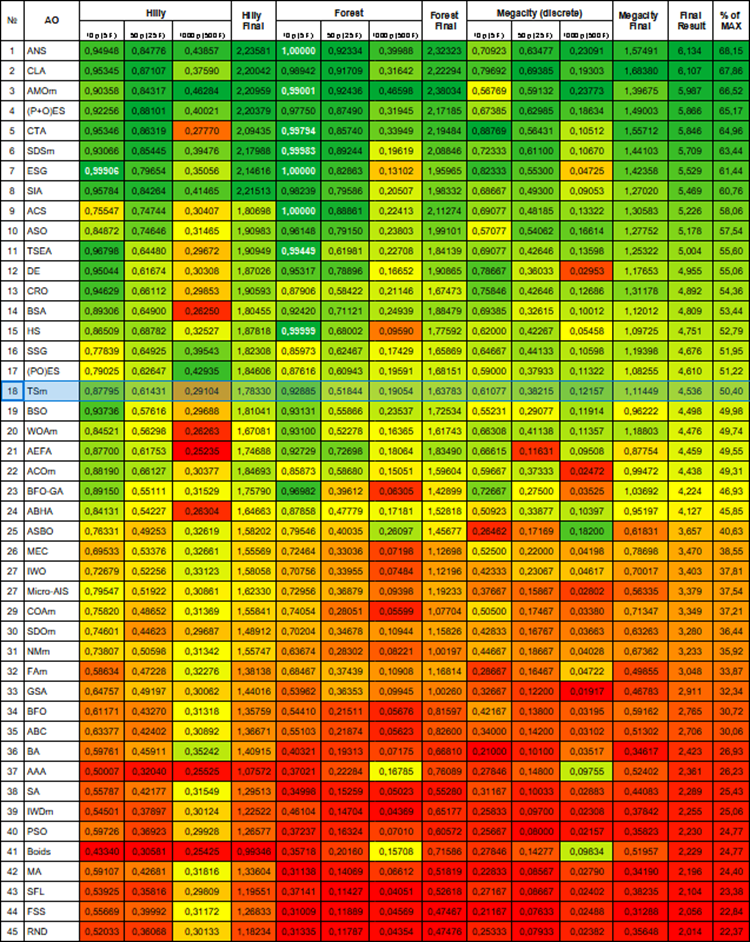
Figura 1. Gradación por colores de los algoritmos según sus respectivas pruebas. Resaltados en blanco, podemos ver los resultados superiores o iguales a 0,99
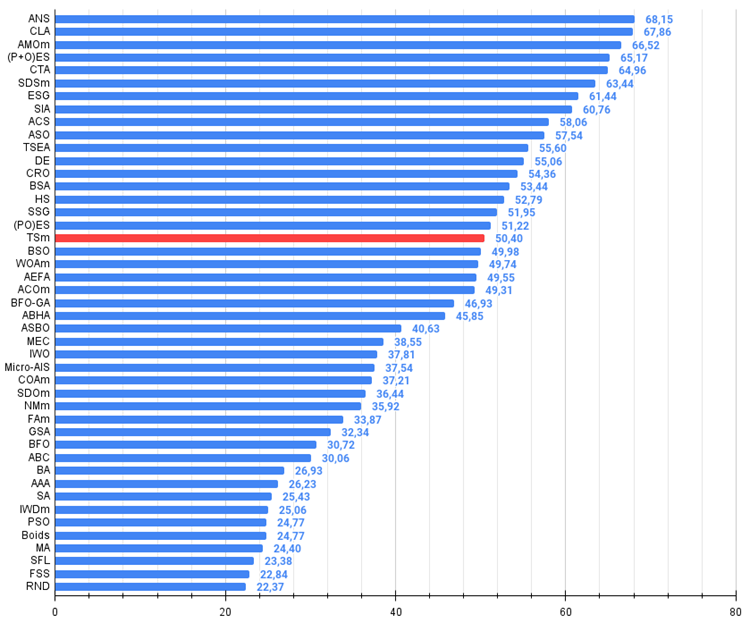
Figura 2. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor,
donde 100 es el máximo resultado teórico posible; el script para calcular la tabla de clasificación está en el archivo)
Ventajas e inconvenientes del algoritmo TSm:
Ventajas:
- Supone una idea prometedora que mejorar y utilizar como base en nuevos algoritmos.
- Buena escalabilidad.
- Número reducido de parámetros intuitivos (apenas dos, sin considerar la selección del tamaño de la población).
Desventajas:
- La precisión de la convergencia debería ser mayor.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15654
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Gráficos del índice del dólar y del índice del euro — ejemplo de servicio en MetaTrader 5
Gráficos del índice del dólar y del índice del euro — ejemplo de servicio en MetaTrader 5
 Algoritmo de optimización de sociedad anárquica (Anarchic Society Optimization, ASO)
Algoritmo de optimización de sociedad anárquica (Anarchic Society Optimization, ASO)
 Métodos de William Gann (Parte II): Creación del indicador Cuadrado de Gann
Métodos de William Gann (Parte II): Creación del indicador Cuadrado de Gann
 Redes neuronales en el trading: Transformador vectorial jerárquico (HiVT)
Redes neuronales en el trading: Transformador vectorial jerárquico (HiVT)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso