Бильярдный алгоритм оптимизации — Billiards Optimization Algorithm (BOA)
371
0
Содержание
Введение
В мире оптимизационных алгоритмов, где математическая точность встречается с вдохновением из реального мира, рождаются подходы, поражающие своей изобретательностью. Один из таких методов — бильярдный алгоритм оптимизации (Billiards Optimization Algorithm, BOA), черпающий идеи для стратегии поиска из механики классической игры в бильярд.
Представьте себе бильярдный стол, где каждая луза является потенциальным решением, а шары — это искатели этих решений, движущиеся по пространству возможностей. Как опытный игрок в бильярд рассчитывает траекторию шара для точного попадания в лузу, так и BOA направляет свои решения к наилучшим результатам через итеративный процесс поиска и уточнения. Этот алгоритм, разработанный исследователями Хади Гиви и Мари Хубаловской в 2023 году, демонстрирует интересный и необычный подход для решения оптимизационных задач.
В данной статье мы погрузимся в концептуальную основу BOA, исследуем его математическую модель и проанализируем его эффективность в решении мультимодальных задач. Алгоритм, сочетающий простоту концепции с математической точностью, открывает новые горизонты в области вычислительной оптимизации и представляет собой ценное дополнение к арсеналу современных методов оптимизации.
Реализация алгоритма
Алгоритм BOA — это метод оптимизации, вдохновленный игрой в бильярд. Его суть заключается в следующем, представьте, что вы ищете наилучшее решение какой-то задачи, в бильярдной терминологии, это как попытка загнать шар в лузу. На бильярдном столе есть 8 луз, а также множество шаров. В начале работы алгоритма создается группа случайных решений (популяция). Эти решения — как шары на бильярдном столе. Для каждого решения вычисляется значение целевой функции, чтобы определить, насколько оно хорошо.
На каждой итерации алгоритма восемь лучших решений из популяции становятся "лузами" (целями, к которым нужно стремиться). Остальные решения рассматриваются как шары, которые нужно направить к этим лузам. Для каждого шара (решения) случайным образом выбирается одна из луз (лучших решений). Затем вычисляется новое положение шара — новое решение, двигающееся в направлении выбранной лузы. Если новое положение шара дает лучшее значение целевой функции, то шар перемещается в новое положение, а если нет, то он остается на месте.
Математически это выглядит таким образом:
X_new = X + rnd [0.0; 1.0] × (P - I × X)
где:
- X_new — новое положение шара,
- X — текущее положение шара,
- P — положение лузы (или шар, по которому должен ударить текущий шар),
- I — случайный выбор из чисел 1 или 2.
Процесс повторяется много раз, и в итоге шары (решения) должны приблизиться к оптимальному решению задачи.
Преимущество BOA может заключаться в том, что он теоретически должен хорошо балансировать, только лишь за счет одного коэффициента в формуле, между глобальным поиском и локальным поиском. Это достигается за счет случайного коэффициента "I", который обеспечивает либо "недолет" шара (уточнение решений вблизи хороших точек), либо "перелет" (исследование разных областей пространства решений).
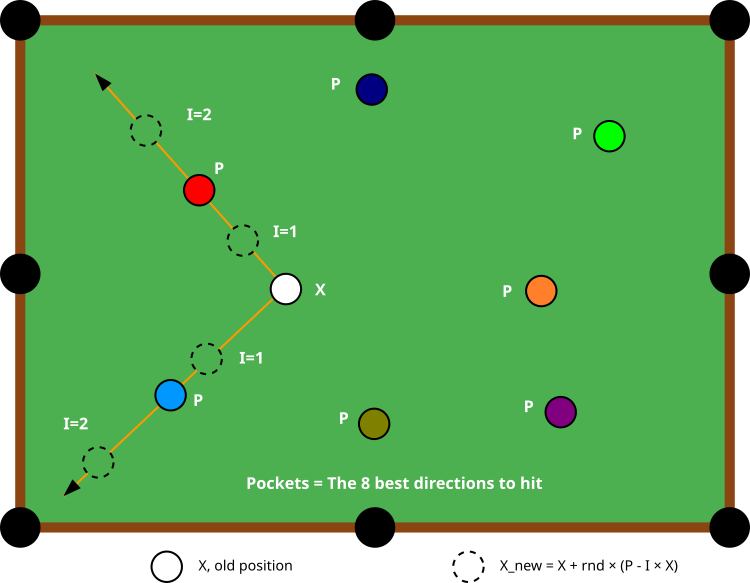
Рисунок 1. Схема работы алгоритма BOA
На рисунке 1 схематично показан принцип работы алгоритма BOA. Центральный элемент — белый шар с маркировкой "X" — представляет текущую позицию агента в пространстве поиска решений. Вокруг этого шара расположены цветные шары с меткой "P" — это "карманы" или "лузы", представляющие 8 лучших решений, найденных на данный момент. Схема демонстрирует, как агент (белый шар) может обновлять свою позицию, двигаясь к различным карманам, а именно, для каждого шага агент случайным образом выбирает один из восьми карманов, как целевое направление движения.
Оранжевые линии со стрелками показывают возможные траектории движения агента к различным карманам (в данном случае к красному, голубому). Пунктирные круги обозначают промежуточные позиции, которые агент может принять при движении, в зависимости от значения "I" (1 или 2). Значение "I" меняет "силу удара" и характер движения: при I=1 позиция смещается в направлении выбранного кармана, а при I=2 агент может совершать более резкие движения, что способствует исследованию большей части пространства решений.
Когда мы полностью выяснили, как работает алгоритм, приступим к написанию псевдокода BOA.
Инициализация
Определяем количество шаров (popSize) и карманов (numPockets).
Создаем популяцию шаров (агентов).
Устанавливаем пространство поиска с минимальными и максимальными границами.
Основной алгоритм
Первый этап: Начальная инициализация (выполняется только один раз)
Для каждого шара в популяции:
Случайно размещаем шары в пространстве поиска.
Сохраняем его начальную позицию.
Устанавливаем начальные значения функции приспособленности в минимальные.
Второй этап: Перемещение шаров
Для каждого шара в популяции:
Для каждой координаты шара:
Выбираем случайный карман (один из numPockets лучших решений).
Обновляем позицию шара по формуле: X_new = X + rnd [0.0; 1.0] × (P - I × X)
Проверяем, чтобы новая позиция оставалась в допустимых границах.
Третий этап: Обновление лучших решений
Для каждого шара:
Если значение функции приспособленности шара лучше глобального лучшего, обновляем глобальное лучшее.
Если значение функции приспособленности шара лучше его собственного лучшего, обновляем его лучшее.
Сортируем шары по их лучшим значениям функции приспособленности.
Первые numPockets агентов после сортировки становятся карманами для следующей итерации.
Повторяем этапы "Перемещение шаров" и "Обновление лучших решений" до тех пор, пока не будет достигнуто условие остановки (например, максимальное число итераций).
Приступаем к написанию кода алгоритма. Класс "C_AO_BOA" является производным от класса "C_AO" (базовый класс популяционных алгоритмов оптимизации) и реализует алгоритм оптимизации BOA. Давайте рассмотрим его ключевые элементы:
- popSize устанавливается в 50, означает количество шаров (агентов) в алгоритме.
- numPockets устанавливается в 8, образует число карманов на бильярдном столе.
- Размер массива "params" изменяется, и два параметра (popSize и numPockets) добавляются в массив "params".
- SetParams () — метод отвечает за установку параметров из массива "params" обратно в локальные переменные "popSize" и "numPockets".
- Init () — метод инициализации настраивает минимальные, максимальные значения и шаги для поиска, а также устанавливает количество эпох.
- Moving () — отвечает за движение шаров в алгоритме.
- Revision () — выполняет проверку и пересмотр позиций/решений агентов.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BOA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_BOA () { } C_AO_BOA () { ao_name = "BOA"; ao_desc = "Billiards Optimization Algorithm"; ao_link = "https://www.mql5.com/ru/articles/17325"; popSize = 50; // число шаров (агентов) numPockets = 8; // число карманов на бильярдном столе ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "numPockets"; params [1].val = numPockets; } void SetParams () { popSize = (int)params [0].val; numPockets = (int)params [1].val; } bool Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0); // количество эпох void Moving (); void Revision (); //---------------------------------------------------------------------------- int numPockets; // число карманов (лучших решений) private: //------------------------------------------------------------------- }; //——————————————————————————————————————————————————————————————————————————————
Метод "Init" в классе "C_AO_BOA" отвечает за инициализацию алгоритма BOA. В начале метода вызывается функция "StandardInit ()", передавая ей массивы минимальных и максимальных значений, а также шагов. Эта функция отвечает за выполнение общих действий и инициализаций, которые должны быть выполнены для всех производных классов алгоритмов оптимизации (включая начальную настройку диапазонов), а также подготовку базовых агентов поиска в алгоритме. Если "StandardInit ()" возвращает "false" (инициализация прошла неудачно), то метод "Init" также возвращает "false". Если все прошло успешно, метод возвращает "true".
//—————————————————————————————————————————————————————————————————————————————— //--- Инициализация bool C_AO_BOA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- return true; } //——————————————————————————————————————————————————————————————————————————————
Метод "Moving" реализует основной шаг алгоритма BOA и управляет перемещением агентов (шаров), в пространстве решений. Сначала проверяется условие "if (!revision)", что позволяет определить, вызывается ли метод в первый раз. Если "revision=false", необходимо инициализировать позиции агентов. Для этого выполняется цикл по всем агентам, определенным как "popSize", в рамках которого выполняется вложенный цикл по координатам, задающим параметры решений каждого агента.
На этапе генерации начальных позиций, случайное значение для каждой координаты агента выбирается в заданном диапазоне, а функция u.SeInDiSp () приводит значение к допустимому, учитывая шаг. Начальная позиция агента сохраняется в a[p].cB[c] как лучшее индивидуальное решение шара (на первой итерации первоначальное решение равнозначно лучшему из известных), и после установки "revision=true" метод завершает выполнение, что предотвращает повторную инициализацию значений.
На второй и последующих итерациях запускается цикл по всем агентам для перемещения. В процессе обновления координат выполняются вложенные циклы по всем агентам и их координатам, где случайным образом выбирается один из лучших доступных карманов для обновления текущей позиции агента. Позиция обновляется за счет предыдущей позиции, к которой прибавляется случайное изменение, основанное на позиции выбранного кармана. Функция u.RNDprobab () возвращает случайное число в диапазоне [0.0; 1.0], чтобы добавить случайный шум, а у функции u.RNDintInRange (1, 2) случайное значение 1 или 2 умножается на позицию агента.
После обновления позиции, происходит ее коррекция, приводящая обновленное значение к заданному диапазону, с учетом минимальных и максимальных значений, а также шага изменения.
//—————————————————————————————————————————————————————————————————————————————— //--- Основной шаг алгоритма void C_AO_BOA::Moving () { //---------------------------------------------------------------------------- // Начальная инициализация if (!revision) { for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { a [p].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [p].c [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); a [p].cB [c] = a [p].c [c]; // Сохраняем начальную позицию } } revision = true; return; } //---------------------------------------------------------------------------- for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { int pocketID = u.RNDminusOne (numPockets); a [p].c [c] = a [p].cB [c] + u.RNDprobab () * (a [pocketID].cB [c] - u.RNDintInRange (1, 2) * a [p].cB [c]); a [p].c [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————Метод "Revision" отвечает за обновление лучшего глобального решения в алгоритме BOA, а так же обновляет лучшие индивидуальные решения шаров. В конце метода происходит сортировка шаров по их лучшим индивидуальным решениям.
//—————————————————————————————————————————————————————————————————————————————— //--- Обновление лучшего решения с учетом жадного выбора и вероятности принятия худших решений void C_AO_BOA::Revision () { int bestIND = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; bestIND = i; } if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } if (bestIND != -1) ArrayCopy (cB, a [bestIND].c, 0, 0, WHOLE_ARRAY); S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Результаты тестов
Теперь посмотрим, как работает алгоритм BOA:=============================
5 Hilly's; Func runs: 10000; result: 0.63960620766331
25 Hilly's; Func runs: 10000; result: 0.3277725645995603
500 Hilly's; Func runs: 10000; result: 0.2514878043770147
=============================
5 Forest's; Func runs: 10000; result: 0.3885662762060409
25 Forest's; Func runs: 10000; result: 0.1955657530616877
500 Forest's; Func runs: 10000; result: 0.15336230733273673
=============================
5 Megacity's; Func runs: 10000; result: 0.5415384615384615
25 Megacity's; Func runs: 10000; result: 0.19046153846153846
500 Megacity's; Func runs: 10000; result: 0.10530769230769324
=============================
All score: 2.79367 (31.04%)
Как можно заметить, показатели алгоритма достаточно слабые, и он не попадает в нашу рейтинговую таблицу, поэтому я решил более пристально пересмотреть алгоритм, — мне пришли некоторые мысли, как заставить его работать. Давайте снова посмотрим на формулу перемещения шаров:
X_new = X + rnd [0.0; 1.0] × (P - I × X)
В этой формуле коэффициент "I" применяется к значению текущей координаты шара, что имеет неясный физический смысл, так как фактически масштабирование применяется к абсолютному значению координаты. Естественным действием представляется вынести этот коэффициент за скобки, чтобы обеспечить масштабирование к разнице между "карманом" и значением координаты шара. Тогда полученная запись описывает действительно физический смысл, либо шар не долетит до кармана, либо перелетит его, вариабельность чего обеспечивается дополнительным шумовым фактором случайного числа в диапазоне [0.0, 1.0].
В итоге получим формулу перемещения шаров:
X_new = X + rnd [0.0; 1.0] × (P -X) × I
Итак, ниже привожу полностью код модифицированной версии метода Moving (), в котором показана закомментированная строка по формуле авторов и ниже — мой вариант формулы.
//—————————————————————————————————————————————————————————————————————————————— //--- Основной шаг алгоритма void C_AO_BOA::Moving () { //---------------------------------------------------------------------------- // Начальная инициализация if (!revision) { for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { a [p].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [p].c [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); a [p].cB [c] = a [p].c [c]; // Сохраняем начальную позицию как лучшее индивидуальное решение } } revision = true; return; } //---------------------------------------------------------------------------- for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { int pocketID = u.RNDminusOne (numPockets); //a [p].c [c] = a [p].cB [c] + u.RNDprobab () * (a [pocketID].cB [c] - u.RNDintInRange (1, 2) * a [p].cB [c]); a [p].c [c] = a [p].cB [c] + u.RNDprobab () * (a [pocketID].cB [c] - a [p].cB [c]) * u.RNDintInRange (1, 2); a [p].c [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Теперь, после проведенных изменений посмотрим, как алгоритм работает с параметрами, с которыми версия авторов показывала наилучшие результаты:
BOA|Billiards Optimization Algorithm|50.0|8.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8727603657603271
25 Hilly's; Func runs: 10000; result: 0.7117647027521633
500 Hilly's; Func runs: 10000; result: 0.25339119302510993
=============================
5 Forest's; Func runs: 10000; result: 0.9228482722678735
25 Forest's; Func runs: 10000; result: 0.7601448268715335
500 Forest's; Func runs: 10000; result: 0.3498925749480034
=============================
5 Megacity's; Func runs: 10000; result: 0.6184615384615385
25 Megacity's; Func runs: 10000; result: 0.45876923076923076
500 Megacity's; Func runs: 10000; result: 0.14586153846153965
=============================
All score: 5.09389 (56.60%)
Проведя ещё несколько экспериментов, я получил параметры, при которых получаем результаты еще лучше:
BOA|Billiards Optimization Algorithm|50.0|25.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.957565927297626
25 Hilly's; Func runs: 10000; result: 0.8259872884790693
500 Hilly's; Func runs: 10000; result: 0.2523458952211869
=============================
5 Forest's; Func runs: 10000; result: 0.9999999999999929
25 Forest's; Func runs: 10000; result: 0.900362056289584
500 Forest's; Func runs: 10000; result: 0.305018130407844
=============================
5 Megacity's; Func runs: 10000; result: 0.7353846153846153
25 Megacity's; Func runs: 10000; result: 0.5252307692307692
500 Megacity's; Func runs: 10000; result: 0.09563076923077005
=============================
All score: 5.59753 (62.19%)
Давайте рассмотрим визуализацию работы алгоритма BOA на тестовых функциях. В пространстве поиска не наблюдается никакого особого характерного поведения; движения "шаров" выглядят хаотичными. Особенно бросается в глаза, что алгоритм успешно справляется с задачами малой и средней размерности, однако, на задачах большой размерности возникают проблемы со сходимостью. Это особенно заметно на гладкой функции Hilly, где результативность оказывается даже хуже, чем на дискретной Megacity, что является крайне редким явлением, по сравнению с другими популяционными алгоритмами. Также следует отметить тенденцию алгоритма к застреванию в локальных минимумах при решении задач малой размерности.
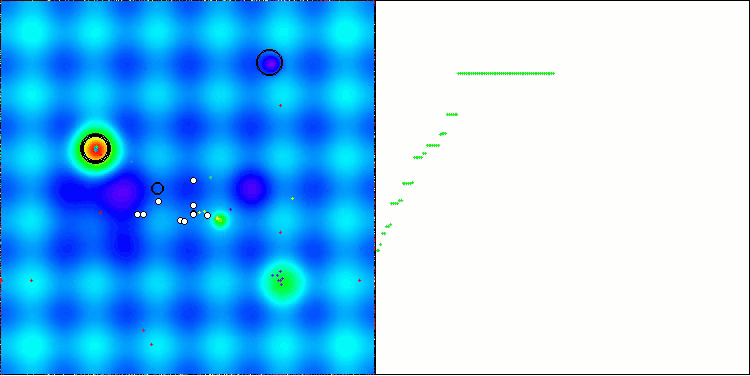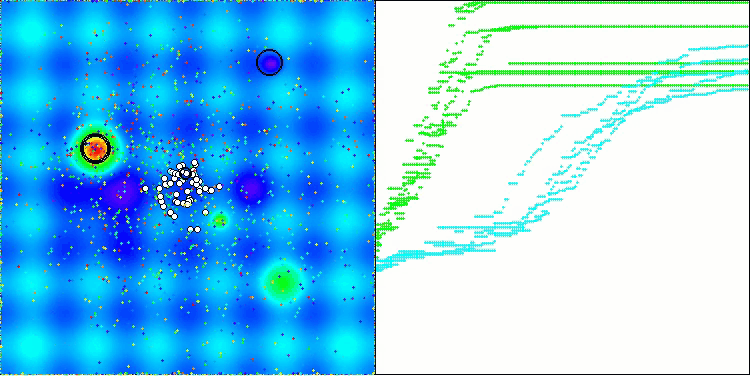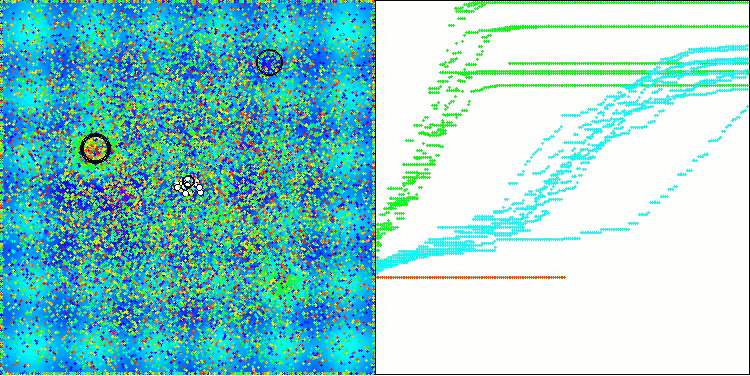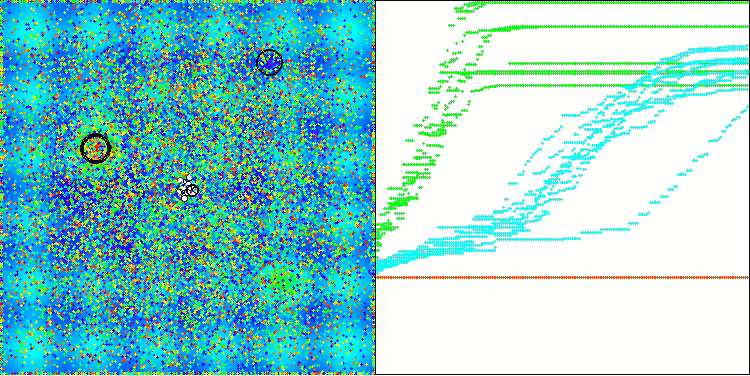
BOA на тестовой функции Hilly
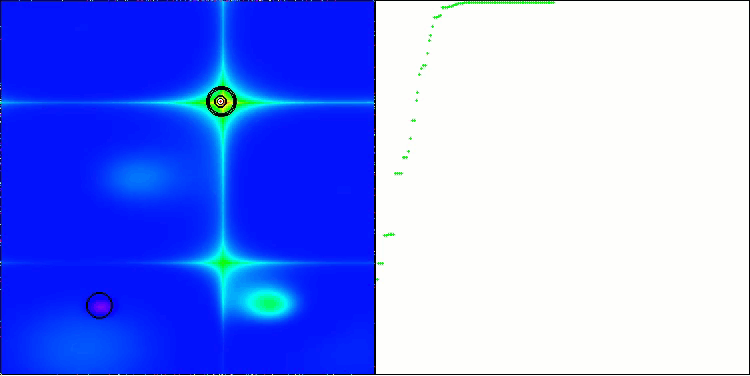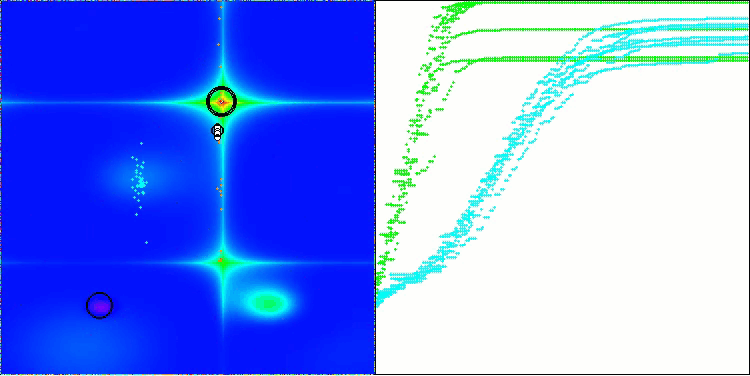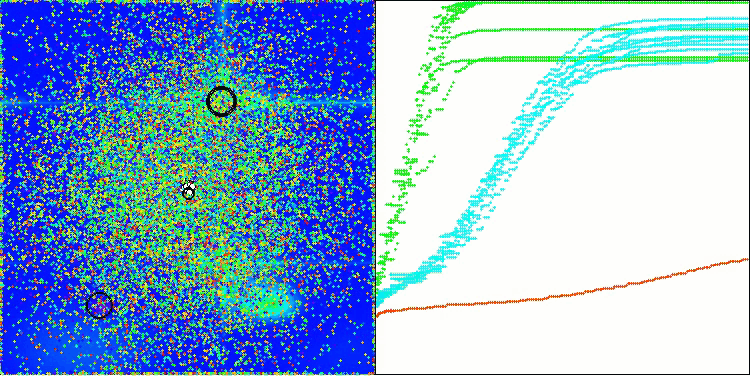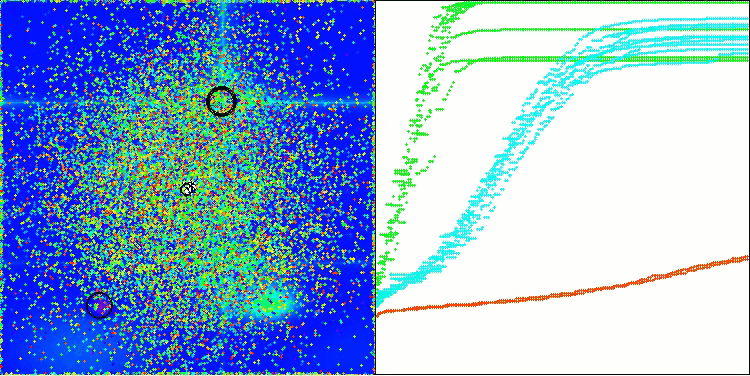
BOA на тестовой функции Forest
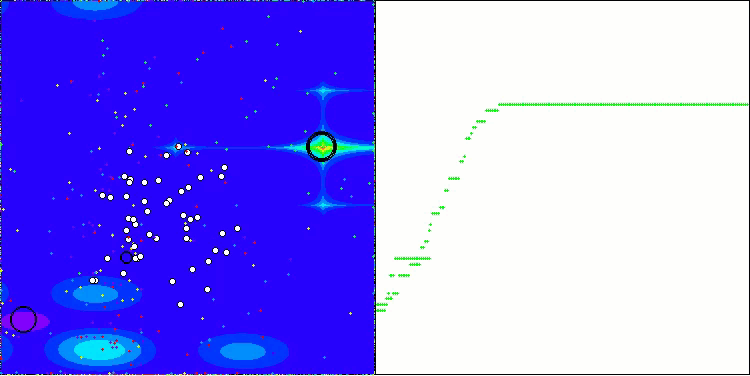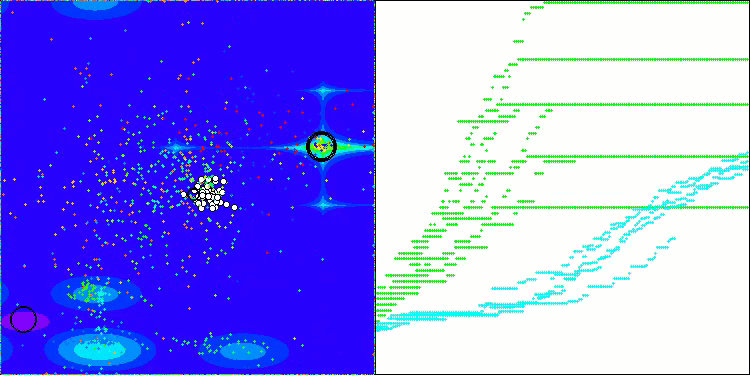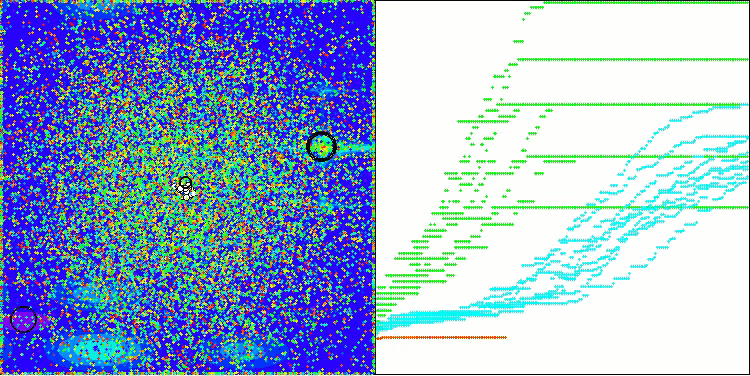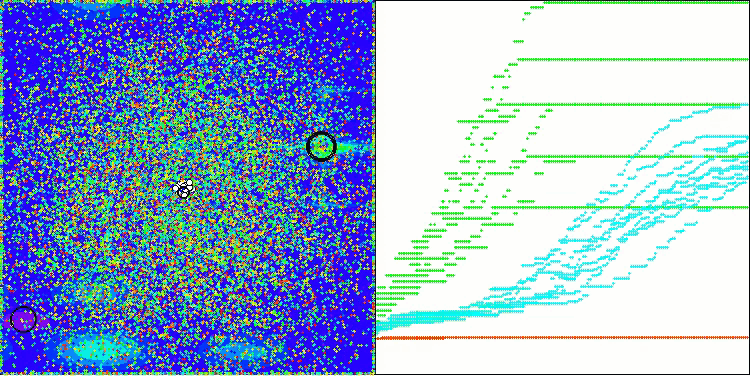
BOA на тестовой функции Megacity
Подведем итоги тестирования и посмотрим результативность. Алгоритм оказался довольно высоко — на 8 позиции в рейтинге самых лучших алгоритмов оптимизации, имея при этом серьезные недостатки.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 13 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 14 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 15 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 16 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 17 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 18 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 19 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 20 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 21 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 22 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 23 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 24 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 25 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 26 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 27 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 28 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 29 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 30 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 31 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 32 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 33 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 34 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 35 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 36 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 37 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 38 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 39 | CGO | chaos game optimization | 0,57256 | 0,37158 | 0,32018 | 1,26432 | 0,61176 | 0,61931 | 0,62161 | 1,85267 | 0,37538 | 0,21923 | 0,19028 | 0,78490 | 3,902 | 43,35 |
| 40 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 41 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 42 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 43 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 44 | CSA | circle search algorithm | 0,66560 | 0,45317 | 0,29126 | 1,41003 | 0,68797 | 0,41397 | 0,20525 | 1,30719 | 0,37538 | 0,23631 | 0,10646 | 0,71815 | 3,435 | 38,17 |
| 45 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Модифицированный бильярдный алгоритм оптимизации (BOAm) продемонстрировал интересные результаты на тестовых функциях. Анализ представленных данных показывает, что алгоритм достигает наилучших показателей на задачах малой и средней размерности, набирая максимальные значения в тестах Hilly (0.957), Forest (0.999) и Megacity (0.735) при достижении 10 000 итераций. Это свидетельствует о его высокой эффективности в поиске оптимальных решений для задач умеренной сложности. Однако, производительность существенно снижается при увеличении размерности проблемы, что видно по результатам в сценариях с 1000 переменными, где показатели падают до 0.252, 0.305 и 0.095 соответственно.
Особенно важно отметить значительное улучшение производительности в модифицированной версии алгоритма, которая набирает 62.19% от максимально возможного результата, что вдвое превышает показатель оригинальной версии 31.04%. Это впечатляющее улучшение было достигнуто лишь изменением одной строки кода, касающейся формулы обновления позиции шаров.
Простота алгоритма является одновременно его преимуществом и ограничением — он интуитивно понятен, легко реализуем и основан на элегантной концепции игры в бильярд, но может требовать дополнительных модификаций для эффективной работы с высокоразмерными задачами. В целом, оказавшись в первой десятке алгоритмов рейтинговой таблицы, BOAm представляет собой перспективный метаэвристический подход с хорошим балансом между исследованием и эксплуатацией пространства решений.
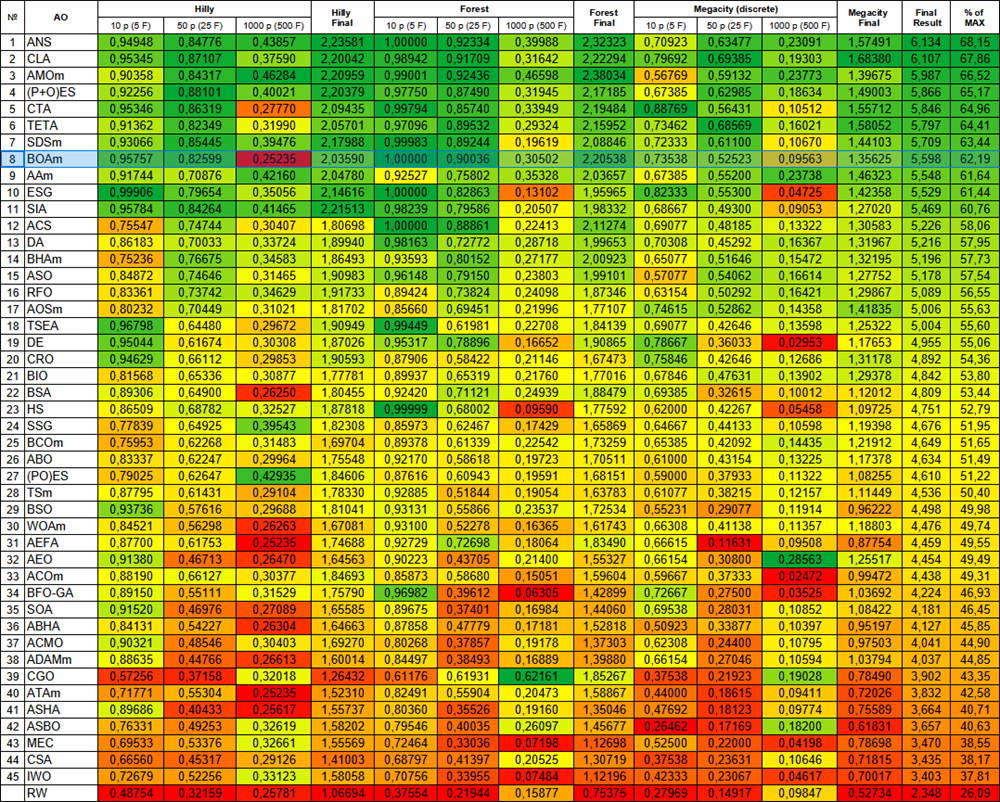
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
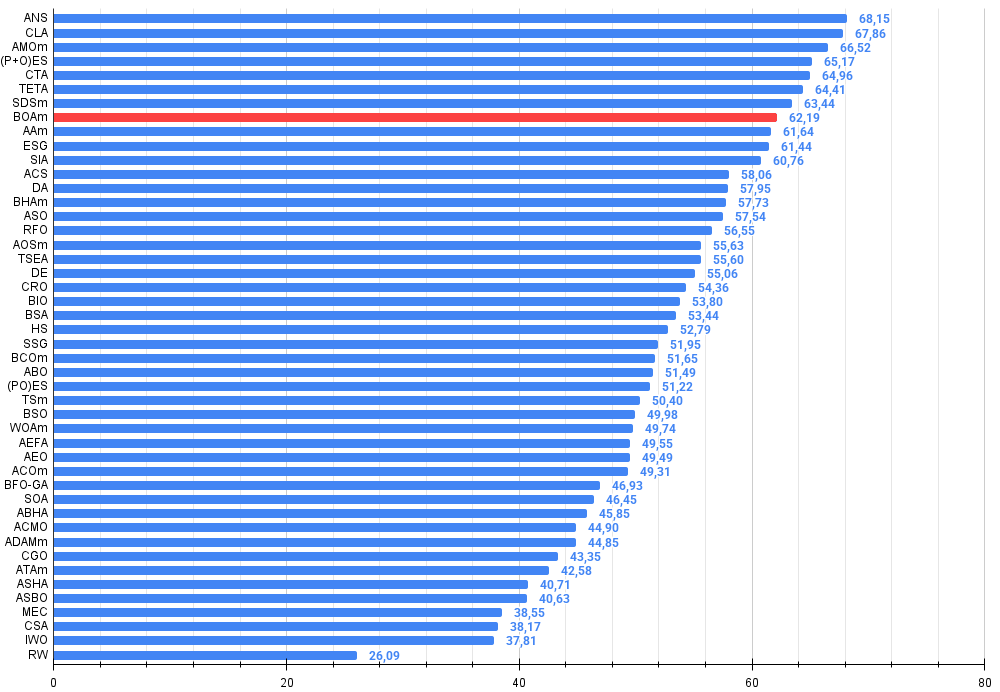
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма BOA:
Плюсы:
- Очень мало внешних параметров.
- Простая реализация.
- Хорошо показывает себя на задачах малой и средней размерности.
- Отличные результаты на задачах с "острыми" экстремумами (типа функции Forest).
Минусы:
- Застревает в локальных экстремумах на задачах низкой размерности.
- Очень низкая скорость и точность сходимости на "гладких" задачах (типа функции Hilly) высококой размерности.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_BOAm.mq5 | Скрипт | Испытательный стенд для BOAm |
MQL5-советник, интегрированный в Telegram (Часть 3): Отправка скриншотов графиков с подписями из MQL5 в Telegram
Нейросети в трейдинге: Интеграция теории хаоса в прогнозирование временных рядов (Окончание)
Формулировка динамического советника на нескольких парах (Часть 1): Корреляция и обратная корреляция валютных пар
Переосмысливаем классические стратегии (Часть V): Анализ нескольких инструментов в валютной паре USDZAR
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования