
Algoritmo de búsqueda orbital atómica - Atomic Orbital Search (AOS) Modificación
Contenido
- Introducción
- Implementación del algoritmo
- Ejemplo de uso de algoritmos de la clase C_AO
- Resultados de las pruebas
Introducción
En la primera parte de este artículo, analizaremos con detalle el algoritmo AOS (Atomic Orbital Search), sus fundamentos inspirados en el modelo orbital atómico y los mecanismos que lo sustentan. Asimismo, discutiremos cómo el algoritmo utiliza distribuciones de probabilidad y dinámicas de interacción para encontrar soluciones óptimas en problemas de optimización complejos.
En la segunda parte del artículo, nos centraremos en modificar el algoritmo del AOS, ya que no podemos dejar pasar una idea tan sobresaliente sin intentar mejorarla. Luego analizaremos el concepto de mejora del algoritmo, centrándonos en operadores específicos que son intrínsecos al método y pueden mejorar su eficacia y adaptabilidad.
El trabajo sobre el algoritmo AOS me ha descubierto muchos aspectos interesantes relacionados con sus métodos de búsqueda en el espacio de soluciones. Durante mi investigación, también se me han ocurrido varias ideas sobre cómo se podría mejorar este interesante algoritmo. En particular, me he centrado en reelaborar los métodos existentes que pueden potenciar el rendimiento del algoritmo mejorando su capacidad para explorar espacios de soluciones complejos. Hoy estudiaremos cómo integrar estas mejoras en la estructura actual del algoritmo AOS para convertirlo en una herramienta aún más potente para resolver problemas de optimización. Así pues, nuestro objetivo no consistirá solo en analizar los mecanismos existentes, sino también proponer otros enfoques que puedan mejorar significativamente las capacidades del algoritmo AOS.
Implementación del algoritmo
En el artículo anterior hemos analizado con detalle los componentes clave del algoritmo AOS. Recordemos que en este algoritmo la población se trata como una molécula, mientras que la región de coordenadas admisibles en la que se buscan soluciones óptimas se representa como un átomo. Cada átomo se compone de diferentes capas que ayudan a organizar y guiar la búsqueda.
Los valores específicos en coordenadas obtenidos durante la optimización pueden interpretarse como electrones. Estos electrones, mientras se hallan dentro del átomo, representan posibles soluciones a uno de los parámetros del problema que estamos optimizando. Así, cada molécula (población) tiende a encontrar los valores óptimos (electrones) dentro de una región determinada (átomo).
En la versión original del algoritmo AOS, la energía de la capa BEk se define como la media aritmética de las energías de los electrones de la capa, mientras que el acoplamiento BSk se define como la media aritmética de sus coordenadas. La energía de BEk se usa para realizar una comparación con la energía de los electrones y determinar cómo se transportan posteriormente. El enlace BSk se usa para calcular el incremento de la posición del electrón como la diferencia entre la mejor posición del electrón LEk en la capa y el enlace BSk utilizando la siguiente fórmula: Xki[t+1] = Xkit + αi × (βi × LEk − γi × BSk).
Le propongo abandonar la posición media de los electrones BSk en favor de una mejor posición personal de los electrones. Así, el electrón se moverá hacia la mejor solución de su capa basándose en los logros individuales y no en la solución media de toda la capa. Además, los dos componentes aleatorios βi y γi parecen redundantes, dado que ya existe un componente aleatorio externo αi. Esto reducirá en tres veces el tiempo para generar números aleatorios en esta fórmula sin perder el sentido físico.
Veamos ahora la estructura que describe una capa en un átomo. Los elementos que se eliminarán del código aparecen destacados en rojo://—————————————————————————————————————————————————————————————————————————————— struct S_Layer { int pc; // particle counter double BSk; // connection state double BEk; // binding energy double LEk; // minimum energy void Init () { pc = 0; BSk = 0.0; BEk = 0.0; LEk = 0.0; } }; //——————————————————————————————————————————————————————————————————————————————
Vamos a analizar el código del método "CalcLayerParams", que realiza el cálculo de las características de la capa como energía y conectividad. Las líneas resaltadas en rojo se eliminarán porque ya no serán necesarias. Recordemos que este método desempeña un papel clave en la estrategia de búsqueda de AOS para evitar que el algoritmo se atasque en trampas locales. Como el nivel de energía de las capas no depende de su ubicación (la energía disminuye desde el centro hacia las capas exteriores del átomo), sino que viene determinado por la presencia de extremos locales significativos (la capa exterior puede tener una energía superior a la de las capas interiores), las capas sirven para corregir el movimiento de los electrones en el espacio de búsqueda.
El número aleatorio de capas en cada época ayuda a evitar que el algoritmo se atasque en trampas locales al no permitir que los electrones se estanquen en una sola de las capas. La versión modificada también evita la necesidad de calcular la energía media de todo el átomo, por lo que eliminaremos las líneas correspondientes.

Figura 1. Diferencia en la dirección y el tamaño del desplazamiento del electrón e según el número de capas del átomo
La figura 1 ilustra las diferencias en el comportamiento de los electrones en átomos con distintos números de capas en el algoritmo AOS. La parte superior muestra un átomo con tres capas, donde el electrón se encuentra en la capa L1 con el valor de la función objetivo B1 y se desplaza hacia el mejor valor local LEk1. La parte inferior de la figura ilustra un átomo con dos capas, en el que el electrón se encuentra también en la capa L1 y se desplaza hacia el mejor valor local LEk1 con el valor de la función objetivo B1 (en el caso con las tres capas sería el punto LEk2).
Los elementos clave de la figura son:
- B0, B1, B2 — designaciones de los valores locales de la función objetivo para las capas correspondientes,
- LEk0, LEk1, LEk2 — mejores soluciones en sus respectivas capas,
- L0, L1, L2 — capas del átomo,
- e — electrón,
- MIN, MAX — límites de las capas exteriores de los átomos (condiciones de contorno de los parámetros optimizados del problema).
//—————————————————————————————————————————————————————————————————————————————— // Calculate parameters for each layer void C_AO_AOS::CalcLayerParams () { double energy; // Handle each coordinate (atom) for (int c = 0; c < coords; c++) { atoms [c].Init (maxLayers); // Handle each layer for (int L = 0; L < currentLayers [c]; L++) { energy = -DBL_MAX; // Handle each electron for (int e = 0; e < popSize; e++) { if (electrons [e].layerID [c] == L) { atoms [c].layers [L].pc++; atoms [c].layers [L].BEk += a [e].f; atoms [c].layers [L].BSk += a [e].c [c]; if (a [e].f > energy) { energy = a [e].f; atoms [c].layers [L].LEk = a [e].c [c]; } } } // Calculate average values for the layer if (atoms [c].layers [L].pc != 0) { atoms [c].layers [L].BEk /= atoms [c].layers [L].pc; atoms [c].layers [L].BSk /= atoms [c].layers [L].pc; } } } // Calculate the general state of connections ArrayInitialize (BS, 0); for (int c = 0; c < coords; c++) { for (int e = 0; e < popSize; e++) { BS [c] += a [e].c [c]; } BS [c] /= popSize; } } //——————————————————————————————————————————————————————————————————————————————
Para actualizar las mejores soluciones individuales, añadiremos código al método "Revision" en la clase de la versión modificada "C_AO_AOSm".
//—————————————————————————————————————————————————————————————————————————————— // Method of revising the best solutions void C_AO_AOSm::Revision () { int bestIndex = -1; // Find the best solution in the current iteration for (int i = 0; i < popSize; i++) { // Update the global best solution if (a [i].f > fB) { fB = a [i].f; bestIndex = i; } // Update the personal best solution if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } // Update the best coordinates if a better solution is found if (bestIndex != -1) ArrayCopy (cB, a [bestIndex].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
En el método "UpdateElectrons", eliminaremos las variables "β" y "γ", ya que no son necesarias para generar los números aleatorios correspondientes. Además, excluiremos la división del incremento de electrones por el número de capas en caso de avanzar hacia la solución global. Francamente, la solución de los autores me parece controvertida, y el sentido físico de este planteamiento no está del todo claro. Es posible que los autores hayan intentado hacer variable el grado de desplazamiento de los electrones en la dirección de la solución global cambiándolo según número de capas: cuantas menos capas, más intenso debería ser el desplazamiento (aunque mis experimentos han demostrado que esto no nos ofrece nada).
//—————————————————————————————————————————————————————————————————————————————— // Update electron positions void C_AO_AOS::UpdateElectrons () { double α; // speed coefficient double β; // best solution weight coefficient double γ; // average state weight coefficient double φ; // transition probability double newPos; // new position double LE; // best energy double BSk; // connection state int lID; // layer ID // Handle each particle for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { φ = u.RNDprobab (); if (φ < PR) { // Random scatter newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); } else { lID = electrons [p].layerID [c]; α = u.RNDfromCI (-1.0, 1.0); β = u.RNDprobab (); γ = u.RNDprobab (); // If the current particle energy is less than the average layer energy if (a [p].f < atoms [c].layers [lID].BEk) { // Moving towards the global optimum---------------------------- LE = cB [c]; newPos = a [p].c [c]+ α * (β * LE - γ * BS [c]) / currentLayers [c]; } else { // Movement towards the local optimum of the layer------------------------ LE = atoms [c].layers [lID].LEk; BSk = atoms [c].layers [lID].BSk; newPos = a [p].c [c] + α * (β * LE - γ * BSk); } } // Limiting the new position within the search range taking into account the step a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Además, en el método "UpdateElectrons" de la clase "C_AO_AOSm", en lugar de la dispersión aleatoria del electrón por el espacio de búsqueda, implementaremos el desplazamiento del electrón hacia el centro del núcleo con cierta probabilidad. En esencia, esto implica sustituir el valor en alguna coordenada por el valor de la solución global, lo que debería mejorar las propiedades combinatorias del algoritmo, mientras que la dispersión aleatoria se ha diseñado para ofrecer diversidad en la población de soluciones, pero esta propiedad garantizaba que los electrones se repartieran en una distribución lognormal en la que había una probabilidad distinta de cero de que un electrón chocara con cualquier punto del espacio mientras viajaba.
Los cambios en las fórmulas de desplazamiento de los electrones se muestran en verde, ahora el incremento se calculará como la diferencia entre la mejor solución local de la capa y la mejor solución individual del electrón.
//—————————————————————————————————————————————————————————————————————————————— // Update electron positions void C_AO_AOSm::UpdateElectrons () { double α; // speed coefficient double φ; // transition probability double newPos; // new position double LE; // best energy double BSk; // connection state int lID; // layer ID // Handle each particle for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { φ = u.RNDprobab (); if (φ < PR) { // Random jump to center newPos = cB [c]; } else { lID = electrons [p].layerID [c]; α = u.RNDfromCI (-1.0, 1.0); // If the current particle energy is less than the average layer energy if (a [p].f < atoms [c].layers [lID].BEk) { // Moving towards the global optimum---------------------------- LE = cB [c]; newPos = a [p].cB [c]+ α * (LE - a [p].cB [c]); } else { // Movement towards the local optimum of the layer------------------------ LE = atoms [c].layers [lID].LEk; newPos = a [p].cB [c]+ α * (LE - a [p].cB [c]); } } // Limiting the new position within the search range taking into account the step a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
El método "DistributeParticles" distribuirá los electrones en el espacio de búsqueda usando una distribución lognormal para cada coordenada. Para cada partícula y cada coordenada, se llamará a una función que genera una posición dados los parámetros especificados (valores medio, mínimo y máximo, pico) y luego se aplicará una función adicional para ajustar la posición dentro del rango especificado.
//—————————————————————————————————————————————————————————————————————————————— // Distribution of particles in the search space void C_AO_AOS::DistributeParticles () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Use log-normal distribution to position particles a [i].c [c] = u.LognormalDistribution (cB [c], rangeMin [c], rangeMax [c], peakPosition); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Luego cambiaremos la distribución de los electrones a normal. Esta distribución utilizará una desviación típica igual a 8. Aunque este parámetro podría hacerse externo al algoritmo, hemos optado por no hacerlo. Los valores más pequeños favorecen una exploración más amplia del espacio de búsqueda, mientras que los valores más altos mejoran la precisión de la convergencia al refinar la solución global.
//—————————————————————————————————————————————————————————————————————————————— // Distribution of particles in the search space void C_AO_AOSm::DistributeParticles () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Use a Gaussian distribution to position particles a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Hemos analizado todos los cambios introducidos en la versión original del algoritmo AOS para mejorar su eficacia. Como hemos introducido cambios significativos en la lógica de la estrategia de búsqueda, la versión modificada del algoritmo puede denotarse con la letra "m". En lo sucesivo, solo presentaremos en la tabla de clasificación la versión modificada, el AOSm.
Ejemplo de uso de algoritmos de la clase C_AO
Dado que todos los algoritmos de optimización basados en poblaciones discutidos anteriormente se heredan de la clase general C_AO, esto nos permitirá utilizarlos de manera uniforme y con un mínimo esfuerzo para resolver una variedad de problemas que requieren la selección de parámetros óptimos. El siguiente ejemplo le mostramos un script que optimiza una función objetivo:
1. Al principio del script, podremos elegir el algoritmo de optimización que deseamos utilizar. Si no seleccionamos nada, el script nos comunicará un error y se detendrá.
2. Ajuste de parámetros. El script determinará cuántas veces se ejecutará la función, cuántos parámetros deben optimizarse, el tamaño del grupo de soluciones y cuántas iteraciones se realizarán.
3. Límites de los valores. Para cada parámetro se fijarán valores mínimos y máximos (en este ejemplo, de -10 a 10).
4. El script iniciará el proceso de optimización:
- Generará soluciones (conjuntos de parámetros) y comprobará su calidad mediante una función especial (función objetivo).
- En cada iteración, el algoritmo actualizará sus soluciones en función de las que hayan funcionado mejor.
5. Resultados. Una vez finalizada la optimización, el script proporcionará información sobre qué algoritmo se ha utilizado, cuál es el mejor valor encontrado y cuántas veces se ha ejecutado la función.
6. La función objetivo es un problema abstracto de optimización (en este ejemplo se utilizará la solución al problema de hallar el máximo global de una parábola invertida) que toma parámetros y retorna una estimación de su calidad.
#property script_show_inputs // Specify that the script will show the inputs in the properties window #include <Math\AOs\PopulationAO\#C_AO_enum.mqh> // Connect the library for handling optimization algorithms input E_AO AOexactly = NONE_AO; // Parameter for selecting the optimization algorithm, default is NONE_AO //—————————————————————————————————————————————————————————————————————————————— void OnStart() { //---------------------------------------------------------------------------- int numbTestFuncRuns = 10000; // Total number of function runs int params = 1000; // Number of parameters for optimization int popSize = 50; // Population size for optimization algorithm int epochCount = numbTestFuncRuns / popSize; // Total number of epochs (iterations) for optimization double rangeMin [], rangeMax [], rangeStep []; // Arrays for storing the parameters' boundaries and steps ArrayResize (rangeMin, params); // Resize 'min' borders array ArrayResize (rangeMax, params); // Resize 'max' borders array ArrayResize (rangeStep, params); // Resize the steps array // Initialize the borders and steps for each parameter for (int i = 0; i < params; i++) { rangeMin [i] = -10; // Minimum value of the parameter rangeMax [i] = 10; // Maximum value of the parameter rangeStep [i] = DBL_EPSILON; // Parameter step } //---------------------------------------------------------------------------- C_AO *ao = SelectAO (AOexactly); // Select an optimization algorithm if (ao == NULL) // Check if an algorithm has been selected { Print ("AO not selected..."); // Error message if no algorithm is selected return; } ao.params [0].val = popSize; // Assigning population size.... ao.SetParams (); //... (optional, then default population size will be used) ao.Init (rangeMin, rangeMax, rangeStep, epochCount); // Initialize the algorithm with given boundaries and number of epochs // Main loop by number of epochs for (int epochCNT = 1; epochCNT <= epochCount; epochCNT++) { ao.Moving (); // Execute one epoch of the optimization algorithm // Calculate the value of the objective function for each solution in the population for (int set = 0; set < ArraySize (ao.a); set++) { ao.a [set].f = ObjectiveFunction (ao.a [set].c); // Apply the objective function to each solution } ao.Revision (); // Update the population based on the results of the objective function } //---------------------------------------------------------------------------- // Output the algorithm name, best result and number of function runs Print (ao.GetName (), ", best result: ", ao.fB, ", number of function launches: ", numbTestFuncRuns); delete ao; // Release the memory occupied by the algorithm object } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Definition of the user's objective function, in this case as an example - a paraboloid, F(Xn) ∈ [0.0; 1.0], X ∈ [-10.0; 10.0], maximization double ObjectiveFunction (double &x []) { double sum = 0.0; // Variable for accumulation of the result // Loop through all parameters for (int i = 0; i < ArraySize (x); i++) { // Check if the parameter is in the allowed range if (x [i] < -10.0 || x [i] > 10.0) return 0.0; // If the parameter is out of range, return 0 sum += (-x [i] * x [i] + 100.0) * 0.01; // Calculate the value of the objective function } return sum /= ArraySize (x); } //——————————————————————————————————————————————————————————————————————————————
Resultados de las pruebas
Pasemos a probar la versión modificada del algoritmo.
AOS|Atomic Orbital Search|50.0|10.0|20.0|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.8023218355650774
25 Hilly's; Func runs: 10000; result: 0.7044908398821188
500 Hilly's; Func runs: 10000; result: 0.3102116882841442
=============================
5 Forest's; Func runs: 10000; result: 0.8565993699987462
25 Forest's; Func runs: 10000; result: 0.6945107796904211
500 Forest's; Func runs: 10000; result: 0.21996085558228406
=============================
5 Megacity's; Func runs: 10000; result: 0.7461538461538461
25 Megacity's; Func runs: 10000; result: 0.5286153846153846
500 Megacity's; Func runs: 10000; result: 0.1435846153846167
=============================
All score: 5.00645 (55.63%)
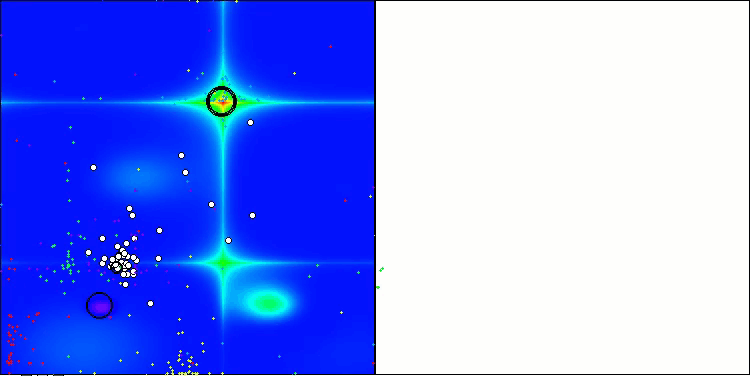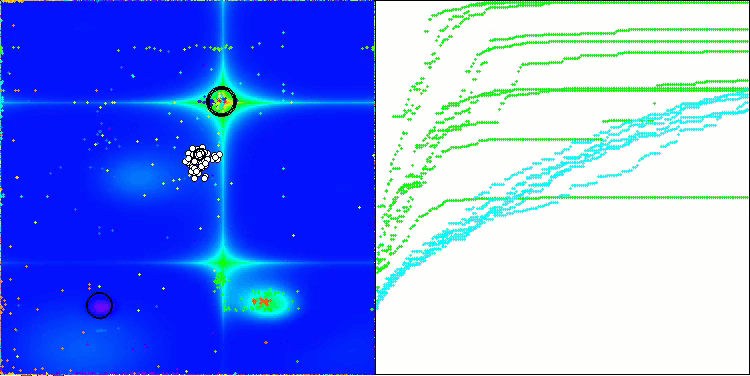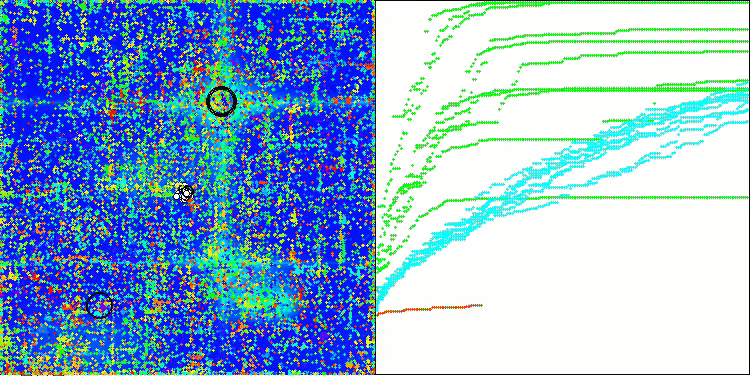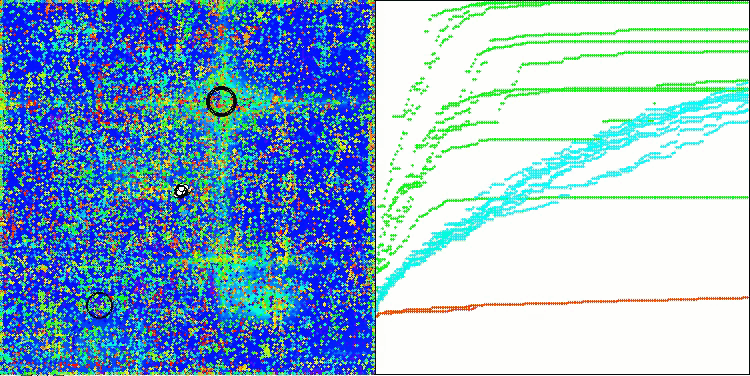
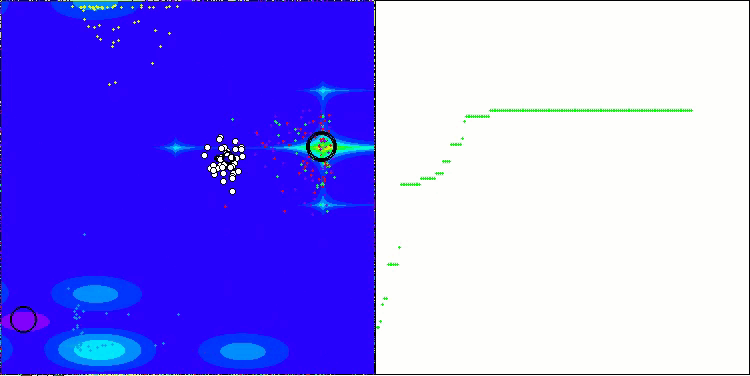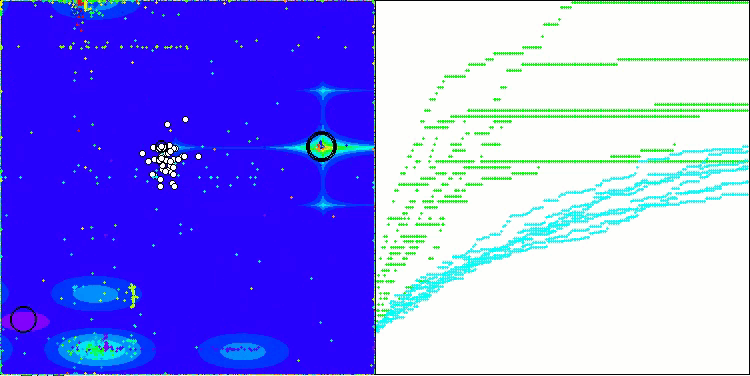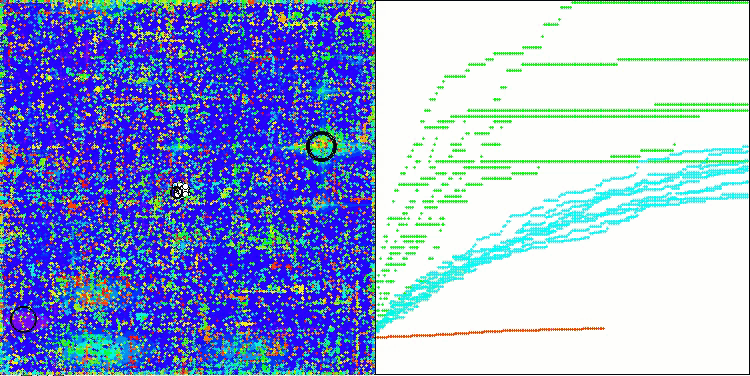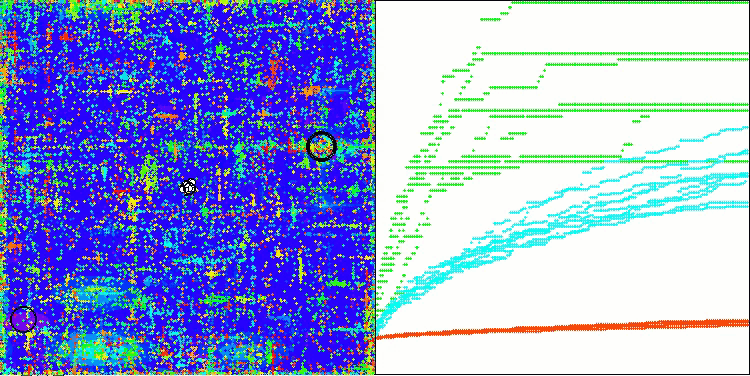
Como podemos observar, los resultados de la versión modificada han mejorado significativamente en comparación con el rendimiento anterior de la versión original, en la que la puntuación total era de 3,00488 (33,39%). Esta mejora se hará patente al analizar la visualización, que muestra no solo una mejora de la convergencia, sino también una elaboración más detallada de los extremos significativos.
Uno de los aspectos clave que merece la pena destacar es el efecto de las soluciones de "aglomeración" en las coordenadas individuales. Este fenómeno se observa tanto en la versión original como en la modificada, lo que pone de relieve un rasgo característico de los algoritmos AOS. La "aglomeración" de soluciones puede indicar que el algoritmo está encontrando eficazmente regiones en las que se hallan posibles soluciones óptimas.
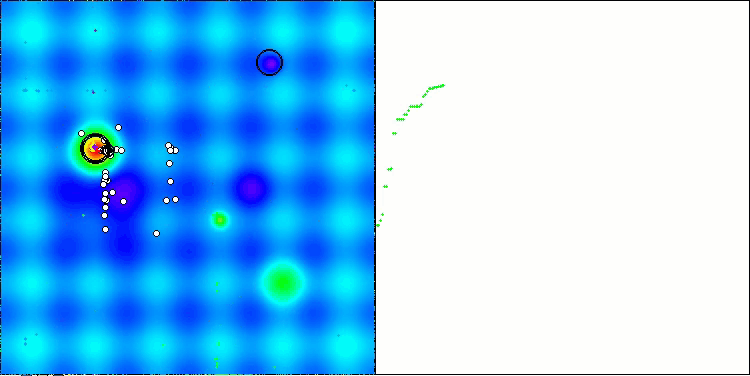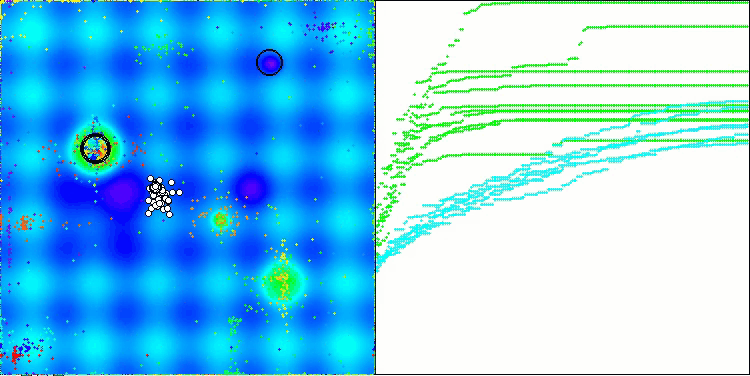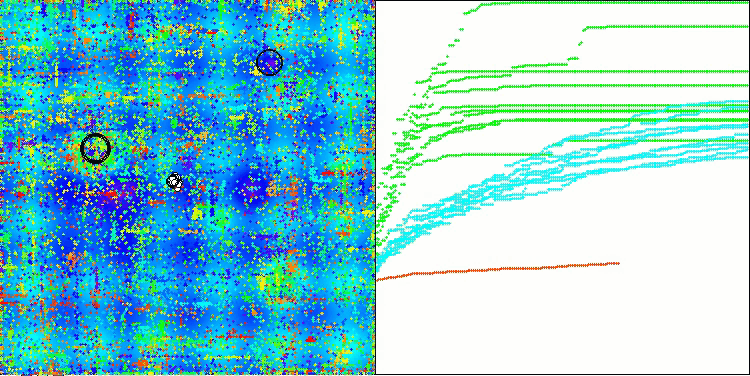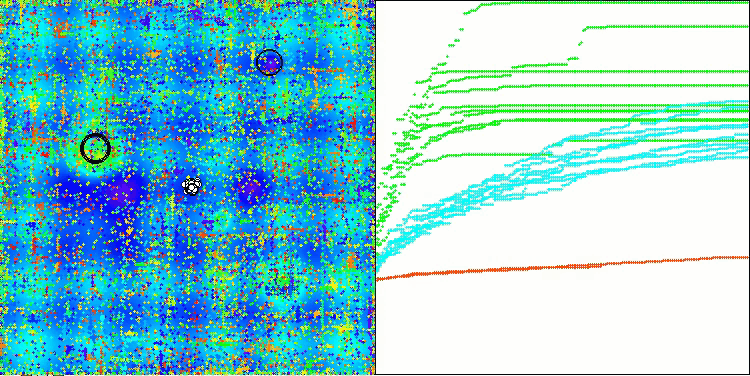
AOSm en la función de prueba Hilly
AOSm en la función de prueba Forest
AOSm en la función de prueba Megacity
La versión modificada del algoritmo Atomic Orbital Search (AOS) ha mejorado notablemente su rendimiento respecto a la versión original y ahora alcanza más del 55% del máximo posible. Es un resultado realmente impresionante. En la tabla de clasificación, el algoritmo ocupa el puesto 12, en la parte superior, lo cual indica unos resultados muy a considerar.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration optimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 12 | AOSm | búsqueda de orbitales atómicos M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 13 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 14 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 15 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 16 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 17 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 18 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 19 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 20 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 21 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 22 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 23 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 24 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 25 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 26 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 27 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 28 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 29 | ABH | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 30 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 31 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 32 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 33 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 34 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 35 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 36 | COAm | cuckoo optimization algorithm M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 37 | SDOm | spiral dynamics optimization M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 38 | NMm | Nelder-Mead method M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 39 | FAm | firefly algorithm M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 40 | GSA | gravitational search algorithm | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 41 | BFO | bacterial foraging optimization | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 42 | ABC | artificial bee colony | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 43 | BA | bat algorithm | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 44 | AAA | algae adaptive algorithm | 0.50007 | 0.32040 | 0.25525 | 1.07572 | 0.37021 | 0.22284 | 0.16785 | 0.76089 | 0.27846 | 0.14800 | 0.09755 | 0.52402 | 2.361 | 26.23 |
| 45 | SA | simulated annealing | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
Conclusiones
En este artículo hemos presentado una versión modificada del algoritmo de búsqueda orbital atómica (AOSm), en la que hemos abandonado la posición promediada de los electrones BSk en las capas del átomo en favor de la mejor posición individual de cada electrón. Esto ha permitido que los electrones se muevan de forma más eficiente hacia la mejor solución en su capa, basándose en los logros personales y no en una media. Además, hemos eliminado los dos componentes aleatorios βi y γi, lo que ha reducido en tres veces el tiempo de generación de números aleatorios sin perder el sentido físico del algoritmo.
En el método "UpdateElectrons", ahora se han eliminado las variables innecesarias y se ha suprimido la división del incremento de electrones por el número de capas al pasar a la solución global. Aunque es posible que los autores de la versión original pretendieran que el grado de movimiento fuera variable, mis experimentos han demostrado que esto no aporta ventajas sustanciales.
También hemos introducido cambios en el método "UpdateElectrons" de la clase "C_AO_AOSm", sustituyendo la dispersión aleatoria de un electrón por un movimiento hacia el centro del núcleo con una probabilidad determinada. Esto ha aumentado las propiedades combinatorias del algoritmo, permitiendo a los electrones apuntar con mayor precisión a una solución global. También hemos sustituido la distribución lognormal por una distribución normal, lo que ha aumentado la precisión de la convergencia al precisar la solución global.
Los resultados de la versión modificada de AOSm han mostrado una mejora significativa, con una puntuación global superior al 55% de la puntuación máxima posible, lo que confirma la gran eficacia y competitividad del algoritmo. El AOSm ocupa el puesto 12 en la tabla de clasificación, lo cual demuestra sus importantes logros entre otros métodos de optimización.
Uno de los aspectos más notables del AOSm es la mejora de la convergencia, que se ha hecho evidente al visualizar los resultados. El algoritmo resuelve los extremos significativos con mayor detalle y demuestra la capacidad de encontrar eficazmente soluciones óptimas en espacios multidimensionales complejos. El efecto de "aglomeración" de soluciones observado tanto en la versión original como en la modificada pone de relieve la capacidad del algoritmo para encontrar y centrarse en regiones con óptimos potenciales, lo cual resulta especialmente útil en problemas de elevada dimensionalidad y estructura compleja.
Un plus adicional a las ventajas de la versión modificada es la reducción del número de parámetros externos, lo que simplifica su uso y ajuste. Dicho sea de paso, para todos los algoritmos presentados anteriormente en los artículos, hemos seleccionado parámetros externos óptimos para lograr el máximo rendimiento en pruebas complejas en diferentes tipos de tareas de prueba, por lo que todos los algoritmos están listos para usar y no requieren ningún ajuste. Este artículo demuestra que a veces los cambios más pequeños en los algoritmos de optimización pueden modificar drásticamente sus propiedades de búsqueda, mientras que cambios significativos en la lógica de la estrategia de búsqueda pueden no suponer una diferencia notable en los resultados. Y, claro está, en los artículos compartimos técnicas que realmente mejoran los resultados de la optimización.
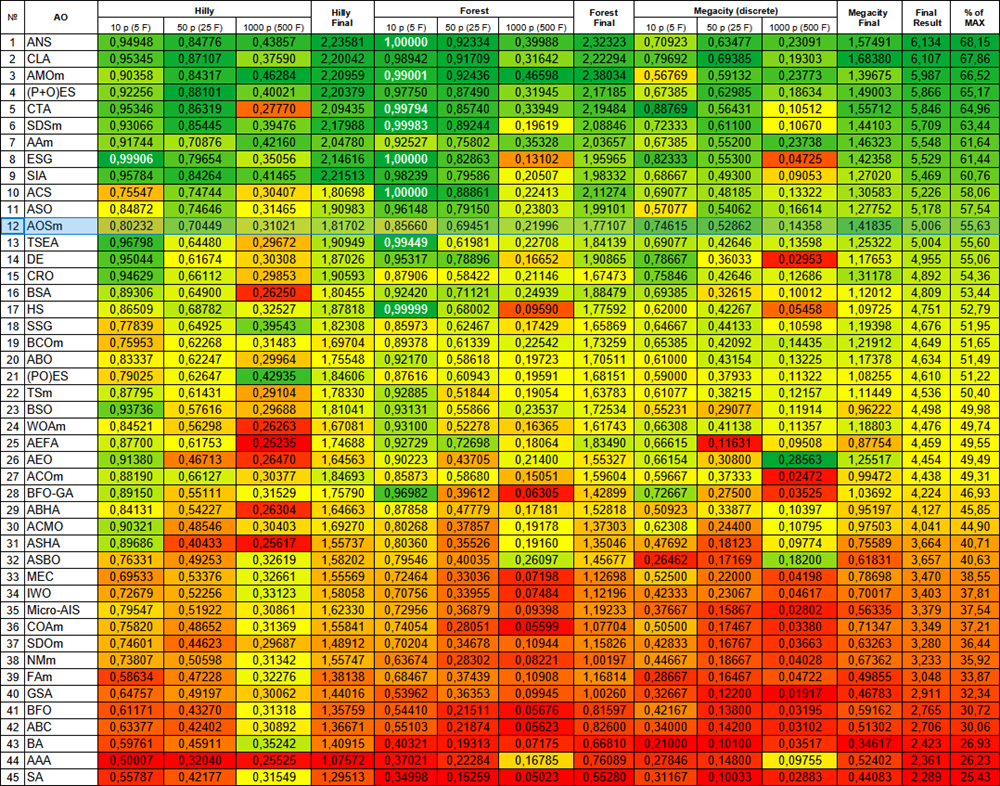
Figura 2. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0.99 se resaltan en blanco
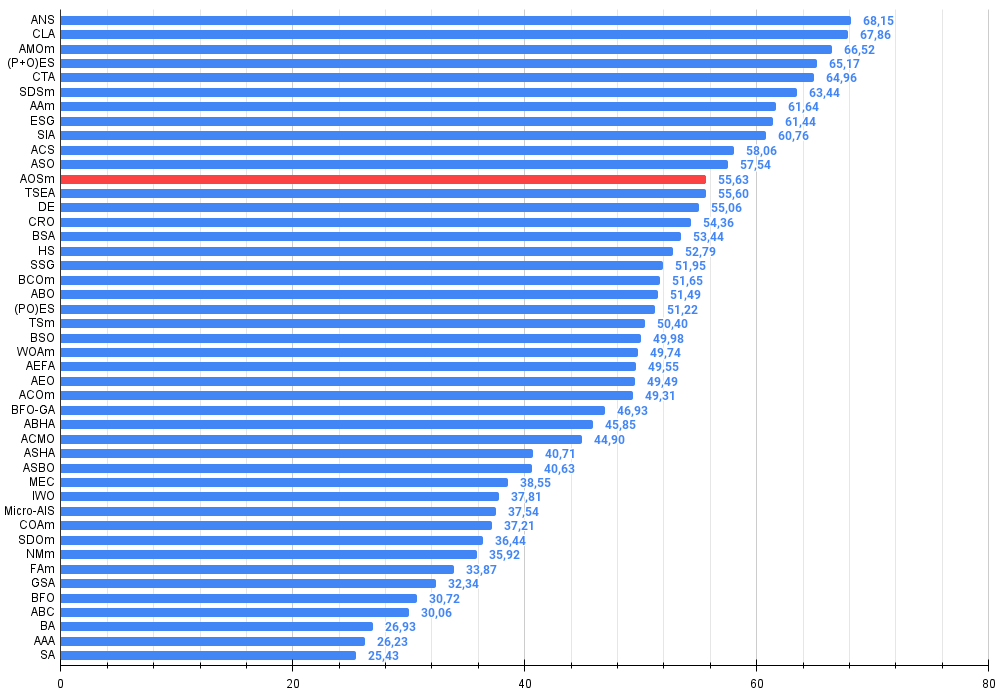
Figura 3. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor,
donde 100 es el máximo resultado teórico posible; el script para calcular la tabla de clasificación está en el archivo)
Ventajas e inconvenientes del algoritmo AOSm:
Ventajas:
- Buen rendimiento en tareas diversas.
- Número reducido de parámetros externos.
- Buena escalabilidad.
- Búsqueda equilibrada tanto por extremos locales como globales.
Desventajas:
- Aplicación bastante compleja.
- Precisión de convergencia media en funciones suaves respecto a otros algoritmos.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | #C_AO.mqh | Archivo de inclusión | Clase padre de algoritmos de optimización basados en la población |
| 2 | #C_AO_enum.mqh | Archivo de inclusión | Enumeración de los algoritmos de optimización basados en la población |
| 3 | TestFunctions.mqh | Archivo de inclusión | Biblioteca de funciones de prueba |
| 4 | TestStandFunctions.mqh | Archivo de inclusión | Biblioteca de funciones del banco de pruebas |
| 5 | Utilities.mqh | Archivo de inclusión | Biblioteca de funciones auxiliares |
| 6 | CalculationTestResults.mqh | Archivo de inclusión | Script para calcular los resultados en una tabla comparativa |
| 7 | Testing AOs.mq5 | Script | Banco de pruebas único para todos los algoritmos de optimización basados en la población |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización |
| 9 | AO_AOSm_AtomicOrbitalSearch.mqh | Archivo de inclusión | Algoritmo de la clase AOSm |
| 10 | Test_AO_AOSm.mq5 | Script | Banco de pruebas para AOSm |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16315
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Redes neuronales en el trading: Mejora de la eficiencia del Transformer mediante la reducción de la nitidez (SAMformer)
Redes neuronales en el trading: Mejora de la eficiencia del Transformer mediante la reducción de la nitidez (SAMformer)
 Operar con noticias de manera sencilla (Parte 4): Mejora del rendimiento
Operar con noticias de manera sencilla (Parte 4): Mejora del rendimiento
 Características del Wizard MQL5 que debe conocer (Parte 43): Aprendizaje por refuerzo con SARSA
Características del Wizard MQL5 que debe conocer (Parte 43): Aprendizaje por refuerzo con SARSA
 Redes neuronales en el trading: Optimización del Transformer para la previsión de series temporales (LSEAttention)
Redes neuronales en el trading: Optimización del Transformer para la previsión de series temporales (LSEAttention)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Gracias por el artículo.
Me senté un rato ayer y hoy en la función Hilly y métodos alglib. Aquí están mis pensamientos.
Para encontrar el máximo de esta función, especialmente cuando el número de parámetros es de 10 y más, no tiene sentido aplicar métodos de gradiente, esta es la tarea de los métodos combinatorios de optimización. Los métodos de gradiente se atascan instantáneamente en el extremo local. Y no importa cuántas veces se reinicie desde un nuevo punto en el espacio de parámetros, la posibilidad de llegar a la región correcta del espacio desde la que el método de gradiente encuentra instantáneamente una solución tiende a cero a medida que aumenta el número de parámetros.
Por ejemplo, el punto del espacio a partir del cual lbfgs o CG para 2(dos) iteraciones encuentran el máximo para cualquier número de parámetros es {x = -1,2 , y = 0,5}.
Pero la posibilidad de entrar en esta región como he dicho es simplemente cero. Debe ser de cien años para generar números aleatorios.
Por lo tanto, es necesario combinar de alguna manera los algoritmos genéticos presentados en el artículo (para que pudieran hacer reconocimiento y reducir el espacio de búsqueda) con métodos de gradiente que encontraran rápidamente el extremo desde un punto más favorable.
Gracias por el artículo.
Gracias por su comentario.
Para encontrar el máximo de una función dada, especialmente cuando el número de parámetros es 10 o más, no tiene sentido utilizar métodos de gradiente.
Sí, es cierto.
Esta es la tarea de los métodos combinatorios de optimización.
Los métodos combinatorios, como la clásica "hormiga", están diseñados para problemas como el "problema del viajante de comercio" y el "problema de la mochila", es decir, para problemas discretos con un paso fijo (borde del grafo). Para problemas multidimensionales "continuos", estos algoritmos no están diseñados en absoluto, por ejemplo, para tareas como el entrenamiento de redes neuronales. Sí, las propiedades combinatorias son muy útiles para los métodos heurísticos estocásticos, pero no son la única propiedad ni la suficiente para resolver con éxito problemas de prueba casi reales. Las propias estrategias de búsqueda en el algo también son importantes.
Las basadas en gradientes simplemente se atascan en un extremo local al instante. Y no importa cuántas veces se reinicie desde un nuevo punto del espacio de parámetros, la posibilidad de llegar a la región correcta del espacio desde la que el método de gradiente encuentra instantáneamente una solución tiende a cero a medida que aumenta el número de parámetros.
Sí, es cierto.
Pero la posibilidad de llegar a esta región, como ya he dicho, es simplemente cero. Se necesitarían unos cien años para generar números aleatorios.
Sí, es cierto. En espacios de baja dimensión (1-2) es muy fácil llegar a la vecindad del global, incluso pueden funcionar para ello generadores aleatorios sencillos. Pero todo cambia completamente cuando la dimensionalidad del problema crece, aquí las propiedades de búsqueda de los algoritmos empiezan a jugar un papel importante, no la Señora Suerte.
Así que necesitamos combinar de alguna manera los algoritmos genéticos presentados en el artículo (que harían exploración, reducirían el espacio de búsqueda) con métodos de gradiente, que entonces encontrarían rápidamente el extremo desde un punto más favorable.
"Genético" - probablemente quieres decir "heurístico". ¿Por qué "el pez necesita un paraguas" y "por qué necesitamos un herrero? No necesitamos un herrero". )))) Hay formas eficientes de resolver problemas complejos multidimensionales en espacio continuo, que se describen en artículos sobre métodos poblacionales. Y para los problemas clásicos de gradiente hay sus propias tareas - problemas unidimensionales analíticamente determinables (en esto no tienen igual, habrá convergencia rápida y exacta).
Y, pregunta, ¿cuáles son tus impresiones sobre la velocidad de la heurística?
SZY:
Oh, cuántos descubrimientos maravillosos
Prepara el espíritu de la iluminación
Y la experiencia, el hijo de los errores
Y el genio, el amigo de las paradojas,
Y el azar, inventor de Dios.
ZZZY. Un momento. En un espacio desconocido de búsqueda nunca es posible saber en ningún momento del tiempo o paso de iteración que se trata realmente de una dirección realmente prometedora hacia lo global. Por lo tanto, es imposible explorar primero y refinar después. Sólo pueden funcionar las estrategias de búsqueda global, que funcionan bien o mal. Cada uno elige por sí mismo el grado de "bondad" y "adecuación a la tarea", para ello se lleva una tabla de valoración para elegir un algoritmo en función de las particularidades de la tarea.
Sí, es cierto. En espacios de baja dimensionalidad (1-2) es muy fácil situarse en la vecindad de un global, los generadores aleatorios simples pueden incluso ser útiles para ello. Pero todo cambia completamente cuando la dimensionalidad del problema crece, aquí las propiedades de búsqueda de los algoritmos, y no la suerte, empiezan a jugar un papel importante.
Entonces fallan
Y, pregunta, ¿cuáles son sus impresiones sobre la velocidad de la heurística?
A pesar de que trabajan rápido. El resultado para 1000 parámetros algo alrededor de 0,4.
Es por eso que intuitivamente pensé que tiene sentido combinar GA y métodos de gradiente para llegar al máximo. De lo contrario, por separado no van a resolver su función. No lo he probado en la práctica.
P.D. Sigo pensando que esta función es demasiado gruesa, en tareas reales (entrenamiento de redes neuronales, por ejemplo) no hay tales problemas, aunque allí también la superficie de error está toda en mínimos locales.
1. No están haciendo un buen trabajo
2. aunque trabajan rápido. El resultado para 1000 parámetros es algo así como 0,4.
3. Por eso pensé intuitivamente que tiene sentido combinar los métodos GA y gradiente para llegar al máximo. De lo contrario, por separado no resolverán tu función. No lo he probado en la práctica.
4. P.D. Sigo pensando que esta función es demasiado gruesa, en tareas reales (entrenamiento de redes neuronales, por ejemplo) no hay tales problemas, aunque allí también la superficie de error está toda en mínimos locales.
1. ¿Qué quieres decir con "no dan abasto"? Hay un límite en el número de accesos a la función objetivo, el que mostró un mejor resultado es el que no puede hacer frente)). ¿Deberíamos aumentar el número de accesos permitidos? Bueno, entonces los más ágiles y adaptados a funciones complejas llegarán a la meta de todos modos. Intente aumentar el número de referencias, el panorama no cambiará.
2. Sí. Y algunos tienen 0,3, y otros 0,2, y otros 0,001. Mejores son los que mostraron 0,4.
3. No servirá de nada, intuitivamente se han probado y vuelto a probar cientos de combinaciones y variaciones. Mejor es el que muestra mejores resultados para un número dado de epochs (iteraciones). Aumenta el número de referencias al objetivo, a ver cuál llega antes a la meta.
4. Si hay líderes en las tareas difíciles, ¿crees que en las tareas fáciles los líderes mostrarán peores resultados que los outsiders? Este no es el caso, por decirlo suavemente. Estoy trabajando en una tarea más "sencilla" pero realista de formación de cuadrículas. Compartiré los resultados como siempre. Será interesante.
Simplemente experimenta, prueba diferentes algoritmos, diferentes tareas, no te estanques en una sola cosa. He intentado proporcionar todas las herramientas para ello.
1. ¿Qué quiere decir "fallar"? Hay un límite en el número de accesos a la función de destino, el que ha mostrado el mejor resultado es el que no da abasto)). ¿Deberíamos aumentar el número de accesos permitidos? Bueno, entonces los más ágiles y adaptados a funciones complejas llegarán a la meta de todos modos. Pruebe a aumentar el número de referencias, el panorama no cambiará.
2. Sí. Y algunos tienen 0,3, y otros 0,2, y otros 0,001. Mejores son los que mostraron 0,4.
3. No servirá de nada, intuitivamente se han probado y vuelto a probar cientos de combinaciones y variaciones. Mejor es el que muestra mejores resultados para un número dado de epochs (iteraciones). Aumente el número de referencias al objetivo, a ver cuál llega antes a la meta.
4. Si hay líderes en las tareas difíciles, ¿crees que en las tareas fáciles los líderes mostrarán peores resultados que los outsiders? Este no es el caso, por decirlo suavemente. Estoy trabajando en una tarea más "sencilla" pero realista de formación de cuadrículas. Compartiré los resultados como siempre. Será interesante.
Sólo experimenta, prueba diferentes algoritmos, diferentes tareas, no te fijes en una sola cosa. He intentado proporcionar todas las herramientas para ello.
Estoy experimentando,
Sobre la tarea realista es correcto probar algoritmos en tareas cercanas al combate.
Es doblemente interesante ver cómo se entrenarán las redes genéticas.