Algoritmo de Irrigación Artificial — Artificial Showering Algorithm (ASHA)
182
0
Contenido
Introducción
Con el vertiginoso crecimiento de los volúmenes de datos en el mundo actual y unas tareas cada vez más complejas y que consumen más energía, la necesidad de métodos de optimización eficientes resulta más importante que nunca. Los algoritmos metaheurísticos de alta convergencia y rápida velocidad de procesamiento descubren nuevos horizontes para resolver diversos problemas en campos que van desde los mercados financieros a la investigación científica.
La velocidad de procesamiento de los datos y la calidad de las soluciones resultantes juegan un papel clave en el éxito de la ejecución de los proyectos. Con plazos ajustados, en los que cada momento puede resultar crítico, los algoritmos metaheurísticos pueden lograr resultados que antes parecían inalcanzables. No solo posibilitan un procesamiento rápido de grandes cantidades de información, sino que también ayudan a encontrar mejores soluciones que los métodos numéricos tradicionales.
El ahorro de recursos es otro aspecto importante a considerar a la hora de optimizar. Con una potencia de cálculo limitada, estos algoritmos necesitan menos tiempo y memoria, lo que resulta especialmente valioso en la computación en nube. La adaptabilidad de los algoritmos a las condiciones cambiantes y su capacidad para reaccionar rápidamente a los nuevos datos los hacen casi ideales para los sistemas dinámicos. Esto mantiene actualizadas las soluciones y mejora la eficacia de la resolución de problemas en el mundo real.
La comparación de distintos algoritmos según sus características, como la velocidad de convergencia, la calidad de las soluciones y la resistencia a quedarse atascado en extremos locales, permite seleccionar los mejores, lo que a su vez fomenta la innovación y el desarrollo de métodos completamente nuevos, a menudo por imitación con la naturaleza, y constituye un paso importante en el campo de la optimización.
El algoritmo de irrigación artificial (Artificial Showering Algorithm, ASHA) es un nuevo método metaheurístico desarrollado para resolver problemas generales de optimización. Este algoritmo se basa en la modelización de los procesos de flujo y acumulación de agua distribuida con la ayuda de equipos controlados por el hombre en un campo ideal. El ASHA modela el proceso de distribución de agua (riego) en un campo, donde el agua representa unidades de recursos y el campo representa el espacio de búsqueda. El algoritmo usa los principios de flujo y acumulación para encontrar soluciones óptimas en problemas sin restricciones. El algoritmo de irrigación artificial (ASHA) fue desarrollado por un grupo de autores: Ali J., M. Said, N. A. Chaudhry, M. Luqman y M. F. Tabassum y publicado en 2015.
Implementación del algoritmo
El método se basa en los siguientes postulados:
- Campo ideal. El espacio de búsqueda es un campo ideal en el que el agua fluye sin resistencia y la infiltración solo se produce en el punto más bajo.
- Ausencia de factores externos. No existe evaporación, ni lluvia, ni flujo de agua.
- Disponibilidad de aspersores. Cada parte del espacio de búsqueda está al alcance de los aspersores sobre el campo.
- Cantidad constante de agua. El agua es abundante y su cantidad en el sistema cerrado permanecerá constante a lo largo de todas las iteraciones.
- Movimiento del agua. Cada unidad de agua posee una tendencia probabilística a desplazarse cuesta abajo.
Descripción del algoritmo ASHA por pasos.
Parámetros del algoritmo:
- f - función objetivo que se debe minimizar
- R*n - espacio de búsqueda n-dimensional
- K - posición actual en el contador de iteraciones
- m - número de unidades de agua (agentes de búsqueda)
- F - velocidad del flujo de agua
- δ - nivel de resistencia (umbral de infiltración)
- ρ₀ - probabilidad inicial
- β - parámetro que controla la velocidad de cambio de la probabilidad
- M - número máximo de iteraciones
Pasos del algoritmo:
1. Inicialización:
Establecemos el valor inicial ρ = ρ₀
Creamos m unidades de agua y las colocamos aleatoriamente en el espacio de búsqueda R*n
2. Valoración del paisaje: para cada unidad de agua, calculamos el valor de la función objetivo f en su posición actual
3. Ciclo básico (repetir M veces): para cada unidad de agua i (1 ≤ i ≤ m):
a) Elegimos un número aleatorio r_i ∈ (0, 1)
(b) Si r_i < ρ:
Seleccionamos una posición x_inferior aleatoria por debajo de la posición actual
Generamos un vector aleatorio s ∈ (0, 1)*n
Calculamos la nueva posición:
x_new = x_old + F × (s ∘ (x_lower x_old))
donde ∘ denota la multiplicación por elementos
Si x_new está en un nivel inferior a x_old:
Aceptamos la nueva posición
De lo contrario:
Generamos un número aleatorio r ∈ (0, 1)
Encontramos la posición x_más baja entre todas las unidades de agua
Calculamos la nueva posición:
x_new = x_old + F × r × (x_lowest x_old)
(c) Comprobación de la infiltración:
Si una unidad de agua ha superado el nivel de resistencia δ:
Creamos una nueva unidad de agua en una posición aleatoria
(d) Comparación con la posición más baja:
Encontramos la unidad de agua con el valor más bajo de la función objetivo
Si la unidad de agua actual tiene un valor inferior, las intercambiamos
(e) Actualización de la probabilidad ρ = max((M - K) / (β × M), ρ₀)
4. Finalización:
Encontramos la unidad de agua con el valor más bajo de la función objetivo
Devolvemos su posición como la mejor solución encontrada
Explicación del algoritmo:
1. El algoritmo simula el proceso de irrigación de un campo, donde cada unidad de agua representa un agente de búsqueda.
2. El espacio de búsqueda se considera un paisaje en el que los valores más bajos de la función objetivo se corresponden con los puntos de menor elevación.
3. Las unidades de agua tienden a "fluir" hacia puntos más bajos del paisaje, lo cual se corresponde con la búsqueda del mínimo de la función objetivo.
4. El parámetro ρ controla el equilibrio entre la exploración del espacio (valores grandes de ρ) y la explotación de las soluciones encontradas (valores pequeños de ρ).
5. El mecanismo de infiltración evita el atasco en mínimos localizados creando nuevas unidades de agua en posiciones aleatorias.
6. La comparación y el intercambio con la posición más baja garantiza que se mantenga la mejor solución encontrada.
7. La actualización dinámica ρ permite al algoritmo pasar gradualmente de la exploración a la explotación conforme aumenta el número de iteraciones.
El algoritmo utiliza la analogía del flujo de agua para la optimización, donde el agua (agentes de búsqueda) intenta encontrar los puntos más bajos del paisaje (mínimos de la función objetivo).
Según los autores, las principales ventajas de este algoritmo son:
- La capacidad para explorar un amplio espacio de soluciones gracias al movimiento aleatorio del agua.
- La capacidad de evitar los mínimos locales mediante un mecanismo de infiltración.
- El comportamiento adaptativo debido al cambio dinámico de la probabilidad ρ.
Veamos con detalle todas las fórmulas utilizadas por el algoritmo.
1. Fórmula para actualizar una posición si se cumple la probabilidad "ρ": x_new = x_old + F × (s ∘ (x_lower - x_old)), donde:
- x_new - nueva posición de la unidad de agua
- x_old - posición actual de la unidad de agua
- F - velocidad de flujo del agua (parámetro del algoritmo)
- s - vector aleatorio en el intervalo (0, 1)
- x_lower - posición seleccionada aleatoriamente por debajo de la posición actual
- ∘ - operador de multiplicación por elementos
La fórmula modela el movimiento del agua por una pendiente. El vector aleatorio "s" añade un elemento de aleatoriedad al movimiento, mientras que "F" controla el tamaño del paso.
2. Fórmula alternativa, en caso de que no se cumpla la probabilidad "ρ", actualización de la posición: x_new = x_old + F × r × (x_lowest - x_old), donde:
- r - número aleatorio en el intervalo (0, 1)
- x_lowest - posición con el valor más bajo de la función objetivo
La fórmula se usa cuando la fórmula básica no produce mejoras. Dirige una unidad de agua hacia el mínimo global.
Como podemos ver en estas fórmulas, el agua siempre tiende hacia posiciones más bajas que su posición actual. Si implementamos el algoritmo solo hasta este paso, probablemente se atasque en los extremos locales.
3. Fórmula de actualización de probabilidades, ρ = max ((M - K) / (β × M), ρ₀), donde:
- ρ - probabilidad actual de movimiento del agua
- M - número máximo de iteraciones
- K - número de la iteración actual
- β - parámetro que controla la velocidad de cambio de la probabilidad
- ρ₀ - probabilidad inicial
Esta fórmula disminuye gradualmente la probabilidad de que el agua se desplace hacia posiciones más bajas seleccionadas al azar y aumenta la probabilidad de que se desplace hacia el mínimo global. Esto permite al algoritmo pasar de explorar el espacio a mejorar las soluciones encontradas.
4. Condición de infiltración, si f (x_current) < δ, entonces se crea una nueva unidad de agua, donde:
- f (x_currente) - valor de la función objetivo en la posición actual
- δ - nivel de resistencia (umbral de infiltración)
Esta condición permite crear nuevas unidades de agua en posiciones aleatorias cuando la unidad de agua actual halla un punto suficientemente bajo. Esto se ha pensado para evitar el atasco en los mínimos localizados.
5. Comparación de posiciones, si f (x_i) < f (x_lowest), se cambian x_i y x_lowest, donde:
- f (x_i) - valor de la función objetivo para la i-ésima unidad de agua
- f (x_lowest) - valor más pequeño encontrado de la función objetivo
Las fórmulas anteriores constituyen la base del algoritmo ASHA.
- La fórmula de actualización de la posición imita el movimiento descendente del agua. El elemento aleatorio (s o r) añade variedad a la búsqueda permitiendo explorar diferentes regiones del espacio de soluciones.
- Se usa una fórmula alternativa de actualización de la posición con probabilidad creciente en cada nueva iteración para garantizar que la mejora de la solución global aumente a lo largo de las iteraciones.
- La fórmula de actualización de la probabilidad ρ proporciona un equilibrio entre exploración y explotación. Al principio del algoritmo, la probabilidad de desplazarse hacia posiciones inferiores del paisaje seleccionadas al azar es alta, lo que favorece una amplia exploración del espacio. Conforme se realizan iteraciones, la probabilidad disminuye, lo cual provoca una exploración más exhaustiva de las áreas prometedoras.
- La condición de infiltración permite al algoritmo "reiniciar" la búsqueda a partir de nuevas posiciones aleatorias al encontrarse una solución suficientemente buena. Esto ayuda a evitar el atasco en mínimos localizados.
- La comparación de posiciones garantiza que el algoritmo siempre "recuerde" la mejor solución encontrada y la use para guiar la búsqueda posterior.
Resumiendo: el algoritmo primero intenta encontrar la mejor posición moviéndose a un punto bajo aleatorio. Si esto falla, intenta desplazarse hacia la mejor posición global encontrada. Esto ofrece un equilibrio entre la búsqueda local y la exploración global del espacio de soluciones.
El principio de infiltración en el algoritmo ASHA puede no resultar obvio a primera vista. Vamos a analizarlo con más detalle:
- Tenemos un parámetro δ (delta) que se denomina nivel de resistencia o umbral de infiltración.
- En cada iteración, para cada unidad de agua, comprobamos si se ha vuelto "demasiado buena", es decir, si ha descendido por debajo de δ.
- Si el valor de la función objetivo para una unidad de agua dada es inferior a δ, se dice que el agua se ha "filtrado" o "infiltrado" en el suelo.
- En este caso, "crearemos" una nueva unidad de agua colocándola en una posición aleatoria del espacio de búsqueda.
Formalmente, esto se puede escribir de la siguiente manera: si f (x_i) < δ, entonces x_i = posición_aleatoria (), donde f (x_i) es el valor de la función objetivo de la i-ésima unidad de agua, y x_i es la posición de la i-ésima unidad de agua.
El objetivo de este mecanismo es evitar que todas las unidades de agua se queden atascadas en el mismo mínimo local; intentar seguir explorando el espacio de búsqueda incluso después de encontrar una buena solución y encontrar potencialmente soluciones aún mejores en zonas inexploradas.
Resulta esencial elegir el valor correcto de δ. Si δ es demasiado pequeño, la infiltración podría no producirse en absoluto; si δ es demasiado grande, el algoritmo podría "reiniciarse" continuamente antes de encontrar una solución óptima. Además, determinar un valor adecuado de δ puede resultar una tarea no trivial, especialmente cuando no conocemos de antemano el rango de valores de la función objetivo y no podemos establecer este parámetro como externo. Así que hemos introducido un contador de intentos de "infiltración" para cada gota, mientras que en el parámetro externo necesitaremos establecer su valor máximo. Con cada nuevo intento, la probabilidad de "infiltración" aumentará según la ley cuadrática, es decir, con aceleración. De esta forma, ninguna gota permanecerá demasiado tiempo en un mismo lugar, lo que evitará que se estanque en extremos localizados.
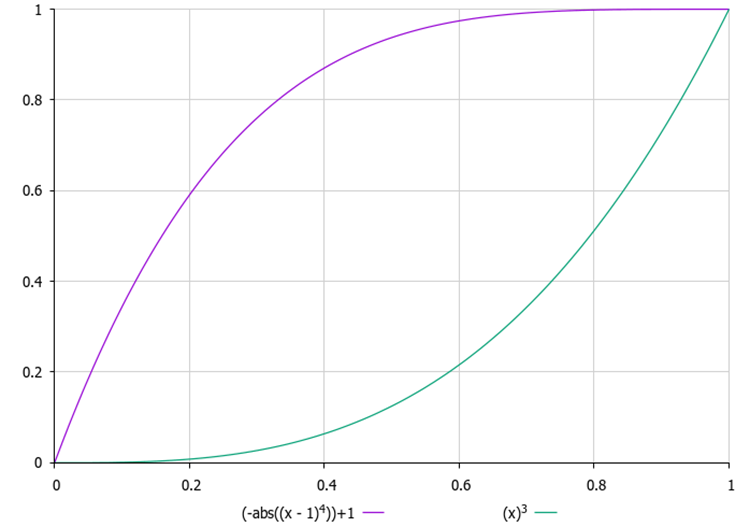
Figura 1. Ejemplos de cambios en la probabilidad de infiltración según el número de intentos
En cuanto al uso de las coordenadas del punto bajo, se suele adoptar el siguiente enfoque:
- Se encuentra la unidad de agua con el valor más bajo de la función objetivo (llamémosla x_lowest).
- La actualización de la posición usa todas las coordenadas de este punto más bajo: x_new = x_old + F × r × (x_lowest - x_old). Aquí x_new, x_old y x_lowest serán vectores que contienen todas las coordenadas.
- Esta ecuación vectorial se aplica a todas las coordenadas de forma simultánea. Es decir, la nueva posición es "atraída" por el punto más bajo por todas las dimensiones del espacio de búsqueda.
Este enfoque permite dirigir la búsqueda hacia la región más prometedora del espacio de soluciones, considerando todas las dimensiones al mismo tiempo.
Ya hemos mencionado más o menos todo lo que queríamos destacar; ahora escribiremos el código del algoritmo. Ah, otra cosa importante: para este algoritmo y posiblemente (de ser necesario) para los siguientes, hemos tenido que ampliar la estructura estándar para almacenar información adicional sobre el agente optimizador; los campos introducidos están marcados en verde.
Recordemos cómo es la estructura estándar del agente de optimización al que accede el programa de usuario, "S_AO_Agent", con adiciones:
1. Campos de la estructura:
- c [] - array de coordenadas actuales del agente en el espacio de búsqueda.
- cP [] - array de las coordenadas anteriores del agente.
- cB [] - array de las mejores coordenadas encontradas por el agente en todo el tiempo.
- f - valor de la función de aptitud para las coordenadas actuales del agente para evaluar el rendimiento del agente en la tarea.
- fP - valor de la función de aptitud de las coordenadas anteriores para rastrear el cambio en el rendimiento del agente.
- fB - valor de la función de aptitud para las mejores coordenadas, conserva el mejor resultado alcanzado por el agente.
- cnt - contador para llevar la cuenta del número de iteraciones.
2. Init () - el método de inicialización toma el número de coordenadas necesarias para el agente y realiza las siguientes acciones:
- redimensiona el array "c" a "coords", asignando memoria para almacenar las coordenadas actuales.
- cambia de forma similar el tamaño del array "cP" para almacenar las coordenadas anteriores y el tamaño del array "cB" para almacenar las mejores coordenadas.
- inicializa el valor actual de la función de aptitud con el valor mínimo posible, permitiendo al agente actualizarlo en la primera valoración.
- inicializa el valor anterior y el mejor valor de la función de aptitud de la misma manera.
- inicializa el contador a cero.
Así, la estructura "S_AO_Agent" permite almacenar información sobre el estado actual del agente, su rendimiento y la historia de cambios. Los cambios introducidos en la estructura no influirán en los algoritmos de optimización ya escritos sobre su base, pero simplificarán la construcción de nuevos algoritmos en el futuro.
//—————————————————————————————————————————————————————————————————————————————— struct S_AO_Agent { double c []; //coordinates double cP []; //previous coordinates double cB []; //best coordinates double f; //fitness double fP; //previous fitness double fB; //best fitness int cnt; //counter void Init (int coords) { ArrayResize (c, coords); ArrayResize (cP, coords); ArrayResize (cB, coords); f = -DBL_MAX; fP = -DBL_MAX; fB = -DBL_MAX; cnt = 0; } }; //——————————————————————————————————————————————————————————————————————————————
La clase "C_AO_ASHA" se hereda de la clase básica "C_AO" y representa la implementación del algoritmo de optimización ASHA; vamos a analizar su estructura y funcionalidad:
- F, δ, β, ρ0 son los parámetros específicos del algoritmo descrito anteriormente que determinan su comportamiento.
- params - array de estructuras que almacena los parámetros del algoritmo. Cada elemento del array contiene el nombre del parámetro y su valor.
El método "SetParams ()" se utiliza para establecer los valores de los parámetros del algoritmo a partir del array "params".
El método "Init ()" inicializa el algoritmo tomando como entrada los límites de búsqueda mínimo y máximo, el paso de búsqueda y el número de épocas.
Los métodos "Moving ()" y "Revision ()" se encargan de desplazar los agentes en el espacio de búsqueda, así como de revisar y actualizar el estado de los agentes y sus posiciones según los criterios de optimización.
Campos privados:
- S_AO_Agent aT [] - array para la población temporal, usado para clasificar la población.
- epochs - número total de épocas utilizadas en el proceso de optimización.
- epochNow - época actual en la que se encuentra el algoritmo.
La clase "C_AO_ASHA" incluye los parámetros, métodos y estructuras necesarios para gestionar el proceso de optimización y la interacción con los agentes.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ASHA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ASHA () { } C_AO_ASHA () { ao_name = "ASHA"; ao_desc = "Artificial Showering Algorithm"; ao_link = "https://www.mql5.com/es/articles/15980"; popSize = 100; //population size F = 0.3; //water flow velocity δ = 2; //resistance level(infiltration threshold) β = 0.8; //parameter that controls the rate of change in probability ρ0 = 0.1; //initial probability ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "F"; params [1].val = F; params [2].name = "δ"; params [2].val = δ; params [3].name = "β"; params [3].val = β; params [4].name = "ρ0"; params [4].val = ρ0; } void SetParams () { popSize = (int)params [0].val; F = params [1].val; δ = (int)params [2].val; β = params [3].val; ρ0 = params [4].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double F; //water flow velocity int δ; //resistance level(infiltration threshold) double β; //parameter that controls the rate of change in probability double ρ0; //initial probability private: //------------------------------------------------------------------- S_AO_Agent aT []; int epochs; int epochNow; }; //——————————————————————————————————————————————————————————————————————————————
El método "Init" se ocupa de inicializar el algoritmo de optimización. Lógica del método:
1. Comprobación de la inicialización estándar: el método llama a "StandardInit", que efectúa las comprobaciones básicas y la inicialización de los parámetros.
2. Establecimiento del contador:
- epochs se establece igual al valor "epochsP" transmitido (número total de iteraciones a realizar por el algoritmo).
- epochNow - se inicializa a cero; el algoritmo acaba de empezar a ejecutarse y aún no ha gastado ninguna época.
3. Reserva de memoria para una población temporal de agentes.
4. Si todos los pasos de inicialización se han realizado correctamente, el método retornará "true", indicando que el algoritmo se ha inicializado como es debido.
El método "Init" es el método clave para preparar el algoritmo para su funcionamiento. Verifica que los parámetros de entrada sean correctos, establece los valores necesarios para controlar el proceso de optimización y asigna memoria a los agentes. Una inicialización exitosa permitirá al algoritmo proceder con otras operaciones, como desplazar y revisar los agentes.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ASHA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; ArrayResize (aT, popSize); return true; } //——————————————————————————————————————————————————————————————————————————————
El método "Moving" implementa la lógica de desplazamiento de los agentes en el espacio de búsqueda dentro del algoritmo ASHA; vamos a desglosarlo paso a paso:
1. El método incrementa el contador de épocas actual para llevar la cuenta del número de iteraciones realizadas.
2. Inicialización (si no se requiere revisión): para cada agente "i" y para cada coordenada "c"
- genera las posiciones iniciales para todos los agentes dentro de los rangos dados utilizando "u.RNDfromCI" y aplica la discretización.
- entonces "revision" se establecerá en "true" y el método finalizará la ejecución.
3. Ciclo principal de agentes en movimiento, para cada agente "i" se realizan las siguientes acciones:
- inf - probabilidad, calculada utilizando "u.Scale" para obtener el valor que depende del contador "cnt" del agente. A continuación, este valor se eleva a la cuarta potencia para aumentar el impacto.
- luego se genera un número aleatorio "rnd" para la toma de decisiones.
4. Ciclo por las coordenadas; para cada coordenada "c" se ejecutan las acciones siguientes:
- se genera un índice "ind" para seleccionar otro agente con una posición inferior en el espacio de búsqueda que se utilizará para actualizar las coordenadas.
- si "i < 1", entonces: si "rnd < inf", las coordenadas del agente actual se actualizarán usando una distribución normal alrededor de las mejores coordenadas "cB" usando"u.GaussDistribution".
- si "i >= 1", entonces: si "rnd < inf", las coordenadas del agente actual se actualizarán de forma similar en relación con las coordenadas del otro agente "a[ind].cB".
- en caso contrario: se conservará el valor antiguo "xOld". Si el número aleatorio generado es menor que "ρ", entonces:
- "xNew" se actualizará basándose en el mejor valor de otro agente "xLower".
- de lo contrario: "xNew" se actualizará según el mejor valor global "xLowest".
- entonces se asignará el nuevo valor "xNew" al agente actual.
5. Corrección de coordenadas: por último, cada nuevo valor de coordenadas se corrige usando "u.SeInDiSp" para que coincida con los rangos y pasos especificados.
El método Moving posibilita tanto la inicialización de las posiciones de los agentes como las actualizaciones durante la optimización basándose en su estado actual y las interacciones con otros agentes.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASHA::Moving () { epochNow++; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double xOld = 0.0; double xNew = 0.0; double xLower = 0.0; double xLowest = 0.0; double ρ = MathMax (β * (epochs - epochNow) / epochs, ρ0); double inf = 0.0; int ind = 0; double rnd = 0.0; for (int i = 0; i < popSize; i++) { inf = u.Scale (a [i].cnt, 0, δ, 0, 1); inf = inf * inf * inf * inf; rnd = u.RNDprobab (); for (int c = 0; c < coords; c++) { ind = (int)u.RNDintInRange (0, i - 1); if (i < 1) { if (rnd < inf) { a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); } } else { if (rnd < inf) { a [i].c [c] = u.GaussDistribution (a [ind].cB [c], rangeMin [c], rangeMax [c], 8); } else { xOld = a [i].c [c]; if (u.RNDprobab () < ρ) { xLower = a [ind].cB [c]; xNew = xOld + F * (u.RNDprobab () * (xLower - xOld)); } else { xLowest = cB [c]; xNew = xOld + F * (u.RNDprobab () * (xLowest - xOld)); } a [i].c [c] = xNew; } } a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
El método "Revision" se encarga de actualizar la información sobre las mejores soluciones (agentes) de la población y de realizar un seguimiento de su aptitud, por etapas:
1. La variable "ind" se inicializa con el valor "-1" y se utiliza para almacenar el índice del agente con el mejor valor de la función aptitud "f".
2. Ciclo por los agentes: el método itera todos los agentes de la población "popSize":
- si el valor de la función de aptitud "f" del agente actual es mayor que su mejor valor actual "fB", entonces "fB" se actualizará y el índice de este agente se almacenará en la variable "ind".
- si el valor de la función de aptitud "f" del agente actual es mayor que su mejor valor local "fB", entonces también se actualizará el mejor valor local "fB" para ese agente.
- luego se copian las coordenadas "c" del agente en "cB", que son sus coordenadas más conocidas.
- el contador "cnt" se reinicia a "0", de lo contrario, si el valor de la función de aptitud no ha mejorado, el contador "cnt" se incrementará.
3. Copiado de las mejores coordenadas: si se ha encontrado un agente con el mejor valor de función (el índice "ind" no es igual a "-1"), sus coordenadas se copiarán en la variable global "cB".
4. Clasificación de los agentes: al final se llama al método "u.Sorting_fB", que clasifica los agentes según su mejor valor local "fB".
El método "Revision" desempeña un papel fundamental en el algoritmo, ya que controla el rendimiento de los agentes y actualiza sus mejores soluciones conocidas.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASHA::Revision () { //---------------------------------------------------------------------------- int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); a [i].cnt = 0; } else { a [i].cnt++; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Resultados de las pruebas
Los resultados de las pruebas del algoritmo ASHA han mostrado un rendimiento medio: =============================
5 Hilly's; Func runs: 10000; result: 0.8968571984324711
25 Hilly's; Func runs: 10000; result: 0.40433437407600525
500 Hilly's; Func runs: 10000; result: 0.25617375427148387
=============================
5 Forest's; Func runs: 10000; result: 0.8036024134603961
25 Forest's; Func runs: 10000; result: 0.35525531625936474
500 Forest's; Func runs: 10000; result: 0.1916000538491299
=============================
5 Megacity's; Func runs: 10000; result: 0.4769230769230769
25 Megacity's; Func runs: 10000; result: 0.1812307692307692
500 Megacity's; Func runs: 10000; result: 0.09773846153846236
=============================
All score: 3.66372 (40.71%)
Observando el trabajo del ASHA en el banco de pruebas, es difícil identificar algún rasgo característico de este algoritmo, no se detectan exploraciones aisladas de zonas prometedoras del espacio de búsqueda.
ASHA en la función de prueba Hilly
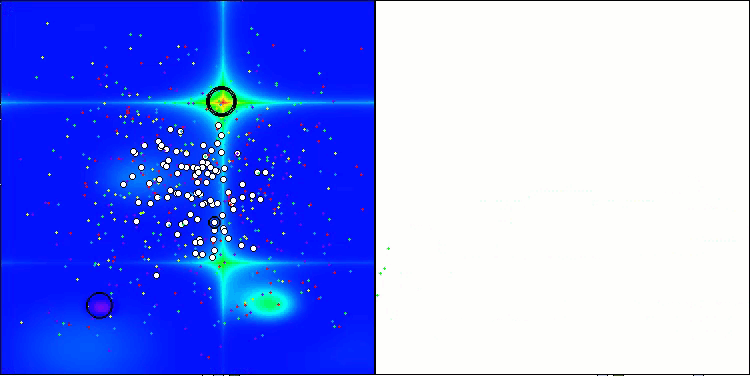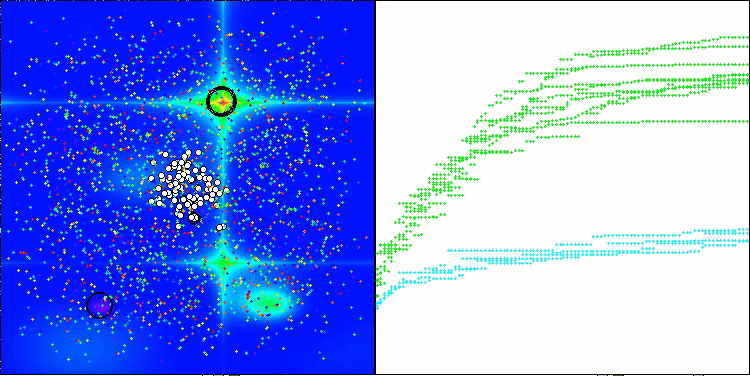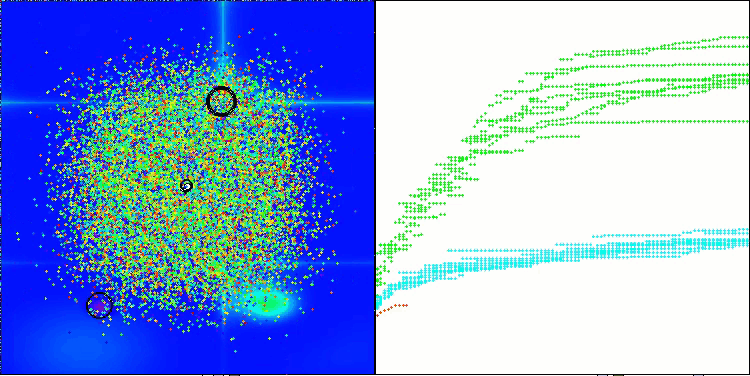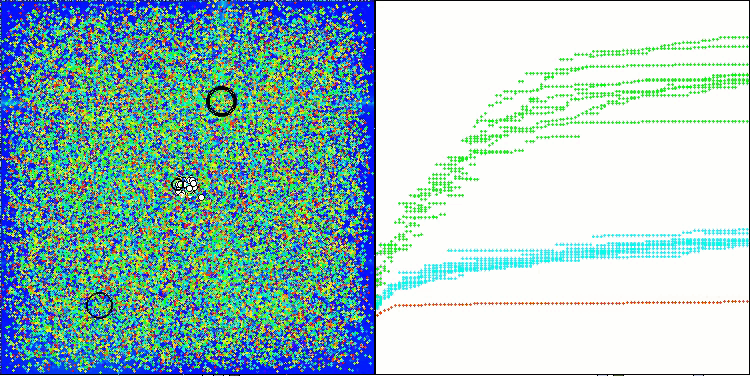
ASHA en la función de prueba Forest
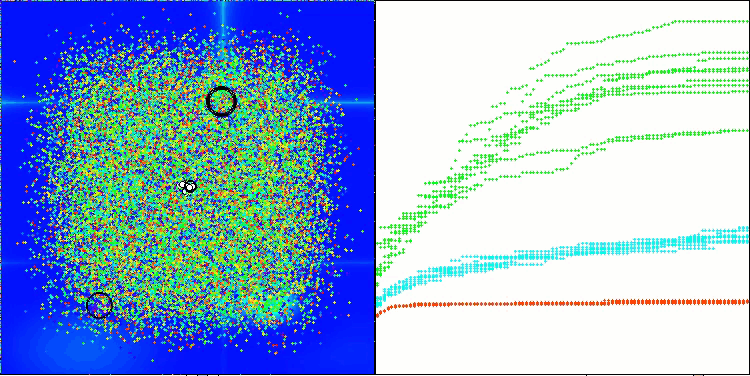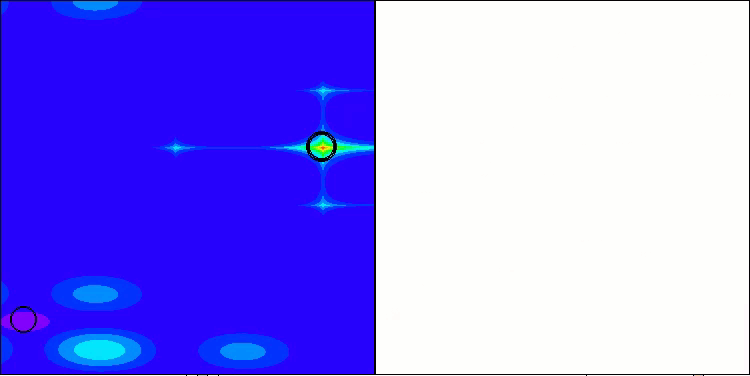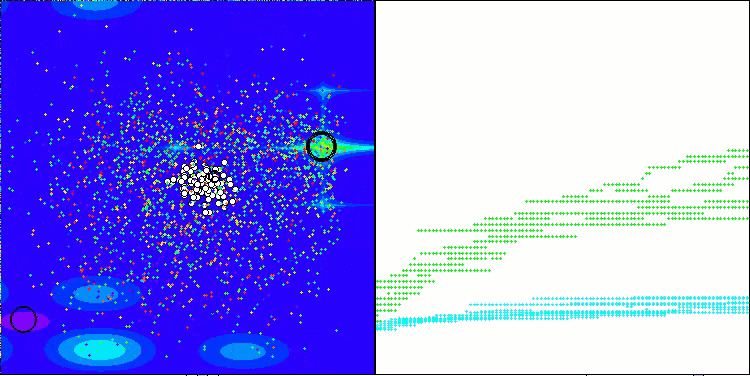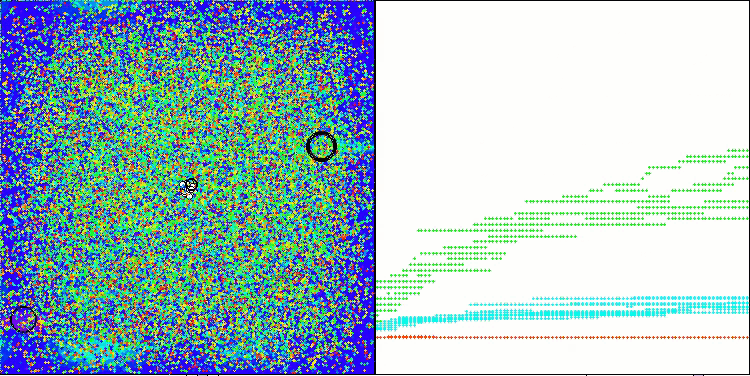
ASHA en la función de prueba Megacity
Según los resultados de las pruebas realizadas, el algoritmo ASHA ocupa el puesto 28 en la tabla de clasificación.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 12 | TSEA | turtle shell evolution algorithm | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 13 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 14 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 15 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 16 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 17 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 18 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 19 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 20 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 21 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 22 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 23 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 24 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 25 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 26 | ABH | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4.127 | 45,85 |
| 27 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 28 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 29 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3.657 | 40,63 |
| 30 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 31 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 32 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 33 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 34 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 35 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 36 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 37 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 38 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 39 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 40 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 41 | AAA | algae adaptive algorithm | 0,50007 | 0,32040 | 0,25525 | 1,07572 | 0,37021 | 0,22284 | 0,16785 | 0,76089 | 0,27846 | 0,14800 | 0,09755 | 0,52402 | 2,361 | 26,23 |
| 42 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 43 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
| 44 | PSO | particle swarm Optimization | 0,59726 | 0,36923 | 0,29928 | 1,26577 | 0,37237 | 0,16324 | 0,07010 | 0,60572 | 0,25667 | 0,08000 | 0,02157 | 0,35823 | 2,230 | 24,77 |
| 45 | Boids | boids algorithm | 0,43340 | 0,30581 | 0,25425 | 0,99346 | 0,35718 | 0,20160 | 0,15708 | 0,71586 | 0,27846 | 0,14277 | 0,09834 | 0,51957 | 2,229 | 24,77 |
Conclusiones
Me ha gustado la idea del algoritmo, pero al ponerlo en práctica y probarlo me ha dado la sensación de que le falta algo. Eso no quiere decir que sus resultados sean los peores, pero está lejos de ser el mejor. Y esto ofrece una oportunidad a los investigadores para seguir trabajando con él, sobre todo por su sencillez, ya que la idea en sí es, en mi opinión, muy prometedora. Además, los autores no han ofrecido una explicación más detallada de la tasa de infiltración, lo cual nos permite interpretarla de diferentes maneras, limitadas únicamente por nuestra propia imaginación.
La principal conclusión de este artículo sería la siguiente: no todas las ideas sencillas son tan eficaces como las más complejas. La eficacia de un algoritmo de optimización es una cuestión compleja e implica elecciones basadas en compromisos. Espero que este algoritmo se convierta en otra página de un gran libro de conocimientos sobre los entresijos y trucos en el arte de encontrar las mejores soluciones.
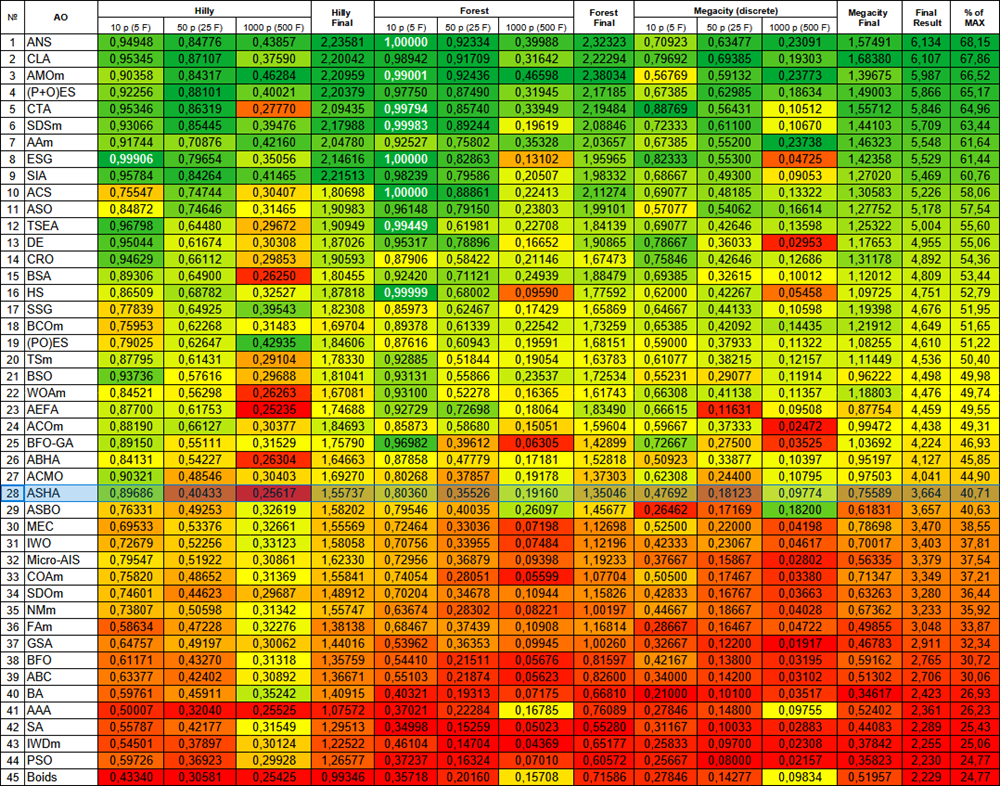
Figura 2. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0,99 aparecen resaltados en blanco.
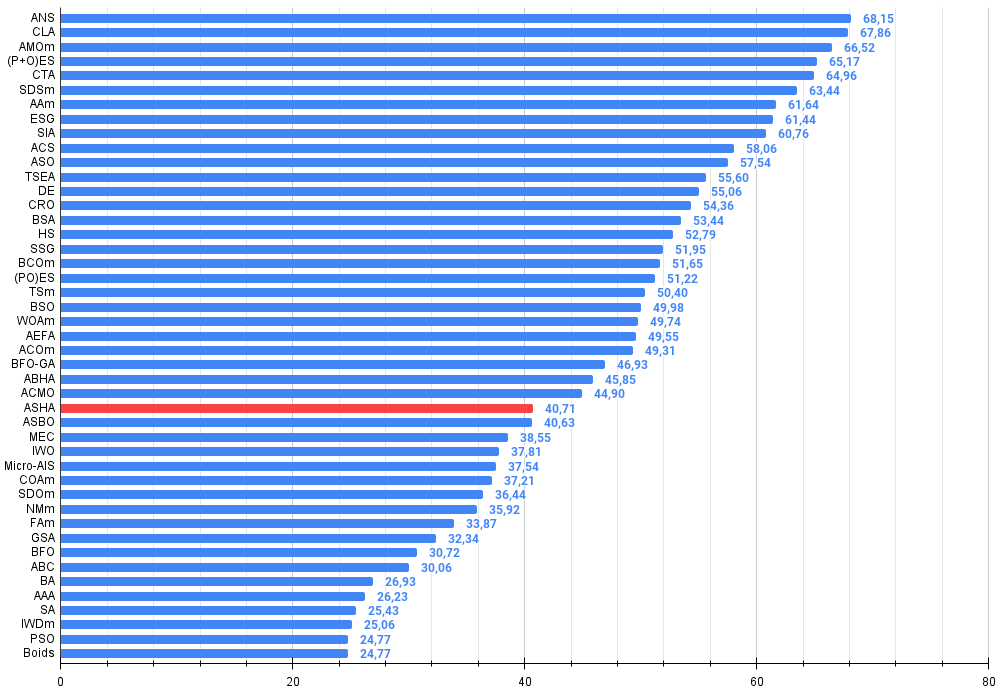
Figura 3. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor,
donde 100 es el máximo resultado teórico posible; el script para calcular la tabla de clasificación está en el archivo)
Ventajas e inconvenientes del algoritmo ASHA:
Ventajas:
- Es rápido.
- Implementación sencilla.
Desventajas:
- Baja precisión de convergencia.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15980
Sistema de arbitraje de alta frecuencia en Python con MetaTrader 5
Métodos de William Gann (Parte III): ¿Funciona la astrología?
Características del Wizard MQL5 que debe conocer (Parte 36): Q-Learning con Cadenas de Markov
Redes neuronales en el trading: Segmentación de datos basada en expresiones de referencia
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso