
Algoritmos de optimización de la población: Algoritmo de enjambre de aves (Bird Swarm Algorithm, BSA)
Contenido:
1. Introducción
2. Descripción del algoritmo
3. Resultados de las pruebas
1. Introducción
Las aves son criaturas asombrosas que ocupan un lugar esencial en la naturaleza y el ecosistema. Se cree que las aves descienden de los dinosaurios, sus parientes más cercanos. Uno de los ejemplos más famosos sería el Archaeopteryx, el ave más antigua conocida, que vivió hace unos 150 millones de años. Con frecuencia actúan como indicadores de la salud del medio ambiente porque los cambios en su número y su comportamiento pueden indicar problemas en el ecosistema, como la contaminación, la pérdida de hábitat y el cambio climático. Existen más de 10 000 especies conocidas de aves en la Tierra, y cada una tiene adaptaciones únicas a su estilo de vida.
Algunas aves pueden volar grandes distancias, otras sumergirse en las aguas a gran profundidad, otras poseen una voz con asombrosas capacidades. Las aves desempeñan un papel importante en el ecosistema, esparcen semillas de plantas, controlan las poblaciones de insectos y otros animales y suponen una fuente de alimento para los depredadores. Muchas especies de aves realizan largas migraciones, se reúnen e interactúan con otros miembros de su especie en una bandada, recorriendo miles de kilómetros juntos en busca de alimento o zonas de cría. Este excepcional fenómeno pone de relieve sus extraordinarias habilidades de navegación, de resistencia, interacción en grupo y cooperación. Las aves son una parte increíblemente diversa e importante de nuestro planeta.
El Bird Swarm Algorithm (BSA) es un apasionante algoritmo evolutivo bioinspirado que utiliza la inteligencia de enjambre, y se basa en las interacciones sociales y el comportamiento de las bandadas de pájaros. Desarrollado por Meng y sus colegas en 2015, el BSA supone un enfoque de optimización único que integra tres aspectos clave del comportamiento de las aves: el vuelo, la búsqueda de alimento y la vigilancia. Entre las bandadas electrónicas, donde cada "pájaro" posee tácticas y estrategias individuales, generando un sistema único de interacción colectiva, lleno de inteligencia algorítmica y creatividad. Aquí no solo resultan importantes los esfuerzos personales, sino también la capacidad de cooperar, compartir y apoyarse mutuamente en la persecución de un objetivo común de optimización.
Los distintos individuos del BSA pueden tener estrategias de búsqueda diferentes. Las aves pueden alternar de forma aleatoria entre el comportamiento de vuelo, la vigilancia y la búsqueda de alimento. El algoritmo de diseño biónico consiste en buscar alimentos basándose en la adaptación global e individual. Las aves también intentan desplazarse al centro de la población, lo cual puede provocar competencia con otras aves, o bien alejarse de la bandada. El comportamiento de las aves incluye el vuelo habitual y la migración, así como el cambio entre los papeles de «productor» y «mendigo». En el mundo de BSA, cada individuo en esa iteración concreta tiene su propia estrategia de búsqueda, lo cual hace que este algoritmo sea multidimensional y pueda exhibir su potencia.
Sin embargo, como muchos algoritmos de inteligencia de enjambre, el BSA puede sufrir de convergencia prematura y quedarse atascado en óptimos locales. Para lograr una convergencia más rápida con una gran precisión de los algoritmos de optimización basados en enjambres, se han usado varios métodos para equilibrar la explotación y la exploración.
El algoritmo BSA basado en el comportamiento de las aves se inspira en las interacciones colectivas en bandada de las aves en la naturaleza, cuyo comportamiento constituye la base de este algoritmo:
- Comportamiento de la bandada. Muchas aves, como los estorninos, las golondrinas y los gansos, muestran un comportamiento de bandada cuando vuelan juntos. Este comportamiento les ayuda a reducir la resistencia del aire y ahorrar energía durante las migraciones o la búsqueda de alimento.
- Comunicación. Las aves usan distintos tipos de comunicación, como sonidos, gestos y posturas, para comunicarse entre sí. Esto les permite coordinar sus acciones, advertir sobre peligros a sus congéneres y coordinar su búsqueda de alimento.
- Adaptabilidad. Las aves tienen un alto grado de adaptabilidad a las cambiantes condiciones del entorno. Pueden reaccionar rápidamente ante el peligro, los cambios meteorológicos y la disponibilidad de alimentos, y también adaptar su comportamiento y sus rutas migratorias según las circunstancias.
- Liderazgo y seguimiento. En una bandada de pájaros, suele haber un líder que define la dirección del vuelo y los demás pájaros le siguen. Esto demuestra el principio de liderazgo y seguimiento, que también se tiene en cuenta en el algoritmo BSA para encontrar eficientemente soluciones óptimas.
El algoritmo BSA usa estos principios del comportamiento de las aves para desarrollar una técnica de optimización eficaz que imite el comportamiento colectivo de las bandadas de pájaros para resolver diversos problemas de optimización. El BSA no es solo un algoritmo, también supone un fascinante viaje al mundo de la optimización, donde las interacciones sociales de las aves se convierten en fuente de inspiración para resolver problemas complejos con eficacia.
2. Descripción del algoritmo
Veamos a echar un vistazo más de cerca a la lógica del algoritmo BSA, que puede parecer compleja y confusa a primera vista. Antes de empezar a escribir el código, desarrollaremos el pseudocódigo del algoritmo que servirá de base para su implementación. Así resultará mucho más fácil entender cómo funciona el BSA.
El Pseudocódigo del Algoritmo de Enjambre de Pájaros (Bird Swarm Algorithm, BSA), es una descripción de alto nivel de un algoritmo que modela el comportamiento de una bandada de pájaros:
1. Inicialización de N soluciones y parámetros asociados
2. Generación de nuevas soluciones:
3. Si el pájaro está volando:
4. Si el pájaro es productor:
5. Búsqueda de un nuevo sector de alimentación
6. De lo contrario:
7. El pájaro mendigo sigue la pista del productor
8. De lo contrario:
9. Si el ave está buscando comida:
10. El pájaro se alimenta
11. De lo contrario:
12. El pájaro se mantiene alerta (vigilante)
13. Evaluación de la idoneidad de las nuevas soluciones
14. Actualización de la solución
15. Si se alcanza el criterio de parada:
16. Finalización del algoritmo
17. De lo contrario:
18. Volver al paso 2
La fórmula del punto 5 para un ave que busca un nuevo sector de alimentación será:
xn = RNDg (min, max, producerPower)
donde:
- xn - nuevo valor de las coordenadas
- RNDg - número aleatorio con distribución normal con el centro de distribución en la coordenada actual
- min y max - límites de la distribución
- producerPower - valor de la desviación típica del productor
La fórmula implica que un ave-productora podrá migrar en cualquier dirección a lo largo del espacio de búsqueda, con una probabilidad mayor en las proximidades de su posición actual. Esto garantizará que las aves exploren nuevas zonas en busca de alimento.
La fórmula del punto 7 para un pájaro mendigo que siga al productor será:
xn = x + (xK - x) * FL * RNDg (-1.0, 1.0, scroungerPower)
donde:
- xn - nuevo valor de las coordenadas
- x - mejor coordenada del mendigo en la historia.
- xK - mejor coordenada del productor en la historia, donde un ave aleatoria con la posición K en la población es elegida como productor
- RNDg - número aleatorio con distribución normal con el centro de la distribución en 0 y los límites "-1.0" y "1.0".
- scroungerPower - valor de la desviación estándar del mendigo
La fórmula muestra que el ave mendiga se orienta hacia sus mejores coordenadas y hacia las mejores coordenadas del mejor individuo de la bandada (el productor no se orientará hacia sus mejores coordenadas, sino hacia las coordenadas actuales). Esto modelará el comportamiento de seguimiento al líder en una manada.
La fórmula del punto 10 aplicable a un ave durante el periodo de alimentación fuera de vuelo será:
xn = x + (p - x) * C * r1 + (g - x) * S * r2
donde:
- xn - nuevo valor de las coordenadas
- x - coordenada actual
- p - mejor coordenada en la historia del ave que toma alimentos
- g - mejores coordenadas demográficas en la historia (mejor solución global)
- r1 - número aleatorio uniforme en el rango [0.0 ... 1.0]
- r2 - número aleatorio uniforme en el intervalo [0.0 ... 1.0]
- C - coeficiente cognitivo, parámetro externo
- S - coeficiente social, parámetro externo
La fórmula describe un momento de ingestión de alimento en el que el comportamiento del ave se basa en su propia experiencia (posición actual y mejor posición en el pasado) y en la experiencia de la bandada.
La fórmula del punto 12 para un ave vigilante será:
xn = x + A1 * (mean [c] - x) * r1 + A2 * (xK - x) * r2
donde:
- xn - nuevo valor de las coordenadas
- x - mejor coordenada de ave vigilante en la historia.
- r1 - número aleatorio uniforme en el rango [0.0 ... 1.0]
- r2 - número aleatorio uniforme en el rango [-1.0 ... 1.0]
- mean [c] - valor medio de la coordenada c-ésima basado en las mejores coordenadas de todas las aves de la bandada
A1 - coeficiente corrector de influencia de las coordenadas promediadas del centro de la bandada:
A1 = a1 * exp (-pFit * N / (sumFit + e))
donde:
- a1 - coeficiente, parámetro externo
- e = DBL_MIN, para evitar la división por 0
- pFit - mejor adaptación de ave vigilante
- sumFit - suma de las mejores adaptaciones de las aves de la bandada
- N - número de aves de la manada
A2 - factor de corrección que considera el efecto de la posición del ave seleccionada para la observación (en el campo de visión del ave vigilante) sobre el comportamiento de esta última. Fórmula para A2:
A2 = a2 * exp (((pFit - pFitK) / (|pFitK - pFit| + e)) * (N * pFitK / (sumFit + e)))
donde:
- a2 - coeficiente, parámetro externo
- e = DBL_MIN, para evitar la división por 0
- pFit - mejor adaptación de ave vigilante
- pFitK - mejor aptitud de un ave K seleccionada al azar en la población (el ave que ha estado a la vista del ave vigilante)
- sumFit - suma de las mejores adaptaciones de las aves de la bandada
- N - número de aves de la manada
De este modo, el ave vigilante observa su entorno, lo cual le permite advertir a tiempo a sus congéneres del peligro. Se trata del comportamiento más complejo de todos los descritos en el algoritmo, pues tiene en cuenta la aptitud de todas las aves de la población, así como la aptitud del propio ave vigilante y del individuo seleccionado para la observación. En esencia, el ave vigilante se desplazará hacia la aptitud general de la población, dada la posición de un congénere que haya entrado en su campo de visión.
El texto resaltado con color en el pseudocódigo corresponde a los elementos lógicos del BSA mostrados en el esquema de la figura 1.
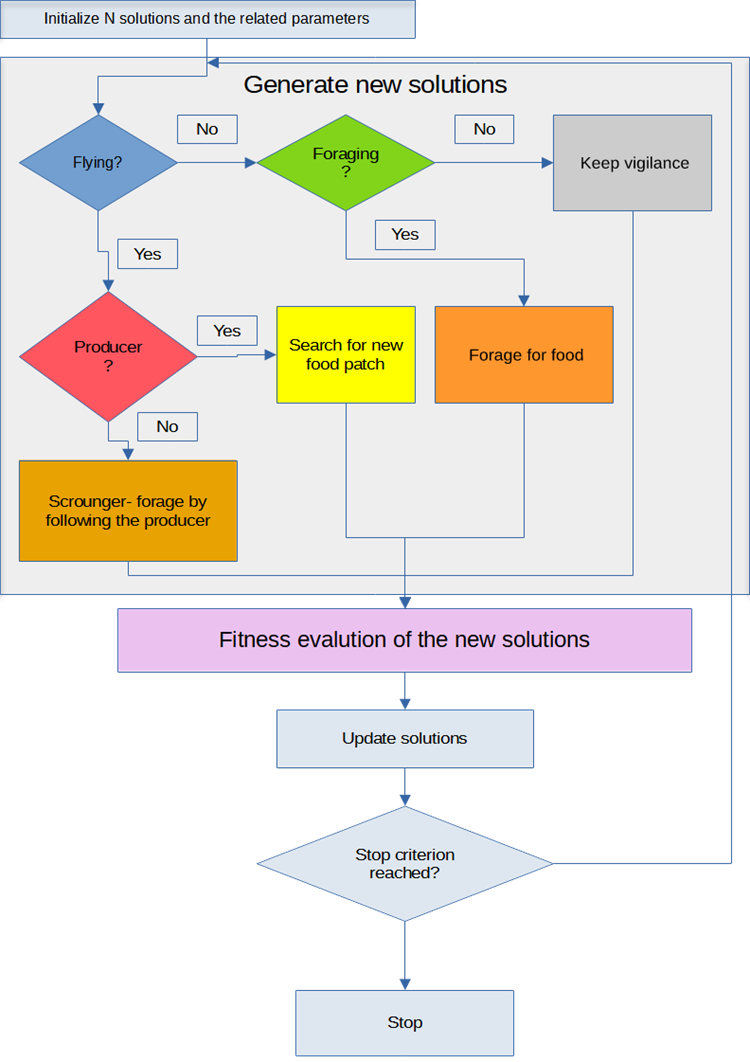
Figura 1. Esquema lógico del algoritmo BSA.
El esquema de la figura 1 supone una visualización del algoritmo BSA y modela el comportamiento de una bandada de pájaros. Las principales características de este algoritmo son:
- La inicialización de las soluciones. El algoritmo comienza inicializando un conjunto de soluciones y sus parámetros vinculados. Esto incluye la distribución inicial de las aves (o soluciones) en el espacio de búsqueda.
- El comportamiento de vuelo. Durante el proceso del algoritmo, cada ave puede "volar" o "no volar". Esta condición influye en la capacidad del ave para descubrir nuevas soluciones.
- El comportamiento de búsqueda de alimentos. Si un ave está "volando" puede convertirse en "productora" y empezar a buscar un nuevo sector de alimento, o puede convertirse en "mendiga", siguiendo al productor.
- El comportamiento de alimentación. Si un ave "no vuela", o bien se está alimentando o bien permanece vigilante. Puede representar un estado de espera, o bien de observación del entorno.
- La evaluación y actualización de las soluciones. Una vez generadas las nuevas soluciones, se evaluará su adaptabilidad o calidad.
- El criterio de parada. El algoritmo continuará el ciclo de generación y actualización de soluciones hasta que se alcance un determinado criterio de parada. Puede tratarse de un determinado número de iteraciones, del alcance de un determinado nivel de calidad de la solución o de cualquier otro criterio.
Me gustaría destacar que el BSA es un algoritmo dinámico que se adapta y evoluciona en el proceso de búsqueda de la solución óptima.
Vamos a escribir el código del algoritmo BSA. Para cada agente, definiremos la estructura "S_BSA_Agent", que supondrá una solución independiente al problema de la optimización, así como la descripción de un ave en la bandada.
La estructura contendrá los siguientes campos:
- cBest[] - array para almacenar las mejores coordenadas del agente.
- fBest - variable para almacenar la mejor estimación de aptitud del agente.
- Init - método de la estructura "S_BSA_Agent" que inicializa los campos de la estructura. Tomará el argumento entero "coords", el número de coordenadas que se utiliza para redimensionar el array "cBest" usando la función "ArrayResize".
Estableceremos un valor inicial de la variable "fBest" igual al valor mínimo posible de un número de tipo double, lo que significará la peor adaptación posible.
//—————————————————————————————————————————————————————————————————————————————— struct S_BSA_Agent { double cBest []; //best coordinates double fBest; //best fitness void Init (int coords) { ArrayResize (cBest, coords); fBest = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Vamos a definir ahora la clase "C_AO_BSA" del algoritmo BSA, que será la sucesora de la clase básica de los algoritmos de población "C_AO" y contendrá los siguientes campos y métodos:
1. Campos públicos:
- ao_name - nombre del algoritmo de optimización.
- ao_desc - descripción del algoritmo de optimización.
- popSize - tamaño de la población.
- params - array de parámetros del algoritmo.
- flyingProb - probabilidad de vuelo.
- producerProb - probabilidad de producción.
- foragingProb - probabilidad de recolección.
- a1 - constante a1 [0...2].
- a2 - constante a2 [0...2].
- C - coeficiente cognitivo.
- S - coeficiente social.
- FL - FL constante [0...2].
- producerPower - desviación estándar en el comportamiento de los productores.
- scroungerPower - desviación estándar en el comportamiento de los mendigos.
2. Métodos:
- C_AO_BSA - constructor de clase que inicializa los campos de la clase.
- SetParams - método para establecer los parámetros del algoritmo.
- Init - método para inicializar el algoritmo. Admite rangos de búsqueda mínimo y máximo, paso de búsqueda y número de épocas.
- Moving - método para desplazar a los agentes.
- Revision - método para revisar a los agentes.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BSA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_BSA () { } C_AO_BSA () { ao_name = "BSA"; ao_desc = "Bird Swarm Algorithm"; popSize = 20; //population size flyingProb = 0.8; //Flight probability producerProb = 0.25; //Producer probability foragingProb = 0.55; //Foraging probability a1 = 0.6; //a1 constant [0...2] a2 = 0.05; //a2 constant [0...2] C = 0.05; //Cognitive coefficient S = 1.1; //Social coefficient FL = 1.75; //FL constant [0...2] producerPower = 7.05; //Producer power scroungerPower = 2.60; //Scrounger power ArrayResize (params, 11); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "flyingProb"; params [1].val = flyingProb; params [2].name = "producerProb"; params [2].val = producerProb; params [3].name = "foragingProb"; params [3].val = foragingProb; params [4].name = "a1"; params [4].val = a1; params [5].name = "a2"; params [5].val = a2; params [6].name = "C"; params [6].val = C; params [7].name = "S"; params [7].val = S; params [8].name = "FL"; params [8].val = FL; params [9].name = "producerPower"; params [9].val = producerPower; params [10].name = "scroungerPower"; params [10].val = scroungerPower; } void SetParams () { popSize = (int)params [0].val; flyingProb = params [1].val; producerProb = params [2].val; foragingProb = params [3].val; a1 = params [4].val; a2 = params [5].val; C = params [6].val; S = params [7].val; FL = params [8].val; producerPower = params [9].val; scroungerPower = params [10].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); void Injection (const int popPos, const int coordPos, const double value); //---------------------------------------------------------------------------- double flyingProb; //Flight probability double producerProb; //Producer probability double foragingProb; //Foraging probability double a1; //a1 constant [0...2] double a2; //a2 constant [0...2] double C; //Cognitive coefficient double S; //Social coefficient double FL; //FL constant [0...2] double producerPower; //Producer power double scroungerPower; //Scrounger power S_BSA_Agent agent []; private: //------------------------------------------------------------------- double mean []; //represents the element of the average position of the whole bird’s swarm double N; double e; //epsilon void BirdProducer (int pos); void BirdScrounger (int pos); void BirdForaging (int pos); void BirdVigilance (int pos); }; //——————————————————————————————————————————————————————————————————————————————
El método "Init" de la clase "C_AO_BSA" se utilizará para inicializar las variables de la clase basándose en los parámetros transmitidos. Este método realiza una inicialización estándar usando el método "StandardInit", que admite los rangos de búsqueda mínimo y máximo, así como el paso de búsqueda.
Si la inicialización estándar se ha realizado correctamente, el método continuará inicializando las variables "N" y "e". El valor de "N" se establecerá igual al tamaño de la población "popSize", mientras que "e"-épsilon se inicializará con el valor mínimo de un número de tipo double.
A continuación, el método redimensiona el array "agent" a "popSize". Para cada elemento del "agente", se llama al método "Init" con el parámetro "coords". El array "mean" también se redimensionará a "coords", este array se utilizará para almacenar las coordenadas de las aves promediadas según la población.
El método retornará "true" si la inicialización se ha realizado correctamente y "false" en caso contrario.
Este método realizará la configuración inicial del algoritmo de optimización BSA con los parámetros especificados y lo preparará para realizar la optimización.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_BSA::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) //number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (agent, popSize); for (int i = 0; i < popSize; i++) agent [i].Init (coords); ArrayResize (mean, coords); N = popSize; e = DBL_MIN; return true; } //——————————————————————————————————————————————————————————————————————————————
El método "Moving" de la clase "C_AO_BSA" se utilizará para desplazar agentes durante el proceso de optimización. El método ejecutará las siguientes acciones:
- Si "revision" es "false", las coordenadas de los agentes "a[i].c[c]" se inicializarán utilizando valores aleatorios dentro de los rangos dados. A continuación, la bandera "revisión" se establecerá en "true" y el método finalizará.
- Si "revision" no es igual a "false", se calcularán las nuevas coordenadas para cada agente utilizando fórmulas y probabilidades.
En la segunda y siguientes épocas, el método llamará a las funciones que determinarán el comportamiento de cada ave de la bandada según las probabilidades ejecutadas:
- Si la probabilidad de vuelo - "flyingProb" se ha ejecutado, el agente "volará". En este caso, hay dos comportamientos posibles:
- Si la probabilidad es menor que "producerProb", entonces el agente será un "productor" y estará buscando un nuevo lugar para comer.
- De lo contrario, el agente será un "mendigo" y seguirá al productor.
- Si "no vuela", serán posibles los dos comportamientos siguientes:
- Si la probabilidad es menor que "foragingProb", entonces el agente "recolectará" la comida.
- En caso contrario, el agente se encontrará en estado de "vigilancia".
Este método se encarga de actualizar las coordenadas de los agentes en el algoritmo de optimización BSA según la época actual, los valores aleatorios y las probabilidades.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BSA::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { //bird is flying------------------------------------------------------------ if (u.RNDprobab () < flyingProb) { //bird producer if (u.RNDprobab () < producerProb) BirdProducer (i); //bird is looking for a new place to eat //bird is not a producer else BirdScrounger (i); //scrounger follows the producer } //bird is not flying-------------------------------------------------------- else { //bird foraging if (u.RNDprobab () < foragingProb) BirdForaging (i); //bird feeds //bird is not foraging else BirdVigilance (i); //bird vigilance } } } //——————————————————————————————————————————————————————————————————————————————
El método "BirdProducer" de la clase "C_AO_BSA" se utiliza para modelar el comportamiento del "productor" en el algoritmo BSA. El método ejecutará las siguientes acciones:
- Inicializa la variable "x", que se usará para almacenar la posición actual del ave.
- A continuación, se realizarán los siguientes pasos para cada coordenada del agente:
- El valor "x" se establecerá igual a la coordenada actual del agente.
- El valor "x" se actualizará usando una distribución gaussiana en la que la media será igual a la coordenada actual y el rango y la desviación típica estarán definidos por "rangeMin", "rangeMax" y "producerPower".
- El nuevo valor de la coordenada del agente se establecerá mediante el método "SeInDiSp", que ajustará el valor "x" según el rango y el paso de búsqueda.
Este método modelará el comportamiento del "productor" en el algoritmo BSA, que busca nuevas ubicaciones de fuentes de alimento (es decir, nuevas soluciones potenciales) usando una distribución gaussiana para explorar el espacio de búsqueda.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BSA::BirdProducer (int pos) { double x = 0.0; //bird position for (int c = 0; c < coords; c++) { x = a [pos].c [c]; x = u.GaussDistribution (x, rangeMin [c], rangeMax [c], producerPower); a [pos].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
El método que modela el comportamiento del "mendigo" será la función "BirdScrounger" de la clase "C_AO_BSA". Realizará las siguientes acciones:
- 1. Inicializará las variables "K", "x" y "xK". "K" será la posición de un ave seleccionada al azar en la bandada, "x" será la mejor posición del ave y "xK" será la mejor posición actual de un ave seleccionada al azar en la bandada.
- 2. Ejecutará un ciclo a través de todas las coordenadas.
- Seleccionará un ave al azar que no será el ave actual.
- Actualizará "x" y "xK" basándose en las mejores posiciones del ave actual y de un ave seleccionada al azar.
- Actualizará "x" utilizando una distribución gaussiana.
- Por último, actualizará la posición actual del ave mediante el método "SeInDiSp", y además ajustará el valor "x" según el rango de búsqueda y el paso.
Este método modelará el comportamiento del "mendigo" en el algoritmo BSA, utilizando una distribución gaussiana que seguirá al "productor" (es decir, afinará su propia ubicación con respecto a la posición del productor).
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BSA::BirdScrounger (int pos) { int K = 0; //position of a randomly selected bird in a swarm double x = 0.0; //best bird position double xK = 0.0; //current best position of a randomly selected bird in a swarm for (int c = 0; c < coords; c++) { do K = u.RNDminusOne (popSize); while (K == pos); x = agent [pos].cBest [c]; xK = agent [K].cBest [c]; x = x + (xK - x) * FL * u.GaussDistribution (0, -1.0, 1.0, scroungerPower); a [pos].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
Para un ave que no vuela en ese momento y está ocupada comiendo, se ha previsto el método "BirdForaging" de la clase "C_AO_BSA". Dentro de un ciclo a través de todas las coordenadas, el método hará lo siguiente:
- Actualizará "x", "p" y "g" en función de la posición actual y la mejor posición del ave, así como de la mejor posición global.
- Generará dos números aleatorios "r1" y "r2".
- Actualizará "x" utilizando estos números aleatorios, así como las constantes "C" y "S".
- Corregirá la posición del ave obtenida usando la función "SeInDiSp".
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BSA::BirdForaging (int pos) { double x = 0.0; //current bird position double p = 0.0; //best bird position double g = 0.0; //best global position double r1 = 0.0; //uniform random number [0.0 ... 1.0] double r2 = 0.0; //uniform random number [0.0 ... 1.0] for (int c = 0; c < coords; c++) { x = a [pos].c [c]; p = agent [pos].cBest [c]; g = cB [c]; r1 = u.RNDprobab (); r2 = u.RNDprobab (); x = x + (p - x) * C * r1 + (g - x) * S * r2; a [pos].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
El último y más complejo método que modelará el comportamiento de un ave vigilante es "BirdVigilance". Realizará las siguientes acciones:
- Calculará la suma de los mejores valores de adaptación de todas las aves de la bandada.
- Calculará el valor medio de cada coordenada para todas las aves de la bandada.
- Seleccionará un ave al azar que no será el ave actual.
- Actualizará "pFit" y "pFitK" basándose en los mejores valores de adaptación del ave actual y de un ave seleccionada al azar.
- Calculará "A1" y "A2" utilizando una función exponencial que dependerá de "pFit", "pFitK", "N", "sumFit" y "e".
- Ejecutará un ciclo a través de todas las coordenadas:
- Generará dos números aleatorios "r1" y "r2".
- Actualizará "x" y "xK" basándose en las mejores posiciones del ave actual y de un ave seleccionada al azar.
- Actualizará "x" utilizando "A1", "A2", "r1" y "r2".
- Corregirá la posición actual del ave mediante la función "SeInDiSp".
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BSA::BirdVigilance (int pos) { int K = 0; //position of a randomly selected bird in a swarm double sumFit = 0.0; //best birds fitness sum double pFitK = 0.0; //best fitness of a randomly selected bird double pFit = 0.0; //best bird fitness double A1 = 0.0; double A2 = 0.0; double r1 = 0.0; //uniform random number [ 0.0 ... 1.0] double r2 = 0.0; //uniform random number [-1.0 ... 1.0] double x = 0.0; //best bird position double xK = 0.0; //best position of a randomly selected bird in a swarm ArrayInitialize (mean, 0.0); for (int i = 0; i < popSize; i++) sumFit += agent [i].fBest; for (int c = 0; c < coords; c++) { for (int i = 0; i < popSize; i++) mean [c] += a [i].c [c]; mean [c] /= popSize; } do K = u.RNDminusOne (popSize); while (K == pos); pFit = agent [pos].fBest; pFitK = agent [K].fBest; A1 = a1 * exp (-pFit * N / (sumFit + e)); A2 = a2 * exp (((pFit - pFitK) / (fabs (pFitK - pFit) + e)) * (N * pFitK / (sumFit + e))); for (int c = 0; c < coords; c++) { r1 = u.RNDprobab (); r2 = u.RNDfromCI (-1, 1); x = agent [pos].cBest [c]; xK = agent [K].cBest [c]; x = x + A1 * (mean [c] - x) * r1 + A2 * (xK - x) * r2; a [pos].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
Finalmente, se utilizará el método "Revision" de la clase "C_AO_BSA" para actualizar la mejor solución global y actualizar las mejores posiciones de los agentes. El método ejecutará las siguientes acciones:
- Actualizará la mejor solución global.
- Actualizará los mejores valores anteriores de la función de adaptación y de las coordenadas del agente.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BSA::Revision () { //---------------------------------------------------------------------------- int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) ind = i; } if (ind != -1) { fB = a [ind].f; ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > agent [i].fBest) { agent [i].fBest = a [i].f; ArrayCopy (agent [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
3. Resultados de las pruebas
Me gustaría profundizar en los resultados del algoritmo BSA con diferentes conjuntos de características. La puntuación total del BSA en todas las funciones de la prueba ha sido de 4,80947, lo que se corresponde con el 53,44% de la puntuación máxima posible. Este resultado indica la eficacia global del algoritmo, por lo que podemos concluir que el algoritmo BSA tiene potencial para resolver con éxito una gran variedad de problemas de optimización de diferentes funciones.
BSA|Bird Swarm Algorithm|20.0|0.8|0.25|0.55|0.6|0.05|0.05|1.1|1.75|7.05|2.6|
=============================
5 Hilly's; Func runs: 10000; result: 0.8930600046782612
25 Hilly's; Func runs: 10000; result: 0.6489975525320968
500 Hilly's; Func runs: 10000; result: 0.262496551797822
=============================
5 Forest's; Func runs: 10000; result: 0.9241962617798402
25 Forest's; Func runs: 10000; result: 0.7112057472851052
500 Forest's; Func runs: 10000; result: 0.24938963509983267
=============================
5 Megacity's; Func runs: 10000; result: 0.6938461538461538
25 Megacity's; Func runs: 10000; result: 0.3261538461538461
500 Megacity's; Func runs: 10000; result: 0.1001230769230778
=============================
All score: 4.80947 (53.44%)
La visualización del rendimiento del algoritmo permite observar una variación significativa de los resultados con diferentes funciones de prueba. A pesar de explorar con éxito las superficies localizadas, el algoritmo puede atascarse en trampas localizadas. Esto limita su capacidad para alcanzar un óptimo global y puede provocar una falta de estabilidad en la búsqueda de una solución óptima.
La visualización del rendimiento con la función de prueba Skin supone solo un ejemplo del rendimiento del algoritmo y no participa en la tabla de clasificación.
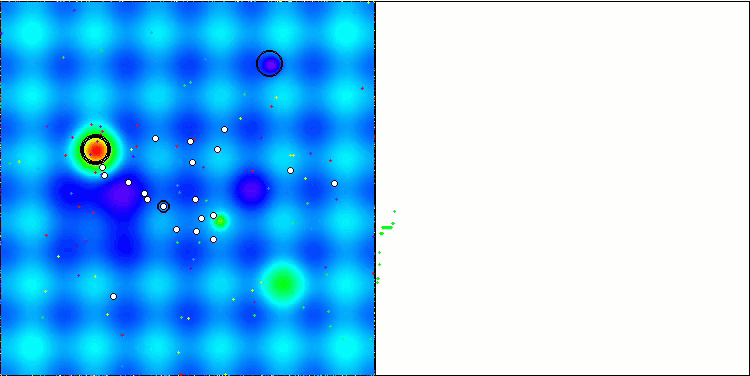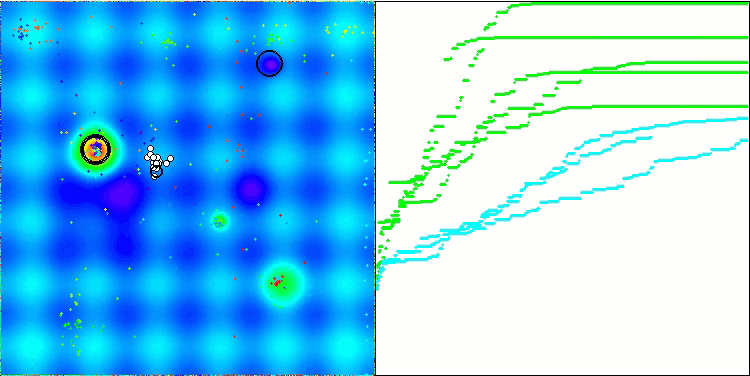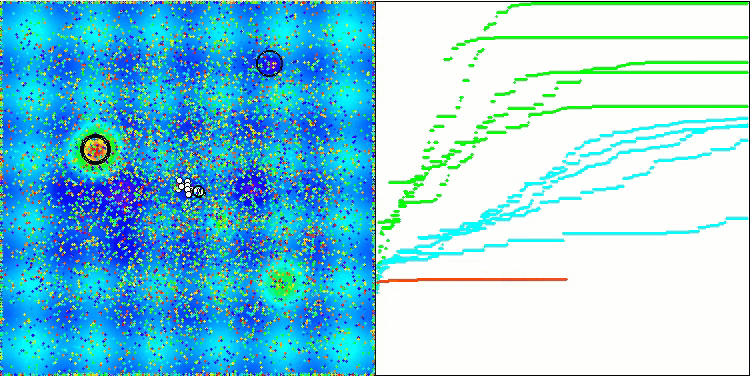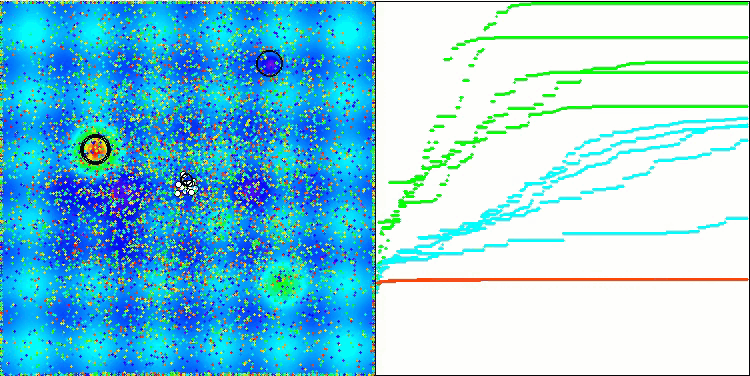
BSA en la función de prueba Hilly.
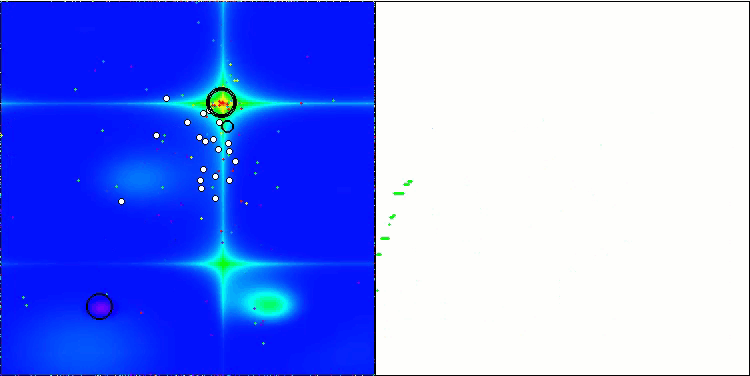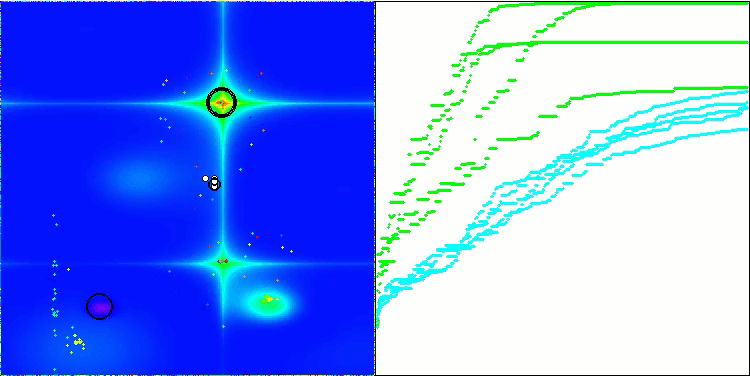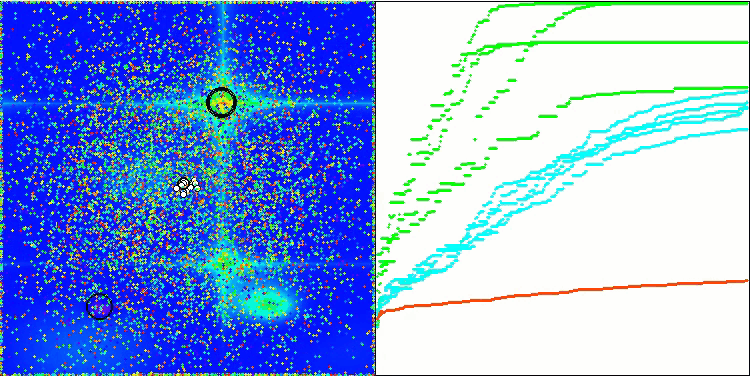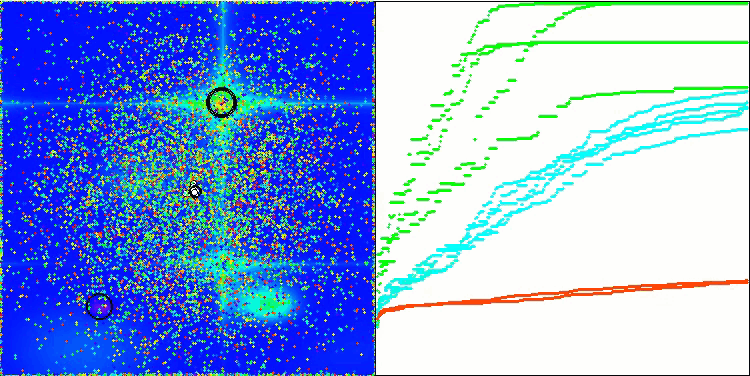
BSA en la función de prueba Forest.
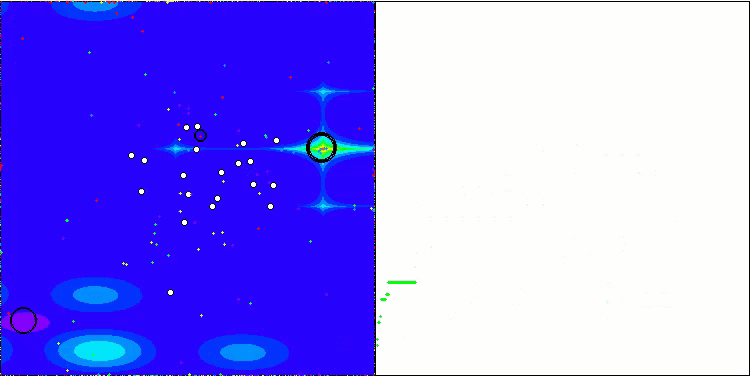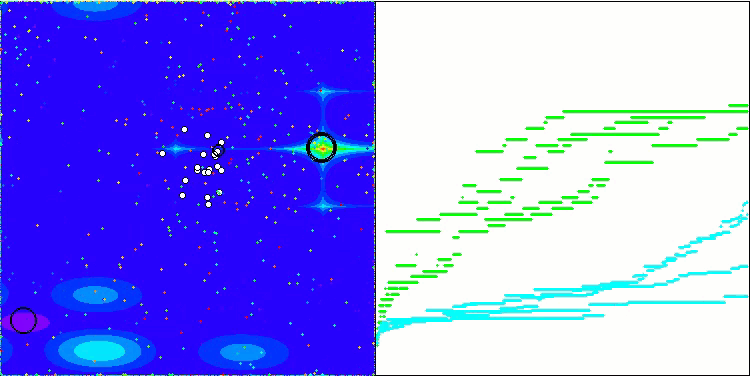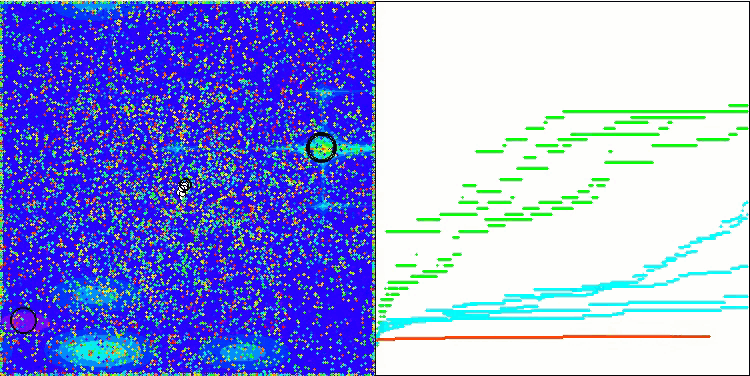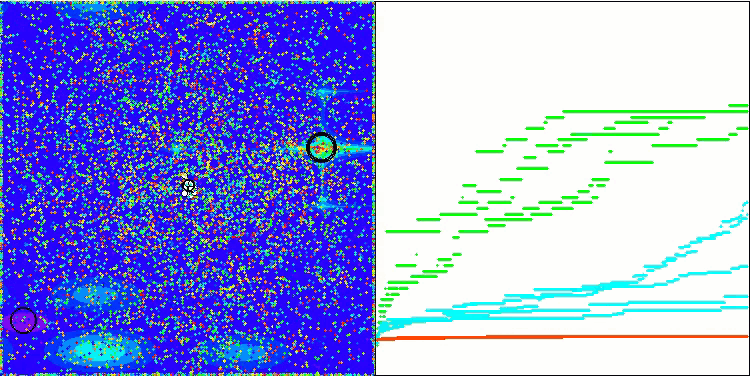
BSA en la función de prueba Megacity.
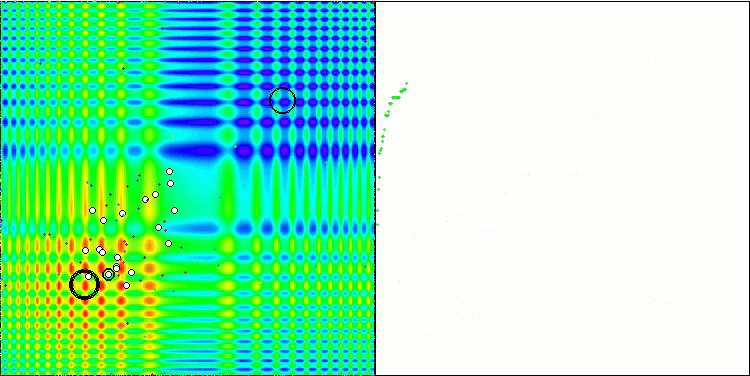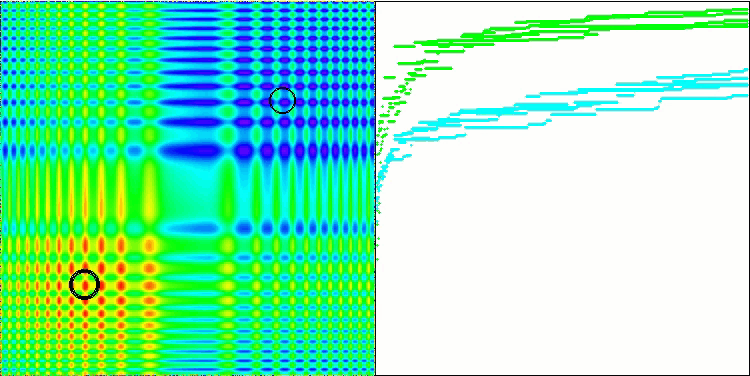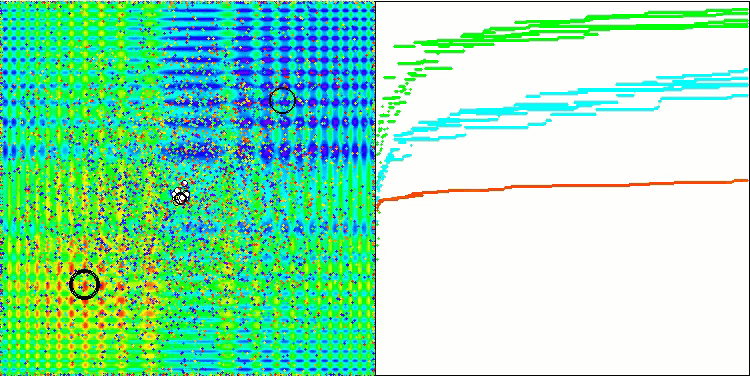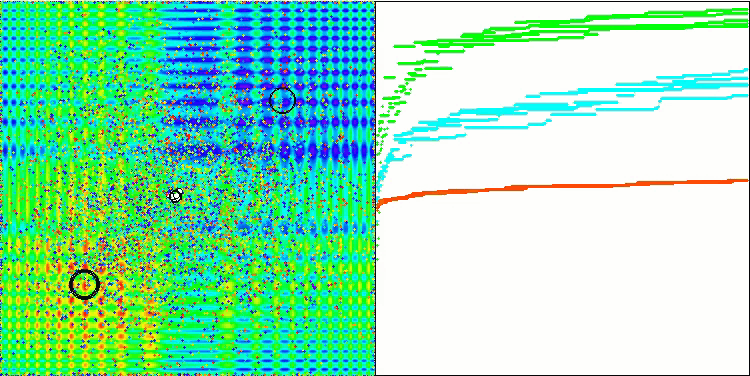
BSA en función de la prueba Skin.
Es importante señalar que en la prueba de la función suave Hilly con un elevado número de variables, el algoritmo ha tenido un rendimiento extremadamente ineficiente, mostrando el resultado más bajo en la tabla de clasificación entre todos los algoritmos considerados, aunque, eso sí, en las funciones Forest y Megacity discreta de alta dimensionalidad, el BSA muestra resultados decentes en comparación con otros algoritmos, incluidos los anteriores en la tabla.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | BGA | binary genetic algorithm | 0,99992 | 0,99484 | 0,50483 | 2,49959 | 1,00000 | 0,99975 | 0,32054 | 2,32029 | 0,90667 | 0,96400 | 0,23035 | 2,10102 | 6,921 | 76,90 |
| 2 | (P+O)ES | (P+O) evolution strategies | 0,99934 | 0,91895 | 0,56297 | 2,48127 | 1,00000 | 0,93522 | 0,39179 | 2,32701 | 0,83167 | 0,64433 | 0,21155 | 1,68755 | 6,496 | 72,18 |
| 3 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 4 | ESG | evolution of social groups | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 5 | SIA | simulated isotropic annealing | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 6 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 7 | BSA | bird swarm algorithm | 0,90857 | 0,73661 | 0,25767 | 1,90285 | 0,90437 | 0,81619 | 0,16401 | 1,88457 | 0,61692 | 0,54154 | 0,10951 | 1,26797 | 5,055 | 56,17 |
| 8 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 9 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 10 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 11 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 12 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 13 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 14 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 15 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 16 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 17 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 18 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 19 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 20 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 21 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 22 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 23 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 24 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 25 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 26 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
| 27 | PSO | particle swarm optimisation | 0,59726 | 0,36923 | 0,29928 | 1,26577 | 0,37237 | 0,16324 | 0,07010 | 0,60572 | 0,25667 | 0,08000 | 0,02157 | 0,35823 | 2,230 | 24,77 |
| 28 | MA | monkey algorithm | 0,59107 | 0,42681 | 0,31816 | 1,33604 | 0,31138 | 0,14069 | 0,06612 | 0,51819 | 0,22833 | 0,08567 | 0,02790 | 0,34190 | 2,196 | 24,40 |
| 29 | SFL | shuffled frog-leaping | 0,53925 | 0,35816 | 0,29809 | 1,19551 | 0,37141 | 0,11427 | 0,04051 | 0,52618 | 0,27167 | 0,08667 | 0,02402 | 0,38235 | 2,104 | 23,38 |
| 30 | FSS | fish school search | 0,55669 | 0,39992 | 0,31172 | 1,26833 | 0,31009 | 0,11889 | 0,04569 | 0,47467 | 0,21167 | 0,07633 | 0,02488 | 0,31288 | 2,056 | 22,84 |
| 31 | RND | random | 0,52033 | 0,36068 | 0,30133 | 1,18234 | 0,31335 | 0,11787 | 0,04354 | 0,47476 | 0,25333 | 0,07933 | 0,02382 | 0,35648 | 2,014 | 22,37 |
| 32 | GWO | grey wolf optimizer | 0,59169 | 0,36561 | 0,29595 | 1,25326 | 0,24499 | 0,09047 | 0,03612 | 0,37158 | 0,27667 | 0,08567 | 0,02170 | 0,38403 | 2,009 | 22,32 |
| 33 | CSS | charged system search | 0,44252 | 0,35454 | 0,35201 | 1,14907 | 0,24140 | 0,11345 | 0,06814 | 0,42299 | 0,18333 | 0,06300 | 0,02322 | 0,26955 | 1,842 | 20,46 |
| 34 | EM | electroMagnetism-like algorithm | 0,46250 | 0,34594 | 0,32285 | 1,13129 | 0,21245 | 0,09783 | 0,10057 | 0,41085 | 0,15667 | 0,06033 | 0,02712 | 0,24412 | 1,786 | 19,85 |
Conclusiones
El algoritmo de enjambre de aves (BSA) es una fascinante herramienta de investigación que cautiva la imaginación con su rica lógica que encarna los diversos estados y estrategias de las bandadas de pájaros. Trabajar en este algoritmo ha resultado interesante por la compleja dinámica que encierra, en la que las acciones individuales y grupales de las aves están sujetas a diferentes condiciones y combinaciones.
La complejidad del BSA también se manifiesta en el gran número de parámetros que requieren un cuidadoso ajuste para conseguir resultados óptimos. Para optimizar los parámetros del algoritmo hemos tenido que escribir un asesor experto para trabajar en el modo de cálculos matemáticos del simulador estándar MetaTrader 5, que ha servido de ayuda para encontrar buenos parámetros externos que han conseguido al algoritmo el 7º lugar en la clasificación. Quizá exista potencial para mejorar aún más los resultados, así que animo a los lectores que deseen experimentar con el algoritmo a poner manos a la obra, con la confianza de saber que aún no se han explotado plenamente todas las posibilidades para obtener los mejores resultados, ya que hay muchas variaciones en el orden de ejecución y la combinación de secuencias de comportamiento de las aves (en el artículo se dan a conocer 4 tipos de comportamiento).
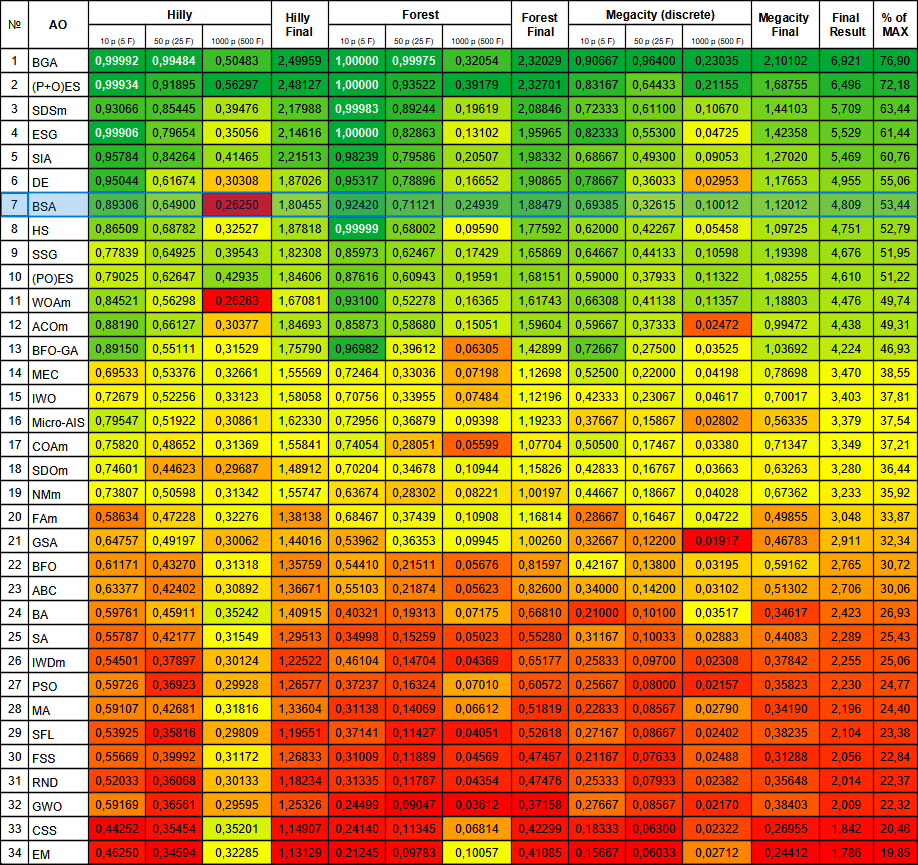
Figura 2. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0,99 aparecen resaltados en blanco.
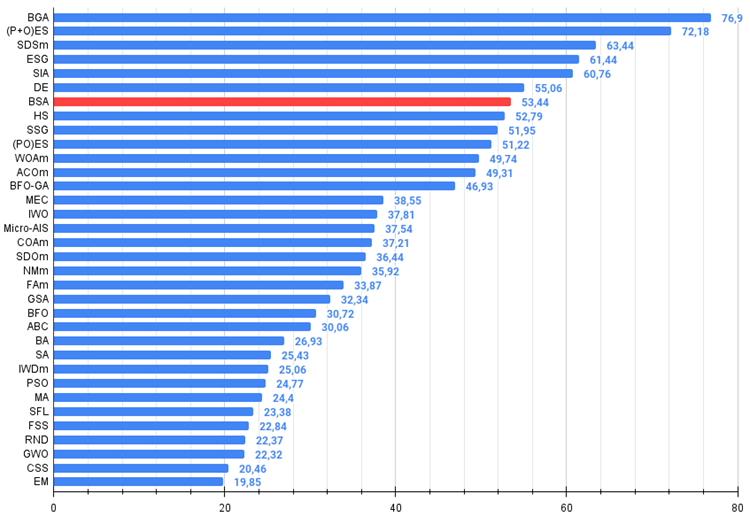
Figura 3. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor),
donde 100 es el máximo resultado teórico posible; hay un script para calcular la tabla de puntuación en el archivo).
Ventajas y desventajas del algoritmo del enjambre de pájaros (BSA):
Ventajas:
- Buenos resultados en la función Forest aguda y Megacity discreta de alta dimensionalidad.
Desventajas:
- Difícil implementación.
- Baja convergencia.
- Baja escalabilidad en funciones suaves como Hilly (problemas con tareas de alta dimensionalidad).
Adjunto al artículo encontrará un archivo con las versiones actuales de los códigos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/14491
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Red neuronal en la práctica: Pseudo inversa (II)
Red neuronal en la práctica: Pseudo inversa (II)
 Algoritmos de optimización de la población: Algoritmo Boids, o algoritmo de comportamiento de bandada (Algoritmo Boids, Boids)
Algoritmos de optimización de la población: Algoritmo Boids, o algoritmo de comportamiento de bandada (Algoritmo Boids, Boids)
 Regresiones espurias en Python
Regresiones espurias en Python
 Características del Wizard MQL5 que debe conocer (Parte 18): Búsqueda de arquitectura neural con vectores propios
Características del Wizard MQL5 que debe conocer (Parte 18): Búsqueda de arquitectura neural con vectores propios
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
¿Qué AO converge más rápido (número de cálculos FF)? No importa hacia dónde converja. Siempre que haya un mínimo de pasos.
Cualquiera de los 5 primeros, muy rápido para converger.
Lástima que no haya un valor numérico para rápido.
Lástima que no exista un valor numérico para la rapidez.
Podrías hacerlo, hacer varias series de pruebas, guardar los valores de FF en cada época, calcular la mejora media en cada época correspondiente. Por supuesto, habrá valores diferentes para cada número de variables. Esto si te pones muy quisquilloso con los indicadores numéricos de "velocidad de convergencia".
En cada primera prueba para las tres funciones de prueba (10 parámetros), el Top 5 de la lista estará muy cerca del máximo teórico ya alrededor de la 100ª época (con una población de 50).
Por supuesto, puede hacerlo, hacer varias series de pruebas, guardar los valores FF en cada época, calcular la mejora media en cada época correspondiente. Por supuesto, para cada número de variables habrá diferentes indicadores. Eso si eres muy quisquilloso con los indicadores numéricos de "velocidad de convergencia".
En cada primera prueba para las tres funciones de prueba (10 parámetros), el Top 5 de la lista estará muy cerca del máximo teórico ya alrededor de la 100ª época (con una población de 50).
~¿5000 FF?
~¿5000 FF?
Sí. Incluso en 50th epoch ya será de alrededor de 70-80% del máximo teórico.
Bueno, esto es, por supuesto, con el parámetro paso 0 (como se hace por mí cuando las pruebas). Si el paso es diferente de 0, la convergencia es aún mayor.