
Billard-Optimierungsalgorithmus (BOA)
Inhalt
Einführung
In der Welt der Optimierungsalgorithmen, wo mathematische Präzision auf Inspiration aus der Praxis trifft, entstehen oft erstaunlich geniale Ansätze. Eine solche Methode ist der Billard-Optimierungsalgorithmus (BOA), der Ideen für eine Suchstrategie aus der Mechanik des klassischen Billardspiels bezieht.
Stellen Sie sich einen Billardtisch vor, bei dem jede Tasche eine potenzielle Lösung darstellt, und die Kugeln sind die Lösungssucher, die sich durch den Raum der Möglichkeiten bewegen. So wie ein geübter Billardspieler die Flugbahn einer Kugel berechnet, um sie genau zu versenken, führt BOA seine Entscheidungen durch einen iterativen Prozess der Suche und Verfeinerung zu optimalen Ergebnissen. Dieser Algorithmus, der von den Forschern Hadi Givi und Marie Hubálovská im Jahr 2023 entwickelt wurde, zeigt einen interessanten und ungewöhnlichen Ansatz zur Lösung von Optimierungsproblemen.
In diesem Artikel gehen wir auf die konzeptionellen Grundlagen von BOA ein, untersuchen sein mathematisches Modell und analysieren seine Effizienz bei der Lösung multimodaler Probleme. Der Algorithmus, der konzeptionelle Einfachheit mit mathematischer Präzision verbindet, eröffnet neue Horizonte im Bereich der rechnergestützten Optimierung und stellt eine wertvolle Ergänzung des Arsenals moderner Optimierungsmethoden dar.
Implementierung des Algorithmus
Der BOA-Algorithmus ist eine Optimierungsmethode, die durch das Billardspiel inspiriert wurde. Stellen Sie sich vor, Sie suchen nach der besten Lösung für ein Problem, in der Billardterminologie ist es so, als würden Sie versuchen, die Kugel in die Tasche zu bekommen. Auf einem Billardtisch gibt es 8 Taschen und viele Kugeln. Zu Beginn des Algorithmus wird eine Gruppe von Zufallslösungen (Population) erstellt. Diese Entscheidungen sind wie Kugeln auf einem Billardtisch. Für jede Lösung wird der Wert der Zielfunktion berechnet, um festzustellen, wie gut sie ist.
Bei jeder Iteration des Algorithmus werden die acht besten Lösungen der Population zu „Taschen“ (anzustrebende Ziele). Die übrigen Lösungen werden als Bälle behandelt, die in diese Taschen gelenkt werden müssen. Für jede Kugel (Lösung) wird eine der Taschen (beste Lösungen) zufällig ausgewählt. Dann wird die neue Position der Kugel berechnet – eine neue Lösung, die sich in Richtung der gewählten Tasche bewegt. Wenn die neue Position der Kugel einen besseren Wert der Zielfunktion ergibt, dann bewegt sich die Kugel an die neue Position, wenn nicht, dann bleibt sie an ihrem Platz.
Mathematisch sieht das so aus:
X_new = X + rnd [0.0; 1.0] × (P - I × X)
wobei:
- X_new – neue Position des Balles,
- X – aktuelle Position des Balles,
- P – Position der Tasche (oder der Kugel, die die aktuelle Kugel treffen soll),
- I – zufällige Auswahl der Zahlen 1 oder 2.
Der Prozess wird viele Male wiederholt, und schließlich sollten sich die Kugeln (Lösungen) der optimalen Lösung des Problems annähern.
Ein Vorteil von BOA könnte darin liegen, dass es theoretisch mit nur einem Koeffizienten in der Gleichung ein gutes Gleichgewicht zwischen globaler Suche und lokaler Suche herstellen sollte. Dies wird durch die Verwendung eines Zufallsverhältnisses I erreicht, das entweder ein „Unterschreiten“ der Kugel (Verfeinerung der Lösungen in der Nähe guter Punkte) oder ein „Überschreiten“ (Erkundung verschiedener Bereiche des Lösungsraums) gewährleistet.
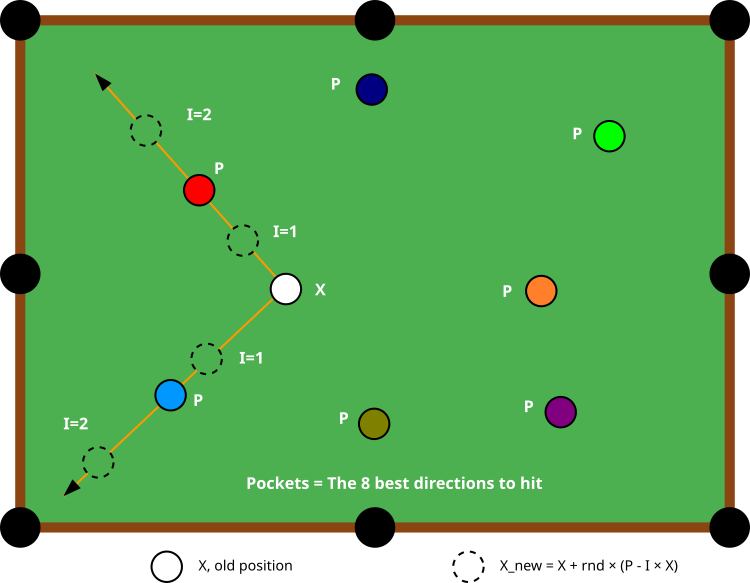
Abbildung 1. Das Flussdiagramm des BOA-Algorithmus
Abbildung 1 zeigt schematisch das Funktionsprinzip des BOA-Algorithmus. Das zentrale Element, ein weißer Ball mit der Aufschrift „X“, stellt die aktuelle Position des Agenten im Lösungssuchraum dar. Um diese Kugel herum befinden sich farbige Kugeln mit der Aufschrift „P“ – das sind „Taschen“ oder „Löcher“, die die 8 besten bisher gefundenen Lösungen darstellen. Das Diagramm veranschaulicht, wie ein Agent (der weiße Ball) seine Position aktualisieren kann, indem er sich auf verschiedene Taschen zubewegt, d. h. bei jedem Schritt wählt der Agent zufällig eine der acht Taschen als Zielrichtung der Bewegung.
Die orangefarbenen Linien mit Pfeilen zeigen die möglichen Wege des Agenten zu verschiedenen Taschen (in diesem Fall zu den roten und blauen). Die gestrichelten Kreise stellen Zwischenpositionen dar, die der Agent während seiner Bewegung einnehmen kann, je nach dem Wert von I (1 oder 2). Der Wert von I ändert die „Stärke des Schlags“ und die Art der Bewegung: bei I=1 verschiebt sich die Position in Richtung der ausgewählten Tasche, und bei I=2 kann der Agent schärfere Bewegungen ausführen, was die Erkundung eines größeren Teils des Lösungsraums erleichtert.
Nachdem wir nun vollständig verstanden haben, wie der Algorithmus funktioniert, beginnen wir mit dem Schreiben von BOA-Pseudocode.
Initialisierung
Bestimme die Anzahl der Kugeln (popSize) und der Taschen (numPockets).
Erstelle eine Population von Bällen (Agenten).
Lege den Suchraum mit minimalen und maximalen Grenzen fest.
Grundlegender Algorithmus
Erste Etappe: Initiale Initialisierung (wird nur einmal durchgeführt)
Für jeden Ball in der Population:
Platziere die Kugeln zufällig im Suchraum.
Speicher die Ausgangsposition.
Setze die Anfangswerte der Fitnessfunktion auf das Minimum.
Zweite Etappe: Bewegliche Bälle
Für jeden Ball in der Population:
Für jede Koordinate der Kugel:
Wähle eine zufällige Tasche (eine der besten Lösungen von numPockets).
Aktualisiere die Position der Kugel anhand der Gleichung: X_new = X + rnd [0.0; 1.0] × (P - I × X).
Prüfe, ob die neue Position innerhalb der zulässigen Grenzen bleibt.
Dritte Stufe: Aktualisierung der besten Lösungen
Für jeden Ball:
Wenn der Wert der Kugelfitnessfunktion besser ist als die globale Bestleistung, aktualisiere die globale Bestleistung.
Wenn der Wert der Fitnessfunktion des Balls besser ist als sein eigener Bestwert, wird sein Bestwert aktualisiert.
Sortiere die Bälle nach ihren besten Werten der Fitnessfunktion.
Die ersten numPockets der Agenten nach dem Sortieren werden zu Taschen für die nächste Iteration.
Wiederhole die Schritte der Ballbewegung und der Aktualisierung der besten Lösung, bis eine Stoppbedingung erreicht ist (z. B. die maximale Anzahl von Iterationen).
Beginnen wir mit dem Schreiben des Algorithmus-Codes. Die Klasse C_AO_BOA ist von der Klasse C_AO (der Basisklasse der Populationsoptimierungsalgorithmen) abgeleitet und implementiert den BOA-Optimierungsalgorithmus. Werfen wir einen Blick auf seine wichtigsten Elemente:
- popSize wird auf 50 gesetzt, was die Anzahl der Bälle (Agenten) im Algorithmus darstellt.
- numPockets auf 8 gesetzt ist, bildet es die Anzahl der Taschen auf einem Billardtisch.
- Die Größe des Arrays params wird geändert und zwei Parameter (popSize und numPockets) werden dem Array params hinzugefügt.
- SetParams () – die Methode ist dafür verantwortlich, die Parameter aus dem Array „params“ zurück in die lokalen Variablen popSize und numPockets zu setzen.
- Init () – die Initialisierungsmethode konfiguriert die Minimal- und Maximalwerte sowie die Schritte für die Suche und legt die Anzahl der Epochen fest.
- Moving () – verwaltet die Bewegung der Kugeln im Algorithmus.
- Revision () – prüft und revidiert die Positionen/Entscheidungen der Agenten
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BOA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_BOA () { } C_AO_BOA () { ao_name = "BOA"; ao_desc = "Billiards Optimization Algorithm"; ao_link = "https://www.mql5.com/en/articles/17325"; popSize = 50; // number of balls (agents) numPockets = 8; // number of pockets on a billiard table ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "numPockets"; params [1].val = numPockets; } void SetParams () { popSize = (int)params [0].val; numPockets = (int)params [1].val; } bool Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0); // number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- int numPockets; // number of pockets (best solutions) private: //------------------------------------------------------------------- }; //——————————————————————————————————————————————————————————————————————————————
Die Methode Init in der Klasse C_AO_BOA ist für die Initialisierung des BOA-Algorithmus zuständig. Zu Beginn der Methode wird die Funktion StandardInit() aufgerufen, der Arrays von Minimal- und Maximalwerten sowie Schritte übergeben werden. Die Funktion ist für die Durchführung allgemeiner Aktionen und Initialisierungen zuständig, die für alle abgeleiteten Klassen von Optimierungsalgorithmen durchgeführt werden müssen (einschließlich der Einrichtung des Anfangsbereichs), sowie für die Vorbereitung der dem Algorithmus zugrunde liegenden Suchagenten. Wenn StandardInit () „false“ zurückgibt (Initialisierung fehlgeschlagen), gibt die Init-Methode ebenfalls „false“ zurück. Wenn alles gut geht, gibt die Methode „true“ zurück.
//—————————————————————————————————————————————————————————————————————————————— //--- Initialization bool C_AO_BOA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode Moving implementiert den Hauptschritt des BOA-Algorithmus und steuert die Bewegung der Agenten (Kugeln) im Lösungsraum. Zunächst wird die Bedingung if (!revision) geprüft, um festzustellen, ob die Methode zum ersten Mal aufgerufen wird. Wenn revision=false, müssen die Agentenpositionen initialisiert werden. Zu diesem Zweck wird eine Schleife über alle als popSize definierten Agenten ausgeführt, innerhalb derer eine verschachtelte Schleife über die Koordinaten ausgeführt wird, die die Entscheidungsparameter jedes Agenten definieren.
In der Phase der Erzeugung der Anfangspositionen wird für jede Koordinate des Agenten ein Zufallswert in einem bestimmten Bereich ausgewählt, und die Funktion u.SeInDiSp() bringt den Wert unter Berücksichtigung der Stufe auf einen akzeptablen Wert. Die Anfangsposition des Agenten wird in a[p].cB[c] als die beste individuelle Lösung des Balls gespeichert (bei der ersten Iteration entspricht die Anfangslösung der besten bekannten Lösung), und nach dem Setzen von revision=true wird die Methode beendet, um eine Neuinitialisierung der Werte zu verhindern.
Bei der zweiten und den folgenden Iterationen wird eine Schleife gestartet, in der sich alle Agenten bewegen müssen. Bei der Koordinatenaktualisierung werden verschachtelte Schleifen über alle Agenten und ihre Koordinaten durchgeführt, wobei eine der besten verfügbaren Taschen zufällig ausgewählt wird, um die aktuelle Position des Agenten zu aktualisieren. Die Position wird auf der Grundlage der vorherigen Position plus einer zufälligen Änderung auf der Grundlage der Position der ausgewählten Tasche aktualisiert. Die Funktion u.RNDprobab() gibt eine Zufallszahl im Bereich [0.0; 1.0] zurück, um Zufallsrauschen hinzuzufügen, während die Funktion u.RNDintInRange(1, 2) einen Zufallswert von 1 oder 2 mit der Position des Agenten multipliziert.
Nach der Aktualisierung der Position wird diese angepasst, wobei der aktualisierte Wert unter Berücksichtigung der Mindest- und Höchstwerte sowie des Änderungsschritts in den angegebenen Bereich gebracht wird.
//—————————————————————————————————————————————————————————————————————————————— //--- The main step of the algorithm void C_AO_BOA::Moving () { //---------------------------------------------------------------------------- // Initial initialization if (!revision) { for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { a [p].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [p].c [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); a [p].cB [c] = a [p].c [c]; // Save the initial position } } revision = true; return; } //---------------------------------------------------------------------------- for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { int pocketID = u.RNDminusOne (numPockets); a [p].c [c] = a [p].cB [c] + u.RNDprobab () * (a [pocketID].cB [c] - u.RNDintInRange (1, 2) * a [p].cB [c]); a [p].c [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————Die Revisionsmethode ist für die Aktualisierung der besten globalen Lösung im BOA-Algorithmus verantwortlich und aktualisiert auch die besten individuellen Lösungen der Kugeln. Am Ende des Verfahrens werden die Kugeln nach ihren besten Einzellösungen sortiert.
//—————————————————————————————————————————————————————————————————————————————— //--- Update the best solution taking into account greedy selection and the probability of making worse decisions void C_AO_BOA::Revision () { int bestIND = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; bestIND = i; } if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } if (bestIND != -1) ArrayCopy (cB, a [bestIND].c, 0, 0, WHOLE_ARRAY); S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Testergebnisse
Schauen wir uns nun an, wie der BOA-Algorithmus funktioniert:=============================
5 Hilly's; Func runs: 10000; result: 0.63960620766331
25 Hilly's; Func runs: 10000; result: 0.3277725645995603
500 Hilly's; Func runs: 10000; result: 0.2514878043770147
=============================
5 Forest's; Func runs: 10000; result: 0.3885662762060409
25 Forest's; Func runs: 10000; result: 0.1955657530616877
500 Forest's; Func runs: 10000; result: 0.15336230733273673
=============================
5 Megacity's; Func runs: 10000; result: 0.5415384615384615
25 Megacity's; Func runs: 10000; result: 0.19046153846153846
500 Megacity's; Func runs: 10000; result: 0.10530769230769324
=============================
All score: 2.79367 (31.04%)
Wie Sie sehen können, ist die Leistung des Algorithmus ziemlich schwach und er schafft es nicht in unsere Rangliste. Deshalb habe ich beschlossen, mir den Algorithmus genauer anzusehen und einige Ideen zu entwickeln, wie man ihn verbessern kann. Schauen wir uns noch einmal die Gleichung für die Bewegung von Bällen an:
X_new = X + rnd [0.0; 1.0] × (P - I × X)
In dieser Gleichung wird das I-Verhältnis auf den Wert der aktuellen Koordinate der Kugel angewandt, was eine unklare physikalische Bedeutung hat, da die Skalierung in Wirklichkeit auf den absoluten Wert der Koordinate angewendet wird. Es liegt auf der Hand, dieses Verhältnis herauszurechnen, um eine Skalierung auf den Unterschied zwischen dem Taschen- und dem Kugelkoordinatenwert zu ermöglichen. Der daraus resultierende Satz hat dann eine wahrhaft physikalische Bedeutung: Entweder erreicht der Ball das Loch nicht oder er fliegt darüber hinweg. Die Variabilität wird durch einen zusätzlichen Rauschfaktor in Form einer Zufallszahl im Bereich [0,0, 1,0] gewährleistet.
Daraus ergibt sich die Gleichung für die Bewegung der Kugeln:
X_new = X + rnd [0.0; 1.0] × (P -X) × I
Im Folgenden finden Sie den vollständigen Code für die geänderte Version der Methode Moving (), die die auskommentierte Zeichenfolge der Gleichung des Autors gefolgt von meiner Version der Gleichung zeigt.
//—————————————————————————————————————————————————————————————————————————————— //--- The main step of the algorithm void C_AO_BOA::Moving () { //---------------------------------------------------------------------------- // Initial initialization if (!revision) { for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { a [p].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [p].c [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); a [p].cB [c] = a [p].c [c]; // Save the initial position as the best individual solution } } revision = true; return; } //---------------------------------------------------------------------------- for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { int pocketID = u.RNDminusOne (numPockets); //a [p].c [c] = a [p].cB [c] + u.RNDprobab () * (a [pocketID].cB [c] - u.RNDintInRange (1, 2) * a [p].cB [c]); a [p].c [c] = a [p].cB [c] + u.RNDprobab () * (a [pocketID].cB [c] - a [p].cB [c]) * u.RNDintInRange (1, 2); a [p].c [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Jetzt, nach den Änderungen, wollen wir sehen, wie der Algorithmus mit den Parametern funktioniert, mit denen die Version der Autoren die besten Ergebnisse zeigte:
BOA|Billiards Optimization Algorithm|50.0|8.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8727603657603271
25 Hilly's; Func runs: 10000; result: 0.7117647027521633
500 Hilly's; Func runs: 10000; result: 0.25339119302510993
=============================
5 Forest's; Func runs: 10000; result: 0.9228482722678735
25 Forest's; Func runs: 10000; result: 0.7601448268715335
500 Forest's; Func runs: 10000; result: 0.3498925749480034
=============================
5 Megacity's; Func runs: 10000; result: 0.6184615384615385
25 Megacity's; Func runs: 10000; result: 0.45876923076923076
500 Megacity's; Func runs: 10000; result: 0.14586153846153965
=============================
All score: 5.09389 (56.60%)
Nach einigen weiteren Experimenten habe ich Parameter gefunden, die noch bessere Ergebnisse liefern:
BOA|Billiards Optimization Algorithm|50.0|25.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.957565927297626
25 Hilly's; Func runs: 10000; result: 0.8259872884790693
500 Hilly's; Func runs: 10000; result: 0.2523458952211869
=============================
5 Forest's; Func runs: 10000; result: 0.9999999999999929
25 Forest's; Func runs: 10000; result: 0.900362056289584
500 Forest's; Func runs: 10000; result: 0.305018130407844
=============================
5 Megacity's; Func runs: 10000; result: 0.7353846153846153
25 Megacity's; Func runs: 10000; result: 0.5252307692307692
500 Megacity's; Func runs: 10000; result: 0.09563076923077005
=============================
All score: 5.59753 (62.19%)
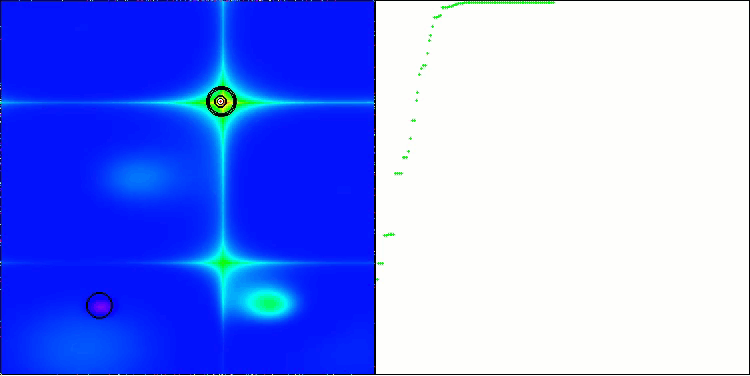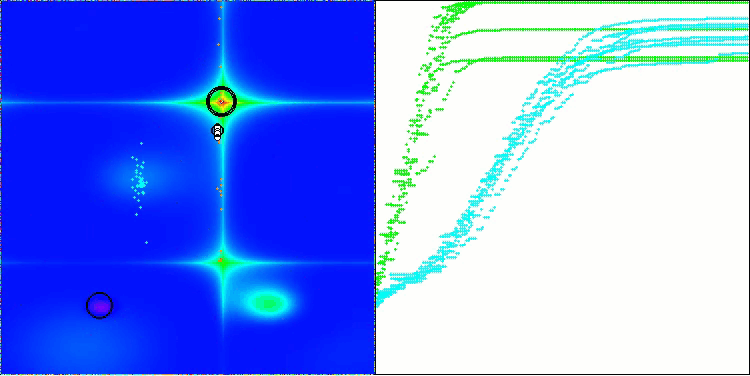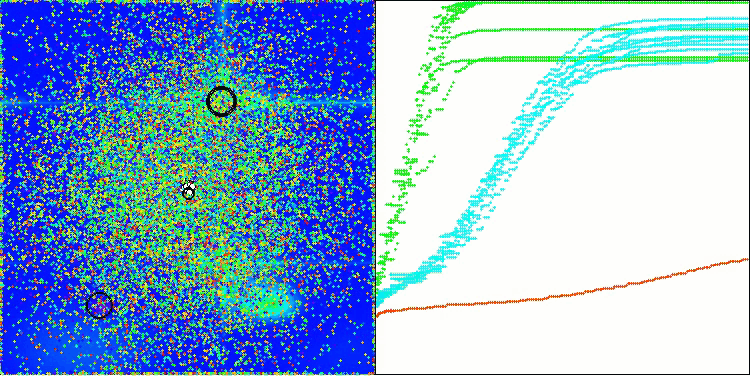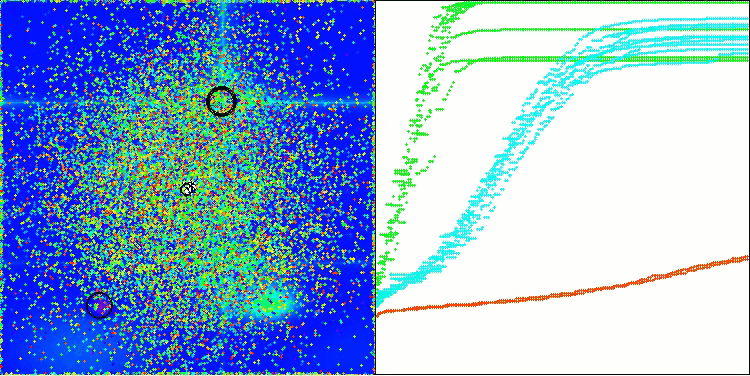
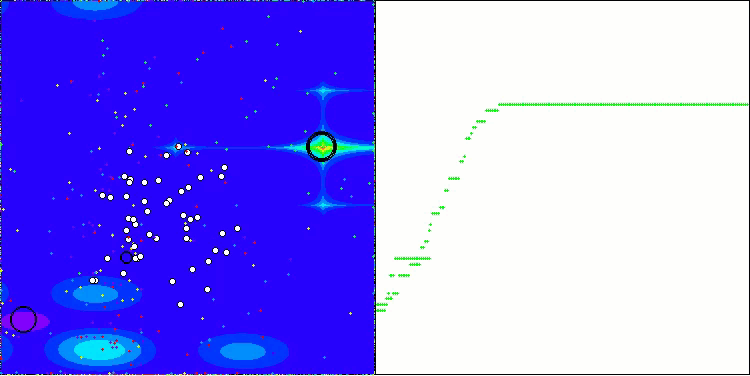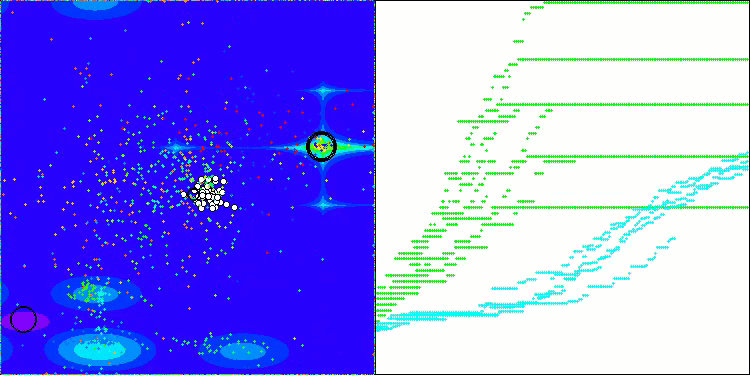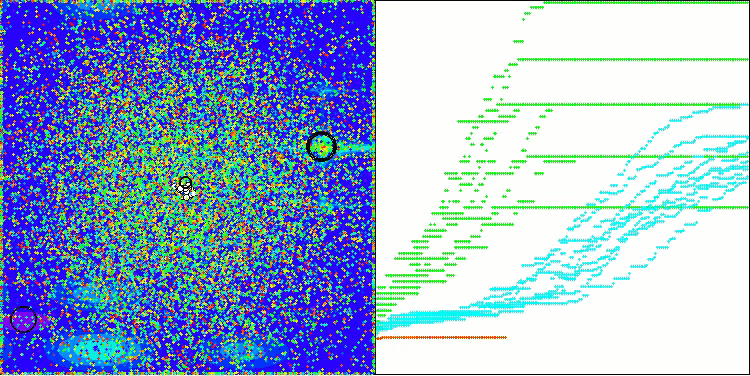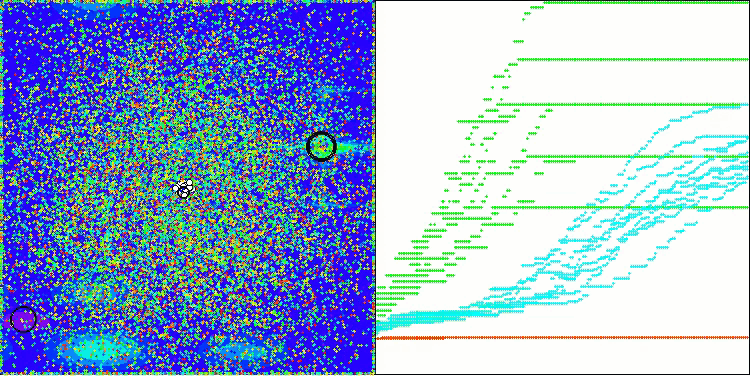
Schauen wir uns die Visualisierung des BOA-Algorithmus für Testfunktionen an. Im Suchraum ist kein besonders charakteristisches Verhalten zu beobachten; die Bewegungen der „Kugeln“ wirken chaotisch. Besonders auffällig ist, dass der Algorithmus Probleme kleiner und mittlerer Dimensionen erfolgreich bewältigt, bei Problemen großer Dimensionen jedoch Konvergenzprobleme auftreten. Besonders auffällig ist dies bei der glatten Hilly-Funktion, wo die Leistung sogar schlechter ist als bei der diskreten Megacity, was im Vergleich zu anderen populationsbasierten Algorithmen ein äußerst seltenes Phänomen ist. Es ist auch erwähnenswert, dass der Algorithmus dazu neigt, bei der Lösung von Problemen kleiner Dimensionen in lokalen Minima stecken zu bleiben.
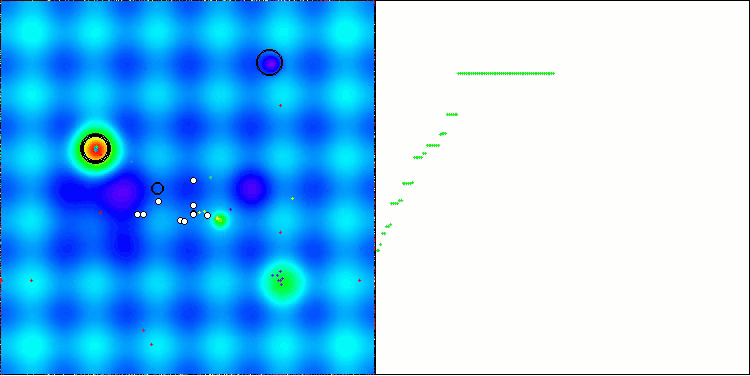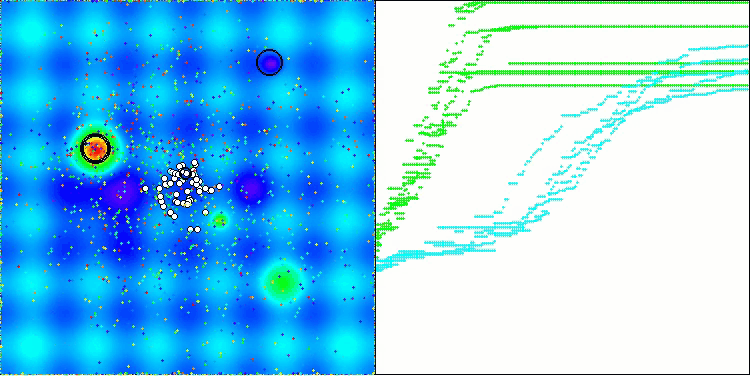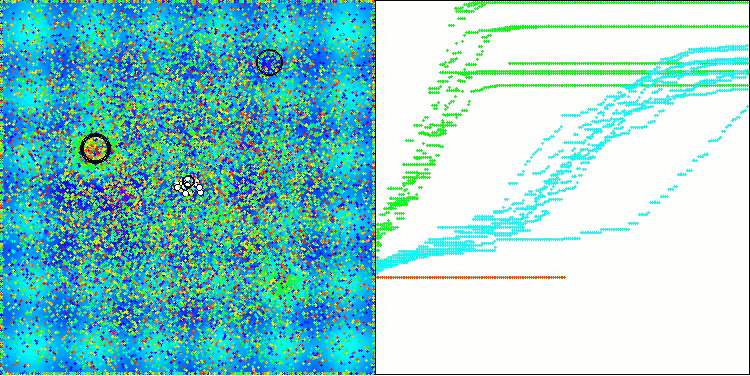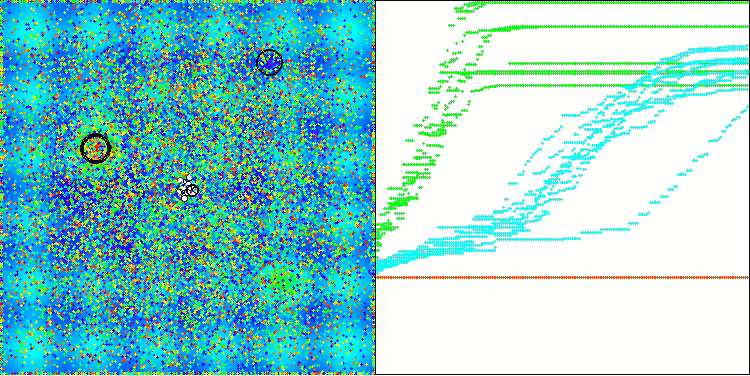
BOA mit der Testfunktion Hilly
BOA mit der Testfunktion Forest
BOA mit der Testfunktion Megacity
Fassen wir die Testergebnisse zusammen und betrachten wir die Effizienz. Der Algorithmus erwies sich als recht effizient und belegte den 8. Platz in der Rangliste der besten Optimierungsalgorithmen, obwohl er erhebliche Mängel aufwies.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Code-Sperr-Algorithmus (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | TETA | Zeit-Evolutions-Reise-Algorithmus (Joo) | 0.91362 | 0.82349 | 0.31990 | 2.05701 | 0.97096 | 0.89532 | 0.29324 | 2.15952 | 0.73462 | 0.68569 | 0.16021 | 1.58052 | 5.797 | 64.41 |
| 7 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 8 | BOAm | Billard-Optimierungsalgorithmus M | 0.95757 | 0.82599 | 0.25235 | 2.03590 | 1.00000 | 0.90036 | 0.30502 | 2.20538 | 0.73538 | 0.52523 | 0.09563 | 1.35625 | 5.598 | 62.19 |
| 9 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 10 | ESG | Entwicklung sozialer Gruppen (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 11 | SIA | Simuliertes isotropes Glühen (Joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 12 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 13 | DA | dialektischer Algorithmus | 0.86183 | 0.70033 | 0.33724 | 1.89940 | 0.98163 | 0.72772 | 0.28718 | 1.99653 | 0.70308 | 0.45292 | 0.16367 | 1.31967 | 5.216 | 57.95 |
| 14 | BHAm | Algorithmus für schwarze Löcher M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 15 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 16 | RFO | Optimierung des Royal Flush (joo) | 0.83361 | 0.73742 | 0.34629 | 1.91733 | 0.89424 | 0.73824 | 0.24098 | 1.87346 | 0.63154 | 0.50292 | 0.16421 | 1.29867 | 5.089 | 56.55 |
| 17 | AOSm | Suche nach atomaren Orbitalen M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 18 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 19 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 20 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 21 | BIO | Optimierung der Blutvererbung (joo) | 0.81568 | 0.65336 | 0.30877 | 1.77781 | 0.89937 | 0.65319 | 0.21760 | 1.77016 | 0.67846 | 0.47631 | 0.13902 | 1.29378 | 4.842 | 53.80 |
| 22 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 23 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 24 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 25 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 26 | ABO | Optimierung des afrikanischen Büffels | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 27 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 28 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 29 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 30 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 31 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 32 | AEO | Algorithmus zur Optimierung auf der Grundlage künstlicher Ökosysteme | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 33 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 34 | BFO-GA | Optimierung der bakteriellen Futtersuche — ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 35 | SOA | einfacher Optimierungsalgorithmus | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 36 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 37 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 38 | ADAMm | adaptive Momentabschätzung M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 39 | CGO | Chaos-Spiel-Optimierung | 0.57256 | 0.37158 | 0.32018 | 1.26432 | 0.61176 | 0.61931 | 0.62161 | 1.85267 | 0.37538 | 0.21923 | 0.19028 | 0.78490 | 3.902 | 43.35 |
| 40 | ATAm | Algorithmus für künstliche Stämme M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 41 | ASHA | Algorithmus für künstliches Duschen | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 42 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 43 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 44 | CSA | Kreis-Such-Algorithmus | 0.66560 | 0.45317 | 0.29126 | 1.41003 | 0.68797 | 0.41397 | 0.20525 | 1.30719 | 0.37538 | 0.23631 | 0.10646 | 0.71815 | 3.435 | 38.17 |
| 45 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| RW | Random Walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Zusammenfassung
Der modifizierte Billard-Optimierungsalgorithmus (BOAm) zeigte interessante Ergebnisse bei Testfunktionen. Die Analyse der präsentierten Daten zeigt, dass der Algorithmus die besten Ergebnisse bei kleinen und mittelgroßen Problemen erzielt und bei 10.000 Iterationen die höchsten Werte in den Tests Hilly (0,957), Forest (0,999) und Megacity (0,735) erreicht. Dies beweist seine hohe Effizienz bei der Suche nach optimalen Lösungen für Probleme von mittlerer Komplexität. Allerdings sinkt die Leistung mit zunehmender Problemgröße erheblich, wie die Ergebnisse für die Szenarien mit 1000 Variablen zeigen, wo die Werte auf 0,252, 0,305 bzw. 0,095 fallen.
Besonders hervorzuheben ist die signifikante Leistungsverbesserung der modifizierten Version des Algorithmus, die 62,19 % des maximal möglichen Ergebnisses erreicht, was doppelt so hoch ist wie die 31,04 % der ursprünglichen Version. Diese beeindruckende Verbesserung wurde durch die Änderung einer einzigen Codezeile erreicht, die die Gleichung für die Aktualisierung der Kugelpositionen betrifft.
Die Einfachheit des Algorithmus ist sowohl sein Vorteil als auch seine Einschränkung – er ist intuitiv, leicht zu implementieren und basiert auf einem eleganten Billardkonzept – kann aber zusätzliche Modifikationen erfordern, um hochdimensionale Probleme effizient zu behandeln. Insgesamt stellt BOAm einen vielversprechenden metaheuristischen Ansatz dar, der ein gutes Gleichgewicht zwischen Exploration und Ausnutzung des Lösungsraums bietet und in der Rangliste zu den zehn besten Algorithmen gehört.
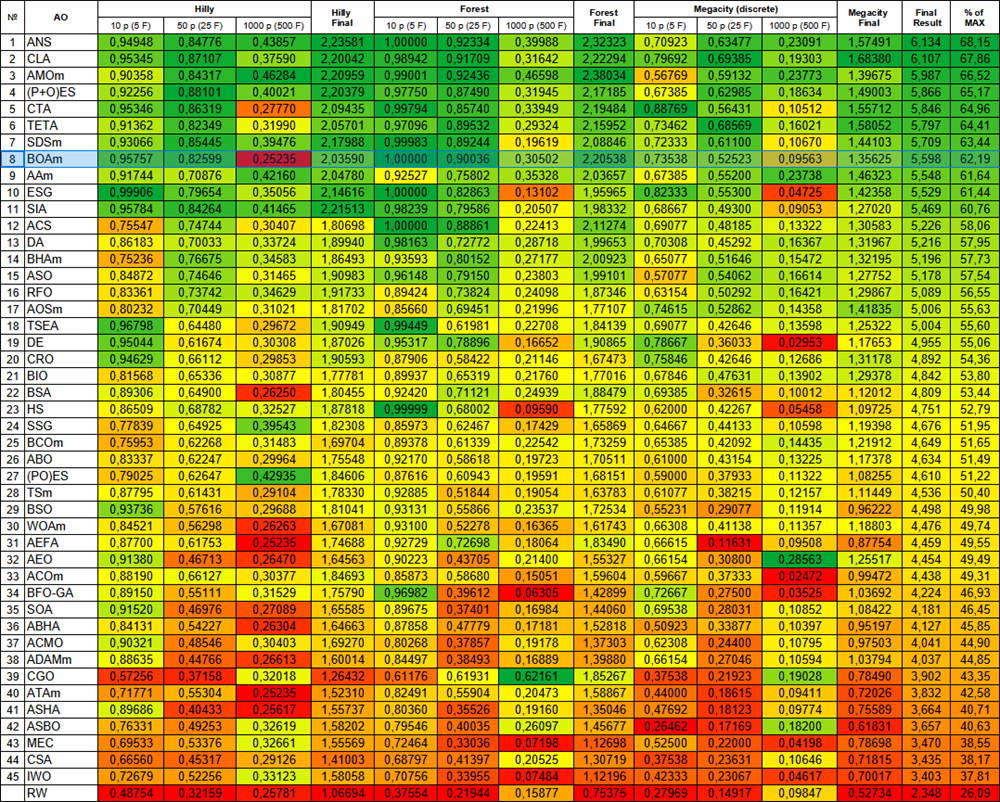
Abbildung 2. Farbabstufung der Algorithmen nach den entsprechenden Tests
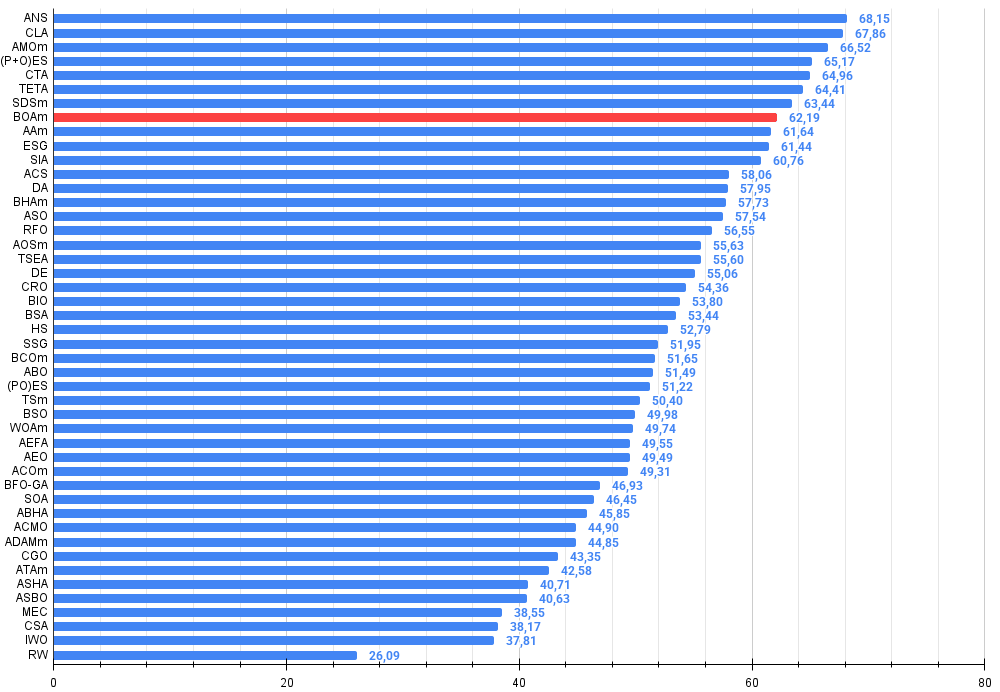
Abbildung 3. Histogramm der Algorithmus-Testergebnisse (Skala von 0 bis 100, je höher, desto besser, wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Bewertungstabelle)
Vor- und Nachteile von BOA:
Vorteile:
- Sehr wenige externe Parameter.
- Einfache Umsetzung.
- Gute Leistung bei kleinen und mittleren Problemen.
- Hervorragende Ergebnisse bei Problemen mit „scharfen“ Extremen (wie der Waldfunktion).
Nachteile
- Bleibt bei niedrigdimensionalen Problemen an lokalen Extremen hängen.
- Sehr geringe Konvergenzgeschwindigkeit und -genauigkeit bei „glatten“ Problemen (wie der Hilly-Funktion) von hoher Dimension.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Elternklasse der Populationsoptimierung Algorithmen |
| 2 | #C_AO_enum.mqh | Include | Enumeration der Algorithmen zur Populationsoptimierung |
| 3 | TestFunctions.mqh | Include | Bibliothek mit Testfunktionen |
| 4 | TestStandFunctions.mqh | Include | Bibliothek mit Funktionen für den Prüfstand |
| 5 | Utilities.mqh | Include | Bibliothek mit Hilfsfunktionen |
| 6 | CalculationTestResults.mqh | Include | Skript zur Berechnung der Ergebnisse in der Vergleichstabelle |
| 7 | Testing AOs.mq5 | Skript | Der einheitliche Prüfstand für alle Algorithmen zur Populationsoptimierung |
| 8 | Simple use of population optimization algorithms.mq5 | Skript | Ein einfaches Beispiel für die Verwendung von Algorithmen zur Populationsoptimierung ohne Visualisierung |
| 9 | Test_AO_BOAm.mq5 | Skript | BOAm Prüfstand |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/17325
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Wie können jahrhundertealte Funktionen Ihre Handelsstrategien aktualisieren?
Wie können jahrhundertealte Funktionen Ihre Handelsstrategien aktualisieren?
 Neuronale Netze im Handel: Zweidimensionale Verbindungsraummodelle (Chimera)
Neuronale Netze im Handel: Zweidimensionale Verbindungsraummodelle (Chimera)
 Algorithmus der erfolgreichen Gastronomen (SRA)
Algorithmus der erfolgreichen Gastronomen (SRA)
 Analyse aller Preisbewegungsoptionen auf dem IBM-Quantencomputer
Analyse aller Preisbewegungsoptionen auf dem IBM-Quantencomputer
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.