
Algoritmo de optimización de Escalera Real - Royal Flush Optimisation (RFO)
Contenido
Introducción
Existen muchos enfoques para resolver problemas de optimización; entre ellos los algoritmos genéticos ocupan un lugar especial por su capacidad para explorar eficazmente el espacio de búsqueda simulando procesos de evolución natural. El algoritmo genético clásico usa la codificación binaria de soluciones, lo cual requiere convertir los números reales a formato binario. Esta transformación no solo introduce una complejidad adicional, sino que también pondera significativamente el algoritmo. En el mundo actual, minimizar el coste del cálculo resulta crucial y la productividad de un método tiende a ser directamente proporcional a su velocidad. Mientras resolvía este problema, se me ocurrió cómo podríamos conservar los operadores genéticos y sustituir los cálculos de conversión de los números reales más difíciles por operaciones más sencillas y que consumieran menos energía.
El algoritmo Royal Flush Optimisation (RFO) que proponemos hoy es un nuevo enfoque para resolver problemas de optimización que conserva las principales ventajas de los algoritmos genéticos, pero utiliza una forma más directa de representar las soluciones. La idea clave consiste en dividir cada coordenada del espacio de búsqueda en sectores, de forma similar a las combinaciones de póquer, compuestas de cartas individuales de un determinado rango. En lugar de trabajar con cadenas de bits, el algoritmo trabaja con rangos de mapas (números de sector), lo que preserva la topología del espacio de búsqueda de forma natural.
En mi opinión, las principales ventajas del enfoque propuesto son tanto la simplicidad de realización y su comprensibilidad intuitiva (el trabajo con "mapas" es más obvio que con cadenas de bits), como el hecho de que no tengamos que codificar y decodificar números reales al preservar las propiedades combinatorias del algoritmo genético. En el artículo presentado analizaremos con detalle la aplicación del algoritmo y las características de los operadores de modificación de decisiones.
La metáfora del póquer no solo da nombre al algoritmo, sino que describe bien su esencia: igual que en el póquer un jugador se esfuerza por reunir la mejor combinación de cartas, el algoritmo combina sectores de distintas soluciones, formando poco a poco "manos" óptimas. Al igual que en el póquer cada carta tiene su propio rango y palo, en el algoritmo cada sector posee su propio significado y posición en el espacio de búsqueda. En este caso, como en el juego real, no solo resulta importante el valor de las cartas individuales, sino también su interacción en la combinación global.
Cabe señalar que este enfoque puede considerarse una generalización de las ideas de optimización discreta en el caso de los espacios continuos, lo que abre interesantes perspectivas de análisis teórico y aplicación práctica. Al igual que el póquer combina elementos de aleatoriedad y estrategia, el RFO combina la búsqueda aleatoria con la optimización dirigida, lo cual lo hace eficaz para problemas multidimensionales complejos.
Implementación del algoritmo
El principio del algoritmo RFO se basa en la idea de representar el espacio de búsqueda como sectores discretos, de forma similar a como en el póquer las cartas tienen determinados rangos. En el algoritmo genético clásico, los valores (parámetros optimizados) de todas las coordenadas se pasan a código binario y se introducen en una secuencia en forma de cromosoma, lo que requiere un coste computacional adicional. En el RFO, abandonamos este enfoque en favor de una presentación más sencilla e intuitiva.
En lugar de la codificación binaria, dividimos cada coordenada del espacio de búsqueda en sectores, asignándoles valores similares a los de las cartas en el póquer, de la jota al as (J, Q, K, A). El número de filas (sectores) se indican en un parámetro externo del algoritmo y puede ser cualquier valor entero. Así, cualquier punto del espacio de búsqueda puede representarse como una combinación de mapas, donde cada mapa corresponde a un sector concreto según su coordenada. Este enfoque no solo simplifica el cálculo, sino que también conserva las propiedades combinatorias del algoritmo genético.
Durante el proceso de optimización, el algoritmo trabaja con "manos", es decir, con conjuntos de cartas que representan distintas soluciones. Los operadores de cruce y mutación se aplican directamente a las "manos" (conjuntos de mapas), donde cada mano es un análogo de un cromosoma, lo que permite explorar el espacio de búsqueda sin necesidad de convertir a código binario y viceversa.
La siguiente ilustración (figura 1) demuestra claramente este principio. En ella se muestra un espacio de búsqueda tridimensional con coordenadas X, Y y Z, donde cada coordenada se divide en sectores correspondientes a los rangos del mapa. A la derecha tenemos ejemplos de "manos": diferentes combinaciones de cartas que el algoritmo genera en el proceso de búsqueda de la solución óptima.
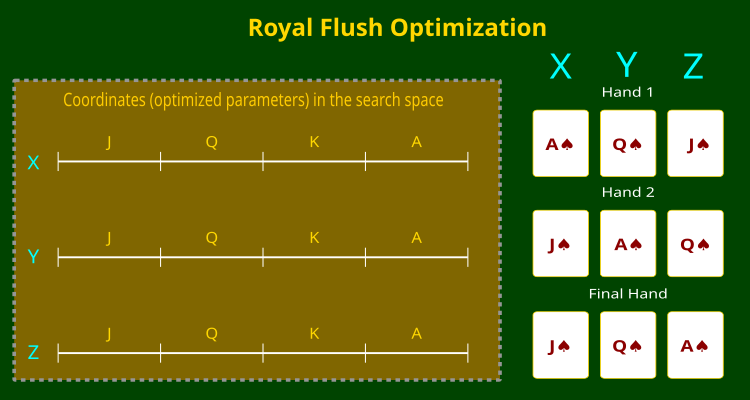
Figura 1. Algoritmo RFO y partición de coordenadas en rangos de mazos de cartas
Vamos ahora a escribir el pseudocódigo del algoritmo Royal Flush Optimisation (RFO):
- Establecemos el número de jugadores de la "mesa de póquer" (tamaño de la población)
- Determinamos el tamaño del "mazo" (número de sectores para cada dimensión)
- Fijamos la probabilidad de "farol" (mutación)
- Creamos un "reparto" inicial: generamos aleatoriamente rangos de mapas para cada coordenada.
- Convertimos los rangos en valores reales con un desplazamiento aleatorio dentro del sector
- Para cada puesto de la mesa:
- Elegimos al "oponente" mediante selección cuadrática (las "manos" más fuertes tienen más posibilidades de ser seleccionadas)
- Copiamos la "mano" (solución) actual
- Realizamos un intercambio de cartas de tres puntos:
- Seleccionamos al azar tres puntos de "corte"
- Clasificación de los puntos de corte
- Seleccionamos aleatoriamente un punto de partida (0 ó 1)
- Intercambiamos las cartas entre nuestra mano actual y la mano de nuestro oponente
- Podemos "tirarnos un farol" (probabilidad de mutación): un cambio aleatorio en el rango de una carta con una probabilidad determinada.
- Convertimos los rangos de mapa obtenidos en valores de coordenadas reales
- Calculamos el valor de cada "mano" (valor de la función objetivo)
- Memorizamos la mejor combinación encontrada (mejor solución global)
- Combinamos las manos actuales con la baraja anterior
- Clasificamos todas las "manos" según su valor
- Las mejores "manos" pasan a la siguiente generación
Vamos a escribir el código del algoritmo. Escribiremos una estructura "S_RFO_Agent" que represente un objeto que contenga información sobre una "mano" en el contexto del juego.
Campos de la estructura:
- card [] — array para almacenar el valor real de la carta.
- f — valor de la mano (valor de la función de aptitud).
- cardRanks [] — array de números enteros que representan "rangos de carta" (números de sector).
Método Init () — inicializa la estructura, toma el parámetro "coords" que especifica el número de cartas en la "mano".
//—————————————————————————————————————————————————————————————————————————————— // Structure for representing a single "hand" struct S_RFO_Agent { double card []; // cards double f; // value of the fitness function ("hand value") int cardRanks []; // sector numbers ("map ranks") void Init (int coords) { ArrayResize (cardRanks, coords); ArrayResize (card, coords); f = -DBL_MAX; // initialization with minimum value } }; //——————————————————————————————————————————————————————————————————————————————
La clase "C_AO_RFO" implementa el algoritmo y hereda propiedades y métodos de la clase básica "C_AO". Veámosla con más detalle.
Constructor C_AO_RFO () — los valores de las variables de clase se establecen, los parámetros se inicializan:- popSize — tamaño de la población (mesa de póquer) se fija en 50.
- deckSize — número de cartas de la baraja (o sectores) - 1000.
- dealerBluff — probabilidad de farol (mutación) se fija en el 3% (0,03).
- Array params — se utiliza para almacenar parámetros, se cambia al tamaño 3 y se rellena con los valores correspondientes a "popSize", "deckSize" y "dealerBluff".
Método SetParams () — recupera los valores del array "params" y los asigna a las variables de clase correspondientes.
Método Init ()— se ha diseñado para inicializar la clase con los parámetros transmitidos, como los valores mínimo y máximo de los parámetros a optimizar y su paso.
Métodos Moving() y Revision() — se utilizan para realizar operaciones relacionadas con barajado las cartas en la "mano" y revisar la mejor combinación de cartas.
Campos de la clase:- deckSize — número de sectores en la dimensión.
- dealerBluff — probabilidad de mutación.
- deck [], tempDeck [], hand [] — arrays del tipo "S_RFO_Agent" que representan el mazo principal, el mazo temporal para la clasificación y la mano actual (descendientes) respectivamente.
- cutPoints — número de puntos de "corte" de conjuntos de cartas en nuestra mano que se utilizan para combinar variantes de conjuntos de cartas.
- tempCuts [] y finalCuts [] — arrays para almacenar los índices temporales y finales de los puntos de los "cortes".
- Los métodos utilizados en Evolution () se encargan de ejecutar la evolución básica de permutaciones de cartas, mientras que DealCard () es responsable de convertir el sector a su valor real. El método "ShuffleRanks ()" se encarga de la mutación de rangos (selección aleatoria entre los rangos disponibles).
//—————————————————————————————————————————————————————————————————————————————— class C_AO_RFO : public C_AO { public: C_AO_RFO () { ao_name = "RFO"; ao_desc = "Royal Flush Optimization"; ao_link = "https://www.mql5.com/es/articles/17063"; popSize = 50; // "poker table" (population) size deckSize = 1000; // number of "cards" in the deck (sectors) dealerBluff = 0.03; // "bluff" (mutation) probability ArrayResize (params, 3); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "deckSize"; params [1].val = deckSize; params [2].name = "dealerBluff"; params [2].val = dealerBluff; } void SetParams () { popSize = (int)params [0].val; deckSize = (int)params [1].val; dealerBluff = params [2].val; } bool Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0); // number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- int deckSize; // number of sectors in the dimension double dealerBluff; // mutation probability S_RFO_Agent deck []; // main deck (population) S_RFO_Agent tempDeck []; // temporary deck for sorting S_RFO_Agent hand []; // current hand (descendants) private: //------------------------------------------------------------------- int cutPoints; // number of cutting points int tempCuts []; // temporary indices of cutting points int finalCuts []; // final indices taking the beginning and end into account void Evolution (); // main process of evolution double DealCard (int rank, int suit); // convert sector to real value void ShuffleRanks (int &ranks []); // rank mutation }; //——————————————————————————————————————————————————————————————————————————————
El método "Init" está diseñado para inicializar el objeto de la clase "C_AO_RFO".
El método comienza llamando una función que realiza la inicialización estándar de los parámetros especificados, como los valores mínimos y máximos, así como los pasos para cambiar los parámetros. Si esta inicialización falla, el método finaliza la ejecución y retorna el valor "false". Una vez inicializados los parámetros con éxito, el método procede a preparar las estructuras de datos para almacenar la información sobre las "manos" y "barajas". Esto implica redimensionar las arrays para que contengan "manos" y "barajas" que coincidan con la cantidad de la población.
A continuación, el método inicializa cada elemento del array de "manos" con un método especial que las ajusta a las coordenadas especificadas. Del mismo modo, también se preparan e inicializan los arrays de "mazo" y "mazo temporal". El método establece el número de puntos de corte necesarios para el algoritmo de cruce. En este caso, se fijan tres puntos de corte (el mejor valor encontrado tras los experimentos realizados). A continuación, los arrays se configuran para almacenar los puntos de corte temporal y final. Al final, el método devuelve "true", lo cual confirma que la inicialización se ha completado con éxito.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_RFO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- // Initialize structures for storing "hands" and "decks" ArrayResize (hand, popSize); for (int i = 0; i < popSize; i++) hand [i].Init (coords); ArrayResize (deck, popSize * 2); ArrayResize (tempDeck, popSize * 2); for (int i = 0; i < popSize * 2; i++) { deck [i].Init (coords); tempDeck [i].Init (coords); } // Initialize arrays for cutting points cutPoints = 3; // three cutting points for a "three-card" crossover ArrayResize (tempCuts, cutPoints); ArrayResize (finalCuts, cutPoints + 2); return true; } //——————————————————————————————————————————————————————————————————————————————
El método "Moving" se encarga del proceso de "mover" o actualizar el estado de la población dentro del algoritmo RFO.
Comprobación del estado— el método inicia la ejecución comprobando la condición que determina si se ha completado la inicialización del "reparto" de cartas. Si no es así (revision == false), el método realiza la inicialización.
Inicialización de la distribución inicial — el método recorre todos los elementos de la población, y se crea un conjunto de cartas para cada elemento de la población (cada "mano"). El ciclo interno recorre cada número necesario de cartas y realiza los siguientes pasos:
- Se selecciona al azar el rango de una carta de la baraja.
- A continuación, se llama a un método para repartir la carta según el rango generado.
- El mapa resultante se corrige usando una función que comprueba si está dentro del rango especificado y realiza los cambios necesarios según los parámetros especificados.
- Por último, el valor del mapa obtenido se escribe en el array "a".
Actualización de estado — una vez finalizada la inicialización, "revision" se establece en "true", lo cual indica que la distribución inicial se ha completado y no es necesario volver a inicializarla.
Llamada al método Evolution () — si ya se ha realizado la distribución inicial, el método procede a realizar el proceso evolutivo de barajado y distribuir las cartas en "manos".
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RFO::Moving () { //---------------------------------------------------------------------------- if (!revision) { // Initialize the initial "distribution" for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { hand [i].cardRanks [c] = u.RNDminusOne (deckSize); hand [i].card [c] = DealCard (hand [i].cardRanks [c], c); hand [i].card [c] = u.SeInDiSp (hand [i].card [c], rangeMin [c], rangeMax [c], rangeStep [c]); a [i].c [c] = hand [i].card [c]; } } revision = true; return; } //---------------------------------------------------------------------------- Evolution (); } //——————————————————————————————————————————————————————————————————————————————
El método Revision se encarga de encontrar la mejor "combinación" en las "manos", evaluar su aptitud y actualizar la baraja global.
Buscando la mejor combinación:
- El método comienza inicializando la variable "bestHand", que almacenará el índice de la mejor mano entre todos los miembros de la población.
- A continuación, se ejecuta un ciclo que recorre todos los elementos de la población (de 0 a popSize). Dentro del ciclo, el método compara el valor de aptitud de cada mano "a" con el mejor valor actual "fB".
- Si el valor de aptitud de la mano actual es mayor que "fB", se realiza una actualización con el nuevo mejor valor y se asigna a la variable "bestHand" el índice de esa "mano".
Si se ha encontrado la mejor mano, sus cartas se copian en el array "cB", conservando así el estado de la mejor combinación (mejor solución global). A continuación, el método actualiza los valores de aptitud de cada mano en el array "hand", igualándolos a los valores correspondientes del array "a". De este modo se garantiza que los datos de aptitud de cada mano estén actualizados. Tras actualizar los valores de aptitud, las manos actuales del array "hand" se añaden al array "deck" total, empezando en la posición "popSize" (es decir, al final de la población, su segunda mitad).
Por último, el método realiza una clasificación en el array "deck", utilizando un array temporal separado "tempDeck" para clasificar el mazo por valor de combinaciones. Esto nos permite utilizar la mayor probabilidad de seleccionar combinaciones valiosas de mapas en la selección y luego combinarlas.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RFO::Revision () { // Search for the best "combination" int bestHand = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; bestHand = i; } } if (bestHand != -1) ArrayCopy (cB, a [bestHand].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- // Update fitness values for (int i = 0; i < popSize; i++) { hand [i].f = a [i].f; } // Add current hands to the general deck for (int i = 0; i < popSize; i++) { deck [popSize + i] = hand [i]; } // Sort the deck by combination value u.Sorting (deck, tempDeck, popSize * 2); } //——————————————————————————————————————————————————————————————————————————————
El método "Evolution" es responsable de la lógica básica del algoritmo, en el que las cartas se intercambian entre las "manos" de los jugadores en la mesa, el "farol" y la actualización de los valores reales de las cartas.
El método comienza con un ciclo que recorre todos los elementos de la población. Para cada elemento, se realizan los siguientes pasos:
Elección del oponente:
- La generación de números aleatorios se utiliza para seleccionar un oponente, que luego se eleva al cuadrado para mejorar la selección (la probabilidad de seleccionar un oponente se cruza con su puntuación). Esto hace que resulte más probable elegir la mejor combinación de manos.
- El número aleatorio se escala usando la función "u.Scale" para obtener el índice del oponente.
La mano actual (del array "deck") se copia en el array "hand". El método genera puntos de "corte" aleatorios del conjunto de cartas de nuestra mano. Estos puntos determinan qué cartas se intercambiarán entre las dos manos. Los puntos de corte se clasifican y se les añaden límites; el primer límite se fija en "0" y el último en "coords - 1". El método selecciona un punto de partida aleatorio para empezar a intercambiar cartas usando "u.RNDbool ()". Una vez realizado el intercambio de cartas, se da la probabilidad de un "farol".
Conversión de rangos a valores reales:- El ciclo final convierte los rangos de las cartas en sus valores usando el método "DealCard" y comprueba si se cumplen los límites definidos.
- A continuación, se actualizan los valores del array "a", que contiene los mapas finales.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RFO::Evolution () { // For each position at the table for (int i = 0; i < popSize; i++) { // Select an opponent based on their rating (probability squared to enhance selection) double rnd = u.RNDprobab (); rnd *= rnd; int opponent = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1); // Copy the current hand hand [i] = deck [i]; // Define cutting points for card exchange for (int j = 0; j < cutPoints; j++) { tempCuts [j] = u.RNDminusOne (coords); } // Sort cutting points and add borders ArraySort (tempCuts); ArrayCopy (finalCuts, tempCuts, 1, 0, WHOLE_ARRAY); finalCuts [0] = 0; finalCuts [cutPoints + 1] = coords - 1; // Random selection of a starting point for exchange int startPoint = u.RNDbool (); // Exchange cards between hands for (int j = startPoint; j < cutPoints + 2; j += 2) { if (j < cutPoints + 1) { for (int len = finalCuts [j]; len < finalCuts [j + 1]; len++) hand [i].cardRanks [len] = deck [opponent].cardRanks [len]; } } // Possibility of "bluffing" (mutation) ShuffleRanks (hand [i].cardRanks); // Convert ranks to real values for (int c = 0; c < coords; c++) { hand [i].card [c] = DealCard (hand [i].cardRanks [c], c); hand [i].card [c] = u.SeInDiSp (hand [i].card [c], rangeMin [c], rangeMax [c], rangeStep [c]); a [i].c [c] = hand [i].card [c]; } } } //——————————————————————————————————————————————————————————————————————————————
El método "DealCard" es un elemento clave del algoritmo de optimización RFO, que convierte sectores discretos del espacio de búsqueda en valores de coordenadas continuas. El método toma dos parámetros como entrada: "rank" - rango de la carta y "suit" - el índice de coordenadas (palo).
El proceso de conversión consta de dos etapas. En primer lugar, el tamaño de un sector (suitRange) se calcula dividiendo el ámbito de búsqueda completo por el número de sectores. A continuación, se genera un valor específico dentro del sector seleccionado. El desplazamiento aleatorio "u.RNDprobab ()" garantiza que el espacio dentro de cada sector se explore de manera uniforme, mientras que "rank" define la posición básica en el espacio de búsqueda.
Este enfoque combina una representación discreta de las soluciones entre sectores con un espacio de búsqueda continuo, logrando un equilibrio entre la búsqueda global y la local.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_RFO::DealCard (int rank, int suit) { // Convert the map rank to a real value with a random offset within the sector double suitRange = (rangeMax [suit] - rangeMin [suit]) / deckSize; return rangeMin [suit] + (u.RNDprobab () + rank) * suitRange; } //——————————————————————————————————————————————————————————————————————————————
El método "ShuffleRanks" implementa el mecanismo de mutación en el algoritmo RFO, actuando como un "farol" cuando se trata de rangos de cartas. Tomando como entrada un array de rangos por referencia, el método recorre cada coordenada y, con una probabilidad "dealerBluff", sustituye el rango actual por un valor aleatorio del diapasón de rangos válidos de la baraja. Este proceso puede compararse a la situación de póquer en la que un jugador cambia repentinamente la carta de su mano, introduciendo un elemento de imprevisibilidad en el juego. Este mecanismo de mutación está diseñado para ayudar al algoritmo a no atascarse en óptimos locales y mantener una diversidad de posibles soluciones durante el proceso de optimización.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RFO::ShuffleRanks (int &ranks []) { // Rank shuffle (mutation) for (int i = 0; i < coords; i++) { if (u.RNDprobab () < dealerBluff) ranks [i] = (int)MathRand () % deckSize; } } //——————————————————————————————————————————————————————————————————————————————
Resultados de las pruebas
Impresión de los resultados de la prueba del algoritmo RFO:
RFO|Royal Flush Optimization|50.0|1000.0|0.03|
=============================
5 Hilly's; Func runs: 10000; result: 0.8336125672709654
25 Hilly's; Func runs: 10000; result: 0.7374210861383783
500 Hilly's; Func runs: 10000; result: 0.34629436610445113
=============================
5 Forest's; Func runs: 10000; result: 0.8942431024645086
25 Forest's; Func runs: 10000; result: 0.7382367793268382
500 Forest's; Func runs: 10000; result: 0.24097956383750824
=============================
5 Megacity's; Func runs: 10000; result: 0.6315384615384616
25 Megacity's; Func runs: 10000; result: 0.5029230769230771
500 Megacity's; Func runs: 10000; result: 0.16420769230769366
=============================
All score: 5.08946 (56.55%)
Una puntuación final del 56,55% es un resultado muy respetable. En la visualización, el algoritmo no muestra ningún comportamiento concreto, es como un deambular caótico de puntos individuales.
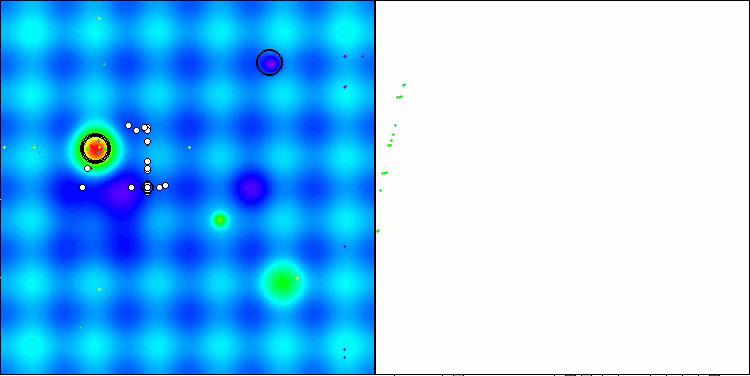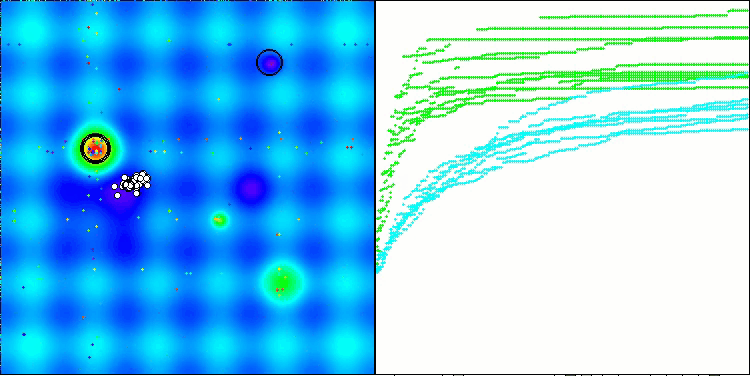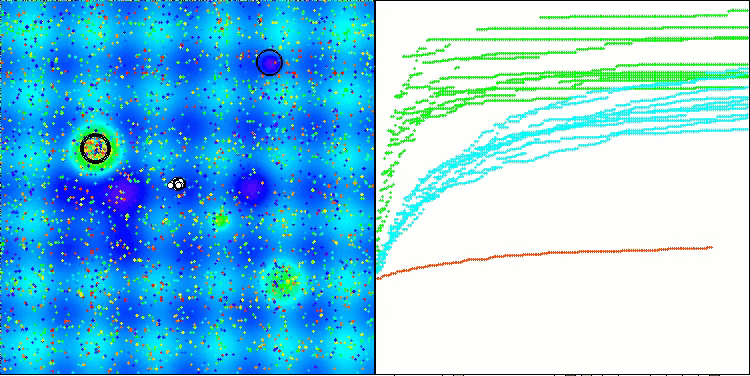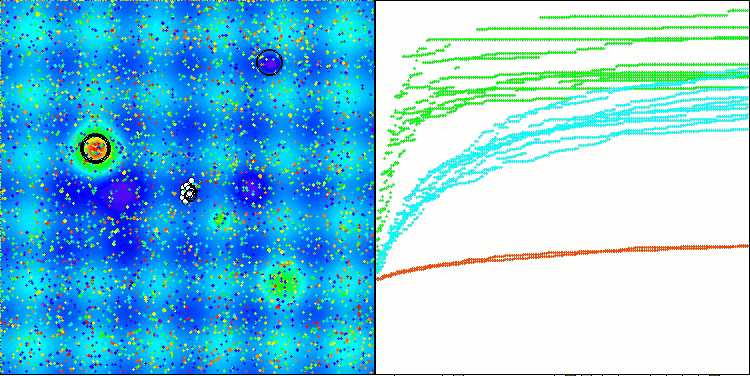
RFO en la función de prueba Hilly
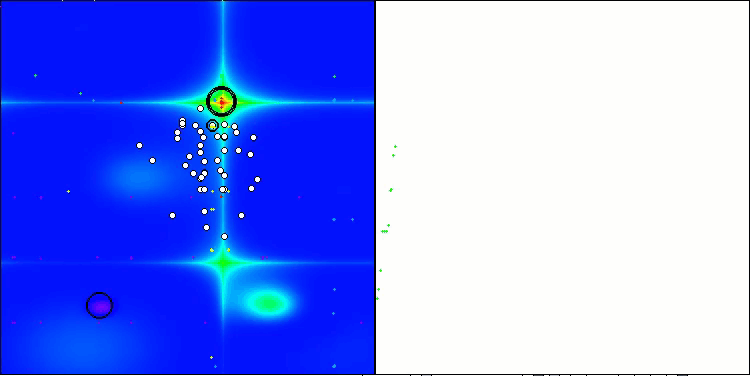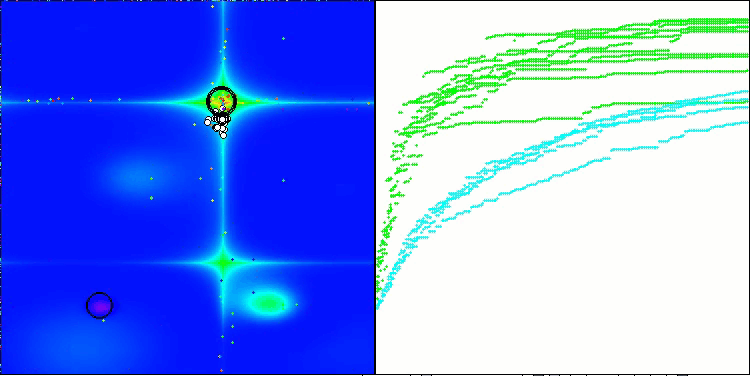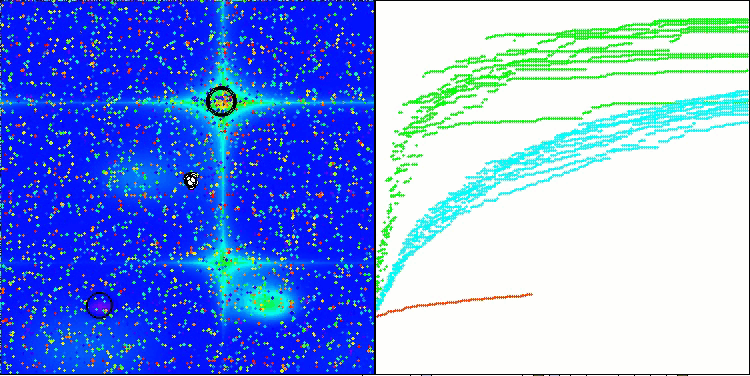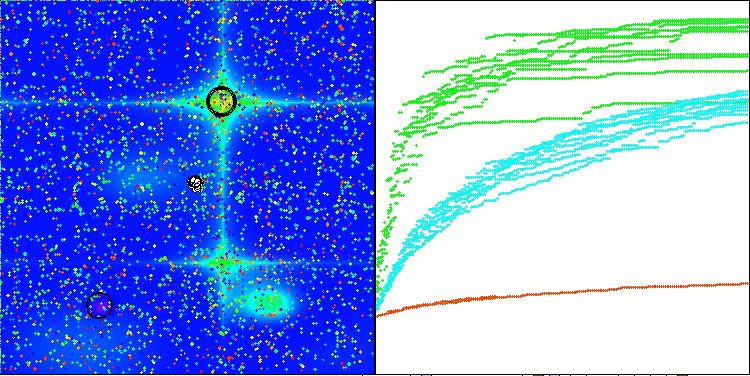
RFO en la función de prueba del bosque
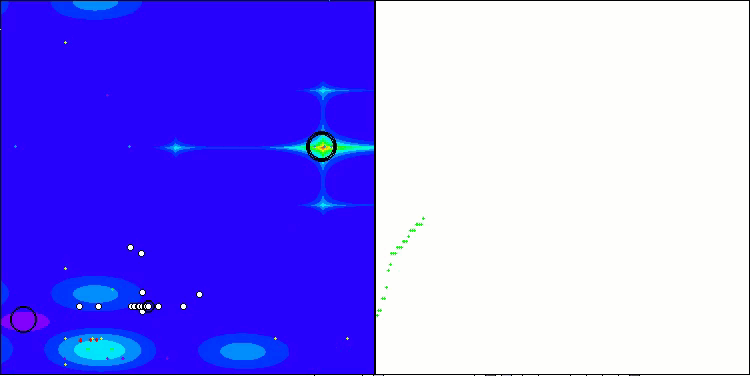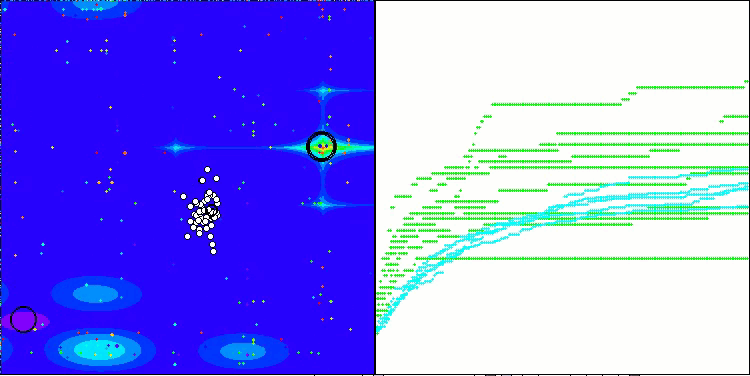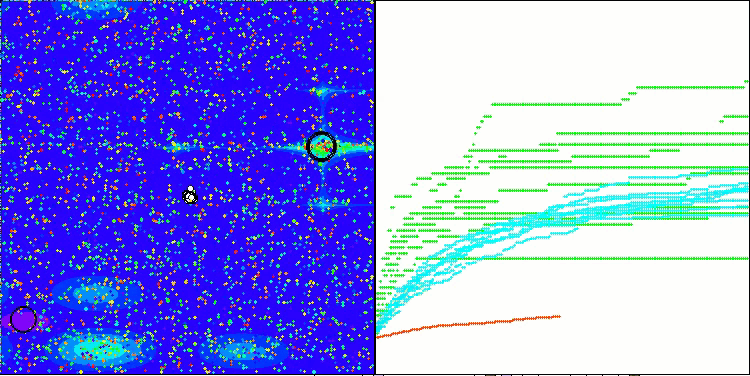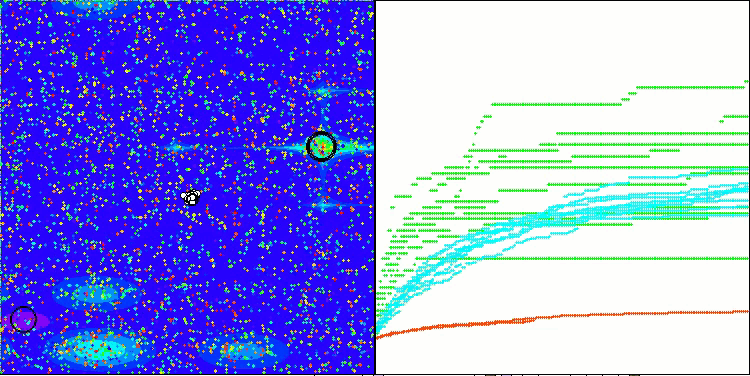
RFO en la función de prueba de Megacity
Según los resultados de la prueba, el algoritmo de optimización RFO ocupa el puesto 15, uniéndose a la lista de los algoritmos más potentes conocidos.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration optimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0.91362 | 0.82349 | 0.31990 | 2.05701 | 0.97096 | 0.89532 | 0.29324 | 2.15952 | 0.73462 | 0.68569 | 0.16021 | 1.58052 | 5.797 | 64.41 |
| 7 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 8 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 9 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 10 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 11 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 12 | DA | dialectical algorithm | 0.86183 | 0.70033 | 0.33724 | 1.89940 | 0.98163 | 0.72772 | 0.28718 | 1.99653 | 0.70308 | 0.45292 | 0.16367 | 1.31967 | 5.216 | 57.95 |
| 13 | BHAm | black hole algorithm M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 14 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 15 | RFO | royal flush optimization (joo) | 0.83361 | 0.73742 | 0.34629 | 1.91733 | 0.89424 | 0.73824 | 0.24098 | 1.87346 | 0.63154 | 0.50292 | 0.16421 | 1.29867 | 5.089 | 56.55 |
| 16 | AOSm | búsqueda de orbitales atómicos M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 17 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 18 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 19 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 20 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 21 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 22 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 23 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 24 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 25 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 26 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 27 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 28 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 29 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 30 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 31 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 32 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 33 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 34 | ABH | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 35 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 36 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 37 | ATAm | artificial tribe algorithm M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 38 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 39 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 40 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 41 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 42 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 43 | COAm | cuckoo optimization algorithm M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 44 | SDOm | spiral dynamics optimization M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 45 | NMm | Nelder-Mead method M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| R.W. | random walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Conclusiones
En la investigación y el desarrollo de nuevos métodos de optimización, con frecuencia nos enfrentamos a la necesidad de encontrar un equilibrio entre eficacia y complejidad de aplicación. Los trabajos sobre el algoritmo Royal Flush Optimisation (RFO) han arrojado algunos resultados interesantes que plantean interrogantes sobre la naturaleza de los procesos de optimización y las maneras de mejorarlos.
Viendo cómo el algoritmo alcanza el 57% del rendimiento máximo teóricamente posible, observamos un fenómeno interesante: a veces la simplificación puede ser más valiosa que la complicación. El RFO demuestra que el abandono de la compleja codificación binaria en favor de un enfoque más sencillo basado en sectores puede suponer una aceleración significativa del algoritmo, manteniendo al mismo tiempo una calidad razonablemente alta de las soluciones. Esto resulta similar a lo que ocurre en el póquer, donde a veces una estrategia más sencilla pero rápida puede ser más eficaz que una estrategia compleja y lenta.
Reflexionando sobre el lugar que ocupa el RFO en la familia de los algoritmos de optimización, podemos establecer una analogía con la evolución de los vehículos. Al igual que se necesitan modelos urbanos de bajo consumo junto a potentes deportivos, en el mundo de los algoritmos de optimización también hay espacio para métodos que se centren en distintas prioridades. El RFO puede considerarse una variante "económica" del algoritmo genético, que ofrece un compromiso razonable entre rendimiento y eficiencia de recursos.
Como conclusión, cabe señalar que el desarrollo del RFO ofrece interesantes perspectivas para futuras investigaciones. Tal vez este sea solo el primer paso en el desarrollo de toda una familia de algoritmos basados en el enfoque sectorial de la optimización. La sencillez y elegancia del método, combinadas con su eficacia práctica, pueden servir de inspiración para nuevos algoritmos que puedan equilibrar rendimiento y eficacia computacional.
Debemos señalar que la partición en sectores se realiza virtualmente, sin asignar memoria en forma de arrays. El marco RFO es un excelente punto de partida para seguir desarrollando versiones mejoradas del algoritmo de póquer.
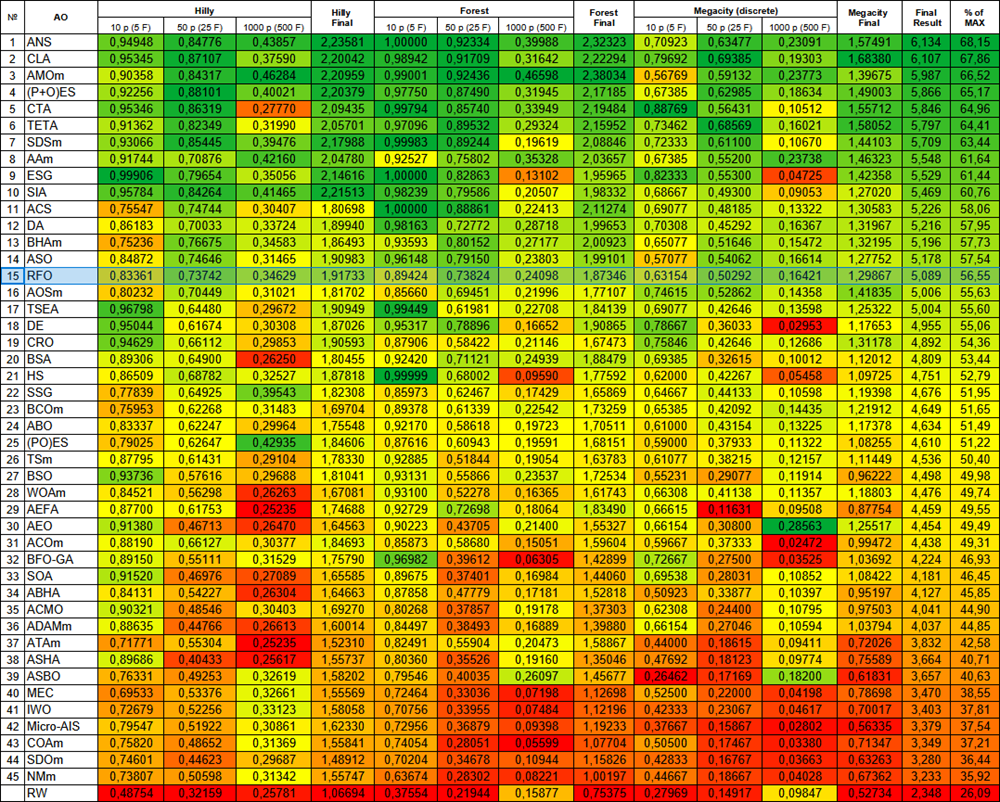
Figura 2. Clasificación por colores de los algoritmos según las pruebas respectivas
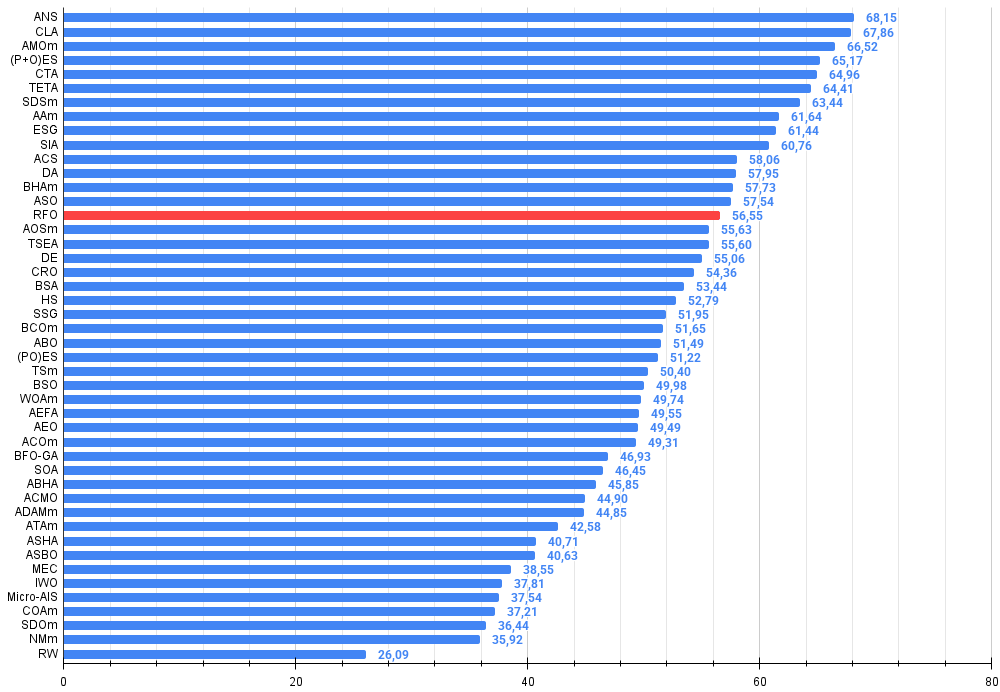
Figura 3. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de puntuación está en el archivo)
Ventajas e inconvenientes del algoritmo RFO:
Ventajas:
- Pocos parámetros externos (solo dos), sin contar el tamaño de la población.
- Implementación sencilla.
- Es rápido.
- Equilibrado, buen rendimiento en tareas de varias dimensionalidades.
Desventajas:
- Precisión media de convergencia.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | #C_AO.mqh | Archivo de inclusión | Clase padre de algoritmos de optimización basados en la población |
| 2 | #C_AO_enum.mqh | Archivo de inclusión | Enumeración de los algoritmos de optimización basados en la población |
| 3 | TestFunctions.mqh | Archivo de inclusión | Biblioteca de funciones de prueba |
| 4 | TestStandFunctions.mqh | Archivo de inclusión | Biblioteca de funciones del banco de pruebas |
| 5 | Utilities.mqh | Archivo de inclusión | Biblioteca de funciones auxiliares |
| 6 | CalculationTestResults.mqh | Archivo de inclusión | Script para calcular los resultados en una tabla comparativa |
| 7 | Testing AOs.mq5 | Script | Banco de pruebas único para todos los algoritmos de optimización basados en la población |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización |
| 9 | Test_AO_RFO.mq5 | Script | Banco de pruebas para RFO |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/17063
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Automatización de estrategias de trading en MQL5 (Parte 3): Sistema RSI de recuperación de zona para la gestión dinámica de operaciones
Automatización de estrategias de trading en MQL5 (Parte 3): Sistema RSI de recuperación de zona para la gestión dinámica de operaciones
 Desarrollo de un kit de herramientas para el análisis de la acción del precio (Parte 6): Recolector de señales de reversión a la media
Desarrollo de un kit de herramientas para el análisis de la acción del precio (Parte 6): Recolector de señales de reversión a la media
 Reimaginando las estrategias clásicas en MQL5 (Parte 13): Minimizar el retraso en los cruces de medias móviles
Reimaginando las estrategias clásicas en MQL5 (Parte 13): Minimizar el retraso en los cruces de medias móviles
 Redes neuronales en el trading: Transformador jerárquico de doble torre (Final)
Redes neuronales en el trading: Transformador jerárquico de doble torre (Final)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
En todos los casos en los que es necesario encontrar la mejor solución entre muchas posibles. Por ejemplo, asesores con autooptimización.