
Algoritmo de optimización caótica — Chaos optimization algorithm (COA)
Contenido
Introducción
En los problemas informáticos modernos, especialmente en los mercados financieros y el trading algorítmico, los métodos de optimización eficientes juegan un papel crucial. Entre los muchos algoritmos de optimización global, los enfoques inspirados en los fenómenos naturales ocupan un lugar especial. El algoritmo de optimización del caos (Chaos Optimization Algorithm, COA) es una solución innovadora que combina la teoría del caos y los métodos de optimización global.
En este artículo, presentamos un algoritmo de optimización caótica mejorado que explota las propiedades fundamentales de los sistemas caóticos: ergodicidad, sensibilidad a las condiciones iniciales y comportamiento cuasistocástico. El algoritmo usa mapeos caóticos para explorar eficientemente el espacio de búsqueda e intentar evitar óptimos locales, un problema que a menudo surge en los métodos de optimización.
La peculiaridad del algoritmo presentado es que combina la búsqueda caótica con el método de dirección de gradiente ponderado y mecanismos adaptativos que permiten el ajuste dinámico de los parámetros de búsqueda. Al utilizar varios tipos de mapeos caóticos (logísticos, sinusoidales y tipo tienda), el algoritmo muestra una buena resistencia al estancamiento y la capacidad de encontrar óptimos globales en funciones multiextremas complejas. Como de costumbre, analizaremos el algoritmo completo y luego probaremos sus capacidades utilizando nuestras funciones de prueba ahora estándar.
Implementación del algoritmo
El algoritmo consta de tres etapas principales:
- la búsqueda caótica con la primera onda portadora, donde se inicializan las variables iniciales del caos; luego se generan valores sucesivos de las variables caóticas a través de un mapeo logístico, y las variables del caos se mapean sobre el rango de variables a optimizar, y se recuerda la mejor solución encontrada;
- la búsqueda a lo largo de la dirección del gradiente ponderado;
- la búsqueda caótica con una segunda onda portadora, donde se realiza una búsqueda local alrededor de la mejor solución, con un enfoque fractal para implementar el tamaño del paso.
En la imagen a continuación, intentamos ilustrar la esencia del algoritmo de optimización caótica, cuya idea principal consiste en utilizar el caos como una herramienta de optimización útil, en lugar de un proceso aleatorio. El óptimo global (resplandor amarillo que brilla en el centro) es el objetivo que queremos encontrar. Las partículas brillantes de color azul son agentes de búsqueda que se mueven en trayectorias caóticas; estas trayectorias se muestran usando líneas brillantes que demuestran la naturaleza no lineal del movimiento.
Demostración de propiedades clave del comportamiento caótico: determinismo (las trayectorias son suaves, no aleatorias), ergodicidad (las partículas exploran todo el espacio), sensibilidad a las condiciones iniciales (diferentes partículas se mueven a lo largo de trayectorias distintas), mientras que la dinámica de búsqueda muestra un brillo de intensidad variable, indicando la "energía" de la búsqueda en diferentes áreas, donde los círculos concéntricos alrededor del óptimo simbolizan áreas de atracción; el desenfoque y los gradientes transmiten la continuidad del espacio de búsqueda. Principales etapas del algoritmo:
- búsqueda amplia lejos del centro (partículas distantes),
- aproximación gradual a zonas prometedoras (trayectorias promedio),
- búsqueda local cerca del óptimo (partículas cercanas al centro).
El resultado sería una especie de "retrato" de optimización caótica, donde el caos se presenta no como desorden, sino como un proceso controlado de exploración del espacio de soluciones.

Figura 1. Visualización de la optimización caótica
El esquema visual del algoritmo presentado a continuación refleja las tres etapas principales:
- First Carrier Wave Search (bloque azul) utiliza un mapeo caótico para la búsqueda global y además transforma las variables caóticas en el espacio de búsqueda.
- Weighted Gradient Search (bloque naranja) es un método de gradiente ponderado que incluye el procesamiento de restricciones a través de coeficientes de ponderación,
- Second Carrier Wave Search (bloque violeta) representa la búsqueda local en torno a la mejor solución y el ajuste adaptativo del parámetro α.
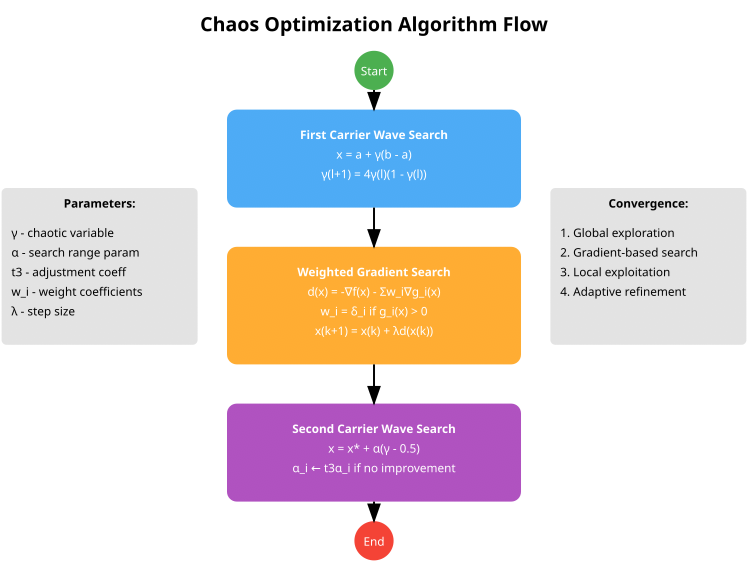
Figura 2. Esquema de funcionamiento del algoritmo de optimización caótica
El esquema representa la estructura básica de tres etapas del algoritmo COA (CHAOS). En nuestra implementación, y ha habido varias, hemos optado por una versión más avanzada y práctica del algoritmo, ampliando la estructura del agente y añadiendo un contador de movimiento, un contador de estancamiento y variables caóticas para cada dimensión. También tenía importancia agregar variedad a los mapeos caóticos, pues los autores se basaban solo en el mapeo logístico; nuestra versión ha sido capaz de añadir mapeos sinusoidales y de tienda. Esta implementación incluye la adaptación automática de los parámetros de penalización y la adaptación de los parámetros de búsqueda dependiendo del éxito con ajuste de la inercia. Además, hemos añadido una inicialización más compleja utilizando el hipercubo latino.
Ahora vamos a escribir el pseudocódigo del algoritmo:
Inicialización del algoritmo
- Configuración de parámetros del algoritmo:
- tamaño de la población (popSize)
- número de iteraciones de la primera fase (S1)
- número de iteraciones de la segunda fase (S2)
- parámetro de penalización (sigma)
- coeficiente de corrección (t3)
- constante menor para coeficientes de ponderación (eps)
- parámetro de inercia
- parámetro de influencia social (socialFactor)
- probabilidad de mutación (mutationRate)
- Agentes de inicialización:
- Para cada agente de la población:
- inicializamos las variables caóticas (gamma) con diferentes valores iniciales
- restablecemos los vectores de velocidad
- ponemos el contador de estancamiento a 0
- Para cada agente de la población:
- Inicialización de parámetros de búsqueda (alfa):
- adaptamos los parámetros según el tamaño del espacio de búsqueda
- alpha[c] = 0.1 * (rangeMax[c] - rangeMin[c]) / sqrt(coords)
Fase 1: Población inicial con distribución caótica
- Creación de una población inicial usando el hipercubo latino:
- generamos los valores para cada dimensión
- mezclamos los valores para garantizar una distribución uniforme
- asignamos los valores a un rango de variables
- Aplicación de varias estrategias de inicialización de agentes:
- para el primer cuarto de los agentes: distribución uniforme
- para el segundo cuarto: clusterización en torno a varios puntos
- para el tercero: posiciones aleatorias con desplazamiento hacia los límites
- para el último: posiciones caóticas con diferentes mapeos
Fase 2: Búsqueda caótica con la primera onda portadora
- Para cada iteración hasta S1:
- Para cada agente de la población:
- si se activa la probabilidad de mutación, aplicamos la mutación
- de lo contrario, para cada coordenada:
- actualizamos la variable caótica a través del mapeo elegido (logístico, sinusoidal o de tienda)
- determinamos la estrategia (búsqueda global o local) en función de la fase de optimización
- Para la búsqueda global: utilizamos valores aleatorios para determinar la nueva posición
- Para la búsqueda local: combinamos la atracción hacia las mejores soluciones con la perturbación caótica
- actualizamos la velocidad considerando la inercia
- aplicamos límites de velocidad y posición
- comprobamos si hay infracciones de las restricciones y aplicamos la corrección
- Evaluación y actualización:
- calculamos la función de penalización para cada agente
- actualizamos las mejores soluciones personales y globales
- actualizamos dinámicamente el parámetro de penalización
- adaptamos el parámetro de búsqueda (alfa) según el éxito
- Para cada agente de la población:
Fase 3: Búsqueda caótica con una segunda onda portadora
- Para cada iteración de S1 a S1+S2:
- comprobamos la convergencia
- para cada agente de la población:
- si se detecta convergencia, aplicamos la mutación aleatoria a algunos agentes
- de lo contrario, para cada coordenada:
- actualizamos la variable caótica
- reducimos el radio de búsqueda de forma adaptativa
- seleccionamos una línea básica dando prioridad a las mejores soluciones
- añadimos perturbaciones caóticas y ruido de Levy para saltos largos aleatorios
- actualizamos velocidad y posición con inercia
- aplicamos restricciones de posición
- Evaluación y actualización:
- calculamos la función de penalización para cada agente
- actualizamos las mejores soluciones personales y globales
- actualizamos la historia de la mejor solución global para determinar la convergencia
- restablecemos los agentes bloqueados si es necesario
Funciones auxiliares
- Mapeos caóticos:
- LogisticMap(x): x[n+1] = rx[n](1-x[n]) con comprobación de la corrección
- SineMap(x): x[n+1] = sin(π*x[n]) con normalización
- TentMap(x): x[n+1] = μ*min(x[n], 1-x[n]) con comprobación de la corrección
- SelectChaosMap(x, tipo): selecciona un mapeo según el tipo
- Restricciones de procesamiento y penalizaciones:
- CalculateConstraintValue(agent, coord): calcula la infracción de la restricción
- CalculateConstraintGradient(agent, coord): calcula el gradiente de restricción
- CalculateWeightedGradient(agent, coord): calcula el gradiente ponderado
- CalculatePenaltyFunction(agent): calcula el valor de la función de penalización
- Procesamiento del estancamiento y la convergencia:
- IsConverged(): comprueba la convergencia basándose en la historia de mejores soluciones
- ResetStagnatingAgents(): restablece los agentes estancados
- ApplyMutation(agent): aplicar diferentes tipos de mutaciones
- UpdateSigma(): actualiza dinámicamente el parámetro de penalización
- UpdateBestHistory(newBest): actualiza la historia de los mejores valores
Ahora podemos describir la implementación del algoritmo COA (CHAOS). En este artículo, analizaremos todos los métodos de implementación clave, y ya en el siguiente, pasaremos directamente a las pruebas y los resultados de rendimiento del algoritmo. Ahora escribiremos la estructura "S_COA_Agent", los campos de la estructura:
- gamma [] — conjunto de variables caóticas de tipo pseudoaleatorio utilizadas para introducir elementos de aleatoriedad y diversidad en el comportamiento del agente,
- velocity [] — array de velocidades, permite que el agente se desplace de forma más dinámica a través del espacio, considerando la inercia,
- stagnationCounter — contador que aumenta si el agente no muestra mejora en su solución; ayuda a implementar mecanismos para reiniciar estrategias en caso de estancamiento.
El método "Init()" se crean y establecen los valores iniciales de los arrays. Para "gamma[]", se utiliza una distribución uniforme entre 0,1 y 0,9 para introducir variedad en las condiciones iniciales de las variables caóticas. Las velocidades "velocity []" comienzan en valores cero, el contador de estancamiento se establece en cero.
//—————————————————————————————————————————————————————————————————————————————— // Улучшенная структура агента с дополнительными полями struct S_COA_Agent { double gamma []; // хаотические переменные double velocity []; // скорость перемещения (для усиления инерции) int stagnationCounter; // счётчик стагнации void Init (int coords) { ArrayResize (gamma, coords); ArrayResize (velocity, coords); // Равномерное распределение значений для gamma for (int i = 0; i < coords; i++) { // Используем различные начальные значения для лучшего разнообразия gamma [i] = 0.1 + 0.8 * (i % coords) / (double)MathMax (1, coords - 1); // Инициализация скорости нулями velocity [i] = 0.0; } stagnationCounter = 0; } }; //——————————————————————————————————————————————————————————————————————————————
La clase "C_AO_COA_chaos" se deriva de la clase básica "C_AO" y es una implementación del algoritmo COA(CHAOS). Incluye los métodos y parámetros necesarios para su funcionamiento, así como funciones adicionales para controlar el comportamiento de los agentes, basándose en los conceptos de búsqueda caótica. Componentes de la clase:
- SetParams() — método para establecer los parámetros de algoritmo,
- Init() — método de inicialización que acepta rangos y parámetros para que el algoritmo funcione.
- Moving() — método responsable de desplazar agentes en el espacio de soluciones,
- Revision() — método para revisar las posiciones de los agentes.
- S1, S2 — número de iteraciones en dos fases del algoritmo.
- sigma, t3, eps, inertia, socialFactor, mutationRate — parámetros que influyen en el comportamiento de los agentes y del algoritmo en su conjunto.
- alpha[] — array de parámetros que se usa para realizar búsquedas.
- agent[] — array de agentes que conforman la población del algoritmo.
- métodos para calcular gradientes, valores de restricción y funciones de penalización, y comprobar la admisibilidad de las soluciones (IsFeasible),
- métodos para mapeos caóticos (LogisticMap, SineMap, TentMap, SelectChaosMap).
- variables que almacenan información sobre la época actual (epochs, epochNow) y el valor de penalización dinámico (currentSigma),
- globalBestHistory[] — array para almacenar los mejores valores globales en múltiples iteraciones,
- Índice de la historia (historyIndex) para rastrear la posición en el array de mejores valores,
- Métodos para gestionar la población de agentes (InitialPopulation), ejecutar las diferentes fases de búsqueda (FirstCarrierWaveSearch, SecondCarrierWaveSearch), mutar agentes (ApplyMutation), actualizar la penalización (UpdateSigma) y comprobar la convergencia (IsConverged), además de reiniciar agentes estancados (ResetStagnatingAgents).
Entonces, la clase "C_AO_COA_chaos" es un componente complejo de un sistema de optimización que usa agentes para encontrar soluciones. Integra los parámetros, los métodos y la lógica necesarios para controlar los agentes dentro de un algoritmo, incluyendo estrategias tanto deterministas como caóticas.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_COA_chaos : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_COA_chaos () { } C_AO_COA_chaos () { ao_name = "COA(CHAOS)"; ao_desc = "Chaos Optimization Algorithm"; ao_link = "https://www.mql5.com/es/articles/16729"; // Внутренние параметры (не настраиваются извне) inertia = 0.7; socialFactor = 1.5; mutationRate = 0.05; // Параметры по умолчанию popSize = 50; S1 = 30; S2 = 20; sigma = 2.0; t3 = 1.2; eps = 0.0001; // Инициализация массива параметров для интерфейса C_AO ArrayResize (params, 6); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "S1"; params [1].val = S1; params [2].name = "S2"; params [2].val = S2; params [3].name = "sigma"; params [3].val = sigma; params [4].name = "t3"; params [4].val = t3; params [5].name = "eps"; params [5].val = eps; } void SetParams () { // Обновление внутренних параметров из массива params popSize = (int)params [0].val; S1 = (int)params [1].val; S2 = (int)params [2].val; sigma = params [3].val; t3 = params [4].val; eps = params [5].val; } bool Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0); // количество эпох void Moving (); void Revision (); //---------------------------------------------------------------------------- // Внешние параметры алгоритма int S1; // итерации первой фазы int S2; // итерации второй фазы double sigma; // параметр штрафа double t3; // коэффициент корректировки alpha double eps; // малое число для весовых коэффициентов // Внутренние параметры алгоритма double inertia; // параметр инерции для движения (внутренний) double socialFactor; // параметр социального влияния (внутренний) double mutationRate; // вероятность мутации (внутренний) S_COA_Agent agent []; // массив агентов private: //------------------------------------------------------------------- int epochNow; double currentSigma; // Динамический параметр штрафа double alpha []; // параметры поиска double globalBestHistory [10]; // История значений глобального лучшего решения int historyIndex; // Вспомогательные методы double CalculateWeightedGradient (int agentIdx, int coordIdx); double CalculateConstraintValue (int agentIdx, int coordIdx); double CalculateConstraintGradient (int agentIdx, int coordIdx); double CalculatePenaltyFunction (int agentIdx); // Метод для проверки допустимости решения bool IsFeasible (int agentIdx); // Хаотические отображения double LogisticMap (double x); double SineMap (double x); double TentMap (double x); double SelectChaosMap (double x, int type); void InitialPopulation (); void FirstCarrierWaveSearch (); void SecondCarrierWaveSearch (); void ApplyMutation (int agentIdx); void UpdateSigma (); void UpdateBestHistory (double newBest); bool IsConverged (); void ResetStagnatingAgents (); }; //——————————————————————————————————————————————————————————————————————————————
El método "Init" de la clase "C_AO_COA" es responsable de la configuración inicial y la preparación del algoritmo para su funcionamiento. Realiza varias tareas importantes: primero, y ejecuta la inicialización básica utilizando el método "StandardInit()", que configura los rangos, los pasos y otros parámetros. Si no tiene éxito, el método finalizará con error.
A continuación, se establecen los parámetros relacionados con el número de épocas, la época actual (epochNow) y el coeficiente de penalización (currentSigma). Luego se inicializa una historia de las mejores decisiones para ayudar a seguir el progreso. Después se comprueba el tamaño de los arrays de rangos de valores mínimos y máximos a buscar. Si los tamaños no coinciden o no se especifican, se cancela la inicialización.
A continuación, se inicializan los arrays en los que se almacenan los agentes, los coeficientes alfa y las mejores soluciones encontradas. Cada agente recibe una posición inicial según varias estrategias:
- Algunos agentes se distribuyen uniformemente en todo el rango,
- otros "clustering" se distribuyen alrededor de varios puntos dentro de un rango,
- otra parte se posiciona aleatoriamente considerando los límites,
- El resto usa funciones de mapeo caótico para obtener soluciones iniciales.
El método de inicialización "Init" de la clase "C_AO_COA_chaos" establece los parámetros iniciales y los arrays necesarias para encontrar la solución óptima. El proceso implica la verificación de la exactitud de los datos de entrada, la configuración de los rangos de búsqueda, la inicialización de un array de agentes con diferentes estrategias de posición inicial y el establecimiento de los valores de las variables globales, como la mejor solución encontrada. Durante la ejecución del método, se crean las estructuras de datos necesarias para el posterior proceso de optimización iterativa y se establecen los parámetros que regulan el comportamiento de los agentes y del algoritmo en su conjunto.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_COA_chaos::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochNow = 0; currentSigma = sigma; historyIndex = 0; // Инициализация истории лучших значений for (int i = 0; i < 10; i++) globalBestHistory [i] = -DBL_MAX; // Проверка и инициализация основных массивов int arraySize = ArraySize (rangeMinP); if (arraySize <= 0 || arraySize != ArraySize (rangeMaxP) || arraySize != ArraySize (rangeStepP)) { return false; } ArrayResize (agent, popSize); ArrayResize (alpha, coords); // Адаптивная инициализация alpha в зависимости от диапазона поиска for (int c = 0; c < coords; c++) { // alpha зависит от размера пространства поиска double range = rangeMax [c] - rangeMin [c]; alpha [c] = 0.1 * range / MathSqrt (MathMax (1.0, (double)coords)); } // Инициализация агентов с разнообразными стратегиями for (int i = 0; i < popSize; i++) { agent [i].Init (coords); for (int c = 0; c < coords; c++) { double position; // Различные стратегии инициализации if (i < popSize / 4) { // Равномерное распределение по пространству position = rangeMin [c] + (i * (rangeMax [c] - rangeMin [c])) / MathMax (1, popSize / 4); } else if (i < popSize / 2) { // Кластеризация вокруг нескольких точек int cluster = (i - popSize / 4) % 3; double clusterCenter = rangeMin [c] + (cluster + 1) * (rangeMax [c] - rangeMin [c]) / 4.0; position = clusterCenter + u.RNDfromCI (-0.1, 0.1) * (rangeMax [c] - rangeMin [c]); } else if (i < 3 * popSize / 4) { // Случайные позиции с смещением в сторону границ double r = u.RNDprobab (); if (r < 0.5) position = rangeMin [c] + 0.2 * r * (rangeMax [c] - rangeMin [c]); else position = rangeMax [c] - 0.2 * (1.0 - r) * (rangeMax [c] - rangeMin [c]); } else { // Хаотические позиции с использованием разных отображений int mapType = i % 3; double chaosValue = SelectChaosMap (agent [i].gamma [c], mapType); position = rangeMin [c] + chaosValue * (rangeMax [c] - rangeMin [c]); } a [i].cB [c] = u.SeInDiSp (position, rangeMin [c], rangeMax [c], rangeStep [c]); } } return true; } //——————————————————————————————————————————————————————————————————————————————
El método "LogisticMap" implementa el mapeo logístico, que se usa para generar secuencias caóticas. Esta función se utiliza en el algoritmo para introducir aleatoriedad y variedad en la búsqueda de soluciones. La idea principal del método consiste en calcular un nuevo valor de estado basado en el actual utilizando la fórmula del mapeo logístico con un parámetro que varía ligeramente para aumentar la aleatoriedad extraída.
Antes del cálculo, se verifica que el valor de entrada sea correcto y esté dentro del rango; si no coincide, se reemplaza con un número aleatorio dentro del rango indicado. Después de calcular el nuevo valor, también se verifica que esté dentro de un rango aceptable y, si es necesario, se reemplaza con un número aleatorio para mantener la estabilidad de la función. Como resultado, la lógica interna garantiza que el siguiente estado se genere dentro de límites aceptables.
//—————————————————————————————————————————————————————————————————————————————— // Улучшенные хаотические отображения double C_AO_COA_chaos::LogisticMap (double x) { // Защита от некорректных входных значений if (x < 0.0 || x > 1.0 || MathIsValidNumber (x) == false) { x = 0.2 + 0.6 * u.RNDprobab (); } // x(n+1) = r*x(n)*(1-x(n)) double r = 3.9 + 0.1 * u.RNDprobab (); // Слегка рандомизированный параметр для избежания циклов double result = r * x * (1.0 - x); // Дополнительная проверка корректности if (result < 0.0 || result > 1.0 || MathIsValidNumber (result) == false) { result = 0.2 + 0.6 * u.RNDprobab (); } return result; } //——————————————————————————————————————————————————————————————————————————————
El método "SineMap" implementa un mapeo caótico basado en la función de seno. Toma el estado actual, verifica su corrección y, si es incorrecto o está fuera del rango [0, 1], lo reemplaza con un valor aleatorio en dicho rango. Luego calcula un nuevo valor usando la función de seno, lo normaliza para que vuelva a estar en el rango [0, 1] y realiza una verificación adicional.
Si el valor final se encuentra fuera de los límites o no es válido, se reemplaza nuevamente con un número aleatorio en el rango [0.2, 0.8]. Como resultado, el método retorna un nuevo estado que se obtiene en función del actual mediante el mapeo caótico.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::SineMap (double x) { // Защита от некорректных входных значений if (x < 0.0 || x > 1.0 || MathIsValidNumber (x) == false) { x = 0.2 + 0.6 * u.RNDprobab (); } // x(n+1) = sin(π*x(n)) double result = MathSin (M_PI * x); // Нормализация результата к диапазону [0, 1] result = (result + 1.0) / 2.0; // Дополнительная проверка корректности if (result < 0.0 || result > 1.0 || MathIsValidNumber (result) == false) { result = 0.2 + 0.6 * u.RNDprobab (); } return result; } //——————————————————————————————————————————————————————————————————————————————
El método "TentMap" implementa un mapeo de "tiendas" para generar una secuencia caótica. El método toma un valor de entrada "x" que debe estar entre 0 y 1 y verifica que "x" sea correcto y, si es necesario, lo reemplaza con un valor aleatorio dentro del rango aceptable. A continuación, usando un parámetro "mu" cercano a 2, se calcula un nuevo valor basado en una función lineal por partes característica para el mapeo de "tienda".
Después del cálculo, se realiza otra comprobación para garantizar que el valor sea válido y, si es necesario, se normaliza mediante un número aleatorio. Luego, el método retorna un nuevo valor generado aleatoriamente.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::TentMap (double x) { // Защита от некорректных входных значений if (x < 0.0 || x > 1.0 || MathIsValidNumber (x) == false) { x = 0.2 + 0.6 * u.RNDprobab (); } // Tent map: x(n+1) = μ*min(x(n), 1-x(n)) double mu = 1.99; // Параметр близкий к 2 для хаотического поведения double result; if (x <= 0.5) result = mu * x; else result = mu * (1.0 - x); // Дополнительная проверка корректности if (result < 0.0 || result > 1.0 || MathIsValidNumber (result) == false) { result = 0.2 + 0.6 * u.RNDprobab (); } return result; } //——————————————————————————————————————————————————————————————————————————————
El método "SelectChaosMap" está diseñado para seleccionar y aplicar una función de mapeo caótico dependiendo del tipo especificado. Toma un valor "x" y un parámetro "tipo" que indica el tipo específico de mapeo caótico. La idea básica del método consiste en utilizar el resto de la división del tipo por 3 para determinar la opción de mapeo, lo que posibilita una elección cíclica entre tres mapas caóticos diferentes: logístico, sinusoidal y de tienda. Dependiendo del resultado, se llama la función correspondiente, que transforma el valor de entrada "x" en uno nuevo, usando la dinámica caótica seleccionada.
Si por alguna razón el tipo no cae dentro del rango esperado (0, 1, 2), el mapa logístico se aplica por defecto. Cada uno de estos mapas modela un comportamiento caótico y se usa para generar números diversos e impredecibles como parte del proceso de optimización.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::SelectChaosMap (double x, int type) { // Выбор хаотического отображения на основе типа switch (type % 3) { case 0: return LogisticMap (x); case 1: return SineMap (x); case 2: return TentMap (x); default: return LogisticMap (x); } } //——————————————————————————————————————————————————————————————————————————————
El método "InitialPopulation" está diseñado para inicializar la población inicial del algoritmo de optimización usando la técnica "Latin Hypercube Sampling (LHS)". El LHS es un método de muestreo estratificado que ofrece una cobertura más uniforme del espacio de búsqueda multivariado en comparación con el muestreo aleatorio, mejorando así la calidad de la población inicial.
El método comienza declarando arrays para los valores del hipercubo latino y valores temporales que servirán de ayuda en la generación. El método intenta asignar memoria para los arrays requeridos y, si la asignación de memoria falla, se produce un escenario de respaldo que crea la población inicial de manera aleatoria. Esto garantiza que el programa no se bloquee debido a la falta de memoria.
A continuación, el método genera valores para el hipercubo latino. Para cada coordenada, se crea un array clasificado de valores, que luego se mezcla aleatoriamente. Los valores mezclados se asignan al array de hipercubo. Los valores del hipercubo latino se transforman en coordenadas de individuos en el espacio de búsqueda. El cálculo se realiza usando los rangos especificados y los valores obtenidos se limitan al rango y paso requeridos.
Al final, el método establece una bandera que indica que la población inicial ha sido modificada o creada. La ventaja de este enfoque consiste en que crea una población inicial más diversificada.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::InitialPopulation () { // Создаем Latin Hypercube для начальной популяции double latinCube []; // Одномерный массив для хранения значений гиперкуба double tempValues []; // Временный массив для хранения и перемешивания значений ArrayResize (latinCube, popSize * coords); ArrayResize (tempValues, popSize); // Генерируем Латинский гиперкуб for (int c = 0; c < coords; c++) { // Создаем упорядоченные значения for (int i = 0; i < popSize; i++) { tempValues [i] = (double)i / popSize; } // Перемешиваем значения for (int i = popSize - 1; i > 0; i--) { int j = (int)(u.RNDprobab () * (i + 1)); if (j < popSize) { double temp = tempValues [i]; tempValues [i] = tempValues [j]; tempValues [j] = temp; } } // Присваиваем перемешанные значения for (int i = 0; i < popSize; i++) { latinCube [i * coords + c] = tempValues [i]; } } // Преобразуем значения Латинского гиперкуба в координаты for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double x = rangeMin [c] + latinCube [i * coords + c] * (rangeMax [c] - rangeMin [c]); a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
El método "FirstCarrierWaveSearch" implementa una etapa de búsqueda en el algoritmo destinada a encontrar un equilibrio entre la exploración global del espacio y la explotación local de soluciones conocidas. Su tarea principal es actualizar las posiciones y velocidades de los agentes, prosiguiendo con la búsqueda y mejora de posibles soluciones. Al comienzo del método, se define un coeficiente que controla el grado de exploración en la época de búsqueda actual. Dicho coeficiente disminuye de forma cuadrática a medida que avanzan las épocas, lo que garantiza un cambio gradual en el énfasis desde las operaciones de búsqueda global a la mejora local. Luego, para cada agente de la población, se realiza una prueba de mutación: con cierta probabilidad, se ejecuta una mutación para aumentar la diversidad de soluciones. Después de eso, para cada dirección de búsqueda (coordenadas):
- Se selecciona el tipo de mapeo caótico utilizado para generar nuevas soluciones potenciales,
- se determina la estrategia de búsqueda: global o local.
En la búsqueda global, el agente actualiza su posición usando un componente caótico y la velocidad se ajusta según la inercia y la dirección del movimiento. En el caso de la búsqueda local, el agente se centra en las mejores soluciones encontradas, realizando una atracción ponderada hacia ellas con una pequeña variación aleatoria para evitar ciclos. En ambos casos, la velocidad está limitada para evitar saltos que terminen demasiado fuera de los límites del espacio de búsqueda. Las posiciones de los agentes se actualizan considerando las restricciones del espacio de búsqueda y, de ser necesario, se realizan correcciones si se detectan violaciones de las restricciones. En este caso se ajustan las posiciones y se reducen las velocidades para suavizar los pasos posteriores.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::FirstCarrierWaveSearch () { // Адаптивный баланс между исследованием и эксплуатацией double globalPhase = (double)epochNow / S1; double explorationRate = 1.0 - globalPhase * globalPhase; // Квадратичное снижение // Для каждого агента for (int i = 0; i < popSize; i++) { // Применяем мутации с некоторой вероятностью для усиления разнообразия if (u.RNDprobab () < mutationRate * (1.0 + explorationRate)) { ApplyMutation (i); continue; } for (int c = 0; c < coords; c++) { // Выбор хаотического отображения с равномерным распределением int mapType = ((i + c + epochNow) % 3); // Безопасная проверка доступа к массиву gamma if (c < ArraySize (agent [i].gamma)) { agent [i].gamma [c] = SelectChaosMap (agent [i].gamma [c], mapType); } else { continue; // Пропускаем, если индекс некорректен } // Определяем соотношение между глобальным и локальным поиском double strategy = u.RNDprobab (); double x; if (strategy < explorationRate) { // Глобальный поиск с хаотическим компонентом x = rangeMin [c] + agent [i].gamma [c] * (rangeMax [c] - rangeMin [c]); // Добавляем компонент скорости для сохранения направления движения agent [i].velocity [c] = inertia * agent [i].velocity [c] + (1.0 - inertia) * (x - a [i].c [c]); } else { // Локальный поиск вокруг лучших решений double personalAttraction = u.RNDprobab (); double globalAttraction = u.RNDprobab (); // Взвешенное притяжение к лучшим решениям double attractionTerm = //personalAttraction * (agent [i].cPrev [c] - a [i].c [c]) + personalAttraction * (a [i].cB [c] - a [i].c [c]) + socialFactor * globalAttraction * (cB [c] - a [i].c [c]); // Хаотическое возмущение для предотвращения застревания double chaosRange = alpha [c] * explorationRate; double chaosTerm = chaosRange * (2.0 * agent [i].gamma [c] - 1.0); // Обновление скорости с инерцией agent [i].velocity [c] = inertia * agent [i].velocity [c] + (1.0 - inertia) * (attractionTerm + chaosTerm); } // Ограничиваем скорость для предотвращения слишком больших шагов double maxVelocity = 0.1 * (rangeMax [c] - rangeMin [c]); if (MathAbs (agent [i].velocity [c]) > maxVelocity) { agent [i].velocity [c] = maxVelocity * (agent [i].velocity [c] > 0 ? 1.0 : -1.0); } // Применяем скорость к позиции x = a [i].c [c] + agent [i].velocity [c]; // Применяем ограничения поискового пространства a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); // Проверяем ограничения и применяем плавную коррекцию double violation = CalculateConstraintValue (i, c); if (violation > eps) { double gradient = CalculateWeightedGradient (i, c); double correction = -gradient * violation * (1.0 - globalPhase); a [i].c [c] = u.SeInDiSp (a [i].c [c] + correction, rangeMin [c], rangeMax [c], rangeStep [c]); // Сбрасываем скорость при коррекции нарушений agent [i].velocity [c] *= 0.5; } } } } //——————————————————————————————————————————————————————————————————————————————
El método “SecondCarrierWaveSearch” supone una etapa de optimización que se desarrolla después de la búsqueda inicial y tiene como objetivo profundizar y refinar las soluciones encontradas. El objetivo principal de este método es mejorar los resultados obtenidos en la etapa anterior mediante la aplicación de estrategias de búsqueda más sofisticadas y la adaptación de parámetros.
El método comienza su trabajo calculando un parámetro que refleja la fase de búsqueda local, que se intensifica con el tiempo. Esto permite que el algoritmo pase gradualmente de una búsqueda amplia a una exploración más detallada y precisa del área con soluciones ya conocidas. Al comienzo del método, se efectúa una comprobación para ver si se ha logrado la convergencia. Si el algoritmo ha alcanzado un estado estable, algunos agentes sufren mutaciones para aumentar la diversidad de soluciones y evitar extremos locales.
Para cada agente, se hace una búsqueda secuencial de nuevas soluciones en su espacio. Luego se definen mapeos caóticos que ayudan a introducir elementos de aleatoriedad. El parámetro de búsqueda disminuye conforme nos acerquemos a la solución óptima. Esto ofrece un enfoque más estrecho a la hora de buscar cerca de las mejores soluciones actuales. Al actualizar cada posición, se consideran los logros pasados de los agentes. Así, se determina un punto básico, que puede ser el óptimo global absoluto o los logros personales previos del agente, lo que ayuda a tener en cuenta tanto los resultados individuales como los generales de toda la población.
El proceso de actualización de posiciones usa tanto el sesgo caótico como el ruido aleatorio (por ejemplo, ruido de Levy), lo que agrega un elemento de aleatoriedad y facilita la búsqueda de soluciones nuevas y potencialmente mejores. El método considera la inercia al actualizar las velocidades de los agentes, lo que permite cambios más suaves y evita movimientos agresivos. Como resultado, las posiciones actualizadas están limitadas por los límites especificados, lo cual garantiza que se cumplan las condiciones del problema.
El método "SecondCarrierWaveSearch" tiene como objetivo una optimización más precisa y profunda de las soluciones existentes.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::SecondCarrierWaveSearch () { // Уточняющий локальный поиск с адаптивными параметрами double localPhase = (double)(epochNow - S1) / S2; double intensificationRate = localPhase * localPhase; // Квадратичное увеличение интенсификации // Проверка на сходимость алгоритма bool isConverged = IsConverged (); // Для каждого агента for (int i = 0; i < popSize; i++) { // Если обнаружена сходимость, добавляем случайную мутацию к некоторым агентам if (isConverged && i % 3 == 0) { ApplyMutation (i); continue; } for (int c = 0; c < coords; c++) { // Выбор хаотического отображения с равномерным распределением int mapType = ((i * c + epochNow) % 3); agent [i].gamma [c] = SelectChaosMap (agent [i].gamma [c], mapType); // Адаптивный радиус поиска с сужением к концу оптимизации double adaptiveAlpha = alpha [c] * (1.0 - 0.8 * intensificationRate); // Выбор базовой точки с приоритетом лучших решений double basePoint; if (a [i].f > a [i].fB) { basePoint = a [i].c [c]; // Текущее положение лучше } else { double r = u.RNDprobab (); if (r < 0.7 * (1.0 + intensificationRate)) // Увеличиваем притяжение к глобальному лучшему { basePoint = cB [c]; // Глобальное лучшее } else { basePoint = a [i].cB [c]; // Личное лучшее } } // Локальный поиск с хаотическим компонентом double chaosOffset = adaptiveAlpha * (2.0 * agent [i].gamma [c] - 1.0); // Добавляем шум Леви для случайных дальних прыжков (тяжелый хвост распределения) double levyNoise = 0.0; if (u.RNDprobab () < 0.1 * (1.0 - intensificationRate)) { // Упрощенное приближение шума Леви double u1 = u.RNDprobab (); double u2 = u.RNDprobab (); if (u2 > 0.01) // Защита от деления на очень малые числа { levyNoise = 0.01 * u1 / MathPow (u2, 0.5) * adaptiveAlpha * (rangeMax [c] - rangeMin [c]); } } // Обновляем скорость с инерцией agent [i].velocity [c] = inertia * (1.0 - 0.5 * intensificationRate) * agent [i].velocity [c] + (1.0 - inertia) * (chaosOffset + levyNoise); // Применяем скорость к позиции double x = basePoint + agent [i].velocity [c]; // Ограничиваем позицию a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
En el próximo artículo, continuaremos analizando los métodos restantes del algoritmo, realizaremos pruebas y resumiremos los resultados.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16729
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Utilizando redes neuronales en MetaTrader
Utilizando redes neuronales en MetaTrader
 Automatización de estrategias de trading en MQL5 (Parte 15): Patrón armónico Cypher de acción del precio con visualización
Automatización de estrategias de trading en MQL5 (Parte 15): Patrón armónico Cypher de acción del precio con visualización
 Particularidades del trabajo con números del tipo double en MQL4
Particularidades del trabajo con números del tipo double en MQL4
 Simulación de mercado (Parte 18): Iniciando SQL (I)
Simulación de mercado (Parte 18): Iniciando SQL (I)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso