Algoritmo de tiro con arco - Archery Algorithm (AA)

Contenido

1. Introducción
2. Implementación del algoritmo
3. Resultados de las pruebas

Introducción

Con tareas cada vez más complejas y recursos cada vez más escasos, la optimización se está convirtiendo no solo en una necesidad, sino en un verdadero arte algorítmico en el mundo actual. ¿Cómo encontrar la mejor solución entre las muchas posibles? ¿Cómo minimizar los costes, aumentar la eficacia y maximizar los beneficios? Estas cuestiones preocupan a especialistas de muy diversos campos, de la economía a la ingeniería, de los sistemas sociales a la ecología. Antes de proceder a resolver un problema de optimización, resulta esencial modelar correctamente el problema, identificando las variables clave y las relaciones matemáticas que reproducirán adecuadamente la realidad. La optimización se usa ampliamente en las finanzas y el trading, ayudando no solo a desarrollar nuevas estrategias de inversión, sino también a mejorar las existentes. No obstante, a pesar de la universalidad de los enfoques, los métodos de optimización pueden dividirse a grandes rasgos en dos categorías: deterministas y estocásticos.

Los métodos deterministas, como el descenso de gradiente, ofrecen soluciones rigurosas y predecibles usando derivadas matemáticas para encontrar el óptimo, lo cual permite modelar eficazmente diversos escenarios; sin embargo, una vez que los problemas se vuelven no lineales o multidimensionales, su eficacia puede disminuir drásticamente. En estos casos, los métodos estocásticos acuden al rescate, usando como base procesos aleatorios para encontrar soluciones aceptables en entornos complejos, lo cual los hace especialmente útiles en mercados volátiles.

Las combinaciones de métodos deterministas y estocásticos juegan un papel fundamental en los enfoques modernos de la optimización. Combinando estos dos enfoques, los analistas pueden crear modelos más flexibles y adaptables que consideren tanto las condiciones estables como las cambiantes. Esto no solo mejora la calidad de las previsiones, sino que también minimiza los riesgos, algo fundamental para el éxito de la gestión de las inversiones.

En este artículo, presentaremos un nuevo enfoque para resolver problemas de optimización, el Algoritmo de Tiro con Arco (AA). El algoritmo fue desarrollado por Fatemeh Ahmadi Zeidabadi y sus colegas y se publicó en febrero de 2022. Este método, inspirado en el arte del tiro con arco, ofrece soluciones casi óptimas actualizando la posición de los miembros de la población en el espacio de búsqueda partiendo de un elemento seleccionado al azar. Hoy comprobaremos la eficacia de AA en funciones objetivo estándar y compararemos los resultados con algoritmos que ya conocemos. Profundizando en los detalles, desvelaremos cómo este enfoque innovador puede cambiar nuestra forma de pensar sobre la optimización y abrir nuevos horizontes para resolver problemas complejos.

Implementación del algoritmo

El Algoritmo de Tiro con Arco (AA) es un método de optimización estocástica completamente nuevo desarrollado para encontrar soluciones óptimas en problemas de optimización e inspirado en el comportamiento de un arquero que apunta a una diana.  El AA simula el proceso de disparo de flechas a una diana. Cada miembro de la población representa una solución potencial al problema de optimización, y sus posiciones en el espacio de búsqueda se actualizan según el rendimiento de un miembro "objetivo" elegido aleatoriamente, proceso similar a la forma en que un tirador ajusta su mira según dónde quiere disparar.

La población se representa como una matriz en la que cada fila corresponde a un miembro (solución) y cada columna a una dimensión del problema. Esto permite evaluar y actualizar de forma estructurada las soluciones según sus valores de función objetivo. El rendimiento de cada miembro se evalúa usando una función objetivo que cuantifica la calidad de la solución encontrada. Los resultados se almacenan en un vector, lo cual permite al algoritmo comparar el rendimiento de distintas soluciones.

El objetivo se divide en secciones, y la anchura de cada sección se corresponde con la productividad de los miembros de la población. Luego se calcula una función de verosimilitud para determinar la probabilidad de que cada miembro sea seleccionado según su valor de función objetivo, teniendo los arqueros más eficientes una mayor probabilidad de ser seleccionados. Después se selecciona aleatoriamente un miembro de la población según la probabilidad acumulada, imitando la selección del objetivo del tirador. Dicha selección afecta al modo en que se actualizan las posiciones de los demás miembros. El algoritmo actualiza la posición de cada flecha en el espacio de búsqueda usando determinadas ecuaciones. La actualización dependerá de si el arquero seleccionado tiene un valor de función objetivo mejor o peor que el actual. Este proceso incorpora la aleatoriedad para explorar el espacio de búsqueda. El AA funciona de forma iterativa, actualizando la población hasta que se alcanza una condición de parada (número máximo de iteraciones). Durante este proceso, el algoritmo efectúa un seguimiento de la mejor solución encontrada.

La versión original del algoritmo AA presentada anteriormente describe la matriz como una población, y los vectores como miembros de la población. Sin embargo, en el texto no se especifican operaciones concretas propias del trabajo con matrices. De hecho, el algoritmo implica acciones estándar del agente de búsqueda, como sucede en la mayoría de los algoritmos discutidos anteriormente.

También cabe señalar que la frase "el objetivo se divide en secciones, y la anchura de cada sección se corresponde con la productividad de los miembros de la población" implica el uso del método de la ruleta para la selección. En este caso, la probabilidad de elegir un sector es proporcional a su anchura.

De este modo, un lenguaje complejo que describe muchos conceptos puede explicarse de forma mucho más simple, lo cual puede facilitar mucho la comprensión de la idea.

Así pues, un algoritmo de tiro con arco supone un método de optimización basado en la población que utiliza los principios del tiro al blanco para guiar la búsqueda de soluciones óptimas. El algoritmo combina elementos de aleatoriedad usando una distribución normal para explorar y explotar el espacio de búsqueda. Componentes clave del algoritmo:

1. Población de agentes (arqueros)
2. Vector de probabilidades y probabilidades acumuladas
3. Mecanismo de herencia (no presente en la versión original)
4. Mecanismo de actualización de posiciones
5. Parámetro de intensidad del entrenamiento (I)

En primer lugar, presentaremos el pseudocódigo del algoritmo:

Inicialización:
    Creamos una población de agentes popSize
    Para cada agente:
        Inicializamos una posición aleatoria dentro del rango de búsqueda
        Inicializamos la posición anterior y la adaptabilidad

Ciclo principal:
    Hasta que se alcance la condición de parada:
        Para cada agente i de la población
            Calculamos el vector de probabilidades P y las probabilidades acumuladas C
            
            Para cada coordenada c:
                Seleccionamos al arquero k utilizando la probabilidad acumulada
                
                Si (número_aleatorio < probabilidad_de_herencia):
                    nueva_posición [c] = posición_arquero_k [c]
                De lo contrario:
                    I = redondeo (1 + número_aleatorio_de_0_a_1) // Parámetro de intensidad del entrenamiento
                    random_gaussian = generar_número_gaussiano (media = 0, min =-1, max = 1)
                    
                    Si (adaptación_arquero_k > adaptación_agente_i):
                        nueva_posición [c] = posición_anterior [c] + random_gaussian * (posición_arquero_k [c] - I * posición_anterior [c])
                    De lo contrario:
                        nueva_posición [c] = posición_anterior [c] + random_gaussian * (posición_anterior [c] - I * posición_arquero_k [c])
                
                Limitamos la nueva_posición [c] dentro del rango de búsqueda
            
            Actualizamos la posición del agente i
        
        Evaluamos la adaptabilidad de todos los agentes
        Actualizamos la mejor solución global
        Para cada agente:
            Si la nueva adaptación es mejor que la anterior:
                Actualizamos la posición anterior y la adaptabilidad

Retornamos la mejor solución encontrada

Peculiaridades de implementación en el código:

1. El algoritmo usa un enfoque probabilístico para seleccionar los arqueros de los que aprender.
2. El mecanismo de herencia permite a los agentes copiar directamente las posiciones de los arqueros que han tenido éxito con cierta probabilidad.
3. Las actualizaciones de posición usan una distribución gaussiana para introducir aleatoriedad en el proceso de entrenamiento de los arqueros.
4. El algoritmo almacena las mejores posiciones anteriores de los agentes, lo cual le permite tener cierta "memoria" de las buenas decisiones.
5. La aplicación incluirá un mecanismo para limitar los nuevos elementos dentro del rango de búsqueda permitido.
6. El parámetro de intensidad de aprendizaje (I) descrito por los autores se usará para regular el grado de influencia de la posición actual en la nueva posición.

El parámetro I (intensidad de entrenamiento) es una variable aleatoria que puede tomar el valor de 1 o 2. Se define del siguiente modo: I = redondeo a número entero (1 + número generado aleatoriamente entre 0 y 1). Esto significa que I será igual a 1 con una probabilidad 0,5 y 2 con la misma probabilidad. Papel del parámetro I en el algoritmo:

1. Cuando I = 1, el algoritmo realiza ajustes de posición más pequeños.
2. Cuando I = 2, el algoritmo puede realizar cambios de posición más bruscos.

Vamos a pasar directamente a escribir el código del algoritmo. La estructura "arquero", "S_AA_Agent", representa un agente en el algoritmo de optimización con un conjunto de coordenadas en el espacio de decisión y contiene información sobre su rendimiento según la aptitud. 

• cPrev [] - el array almacena las coordenadas anteriores del agente.
  
• fPrev - esta variable almacena el anterior valor de aptitud del agente.   

El método "Init" prepara al agente para el funcionamiento estableciendo los valores iniciales para sus coordenadas y aptitud. A continuación, establecemos el valor de "fPrev" en el valor mínimo posible para el tipo "double" porque aún no se ha calculado la adaptabilidad.

//——————————————————————————————————————————————————————————————————————————————
struct S_AA_Agent
{
    double cPrev []; // previous coordinates
    double fPrev;    // previous fitness

    void Init (int coords)
    {
      ArrayResize (cPrev, coords);
      fPrev = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Luego analizamos la clase "C_AO_AAm", que implementa el algoritmo propiamente dicho y hereda de la clase "C_AO". 

• popSize - indica el tamaño de la población.
• inhProbab - representa el valor de la probabilidad de heredar una característica de otro arquero.

A continuación, se inicializa un array "params" de tamaño 2, donde se almacenan los parámetros del algoritmo: el tamaño de la población y la probabilidad de herencia.

• SetParams - el método establece los parámetros del algoritmo basándose en los valores almacenados en el array "params". Después extraemos los valores "popSize" y "inhProbab", convirtiéndolos a sus respectivos tipos.
• Init - el método inicializa el algoritmo tomando los límites de búsqueda mínimos y máximos, el paso de búsqueda y el número de épocas.
• Moving y Revision - los métodos son responsables de la lógica de movimiento de los agentes en el espacio de soluciones y de su revisión (actualización). 

S_AA_Agent agent [] - array de agentes que serán usados para realizar la optimización.

La clase "C_AO_AAm" implementa el algoritmo de optimización, mientras que los métodos "SetParams", "Init", "Moving" y "Revision" controlan la configuración y el comportamiento del algoritmo mientras se ejecuta. 

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AAm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AAm () { }
  C_AO_AAm ()
  {
    ao_name = "AAm";
    ao_desc = "Archery Algorithm M";
    ao_link = "https://www.mql5.com/es/articles/15782";

    popSize   = 50;    // population size
    inhProbab = 0.3;

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "inhProbab"; params [1].val = inhProbab;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    inhProbab = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], // minimum search range
             const double &rangeMaxP  [], // maximum search range
             const double &rangeStepP [], // step search
             const int     epochsP = 0);  // number of epochs

  void Moving ();
  void Revision ();

  //----------------------------------------------------------------------------
  double  inhProbab; //probability of inheritance

  S_AA_Agent agent [];

  private: //-------------------------------------------------------------------
};
//——————————————————————————————————————————————————————————————————————————————

El método "Init" de la clase "C_AO_AAm" se ocupa de inicializar el algoritmo de optimización. Toma cuatro parámetros: los arrays para los límites de búsqueda mínimos y máximos, el paso de búsqueda y el número de épocas, que por defecto es cero.

• Si la inicialización estándar tiene éxito, el método redimensionará el array "agent" para que coincida con el tamaño de población establecido "popSize". Esto permitirá crear el número necesario de agentes que se utilizarán en el algoritmo.
• En el ciclo "for", cada agente del array se inicializa usando el método "Init", que establece las coordenadas iniciales de cada agente.
  

Al final, el método retorna "true", indicando que la inicialización del algoritmo se ha completado con éxito. Así, el método "Init" se ocupa de preparar el algoritmo para su funcionamiento, configurando los parámetros necesarios y creando los agentes que participarán en el proceso de optimización.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AAm::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

El método "Moving" de la clase "C_AO_AAm" se encarga de desplazar los agentes en el espacio de soluciones según sus posiciones actuales y los valores de la función que están optimizando. Vamos a desglosarlo pieza por pieza:

• Si llamamos al método por primera vez ("revision" es "false"), se inicializará un valor aleatorio para cada agente y cada coordenada dentro de los límites "rangeMin" y "rangeMax" dados.
• A continuación, este valor se ajusta mediante el método "SeInDiSp", que garantiza que el valor coincida con el paso indicado.

Después, la bandera "revision" se establece en "true" y el método finalizará.

• A continuación, se crean dos arrays: "P" para las probabilidades y "C" para las probabilidades acumuladas.
• Luego se encuentra el peor valor de la función "F_worst" para normalizar los valores de la función de aptitud de los agentes.
• A continuación, calculamos las probabilidades de cada agente, que se normalizan para que su suma sea igual a 1.
• Las probabilidades acumuladas "C" se calculan a partir de las probabilidades "P".
• Para cada agente y cada coordenada, se selecciona un tirador compañero, un agente según la probabilidad acumulada.
• Si el valor aleatorio es menor que la probabilidad de herencia dada "inhProbab", el agente tomará la coordenada del agente seleccionado (asegurando la herencia de características con la probabilidad dada).
  
• En caso contrario, el agente actualiza su posición basándose en una fórmula que considera la posición actual, un valor aleatorio y la posición del tirador compañero.
• Por último, el nuevo valor de coordenadas también se corrige usando el método "SeInDiSp".

El método Moving ejecuta el movimiento de los agentes en el espacio de decisión dadas sus posiciones actuales y los valores de las funciones y utiliza métodos probabilísticos para seleccionar las direcciones de movimiento y actualizar las posiciones.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //-------------------------------------------------------------------------
  // Calculate probability vector P and cumulative probability C
  double P [], C [];
  ArrayResize (P, popSize);
  ArrayResize (C, popSize);
  double F_worst = DBL_MAX;
  double sum = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f < F_worst) F_worst = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] =  a [i].f - F_worst;
    sum += P [i];
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] /= sum;
    C [i] = (i == 0) ? P [i] : C [i - 1] + P [i];
  }

  double x;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Select archer (k) using cumulative probability
      int k = 0;
      double r = u.RNDprobab ();
      while (k < popSize - 1 && C [k] < r) k++;

      if (u.RNDbool () < inhProbab)
      {
        x = a [k].c [c];
      }
      else
      {
        // Update position using Eq. (5) and (6)
        double I   = MathRound (1 + u.RNDprobab ());
        double rnd = u.GaussDistribution (0, -1, 1, 8);

        if (a [k].f > a [i].f)
        {
          x = agent [i].cPrev [c] + rnd * (a [k].c [c] - I * agent [i].cPrev [c]);
        }
        else
        {
          x = agent [i].cPrev [c] + rnd * (agent [i].cPrev [c] - I * a [k].c [c]);
        }
      }

      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "Revision" de la clase "C_AO_AAm" se ocupa de actualizar la información sobre los mejores agentes de la población. El método efectúa las siguientes acciones:

• La variable "ind" se inicializará con el valor "-1". Se usará para almacenar el índice del agente con el mejor valor de característica.
• El ciclo "for" itera todos los agentes de la población "popSize" y si el valor de la característica del agente actual "a[i].f" es mayor que el valor de la mejor característica actual "fB":
• se actualiza "fB" al nuevo mejor valor "a[i].f".
• el índice de este agente se almacena en la variable "ind".

Una vez finalizado el ciclo, si "ind" no es igual a "-1", se llamará la función "ArrayCopy", que copiará las coordenadas del mejor agente del array "a" al array "cB". También se ejecutará un segundo ciclo "for" en todos los agentes de la población:

• Si el valor de la función del agente actual "a[i].f" es mayor que su anterior valor de la función de aptitud "agente[i].fPrev":
• actualizamos el valor "fPrev" anterior de este agente.
• las coordenadas actuales del agente se copian en el array "cPrev" usando "ArrayCopy".

El métodoRevision se utiliza para actualizar la información sobre la mejor solución global y para actualizar las mejores posiciones de los agentes.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAm::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > agent [i].fPrev)
    {
      agent [i].fPrev = a [i].f;
      ArrayCopy (agent [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Resultados de las pruebas

Hemos modificado ligeramente este algoritmo. El algoritmo original de los autores no intercambia directamente información entre los arqueros. El intercambio se realiza indirectamente mediante la interacción de coordenadas a través de la distribución normal, por lo que me ha parecido necesario añadir el intercambio de esta información. Para ello, hemos añadido un parámetro adicional "inhProbab" que se encarga de realizar dicho intercambio con una probabilidad determinada.

if (u.RNDbool () < inhProbab)
{
  x = a [k].c [c];
}

Los resultados presentados a continuación se corresponden con la versión original del algoritmo, tal como la concibieron los autores.

AA|Archery Algorithm|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6699547926310098
25 Hilly's; Func runs: 10000; result: 0.37356238340164605
500 Hilly's; Func runs: 10000; result: 0.257542163368952
=============================
5 Forest's; Func runs: 10000; result: 0.38166669771790607
25 Forest's; Func runs: 10000; result: 0.199300365268835
500 Forest's; Func runs: 10000; result: 0.15337954055780398
=============================
5 Megacity's; Func runs: 10000; result: 0.4076923076923077
25 Megacity's; Func runs: 10000; result: 0.17907692307692308
500 Megacity's; Func runs: 10000; result: 0.10004615384615476
=============================
All score: 2.72222 (30.25%)

El algoritmo obtiene una puntuación del 30,25% en los resultados de la prueba; sin embargo, con mi modificación, el algoritmo ha mejorado su rendimiento en más de un 13%. A continuación le mostramos los resultados de la versión modificada:

AAm|Archery Algorithm M|50.0|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.9353194829441194
25 Hilly's; Func runs: 10000; result: 0.6798262991897616
500 Hilly's; Func runs: 10000; result: 0.2596620178276653
=============================
5 Forest's; Func runs: 10000; result: 0.5735062785421186
25 Forest's; Func runs: 10000; result: 0.22007188891556378
500 Forest's; Func runs: 10000; result: 0.1486980566819649
=============================
5 Megacity's; Func runs: 10000; result: 0.6307692307692309
25 Megacity's; Func runs: 10000; result: 0.344
500 Megacity's; Func runs: 10000; result: 0.10193846153846249
=============================
All score: 3.89379 (43.26%)

Así que he decidido decantarme por un algoritmo con modificaciones y ponerlo en la tabla de clasificación. Más abajo puede ver cómo funciona el algoritmo en la visualización. Creo que es lo suficientemente bueno: claro que existe una dispersión en los resultados, sin embargo, no es sustancial y solo se da en funciones con un pequeño número de coordenadas.

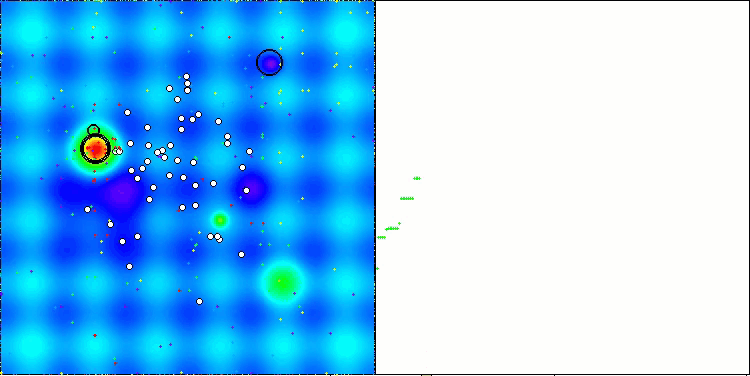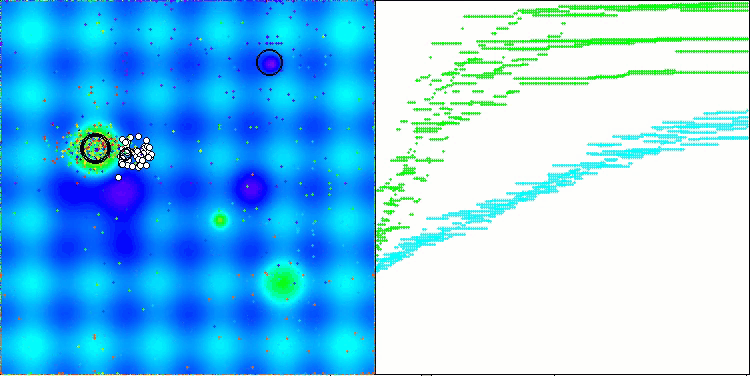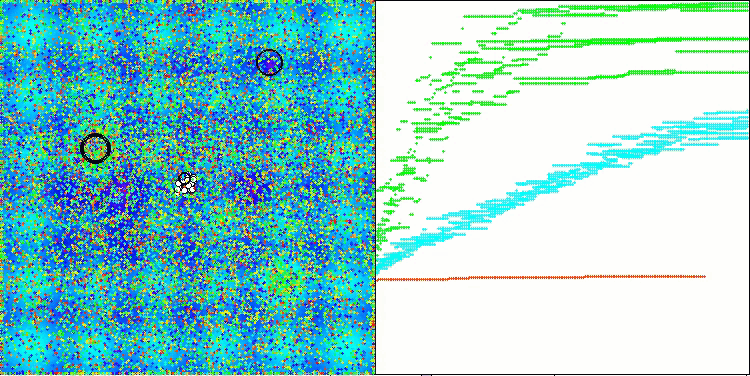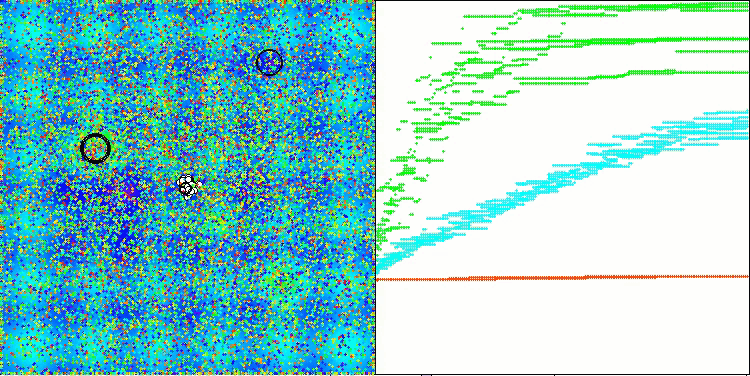
AAm en la función de prueba Hilly

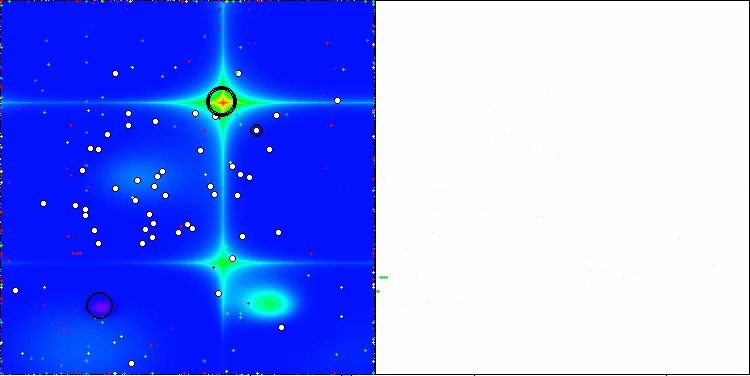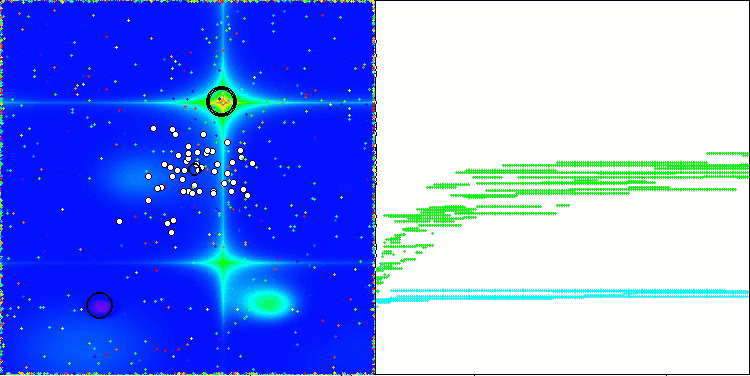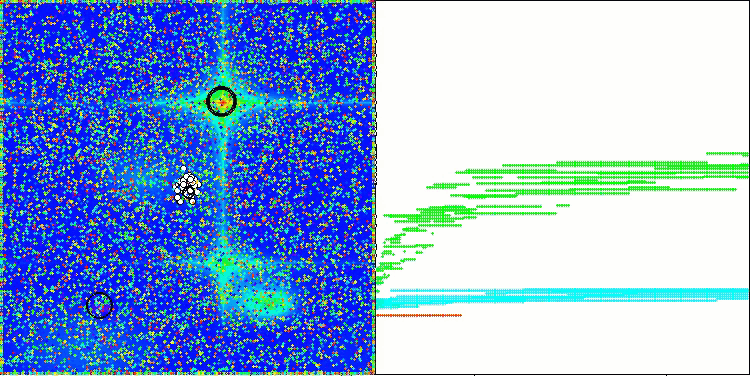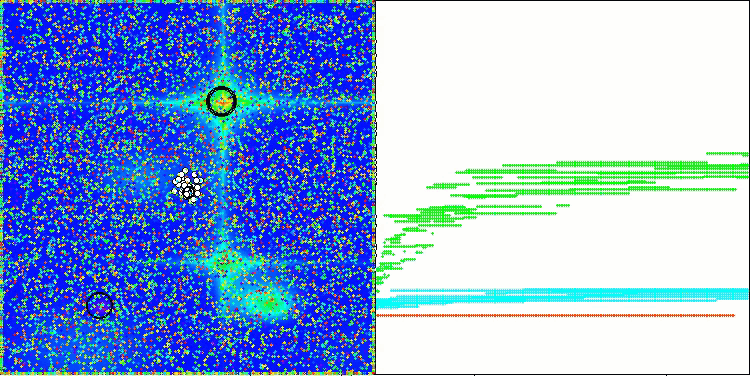
AAm en la función de prueba Forest

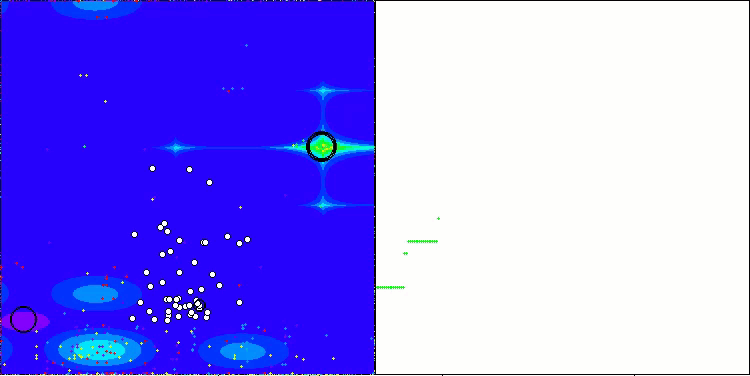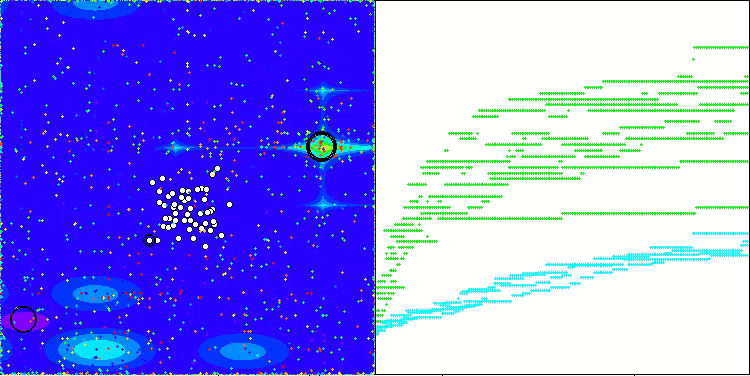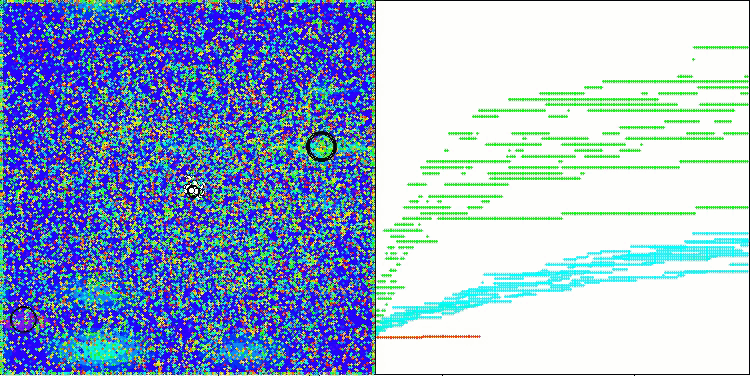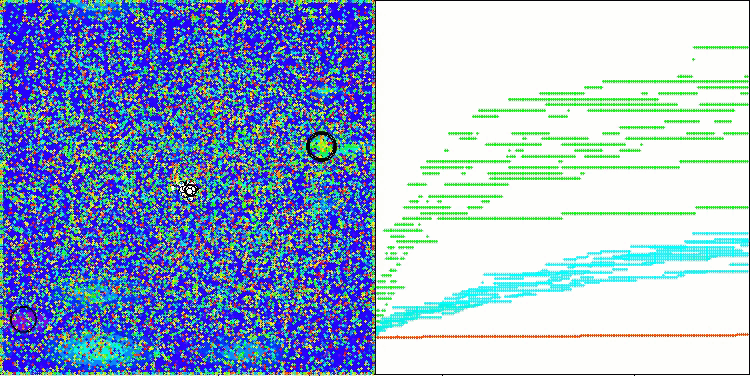
AAm sobre la función de prueba Megacity

La versión modificada del algoritmo ocupa el puesto 26 en cuanto a rendimiento.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% de MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
2	CLA	code lock algorithm	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	AMOm	animal migration optimization M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5,987	66,52
4	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
5	CTA	comet tail algorithm	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
6	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
7	ESG	evolution of social groups	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
8	SIA	simulated isotropic annealing	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
9	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
10	ASO	anarchy society optimization	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5,178	57,54
11	TSEA	turtle shell evolution algorithm	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
12	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
13	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
14	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
15	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
16	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
17	BCOm	bacterial chemotaxis optimization M	0,75953	0,62268	0,31483	1,69704	0,89378	0,61339	0,22542	1,73259	0,65385	0,42092	0,14435	1,21912	4,649	51,65
18	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
19	TSm	tabu search M	0,87795	0,61431	0,29104	1,78330	0,92885	0,51844	0,19054	1,63783	0,61077	0,38215	0,12157	1,11449	4,536	50,40
20	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
21	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
22	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
23	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
24	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
25	ABH	artificial bee hive algorithm	0,84131	0,54227	0,26304	1,64663	0,87858	0,47779	0,17181	1,52818	0,50923	0,33877	0,10397	0,95197	4.127	45,85
26	AAm	archery algorithm M	0,93532	0,67983	0,25966	1,87481	0,57351	0,22007	0,14870	0,94228	0,63077	0,34400	0,10194	1,07671	3,894	43,26
27	ASBO	adaptive social behavior optimization	0,76331	0,49253	0,32619	1,58202	0,79546	0,40035	0,26097	1,45677	0,26462	0,17169	0,18200	0,61831	3.657	40,63
28	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
29	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
30	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
31	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
32	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
33	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
34	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
35	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
36	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72
37	ABC	artificial bee colony	0,63377	0,42402	0,30892	1,36671	0,55103	0,21874	0,05623	0,82600	0,34000	0,14200	0,03102	0,51302	2,706	30,06
38	BA	bat algorithm	0,59761	0,45911	0,35242	1,40915	0,40321	0,19313	0,07175	0,66810	0,21000	0,10100	0,03517	0,34617	2,423	26,93
39	AAA	algae adaptive algorithm	0,50007	0,32040	0,25525	1,07572	0,37021	0,22284	0,16785	0,76089	0,27846	0,14800	0,09755	0,52402	2,361	26,23
40	SA	simulated annealing	0,55787	0,42177	0,31549	1,29513	0,34998	0,15259	0,05023	0,55280	0,31167	0,10033	0,02883	0,44083	2,289	25,43
41	IWDm	intelligent water drops M	0,54501	0,37897	0,30124	1,22522	0,46104	0,14704	0,04369	0,65177	0,25833	0,09700	0,02308	0,37842	2,255	25,06
42	PSO	particle swarm Optimization	0,59726	0,36923	0,29928	1,26577	0,37237	0,16324	0,07010	0,60572	0,25667	0,08000	0,02157	0,35823	2,230	24,77
43	Boids	boids algorithm	0,43340	0,30581	0,25425	0,99346	0,35718	0,20160	0,15708	0,71586	0,27846	0,14277	0,09834	0,51957	2,229	24,77
44	MA	monkey algorithm	0,59107	0,42681	0,31816	1,33604	0,31138	0,14069	0,06612	0,51819	0,22833	0,08567	0,02790	0,34190	2,196	24,40
45	SFL	shuffled frog-leaping	0,53925	0,35816	0,29809	1,19551	0,37141	0,11427	0,04051	0,52618	0,27167	0,08667	0,02402	0,38235	2,104	23,38

Conclusiones

Hoy hemos presentado dos versiones del algoritmo: la del autor y mi versión modificada, que incluye pequeños cambios pero ofrece una mejora significativa del rendimiento. Este artículo demuestra claramente que incluso pequeños ajustes en la lógica de un algoritmo pueden dar lugar a notables aumentos de eficiencia en diversas tareas. También se pone de manifiesto que las descripciones complejas de un algoritmo pueden dificultar la comprensión del funcionamiento del mismo, lo que a su vez obstaculiza su mejora. Por el contrario, los conceptos complejos expresados en un lenguaje simple abren el camino a soluciones más eficaces.

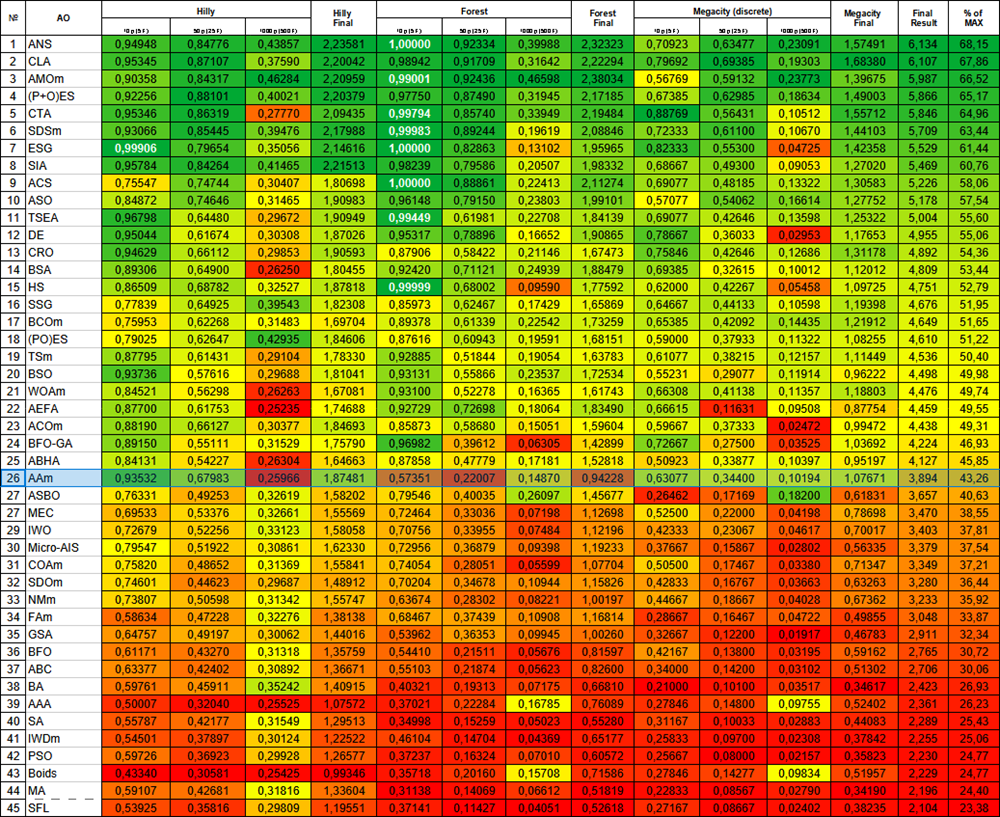
Figura 1. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0,99 aparecen resaltados en blanco.

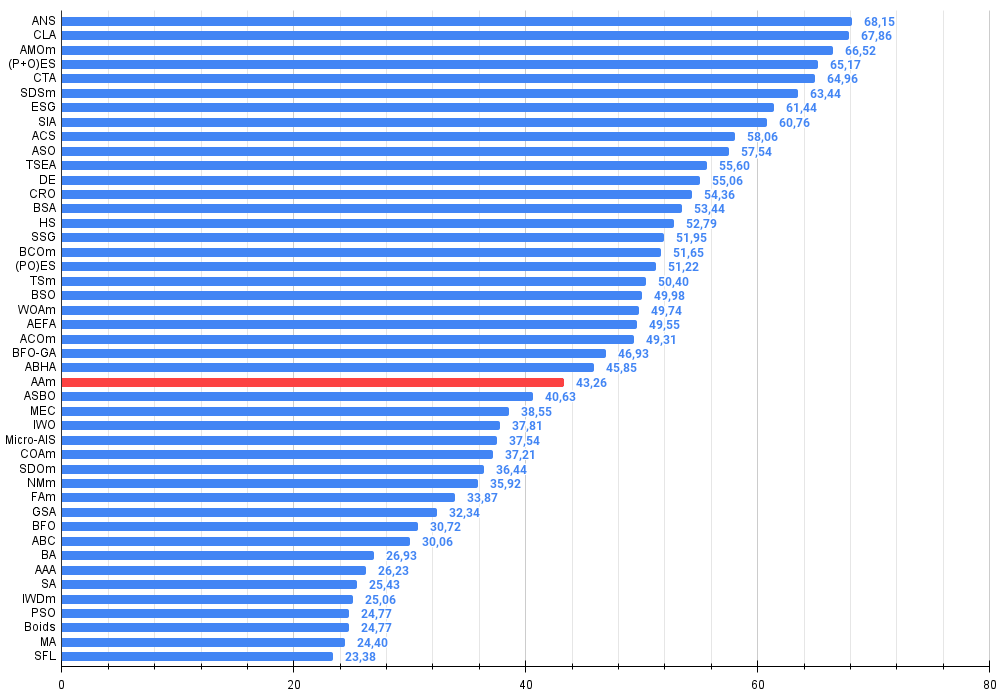
Figura 2. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible; el script para calcular la tabla de puntuación se encuentra en el archivo)

Cuando el artículo estaba casi listo para su publicación, se me ocurrió una idea que decidí poner a prueba. ¿Y si, siguiendo la lógica de los autores sobre las dianas y los arqueros que usan el método de la "ruleta" para la selección, cambiamos el tamaño de las propias dianas de forma inversamente proporcional a la calidad de las soluciones encontradas? Si la solución es buena, habrá que perfeccionarla y explorar su vecindad. De lo contrario, si el resultado es insignificante, deberemos ampliar el área de búsqueda para identificar nuevas zonas potencialmente prometedoras.

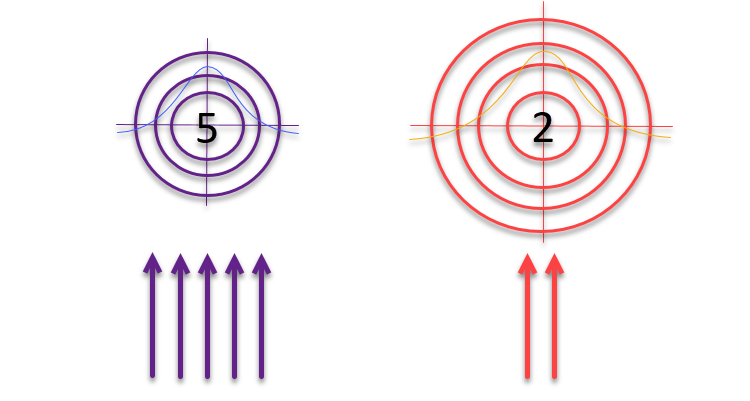
Figura 3. El número de flechas que alcanzan los objetivos es directamente proporcional a la calidad de los propios objetivos, mientras que el tamaño de los objetivos es inversamente proporcional a la calidad de los mismos. 

Veamos un código que usa la idea de que los objetivos aumentan de forma inversamente proporcional a su calidad.

void C_AO_AAm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //-------------------------------------------------------------------------
  // Calculate probability vector P and cumulative probability C
  double P [], C [];
  ArrayResize (P, popSize);
  ArrayResize (C, popSize);
  double F_worst = DBL_MAX; // a[ArrayMaximum(a, WHOLE_ARRAY, 0, popSize)].f;
  double sum = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f < F_worst) F_worst = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] =  a [i].f - F_worst; ////F_worst - a[i].f;
    sum += P [i];
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] /= sum;
    C [i] = (i == 0) ? P [i] : C [i - 1] + P [i];
  }

  double x;
  
  double maxFF = fB;
  double minFF = DBL_MAX;
  double prob1;
  double prob2;
  
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f < minFF) minFF = a [i].f;
  } 

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Select archer (k) using cumulative probability
      int k = 0;
      double r = u.RNDprobab ();
      while (k < popSize - 1 && C [k] < r) k++;

      if (u.RNDbool () < inhProbab)
      {
        x = a [k].c [c];
      }
      else
      {
        
        // Update position using Eq. (5) and (6)
        //double I   = MathRound (1 + u.RNDprobab ());
        double rnd = u.GaussDistribution (0, -1, 1, 8);
        /*
        if (a [k].f > a [i].f)
        {
          x = agent [i].cPrev [c] + rnd * (a [k].c [c] - I * agent [i].cPrev [c]);
        }
        else
        {
          x = agent [i].cPrev [c] + rnd * (agent [i].cPrev [c] - I * a [k].c [c]);
        }
        */
        
        prob1 = u.Scale (a [i].f, minFF, maxFF, 0, 1);
        prob2 = u.Scale (a [k].f, minFF, maxFF, 0, 1);
        
        x = agent [i].cPrev [c] + rnd * (a [k].c [c] - agent [i].cPrev [c]) * (1 - prob1 - prob2);  
        
      }

      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//—

1. En la sección comentada, la versión original usaba una construcción condicional "if-else" para determinar cómo actualizar la posición del agente. Esta lógica ha sido eliminada y sustituida por un nuevo cálculo.

2. Tres nuevas líneas de código:

prob1 = u.Scale(a[i].f, minFF, maxFF, 0, 1);
prob2 = u.Scale(a[k].f, minFF, maxFF, 0, 1);

x = agent[i].cPrev[c] + rnd * (a[k].c[c] - agent[i].cPrev[c]) * (1 - prob1 - prob2);

Estas líneas introducen un nuevo enfoque para calcular la posición actualizada:

(a) Se calculan dos valores de "prob1" y "prob2", usando la función "Scale", que normaliza los valores de aptitud de los agentes "i" y "k" en un diapasón de 0 a 1, usando como base los valores de aptitud máximos y mínimos, "minFF" y "maxFF".

b) A continuación, se calcula la nueva posición "x" utilizando estas probabilidades. Esta utiliza la anterior posición "i" del agente "agent [i].cPrev [c]", la posición "k" del arquero "a [k].c [c]" elegido y el factor aleatorio "rnd".

c) Ahora el movimiento se ve afectado por la suma de la aptitud de ambos agentes restada de 1. Este factor sirve como factor de escalado, permitiendo que la diana se ensanche o estreche de forma inversamente proporcional a la aptitud de los arqueros seleccionados. Cuanto menos experimentados sean los arqueros, mayor será la dispersión de las flechas, pero la distribución de las probabilidades de dar en el blanco seguirá una distribución normal.

Veamos ahora los resultados:

AAm|Archery Algorithm M|50.0|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.9174358826544864
25 Hilly's; Func runs: 10000; result: 0.7087620527831496
500 Hilly's; Func runs: 10000; result: 0.42160091427958263
=============================
5 Forest's; Func runs: 10000; result: 0.9252690259821034
25 Forest's; Func runs: 10000; result: 0.7580206359203926
500 Forest's; Func runs: 10000; result: 0.353277934084795
=============================
5 Megacity's; Func runs: 10000; result: 0.6738461538461538
25 Megacity's; Func runs: 10000; result: 0.552
500 Megacity's; Func runs: 10000; result: 0.23738461538461658
=============================
All score: 5.54760 (61.64%)

No podemos sino estar contentos con los resultados: el rendimiento del algoritmo ha mejorado notablemente. En la siguiente visualización podemos ver la convergencia segura del algoritmo y la identificación de zonas significativas de la superficie de la función.

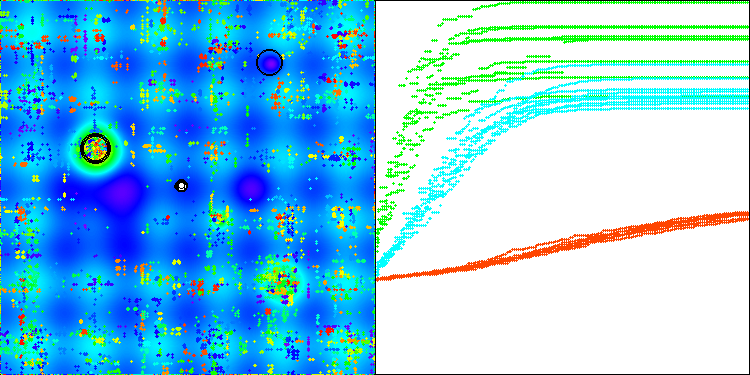
AAm en la función de prueba Hilly

Hagamos otro pequeño experimento. Los resultados anteriores se obtienen restando a la unidad la suma de las probabilidades de los arqueros.

//x = agent [i].cPrev [c] + rnd * (a [k].c [c] - agent [i].cPrev [c]) * (1 - prob1 - prob2); 
 x = agent [i].cPrev [c] + rnd * (a [k].c [c] - agent [i].cPrev [c]) * (2 - prob1 - prob2);  

El principal cambio consiste en restar la suma no a la unidad, sino a dos. Veamos cómo una acción tan simple puede influir en el comportamiento del algoritmo:

• en la versión anterior, el resultado de dicha operación puede ser negativo si la adaptabilidad de ambos arqueros es alta, provocando un efecto de "mutación" en las coordenadas resultantes del nuevo arquero.
  
• en la nueva versión, el multiplicador dará un valor entre 0 y 2.

Este cambio provoca un movimiento más disperso de los agentes, además da una exploración más agresiva del espacio de soluciones, ya que los agentes darán pasos más largos cada vez que se actualice una posición.

De esta forma, como podemos ver en la impresión de los resultados del algoritmo, este cambio ha mejorado la convergencia del algoritmo en funciones de dimensionalidad media, pero también ha provocado un deterioro en funciones de dimensionalidad alta (marcadas en amarillo), aunque en general el algoritmo ha obtenido una puntuación global más alta.

AAm|Archery Algorithm M|50.0|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.9053229410164233
25 Hilly's; Func runs: 10000; result: 0.8259118221071665
500 Hilly's; Func runs: 10000; result: 0.2631661675236262
=============================
5 Forest's; Func runs: 10000; result: 0.9714247249319152
25 Forest's; Func runs: 10000; result: 0.9091052022399436
500 Forest's; Func runs: 10000; result: 0.2847632249786224
=============================
5 Megacity's; Func runs: 10000; result: 0.7169230769230768
25 Megacity's; Func runs: 10000; result: 0.6378461538461538
500 Megacity's; Func runs: 10000; result: 0.10473846153846252
=============================
All score: 5.61920 (62.44%)

El resultado anterior parece más práctico y seguirá siendo la variante principal de la versión modificada del algoritmo AAm. Aquí tenemos nuevamente la tabla de clasificación con gradiente térmico, en la que AAm ocupa ahora un respetable 7º puesto. El algoritmo puede definirse como muy equilibrado (buena convergencia en funciones de diferente dimensionalidad) y puede recomendarse para resolver diversos problemas.

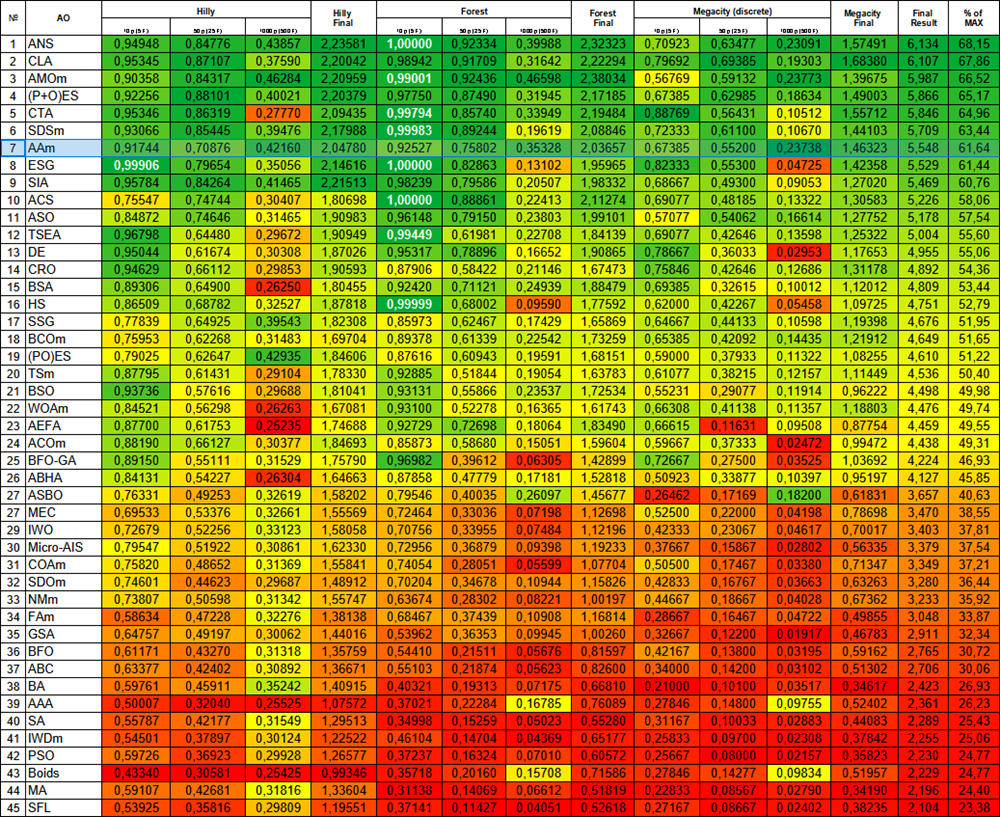
Figura 4. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0,99 aparecen resaltados en blanco.

Ventajas e inconvenientes del algoritmo AAm:

Ventajas:

1. Bastante rápido.
2. Autoadaptativo.
   
3. Solo un parámetro externo.
4. Buena convergencia.
5. Buena escalabilidad.
6. Aplicación sencilla (a pesar de la compleja descripción de los autores).
   

Desventajas:

1. Ligera tendencia a atascarse en funciones de baja dimensionalidad.
   

La adición de nuevos algoritmos a la tabla de clasificación ha empezado a causar dificultades: se ha vuelto poco legible. Por lo tanto, hemos decidido limitar el número de participantes en la comparación a 45 algoritmos, y ahora la competición tiene un formato de todos contra todos. Para facilitar y aclarar a los lectores el acceso a todos los artículos, hemos preparado un archivo HTML con una lista de todos los algoritmos anteriormente comentados, ordenados según su clasificación en una tabla. Este fichero se encuentra en el archivo anexo a los artículos desde hace algún tiempo, y para los que lo abren por primera vez, hay una pequeña sorpresa.

Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5