Optimización de la quimiotaxis bacteriana - Bacterial Chemotaxis Optimisation (BCO)

Contenido

1. Introducción
2. Implementación del algoritmo
3. Resultados de las pruebas

Introducción

En el campo de la optimización, muchos investigadores y desarrolladores se inspiran en procesos biológicos que suceden en la naturaleza, como la evolución, las interacciones sociales o el comportamiento de la búsqueda de alimento de los organismos vivos. Y esto conduce al desarrollo de técnicas de optimización completamente nuevas e innovadoras. Los estudios han demostrado que estos métodos suelen superar a los enfoques heurísticos clásicos y a los basados en gradientes, sobre todo cuando se trata de resolver problemas multimodales, no diferenciables y discretos. Uno de estos métodos es el algoritmo de quimiotaxis propuesto por primera vez por Bremermannn y sus colegas; nosotros ya analizamos el algoritmo de optimización por forrajeo bacteriano (BFO) en su momento. Este modela la respuesta de las bacterias a los quimioatrayentes en gradientes de concentración. Bremermann analizó la quimiotaxis en gradientes tridimensionales y la aplicó al entrenamiento de redes neuronales. Aunque este algoritmo se basa en los principios de la quimiotaxis bacteriana, ciertos nuevos descubrimientos biológicos han proporcionado un modelo más detallado de este proceso.

En este artículo, intentaremos analizar el modelo mencionado como una nueva estrategia de optimización. Las principales diferencias entre el nuevo modelo y el algoritmo de quimiotaxis clásico son las siguientes:

1. Las bacterias del nuevo modelo usan información sobre los valores de concentración.
2. No continúan en la misma dirección cuando aumentan las concentraciones de quimioatrayentes.

Las bacterias son organismos unicelulares, es decir, una de las formas de vida más simples de la Tierra. A pesar de su simplicidad, son capaces de captar información sobre su entorno, orientarse con ella y utilizarla eficazmente para sobrevivir. La respuesta de las bacterias a los cambios del entorno ha sido objeto de intensas investigaciones en las últimas décadas, y también ha atraído la atención de los científicos que trabajan en el campo de la optimización. Los algoritmos de optimización pueden considerarse sistemas que recopilan información sobre el panorama funcional y la utilizan para alcanzar un grado óptimo. La simplicidad de la idea de la quimiotaxis bacteriana la convierte en un atractivo punto de partida para construir dicho tipo de algoritmos.

Diversos estudios han descubierto que las bacterias intercambian información entre sí, aunque no se sabe mucho sobre los mecanismos de dicha comunicación. Por lo general, las bacterias se contemplan como individuos y la interacción social no se tiene en cuenta en los modelos. Esto los distingue de los modelos de interacción que describen el comportamiento de los insectos sociales (como hormigas, abejas, avispas o termitas), que actúan como sistemas con inteligencia colectiva, lo cual abre distintas posibilidades para resolver diferentes problemas.

La adaptación es otro aspecto importante de la quimiotaxis. Las bacterias son capaces de cambiar su sensibilidad a condiciones químicas constantes, lo cual les permite responder eficazmente a los cambios del entorno. Esta cualidad no solo las hace resistentes, sino también muy eficaces en la búsqueda de recursos.

En este estudio, los autores se centraron en modelos microscópicos que tienen en cuenta la quimiotaxis de bacterias individuales, en contraposición a los modelos macroscópicos que analizan el movimiento de las colonias. El algoritmo fue desarrollado por S. D. Müller y P. Koumatsakas, cuyas ideas principales se presentaron y publicaron en 2002.

Implementación del algoritmo

La idea que subyace en el algoritmo de quimiotaxis bacteriana (BCO) consiste en usar los principios biológicos observados en el comportamiento bacteriano para resolver problemas de optimización. El algoritmo modela cómo responden las bacterias a los gradientes de sustancias químicas en el entorno, lo cual les permite encontrar condiciones más favorables para vivir. Ideas básicas del algoritmo:

1. El algoritmo describe el movimiento bacteriano como una secuencia de trayectorias rectilíneas conectadas por giros instantáneos. Cada movimiento se caracteriza por su velocidad, dirección y duración.
2. El sentido de rotación de la bacteria viene determinado por una distribución de probabilidades, lo cual permite variaciones aleatorias del movimiento.
3. El algoritmo usa la información sobre los gradientes de la función para guiar a la bacteria hacia la solución óptima, minimizando el número de iteraciones necesarias para alcanzar el objetivo.

El pseudocódigo detallado del algoritmo BCO describe los pasos principales del algoritmo, incluida la inicialización, el ciclo principal de optimización con los pasos de movimiento y revisión, y las funciones auxiliares.

Inicialización.

1. Establecer los parámetros:

• popSize: tamaño de la población (número de bacterias)
• hs: número de pasos para calcular el cambio medio
• T0: temperatura inicial
• b: parámetro
• tau_c: parámetro
• v: velocidad

2. Crear un array de bacterias del tamaño popSize

3. Para cada bacteria, i abarca de 0 hasta popSize-1:

• Inicializar fPrev con el valor -DBL_MAX
• Crear un array fHistory de tamaño hs y rellenarlo de ceros

Ciclo básico de optimización. Repetir hasta que se alcance la condición de parada:

La etapa de movimiento para cada bacteria i de 0 a popSize será 1:

1. Obtener el valor actual de la función objetio f_tr

2. Obtener el valor anterior de la función objetivo f_pr de bacterium [i].fPrev

3. Si f_tr <= f_pr: T = T0

    En caso contrario: calcular b_corr = CalculateB corregido (f_tr, f_pr, i)

• T = T0 * exp (b_corr * (f_tr - f_pr))

4. Generar tau a partir de una distribución exponencial con parámetro T.

5. Calcular los ángulos new_angles [] para las dimensiones coords - 1: para cada ángulo j de 0 a coords - 2:

• theta = CalculateRotationAngle ()
• mu = 62 * (1 - cos (theta)) * π / 180
• sigma = 26 * (1 - cos (theta)) * π / 180
• new_angles [j] = número aleatorio de la distribución gaussiana con parámetros (mu, mu-π, mu+π)

6. Calcular la nueva posición:

• l = v * tau
• CalculateNewPosition (l, new_angles, new_position, current_position)

7. Actualizar la posición de la bacteria restringiendo los valores dentro de rangeMin y rangeMax

8. Actualizar bacterium [i].fPrev con el valor f_tr

Fase de revisión.

1. Actualizar la mejor solución global cB con el valor de aptitud fB

2. Para cada bacteria i de 0 a popSize - 1. Actualizar la historia de valores de la función objetivo fHistory:

• Desplazar todos los valores una posición a la izquierda
• Añadir el valor actual de la función objetivo al final de la historia

Funciones auxiliares:

CalculateCorrectedB (f_tr, f_pr, bacteriumIndex)

1. Calcular delta_f_tr = f_tr - f_pr

2. Calcular delta_f_pr = cambio medio en los últimos pasos hs.

3. Si |delta_f_pr| < epsilon: Retornar b

   De lo contrario: Retornar b * (1 / (|delta_f_tr / delta_f_pr| + 1) + 1 / (|f_pr| + 1))

CalculateRotationAngle ()

1. Calcular cos_theta = exp (-tau_c / T0)

2. Retornar arccos (cos_theta)

CalculateNewPosition (l, angles, new_position, current_position)

1. Calcular new_position [0] considerando todos los ángulos

2. Para cada coordenada i de 1 a coords - 1:

   Calcular new_position [i] con respecto a los ángulos correspondientes

3. Aplicar una dirección aleatoria (1 o -1) a cada coordenada

GenerateFromExponentialDistribution (T)

Retornar -T * ln (número aleatorio de 0 a 1)

Vamos a escribir el código del algoritmo. Para representar la bacteria como solución al problema de optimización, describiremos la estructura "S_BCO_Bacterium".

1. Campos de la estructura:

• fPrev - valor anterior de la función objetivo.
  
• fHistory [] - array con la historia de los valores de la función objetivo.
  

2. Init - el método de inicialización realiza las siguientes acciones:

• cambia el tamaño del array "fHistory" al valor "historySize".
• todos los elementos del array "fHistory" se inicializan con el valor "0.0".
• fPrev - establece el valor anterior de la función objetivo en el valor mínimo posible.

Se trata de monitorear los cambios en los valores de la función objetivo a lo largo de un número determinado de iteraciones (movimientos individuales).

//——————————————————————————————————————————————————————————————————————————————
struct S_BCO_Bacterium
{
    double fPrev;        // previous value of the objective function
    double fHistory [];  // history of objective function values

    void Init (int coords, int historySize)
    {
      ArrayResize     (fHistory, historySize);
      ArrayInitialize (fHistory, 0.0);
      fPrev = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Luego describiremos la clase del algoritmo "C_AO_BCO". Vamos a desglosarla pieza por pieza.

1. El constructor inicializará los parámetros externos del algoritmo.

2. El método "SetParams" actualizará los valores de los parámetros del array "params".

3. Los métodos "Moving" y "Revision" se encargarán de desplazar las bacterias y revisar sus posiciones.

4. La clase definirá varios métodos privados que se utilizarán para diversos cálculos relacionados con el algoritmo: "CalculateAverageDeltaFpr", "CalculateNewAngles", "CalculateNewPosition", "GenerateFromExponentialDistribution", "CalculateCorrectedB", "CalculateRotationAngle", "RNDdir", bacterium - array de bacterias (población). Parámetros de la clase:

• hs - número de pasos para calcular el cambio medio.
• T0 - temperatura inicial.
• b - parámetro.
• tau_c - parámetro.
• v - velocidad.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BCO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BCO () { }
  C_AO_BCO ()
  {
    ao_name = "BCO";
    ao_desc = "Bacterial Chemotaxis Optimization";
    ao_link = "https://www.mql5.com/es/articles/15711";

    popSize = 50;     // population size (number of bacteria)
    hs      = 10;     // number of steps to calculate average change
    T0      = 1.0;    // initial temperature
    b       = 0.5;    // parameter b
    tau_c   = 1.0;    // parameter tau_c
    v       = 1.0;    // velocity

    ArrayResize (params, 6);

    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "hs";      params [1].val = hs;
    params [2].name = "T0";      params [2].val = T0;
    params [3].name = "b";       params [3].val = b;
    params [4].name = "tau_c";   params [4].val = tau_c;
    params [5].name = "v";       params [5].val = v;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
    hs      = (int)params [1].val;
    T0      = params      [2].val;
    b       = params      [3].val;
    tau_c   = params      [4].val;
    v       = params      [5].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    hs;
  double T0;
  double b;
  double tau_c;
  double v;

  S_BCO_Bacterium bacterium [];

  private: //-------------------------------------------------------------------
  double CalculateAverageDeltaFpr            (int bacteriumIndex);
  void   CalculateNewAngles                  (double &angles []);
  void   CalculateNewPosition                (double l, const double &angles [], double &new_position [], const double &current_position []);
  double GenerateFromExponentialDistribution (double T);
  double CalculateCorrectedB                 (double f_tr, double f_pr, int bacteriumIndex);
  double CalculateRotationAngle              ();
  int    RNDdir                              ();
};

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BCO::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (bacterium, popSize);
  for (int i = 0; i < popSize; i++) bacterium [i].Init (coords, hs);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

El método "Moving" de la clase "C_AO_BCO" se encargará de desplazar la bacteria en el espacio de búsqueda. Veamos cómo funciona:

1. Si "revision" es igual a "false", significa que las bacterias tendrán una posición inicial.

• Para cada bacteria "a[i]", se generarán coordenadas aleatorias dentro de un rango determinado.
• La función "u.RNDfromCI" generará un valor aleatorio, mientras que "u.SeInDiSp" lo corregirá con el paso dado.

2. Ciclo de movimiento básico si "revision" es igual a "true". El método cumple la lógica básica del movimiento bacteriano. Definición de temperatura "T":

• Si el valor actual de la función "f_tr" es mejor o igual que el valor "f_pr" anterior, se utilizará la temperatura inicial "T0".
• En caso contrario, la temperatura se corregirá mediante la función "CalcularCorregidoB", que considerará la diferencia entre el valor actual y el anterior de la función de adaptación. 
• En la generación del tiempo de desplazamiento "tau": se utilizará una distribución exponencial para generar el tiempo de desplazamiento.
• Los nuevos ángulos de desplazamiento y la nueva posición se calcularán partiendo de la longitud de desplazamiento "l" y los nuevos ángulos.
• La nueva posición se ajustará al rango y al paso especificados.
• Al final del ciclo, se actualizará el valor anterior de la función de aptitud de cada bacteria.

El método Moving implementará la lógica básica de desplazamiento de las bacterias en el espacio de búsqueda, adaptando su comportamiento según los resultados de las iteraciones anteriores. Así, utilizará elementos aleatorios y mecanismos adaptativos para encontrar una solución óptima.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    double f_tr = a [i].f;
    double f_pr = bacterium [i].fPrev;

    double T;
    
    if (f_tr <= f_pr)
    {
      T = T0;
    }
    else
    {
      double b_corr = CalculateCorrectedB (f_tr, f_pr, i);
      
      T = T0 * exp (b_corr * (f_tr - f_pr));
    }

    double tau = GenerateFromExponentialDistribution (T);

    double new_angles [];
    ArrayResize (new_angles, coords - 1);
    CalculateNewAngles (new_angles);

    double l = v * tau;
    double new_position [];
    ArrayResize (new_position, coords);
    CalculateNewPosition (l, new_angles, new_position, a [i].c);

    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = u.SeInDiSp (new_position [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    bacterium [i].fPrev = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "Revision" de la clase "C_AO_BCO" se encargará de actualizar la información sobre las mejores soluciones encontradas y la historia de los valores de la función de aptitud de cada bacteria.

1. La variable "ind" se inicializará con el valor "-1". Se usará para almacenar el índice de la bacteria con el mejor valor de función encontrado.

2. Localización del mejor valor de la función:

• El método iterará todas las bacterias de la población "popSize" y buscará una que tenga un valor de función "f" mayor que el mejor valor actual "fB".
• Si se encuentra una bacteria con un valor de función superior, "fB" se actualizará y el índice de esa bacteria se almacenará en "ind".

3. Si se encuentra una bacteria con el índice "ind" (es decir, "ind" no es igual a "-1"), las coordenadas de esta bacteria se copiarán en el array "cB", que representará las coordenadas de la mejor solución actual.

4. La historia de valores de función se actualizará para cada bacteria. El método recorrerá cada elemento de "fHistory", desplazando los valores una posición a la izquierda para hacer sitio al nuevo valor. Al final de cada iteración, el valor de aptitud actual "a[i].f" de cada bacteria se escribirá en el último elemento del array "fHistory".

Así, el método revision cumplirá dos funciones principales:

• La actualización del mejor valor de la función de aptitud y las coordenadas correspondientes.
• La actualización de la historia de valores de la función de aptitud de cada bacteria, lo cual permitirá monitorear los cambios en su estado a lo largo de su historia de desplazamientos. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1)
  {
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 1; j < hs; j++)
    {
      bacterium [i].fHistory [j - 1] = bacterium [i].fHistory [j];
    }

    bacterium [i].fHistory [hs - 1] = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "CalculateAverageDeltaFpr" de la clase "C_AO_BCO" está diseñado para calcular los cambios medios en los valores de la función de aptitud (delta) para una bacteria concreta entre sus dos posiciones vecinas, basándose en la historia de valores de aptitud.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BCO::CalculateAverageDeltaFpr (int bacteriumIndex)
{
  double sum = 0;

  for (int i = 1; i < hs; i++)
  {
    sum += bacterium [bacteriumIndex].fHistory [i] - bacterium [bacteriumIndex].fHistory [i - 1];
  }

  return sum / (hs - 1);
}
//——————————————————————————————————————————————————————————————————————————————

El método "CalculateNewAngles" de la clase "C_AO_BCO" está diseñado para calcular nuevos ángulos basados en la lógica relacionada con la rotación y la distribución, y realiza las siguientes acciones:

• Recorre el array en busca de nuevos ángulos y calcula un nuevo valor para cada ángulo.
• Usa los parámetros que dependen del coseno del ángulo para generar valores que utilizan una distribución gaussiana.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::CalculateNewAngles (double &angles [])
{
  for (int i = 0; i < coords - 1; i++)
  {
    double theta = CalculateRotationAngle ();
    double mu    = 62 * (1 - MathCos (theta)) * M_PI / 180.0;
    double sigma = 26 * (1 - MathCos (theta)) * M_PI / 180.0;

    angles [i] = u.GaussDistribution (mu, mu - M_PI, mu + M_PI, 8);
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "CalculateNewPosition" de la clase "C_AO_BCO" está diseñado para calcular las coordenadas de la nueva posición basándose en las coordenadas actuales, los ángulos y el parámetro "l". 

1. Parámetros de entrada del método:

• l - coeficiente que afecta al cambio de posición.
• angles [] - array de ángulos que se utilizan para calcular la nueva posición.
• new_position [] - array donde se escribirán las nuevas coordenadas.
• current_position [] - array de coordenadas actuales.

2. La primera coordenada "new_position [0]" se calculará como la suma de la coordenada "current_position [0]" actual y el producto de "l" por la diferencia entre "rangeMax [0]" y "rangeMin [0]".

3. A continuación, la primera coordenada se multiplicará por los cosenos de los ángulos del array "angles", empezando por el primero hasta el penúltimo.

4. El resultado se multiplicará por el valor devuelto por la función "RNDdir ()", que generará una dirección aleatoria "-1" o "1".

5. Para cada coordenada "new_position [i]" siguiente, donde "i" estará comprendida entre "1" y "coords - 2", se calculará una nueva posición basada en la posición actual y el seno del ángulo correspondiente.

6. Cada nueva coordenada se multiplicará también por los cosenos de los ángulos desde el índice actual "i" hasta el penúltimo.

7. Dirección aleatoria para el resto de coordenadas, el resultado también se multiplicará por el valor devuelto por "RNDdir ()".

8. Procesamiento de la última coordenada, si el número de coordenadas es superior a 1, se calculará una nueva posición para la última coordenada "new_position [coords - 1]" basada en la posición actual y el seno del último ángulo.

Así, el método "CalculateNewPosition" realizará las siguientes acciones:

• Calculará las nuevas coordenadas a partir de las coordenadas y ángulos actuales.
• Considerará el efecto de la dirección aleatoria en cada coordenada.
• Aplicará las funciones trigonométricas (seno y coseno) para tener en cuenta los ángulos.

Así, este método se utilizará para modelizar el movimiento de las bacterias en el espacio dada su posición actual y unos ángulos determinados.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::CalculateNewPosition (double l, const double &angles [], double &new_position [], const double &current_position [])
{
  new_position [0] = current_position [0] + l * (rangeMax [0] - rangeMin [0]);
 
  for (int k = 0; k < coords - 1; k++)
  {
    new_position [0] *= MathCos (angles [k]);
  }
 
  new_position [0] *= RNDdir ();

  for (int i = 1; i < coords - 1; i++)
  {
    new_position [i] = current_position [i] + l * MathSin (angles [i - 1]) * (rangeMax [0] - rangeMin [0]);
    
    for (int k = i; k < coords - 1; k++)
    {
      new_position [i] *= MathCos (angles [k]);
    }
    
    new_position [i] *= RNDdir ();
  }

  if (coords > 1)
  {
    new_position [coords - 1] = current_position [coords - 1] + l * MathSin (angles [coords - 2]);
  }
 
}
//——————————————————————————————————————————————————————————————————————————————

A continuación, describiremos brevemente el método "RNDdir" de la clase "C_AO_BCO", que está diseñado para generar la dirección aleatoria que puede tomar uno de dos valores: -1 o 1.

//——————————————————————————————————————————————————————————————————————————————
int C_AO_BCO::RNDdir ()
{
  if (u.RNDbool () < 0.5) return -1;
 
  return 1;
}
//——————————————————————————————————————————————————————————————————————————————

Vamos a repasar brevemente los métodos de la clase "C_AO_BCO".

El método "GenerateFromExponentialDistribution" ejecutará:

• la generación de un número aleatorio usando distribución exponencial con el parámetro "T".
• después utilizará un número aleatorio del intervalo (0, 1), calculará su logaritmo y lo multiplicará por "-T".
• así obtendremos un número aleatorio distribuido según la ley exponencial.

 El método "CalculateCorrectedB" ejecutará:

• el cálculo del valor "b" ajustado a partir de la diferencia entre "f_tr" y "f_pr" (aptitud actual y anterior).
• luego calculará la diferencia entre "f_tr" y "f_pr", obtendrá el valor medio de la bacteria y retornará el valor "b" ajustado en función de éste.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BCO::GenerateFromExponentialDistribution (double T)
{
  return -T * MathLog (u.RNDprobab ());
}

double C_AO_BCO::CalculateCorrectedB (double f_tr, double f_pr, int bacteriumIndex)
{
  double delta_f_tr = f_tr - f_pr;
  double delta_f_pr = CalculateAverageDeltaFpr (bacteriumIndex);

  if (MathAbs (delta_f_pr) < DBL_EPSILON)
  {
    return b;
  }
  else
  {
    return b * (1 / (MathAbs (delta_f_tr / delta_f_pr) + 1) + 1 / (MathAbs (f_pr) + 1));
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "CalculateRotationAngle" de la clase "C_AO_BCO" será el último. El método calculará el ángulo de rotación basándose en los parámetros dados y retornará el valor en radianes.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BCO::CalculateRotationAngle ()
{
  double cos_theta = MathExp (-tau_c / T0);
  return MathArccos (cos_theta);
}
//——————————————————————————————————————————————————————————————————————————————

Vamos a poner a prueba la versión original del algoritmo y a ver los resultados:

BCO|Bacterial Chemotaxis Optimization|50.0|10.0|1.0|0.5|1.0|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.42924491510564006
25 Hilly's; Func runs: 10000; result: 0.282259866768426
500 Hilly's; Func runs: 10000; result: 0.2515386629014219
=============================
5 Forest's; Func runs: 10000; result: 0.2476662231845009
25 Forest's; Func runs: 10000; result: 0.17824381036550777
500 Forest's; Func runs: 10000; result: 0.15324081202657283
=============================
5 Megacity's; Func runs: 10000; result: 0.2430769230769231
25 Megacity's; Func runs: 10000; result: 0.11415384615384619
500 Megacity's; Func runs: 10000; result: 0.09444615384615461
=============================
All score: 1.99387 (22.15%)

Los resultados obtenidos son tan poco significativos que no tiene sentido incluirlos en la tabla de clasificación. Al diseñar el algoritmo y escribir el código según la descripción del texto del autor, hemos tenido que ajustar algunas fórmulas: algunas no tenían sentido matemático (por ejemplo, dividir un número por un vector), mientras que otras degeneraban en valores extremadamente pequeños o extremadamente grandes incomparables con las dimensionalidades del problema, al tiempo que yo imprimía los resultados de las funciones para cada una de las fórmulas presentadas y los analizaba. De esta forma, tal y como lo describen los autores, el algoritmo no puede funcionar en principio.

Además, las operaciones con ángulos que usan una distribución normal en sus cálculos pueden simplificarse enormemente, ya que el significado físico de estas operaciones supone que en cada coordenada uno puede simplemente posponer un nuevo incremento desde la ubicación actual de la bacteria. Por consiguiente, hemos decidido desarrollar nuestra propia implementación de la quimiotaxis bacteriana, adhiriéndonos a los conceptos e ideas básicas del algoritmo en la medida de lo posible.

Así pues, le presentamos el pseudocódigo de nuestra versión del algoritmo:

Inicialización:
1. Crear una población de bacterias popSize
2. Para cada bacteria i:
    Inicializar con un valor cero la historia de los valores de la función objetivo f_history [i] de tamaño hs.
    Fijar el valor inicial f_prev [i] = -DBL_MAX

Ciclo primario:
Hasta que se alcance la condición de parada:

1. Si esta es la primera iteración:
   Para cada bacteria i:
     Inicializar aleatoriamente la posición x [i] en el espacio de búsqueda
     x [i].[j] ∈ [x_min [j], x_max [j]] para cada coordenada j

2. De lo contrario:
   Para cada bacteria i:
     a. Calcular el cambio medio de la función objetivo:
        delta_ave [i] = (1 / (hs - 1)) * sum (f_history [i].[k] - f_history [i].[k-1] for k in 1..hs-1) + epsilon
     
     b. Calcular el cambio relativo de la adaptabilidad:
        delta [i] = 1 - |f (x [i]) - f_prev [i]| / delta_ave [i]
        delta [i] = max (delta [i], 0.0001)
     
     c. Para cada coordenada j:
        Con una probabilidad de 0,5:
          dist [j] = (x_max [j] - x_min [j]) * delta [i]
          x [i].[j] = N (x [i].[j], x [i].[j] - dist [j], x [i].[j] + dist [j])
          Limitar x [i].[j] dentro de [x_min [j], x_max [j]]
        De lo contrario:
          x [i].[j] = x_best [j]
     
     d. Actualizar f_prev [i] = f (x [i])

3. Estimar la función objetivo f (x [i]) para cada bacteria

4. Actualizar la mejor solución encontrada:
   Si existe i: f (x [i]) > f (x_best), entonces x_best = x [i]

5. Actualizar la historia de valores de la función objetivo para cada bacteria:
   Desplazar valores en f_history [i]
   Añadir un nuevo valor: f_history [i].[hs - 1] = f (x [i])

Finalización:
Retornar la mejor solución encontrada x_best

Donde:

• x [i] - posición de la i-ésima bacteria
• f (x) - función objetivo
• hs - tamaño de la historia
• epsilon - constante menor para evitar la división por cero
• N (μ, a, b) - distribución normal truncada con media μ y límites [a, b]

Así, nuestro pseudocódigo modificado reflejará la estructura básica y la lógica del algoritmo BCO. Vamos a centrarnos en los puntos principales:

• El algoritmo usa una población de bacterias, cada una de las cuales representará una solución potencial.
• En cada iteración, las bacterias se desplazarán por el espacio de búsqueda utilizando las información sobre sus resultados anteriores.
• El movimiento se basará en el cambio relativo de la función objetivo, lo cual permitirá al algoritmo adaptarse al paisaje de optimización.
• El algoritmo almacenará la historia de los valores de la función objetivo para cada bacteria, que se utilizará para calcular el cambio medio.
• Con cierta probabilidad, la bacteria se desplazará hacia la mejor solución conocida en lugar de explorar una nueva zona (sería un análogo de la herencia de rasgos en genética).
  
• Después de cada movimiento, se evaluarán las nuevas posiciones y se actualizará la mejor solución encontrada.

La versión BCOm combina elementos de búsqueda local (desplazamiento de bacterias individuales) y la búsqueda global (intercambio de información a través de la mejor solución conocida).

Veamos las principales diferencias entre las dos versiones del algoritmo. En primer lugar, hemos simplificado el mecanismo de movimiento de las bacterias, abandonando el complejo sistema con ángulos de rotación y temperatura. En segundo lugar, la nueva versión se basa menos en la historia de cambios para ajustar el comportamiento bacteriano, usando un enfoque más directo para actualizar las posiciones. En lugar de una combinación de las distribuciones exponencial y normal, el nuevo algoritmo usa una distribución normal para actualizar las coordenadas. La consecuencia de los cambios introducidos ha sido la reducción a uno del número de parámetros (excluido el tamaño de la población) que controlan el comportamiento del algoritmo, lo cual ha cambiado la forma de afinar el algoritmo y ha simplificado el control del proceso de optimización.

En general, el nuevo pseudocódigo implica cálculos más sencillos en cada paso de optimización, lo que también debería tener un efecto positivo en la velocidad del algoritmo (la versión original realizaba múltiples cálculos del seno y el coseno de los ángulos de rotación para cada coordenada de cada bacteria). Nuestro enfoque establece un equilibrio ligeramente diferente entre la exploración de un nuevo espacio de soluciones y la explotación de las buenas soluciones ya encontradas.

Estos cambios en la lógica han dado lugar a un algoritmo más sencillo y presumiblemente (a la espera de los resultados de las pruebas) más eficaz. Vamos a escribir el código.

Dejaremos inalterada la estructura "S_BCO_Bacteria" que representa a cada bacteria. Está diseñada para almacenar información sobre la bacteria y su historia de valores de función objetivo.

En el método "Init" de la clase "C_AO_BCOm", responsable de la inicialización de los parámetros del algoritmo, añadiremos la definición de la distancia de movimiento admisible para cada coordenada.

Así, el método "Init" de la clase "C_AO_BCOm" se encargará de inicializar los parámetros del algoritmo de optimización. Luego comprobaremos las condiciones de inicialización estándar, crearemos los arrays necesarios y los rellenaremos con valores.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BCOm::Init (const double &rangeMinP  [], //minimum search range
                      const double &rangeMaxP  [], //maximum search range
                      const double &rangeStepP [], //step search
                      const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (bacterium, popSize);
  for (int i = 0; i < popSize; i++) bacterium [i].Init (coords, hs);

  ArrayResize (allowedDispl, coords);
  for (int c = 0; c < coords; c++) allowedDispl [c] = rangeMax [c] - rangeMin [c];

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Ahora analizaremos el método "Moving" de la clase "C_AO_BCOm", que se encarga de desplazar las bacterias en el espacio de búsqueda. Vamos a desglosarla pieza por pieza.

1. En la primera iteración, las acciones del método no han cambiado: se inicializarán las coordenadas de las bacterias con valores aleatorios dentro de un rango dado.

2. El algoritmo básico desplazamiento: se declararán las variables para almacenar los valores como "Δ", "ΔAve", y "dist" y para cada individuo de la población:

• El valor medio "ΔAve" se calculará con la función "CalculateAverageDeltaFpr (i)".
• El cambio relativo "Δ" se calculará y se utilizará para determinar el grado de cambio en la posición de la bacteria.
• Si "Δ" es demasiado pequeño, se fijará en 0,0001.

3. Cambio de coordenadas:

• Para cada coordenada, se probará una probabilidad aleatoria (50%).
• Si se cumple la condición, se calculará la distancia "dist", que depende de "allowedDispl [c]" y "Δ".
• El nuevo valor "x" se calculará mediante la función "GaussDistribution", teniendo en cuenta los límites "xMin" y "xMax".
• Si "x" está fuera de rango, se corregirá utilizando "RNDfromCI".
• Por último, el nuevo valor de las coordenadas se almacenará teniendo en cuenta el paso "rangeStep".

4. Se conservará el valor anterior de la función de aptitud "f" para cada individuo del array "bacteria". Se utilizarán los arrays "a" y "bacteria". Las funciones "RNDfromCI", "SeInDiSp", "GaussDistribution" se encargarán de generar números aleatorios y distribuciones, así como de normalizar los valores de las coordenadas.

Así, la función "Moving ()" se encargará de inicializar y actualizar la posición de los individuos en la población dentro del algoritmo. Este utilizará probabilidades y distribuciones aleatorias para controlar el movimiento de las bacterias. Sin embargo, la diferencia clave con respecto a la versión original será la forma más sencilla y eficaz de realizar el gradiente de la función de aptitud. Cuando la diferencia de estado de la bacteria en el paso actual disminuya en comparación con el paso anterior, su movimiento se acelerará. Por el contrario, la bacteria se ralentizará cuando se encuentra en un entorno externo favorable. Esto resulta contrario al comportamiento natural de las bacterias, que entran en un estado de depresión y anabiosis en un entorno agresivo.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCOm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double x    = 0.0;
  double xMin = 0.0;
  double xMax = 0.0;
  double Δ    = 0.0;
  double ΔAve = 0.0;
  double dist = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    ΔAve = CalculateAverageDeltaFpr (i) + DBL_EPSILON;

    Δ = fabs (a [i].f - bacterium [i].fPrev) / ΔAve;

    Δ = 1.0 - Δ;

    if (Δ < 0.0001) Δ = 0.0001;

    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < 0.5)
      {
        dist = allowedDispl [c] * Δ;

        x    = a [i].c [c];
        xMin = x - dist;
        xMax = x + dist;

        x = u.GaussDistribution (x, xMin, xMax, 8);

        if (x > rangeMax [c]) x = u.RNDfromCI (xMin, rangeMax [c]);
        if (x < rangeMin [c]) x = u.RNDfromCI (rangeMin [c], xMax);

        a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
      else a [i].c [c] = cB [c];
    }

    bacterium [i].fPrev = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "Revision ()" de la clase "C_AO_BCOm", encargado de actualizar la información sobre la población y la historia de valores de la función objetivo, no ha cambiado.

Resultados de las pruebas

Veamos ahora cómo funciona la nueva versión del algoritmo BCOm:

BCO|Bacterial Chemotaxis Optimization|50.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.759526049526603
25 Hilly's; Func runs: 10000; result: 0.6226756163411526
500 Hilly's; Func runs: 10000; result: 0.31483373090540534
=============================
5 Forest's; Func runs: 10000; result: 0.8937814268120954
25 Forest's; Func runs: 10000; result: 0.6133909133246214
500 Forest's; Func runs: 10000; result: 0.22541842289630293
=============================
5 Megacity's; Func runs: 10000; result: 0.653846153846154
25 Megacity's; Func runs: 10000; result: 0.42092307692307684
500 Megacity's; Func runs: 10000; result: 0.14435384615384755
=============================
All score: 4.64875 (51.65%)

Probablemente, la experiencia acumulada y una mirada crítica a la información disponible sobre la versión original hayan tenido su efecto, y la nueva versión del algoritmo haya demostrado ser más potente en la aplicación práctica que la original.

En la visualización del rendimiento del algoritmo BCOm, podemos observar una buena exploración de partes significativas del hiperespacio, lo cual indica una gran capacidad para explorar la superficie de la función que se está optimizando.

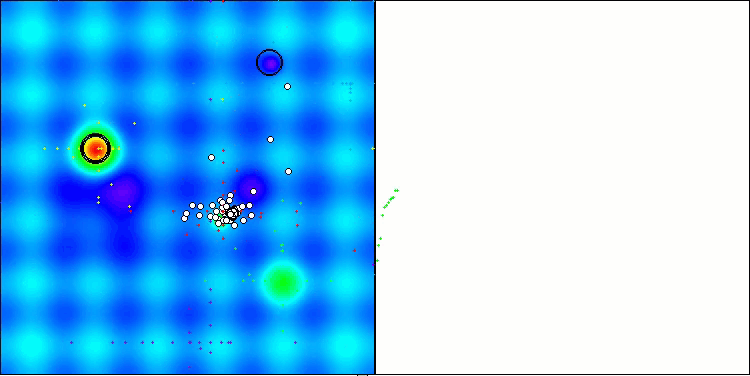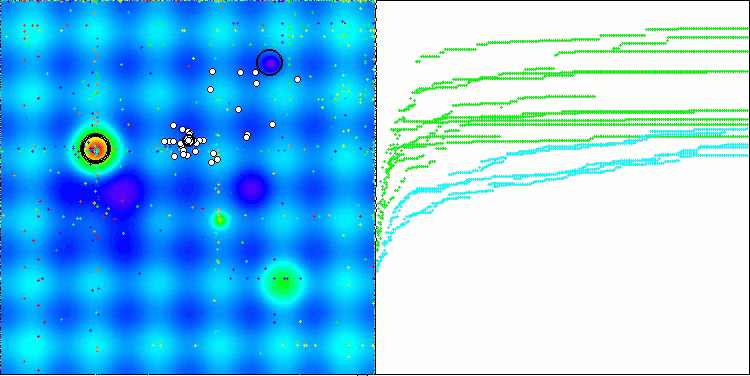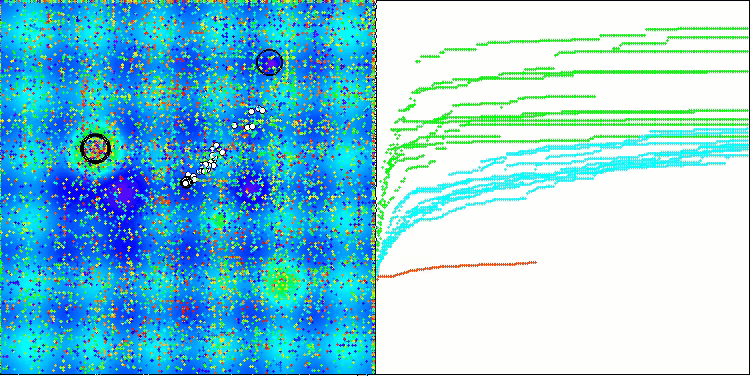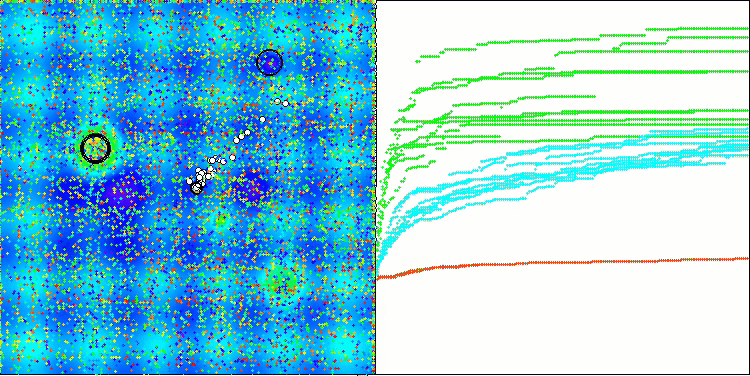
BCOm en la función de prueba Hilly

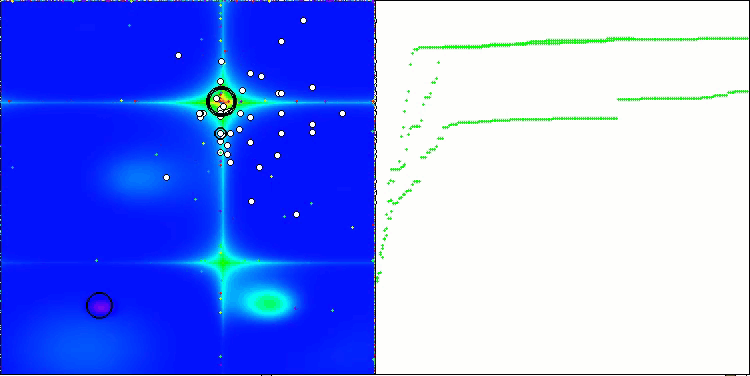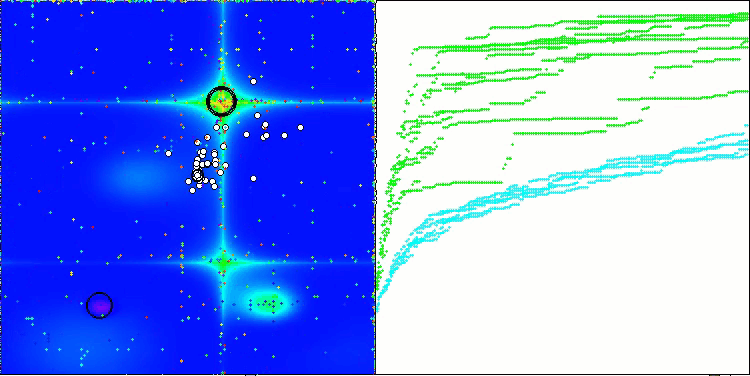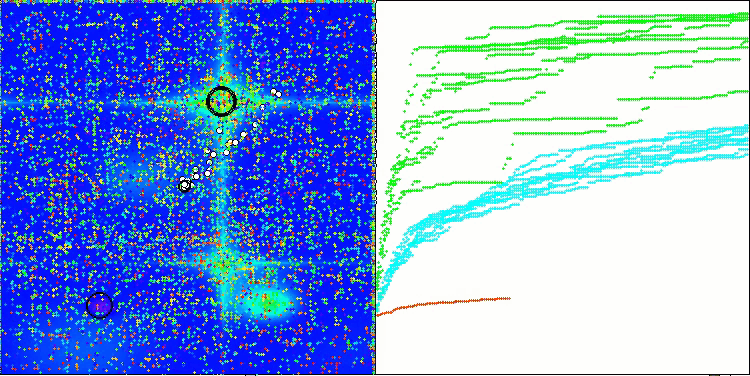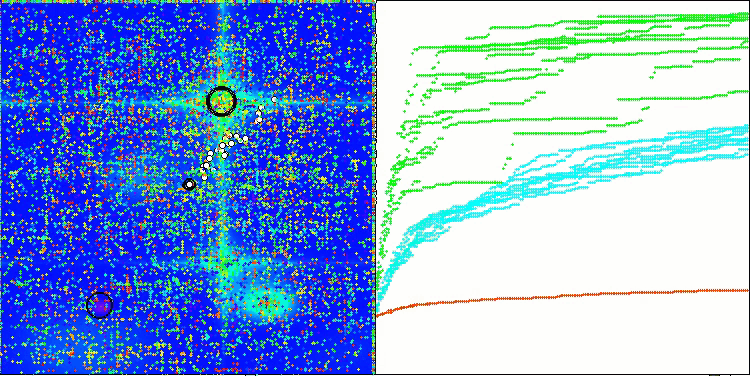
BCOm en la función de prueba Forest

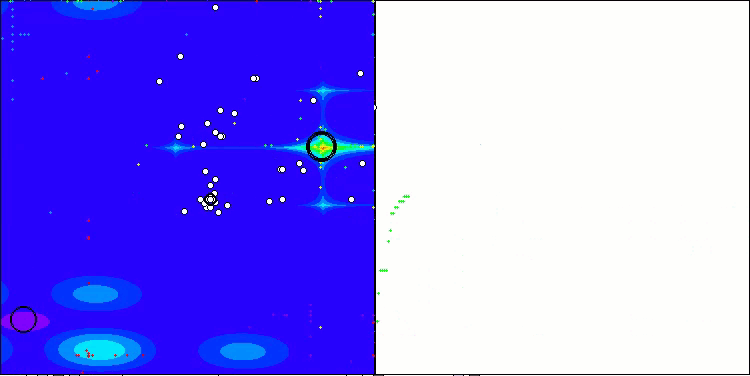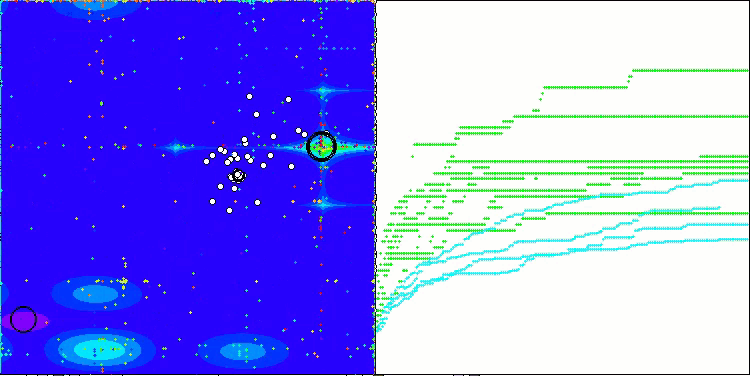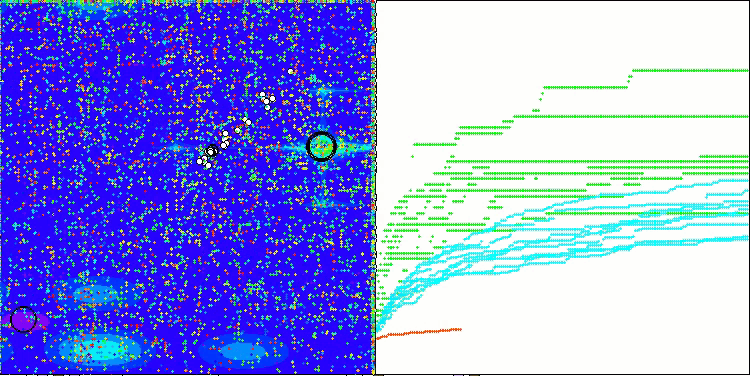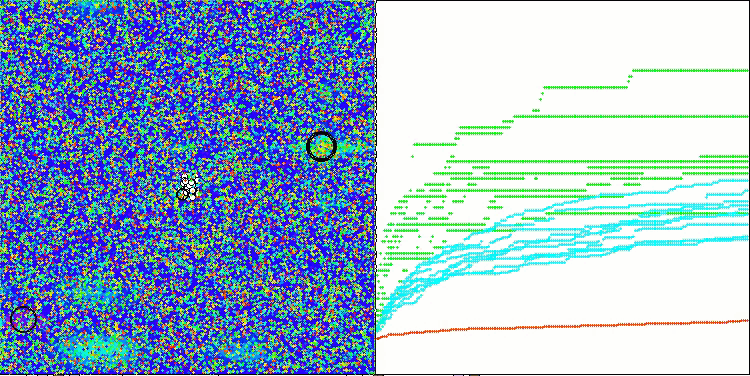
BCOm sobre la función de prueba Megacity

Al final de las pruebas, el algoritmo ha ocupado un estable 17º puesto en la clasificación general de los algoritmos de optimización.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% de MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
2	CLA	code lock algorithm	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	AMOm	animal migration ptimization M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5,987	66,52
4	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
5	CTA	comet tail algorithm	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
6	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
7	ESG	evolution of social groups	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
8	SIA	simulated isotropic annealing	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
9	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
10	ASO	anarchy society optimization	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5,178	57,54
11	TSEA	turtle shell evolution algorithm	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
12	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
13	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
14	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
15	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
16	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
17	BCOm	bacterial chemotaxis optimization M	0,75953	0,62268	0,31483	1,69704	0,89378	0,61339	0,22542	1,73259	0,65385	0,42092	0,14435	1,21912	4,649	51,65
18	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
19	TSm	tabu search M	0,87795	0,61431	0,29104	1,78330	0,92885	0,51844	0,19054	1,63783	0,61077	0,38215	0,12157	1,11449	4,536	50,40
20	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
21	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
22	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
23	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
24	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
25	ABH	artificial bee hive algorithm	0,84131	0,54227	0,26304	1,64663	0,87858	0,47779	0,17181	1,52818	0,50923	0,33877	0,10397	0,95197	4.127	45,85
26	ASBO	adaptive social behavior optimization	0,76331	0,49253	0,32619	1,58202	0,79546	0,40035	0,26097	1,45677	0,26462	0,17169	0,18200	0,61831	3.657	40,63
27	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
28	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
29	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
30	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
31	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
32	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
33	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
34	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
35	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72
36	ABC	artificial bee colony	0,63377	0,42402	0,30892	1,36671	0,55103	0,21874	0,05623	0,82600	0,34000	0,14200	0,03102	0,51302	2,706	30,06
37	BA	bat algorithm	0,59761	0,45911	0,35242	1,40915	0,40321	0,19313	0,07175	0,66810	0,21000	0,10100	0,03517	0,34617	2,423	26,93
38	AAA	algae adaptive algorithm	0,50007	0,32040	0,25525	1,07572	0,37021	0,22284	0,16785	0,76089	0,27846	0,14800	0,09755	0,52402	2,361	26,23
39	SA	simulated annealing	0,55787	0,42177	0,31549	1,29513	0,34998	0,15259	0,05023	0,55280	0,31167	0,10033	0,02883	0,44083	2,289	25,43
40	IWDm	intelligent water drops M	0,54501	0,37897	0,30124	1,22522	0,46104	0,14704	0,04369	0,65177	0,25833	0,09700	0,02308	0,37842	2,255	25,06
41	PSO	particle swarm Optimization	0,59726	0,36923	0,29928	1,26577	0,37237	0,16324	0,07010	0,60572	0,25667	0,08000	0,02157	0,35823	2,230	24,77
42	Boids	boids algorithm	0,43340	0,30581	0,25425	0,99346	0,35718	0,20160	0,15708	0,71586	0,27846	0,14277	0,09834	0,51957	2,229	24,77
43	MA	monkey algorithm	0,59107	0,42681	0,31816	1,33604	0,31138	0,14069	0,06612	0,51819	0,22833	0,08567	0,02790	0,34190	2,196	24,40
44	SFL	shuffled frog-leaping	0,53925	0,35816	0,29809	1,19551	0,37141	0,11427	0,04051	0,52618	0,27167	0,08667	0,02402	0,38235	2,104	23,38
45	FSS	fish school search	0,55669	0,39992	0,31172	1,26833	0,31009	0,11889	0,04569	0,47467	0,21167	0,07633	0,02488	0,31288	2,056	22,84

Conclusiones

Hoy hemos presentado al lector las versiones original BCO y modificada BCOm del algoritmo. La versión original, recreada a partir de información disponible de código abierto, está sobrecargada con pesados cálculos trigonométricos y con débiles propiedades de búsqueda, y muestra "meteduras de pata" matemáticas. Por ello, hemos tenido que replantearnos el algoritmo completo y analizar en profundidad la estrategia de búsqueda y crear una nueva versión modificada. Los cambios en la lógica del algoritmo han dado lugar a cálculos más sencillos en cada paso de optimización, lo cual ha tenido un efecto positivo en la velocidad de ejecución del código. El nuevo algoritmo también establece un equilibrio diferente entre la exploración de un nuevo espacio de soluciones y la explotación de las buenas soluciones ya encontradas.

Aunque el planteamiento actualizado resulta ligeramente contrario al comportamiento natural de las bacterias, ha demostrado ser muy eficaz en aplicaciones prácticas. La visualización del rendimiento del algoritmo ha mostrado su capacidad para explorar en profundidad regiones significativas del hiperespacio, lo que también indica su mejor capacidad de exploración. Al final, la nueva versión del algoritmo ha resultado más potente y eficiente que la original.

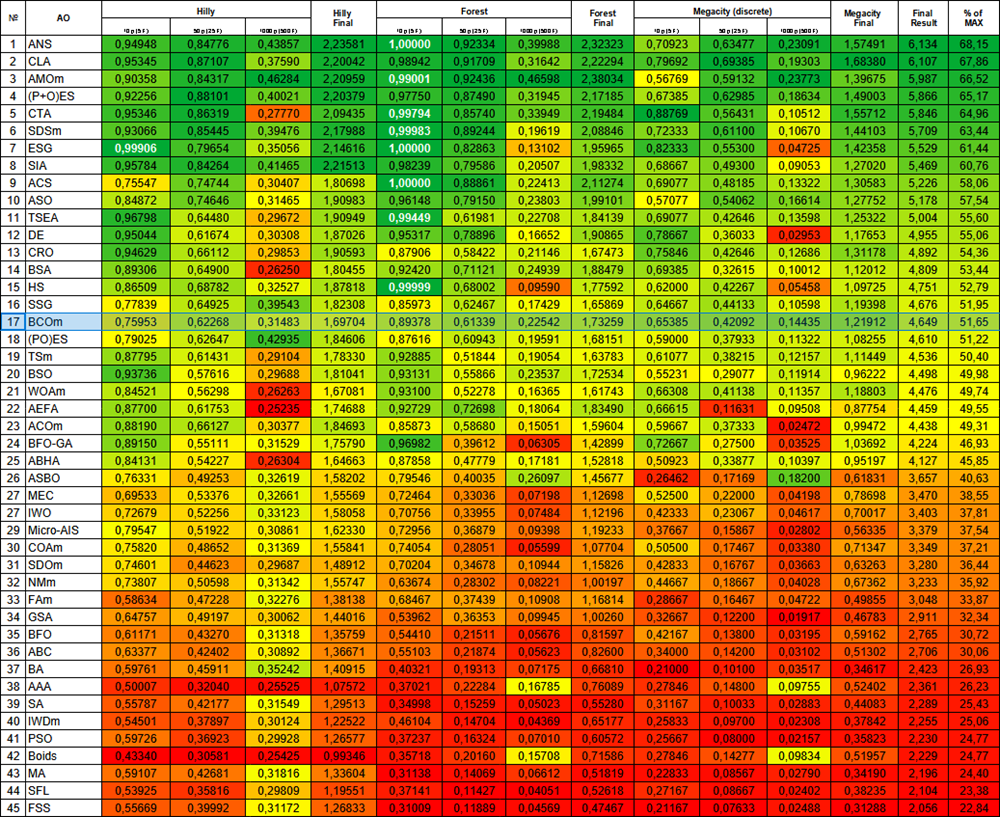
Figura 1. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0,99 aparecen resaltados en blanco.

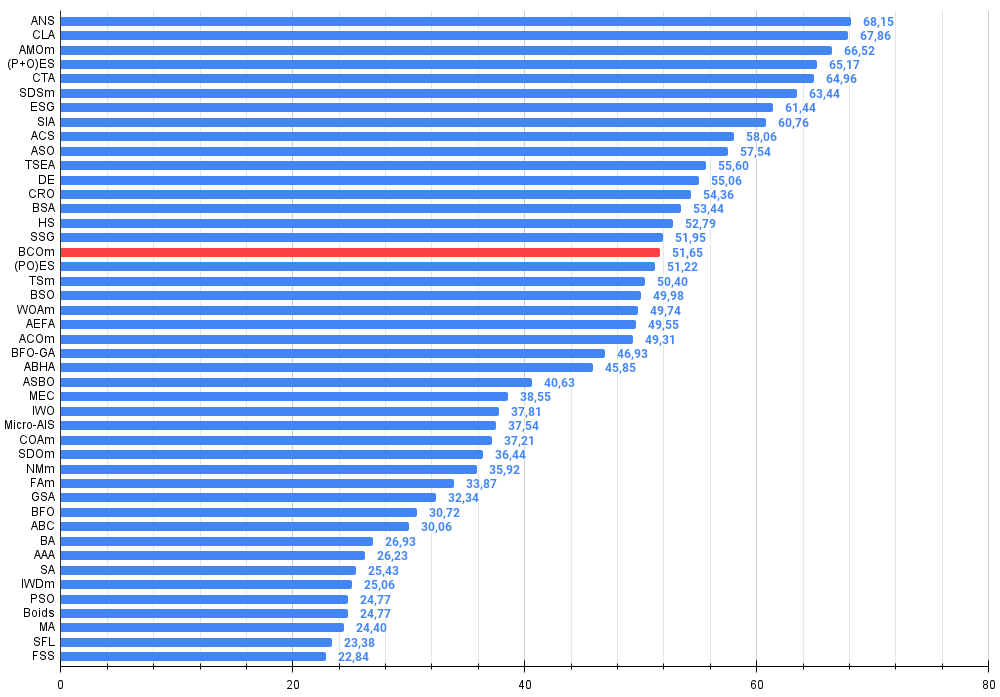
Figura 2. Histograma de los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor,

donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de clasificación está en el archivo)

Ventajas e inconvenientes del algoritmo BCOm:

Ventajas:

1. Es rápido.
2. Autoadaptable.
   
3. Posee una buena escalabilidad.
4. Solo un parámetro externo.
   

Desventajas:

1. Gran dispersión de resultados en funciones de pequeña dimensionalidad.
   

Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/es/code/49355