Características del Wizard MQL5 que debe conocer (Parte 54): Aprendizaje por refuerzo con SAC híbrido y tensores

Introducción

Soft Actor Critic (SAC) es uno de los algoritmos utilizados en el aprendizaje por refuerzo cuando se entrena una red neuronal. En resumen, el aprendizaje por refuerzo es un método emergente de entrenamiento en el aprendizaje automático, junto con el aprendizaje supervisado y el aprendizaje no supervisado.

Búfer de reproducción

El búfer de reproducción es un componente muy importante del algoritmo SAC fuera de política en el aprendizaje por refuerzo, ya que mantiene las experiencias pasadas de estado, acción, recompensa, siguiente estado y el indicador de finalización (para registrar si un episodio ha finalizado o está en curso) en minilotes de muestra para el entrenamiento. Su objetivo principal es descorrelacionar diversas experiencias, de modo que el agente sea capaz de aprender de un conjunto más diverso de experiencias, lo que tiende a mejorar la estabilidad del aprendizaje y la eficiencia de la muestra.

Al implementar SAC, podemos utilizar el lenguaje MQL5, pero las redes creadas no serían tan eficientes para entrenar como las creadas en Python con bibliotecas de código abierto como TensorFlow o PyTorch. Por lo tanto, tal y como vimos en el último artículo sobre aprendizaje por refuerzo, en el que se utilizó Python para modelar una red SAC rudimentaria, continuamos con Python, pero esta vez con el objetivo de explorar y aprovechar sus gráficos Tensor. En principio, hay dos formas de implementar un búfer de reproducción en Python. El enfoque manual o el enfoque basado en tensores. 

Con el enfoque manual, se utilizan estructuras de datos básicas de Python, como listas o matrices NumPy. Sin embargo, con el método basado en Tensor, se emplean marcos de aprendizaje profundo como TensorFlow o PyTorch, siendo este enfoque más eficiente para la aceleración de la GPU debido a la integración perfecta con los procesos de entrenamiento de redes neuronales. En el enfoque manual, el búfer de reproducción se crea con matrices «NumPy», lo cual es sencillo y eficaz para problemas a pequeña escala. Esto podría gestionarse de la siguiente manera:

import numpy as np

class ReplayBuffer:
    def __init__(self, max_size, state_dim, action_dim):
        self.max_size = max_size
        self.states = np.zeros((max_size, state_dim), dtype=np.float32)
        self.actions = np.zeros((max_size, action_dim), dtype=np.float32)
        self.rewards = np.zeros(max_size, dtype=np.float32)
        self.next_states = np.zeros((max_size, state_dim), dtype=np.float32)
        self.dones = np.zeros(max_size, dtype=np.float32)
        self.ptr = 0
        self.size = 0

    def add(self, state, action, reward, next_state, done):
             
        ...

    def sample(self, batch_size):
        idx = np.random.randint(0, self.size, size=batch_size)
        return (
            self.states[idx],
            ...

             self.dones[idx],
        )

Aunque este enfoque es relativamente sencillo de implementar y muy similar al que utilizamos en el artículo anterior sobre SAC, es posible que no se adapte bien a problemas más grandes o a la aceleración por GPU.

Con el método basado en Tensor, el búfer de reproducción se codifica con PyTorch o TensorFlow. Esto último, según mi experiencia (hasta ahora), parece un poco problemático. He conseguido configurar una GPU para que funcione con TensorFlow, pero la naturaleza específica de toda la cadena de controladores y versiones de bibliotecas de software asociadas que deben estar presentes para una versión concreta no solo de TensorFlow, sino también de Python, cuando se utiliza una GPU determinada, es sin duda abrumadora.

Más tarde probé PyTorch y, tal vez gracias a mi experiencia previa con TensorFlow, el proceso fue mucho más fluido. La integración de PyTorch en el entrenamiento de redes neuronales con aceleración GPU es tan fluida que un conjunto de datos de casi un millón de filas, cuando se introduce en una red bastante compleja de 10 millones de parámetros, puede ejecutarse en una sola época en unos 4 minutos en una NVIDIA T4 muy básica. Podemos realizar una implementación rudimentaria en Python de la siguiente manera:

import torch

class ReplayBuffer:
    def __init__(self, max_size, state_dim, action_dim):
        self.max_size = max_size
        self.states = torch.zeros((max_size, state_dim), dtype=torch.float32)
        ...

        self.ptr = 0
        self.size = 0

    def add(self, state, action, reward, next_state, done):
        self.states[self.ptr] = torch.tensor(state, dtype=torch.float32)
        self.actions[self.ptr] = torch.tensor(action, dtype=torch.float32)
        self.rewards[self.ptr] = torch.tensor(reward, dtype=torch.float32)
        self.next_states[self.ptr] = torch.tensor(next_state, dtype=torch.float32)
        self.dones[self.ptr] = torch.tensor(done, dtype=torch.float32)
        self.ptr = (self.ptr + 1) % self.max_size
        self.size = min(self.size + 1, self.max_size)

    def sample(self, batch_size):
        idx = torch.randint(0, self.size, (batch_size,))
        return (
            self.states[idx],
            self.actions[idx],
            self.rewards[idx],
            self.next_states[idx],
            self.dones[idx],
        )

Este método es muy eficiente, ya que se integra directamente con las canalizaciones de optimización y autógradación de PyTorch. En resumen, la comparación entre el enfoque manual y el tensor presenta las siguientes ventajas: el enfoque manual destaca por su sencillez de implementación, sin depender de marcos de aprendizaje profundo. Las desventajas, por otro lado, son la escalabilidad limitada y la ausencia de aceleración por GPU. Con el enfoque basado en tensores, las ventajas son la integración perfecta con redes neuronales, la aceleración de GPU y los problemas a gran escala, mientras que las desventajas serían la necesidad de tener un conocimiento razonable de las complejas implementaciones de TensorFlow/PyTorch.

Por lo tanto, como regla general, se debe elegir el enfoque teniendo en cuenta la magnitud del problema y la disponibilidad de hardware; los métodos basados en tensores son los preferidos para problemas a gran escala o para el entrenamiento con GPU. Además, si su entorno tiene estados de tamaño variable, como en el caso de las imágenes, entonces el método basado en tensores sería el más adecuado. Además, SAC se puede mejorar con la reproducción de experiencia priorizada (PER), en la que el muestreo del búfer de reproducción se basa en la importancia relativa de cada estado en el búfer mediante la medición del error de diferencia temporal u otras métricas clave. La implementación de PER es más fácil con búferes de reproducción basados en tensores, ya que permite actualizaciones de prioridad y muestreos eficientes.

Al igual que con cualquier listado de código, antes de la implementación siempre es buena idea realizar algunas pruebas y depurar, y con un búfer de reproducción, esto se puede llevar a cabo añadiendo datos ficticios y verificando que el muestreo funciona correctamente. Además, hay que asegurarse de que el búfer de reproducción maneje casos extremos como estar vacío o estar lleno. Las aserciones de Python o las pruebas unitarias se pueden utilizar para validar la funcionalidad. Una vez que el búfer de reproducción está listo, lo siguiente es la integración en el bucle de entrenamiento SAC mediante el almacenamiento de experiencias después de cada paso de entrenamiento y, a continuación, el muestreo de minilotes para las actualizaciones.

A menudo se busca un equilibrio al establecer el tamaño del búfer de reproducción, ya que debe ser lo suficientemente grande como para almacenar un conjunto diverso de experiencias, pero no tan grande como para ralentizar el proceso de muestreo. El búfer de reproducción se puede optimizar en cuanto a velocidad y memoria utilizando estructuras de datos eficientes como los tensores PyTorch, evitando copias innecesarias de datos y preasignando memoria para el búfer. El análisis del búfer de reproducción puede ayudar a identificar y solucionar los cuellos de botella que afectan al rendimiento.

En resumen, una buena implementación del búfer SAC es esencial para el éxito de SAC y de muchos algoritmos fuera de la política. Garantiza una formación estable y eficaz mediante la provisión de experiencias diversas y descorrelacionadas.

Red de críticos

En los algoritmos SAC, la red crítica estima el valor Q (o valor de acción del estado, o la siguiente acción que debe realizar el actor) cuando se le presenta el estado actual del entorno y la elección del actor sobre la siguiente acción. SAC involucra dos de estas redes críticas para reducir el sesgo de sobreestimación y también mejorar la estabilidad del aprendizaje. Como una red neuronal que toma como entrada 2 conjuntos de datos restringidos de la distribución de probabilidad de las acciones de la red actor y las "coordenadas" de los estados del entorno, por lo tanto, la elección de usar NumPy o tensores dependerá del tamaño del problema (tal como se define por el tamaño de la red y el volumen de datos a usar en el entrenamiento) y también de la disponibilidad del hardware.

Con una implementación manual no tensorial de redes críticas, NumPy resulta útil para operaciones de matriz y actualizaciones de gradientes. En los casos en que las redes tienen menos de 5 capas con tamaños no mayores a 15 cada una o para fines educativos e ilustrativos, esta podría ser una solución viable. Con este enfoque, los pases de propagación hacia adelante y hacia atrás se implementan manualmente, lo que podría ser propenso a errores y no tan eficiente al escalar a grandes conjuntos de datos de entrenamiento. Así es como podría verse una implementación manual de Python:

import numpy as np

class CriticNetwork:
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        self.state_dim = state_dim
        self.action_dim = action_dim
        self.hidden_dim = hidden_dim

        # Initialize weights and biases
        self.W1 = np.random.randn(state_dim + action_dim, hidden_dim)
        self.b1 = np.zeros(hidden_dim)
        self.W2 = np.random.randn(hidden_dim, hidden_dim)
        self.b2 = np.zeros(hidden_dim)
        self.W3 = np.random.randn(hidden_dim, 1)
        self.b3 = np.zeros(1)

    def forward(self, state, action):
        x = np.concatenate([state, action], axis=-1)
        x = np.maximum(0, x @ self.W1 + self.b1)  # ReLU activation
        x = np.maximum(0, x @ self.W2 + self.b2)  # ReLU activation
        q_value = x @ self.W3 + self.b3
        return q_value

    def update(self, states, actions, targets, learning_rate=1e-3):
        # Manual gradient descent (simplified)
        q_values = self.forward(states, actions)
        error = q_values - targets
        # Backpropagation and weight updates (not shown for brevity)

Como ya se señaló, este enfoque no es escalable para redes o conjuntos de datos grandes y carece de aceleración de GPU. Si, por otro lado, elegimos utilizar tensores, con PyTorch podremos aprovechar la diferenciación automática y la aceleración de la GPU. Estas propiedades son un buen augurio para problemas a gran escala e implementaciones a nivel de producción. Un ejemplo de codificación muy básico de esto podría ser el siguiente:

import torch
import torch.nn as nn
import torch.nn.functional as F

class CriticNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        super(CriticNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim + action_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc3 = nn.Linear(hidden_dim, 1)

    def forward(self, state, action):
        x = torch.cat([state, action], dim=-1)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        q_value = self.fc3(x)
        return q_value

PyTorch en particular viene con algunas bibliotecas cruciales, a saber, 'torch.optim' para manejar la optimización de la red y 'torch.nn' para configurar la arquitectura de la red. Todo esto se logra mediante un enfoque altamente escalable y eficiente.

Entonces, si bien es posible aplicar un enfoque manual, como se muestra en la lista de muestra anterior, y ofrece las ventajas de la simplicidad y de no tener que depender de marcos de aprendizaje profundo, su incapacidad para escalar o incluso aprovechar adecuadamente las GPU es un obstáculo para su adopción.

El uso de tensores en redes críticas también presentaría ventajas y desventajas similares a las descritas anteriormente con el búfer de reproducción, lo que implica en términos generales, como ya se concluyó, que el enfoque manual a menudo es adecuado en situaciones en las que los problemas que se resuelven son muy pequeños y es importante ilustrar o "enseñar" las complejidades de las redes neuronales. En la práctica, sin embargo, los tensores son más prácticos por las razones ya compartidas.

Las redes SAC, si recordamos, utilizan dos redes críticas (a menudo denominadas Q1 y Q2) para mitigar el sesgo de sobreestimación. Por tanto, el valor Q objetivo se determina como el mínimo de los dos valores Q producidos por las redes. Para ilustrarlo, las redes críticas, como parte del resultado de la red de actores, producen un vector con recompensas estimadas para tomar cada una de las acciones disponibles.

Entonces, naturalmente, dentro de cada uno de estos vectores, el índice/acción con el valor más alto pronosticaría la recompensa más alta. El propósito principal de las redes críticas es determinar de manera conservadora el gradiente para propagar hacia atrás la red del actor.

Durante la actualización de la red del actor, se calcula el gradiente de la función objetivo y se propaga hacia atrás a través de la red del actor desde el mínimo de los dos valores Q. La elección mínima asegura que el actor esté optimizado para elegir acciones que sean robustas a los errores de sobreestimación en los críticos.

Estas redes críticas que proporcionan el gradiente a la función objetivo que actualiza la red del actor también necesitan ser entrenadas. Pero dado que están estimando recompensas futuras de sus acciones, ¿cómo se establece su objetivo de entrenamiento? La respuesta es que para las actualizaciones críticas, SAC no utiliza directamente el mínimo de los dos valores Q. En su lugar, se realiza una actualización para cada crítico (Q1 y Q2) utilizando el objetivo derivado de la ecuación de Bellman suave.

class DoubleCriticNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        super(DoubleCriticNetwork, self).__init__()
        self.Q1 = CriticNetwork(state_dim, action_dim, hidden_dim)
        self.Q2 = CriticNetwork(state_dim, action_dim, hidden_dim)

    def forward(self, state, action):
        q1 = self.Q1(state, action)
        q2 = self.Q2(state, action)
        return q1, q2

Además, las redes objetivo en SAC son otro conjunto separado de redes (una para cada crítico Q1 y Q2) que se utilizan para calcular los valores Q objetivo que son clave en la propagación hacia atrás de estas redes críticas. Ellos mismos se actualizan lentamente a través del promedio polyak, para tener estabilidad durante el entrenamiento. El uso de redes objetivo surge de la necesidad de proporcionar un objetivo estable para la ecuación de Bellman sin el cual, se argumenta, las estimaciones del valor Q de las redes críticas divergirían u oscilarían debido al bucle de retroalimentación entre los valores Q y los objetivos.

for target_param, param in zip(target_critic.parameters(), critic.parameters()):
    target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data)
```
where `tau` is the polyak averaging coefficient (e.g., 0.005).

La función de pérdida para los críticos sería entonces el error cuadrático medio (MSE) entre el valor Q previsto y el valor Q objetivo, según lo establecido por la ecuación de Bellman con la ayuda de las redes objetivo mencionadas anteriormente.

target_q_value = reward + (1 - done) * gamma * min(Q1_target(next_state, next_action), Q2_target(next_state, next_action))
```
where `gamma` is the discount factor.

Entonces, para entrenar a los críticos, se tomaría una muestra de un mini lote del buffer de reproducción y se calcularía el valor Q objetivo. Con esto las redes críticas se actualizarían por gradiente descendente. Se puede utilizar un optimizador como Adam para hacer que el entrenamiento sea más eficiente.

optimizer = torch.optim.Adam(critic.parameters(), lr=learning_rate)

La depuración y las pruebas se pueden realizar introduciendo entradas ficticias y verificando la forma y los valores de la salida. Se debe garantizar que la red pueda adaptarse a un conjunto de datos pequeño. Como ya se mencionó, las afirmaciones de Python se pueden utilizar para validar datos de entrada. Las redes críticas se integran en el ciclo de entrenamiento SAC calculando valores Q, actualizando la pérdida crítica y sincronizando las redes de destino. Es importante garantizar que la red crítica se actualice junto con las redes de actores y valores, por lo que los tensores y, en particular, el uso de GPU son de gran importancia aquí.

También se podrían adoptar algunos consejos de optimización adicionales para las redes críticas, y en primer lugar estos incluyen la normalización por lotes o la normalización por capas. En segundo lugar, experimentar con diferentes funciones de activación como ReLU o Leaky podría producir resultados diferentes dependiendo de los datos probados y la naturaleza de la red que se emplee. Además, se pueden ajustar hiperparámetros como la tasa de aprendizaje y la profundidad de la red. El seguimiento de la pérdida crítica durante el entrenamiento es importante para detectar problemas como sobreajuste e inestabilidad.

Para concluir, la red de críticos es un componente crucial del SAC, fundamental para estimar los valores Q y orientar las actualizaciones de políticas de los actores. Una red crítica bien implementada garantiza un aprendizaje estable y eficiente.

Redes de valor

Esta red, también conocida como función estado-valor, es una parte opcional de SAC que podríamos elegir utilizar. Su propósito es estimar la recompensa acumulada esperada de un estado bajo la política actual utilizando la función de valor blando. Si bien el uso de una red de valor es “opcional”, conlleva muchas ventajas si se implementa correctamente. En primer lugar, porque incorpora explícitamente la entropía, la función de valor blando incentiva a la política a explorar de manera más eficiente y efectiva. La acción de la función de valor suave tiende a proporcionar un objetivo más suave para el entrenamiento, lo que puede ayudar a estabilizar el proceso de aprendizaje.

Esta estabilidad es muy beneficiosa cuando se enfrentan datos de entrada de alta dimensión (cuando el vector de datos de entrada es grande en tamaño >10) o los espacios de acción son de naturaleza continua (por ejemplo, una opción de acción de (0,14, 0,67, 1,51) en lugar de (comprar, vender, mantener)) o cuando los entornos de datos se enfrentan a múltiples óptimos locales (escenario en el que muchas configuraciones de peso de red diferentes parecen dar resultados decentes cuando cada configuración se entrena en conjuntos de datos o entornos separados, pero ninguna de estas configuraciones de peso puede generalizar o mantener su rendimiento en conjuntos de datos más amplios).

Para resumir, las redes de valor en SAC se utilizan para estimar el rendimiento esperado de un estado independientemente de cualquier acción, lo que ayuda a reducir las variaciones en las estimaciones del valor Q al proporcionar un objetivo suave. Los argumentos a favor del uso de tensores frente al manual son muy similares a los dados para la red crítica anterior. La mayoría de las redes SAC modernas no implementan la red de valor, sino que se centran en las 2 redes de destino adicionales para ayudar a establecer los objetivos de entrenamiento para las 2 redes críticas.

Además de utilizar una única red de valor anterior para moderar los objetivos de entrenamiento de la red crítica, también podríamos utilizar 2 redes de valor. En este escenario, también se utilizan una red de valor y una red de valor objetivo para estimar la función de valor, que predice el rendimiento esperado (recompensa acumulada) de cualquier estado dado. La red de valor objetivo en particular se utiliza para estabilizar el entrenamiento, no solo en este caso sino también con redes Deep-QN. Al ser una copia de la red de valor, se actualiza con menos frecuencia y proporciona un objetivo estable para el entrenamiento.

Red de actores

Esta es la red principal y también se la conoce como red de políticas. Toma como entrada estados del entorno y genera como salida dos vectores, media y desviación estándar, que sirven como parámetros de una distribución de probabilidad sobre acciones que pueden usarse para muestrear estocásticamente. Las dos redes críticas, sus redes de destino correspondientes y la red de valor, si se utiliza, sirven para ayudar a la propagación hacia atrás y al entrenamiento de esta red.

Al ser una red, deberíamos beneficiarnos significativamente del uso del tensor, dado el papel central que desempeña en SAC. Además, dado que todas las redes mencionadas anteriormente dependen del entrenamiento de esta red, la red de actores, entonces el uso de GPU para paralelizar y permitir el entrenamiento concurrente de estas múltiples redes es algo que se debería buscar explorar, ya que aporta mucha eficiencia.

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.distributions as dist

class ActorNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        super(ActorNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc_mean = nn.Linear(hidden_dim, action_dim)
        self.fc_log_std = nn.Linear(hidden_dim, action_dim)

    def forward(self, state):
        x = F.relu(self.fc1(state))
        x = F.relu(self.fc2(x))
        mean = self.fc_mean(x)
        log_std = self.fc_log_std(x)
        return mean, log_std

    def sample_action(self, state):
        mean, log_std = self.forward(state)
        std = torch.exp(log_std)
        normal = dist.Normal(mean, std)
        action = normal.rsample()  # Reparameterization trick
        return torch.tanh(action), normal.log_prob(action).sum(dim=-1, keepdim=True)

La red de actores, como ya hemos señalado en el último artículo de SAC, genera dos "vectores" de datos clave: la media y la desviación estándar de una distribución gaussiana. Estos dos se combinan para determinar la siguiente acción de manera estocástica, lo que es importante para la exploración y optimización en espacios de acción continua. La media representa el centro de la dispersión o distribución de la acción, mientras que la desviación estándar controla la dispersión o aleatoriedad de la distribución. Estos dos definen una distribución gaussiana de la cual se pueden seleccionar acciones. El código Python a continuación ayuda a lograr esto.

import torch

def select_action(mean, log_std):
    """
    Given the SAC actor's output (mean and log_std), this function selects an action index.
    
    Args:
        mean (torch.Tensor): Mean of the action distribution, shape (n_actions,)
        log_std (torch.Tensor): Log standard deviation, shape (n_actions,)

    Returns:
        int: The index of the selected action.
    """
    std = log_std.exp()  # Convert log standard deviation back to standard deviation
    ....  
    return selected_index

# Example inputs
mean = torch.tensor([0.2, -0.5, 1.0, 0.3])  # Example mean values for 4 actions
log_std = torch.tensor([-1.0, -0.7, -0.2, -0.5])  # Example log std values

# Select action
action_index = select_action(mean, log_std)
print("Selected Action Index:", action_index)

En la práctica, sin embargo, tendríamos que ejecutar esta función en MQL5 porque después de entrenar el modelo en Python se exportaría como un archivo ONNX y como ONNX sus salidas en cualquier paso hacia adelante serían similares a lo que se usó en Python durante el entrenamiento. Entonces, dado que estas dos salidas se recibirían en MQL5, esta función de selección de acción también tendría que estar en MQL5.

Estas dos salidas definen una distribución gaussiana o normal de la que se eligen las acciones. La elección de las acciones se realiza de forma estocástica para fomentar la exploración de modo que el agente no elija siempre la misma acción para un estado determinado. Durante la propagación hacia atrás, para lograr mayor eficiencia, se utiliza la reparametrización para que los gradientes puedan fluir a través del proceso de muestreo.

Además, a partir de nuestra función Python anterior, dado que la mayoría de las acciones en aplicaciones del mundo real tienen un alcance o están limitadas, SAC aplica la función Tanh para comprimir las acciones muestreadas para que estén en el rango de -1 a +1. Esto garantiza que la acción se mantenga dentro de un rango manejable mientras se preserva la naturaleza estocástica del proceso.

Agente

El agente en SAC, que representamos aquí como la clase de agente en Python, combina la optimización de políticas (red de actores) con la aproximación de la función de valor (el emparejamiento de las dos redes críticas, la red de valor y la red de valor objetivo). El agente debe ser altamente eficiente en el procesamiento de muestras y poder gestionar espacios de acción continua. Esto se debe a que reúne no solo estas redes sino también el búfer de reproducción con el objetivo de aprender una "política óptima" o pesos y sesgos adecuados para la red del actor.

Dada la naturaleza de visión general de alto nivel del agente, tal vez no sea necesario decir que los tensores serían esenciales para que el entrenamiento de la red se realice con cierta eficiencia. A continuación se muestra un resumen en Python de cómo se podría hacer esto:

import torch
import torch.nn.functional as F
import torch.optim as optim

class SACAgent:
    def __init__(self, state_dim, action_dim, hidden_dim=256, replay_buffer_size=1e6, batch_size=256, gamma=0.99, tau=0.005, alpha=0.2):
        self.state_dim = state_dim
        ...

        self.alpha = alpha

        # Initialize networks and replay buffer
        self.actor = ActorNetwork(state_dim, action_dim, hidden_dim)
        ....

        self.value_optimizer = optim.Adam(self.value_network.parameters(), lr=3e-4)

    def select_action(self, state):
        state = torch.FloatTensor(state).unsqueeze(0)
        action, _ = self.actor.sample_action(state)
        return action.detach().numpy()[0]

    def update(self):
        # Sample a batch from the replay buffer
        states, actions, rewards, next_states, dones = self.replay_buffer.sample(self.batch_size)

        # Convert to tensors
        states = torch.FloatTensor(states)
        ...

        dones = torch.FloatTensor(dones).unsqueeze(1)

        # Update value network
        target_value = self.target_value_network(next_states)
        ...

        # Update critic networks
        q1_value = self.critic1(states, actions)
             
        ...

        self.critic2_optimizer.step()

        # Update actor network
        new_actions, log_probs = self.actor.sample_action(states)
             
        ...

        self.actor_optimizer.step()

        # Update target networks
        for target_param, param in zip(self.target_value_network.parameters(), self.value_network.parameters()):
            target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)

Dado que utilizamos tensores con PyTorch, es importante destacar que la asignación manual de un dispositivo GPU, si está disponible, contribuye en gran medida a garantizar que los tensores se ejecuten de la manera más eficiente posible.

Entorno

El entorno es donde se definen los conjuntos de datos de entrenamiento y de objetivos/acción. Básicamente, define el problema que el agente está intentando resolver proporcionándole señales de estado, recompensa y finalización en función de sus acciones. El entorno se puede implementar manualmente (es decir, desde los primeros principios) o por herencia utilizando bibliotecas como Gym de OpenAI para entornos estandarizados. Un entorno basado en tensores podría implementarse de la siguiente manera:

import torch

class TensorEnvironment:
    def __init__(self):
        self.state_space = 4  # Example: state dimension
        self.action_space = 2  # Example: action dimension
        self.state = torch.zeros(self.state_space)  # Initial state

    def reset(self):
        self.state = torch.randn(self.state_space)  # Reset to a random state
        return self.state

    def step(self, action):
        # Define transition dynamics and reward function
        next_state = self.state + action  # Simple transition
        ...

        self.state = next_state
        return next_state, reward, done, {}

    def render(self):
        print(f"State: {self.state}")

Luego se usaría un bucle para recopilar experiencias y actualizar el agente periódicamente:

for episode in range(num_episodes):
    state = env.reset()
    episode_reward = 0
    for step in range(max_steps):
        action = agent.select_action(state)
        next_state, reward, done, _ = env.step(action)
        agent.replay_buffer.add(state, action, reward, next_state, done)
        state = next_state
        episode_reward += reward
        if len(agent.replay_buffer) > batch_size:
            agent.update()
        if done:
            break
    print(f"Episode {episode}, Reward: {episode_reward}")

Prueba

Probamos nuestro SAC híbrido basado en tensores que, además de tener una red de actores y 2 redes de críticos, utiliza una red de valor y una red de valor objetivo en lugar de las 2 redes objetivo (que entrenan a los críticos). Utilizamos el par EURUSD en el marco temporal de 4 horas para el año 2023.

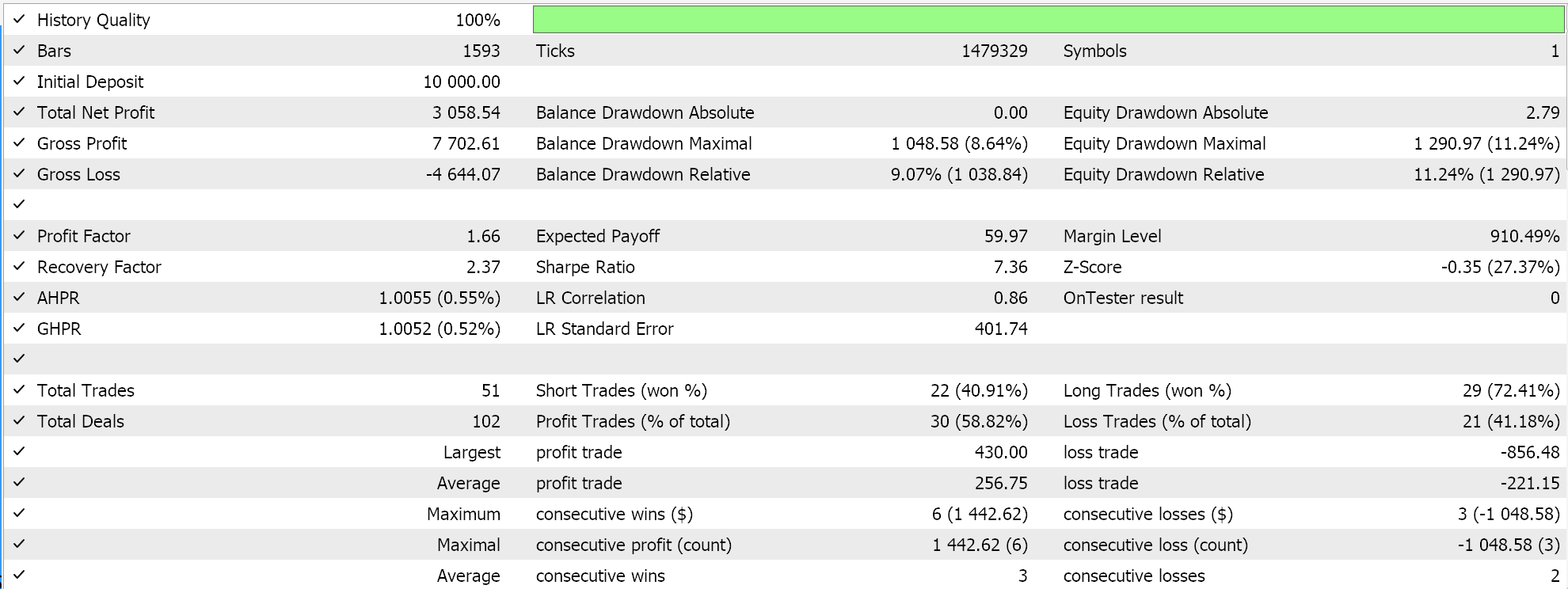
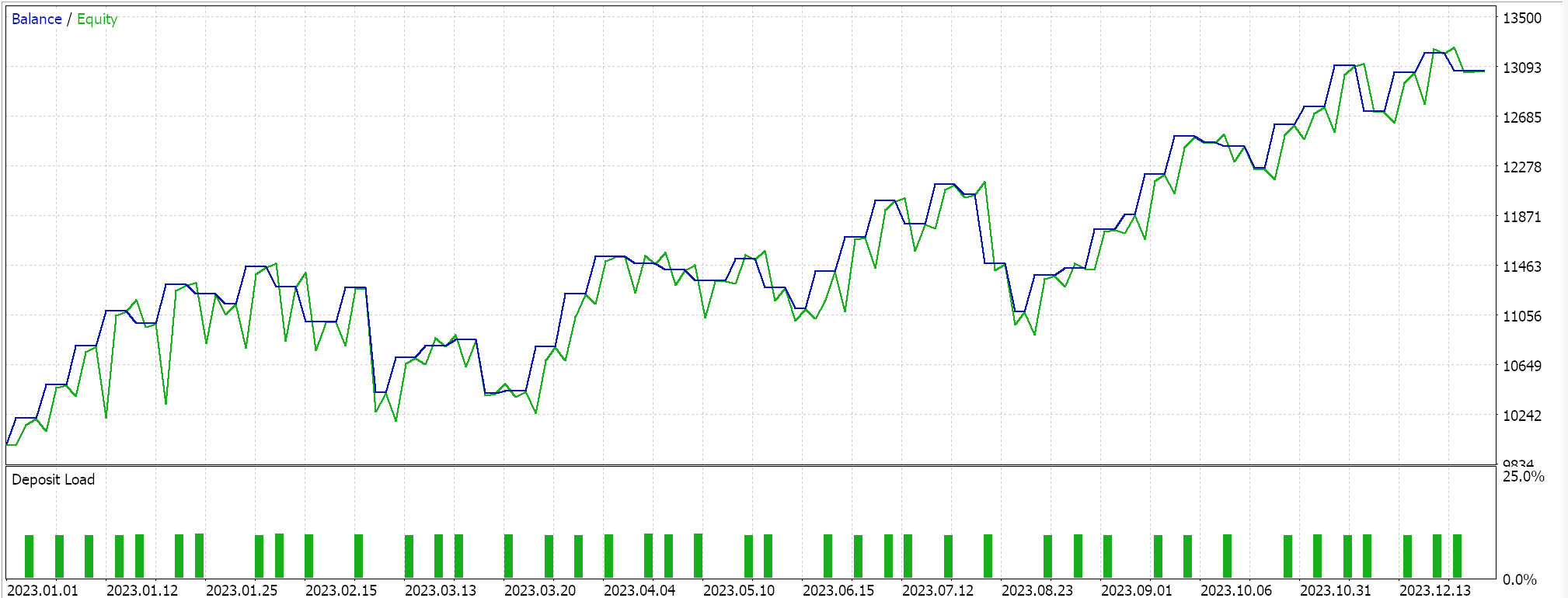
Tanto TensorFlow como PyTorch permiten no solo el entrenamiento de modelos, sino también su validación cruzada. TensorFlow permite pasar valores de datos de validación x e y a su función de ajuste, mientras que PyTorch esencialmente permite lo mismo al pasar estos datos a un data_loader. Una ejecución de prueba en un Asesor Experto compilado en MQL5 que no realiza una validación cruzada (o inferencia) nos da los siguientes resultados para EURUSD durante 2023:

Usamos, como en el último artículo de SAC, ONNX para exportar el modelo desde Python e importarlo a MQL5. Hemos estado trabajando con 5 redes neuronales y, sin embargo, solo una está haciendo los pronósticos que necesitamos, ya que las otras 4 ayudan simplemente en la propagación hacia atrás. La red que necesitamos y exportamos es la red de actores. Sin embargo, esta red genera no uno, sino dos vectores, como ya se mencionó. La media y la desviación estándar. Por lo tanto, antes de poder utilizar el modelo ONNX en MQL5, necesitamos definir con precisión las formas de salida de este modelo. La forma de entrada es sencilla. Establecemos las formas en MQL5 de la siguiente manera:

//+------------------------------------------------------------------+
//| Validation arch protected data.                                  |
//+------------------------------------------------------------------+
bool CSignalSAC::ValidationSettings(void)
{  if(!CExpertSignal::ValidationSettings())
      return(false);
//--- initial data checks
   if(m_period != PERIOD_H4)
   {  Print(" time frame should be H4 ");
      return(false);
   }
   if(m_actor_handle == INVALID_HANDLE)
   {  Print("Actor OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   // Set input shapes
   const long _actor_in_shape[] = {1, __STATES};
   // Set output shapes
   const long _actor_out_shape[] = {1, __ACTIONS};
   if(!OnnxSetInputShape(m_actor_handle, ONNX_DEFAULT, _actor_in_shape))
   {  Print("Actor OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_actor_handle, 0, _actor_out_shape))
   {  Print("Actor OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_actor_handle, 1, _actor_out_shape))
   {  Print("Actor OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
//read best weights
//--- ok
   return(true);
}

Esto se maneja en la función de validación de nuestra clase de señal personalizada, ya que el modelo ONNX no se ejecutará a menos que estas formas estén definidas con precisión. Los nuevos lectores pueden encontrar guías sobre cómo montar un Asesor Experto a partir de un archivo de señal personalizado .mqh aquí y aquí.

Conclusión

Hemos implementado un algoritmo de aprendizaje de refuerzo Soft Actor Critic en Python con la ayuda de tensores. Los tensores son cruciales en el aprendizaje automático porque brindan enormes ganancias de eficiencia al entrenar modelos, un aspecto que es muy importante especialmente para los comerciantes. El tamaño de los conjuntos de datos de entrenamiento y la necesidad de redes diseñadas de manera más compleja tienden a conducir a procesos de entrenamiento más lentos. Por lo tanto, este inconveniente se soluciona no solo utilizando tensores, sino también aprovechando la potencia de las GPU.

Nombre	Descripción
hybrid_sac.mq5	Asesor experto ensamblado por Wizard MQL5 con encabezado que muestra los archivos utilizados.
SignlWZ_54.mqh	Archivo de clase de señal personalizada.
model.onnx	Archivo de red ONNX.