Algoritmo de búsqueda cooperativa artificial (Artificial Cooperative Search, ACS)
208
0
Contenido
1. Introducción
2. Ejecución del algoritmo
3. Resultados de las pruebas
1. Introducción
La naturaleza es una fuente inagotable de inspiración para científicos e ingenieros que buscan crear soluciones innovadoras. Uno de estos fenómenos notables es el mutualismo: una interacción biológica mutuamente beneficiosa entre diferentes especies. Los organismos vivos que participan en relaciones mutualistas se esfuerzan por obtener beneficios mutuos de esta interacción, orientada al desarrollo y la diversidad de la población. Para entender esto, daré varios ejemplos de relaciones mutualistas (simbióticas) entre organismos vivos, en las que reciben beneficios mutuos:
1. Plantas con flores y polinizadores:
- Las plantas producen néctar y otras recompensas para atraer polinizadores como insectos, pájaros y murciélagos.
- Los polinizadores, a su vez, transfieren el polen de una flor a otra, lo que promueve la reproducción de la planta.
2. Hongos y raíces de las plantas (micorrizas):
- Los hongos penetran en las raíces de las plantas y reciben de ellas compuestos orgánicos (productos de la fotosíntesis).
- Los hongos, a su vez, amplían la superficie de absorción de las raíces, aumentando la disponibilidad de agua y minerales para las plantas.
3. Termitas y bacterias simbióticas:
- Las termitas contienen bacterias simbióticas en sus intestinos que les ayudan a digerir la celulosa, el componente principal de la madera.
- Las bacterias obtienen nutrientes de las termitas y las termitas obtienen la capacidad de digerir la fibra.
Estos ejemplos demuestran cómo los organismos vivos interactúan para obtener beneficios mutuos y aumentar sus posibilidades de supervivencia.
El algoritmo ACS también se inspira en el comportamiento migratorio de los superorganismos eusociales que comparten un entorno común. A continuación se presentan algunos ejemplos de dicho comportamiento migratorio de superorganismos eusociales:
1. Las colonias de hormigas:
- Durante una migración de colonia, las hormigas transportan consigo larvas, pupas y otros elementos importantes del nido.
2. Las familias de abejas:
- Al enjambrar, las colonias de abejas pueden migrar temporalmente de su colmena para iniciar una nueva colonia en otro lugar.
- Durante la migración de un enjambre, las abejas transportan reinas, larvas y los suministros de miel necesarios para establecer un nuevo nido.
Una característica común de estos ejemplos es que los superorganismos eusociales, como las hormigas, las termitas, las abejas y las avispas, son capaces de trasladar colectivamente sus colonias en respuesta a cambios ambientales o al agotamiento de recursos. Esta capacidad migratoria les permite adaptarse a las condiciones cambiantes y asegura la supervivencia de todo el superorganismo. La interacción biológica mutualista y cooperativa de dos superorganismos eusociales que viven en el mismo entorno sirvió de inspiración para el algoritmo ACS. En este algoritmo, el concepto de hábitat corresponde al concepto de espacio de búsqueda relacionado con el problema de optimización correspondiente.
Conceptualmente, el algoritmo ACS ve las soluciones aleatorias al problema correspondiente como superorganismos artificiales que migran a áreas de alimentación más productivas. Los dos superorganismos principales, denominados α y β, contienen subsuperorganismos artificiales iguales al tamaño de la población. El tamaño de la población corresponde al número de individuos de estos subsuperorganismos. En el proceso de coevolución, los superorganismos α y β interactúan como depredadores y presas, utilizando dos poblaciones dinámicas para explorar eficientemente el espacio de búsqueda y encontrar el óptimo global para problemas de optimización numérica.
El algoritmo ACS fue propuesto por Pinar Civicioglu en 2013. Comienza utilizando dos poblaciones base que contienen soluciones candidatas dentro de la región de confianza. A continuación, el algoritmo crea dos nuevas poblaciones, depredadores y presas, mediante la asignación de valores de las poblaciones iniciales α y β utilizando pasos aleatorios y una matriz binaria. Además, la quinta población se calcula a partir de los valores de las poblaciones de depredadores y presas. El proceso consiste en actualizar las poblaciones iniciales durante un número determinado de iteraciones, tomando la mejor solución de estas dos poblaciones.
La migración y evolución de dos superorganismos artificiales que interactúan biológicamente entre sí para alcanzar el extremo global de la función objetivo, y el proceso similar al comportamiento cooperativo en la naturaleza, son la clave del alto rendimiento de ACS en problemas de optimización numérica. Este enfoque único de las interacciones biológicamente motivadas entre poblaciones permite al algoritmo ACS alcanzar una impresionante velocidad de convergencia y una elevada precisión de las soluciones. Gracias a su capacidad para encontrar soluciones óptimas de forma rápida y precisa, ACS ha demostrado ser una potente herramienta para resolver una amplia gama de problemas de optimización numérica.
En este artículo, describiré en detalle el concepto en el que se basa el algoritmo ACS y demostraré sus notables capacidades. Los lectores comprenderán en profundidad cómo la inspiración biológica puede implementarse con éxito en algoritmos avanzados de optimización capaces de resolver problemas complejos con gran eficacia.
2. Implementación del algoritmo
El algoritmo de búsqueda cooperativa artificial (ACS) funciona del siguiente modo:
1. Inicialización. Se establecen el tamaño de la población «popSize», el número de variables «N», los límites inferior «XLow» y superior «XHi» de las variables, así como la probabilidad de interacción biológica «Probab». A continuación, se generan las posiciones iniciales de las poblaciones «A» y «B» y se calculan sus valores de aptitud «YA» e «YB».
2. Bucle por iteraciones. En cada iteración se realizan los siguientes pasos:
- Selección. Se determina qué conjunto de agentes de las poblaciones A o B se utilizará como «depredador» en la iteración actual.
- Barajando la "presa". Las posiciones de los agentes en el conjunto seleccionado se mezclan.
- Mutación. Las posiciones de los agentes se actualizan utilizando un factor de escala R generado aleatoriamente. Los «depredadores» mutan utilizando información sobre los vectores de decisión de las «presas».
- Rellenar la matriz binaria M. La matriz binaria M se crea para determinar qué variables se actualizarán en la iteración actual.
- Actualización de las posiciones de los agentes. Las posiciones de los agentes se actualizan teniendo en cuenta los valores de la matriz M. Si el valor en M es 1, se actualiza la variable agente correspondiente.
- Control fronterizo. Si la posición actualizada del agente está fuera de los límites especificados, se ajusta.
- Actualización de la selección. En esta fase, las mejores soluciones se guardan para la siguiente iteración del algoritmo.
- Actualización de la mejor solución global. Si se encuentra una solución mejor, se guarda.
3. Devuelve el resultado. Al final del algoritmo, se devuelve la mejor solución global y su valor de aptitud.
El algoritmo presenta algunos operadores únicos, como el operador de barajado «presa» y el operador de mutación, que implican el uso de la matriz binaria M.
La matriz M es una matriz bidimensional con filas «popSize» (el número de candidatos de la población) y columnas «N» (el número de variables de cada candidato). Cada elemento de la matriz puede ser 0 ó 1. La matriz M se utiliza para determinar qué candidatos se seleccionarán para su posterior renovación en la población. Los valores 0 y 1 de la matriz indican si el candidato correspondiente se seleccionará para la actualización en función de los valores aleatorios de Rand y la probabilidad de interacción Probab.
La matriz M ayuda a regular la selección de candidatos a la renovación en la población. Así, la matriz M desempeña un papel clave en la evolución de la población y la búsqueda de la solución óptima en ACS.
Veamos en detalle cada paso del algoritmo ACS en pseudocódigo:
1. Inicialización:
- Se establecen los siguientes parámetros:
- popSize - tamaño de la población
- N - número de variables
- MaxIter - número máximo de iteraciones
- XLow - límite inferior de las variables
- XHi - límite superior de las variables
- Probab - probabilidad de interacción biológica
- Rand - función que devuelve números distribuidos uniformemente en el rango (0, 1)
- GlobMax se inicializa con el valor negativo DBL_MAX
2. Bucle principal:
- Para cada elemento de la población (I = 1 a popSize):
- Para cada variable (J = 1 a N):
- Se calculan los valores iniciales A(I,J) y B(I,J) en el intervalo [XLow(J), XHi(J)]
- Se calculan los valores iniciales de la función objetivo YA(I) = Fx(A(I,:)) e YB(I) = Fx(B(I,:))
- Comienza el bucle principal por (Iter = 1 a MaxIter) iteraciones
3. Selección:
- Elegimos al azar si A o B se usará como depredador (Predator):
- Si Rand < 0.5, Predator = A, Ypred = YA, Key = 1
- De lo contrario, Predator = B, Ypred = YB, Key = 2
- Elegimos al azar si A o B se va a utilizar como presa (Prey):
- Si Rand < 0.5, Prey = A
- De lo contrario, Prey = B
- Las presas se barajan aleatoriamente
- El parámetro R se calcula:
- Si Rand < 0,5, R = 4 * Rand * (Rand - Rand)
- En caso contrario, R = 1/exp(4 * Rand)
- Se crea la matriz binaria M de popSize x N llena de unos
- Algunos elementos de la matriz M se ponen aleatoriamente a 0 con la probabilidad Probab
- Si Rand < Probab, algunos elementos de la matriz M se ponen aleatoriamente a 0 o 1
- Para cada fila de la matriz M, si la suma de los elementos es N, se selecciona aleatoriamente un elemento y se pone a 0
.
4. Mutación:
- Se calcula el nuevo valor X = Predator + R * (Prey - Predator)
- Para cada elemento de la población (I = 1 a popSize) y cada variable (J = 1 a N):
- Si el elemento correspondiente de la matriz M es superior a 0, entonces X(I,J) = Predator(I,J)
- Si X(I,J) está fuera del intervalo [XLow(J), XHi(J)], entonces X(I,J) se establece en un valor aleatorio dentro de ese intervalo
5. Actualización de la selección:
- Para cada elemento de la población (I = 1 a popSize):
- Si Fx(X(I,:)) < Ypred(i), entonces Predator(I,:) = X(I,:) e Ypred(I) = Fx(X(I,:))
- Si Key = 1, entonces A = Predator y YA = Ypred, de lo contrario B = Predator e YB = Ypred
- Ybest = min(Ypred)
- Ibest = Índice de la fila del depredador correspondiente a Ybest
- Si Ybest > GlobMax, entonces GlobMax = Ybest y GlobMax = Predator(Ibest,:)
6. Devuelve el resultado:
- Devuelve el vector GlobMax y GlobMaxX
Pasemos a la descripción de la implementación del algoritmo ACS. Utilizaremos la estructura más simple «S_D » para describir la población (de las que hay cinco en el algoritmo):
- c [] es un array para almacenar coordenadas (parámetros optimizados de la tarea)
- Init (int coords) - método que cambia el tamaño de la matriz c al tamaño especificado en coords (número de coordenadas) mediante la función ArrayResize
En general, esta estructura se utiliza para crear un objeto que contiene una matriz de números reales. El método Init se utiliza para redimensionar el array.
//—————————————————————————————————————————————————————————————————————————————— struct S_D { void Init (int coords) { ArrayResize (c, coords); } double c []; }; //——————————————————————————————————————————————————————————————————————————————
Para describir la matriz M, cree la estructura S_C, que es diferente de la estructura del tipo de campo S_D:
- c[] - matriz que almacena los símbolos matriciales «0» y «1».
- Init (int coords) - el método cambia el tamaño de la matriz c al tamaño especificado en coords utilizando la función ArrayResize.
//—————————————————————————————————————————————————————————————————————————————— struct S_C { void Init (int coords) { ArrayResize (c, coords); } char c []; }; //——————————————————————————————————————————————————————————————————————————————
El algoritmo se describirá como la clase C_AO_ACS derivada de la clase base C_AO y contendrá los siguientes campos:
- ~C_AO_ACS () { } - destructor de la clase llamado cuando se elimina el objeto de la clase. En este caso, el destructor está vacío.
- C_AO_ACS () - constructor de la clase que inicializa los miembros de datos de la clase, redimensiona la matriz params y asigna valores por defecto a los parámetros del algoritmo.
- SetParams () - el método establece los valores popSize y bioProbab basándose en los valores de la matriz params.
- Init () - método toma varios argumentos y devuelve un valor booleano.
- Moving () y Revision () son métodos que contienen la lógica principal del algoritmo.
- bioProbab - miembro de datos que almacena la probabilidad de una interacción biológica.
- S_D A [], S_D B [], S_D Predator [], S_D Prey [], S_C M [], double YA [], double YB [], double Ypred [], int Key, int phase - datos de clase miembros privados.
- ArrayShuffle () - método privado que baraja los elementos del array.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ACS : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ACS () { } C_AO_ACS () { ao_name = "ACS"; ao_desc = "Artificial Cooperative Search"; ao_link = "https://www.mql5.com/ru/articles/15004"; popSize = 1; //population size bioProbab = 0.9; //biological interaction probability ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "bioProbab"; params [1].val = bioProbab; } void SetParams () { popSize = (int)params [0].val; bioProbab = params [1].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double bioProbab; //biological interaction probability private: //------------------------------------------------------------------- S_D A []; S_D B []; S_D Predator []; S_D Prey []; S_C M []; double YA []; double YB []; double Ypred []; int Key; int phase; void ArrayShuffle (double &arr []); }; //——————————————————————————————————————————————————————————————————————————————
A continuación, presenta el método Init de la clase C_AO_ACS. El método inicializa el objeto de clase:
- Init () - declaración del método. Toma cuatro argumentos: rango de búsqueda mínimo «rangeMinP», rango de búsqueda máximo «rangeMaxP», paso de búsqueda «rangeStepP» y el número de épocas «epochsP», que es 0 por defecto.
- if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; - llama a la función StandardInit que realiza la inicialización estándar de la clase base. Si StandardInit devuelve falso, Init termina inmediatamente y devolvera falso.
- En el bucle for (int i = 0; i < popSize; i++), cada elemento de las matrices A, B, Predator, Prey y M se inicializa mediante el método Init.
- ArrayResize (YA, popSize) y filas similares cambian el tamaño de las matrices YA, YB y Ypred a popSize.
- ArrayInitialize (YA, -DBL_MAX) y filas similares inicializan todos los elementos de las matrices YA, YB y Ypred utilizando el valor -DBL_MAX.
- En el bucle anidado for, cada elemento c de cada objeto en las matrices A y B se inicializa utilizando un valor aleatorio dentro del rango dado.
- phase = 0 establece 'phase' en 0.
El algoritmo original no tiene una división de la lógica en fases. Tuve que añadir fases para implementar el algoritmo en el estilo que he adoptado para todos los algoritmos de población. Esto era necesario porque el ACS utiliza un cálculo previo de la aptitud del agente para las poblaciones А y B. Se ha añadido una división de fases para realizar estas operaciones secuencialmente en los métodos.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ACS::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) //number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (A, popSize); ArrayResize (B, popSize); ArrayResize (Predator, popSize); ArrayResize (Prey, popSize); ArrayResize (M, popSize); for (int i = 0; i < popSize; i++) { A [i].Init (coords); B [i].Init (coords); Predator [i].Init (coords); Prey [i].Init (coords); M [i].Init (coords); } ArrayResize (YA, popSize); ArrayResize (YB, popSize); ArrayResize (Ypred, popSize); ArrayInitialize (YA, -DBL_MAX); ArrayInitialize (YB, -DBL_MAX); ArrayInitialize (Ypred, -DBL_MAX); // Initialization for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { A [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab(); B [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab(); } } phase = 0; return true; } //——————————————————————————————————————————————————————————————————————————————
El método Moving de la clase C_AO_ACS implementa la lógica básica del movimiento de individuos en el algoritmo. Este método realiza varias operaciones, como la copia de matrices, la selección, la permutación, la mutación y el cruce.
- if (phase == 0) - los individuos de la población A se copian en esta fase.
- if (phase == 1) - en esta fase devolvemos la aptitud de los individuos de la población А y copiamos los individuos de la población B.
- if (phase == 2) - en esta fase devolvemos la aptitud de los individuos de la población B y a continuación se ejecuta toda la lógica posterior del algoritmo.
- Selección - el bloque realiza la selección. En función de un número aleatorio, las matrices A o B se copian en la matriz Predator, mientras que los valores correspondientes se copian en la matriz Ypred.
- Permutación de presa - aquí se realiza la permutación de los elementos de la matriz Prey.
- R - se declara una variable, que se inicializa con uno de los dos valores posibles en función del número aleatorio.
- Rellenar matriz binaria M con unos - la matriz binaria M se rellena aquí con unos.
- Operaciones adicionales con la matriz M - el bloque realiza operaciones adicionales con la matriz M, incluyendo el cambio de algunos de sus elementos a 0 o 1, dependiendo del número aleatorio y de la probabilidad bioProbab de interacción biológica.
- Mutación: el bloque realiza una mutación, en la que los elementos de la matriz a cambian en función de los elementos de las matrices Predator y Prey, así como del valor R.
- Cruzamiento: el bloque realiza una operación de cruce, en la que algunos elementos de la matriz a se sustituyen por los elementos de la matriz Predator.
- Control de límites - el bloque realiza un control de límites, en el que los elementos de la matriz a fuera del rango especificado de parámetros optimizados se sustituyen por valores aleatorios dentro del rango.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACS::Moving () { //---------------------------------------------------------------------------- if (phase == 0) { for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c); phase++; return; } //---------------------------------------------------------------------------- if (phase == 1) { for (int i = 0; i < popSize; i++) YA [i] = a [i].f; for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c); phase++; return; } //---------------------------------------------------------------------------- if (phase == 2) { for (int i = 0; i < popSize; i++) YB [i] = a [i].f; phase++; } //---------------------------------------------------------------------------- // Selection if (u.RNDprobab () < 0.5) { for (int i = 0; i < popSize; i++) { ArrayCopy (Predator [i].c, A [i].c); } ArrayCopy (Ypred, YA); Key = 1; } else { for (int i = 0; i < popSize; i++) { ArrayCopy (Predator [i].c, B [i].c); } ArrayCopy (Ypred, YB); Key = 2; } if (u.RNDprobab () < 0.5) { for (int i = 0; i < popSize; i++) { ArrayCopy (Prey [i].c, A [i].c); } } else { for (int i = 0; i < popSize; i++) { ArrayCopy (Prey [i].c, B [i].c); } } // Permutation of Prey for (int i = 0; i < popSize; i++) { ArrayShuffle (Prey [i].c); } double R; if (u.RNDprobab () < 0.5) { R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0); } else R = 1 / MathExp (4 * MathRand () / 32767.0); // Fill binary matrix M with 1s for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { M [i].c [j] = 1; } } // Additional operations with matrix M for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { if (u.RNDprobab () < bioProbab) { M [i].c [j] = 0; } } } for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { if (u.RNDprobab () < bioProbab) { M [i].c [j] = 1; } else { M [i].c [j] = 0; } } } for (int i = 0; i < popSize; i++) { int sum = 0; for (int c = 0; c < coords; c++) sum += M [i].c [c]; if (sum == coords) { int j = MathRand () % coords; M [i].c [j] = 0; } } // Mutation for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]); // Crossover if (M [i].c [j] > 0) { a [i].c [j] = Predator [i].c [j]; } // Boundary control if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j]) { a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab (); } } } for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } } //——————————————————————————————————————————————————————————————————————————————
Método de revisión de la clase C_AO_ACS. El método realiza una serie de operaciones: ordenación y copia inversa de matrices, así como actualización del mejor valor de la solución global.
- if (phase < 3) return - la lógica básica del método no se ejecuta hasta que se completan las tres fases de preparación de las poblaciones para una interacción posterior.
- Actualización de la selección - el bloque actualiza la selección de individuos. Para cada individuo de la matriz a, comprobamos si su valor de aptitud f supera el valor apropiado de la matriz Ypred.
- if (Key == 1) y else - en estos bloques, dependiendo del valor de Key, los elementos de la matriz Predator se copian de la matriz A o B, mientras que los valores correspondientes de Ypred se copian de la matriz YA o YB.
- ArraySort (Ypred); ArrayReverse (Ypred, 0, WHOLE_ARRAY) - la matriz Ypred que contiene los valores de aptitud se ordena y luego se invierte para que los valores estén en orden descendente.
- Ybest = Ypred [0]; int Ibest = ArrayMaximum (Ypred) - aquí Ybest es un valor máximo en Ypred, mientras que Ibest es un índice de este valor máximo.
- if (Ybest > fB) - Si Ybest supera el valor actual de fB, entonces se actualiza fB, mientras que los elementos apropiados de las matrices a y cB se copian de la matriz Predator.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACS::Revision () { if (phase < 3) return; // Selection update for (int i = 0; i < popSize; i++) { double d = a [i].f; if (d > Ypred [i]) { ArrayCopy (Predator [i].c, a [i].c); Ypred [i] = d; } } if (Key == 1) { for (int i = 0; i < popSize; i++) { ArrayCopy (A [i].c, Predator [i].c); } ArrayCopy (YA, Ypred); } else { for (int i = 0; i < popSize; i++) { ArrayCopy (B [i].c, Predator [i].c); } ArrayCopy (YB, Ypred); } ArraySort (Ypred); ArrayReverse (Ypred, 0, WHOLE_ARRAY); double Ybest = Ypred [0]; int Ibest = ArrayMaximum (Ypred); if (Ybest > fB) { fB = Ybest; ArrayCopy (a [Ibest].c, Predator [Ibest].c); ArrayCopy (cB, Predator [Ibest].c); } } //——————————————————————————————————————————————————————————————————————————————
El método ArrayShuffle de la clase C_AO_ACS baraja aleatoriamente los elementos del array.
- for (int i = n - 1; i > 0; i--) - el bucle itera a través de la matriz arr en orden inverso, empezando por el último elemento.
- j = MathRand () % (i + 1) - aquí j es un número aleatorio comprendido entre 0 e i.
- tmp = arr [i]; arr [i] = arr [j]; arr [j] = tmp - estas filas realizan el intercambio de los elementos arr[i] y arr[j].
Como resultado, los elementos de la matriz arr se barajan aleatoriamente.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACS::ArrayShuffle (double &arr []) { int n = ArraySize (arr); for (int i = n - 1; i > 0; i--) { int j = MathRand () % (i + 1); double tmp = arr [i]; arr [i] = arr [j]; arr [j] = tmp; } } //——————————————————————————————————————————————————————————————————————————————
3. Resultados de la prueba
La originalidad del algoritmo queda confirmada por las pruebas realizadas. Este algoritmo es único en su capacidad de lograr excelentes resultados cuando se reduce la población. A medida que aumenta el número de iteraciones, el algoritmo puede tener un 100% de convergencia en funciones de prueba individuales, lo que lo distingue de otros algoritmos, para los cuales cualquier aumento en el número de ejecuciones de funciones de aptitud todavía no brinda la oportunidad de converger. Este rasgo se caracteriza por su resistencia a quedar atrapado en «trampas» locales.
Veamos cómo cambian los resultados del algoritmo dependiendo del tamaño de la población. Normalmente utilizo un promedio de 50 individuos en una población. Sin embargo, durante las pruebas, este algoritmo comienza a mostrar resultados decentes con tamaños de población más bajos.
En el caso de 10 individuos en la población y quedando el número de lanzamientos de la función de aptitud en 10.000, el algoritmo alcanza el resultado de 49,97%.
ACS|Artificial Cooperative Search|10.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.8213829114300768
25 Hilly's; Func runs: 10000; result: 0.5418951009344799
500 Hilly's; Func runs: 10000; result: 0.2811381329747021
=============================
5 Forest's; Func runs: 10000; result: 0.9750514085798038
25 Forest's; Func runs: 10000; result: 0.5078176955906151
500 Forest's; Func runs: 10000; result: 0.20112458337102135
=============================
5 Megacity's; Func runs: 10000; result: 0.736923076923077
25 Megacity's; Func runs: 10000; result: 0.31446153846153846
500 Megacity's; Func runs: 10000; result: 0.11721538461538572
=============================
All score: 4.49701 (49.97%)
En el caso de 3 individuos en la población y quedando el número de lanzamientos de la función de aptitud en 10.000, el algoritmo alcanza el resultado de 55,23%.
ACS|Artificial Cooperative Search|3.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.8275253778390631
25 Hilly's; Func runs: 10000; result: 0.6349216357701294
500 Hilly's; Func runs: 10000; result: 0.29382093872076825
=============================
5 Forest's; Func runs: 10000; result: 0.9998874875962974
25 Forest's; Func runs: 10000; result: 0.6985911632646721
500 Forest's; Func runs: 10000; result: 0.2132502183011688
=============================
5 Megacity's; Func runs: 10000; result: 0.7507692307692307
25 Megacity's; Func runs: 10000; result: 0.4270769230769231
500 Megacity's; Func runs: 10000; result: 0.1252615384615397
=============================
All score: 4.97110 (55.23%)
En el caso de 1 individuo en la población y quedando el número de lanzamientos de la función de aptitud en 10.000, el algoritmo alcanza el resultado de 58,06%.
ACS|Artificial Cooperative Search|1.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.7554725186591347
25 Hilly's; Func runs: 10000; result: 0.7474431551529281
500 Hilly's; Func runs: 10000; result: 0.3040669213089683
=============================
5 Forest's; Func runs: 10000; result: 0.9999999999993218
25 Forest's; Func runs: 10000; result: 0.888607840003743
500 Forest's; Func runs: 10000; result: 0.2241289484506152
=============================
5 Megacity's; Func runs: 10000; result: 0.6907692307692308
25 Megacity's; Func runs: 10000; result: 0.4818461538461539
500 Megacity's; Func runs: 10000; result: 0.1332153846153859
=============================
All score: 5.22555 (58.06%)
Puede preguntarse cómo se produce la interacción en una población con un solo individuo. Como recordará, el algoritmo utiliza cinco poblaciones, y la interacción se produce entre los individuos de estas poblaciones. A pesar del número tan reducido de individuos, el algoritmo preserva la diversidad en las poblaciones y no tiene efecto «cuello de botella».
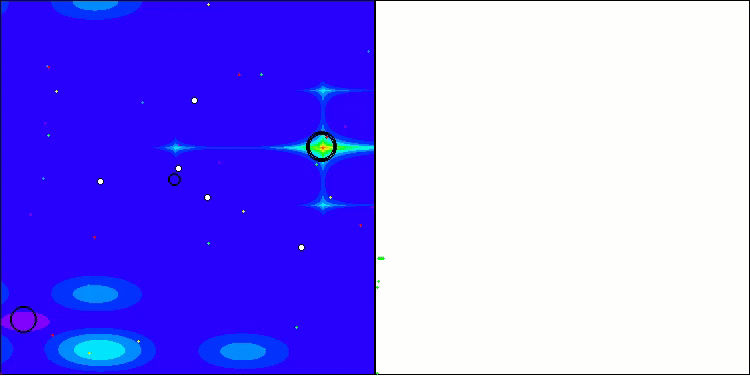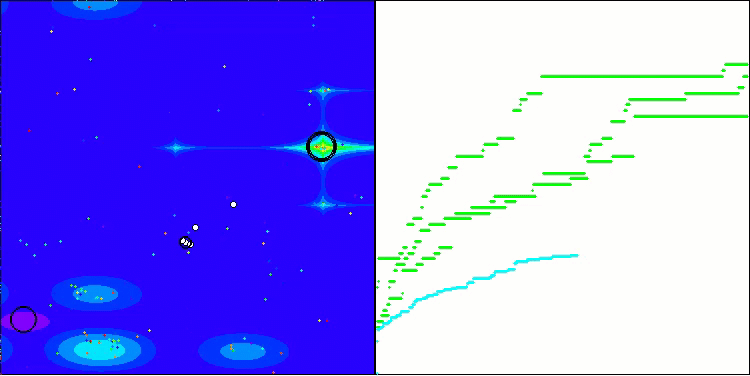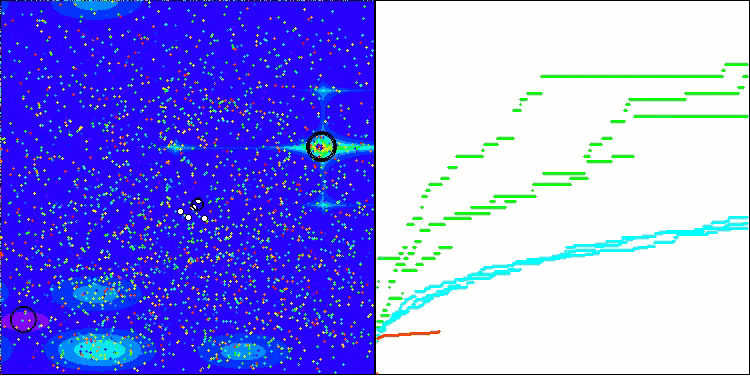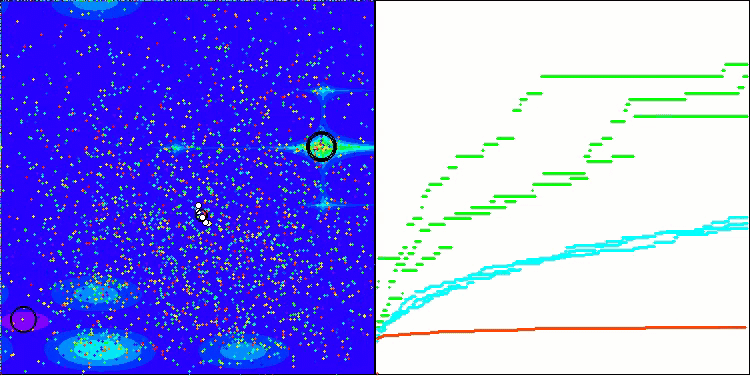
En la visualización, podemos ver la ausencia de cualquier efecto de agrupamiento y el hecho de que los agentes se comportan aparentemente de forma caótica. Los agentes entran en zonas del espacio de búsqueda incluso donde no hay direcciones prometedoras. Este rasgo es claramente visible en los rasgos Forest y Megacity, que presentan amplias zonas llanas con escasa variación del terreno.
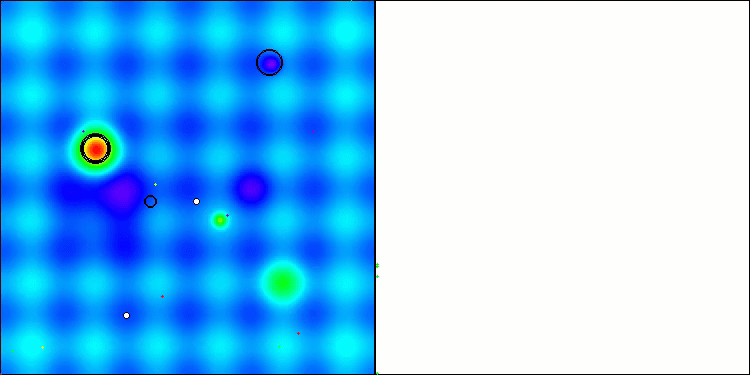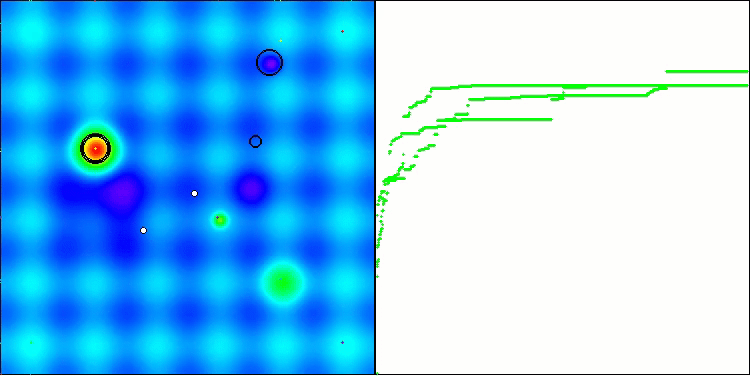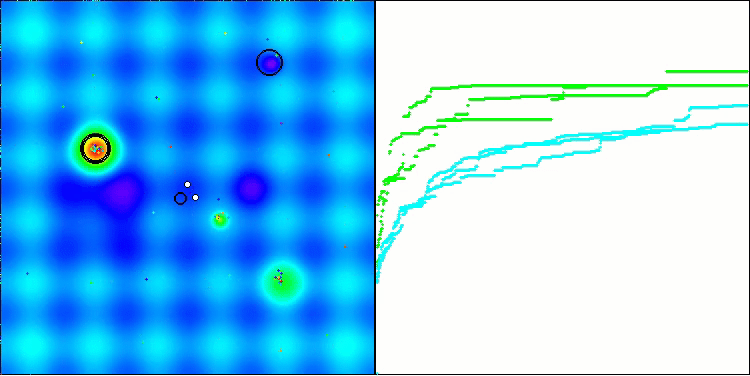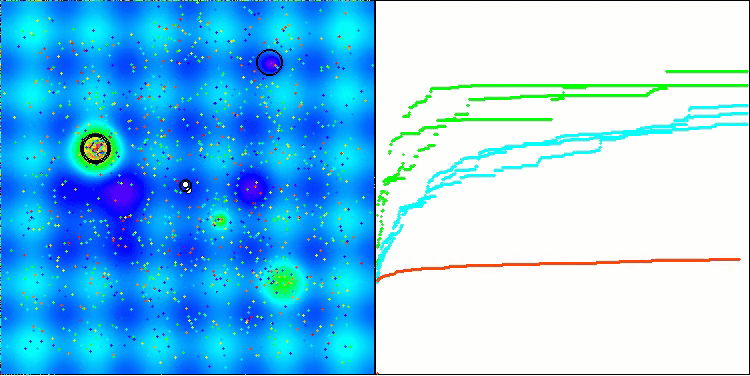
ACS en la función de prueba Hilly (colina).
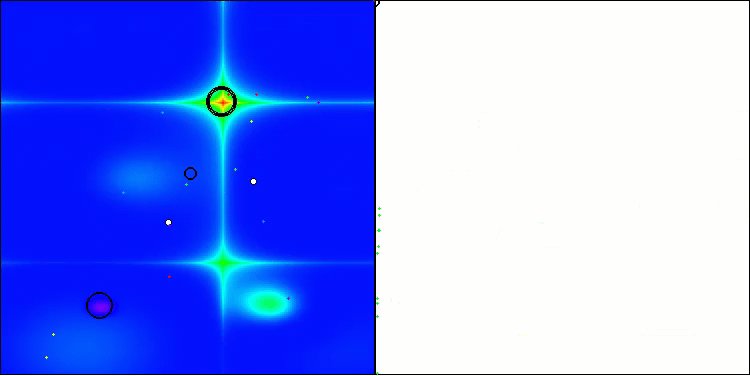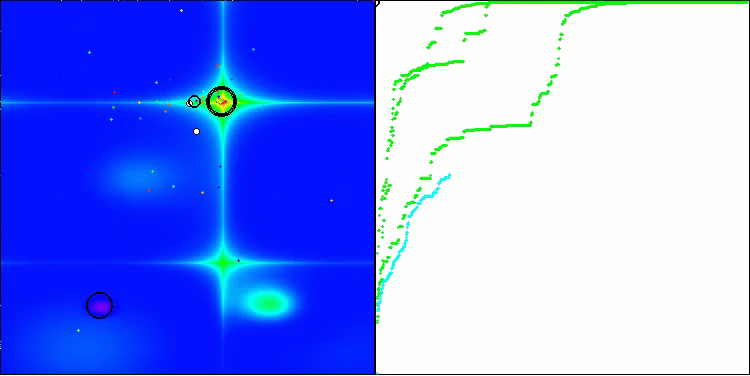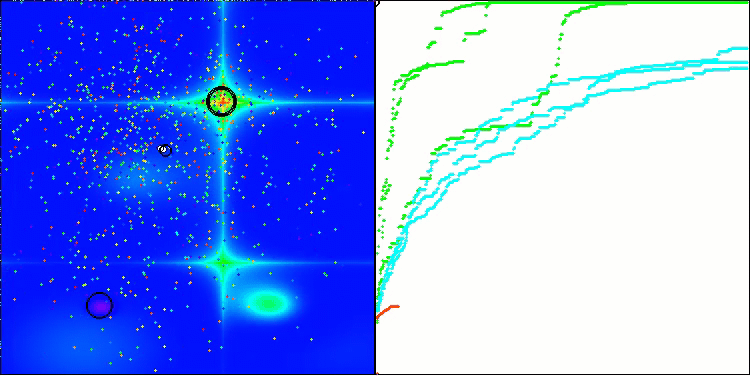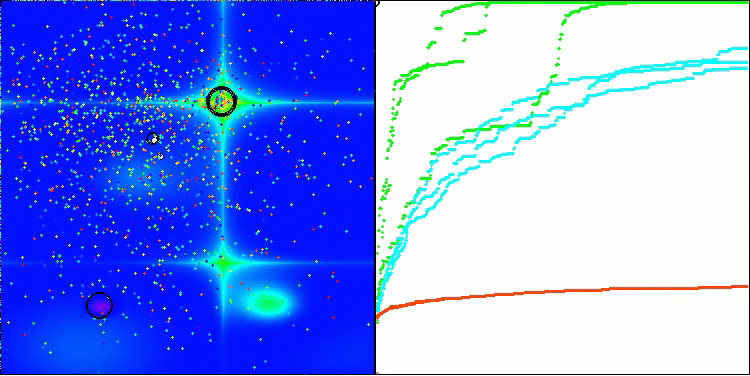
ACS en la función de prueba Forest (bosque).
ACS sobre la función de prueba Megacity (megaciudad).
Según los resultados de la prueba, el algoritmo obtuvo el octavo puesto. ACS destacó especialmente en las funciones Forest y Megacity.
# | AO | Descripción | Hilly | Hilly final | Forest | Forest final | Megacity (discreto) | Megacity final | Resultado final | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | BGA | algoritmo genético binario | 0.99989 | 0.99518 | 0.42835 | 2.42341 | 0.96153 | 0.96181 | 0.32027 | 2.24360 | 0.91385 | 0.95908 | 0.24220 | 2.11512 | 6.782 | 75.36 |
| 2 | CLA | algoritmo de bloqueo del código | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | (P+O)ES | (P+O) estrategias de evolución | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 4 | CTA | algoritmo de cola de cometa | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 5 | SDSm | búsqueda por difusión estocástica M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 6 | ESG | evolución de los grupos sociales | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 7 | SIA | recocido isotrópico simulado | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 8 | ACS | búsqueda cooperativa artificial | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 9 | TSEA | algoritmo de evolución del caparazón de tortuga | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 10 | DE | evolución diferencial | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 11 | BSA | algoritmo del enjambre de aves | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 12 | HS | búsqueda de armonía | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 13 | SSG | siembra y crecimiento de plantones | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 14 | (PO)ES | (PO) estrategias de evolución | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 15 | BSO | tormenta de ideas optimización | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 16 | WOAm | algoritmo de optimización Wale M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 17 | ACOm | optimización de colonias de hormigas M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 18 | BFO-GA | optimización de la alimentación bacteriana - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 19 | MEC | computación mental evolutiva | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 20 | IWO | optimización de malezas invasoras | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 21 | Micro-AIS | sistema inmunitario microartificial | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 22 | COAm | algoritmo de optimización del cuco M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 23 | SDOm | optimización de la dinámica espiral M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 24 | NMm | método de Nelder-Mead M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 25 | FAm | algoritmo Firefly M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 26 | GSA | algoritmo de búsqueda gravitacional | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 27 | BFO | optimización de la alimentación bacteriana | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 28 | ABC | colonia artificial de abejas | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 29 | BA | algoritmo de murciélago | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 30 | SA | recocido simulado | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 31 | IWDm | gotas de agua inteligentes M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 32 | PSO | optimización mediante enjambre de partículas | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 33 | Boids | algoritmo de boids | 0.43340 | 0.30581 | 0.25425 | 0.99346 | 0.35718 | 0.20160 | 0.15708 | 0.71586 | 0.27846 | 0.14277 | 0.09834 | 0.51957 | 2.229 | 24.77 |
| 34 | MA | algoritmo del mono | 0.59107 | 0.42681 | 0.31816 | 1.33604 | 0.31138 | 0.14069 | 0.06612 | 0.51819 | 0.22833 | 0.08567 | 0.02790 | 0.34190 | 2.196 | 24.40 |
| 35 | SFL | salto de rana reorganizado | 0.53925 | 0.35816 | 0.29809 | 1.19551 | 0.37141 | 0.11427 | 0.04051 | 0.52618 | 0.27167 | 0.08667 | 0.02402 | 0.38235 | 2.104 | 23.38 |
| 36 | FSS | búsqueda de bancos de peces | 0.55669 | 0.39992 | 0.31172 | 1.26833 | 0.31009 | 0.11889 | 0.04569 | 0.47467 | 0.21167 | 0.07633 | 0.02488 | 0.31288 | 2.056 | 22.84 |
| 37 | RND | aleatorio | 0.52033 | 0.36068 | 0.30133 | 1.18234 | 0.31335 | 0.11787 | 0.04354 | 0.47476 | 0.25333 | 0.07933 | 0.02382 | 0.35648 | 2.014 | 22.37 |
| 38 | GWO | optimizador de lobo gris | 0.59169 | 0.36561 | 0.29595 | 1.25326 | 0.24499 | 0.09047 | 0.03612 | 0.37158 | 0.27667 | 0.08567 | 0.02170 | 0.38403 | 2.009 | 22.32 |
| 39 | CSS | búsqueda de sistemas cargados | 0.44252 | 0.35454 | 0.35201 | 1.14907 | 0.24140 | 0.11345 | 0.06814 | 0.42299 | 0.18333 | 0.06300 | 0.02322 | 0.26955 | 1.842 | 20.46 |
| 40 | EM | algoritmo similar al electromagnetismo | 0.46250 | 0.34594 | 0.32285 | 1.13129 | 0.21245 | 0.09783 | 0.10057 | 0.41085 | 0.15667 | 0.06033 | 0.02712 | 0.24412 | 1.786 | 19.85 |
Resumen
El algoritmo de búsqueda cooperativa artificial (ACS) ha demostrado ser un enfoque interesante para la optimización, que se manifiesta en el uso de varias poblaciones de agentes que interactúan entre sí, proporcionando diversidad y resistencia a quedarse atascado en óptimos locales, en el uso de operadores especiales, como el barajado de la «presa» y la mutación utilizando una matriz binaria. Esto último le dio al algoritmo originalidad y la capacidad de lograr resultados elevados con un tamaño de población muy pequeño (hasta 1 individuo en cada una de las cinco poblaciones). El enfoque original y la capacidad de trabajar con poblaciones pequeñas (lo que acentúa la resistencia a la degeneración de las colonias) hacen de ACS un algoritmo de optimización realmente prometedor.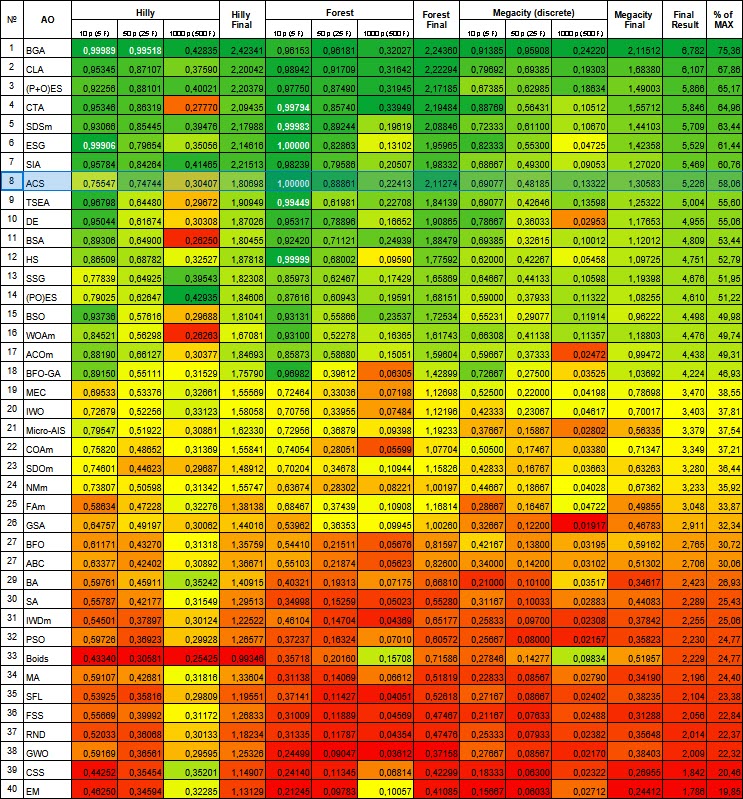 
Figura 1. Gradación por colores de los algoritmos según las pruebas pertinentes. Los resultados superiores o iguales a 0,99 se resaltan en blanco.
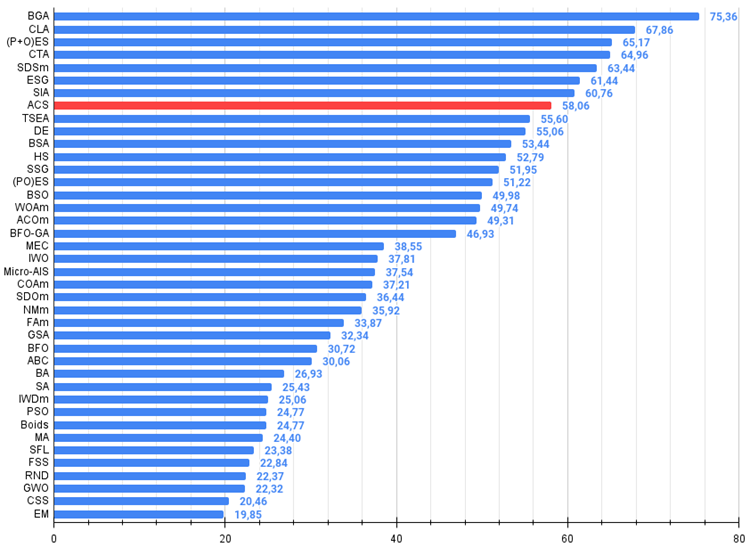
Figura 2. El histograma de los resultados de las pruebas de algoritmos (en una escala de 0 a 100, cuanto más, mejor,
donde 100 es el máximo resultado teórico posible, el archivo contiene un script para calcular la tabla de clasificación)
Ventajas e inconvenientes de ACS:
Ventajas:
- Número reducido de parámetros externos (sólo uno).
- Buena convergencia en varios tipos de funciones.
Desventajas:
- Dispersión de resultados en funciones de baja dimensión.
El artículo va acompañado de un archivo con las versiones actuales de los códigos de los algoritmos. El autor del artículo no se responsabiliza de la exactitud absoluta en la descripción de los algoritmos canónicos. Se han introducido cambios en muchos de ellos para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15004
Redes neuronales: así de sencillo (Parte 93): Predicción adaptativa en los ámbitos de la frecuencia y el tiempo (Parte final)
Redes neuronales: así de sencillo (Parte 92): Predicción adaptativa en los ámbitos de la frecuencia y el tiempo
Desarrollo de un sistema de repetición (Parte 60): Presionando play en el servicio (I)
Desarrollo de un sistema de repetición (Parte 59): Un nuevo futuro
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso