Algoritmo de optimización basado en ecosistemas artificiales — Artificial Ecosystem-based Optimization (AEO)

Contenido

1. Introducción
2. Implementación del algoritmo
3. Resultados de las pruebas

Introducción

En el mundo de la optimización y la inteligencia artificial se buscan constantemente nuevos métodos más eficaces para resolver problemas complejos. Uno de estos enfoques innovadores, el algoritmo de optimización basada en ecosistemas artificiales (OEA), fue desarrollado y presentado en 2019. Este método se inspira en los ecosistemas naturales, imitando las complejas interacciones y procesos que ocurren en los entornos naturales.

El algoritmo AEO se basa en varios principios clave observados en la naturaleza. Al igual que los ecosistemas tienen muchas especies, cada una adaptada a su nicho ecológico, el AEO utiliza una población de soluciones diversas. En este contexto, cada solución puede considerarse una "especie" distinta con características y capacidades de adaptación únicas.

En la naturaleza, la energía se transfiere de un organismo a otro a través de la cadena alimentaria. En el AEO esto se modela a través de la interacción de distintos tipos de "agentes", desde los "herbívoros" hasta los "omnívoros". Aquí la información, de forma similar a la energía, se transfiere entre las soluciones, lo cual contribuye a la calidad general de la población. Los ecosistemas se caracterizan tanto por la competición por los recursos como por las relaciones simbióticas. El algoritmo AEO refleja estos procesos mediante estrategias de actualización de decisiones en las que los agentes pueden "competir" por las mejores posiciones o "cooperar" intercambiando información.

Los ecosistemas naturales están sujetos a cambios cíclicos, lo cual también se refleja en el OEA. El proceso de optimización iterativo consiste en alternar fases de consumo y descomposición, lo cual permite al algoritmo adaptarse a la dinámica del problema. En la naturaleza, sucesos aleatorios como las mutaciones y las catástrofes naturales coexisten con procesos deterministas como la selección natural. El AEO utiliza tanto elementos estocásticos (por ejemplo, la distribución de Levy) como reglas deterministas para actualizar las soluciones, logrando un equilibrio entre la exploración de nuevas áreas y la explotación de las ya encontradas.

Para entender mejor cómo se reflejan los procesos naturales en el algoritmo AEO, veremos algunos ejemplos concretos. En la sabana africana, la energía pasa de la hierba a las cebras (herbívoros), luego a los leones (carnívoros) y finalmente a las hienas (carroñeras). En el AEO, la información sobre las mejores soluciones pasa de la "hierba" (peor solución) a los "herbívoros" (soluciones medias) y los "depredadores" (mejores soluciones), mejorando así la calidad global de la población.

Cuando los organismos mueren, se descomponen, devolviendo nutrientes al ecosistema. Por ejemplo, hojas que caen en el bosque se descomponen, enriqueciendo el suelo y nutriendo nuevas plantas. En el AEO, la fase de descomposición del algoritmo imita este proceso. A la fase de consumo (actualización de las decisiones) le sigue la fase de descomposición, en la que la información de las decisiones actuales se "descompone" y se propaga por todo el espacio de búsqueda, lo cual permite al algoritmo explorar nuevas áreas y evitar quedarse atascado en óptimos locales. En el algoritmo, esto se realiza aplicando una distribución gaussiana a las soluciones actuales en relación con la mejor solución (la mejor solución global actúa como descomponedor), lo que puede verse como una "descomposición" y "redistribución" de la información en el espacio de búsqueda.

Así, el algoritmo AEO supone una elegante síntesis de principios naturales y optimización matemática. No solo ofrece un método eficaz para resolver problemas complejos, sino que también abre una nueva perspectiva sobre la relación entre los procesos naturales y la inteligencia artificial. A continuación, detallaremos la estructura y los mecanismos de este algoritmo para comprender mejor su potencial y su aplicación.

Implementación del algoritmo

Para entender mejor la idea de los autores del algoritmo AEO, volveremos a la ilustración de la figura 1, que muestra la jerarquía de organismos en un ecosistema artificial. El ecosistema completo está formado por organismos numerados convencionalmente del 1 al Xn. En el número 1 tenemos la "hierba" con la máxima energía (valor mínimo de la función de aptitud), mientras que Xn representa al saprofito que realiza la función de descomposición (energía mínima, valor máximo de la función de aptitud).

En la figura, las flechas indican las direcciones de la nutrición: la hierba (número 1) solo puede usar los productos de los saprofitos, los herbívoros (número 2) comen hierba, y los organismos numerados 2, 4 y 5 pueden ser herbívoros (solo comen hierba), carnívoros (los organismos solo pueden comer criaturas cuya energía sea inferior a la suya) y omnívoros (pueden comer tanto hierba como organismos con mayor energía). La parte superior del ecosistema está ocupada por los saprófitos, que descomponen todos los organismos al final de su ciclo vital.

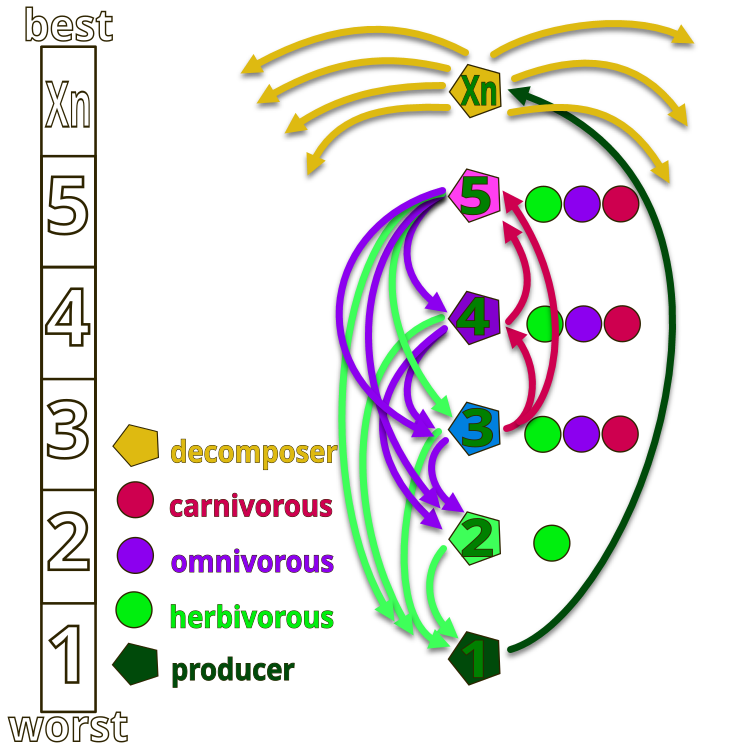
Figura 1. Jerarquía de organismos en el ecosistema artificial del algoritmo AEO

La idea principal del algoritmo consiste en modelar las interacciones entre los componentes del ecosistema para resolver problemas de optimización. El algoritmo se basa en tres principios clave observados en la naturaleza:

1. Producción: en la naturaleza, los productores, como las plantas, transforman la energía solar en compuestos orgánicos.
2. Consumo: los consumidores (herbívoros, carnívoros, omnívoros) usan la energía producida por otros, en particular por las plantas.
3. Descomposición: los saprofitos descomponen la materia orgánica compleja en simple, lo que se modela en el algoritmo como descomposición por decisión.

Principios del algoritmo:

1. Inicialización: se crea una población inicial de soluciones que representan el ecosistema.
2. Producción: en cada iteración, la peor solución se actualiza considerando la mejor y un factor aleatorio.
3. Consumo: las soluciones restantes se actualizan usando las tres estrategias:

• Herbívoros: se actualizan usando como base el productor.
• Depredadores: se actualizan según una mejor solución seleccionada al azar.
• Omnívoros: se actualizan según el criterio del productor y el azar.

4. Descomposición: todas las soluciones pasan por un proceso de "descomposición" que mejora la búsqueda global.
5. Selección: solo se conservan las soluciones mejoradas, lo cual garantiza una mejora gradual de la población.

Así, el algoritmo se basa en el mecanismo de transferencia de energía entre organismos vivos para ayudar a mantener la estabilidad de las especies usando tres operadores: producción, consumo y descomposición.

1. Producción, el peor individuo de la población "X1" se actualiza con respecto al mejor "Xn" con la adición de una coordenada generada aleatoriamente "Xrand" dentro de un rango dado, creando un nuevo individuo mediante el operador de producción. Representación matemática: X1 (t + 1) = (1 - a) * Xn (t) + a * Xrand (t), donde a = (1 - t / T) * r1 (t - época actual, T - épocas totales), r1 - número aleatorio [0; 1]. En este caso, el componente "r1" podrá omitirse, puesto que ya estamos utilizando una coordenada aleatoria en la fórmula.

2. Consumo: un consumidor elegido al azar puede "comerse" al productor para obtener energía. El factor de consumo C se define como: C = 1/2 * (v1 / |v2|), donde v1 y v2 son números aleatorios distribuidos uniformemente en el intervalo [0; 1].

• Herbívoros: Xi (t + 1) = Xi (t) + C * (Xi (t) - X1 (t)).
• Depredadores: Xi (t + 1) = Xi (t) + C * (Xi (t) - Xj (t)).
• Omnívoros: Xi (t + 1) = Xi (t) + C * (r2 * Xi (t) + (1 - r2) * Xj (t)).

3. Descomposición: un saprofito descompone los restos de los individuos muertos, proporcionando nutrientes a los productores. La actualización de la posición de los individuos tras el trabajo saprofito se describe como:

Xi (t + 1) = Xn (t) + D * (e * Xn (t) - h * Xi (t)), donde D = 3u, u ~ N (0, 1), e = r3 * rand (i), h = 2 * r3 - 1 (r3, un número aleatorio en el intervalo [0; 1]).

Así, al principio se genera una población aleatoria y, en cada iteración, se actualiza la posición del primer individuo usando la ecuación (1). Las posiciones de los demás individuos se actualizan seleccionando entre las ecuaciones de (2) con igual probabilidad. En la etapa de descomposición, cada individuo actualiza su posición usando la ecuación p.3. Este proceso continúa hasta que se alcance un criterio de finalización satisfactorio. El último paso retornará el mejor individuo encontrado hasta el momento.

Ahora podemos componer el pseudocódigo del algoritmo AEO:

Algoritmo AEO (Artificial Ecosystem-based Optimization)

Inicialización:
    Establecemos el tamaño de la población (popSize)
    Establecemos el número de épocas (epochs)
    Establecemos el parámetro de distribución de Levy (levisPower)
    Inicializamos la población con soluciones aleatorias dentro de un rango determinado
    Evaluamos la función de aptitud para cada solución
    Encontramos la mejor solución global cB

Para cada época desde 1 hasta epochs:
    // Fase de consumo
    Para cada agente i de la población
        Si i == 0:
            Aplicamos una distribución gaussiana a la solución actual
        En caso contrario, si i == popSize - 1:
            Aplicamos el comportamiento de la hierba (GrassBehavior)
        De lo contrario:
            Seleccionamos aleatoriamente los comportamientos:
                - Comportamiento del herbívoro (HerbivoreBehavior).
                - Comportamiento del carnívoro (CarnivoreBehavior)
                - Comportamiento del omnívoro (OmnivoreBehavior)
    
    // Fase de descomposición
    Para cada agente i de la población
        Para cada coordenada c:
            Elegimos un agente aleatorio j
            Calculamos la distancia D entre cB [c] y a [j].c [c]
            Actualizamos a [i].c [c] utilizando una distribución gaussiana

    // Revisión
    Estimamos la función de aptitud de cada agente
    Actualizamos la mejor solución personalizada para cada agente
    Actualizamos la mejor solución global cB
    Clasificamos la población según el valor de la función de aptitud

Retornamos la mejor solución encontrada cB

Subprocedimientos:

GrassBehaviour (agente):
    α = (1 - época_actual / número_total_de_épocas)
    Para cada coordenada c:
        Xr = valor aleatorio en el intervalo [min [c], max [c]]
        Xn = cB [c]
        X1 = Xn + α * (Xn - Xr)
        agente.c [c] = X1 (considerando las restricciones)

HerbivoreBehavior (agente, índice_coordenadas):
    Xi = agente.cB [índice_coordenadas]
    X1 = peor solución de la población para una coordenada dada
    C = número aleatorio de la distribución de Levy (levisPower)
    Xi = Xi + C * (Xi - X1)
    agente.c [índice_coordenadas] = Xi (considerando las restricciones)

CarnivoreBehavior (agente, índice_del_agente, índice_coordenadas):
    Xi = agente.cB [coordenada]
    j = índice aleatorio < índice_del_agente
    Xj = a [j].cB [índice_coordenadas]
    C = número aleatorio de la distribución de Levy (levisPower)
    Xi = Xi + C * (Xj - Xi)
    agente.c [índice_coordenadas] = Xi (considerando las restricciones)

OmnivoreBehavior (agente, índice_del_agente, índice_coordenadas):
    Xi = agente.cB [coordenada]
    X1 = peor solución de la población para una coordenada dada
    j = índice aleatorio > índice_del_agente
    Xj = a [j].cB [índice_coordenadas]
    C = número aleatorio de la distribución de Levy (levisPower)
    r = número aleatorio entre 0 y 1
    Xi = Xi + C * r * (Xi - X1) + (1 - r) * (Xi - Xj)
    agente.c [índice_coordenadas] = Xi (considerando las restricciones)

Tras describir y analizar el algoritmo con detalle, pasaremos a escribir el código.

El algoritmo usa una distribución de Levy para generar saltos extremadamente distantes pero dispersos en el espacio de búsqueda. Ya hemos aplicado anteriormente esta distribución de números aleatorios, por ejemplo, en el algoritmo de «Búsqueda de cuco», pero no entraremos en los detalles de sus características. La cuestión es que la generación correcta de la distribución de Levy implica el uso de cuatro números aleatorios distribuidos uniformemente, lo cual resulta costoso en sí mismo. Además, la distribución de Levy tiene una cola infinitamente larga (es asimétrica, con una sola cola), lo cual dificulta su uso práctico en algoritmos de optimización, especialmente en presencia de condiciones límite. También debemos comprobar las condiciones límite durante la generación, como la comprobación de 0 antes de calcular el logaritmo natural, y también evitar la división por 0.

Aquí está el código para generar números aleatorios con distribución Levy, sin las comprobaciones anteriores y sin la explicación de la lógica del código:

double LevyFlight()
{
    const double epsilon = 1e-10; // Small value to avoid division by zero
    const double maxValue = 1e10; // Maximum allowed value

    double log1 = MathMax (RNDprobab(), epsilon);
    double log2 = MathMax (RNDprobab(), epsilon);

    double cos1 = MathCos (2 * M_PI * RNDprobab());
    double cos2 = MathCos (2 * M_PI * RNDprobab());

    double U = MathSqrt (-2.0 * MathLog (log1)) * cos1;
    double v = MathSqrt (-2.0 * MathLog (log2)) * cos2;

    double l = 0.5 * MathAbs(U) / MathMax(MathAbs(v), epsilon);

    return l;
}

Para evitar las desventajas de la generación de números con la distribución Levy, escribiremos nuestra propia función "LevyFlightDistribution" con una distribución cercana y la colocaremos en nuestro conjunto estándar de funciones "C_AO_Utilities" para su uso en los algoritmos de optimización. Vamos a desglosarla:

1. Parámetro "levisPower" - grado que determina la forma de la distribución. Cuanto mayor sea el valor "levisPower", más "dispersa" será la distribución.
2. Cálculo del valor mínimo - calcula el valor mínimo que se utilizará para el escalado. Depende de "levisPower" y se calculará como 20^levisPower.
3. Generación de un número aleatorio "r" usando la función "RNDfromCI" en el rango de 1 a 20.
4. Aplicación de la potencia - el número generado "r" se eleva al grado "-levisPower", lo que cambiará su distribución.
5. Escala del resultado - el valor obtenido "r" se escala al intervalo [0, 1]. Para ello, se resta el valor mínimo y se divide por la diferencia entre 1 y el valor mínimo. Así, el resultado siempre estará dentro de [0, 1].
6. Retorno del resultado - la función retorna el valor generado "r" que ahora tiene una distribución cercana a la distribución de Levy, desplazada a 0.

Como vemos, la función genera números aleatorios estrictamente en el rango [0, 1], lo cual resulta muy cómodo en la aplicación práctica; este rango siempre se puede ampliar a cualquier valor aplicando el coeficiente adecuado. Esta función es mucho más rápida y ofrece una distribución muy cercana a la deseada (lado derecho de la distribución relativo al máximo).

//------------------------------------------------------------------------------
//A distribution function close to the Levy Flight distribution.
//The function generates numbers in the range [0.0;1.0], with the distribution shifted to 0.0.
double C_AO_Utilities :: LevyFlightDistribution (double levisPower)
{
  double min = pow (20, -levisPower); //calculate the minimum possible value
  double r = RNDfromCI (1.0, 20);     //generating a number in the range [1; 20]

  r = pow (r, -levisPower);           //we raise the number r to a power
  r = (r - min) / (1 - min);          //we scale the resulting number to [0; 1]

  return r;
}

Vamos a describir ahora el código básico del algoritmo. La clase "C_AO_AEO" deriva de la clase "C_AO" e implementa el algoritmo. Veamos con detalle su estructura, miembros y métodos.

Constructor:

• Establece los valores por defecto para el tamaño de la población y el grado de Levy.
• Crea un array de parámetros "params" y lo inicializa con valores.

Métodos:

• Establece los parámetros "popSize" y "levisPower" del array "params".
• Init () - inicializa el algoritmo con los rangos de búsqueda y el número de épocas indicados. El método retorna "bool", lo cual implica que es posible comprobar si la inicialización se ha realizado correctamente.
• Moving () - procesa el movimiento de los agentes en la época actual actualizando sus coordenadas.
• Revisión () - actualiza la información sobre los agentes y sus mejores soluciones.

Miembros privados y variables:

• levisPower - parámetro utilizado en la distribución Levy.
• epochs - número total de épocas.
• epochNow - época actual.
• consModel - estadio (consumo o descomposición).

S_AO_Agent aT [] - array temporal de agentes usados para clasificar la población.

Métodos privados:

• GrassBehavior () - procesa el comportamiento del agente "hierba".
• HerbivoreBehavior () - procesa el comportamiento del agente herbívoro que "come" hierba (el peor agente).
• CarnivoreBehavior () - procesa el comportamiento de un agente carnívoro que "come" agentes con un valor más alto de la función de aptitud.
• OmnivoreBehavior () - procesa el comportamiento de un agente omnívoro que combina el comportamiento de un herbívoro y que se come a cualquiera con una aptitud menor.

La clase "C_AO_AEO" ofrece la implementación de un algoritmo de optimización basado en un ecosistema artificial, utilizando diferentes tipos de agentes y sus interacciones para encontrar soluciones óptimas. Cada método es responsable de determinados aspectos del algoritmo, como la inicialización, el desplazamiento de los agentes y las actualizaciones de estado.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AEO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AEO () { }
  C_AO_AEO ()
  {
    ao_name = "AEOm";
    ao_desc = "Artificial Ecosystem-based Optimization Algorithm";
    ao_link = "https://www.mql5.com/es/articles/16058";


    popSize    = 50;       // population size
    levisPower = 2;

    ArrayResize (params, 2);

    params [0].name = "popSize";    params [0].val = popSize;
    params [1].name = "levisPower"; params [1].val = levisPower;
  }

  void SetParams ()
  {
    popSize    = (int)params [0].val;
    levisPower = params      [1].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum search range
             const double &rangeMaxP  [],  // maximum search range
             const double &rangeStepP [],  // step search
             const int     epochsP = 0);   // number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double levisPower;


  private: //-------------------------------------------------------------------
  int  epochs;
  int  epochNow;
  int  consModel; // consumption model;
  S_AO_Agent aT [];

  void GrassBehavior     (S_AO_Agent &animal);
  void HerbivoreBehavior (S_AO_Agent &animal, int indCoord);
  void CarnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord);
  void OmnivoreBehavior  (S_AO_Agent &animal, int indAnimal, int indCoord);
};
//——————————————————————————————————————————————————————————————————————————————

Vamos a analizar con detalle el código del método "Init" de la clase "C_AO_AEO". El método "Init" retorna un valor de tipo "bool" que permite determinar el éxito de la inicialización. Comprobación de inicialización estándar: en este bloque se llama al método "StandardInit", que efectúa la inicialización básica de los parámetros transmitidos al método. Si "StandardInit" retorna "false", significará que la inicialización ha fallado y el método "Init" también retornará "false".

Ajuste de variables:

• epochs - establece el número total de épocas obtenido a partir del parámetro "epochsP".
• epochNow - inicializa la época actual con un valor igual a 0, indicando que el algoritmo acaba de empezar.
• consModel - establece el valor del modelo en 0, para que en el futuro pueda pasar de una etapa a la siguiente alternativamente.
  

Cambio del tamaño del array de agentes temporales "aT" por el valor "popSize".

Resultado de retorno: si todas las operaciones anteriores se han realizado correctamente, el método retornará "true", lo cual indicará que la inicialización se ha realizado correctamente.

El método "Init" de la clase "C_AO_AEO" se encarga de la configuración inicial del algoritmo. Comprueba los parámetros estándar, establece los valores para las épocas y la etapa inicial, y prepara un array de agentes para su funcionamiento. Si todos los pasos se completan con éxito, el método retornará "true", indicando que el algoritmo está listo para su ejecución.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AEO::Init (const double &rangeMinP [],
                     const double &rangeMaxP [],
                     const double &rangeStepP [],
                     const int epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs    = epochsP;
  epochNow  = 0;
  consModel = 0;
  ArrayResize (aT, popSize);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Vamos a analizar el código del método "Moving" de la clase "C_AO_AEO". Estructura general del método:  "Moving" se encarga de actualizar el estado de la población de agentes (individuos) según la época actual y del patrón de consumo. Se divide en varios bloques lógicos:

1. Aumento de época: "epochNow++" incrementa el contador de época actual.

2. Inicialización inicial:

• Si "revision" es "false", se producirá la inicialización de las coordenadas de los agentes de la población. Las coordenadas se eligen aleatoriamente a partir de un intervalo dado y luego se redondean al valor más próximo que corresponda al paso.
• Después de ello, "revision" se establece entonces en "true" y el método completa su ejecución.

3. Modelo de consumo:

• Si "consModel" es "0", las coordenadas de los agentes se actualizarán según su comportamiento. 
• Para el primer agente (índice 0), se usan distribuciones gaussianas para inicializar las coordenadas.
• Para el resto de agentes, el comportamiento depende de su índice: el último agente (índice "popSize - 1") llama a la función "GrassBehavior". Para el penúltimo agente y los siguientes (índices "popSize - 2" e inferiores), el comportamiento se determina de forma aleatoria: herbívoro, carnívoro u omnívoro.

4. Descomposición: si "consModel" no es igual a "0", se producirá la descomposición donde para cada agente se actualizarán sus coordenadas usando como base valores aleatorios y la distribución gaussiana. Para cada coordenada, se selecciona un índice aleatorio de otro agente y se calculan nuevas coordenadas a partir de este valor, considerando los límites mínimo y máximo.

El método "Moving" implementa la lógica vinculada al cambio de coordenadas de los agentes según su comportamiento y la época actual. Incluye tanto la inicialización inicial como la actualización del estado de los agentes para reflejar su patrón de consumo.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEO::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  // Consumption ---------------------------------------------------------------
  if (consModel == 0)
  {
    double r = 0.0;

    for (int i = 0; i < popSize; i++)
    {
      if (i == 0)
      {
        for (int c = 0; c < coords; c++)
        {
          a [i].c [c] = u.GaussDistribution (a [i].c [c], rangeMin [c], rangeMax [c], 8);
          a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }

        continue;
      }

      if (i == popSize - 1) GrassBehavior (a [i]);
      else
      {
        if (i >= popSize - 2)
        {
          for (int c = 0; c < coords; c++)
          {
            r = u.RNDprobab ();

            if (r < 0.333) HerbivoreBehavior (a [i], c);
            else
            {
              if (r < 0.667)
              {
                CarnivoreBehavior (a [i], i, c);
              }
              else
              {
                OmnivoreBehavior (a [i], i, c);
              }
            }
          }
        }
        else
        {
          for (int c = 0; c < coords; c++)
          {
            r = u.RNDprobab ();

            if (r < 0.5) CarnivoreBehavior (a [i], i, c);
            else         OmnivoreBehavior  (a [i], i, c);
          }
        }
      }
    }

    consModel++;
    return;
  }

  // Decomposition -------------------------------------------------------------
  int    j   = 0;
  double D   = 0.0;
  double min = 0.0;
  double max = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      j = u.RNDminusOne (popSize);
      D = 3.0 * (cB [c] - a [j].c [c]); // * u.RNDprobab ();
      min = cB [c] - D;
      max = cB [c] + D;

      if (min < rangeMin [c]) min = u.RNDfromCI (rangeMin [c], cB [c]);
      if (max > rangeMax [c]) min = u.RNDfromCI (cB [c], rangeMax [c]);

      a [i].c [c] = u.GaussDistribution (cB [c], min, max, 1);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  consModel = 0;
}
//——————————————————————————————————————————————————————————————————————————————

El método "Revision" de la clase "C_AO_AEO" se encarga de actualizar la información sobre los mejores agentes de la población. Implementa una lógica que rastrea y guarda las mejores soluciones encontradas durante la ejecución del algoritmo.  Estructura del método:

1. Búsqueda del mejor agente:

• Iteramos todos los agentes de la población.
• Comparamos su aptitud (valor "f") con la mejor aptitud actual "fB".
• Si se encuentra un agente con mejor aptitud, actualizaremos fB y recordaremos su índice.

2. Copiado de las coordenadas del mejor agente: si se ha encontrado el mejor agente (el índice no es igual a -1), copiaremos sus coordenadas en el array "cB", que almacena las mejores coordenadas actuales.

3. Actualización de las mejores aptitudes personales de los agentes: iteramos de nuevo todos los agentes y comprobamos si su aptitud actual supera su mejor aptitud personal ("fB"). Si es así, actualizaremos su mejor aptitud personal y copiaremos sus coordenadas actuales en "cB".

4. Clasificación de los agentes: al final llamamos a la función de clasificación para ordenar los agentes según su mejor valor de aptitud personal.

El método "revision" es un elemento importante del algoritmo, ya que garantiza el seguimiento y almacenamiento de las mejores soluciones encontradas.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

El método "GrassBehavior" de la clase "C_AO_AEO" implementa un comportamiento del agente basado en el concepto de "herbívoros", que simboliza la búsqueda de nuevas soluciones en el espacio. Estructura del método:

1. El cálculo del coeficiente "α", se define como "(1,0 - (doble) epochNow / epochs)", lo cual significa que disminuye a medida que aumenta el número de épocas. Esto permite al algoritmo explorar el espacio de forma más activa al principio y centrarse después en mejorar las soluciones halladas.

2. Inicialización de variables:

• X1 - coordenada actual del agente herbívoro .
• Xn - coordenada actual del saprofito.
• Xr - coordenada aleatoria seleccionada del rango especificado.

3. Ciclo por las coordenadas. Para cada coordenada de agente:

• Se genera un valor aleatorio "Xr" dentro del rango especificado "[Xmin, Xmax]".
• La coordenada actual "Xn" se toma del array "cB", que almacena las mejores coordenadas globales actuales (la posición del saprofito en el espacio).
• Se calcula una nueva coordenada "X1" usando la fórmula "X1 = Xn + α * (Xn - Xr)", que permite mezclar el valor actual con un valor aleatorio, reduciendo la influencia de la aleatoriedad a medida que aumenta el número de épocas.
• Por último, la nueva coordenada se limita dentro del rango especificado mediante la función "SeInDiSp".

//——————————————————————————————————————————————————————————————————————————————
// Grass
// (Worst) X1 X2 X3 ...... Xn (Best)
// X1(t+1) = (1 - α) * Xn(t) + α * Xrnd (t)
// α = (1 - t / T) * rnd [0.0; 1.0]
// Xrnd = rnd [Xmin; Xmax]

void C_AO_AEO::GrassBehavior (S_AO_Agent &animal)
{
  //0) (1 - α) * Xn + α * Xrnd
  //1) Xn - α * Xn + α * Xrnd
  //2) Xn + α * (Xrnd - Xn)

  double α = (1.0 - (double)epochNow / epochs);

  double X1 = 0.0;
  double Xn = 0.0;
  double Xr = 0.0;

  for (int c = 0; c < coords; c++)
  {
    Xr = u.RNDfromCI (rangeMin [c], rangeMax [c]);
    Xn = cB [c];

    //X1 = Xn + α * (Xr - Xn);
    X1 = Xn + α * (Xn - Xr);

    animal.c [c] = u.SeInDiSp (X1, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "HerbivoreBehavior" en la clase "C_AO_AEO" implementa el comportamiento del agente herbívoro. Estructura del método:

1. Inicialización de variables:

• Xi - coordenada actual del agente a actualizar.
• X1 - coordenada del peor agente de la población, que corresponde a la máxima energía (o menor aptitud).
• C - valor aleatorio generado mediante la distribución de Levy.

2. Actualización de coordenadas: la coordenada "Xi" se actualiza de acuerdo con la fórmula: Xi (t+1)=Xi (t)+C ⋅ (Xi (t)−X1 (t)).  Esta fórmula significa que un agente cambia su coordenada según la diferencia entre su coordenada actual y la coordenada del peor agente. Esto permite al herbívoro "alimentarse" del peor agente, es decir, explorar incluso áreas de búsqueda poco prometedoras.

3. Restricción de coordenadas: una vez actualizada la coordenada "Xi", se restringe dentro del rango indicado mediante la función "SeInDiSp", que toma como argumentos el nuevo valor, los límites mínimo y máximo, y el paso.

El método HerbivoreBehavior demuestra cómo los agentes herbívoros pueden adaptarse "alimentándose" de los peores miembros de una población.

//——————————————————————————————————————————————————————————————————————————————
// Herbivore
// (Worst) X1 X2 X3 ...... Xn (Best)
// Xi(t+1) = Xi(t) + C * (Xi(t) - X1(t)) for i ∈ [2, n]
// Herbivore eats only the one with the highest energy (eats the one with the worst FF)
void C_AO_AEO::HerbivoreBehavior (S_AO_Agent &animal, int indCoord)
{
  double Xi = animal.c [indCoord];
  double X1 = a [popSize - 1].c [indCoord];
  double C  = u.LevyFlightDistribution (levisPower);

  Xi = Xi + C * (Xi - X1);

  animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]);
}
//——————————————————————————————————————————————————————————————————————————————

El método "CarnivoreBehavior " de la clase "C_AO_AEO " implementa el comportamiento del agente carnívoro dentro del algoritmo. Estructura del método:

1. Inicialización de variables:

• Xi - coordenada actual del agente carnívoro que se va a actualizar.
• j - índice de un agente de sacrificio elegido al azar (el carnívoro "come" agentes con menor energía pero mejor aptitud).
• Xj - coordenada de la presa que se usará para actualizar la coordenada del carnívoro.
• C - valor aleatorio generado mediante la distribución de Levy.
  

2. Actualización de coordenadas: la coordenada "Xi" se actualiza según la fórmula: Xi (t+1) = Xi (t) + C * (Xj (t) - Xi (t)). Esta fórmula significa que el agente carnívoro cambia su coordenada según la diferencia entre la coordenada de la presa y su coordenada actual. Esto permite al carnívoro "alimentarse" a costa de la presa, mejorando su rendimiento.

3. Limitación de coordenadas: una vez actualizada la coordenada "Xi", se limita dentro del rango especificado mediante la función "SeInDiSp ".

El método "CarnivoreBehavior " demuestra cómo los agentes carnívoros pueden adaptarse "alimentándose" de presas con menos energía. Esto les permite mejorar su rendimiento, buscando soluciones más óptimas. 

//——————————————————————————————————————————————————————————————————————————————
// Carnivorous
// (Worst) X1 X2 X3 ...... Xn (Best)
// Xi(t+1) = Xi(t) + C * (Xi(t) - Xj(t)) for i ∈ [3, n]
// Carnivore eats those with less energy (eats those with higher FF)
void C_AO_AEO::CarnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord)
{
  //double Xi = animal.c [indCoord];
  double Xi = animal.cB [indCoord];
  int    j  = u.RNDminusOne (indAnimal);
  //double Xj = a [j].c [indCoord];
  double Xj = a [j].cB [indCoord];
  double C  = u.LevyFlightDistribution (levisPower);

  //Xi = Xi + C * (Xi - Xj);
  Xi = Xi + C * (Xj - Xi);

  animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]);
}
//——————————————————————————————————————————————————————————————————————————————

El método "OmnivoreBehavior" de la clase "C_AO_AEO" describe el comportamiento de un agente omnívoro en el contexto de un algoritmo evolutivo. Estructura del método:

1. Inicialización de variables:

• Xi - coordenada actual del agente omnívoro que hay que actualizar.
• X1 - coordenada del peor agente (el agente con mayor energía).
  
• j - índice aleatorio de otro agente seleccionado de la población que se utilizará para actualizar la coordenada.
• Xj - coordenada del otro agente seleccionado.
• C - valor aleatorio generado mediante la distribución de Levy.
• r - probabilidad aleatoria que se utilizará para mezclar la actualización de coordenadas.

2. Actualización de coordenadas: la coordenada "Xi" se actualiza de acuerdo con la fórmula: Xi (t+1) = Xi (t) + C * r * (Xi (t) - X1 (t)) + (1 - r)  (Xi (t) - Xj (t)). Esta fórmula permite a un agente omnívoro adaptarse "alimentándose" tanto del peor agente (con mayor energía) como de otro agente aleatorio con menor capacidad de adaptación, lo cual flexibiliza su comportamiento.

3. Limitación de coordenadas: una vez actualizada la coordenada "Xi", se restringe dentro de los límites especificados mediante la función "SeInDiSp".

El método "OmnivoreBehavior" demuestra cómo los agentes omnívoros pueden adaptarse y beneficiarse de diferentes fuentes de energía, incluyendo agentes peores y otros agentes seleccionados al azar con menor capacidad de adaptación.

//——————————————————————————————————————————————————————————————————————————————
// Omnivorous
// (Worst) X1 X2 X3 ...... Xn (Best)
// Xi(t+1) = Xi(t) + C * r2 * (Xi(t) - X1(t)) + (1 - r2) * (Xi(t) - Xj(t)) for i ∈ [3, n]
// Omnivore eats everyone who has more energy (grass and small animals, that is, those who have worse FF)
void C_AO_AEO::OmnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord)
{
  //double Xi = animal.c [indCoord];
  double Xi = animal.cB [indCoord];
  //double X1 = a [popSize - 1].c [indCoord];
  double X1 = a [popSize - 1].cB [indCoord];
  int    j  = u.RNDintInRange (indAnimal + 1, popSize - 1);
  //double Xj = a [j].c [indCoord];
  double Xj = a [j].cB [indCoord];
  double C  = u.LevyFlightDistribution (levisPower);
  double r  = u.RNDprobab ();

  Xi = Xi + C * r * (Xi - X1) + (1.0 - r) * (Xi - Xj);

  animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]);
}
//——————————————————————————————————————————————————————————————————————————————

Ahora que hemos escrito el código del algoritmo, por fin podremos empezar a probarlo en nuestras funciones de prueba.

AEO|Artificial Ecosystem-based Optimization Algorithm|50.0|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.6991675795357223
25 Hilly's; Func runs: 10000; result: 0.34855292688850514
500 Hilly's; Func runs: 10000; result: 0.253085011547826
=============================
5 Forest's; Func runs: 10000; result: 0.6907505745478882
25 Forest's; Func runs: 10000; result: 0.23365521509528495
500 Forest's; Func runs: 10000; result: 0.1558073538195803
=============================
5 Megacity's; Func runs: 10000; result: 0.5430769230769231
25 Megacity's; Func runs: 10000; result: 0.20676923076923082
500 Megacity's; Func runs: 10000; result: 0.1004461538461546
=============================
All score: 3.23131 (35.90%)

El algoritmo ha obtenido una puntuación aproximada del 36% en las pruebas, aunque se trata de un resultado medio. Para este algoritmo, hemos decidido revisar el método Moving, y esto es lo que hemos obtenido:

Lógica de movimiento de agentes modificada para dar cabida a diferentes comportamientos (producción, consumo y descomposición) en el método "Moving":

1. La inicialización de la población no ha cambiado.

2. El factor de actualización "α", se calcula según la época actual, disminuyendo a medida que aumenta "epochNow". Este coeficiente se extrae de un método privado separado.

3. Producción (consModel == 0) - en esta parte, los agentes actualizan sus coordenadas usando una fórmula basada en el estado anterior y un valor aleatorio. Esto les permite "producir" nuevos estados.

4. Consumo (consModel == 1). Aquí dividimos a los agentes en tres grupos según un valor aleatorio:

• Herbívoros.
• Carnívoros.
• Omnívoros.

5. Descomposición: en esta etapa, los agentes interactúan entre sí, cambiando sus coordenadas según los valores aleatorios y las interacciones con otros agentes.

6. Restablecimiento del modelo de consumo: al final del método, "consModel" se restablece a "0" para iniciar un nuevo ciclo.

Como podemos ver, el principal cambio en la lógica del algoritmo es la separación de la "Producción" en una etapa independiente. Para ello se reserva una época separada, lo que permite una seria sacudida en la población de organismos. Esto también se ha reflejado en el comportamiento del algoritmo AEO en la visualización: se observan "parpadeos", es decir, pueden observarse etapas individuales del ecosistema artificial incluso visualmente.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEO::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double α = (1.0 - (double)epochNow / epochs);

  double Xi   = 0.0;
  double Xb   = 0.0;
  double Xr   = 0.0;
  double Xj   = 0.0;
  double C    = 0.0;
  int    j    = 0;
  double r    = 0.0;

  // Production ---------------------------------------------------------------- 
  // X(t + 1) = (1 - α) * Xb(t) + α * Xrnd (t)
  // α = (1 - t / T) * rnd [0.0; 1.0]
  // Xrnd = rnd [Xmin; Xmax]
  if (consModel == 0)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        Xb = cB [c];
        Xr = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        //Xi = Xb + α * (Xr - Xb);
        Xi = Xb + α * (Xb - Xr);

        a [i].c [c] = u.SeInDiSp (Xi, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    consModel++;
    return;
  }

  // Consumption --------------------------------------------------------------- 
  if (consModel == 1)
  {
    for (int i = 0; i < popSize; i++)
    {
      if (i > 1)
      {
        for (int c = 0; c < coords; c++)
        {
          r = u.RNDprobab ();

          // Herbivore behavior ------------------------------------------------ 
          //Xi (t + 1) = Xi (t) + C * (Xi (t) - Xb (t));
          if (r < 0.333)
          {
            C  = u.LevyFlightDistribution (levisPower);
            Xb = cB [c];
            //Xi = a [i].c [c];
            Xi = a [i].cB [c];

            //Xi = Xi + C * (Xi - Xb);
            Xi = Xi + C * (Xb - Xi);
          }
          else
          {
            // Carnivore behavior ---------------------------------------------- 
            //Xi (t + 1) = Xi (t) + C * (Xi (t) - Xj (t));
            if (r < 0.667)
            {
              C  = u.LevyFlightDistribution (levisPower);
              j  = u.RNDminusOne (i);
              //Xj = a [j].c [c];
              Xj = a [j].cB [c];
              //Xi = a [i].c [c];
              Xi = a [i].cB [c];

              //Xi = Xi + C * (Xi - Xj);
              Xi = Xi + C * (Xj - Xi);
            }
            // Omnivore behavior ----------------------------------------------- 
            //Xi (t + 1) = Xi (t) + C * r2 * (Xi (t) - Xb (t)) +
            //                    (1 - r2) * (Xi (t) - Xj (t));
            else
            {
              C  = u.LevyFlightDistribution (levisPower);
              Xb = cB [c];
              j  = u.RNDminusOne (i);
              //Xj = a [j].c [c];
              Xj = a [j].cB [c];
              //Xi = a [i].c [c];
              Xi = a [i].cB [c];
              r = u.RNDprobab ();

              //Xi = Xi + C * r * (Xi - Xb) +
              //     (1 - r) * (Xi - Xj);
              Xi = Xi + C * r * (Xb - Xi) +
                   (1 - r) * (Xj - Xi);
            }
          }

          a [i].c [c] = u.SeInDiSp (Xi, rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }
    }

    consModel++;
    return;
  }

  // Decomposition -------------------------------------------------------------
  double D = 0.0;
  double h = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    D = 3 * u.RNDprobab ();
    h = u.RNDprobab () * (u.RNDprobab () < 0.5 ? 1 : -1);
    C = u.LevyFlightDistribution (levisPower);
    j = u.RNDminusOne (popSize);

    for (int c = 0; c < coords; c++)
    {
      double x = a [i].cB [c] + D * (C * a [i].cB [c] - h * a [j].c [c]);
      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  consModel = 0;
}
//——————————————————————————————————————————————————————————————————————————————

Resultados de las pruebas

Ahora podemos volver a probar el algoritmo con nuestros cambios en la lógica. 

AEO|Artificial Ecosystem-based Optimization Algorithm|50.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9137986747745103
25 Hilly's; Func runs: 10000; result: 0.4671288391599192
500 Hilly's; Func runs: 10000; result: 0.2647022528159094
=============================
5 Forest's; Func runs: 10000; result: 0.9022293417142482
25 Forest's; Func runs: 10000; result: 0.4370486099190667
500 Forest's; Func runs: 10000; result: 0.2139965996985526
=============================
5 Megacity's; Func runs: 10000; result: 0.6615384615384616
25 Megacity's; Func runs: 10000; result: 0.30799999999999994
500 Megacity's; Func runs: 10000; result: 0.28563076923076974
=============================
All score: 4.45407 (49.49%)

Cabe destacar que no existe una dispersión significativa en los resultados. El algoritmo sortea con éxito las trampas locales, aunque la precisión de convergencia presenta valores medios. También se nota el "parpadeo" al cambiar de etapa que comentábamos más arriba. El algoritmo se comporta de forma especialmente inusual en la función discreta Megacity, extrayendo grupos de coordenadas en líneas verticales y diagonales separadas que atraviesan zonas significativas de la superficie. Esto se ha reflejado en los resultados de esta función discreta: son los mejores de la tabla de clasificación para la función discreta con 1.000 variables.

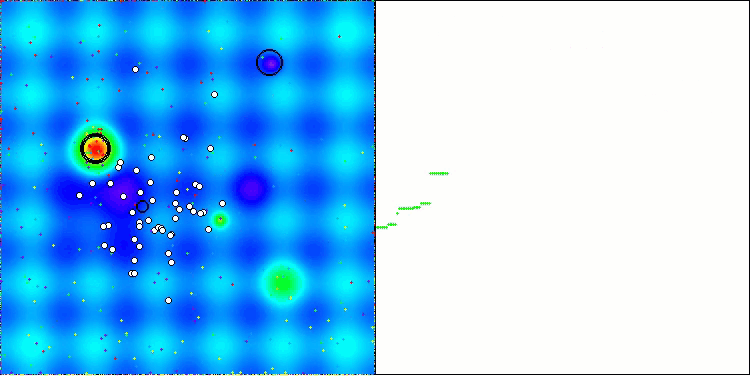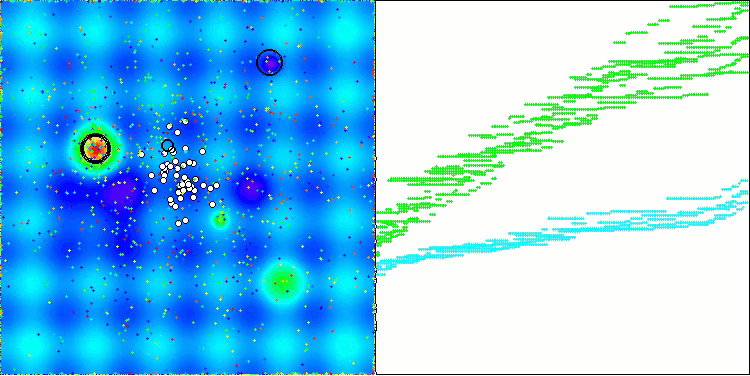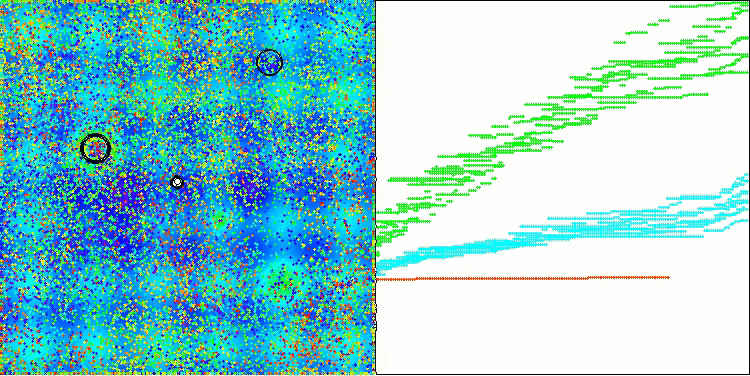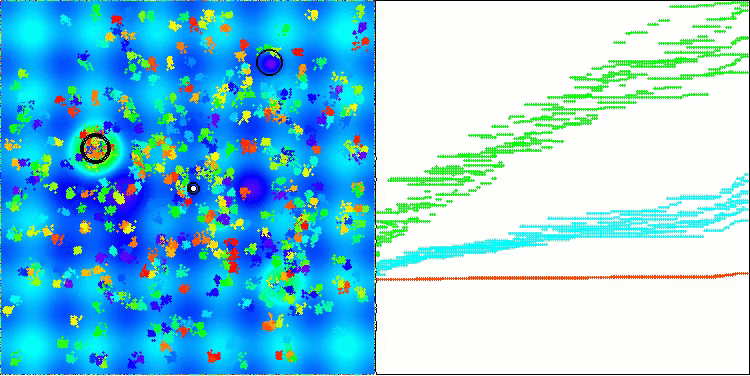
AEO en la función de prueba Hilly

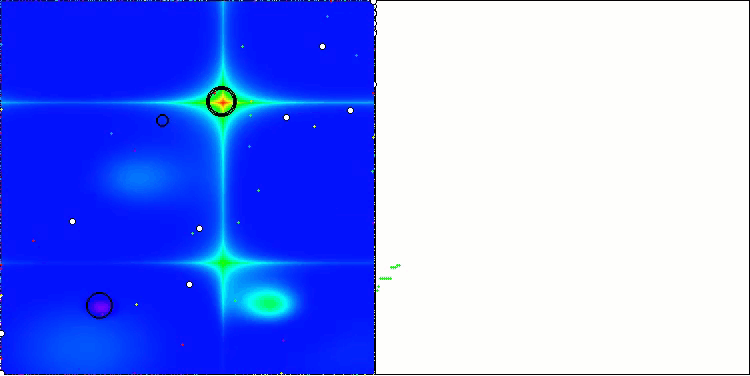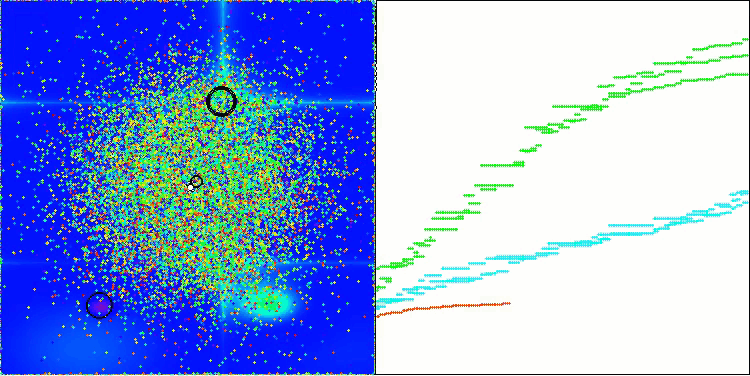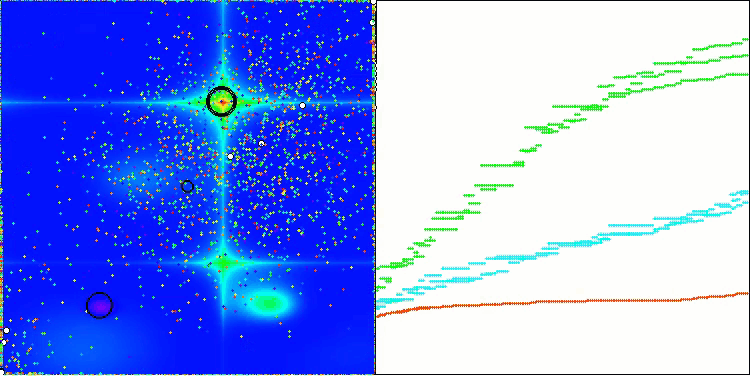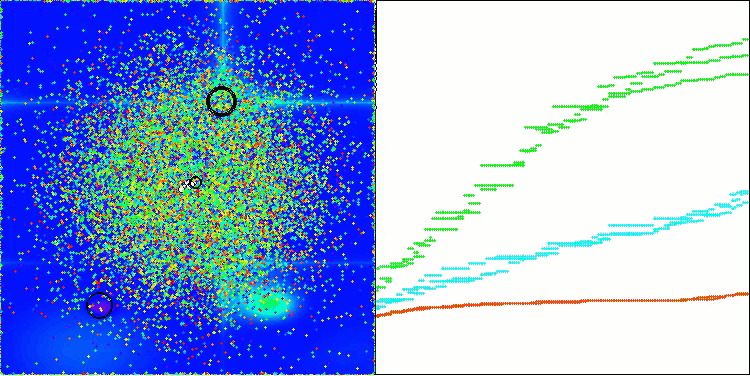
AEO en la función de prueba Forest

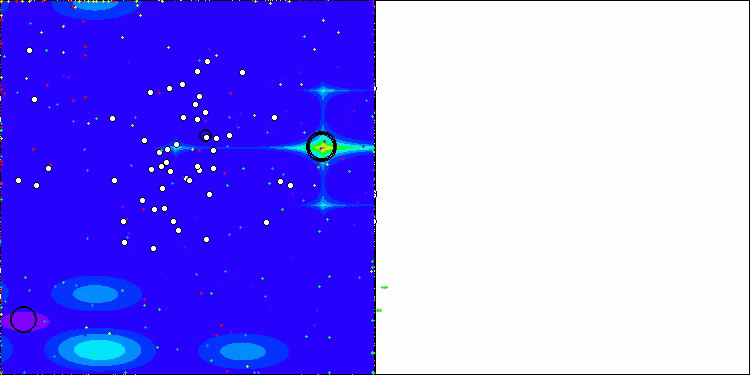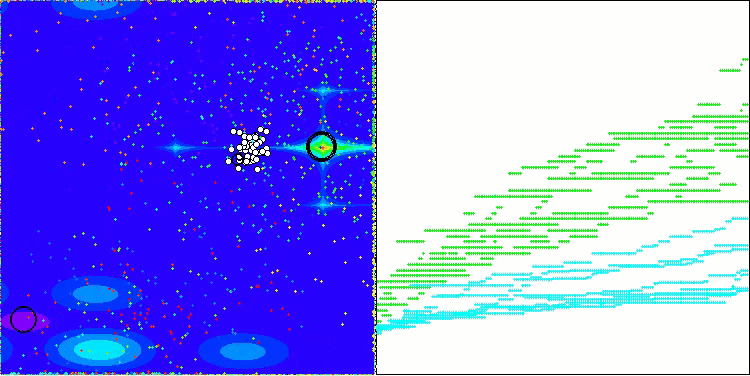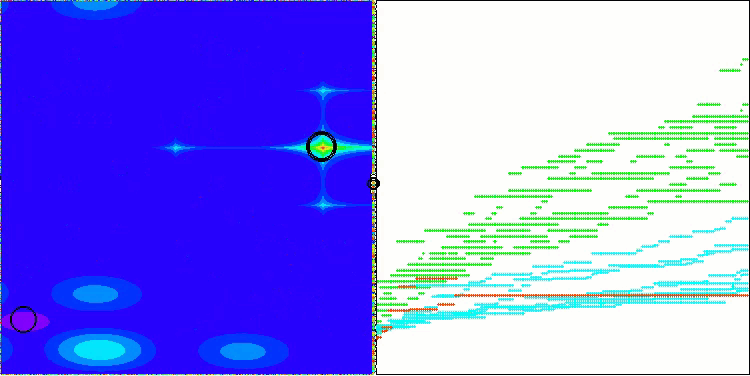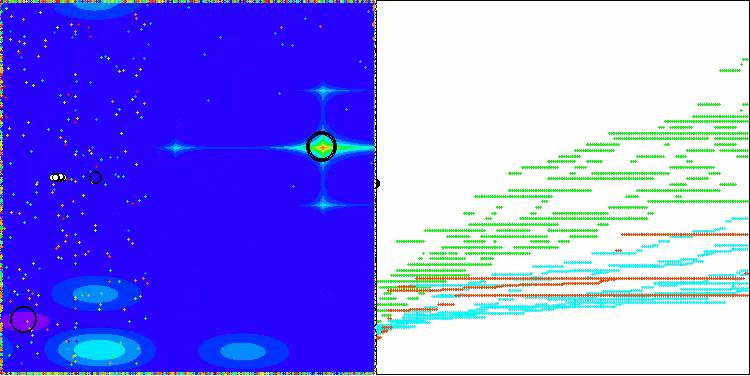
AEO en la función de prueba Megacity

Como podemos ver, el algoritmo ha mejorado notablemente con respecto a la versión original y ahora alcanza aproximadamente el 50% del máximo posible. Es un resultado realmente impresionante. El algoritmo ocupa el puesto 25 en la tabla de clasificación, lo cual también resulta bastante respetable. Lo más impresionante es que AEO ha establecido un nuevo récord en la tabla en la función discreta Megacity, ¡ha mejorado el resultado con 1.000 parámetros hasta en un 5%!

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% de MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
2	CLA	code lock algorithm (joo)	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	AMOm	animal migration optimization M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5,987	66,52
4	(P+O)ES	(P+O) estrategias de evolución	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
5	CTA	comet tail algorithm (joo)	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
6	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
7	AAm	archery algorithm M	0,91744	0,70876	0,42160	2,04780	0,92527	0,75802	0,35328	2,03657	0,67385	0,55200	0,23738	1,46323	5,548	61,64
8	ESG	evolution of social groups (joo)	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
9	SIA	simulated isotropic annealing (joo)	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
10	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
11	ASO	anarchy society optimization	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5,178	57,54
12	TSEA	turtle shell evolution algorithm (joo)	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
13	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
14	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
15	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
16	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
17	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
18	BCOm	bacterial chemotaxis optimization M	0,75953	0,62268	0,31483	1,69704	0,89378	0,61339	0,22542	1,73259	0,65385	0,42092	0,14435	1,21912	4,649	51,65
19	ABO	african buffalo optimization	0,83337	0,62247	0,29964	1,75548	0,92170	0,58618	0,19723	1,70511	0,61000	0,43154	0,13225	1,17378	4,634	51,49
20	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
21	TSm	tabu search M	0,87795	0,61431	0,29104	1,78330	0,92885	0,51844	0,19054	1,63783	0,61077	0,38215	0,12157	1,11449	4,536	50,40
22	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
23	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
24	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
25	AEO	artificial ecosystem-based optimization algorithm	0,91380	0,46713	0,26470	1,64563	0,90223	0,43705	0,21400	1,55327	0,66154	0,30800	0,28563	1,25517	4,454	49,49
26	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
27	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
28	ABH	artificial bee hive algorithm	0,84131	0,54227	0,26304	1,64663	0,87858	0,47779	0,17181	1,52818	0,50923	0,33877	0,10397	0,95197	4.127	45,85
29	ACMO	atmospheric cloud model optimization	0,90321	0,48546	0,30403	1,69270	0,80268	0,37857	0,19178	1,37303	0,62308	0,24400	0,10795	0,97503	4,041	44,90
30	ASHA	artificial showering algorithm	0,89686	0,40433	0,25617	1,55737	0,80360	0,35526	0,19160	1,35046	0,47692	0,18123	0,09774	0,75589	3,664	40,71
31	ASBO	adaptive social behavior optimization	0,76331	0,49253	0,32619	1,58202	0,79546	0,40035	0,26097	1,45677	0,26462	0,17169	0,18200	0,61831	3.657	40,63
32	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
33	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
34	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
35	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
36	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
37	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
38	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
39	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
40	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72
41	ABC	artificial bee colony	0,63377	0,42402	0,30892	1,36671	0,55103	0,21874	0,05623	0,82600	0,34000	0,14200	0,03102	0,51302	2,706	30,06
42	BA	bat algorithm	0,59761	0,45911	0,35242	1,40915	0,40321	0,19313	0,07175	0,66810	0,21000	0,10100	0,03517	0,34617	2,423	26,93
43	AAA	algae adaptive algorithm	0,50007	0,32040	0,25525	1,07572	0,37021	0,22284	0,16785	0,76089	0,27846	0,14800	0,09755	0,52402	2,361	26,23
44	SA	simulated annealing	0,55787	0,42177	0,31549	1,29513	0,34998	0,15259	0,05023	0,55280	0,31167	0,10033	0,02883	0,44083	2,289	25,43
45	IWDm	intelligent water drops M	0,54501	0,37897	0,30124	1,22522	0,46104	0,14704	0,04369	0,65177	0,25833	0,09700	0,02308	0,37842	2,255	25,06

Conclusiones

Características y ventajas del algoritmo:

1. Equilibrio entre investigación y explotación. El AEO ofrece un buen equilibrio entre la exploración global del espacio de soluciones (mediante la producción y el consumo) y la explotación local (mediante la descomposición).

2. Adaptabilidad. El algoritmo se adapta al paisaje de tareas usando diferentes estrategias de actualización de soluciones.

3. Simplicidad. A pesar de la metáfora biológica, el algoritmo resulta relativamente sencillo de aplicar y comprender.

4. Excelentes resultados en funciones discretas de alta dimensionalidad.

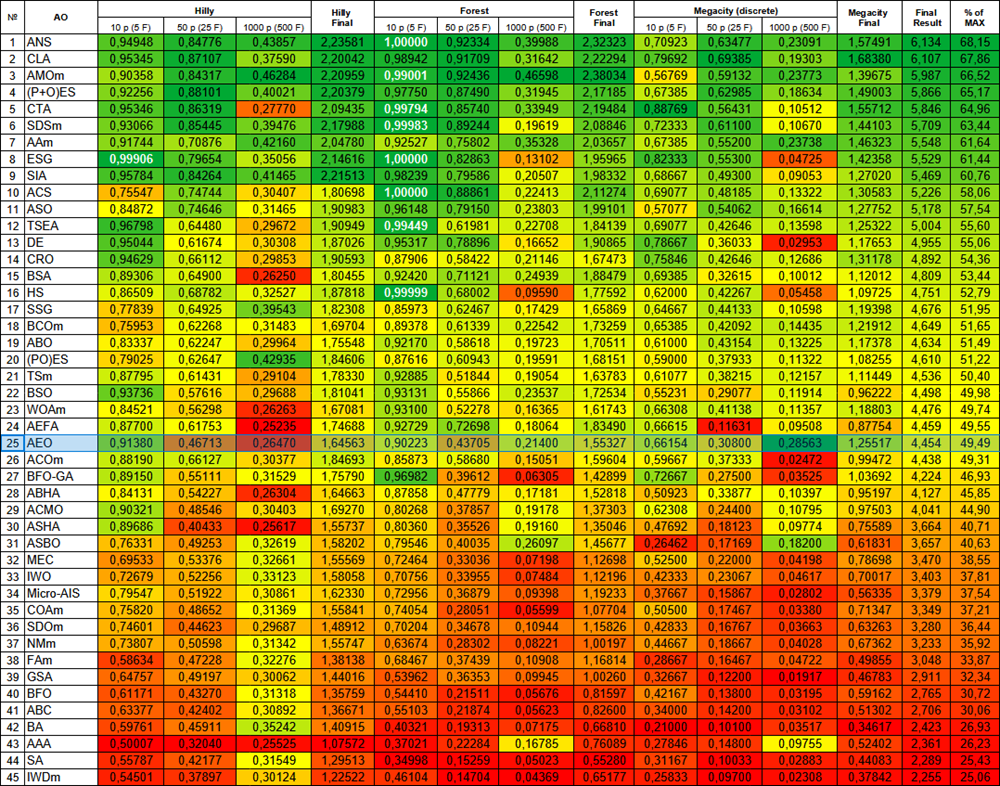
Figura 2. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0.99 se resaltan en blanco.

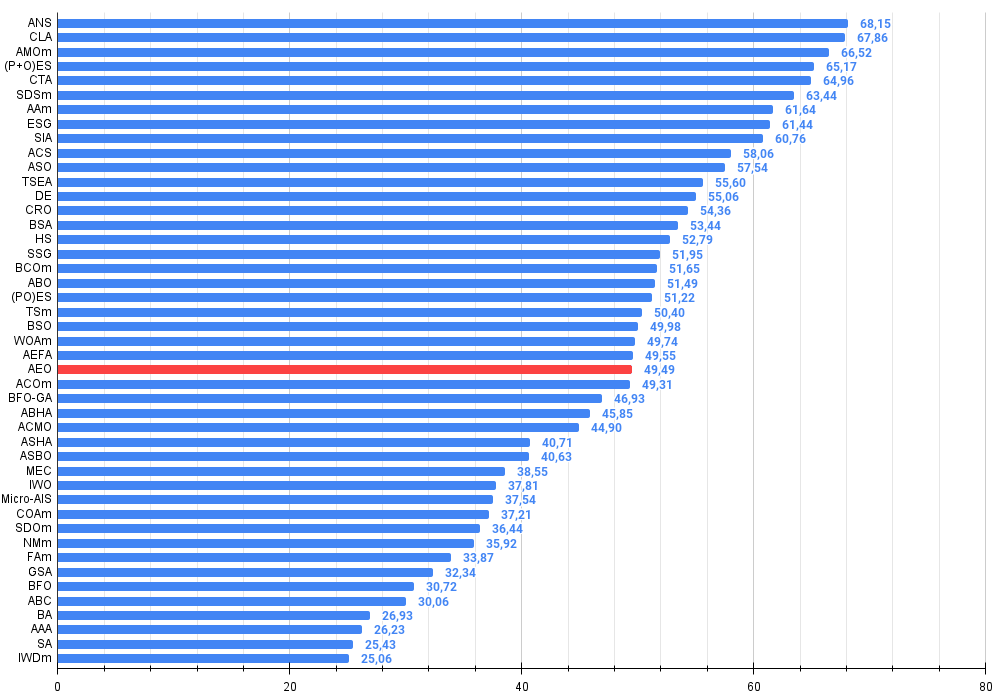
Figura 3. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor,

donde 100 es el máximo resultado teórico posible; el script para calcular la tabla de clasificación está en el archivo)

Ventajas e inconvenientes del algoritmo AEO:

Ventajas:

1. Solo un parámetro externo (aparte del tamaño de la población).
   
2. Buen rendimiento en una función discreta.

Desventajas:

1. No posee la mayor precisión de convergencia.
   

Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5