Redes neuronales en el trading: Integración de la teoría del caos en la previsión de series temporales (Attraos)

Introducción

En los mercados financieros, las series temporales son secuencias de datos de precios, volúmenes comerciales y otros indicadores económicos que cambian con el tiempo debido a diversos factores. Reflejan procesos dinámicos complejos, incluidas las tendencias del mercado, los ciclos y las fluctuaciones a corto plazo impulsadas por las noticias económicas, el comportamiento de los participantes en el mercado y diversas condiciones macroeconómicas. La previsión correcta de series temporales en finanzas desempeña un papel clave en la gestión de riesgos, la construcción de estrategias comerciales, la optimización de carteras y el trading algorítmico. Los errores en las previsiones pueden provocar importantes pérdidas financieras, por lo que el desarrollo de métodos más precisos de análisis de series temporales es una prioridad para analistas, tráders e instituciones financieras.

Los métodos modernos de previsión de series temporales financieras usan ampliamente el aprendizaje automático, incluidas las redes neuronales y los modelos de aprendizaje profundo. Sin embargo, la mayoría de los enfoques tradicionales se basan en métodos estadísticos y modelos lineales, sistemas que encuentran dificultades para analizar datos muy volátiles y caóticos, típicos de los mercados financieros. Los procesos de mercado suelen presentar dependencias no lineales, sensibilidad a las condiciones iniciales y una dinámica compleja. Todo ello hace que predecirlos resulte todo un reto. Los modelos tradicionales tienen dificultades para considerar eventos repentinos del mercado, como crisis, cambios bruscos de liquidez o ventas masivas de activos provocadas por el pánico de los inversores. Por lo tanto, la búsqueda de nuevos enfoques que puedan adaptarse a la compleja dinámica de los mercados financieros es un área de investigación sumamente importante.

Para resolver estos problemas, los autores del framework Attraos, propuesto en el artículo "Attractor Memory for Long-Term Time Series Forecasting: A Chaos Perspective", integran los principios de la teoría del caos tratando las series temporales como proyecciones de baja dimensión de sistemas dinámicos caóticos multidimensionales. Este enfoque permite considerar las dependencias no lineales ocultas entre los datos del mercado y mejorar la precisión de las previsiones. El uso de métodos de dinámica caótica en el análisis de series temporales abre la posibilidad de identificar estructuras estables en los datos de mercado y considerarlas al construir modelos de previsión.

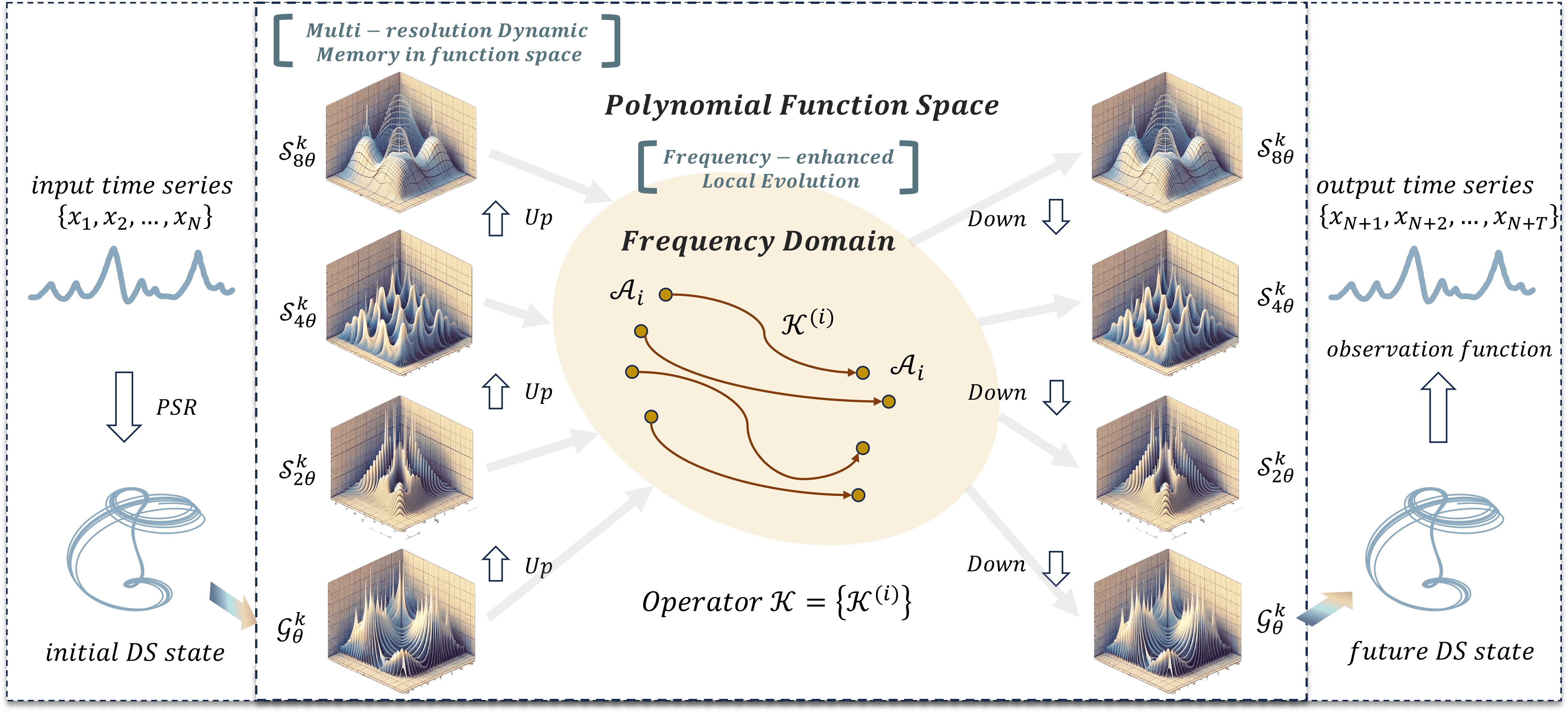
El framework Attraos resuelve dos problemas fundamentales. En primer lugar, modela procesos dinámicos ocultos usando técnicas de reconstrucción del espacio de fases. Esto nos permite identificar patrones ocultos y considerar las interacciones no lineales entre distintas variables del mercado, como las correlaciones entre activos, los indicadores macroeconómicos y la liquidez del mercado. En segundo lugar, Attraos usa una estrategia de evolución local en el dominio de la frecuencia que le permite adaptarse a las condiciones cambiantes del mercado amplificando las diferencias de los atractores. A diferencia de los modelos tradicionales basados en hipótesis fijas sobre la distribución de datos, Attraos se adapta dinámicamente a la estructura cambiante de los mercados financieros, ofreciendo previsiones más precisas en distintos horizontes temporales.

Además, el modelo incluye una unidad de memoria dinámica de resolución múltiple que le permite recordar y tener en cuenta patrones históricos de movimiento de los precios, así como adaptarse a las condiciones cambiantes del mercado. Esto resulta especialmente importante para los mercados financieros, donde los mismos patrones pueden repetirse en diferentes intervalos de tiempo, pero con diferente amplitud e intensidad. La capacidad del modelo para aprender de datos con distintos grados de detalle le confiere una ventaja significativa sobre los planteamientos tradicionales, que a menudo ignoran la naturaleza multiescala de los procesos de mercado.

Los experimentos realizados por los autores del framework demuestran que Attraos supera a los métodos tradicionales de previsión de series temporales, ofreciendo previsiones más precisas con menos parámetros entrenados. Debemos destacar que el uso de la dinámica caótica permite al modelo captar mejor las dependencias a largo plazo y reducir el impacto de los errores acumulados, lo cual resulta fundamental para las estrategias de inversión a medio y largo plazo.

El algoritmo Attraos

En la teoría del caos, los sistemas dinámicos multidimensionales que evolucionan en el tiempo pueden mostrar un comportamiento complejo y aparentemente arbitrario. Sin embargo, un análisis detallado de dichos sistemas revela la existencia de regularidades ocultas que determinan su dinámica.

Según el teorema de Takens, si un sistema es determinista, su espacio de fases puede reconstruirse a partir de observaciones de una de las variables. Esta afirmación se basa en la idea de que, dada una longitud suficiente de series temporales, es posible reconstruir la trayectoria multidimensional de un sistema aunque solo se disponga de datos univariantes. Este enfoque nos permite identificar los atractores ocultos, que son las regiones del espacio de fases a las que tienden las trayectorias del sistema cuando el tiempo de evolución es suficientemente grande.

En el contexto de los mercados financieros, las series temporales como las cotizaciones bursátiles, los pares de divisas y otros activos contienen información sobre la dinámica interna del sistema de mercado. A pesar de la aleatoriedad externa, el comportamiento del mercado puede obedecer a leyes deterministas, que pueden identificarse usando métodos de reconstrucción del espacio de fases. La aplicación de estos métodos permite a los analistas identificar los atractores característicos a partir de los que pueden predecirse los futuros movimientos de los precios.

El framework Attraos se basa en los principios de la teoría del caos y la reconstrucción del espacio de fases, lo que permite crear modelos topológicamente equivalentes de sistemas dinámicos sin necesidad de conocer previamente su naturaleza. La idea principal consiste en representar las series temporales en un espacio de fases multidimensional para revelar patrones ocultos. Esto se logra seleccionando los parámetros clave, la dimensionalidad de incorporación d y el retardo temporal ꚍ, que forman una representación multidimensional de las series temporales:

Este enfoque reduce la influencia del ruido, destaca los elementos estructurales del proceso y mejora la precisión de la predicción. La técnica de reconstrucción del espacio de fase posibilita la construcción de un retrato de fase estable que refleja la dinámica del sistema en el tiempo y permite su análisis y modelización.

El proceso de procesamiento de datos en Attraos comienza con el módulo de reconstrucción del espacio de fases (Phase Space Reconstruction — PSR), que se encarga de seleccionar los valores óptimos de d y τ para representar correctamente la dinámica del sistema. Este paso resulta vital porque unos parámetros elegidos incorrectamente pueden provocar distorsiones significativas en el retrato de fase reconstruido. A continuación, el módulo MDMU (Multidimensional Data Management Unit) realiza la partición de los datos en fragmentos no solapados utilizando tensores multidimensionales. Este proceso reduce la complejidad computacional, acelera la convergencia del modelo y construye la memoria dinámica del sistema captando patrones evolutivos clave. Este enfoque hace que las previsiones sean más estables y resistentes a una posible degradación de los datos. Además, el MDMU utiliza el método de selección adaptativa de los elementos significativos de la serie temporal, que permite excluir dinámicamente los componentes poco informativos y destacar los factores clave que influyen al máximo en la evolución del sistema.

Uno de los elementos más importantes de la arquitectura de Attraos es el módulo LMA (Linear Matrix Approximation), que aplica el método de aproximación matricial lineal. Este aplica la proyección polinómica para extraer las principales características de la dinámica del sistema, usando matrices parametrizadas con estructuras diagonales que definen las "ventanas de medición". Esto posibilita la extracción precisa de las características locales de la dinámica y el ajuste adaptativo del modelo cuando cambian los datos iniciales. El uso de matrices diagonales reduce la complejidad computacional, permitiendo un manejo eficiente de estructuras de datos multidimensionales. La evolución del sistema en este módulo se formaliza con la ayuda de la siguiente expresión:

donde M supone la matriz de estado diagonal parametrizada y ϵ representa el error aleatorio de modelización. Este módulo usa diversas opciones evolutivas, incluidas las proyecciones no lineales adaptativas, para acomodar transformaciones complejas en la dinámica del sistema y mejorar la precisión de las predicciones.

Para procesar los procesos dinámicos, se usa el módulo DP (Discrete Projection), que ejecuta la discretización del sistema utilizando métodos combinados. Concretamente, se aplica una representación matricial exponencial que proporciona una gran precisión al analizar datos secuenciales. Este método garantiza una aproximación correcta de la evolución del sistema y reduce la influencia de la acumulación de errores, lo cual resulta especialmente importante cuando se analizan series temporales largas. Este módulo implementa un mecanismo adaptativo de cuantificación de datos que permite optimizar la precisión de la aproximación sin aumentar significativamente el coste computacional.

Otros mecanismos de adaptación integrados en Attraos son una estrategia de evolución local con refuerzo de frecuencia que ajusta las características de frecuencia de las series temporales y compensa las distorsiones causadas por procesos estocásticos. Esto se logra filtrando los componentes de alta frecuencia y controlando la densidad espectral de los datos. También se aplica una representación multinivel de la estructura dinámica en la que la longitud de la ventana de análisis aumenta gradualmente, lo cual reduce los errores de proyección y mejora la precisión de la aproximación. Este planteamiento nos permite considerar la compleja organización topológica de los atractores a diferentes escalas, lo que resulta especialmente importante para los sistemas dinámicos complejos. La arquitectura del framework también aplica métodos de aprendizaje híbridos que combinan métodos numéricos clásicos y modernos algoritmos de aprendizaje automático para mejorar la adaptabilidad del modelo y su generalizabilidad.

La estabilidad del modelo Attraos se garantiza usando métodos de minimización de error y de control de la desviación del atractor. Para ello, se calcula la distancia entre atractores, se controla su cambio y se ajusta la trayectoria del sistema cuando se detectan desviaciones significativas. Este conjunto de medidas estabiliza las previsiones y garantiza una gran precisión del modelo incluso con dinámicas inestables. El uso de métodos de control estadístico permite detectar automáticamente las zonas de inestabilidad y corregir el modelo en tiempo real. Se han introducido mecanismos de control activo de los parámetros del modelo que permiten cambiar dinámicamente los parámetros de optimización según el estado actual del sistema, lo que aumenta adicionalmente su adaptabilidad y la precisión de las previsiones.

A continuación le mostramos la visualización del framework Attraos realizada por el autor.

Implementación con MQL5

Tras considerar los aspectos teóricos del framework Attraos, abordaremos la parte práctica de nuestro trabajo, en la que implementaremos nuestra visión de los enfoques propuestos utilizando herramientas MQL5.

Empezaremos nuestro trabajo preparando los procesos clave necesarios para el funcionamiento eficaz del algoritmo Attraos. En el algoritmo considerado se usan activamente matrices diagonales. Estas desempeñan un papel importante en los cálculos, ya que permiten simplificar el procesamiento de datos y reducir la cantidad de memoria utilizada.

Una matriz diagonal es una matriz cuadrada cuyos elementos, excepto los de la diagonal principal, son cero. En el álgebra lineal tradicional, dichas matrices se almacenan como arrays bidimensionales de tamaño n*n. Sin embargo, este método resulta ineficaz, porque la gran mayoría de los elementos son ceros. Una solución mejor sería almacenar solo los elementos no iguales a cero de la diagonal como un array unidimensional de longitud n. Este enfoque reduce sustancialmente la cantidad de memoria utilizada y acelera los cálculos al eliminar operaciones innecesarias sobre elementos cero.

El uso de una representación vectorial de una matriz diagonal requiere un algoritmo especial para realizar operaciones de álgebra lineal, concretamente, la multiplicación de una matriz diagonal por una matriz arbitraria. Los algoritmos de multiplicación de matrices que hemos construido anteriormente suponen el almacenamiento explícito de todos los elementos, lo cual da lugar a cálculos redundantes. En este caso, basta con multiplicar cada elemento del vector diagonal por la fila correspondiente de la otra matriz. Esto simplifica enormemente el algoritmo, haciéndolo más eficiente.

Para maximizar el rendimiento, implementaremos el proceso anterior en el lado del contexto OpenCL utilizando las capacidades de cálculo paralelo de los procesadores gráficos. La idea básica es que cada elemento de la matriz resultante se calcule de forma independiente, utilizando solo el elemento deseado del vector diagonal. Esto reducirá la complejidad computacional del algoritmo y acelerará la ejecución.

Multiplicación de una matriz diagonal

El algoritmo para realizar la operación de multiplicación de una matriz diagonal por otra se implementará en el kernel DiagMatMult. Su trabajo se planificará en un espacio de tareas tridimensional. Las dos primeras dimensiones se corresponderán con la dimensionalidad de la segunda matriz, mientras que la tercera dimensión reflejará el número de matrices independientes utilizadas para procesar las proyecciones de secuencias unitarias de las series temporales multivariantes analizadas.

Como ya hemos mencionado, la operación de multiplicar una representación vectorial de una matriz diagonal por una matriz arbitraria implica multiplicar un elemento del vector diagonal por la fila correspondiente de la segunda matriz. Agruparemos los flujos de cálculo en grupos de trabajo para optimizar el rendimiento de la GPU. En cada grupo, solo un flujo realiza un acceso a memoria global, recuperando el elemento deseado del vector diagonal y almacenándolo en memoria local. Los otros flujos utilizan el valor de la memoria local, realizando los cálculos necesarios sin acceso adicional a la memoria global. Esto mejora notablemente la velocidad de ejecución de los algoritmos, reduciendo la sobrecarga de la transferencia de datos entre la memoria global y las unidades de cálculo del procesador.

En los parámetros del kernel DiagMatMult obtenemos punteros a 3 búferes de datos. Dos de ellos contienen los datos iniciales, mientras que el tercero está destinado a guardar los resultados de las operaciones. También hemos añadido la posibilidad de aplicar la función de activación a los resultados de la multiplicación de matrices.

__kernel void DiagMatMult(__global const float * diag,
                          __global const float * matr,
                          __global float * result,
                          int activation)
  {
   size_t row = get_global_id(0);
   size_t col = get_local_id(1);
   size_t var = get_global_id(2);
   size_t rows = get_global_size(0);
   size_t cols = get_local_size(1);

En el cuerpo del kernel, primero realizamos la identificación del flujo de operaciones en las tres dimensiones del espacio de tareas. A continuación, el primer flujo del grupo de trabajo guarda el valor del elemento diagonal en la memoria local y sincroniza los flujos de operación mediante una barrera.

   __local float local_diag[1];
   if(cols==0)
      local_diag[0] = diag[row + var * rows];
   barrier(CLK_LOCAL_MEM_FENCE);

En el siguiente paso, determinamos el desplazamiento en el búfer de matriz arbitraria hasta el elemento deseado.

   int shift = (row  + var * rows) * cols + col;

Nótese aquí que las dimensiones de la matriz arbitraria y de la matriz resultante serán iguales. Por ello, el desplazamiento obtenido también es relevante para la matriz de resultados.

Luego recuperamos el valor del elemento del búfer requerido de matriz arbitraria y lo multiplicamos por el elemento diagonal previamente almacenado en la memoria local. El resultado de la operación lo activamos utilizando la función especificada. Y guardamos el valor obtenido en el búfer de la matriz de resultados.

   float res = local_diag[0] * matr[shift];
//---
   result[shift] = Activation(res, activation);
  }

El kernel presentado anteriormente implementa el algoritmo de pasada directa para multiplicar una matriz diagonal por una matriz arbitraria. Sin embargo, eso supone solo la mitad de la batalla. En el entrenamiento del modelo, necesitaremos propagar el gradiente de error a través de esta operación. Para ello, crearemos otro kernel, DiagMatMultGrad, cuyo algoritmo será algo más complejo.

En los parámetros del kernel, añadimos los búferes para registrar los gradientes de error correspondientes. Pero excluimos el puntero de la función de activación. Se supone que el gradiente de los resultados de la operación ya está corregido para la derivada de la función de activación correspondiente.

__kernel void DiagMatMultGrad(__global const float *diag,
                              __global float *grad_diag,
                              __global const float *matr,
                              __global float * grad_matr,
                              __global const float * grad_result)
  {
   size_t row = get_global_id(0);
   size_t col = get_local_id(1);
   size_t var = get_global_id(2);
   size_t rows = get_global_size(0);
   size_t cols = get_local_size(1);
   size_t vars = get_global_size(2);

En el cuerpo del kernel, identificamos el flujo actual en un espacio de tareas tridimensional cuyos planteamientos de formación se trasladan desde el kernel de pasada directa.

De forma similar al kernel de pasada directa, solo un flujo del grupo de trabajo extrae los valores del elemento deseado de la matriz diagonal en un array local.

   __local float local_diag[LOCAL_ARRAY_SIZE];
   if(cols==0)
      local_diag[0] = diag[row + var * rows];
   barrier(CLK_LOCAL_MEM_FENCE);

Y sincronizamos el funcionamiento de los flujos del grupo de trabajo.

Luego determinamos el desplazamiento en los búferes de las matrices arbitraria y resultante.

   int shift = (row  + var * rows) * cols + col;
//---
   float grad = grad_result[shift];
   float inp = matr[shift];

Almacenamos los valores de los elementos necesarios de estas matrices en variables locales.

Con esto completaremos el trabajo preparatorio. Así que podemos calcular el gradiente de error a nivel de una matriz arbitraria. Para ello, bastará con multiplicar el valor del gradiente de error del elemento correspondiente de la matriz resultante por el elemento de la matriz diagonal almacenado previamente en el array local.

   grad_matr[shift] = IsNaNOrInf(local_diag[0] * grad, 0);
   barrier(CLK_LOCAL_MEM_FENCE);

Después guardamos el resultado de las operaciones en el búfer global correspondiente y sincronizamos los flujos de operaciones dentro del grupo de trabajo.

A continuación deberemos determinar el gradiente de error para los elementos de la matriz diagonal. Y aquí ya tenemos que recopilar los valores de todos los elementos de la fila correspondiente de la memoria resultante. Como comprenderá, deberemos sumar los valores de todos los flujos del grupo de trabajo.

Para ello, organizaremos un ciclo de suma paralela de valores individuales en los elementos del array local.

   int loc = col % LOCAL_ARRAY_SIZE;
#pragma unroll
   for(int c = 0; c < cols; c += LOCAL_ARRAY_SIZE)
     {
      if(c <= col && (c + LOCAL_ARRAY_SIZE) > col)
        {
         if(c == 0)
            local_diag[loc] = IsNaNOrInf(grad * inp, 0);
         else
            local_diag[loc] += IsNaNOrInf(grad * inp, 0);
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }

El número máximo de flujos activos en cada iteración del ciclo está limitado por el número de elementos del array local. Por eso, después de realizar las operaciones de una iteración, nos aseguraremos de sincronizar los flujos del grupo de trabajo y solo entonces pasaremos a la siguiente iteración del ciclo para trabajar con el siguiente lote de flujos activos.

A continuación, añadiremos un ciclo de suma paralela de los elementos del array local.

   int count = min(LOCAL_ARRAY_SIZE, (int)cols);
   int ls = count;
#pragma unroll
   do
     {
      count = (count + 1) / 2;
      if((col + count) < ls)
        {
         local_diag[col] += local_diag[col + count];
         local_diag[col + count] = 0;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

En cada iteración del ciclo, el número de flujos activos disminuirá constantemente. No obstante, deberemos sincronizar constantemente los flujos paralelos de operaciones dentro del grupo de trabajo.

Y para guardar el valor final en el búfer global, solo necesitaremos un flujo por grupo de trabajo.

   if(col == 0)
      grad_diag[row + var * rows] = IsNaNOrInf(local_diag[0], 0);
  }

Este enfoque nos permitirá optimizar los costosos accesos a la memoria global y distribuir al máximo la ejecución de las operaciones entre flujos paralelos, lo que a su vez reducirá el coste de entrenamiento del modelo.

Algoritmo de escaneo paralelo

Seguimos trabajando en la parte del programa OpenCL, pero ahora pasaremos a implementar los algoritmos del framework Attraos. Tenemos que implementar un algoritmo de escaneo paralelo, que se utiliza para actualizar de forma eficiente los valores del array de datos de origen X dadas las matrices de coeficientes de interacción A y los multiplicadores normalizadores H. La idea básica del algoritmo consiste en calcular iterativamente sumas prefijadas con partición binaria, lo que reducirá la complejidad computacional de O(L), típica de los métodos secuenciales, a O(log L).

El array X = {x0, x1, ..., xL-1} se actualiza con respecto a los elementos vecinos mediante la siguiente relación de recurrencia:

donde θ1 y θ2 se determinan durante los pasos iterativos del algoritmo. El vector A representa la matriz de coeficientes de interacción entre elementos vecinos, mientras que H se encarga de normalizar los resultados de los cálculos. Estos parámetros especifican una distribución adaptativa de los pesos, que permite considerar la estructura de los datos procesados y modelar eficazmente las dependencias complejas.

Implementaremos este proceso como parte del kernel de PScan. En los parámetros del kernel obtenemos los punteros a 4 búferes de datos. Tres de ellos contienen los datos de origen y uno registra los resultados.

__kernel void PScan(__global const float* A,
                    __global const float* X,
                    __global const float* H,
                    __global float* X_out)
  {
   const size_t idx = get_local_id(0);
   const size_t dim = get_global_id(1);
   const size_t L = get_local_size(0);
   const size_t D = get_global_size(1);

El funcionamiento de este kernel se planifica en un espacio de tareas bidimensional con flujos agrupados en grupos de trabajo en la primera dimensión. El cuerpo del kernel identifica los flujos en un espacio de tareas indicado y también determina su tamaño.

A continuación, se determina un número de iteraciones num_steps igual al logaritmo binario de la longitud de la secuencia.

   const int num_steps = (int)log2((float)L);

El uso del logaritmo binario garantiza el cálculo del número mínimo de iteraciones para una pasada completa sobre los datos, lo cual asegura una asignación óptima de los recursos del dispositivo informático.

Para optimizar el número de accesos a la costosa memoria global, se crean arrays locales que se utilizan para almacenar valores temporalmente.

   __local float local_A[1024];
   __local float local_X[1024];
   __local float local_H[1024];

Cada flujo carga datos de la memoria global en la memoria local. Esto reducirá la latencia de los accesos a los datos durante las operaciones posteriores y mejorará el rendimiento computacional global.

//--- Load data to local memory
   int offset = dim + idx * D;
   local_A[idx] = A[offset];
   local_X[idx] = X[offset];
   local_H[idx] = H[offset];
   barrier(CLK_LOCAL_MEM_FENCE);

Una vez cargados los datos, nos deberemos asegurar de sincronizar los flujos dentro del grupo de trabajo, asegurándonos de que los datos se lean y escriban correctamente antes de continuar con el cálculo.

A continuación, se realizará la etapa principal de las operaciones, que será la suma paralela de valores. El número de flujos activos se reducirá a la mitad en cada iteración del ciclo.

//--- Scan
#pragma unroll
   for(int step = 0; step < num_steps; step++)
     {
      int halfT = L >> (step + 1);
      if(idx < halfT)
        {
         int base = idx * 2;
         local_X[base + 1] += local_A[base + 1] * local_X[base];
         local_X[base + 1] *= local_H[base + 1];
         local_A[base + 1] *= local_A[base];
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }

En el cuerpo del ciclo, sumaremos los valores del array de datos de origen, a lo que seguirá una normalización basada en el coeficiente H y una actualización de los coeficientes de interacción A, que mantendrá la coherencia de los cálculos en el proceso de actualización iterativo. La optimización con #pragma unroll permite al compilador desplegar el ciclo por anticipado, reduciendo la sobrecarga de bifurcación y proporcionando un procesamiento de datos más eficiente.

Una vez completadas las iteraciones del ciclo, los valores resultantes se transferirán de la memoria local al búfer de resultados global.

//--- Save result
   X_out[offset] = local_X[idx];
  }

Este enfoque permitirá procesar los datos con mucha más rapidez y realizar exploraciones paralelas con un uso optimizado de los recursos informáticos.

El siguiente paso consistirá en construir el algoritmo de propagación inversa de errores del escaneo paralelo implementado anteriormente. Para ello, crearemos un nuevo kernel PScan_CalcHiddenGradient,cuya tarea principal consistirá en realizar la diferenciación de parámetros mediante el escaneo inverso.

En los parámetros del kernel, añadiremos los punteros a los búferes para registrar los gradientes de error correspondientes.

__kernel void PScan_CalcHiddenGradient(__global const float* A,
                                       __global float*  grad_A,
                                       __global const float* X,
                                       __global float*  grad_X,
                                       __global const float* H,
                                       __global float*  grad_H,
                                       __global const float* grad_X_out)
  {
   const size_t idx = get_local_id(0);
   const size_t dim = get_global_id(1);
   const size_t L = get_local_size(0);
   const size_t D = get_global_size(1);
   const int num_steps = (int)log2((float)L);

El algoritmo comenzará por identificar los flujos en un espacio de tareas similar al utilizado en el marco de la pasada inversa. Como la exploración paralela se realiza en múltiples iteraciones, el número de pasos se calculará como el logaritmo binario de la longitud de la secuencia, lo que permitirá descomponer el proceso en una estructura jerárquica con fusión secuencial de valores.

Un aspecto importante de esta implementación será minimizar los accesos a la memoria global, lo cual se conseguirá utilizando los arrays de memoria local. Esto mejorará significativamente el rendimiento porque la memoria local proporciona un acceso más rápido a los datos en comparación con la memoria global. Para almacenar los datos de origen y los valores intermedios de los gradientes de error, se declararán los búferes correspondientes.

   __local float local_A[1024];
   __local float local_X[1024];
   __local float local_H[1024];
   __local float local_grad_X[1024];
   __local float local_grad_A[1024];
   __local float local_grad_H[1024];

Tras declarar los arrays locales, transferiremos a ellos los datos de origen de los búferes globales. Esto permitirá que cada flujo cargue el elemento que le corresponda. A continuación, los flujos se sincronizarán dentro del grupo local para evitar conflictos de acceso.

//--- Load data to local memory
   int offset = idx * D + dim;
   local_A[idx] = A[offset];
   local_X[idx] = X[offset];
   local_H[idx] = H[offset];
   local_grad_X[idx] = grad_X_out[offset];
   local_grad_A[idx] = 0.0f;
   local_grad_H[idx] = 0.0f;
   barrier(CLK_LOCAL_MEM_FENCE);

Luego se realizará el paso clave del algoritmo, el escaneo inverso. Esta etapa se organizará como un proceso iterativo. En cada iteración, se reducirá el tamaño del array a procesar.

//--- Reverse Scan (Backward)
#pragma unroll
   for(int step = num_steps - 1; step >= 0; step--)
     {
      int halfT = L >> (step + 1);
      if(idx < halfT)
        {
         int base = idx * 2;
         // Compute gradients
         float grad_next = local_grad_X[base + 1] * local_H[base + 1];
         local_grad_H[base + 1] = local_grad_X[base + 1] * local_X[base];
         local_grad_A[base + 1] = local_grad_X[base + 1] * local_X[base];
         local_grad_X[base] += local_A[base + 1] * grad_next;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     } 

El cuerpo del ciclo calculará primero el número de flujos activos que participan en una iteración determinada (halfT). Y a continuación, el gradiente de error (grad_next) vendrá determinado por el producto del valor actual por el factor de normalización H correspondiente. A continuación, se calcularán las derivadas de los coeficientes de normalización H y los coeficientes de interacción A a partir del valor actual de X. Para propagar correctamente el error de forma inversa, el valor del gradiente X se corregirá en función del coeficiente de interacción. Y luego deberemos asegurarnos de sincronizar los flujos dentro del grupo de trabajo en cada iteración del ciclo.

Al final de las operaciones del kernel, los gradientes de error actualizados deberán transferirse de nuevo a la memoria global.

//--- Save gradients
   grad_A[offset] = local_grad_A[idx];
   grad_X[offset] = local_grad_X[idx];
   grad_H[offset] = local_grad_H[idx];
  }

Este método de procesamiento de datos ofrece una alta eficiencia computacional debido al uso de la memoria local y al mínimo número de accesos a la memoria global.

Con esto concluirá nuestro trabajo sobre el contexto OpenCL de esta implementación. Podrá ver el código completo del programa OpenCL en el archivo adjunto.

La siguiente etapa de nuestro trabajo consistirá en construir los algoritmos al margen del programa principal. Sin embargo, prácticamente hemos agotado la extensión del artículo. Así que tomaremos un breve descanso y volveremos a la construcción del framework Attraos en el próximo artículo.

Conclusión

En este artículo hemos presentado el framework Attraos, que ofrece un algoritmo de previsión de series temporales basado en métodos de la teoría del caos. Las series temporales se interpretan como proyecciones de sistemas dinámicos caóticos multidimensionales, lo cual permite revelar regularidades ocultas inaccesibles a los modelos estadísticos y de regresión tradicionales. El framework Attraos aplica mecanismos de reconstrucción del espacio de fases y de memoria dinámica, lo que ayuda a identificar dependencias no lineales estables en los datos del mercado y a mejorar la precisión de las previsiones.

A diferencia de los modelos lineales tradicionales, que no consideran las complejas interacciones multivariantes entre variables, Attraos opera con la estructura interna de los atractores caóticos, lo que proporciona no solo una gran precisión en la previsión de los valores posteriores de una serie temporal, sino también su adaptabilidad a las cambiantes condiciones del mercado. Este enfoque nos permite detectar componentes deterministas en procesos que a primera vista parecen arbitrarios. Esto resulta especialmente importante al analizar datos de alta frecuencia y pronosticar la actividad de instrumentos financieros a corto plazo.

En la parte práctica del artículo hemos comenzado a implementar nuestra propia visión de los enfoques propuestos mediante MQL5 con el uso de la tecnología OpenCL, que permite acelerar sustancialmente los cálculos gracias al procesamiento paralelo de datos en procesadores gráficos. Esta solución permite utilizar el método Attraos en sistemas comerciales reales y complejos analíticos automatizados, proporcionando un procesamiento de alta velocidad de grandes volúmenes de información y una rápida adaptación a las cambiantes condiciones del mercado.

En el próximo artículo, continuaremos la aplicación inicial de los enfoques propuestos y la llevaremos a su conclusión lógica, comprobando además la eficacia con datos históricos reales.

Enlaces

• Attractor Memory for Long-Term Time Series Forecasting: A Chaos Perspective
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor experto para recopilar ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema y la arquitectura del modelo
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código del programa OpenCL