
Creación de una estrategia de retorno a la media basada en el aprendizaje automático
Introducción
Este artículo propone otro enfoque original para crear sistemas comerciales basados en el aprendizaje automático. En el artículo anterior ya analizamos cómo aplicar la clusterización a la tarea de la inferencia causal. En este artículo, utilizaremos la clusterización para dividir las series temporales financieras en varios modos con propiedades únicas y, a continuación, construiremos y validaremos sistemas comerciales en cada modo.
Además, veremos algunas formas de etiquetado de ejemplos para estrategias de retorno a la media y las probaremos con el par de divisas EURGBP, que se considera plano, lo que significa que estas estrategias deberían ser totalmente aplicables a él.
Al final del artículo podremos entrenar diferentes modelos de aprendizaje automático en Python y convertirlos en sistemas comerciales para el terminal MetaTrader 5.
Preparando los paquetes necesarios
Los modelos se entrenarán en Python, así que asegúrese de tener instalados los siguientes paquetes:
import math import pandas as pd import pickle from datetime import datetime from catboost import CatBoostClassifier from sklearn.model_selection import train_test_split from sklearn.cluster import KMeans from bots.botlibs.labeling_lib import * from bots.botlibs.tester_lib import tester from bots.botlibs.export_lib import export_model_to_ONNX
Los 3 últimos módulos han sido escritos por mí y se adjuntarán al final del artículo. En cada uno de ellos se pueden importar otros paquetes como Scipy, Numpy, Sklearn, Numba, que también deben ser instalados. Son ampliamente conocidos y están a disposición del público, por lo que su instalación no debería suponer ningún problema.
Si tiene una versión limpia de Python, a continuación encontrará la lista de paquetes que necesitará instalar:
pip install numpy pip install pandas pip install scipy pip install scikit-learn pip install catboost pip install numba
Es posible que también tenga que usar rutas de importación absolutas para las bibliotecas que se adjuntan al final de este artículo, dependiendo de su entorno de desarrollo y de su ubicación.
El código está diseñado de tal forma que no es altamente dependiente de la versión del intérprete de Python o de un paquete en particular, pero es mejor utilizar versiones estables actuales.
Cómo etiquetar los ejemplos para las estrategias de retorno a la media
Recordemos cómo hemos etiquetado las etiquetas en artículos anteriores. Creamos un ciclo en el que la duración de cada transacción individual se fijaba aleatoriamente, por ejemplo, de 1 a 15 barras. A continuación, dependiendo de si el mercado ha subido o bajado durante el número de barras que han transcurrido desde la apertura de la transacción virtual, se ponía una etiqueta de compra o de venta. La función devolvía un marco de datos con las características y etiquetas marcadas, y el conjunto de datos ya estaba totalmente preparado para entrenar posteriormente un modelo de aprendizaje automático con él.
def get_labels(dataset, markup, min = 1, max = 15) -> pd.DataFrame: labels = [] for i in range(dataset.shape[0]-max): rand = random.randint(min, max) curr_pr = dataset['close'].iloc[i] future_pr = dataset['close'].iloc[i + rand] if (future_pr + markup) < curr_pr: labels.append(1.0) elif (future_pr - markup) > curr_pr: labels.append(0.0) else: labels.append(2.0) dataset = dataset.iloc[:len(labels)].copy() dataset['labels'] = labels dataset = dataset.dropna() dataset = dataset.drop( dataset[dataset.labels == 2.0].index) return dataset
Pero ese etiquetado tiene un gran inconveniente: es aleatorio. Al etiquetar los datos de este modo, no estamos estableciendo ninguna idea sobre qué patrones debe aproximar el modelo de aprendizaje automático. Por ello, el resultado de dicho etiquetado y formación también será mayoritariamente aleatorio. Intentamos solucionarlo mediante múltiples entrenamientos de fuerza bruta y haciendo más complejas las propias arquitecturas de los algoritmos, pero el etiquetado en sí seguía sin tener sentido. Debido al muestreo aleatorio, solo algunos modelos podían superar el OOS (prueba con datos nuevos).
En este artículo, proponemos un nuevo enfoque de etiquetado de transacciones basado en el filtrado de la serie temporal original. Veamos enseguida un ejemplo de este tipo de marcado.
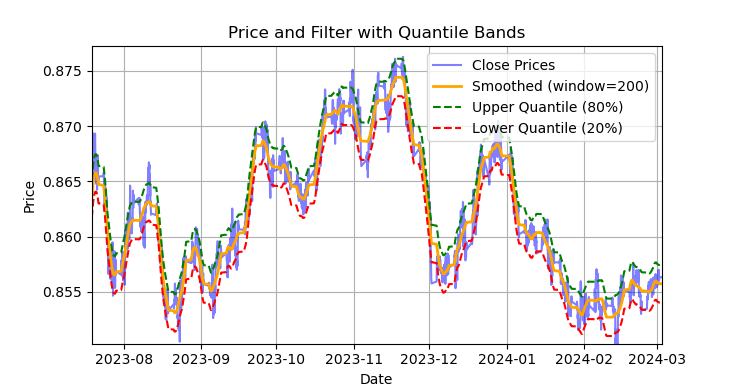
Fig. 1 representación del filtro Savitzky-Golei y bandas (cuantiles)
En la fig. 1 se muestra la línea de suavizado del filtro Savitsky-Golei y las bandas de 20 y 80 cuantiles, que recuerdan en cierto modo a las bandas de Bollinger. La principal diferencia entre el filtro Savitsky-Golei y la media móvil habitual es que no se retrasa respecto a los precios. Debido a esta propiedad, el filtro suaviza bien los precios, mientras que el "ruido" residual supone desviaciones de los valores medios (los valores del propio filtro), que pueden utilizarse para desarrollar una estrategia de regreso a la media. Cuando las bandas superior e inferior se cruzan, se forma una señal de venta o de compra. Si el precio cruza la línea superior, será una señal de venta. Si el precio cruza la línea inferior, será una señal de compra.
El filtro Savitzky-Golei es un filtro digital utilizado para suavizar los datos y suprimir el ruido, preservando al mismo tiempo las características importantes de la señal, como los picos y las tendencias. Fue propuesto por Abraham Savitzky y Marcel J. E. Golei en 1964, y es el primero de este tipo en el mundo. Este filtro se utiliza mucho en el procesamiento de señales y el análisis de datos.
El filtro Savitzky-Golei funciona a partir de la aproximación local de los datos usando un polinomio de grado bajo (normalmente de grado 2-4) usando el método de mínimos cuadrados. Así, se selecciona una vecindad (ventana) para cada punto de datos, y dentro de esa ventana los datos se aproximan mediante un polinomio. Tras la aproximación, el valor en el punto central de la ventana es sustituido por el valor calculado por el polinomio. Esto suaviza el ruido al tiempo que preserva la forma de la onda.
A continuación le mostramos el código para construir y evaluar visualmente el filtro.
def plot_close_filter_quantiles(dataset, rolling=200, quantiles=[0.2, 0.8], polyorder=3): # Calculate smoothed prices smoothed = savgol_filter(dataset['close'], window_length=rolling, polyorder=polyorder) # Calculate difference between prices and filter lvl = dataset['close'] - smoothed # Get quantile values q_low, q_high = lvl.quantile(quantiles).tolist() # Calculate bands based on quantiles upper_band = smoothed + q_high # Upper band lower_band = smoothed + q_low # Lower band # Create plot plt.figure(figsize=(14, 7)) plt.plot(dataset.index, dataset['close'], label='Close Prices', color='blue', alpha=0.5) plt.plot(dataset.index, smoothed, label=f'Smoothed (window={rolling})', color='orange', linewidth=2) plt.plot(dataset.index, upper_band, label=f'Upper Quantile ({quantiles[1]*100:.0f}%)', color='green', linestyle='--') plt.plot(dataset.index, lower_band, label=f'Lower Quantile ({quantiles[0]*100:.0f}%)', color='red', linestyle='--') # Configure display plt.title('Price and Filter with Quantile Bands') plt.xlabel('Date') plt.ylabel('Price') plt.legend() plt.grid(True) plt.show()
Por lo tanto, será un error utilizar este filtro en línea en series temporales no estacionarias, porque los últimos valores pueden redibujarse, pero para etiquetar transacciones en datos existentes resultará bastante adecuado.
Vamos a escribir el código que implementará el etiquetado de ejemplos de entrenamiento mediante el filtro Savitzky-Golei. La función de etiquetado, junto con otras funciones similares, se encuentra en el módulo de python labeling_lib.py, que luego importaremos a nuestro proyecto.
@njit def calculate_labels_filter(close, lvl, q): labels = np.empty(len(close), dtype=np.float64) for i in range(len(close)): curr_lvl = lvl[i] if curr_lvl > q[1]: labels[i] = 1.0 elif curr_lvl < q[0]: labels[i] = 0.0 else: labels[i] = 2.0 return labels def get_labels_filter(dataset, rolling=200, quantiles=[.45, .55], polyorder=3) -> pd.DataFrame: """ Generates labels for a financial dataset based on price deviation from a Savitzky-Golay filter. This function applies a Savitzky-Golay filter to the closing prices to generate a smoothed price trend. It then calculates trading signals (buy/sell) based on the deviation of the actual price from this smoothed trend. Buy signals are generated when the price is significantly below the smoothed trend, anticipating a potential price reversal. Args: dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column. rolling (int, optional): Window size for the Savitzky-Golay filter. Defaults to 200. quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.45, .55]. polyorder (int, optional): Polynomial order for the Savitzky-Golay filter. Defaults to 3. Returns: pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows: - 'labels' column: - 0: Buy - 1: Sell - Rows where 'labels' is 2 (no signal) are removed. - Rows with missing values (NaN) are removed. - The temporary 'lvl' column is removed. """ # Calculate smoothed prices using the Savitzky-Golay filter smoothed_prices = savgol_filter(dataset['close'].values, window_length=rolling, polyorder=polyorder) # Calculate the difference between the actual closing prices and the smoothed prices diff = dataset['close'] - smoothed_prices dataset['lvl'] = diff # Add the difference as a new column 'lvl' to the DataFrame # Remove any rows with NaN values dataset = dataset.dropna() # Calculate the quantiles of the 'lvl' column (price deviation) q = dataset['lvl'].quantile(quantiles).to_list() # Extract the closing prices and the calculated 'lvl' values as NumPy arrays close = dataset['close'].values lvl = dataset['lvl'].values # Calculate buy/sell labels using the 'calculate_labels_filter' function labels = calculate_labels_filter(close, lvl, q) # Trim the dataset to match the length of the calculated labels dataset = dataset.iloc[:len(labels)].copy() # Add the calculated labels as a new 'labels' column to the DataFrame dataset['labels'] = labels # Remove any rows with NaN values dataset = dataset.dropna() # Remove rows where the 'labels' column has a value of 2.0 (no signals) dataset = dataset.drop(dataset[dataset.labels == 2.0].index) # Return the modified DataFrame with the 'lvl' column removed return dataset.drop(columns=['lvl'])
Para acelerar el proceso de etiquetado, usaremos el paquete Numba, del que ya hablamos en el artículo anterior.
La función get_labels_filter() admite el conjunto de datos de origen con los precios y las características construidas sobre ellos, la longitud de la ventana de aproximación para el filtro, los límites de los cuantiles inferior y superior y el grado del polinomio. A la salida, esta función añade etiquetas de compra o venta al conjunto de datos de origen, que puede utilizarse como conjunto de datos de entrenamiento.
El ciclo transversal de la historia se implementa en una función calc_labels_filter independiente que realiza cálculos pesados a través del paquete Numba.
Estas marcas tienen sus propias peculiaridades:
- no todas las transacciones etiquetadas son rentables, porque las variaciones posteriores del precio después de cruzar las bandas no siempre van en la dirección opuesta. Esto puede dar lugar a ejemplos falsamente etiquetados como compra o venta.
- Esta desventaja, en teoría, se compensa por el hecho de que el etiquetado resulta homogéneo y no aleatorio, por lo que los ejemplos falsamente etiquetados pueden considerarse errores de entrenamiento o del sistema comercial en su conjunto, lo que puede dar lugar a un menor sobreentrenamiento en la salida.
A continuación le ofrecemos una descripción completa de la lógica del etiquetado de transacciones:
La función calculate_labels_filter
Datos de entrada:
- close: array de precios de cierre
- lvl: array de desviaciones del precio con respecto a la tendencia suavizada
- q: array de cuantiles que definen las zonas de la señal
Lógica:
1. Inicialización: Crea un array vacío de etiquetas de la misma longitud que close para almacenar las señales.
2. Ciclo por precios: Para cada precio close[i] y la desviación correspondiente lvl[i]:
- Señal "Sell": Si la desviación lvl[i] es mayor que el cuantil superior q[1], el precio estará muy por encima de la tendencia suavizada, lo cual indicará una señal "Sell" (labels[i] = 1.0).
- Señal "Buy": Si la desviación lvl[i] es inferior al cuantil inferior q[0], el precio estará muy por debajo de la tendencia suavizada, lo que indicará una señal "Buy" (labels[i] = 0,0).
- No hay señal: En otros casos (la desviación se encuentra entre los cuantiles), no se generará ninguna señal (labels[i] = 2,0).
3. Retorno del resultado: Devuelve un array labels con señales.
La función get_labels_filter
Datos de entrada:
- dataset: DataFrame con datos financieros que contiene una columna "close" (precios de cierre)
- rolling: tamaño de la ventana para suavizar el filtro Savitzky-Golay
- quantiles: cuantiles para definir zonas de las señales
- polyorder: orden polinómico para el suavizado de Savitzky-Golay
Lógica:
1. Suavizado de precios:
- Calculamos smoothed_prices usando el filtro Savitzky-Golay aplicado a los precios de cierre (dataset['close']).
2. Cálculo de la desviación:
- Calculamos la diferencia (diff) entre los precios de cierre reales y los precios suavizados.
- Añadimos la diferencia como una nueva columna 'lvl' en el DataFrame.
3. Eliminación de valores ausentes:
- Eliminamos las filas con valores ausentes (NaN) de DataFrame.
4. Cálculo de cuantiles:
- Calculamos los cuantiles de la columna "lvl" que se utilizarán para definir las zonas de señales.
5. Cálculo de señales:
- Llamamos a la función calculate_labels_filter, transmitiéndole los precios de cierre, las desviaciones y los cuantiles.
- Obtenemos un array labels con señales.
6. Procesamiento de DataFrame:
- Recortamos el DataFrame a la longitud del array labels.
- Añadimos el array labels como una nueva columna 'labels' en el DataFrame.
- Borramos las líneas donde 'labels' sea 2.0 (no hay señal).
- Eliminamos la columna temporal 'lvl'.
7. Retorno del resultado: Devolvemos el DataFrame modificado con señales "Buy" y "Sell" en la columna 'labels'.
El método de etiquetado anterior se considerará un punto de referencia, a través del cual se demostrarán los principios básicos del etiquetado para la estrategia de retorno a la media. Este es un método de trabajo que podemos usar. Podemos generalizarlo y modificarlo para el caso de filtros múltiples y para considerar la varianza variable de las desviaciones respecto a la media. A continuación le mostramos la función get_labels_multiple_filters que implementa dichos cambios.
@njit def calc_labels_multiple_filters(close, lvls, qs): labels = np.empty(len(close), dtype=np.float64) for i in range(len(close)): label_found = False for j in range(len(lvls)): curr_lvl = lvls[j][i] curr_q_low = qs[j][0][i] curr_q_high = qs[j][1][i] if curr_lvl > curr_q_high: labels[i] = 1.0 label_found = True break elif curr_lvl < curr_q_low: labels[i] = 0.0 label_found = True break if not label_found: labels[i] = 2.0 return labels def get_labels_multiple_filters(dataset, rolling_periods=[200, 400, 600], quantiles=[.45, .55], window=100, polyorder=3) -> pd.DataFrame: """ Generates trading signals (buy/sell) based on price deviation from multiple smoothed price trends calculated using a Savitzky-Golay filter with different rolling periods and rolling quantiles. This function applies a Savitzky-Golay filter to the closing prices for each specified 'rolling_period'. It then calculates the price deviation from these smoothed trends and determines dynamic "reversion zones" using rolling quantiles. Buy signals are generated when the price is within these reversion zones across multiple timeframes. Args: dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column. rolling_periods (list, optional): List of rolling window sizes for the Savitzky-Golay filter. Defaults to [200, 400, 600]. quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.05, .95]. window (int, optional): Window size for calculating rolling quantiles. Defaults to 100. polyorder (int, optional): Polynomial order for the Savitzky-Golay filter. Defaults to 3. Returns: pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows: - 'labels' column: - 0: Buy - 1: Sell - Rows where 'labels' is 2 (no signal) are removed. - Rows with missing values (NaN) are removed. """ # Create a copy of the dataset to avoid modifying the original dataset = dataset.copy() # Lists to store price deviation levels and quantiles for each rolling period all_levels = [] all_quantiles = [] # Calculate smoothed price trends and rolling quantiles for each rolling period for rolling in rolling_periods: # Calculate smoothed prices using the Savitzky-Golay filter smoothed_prices = savgol_filter(dataset['close'].values, window_length=rolling, polyorder=polyorder) # Calculate the price deviation from the smoothed prices diff = dataset['close'] - smoothed_prices # Create a temporary DataFrame to calculate rolling quantiles temp_df = pd.DataFrame({'diff': diff}) # Calculate rolling quantiles for the price deviation q_low = temp_df['diff'].rolling(window=window).quantile(quantiles[0]) q_high = temp_df['diff'].rolling(window=window).quantile(quantiles[1]) # Store the price deviation and quantiles for the current rolling period all_levels.append(diff) all_quantiles.append([q_low.values, q_high.values]) # Convert lists to NumPy arrays for faster calculations (potentially using Numba) lvls_array = np.array(all_levels) qs_array = np.array(all_quantiles) # Calculate buy/sell labels using the 'calc_labels_multiple_filters' function labels = calc_labels_multiple_filters(dataset['close'].values, lvls_array, qs_array) # Add the calculated labels to the DataFrame dataset['labels'] = labels # Remove rows with NaN values and no signals (labels == 2.0) dataset = dataset.dropna() dataset = dataset.drop(dataset[dataset.labels == 2.0].index) # Return the DataFrame with the new 'labels' column return dataset
Esta función es capaz de admitir un número ilimitado de parámetros de suavizado para el filtro Savitzky-Golei. Esto puede suponer una ventaja adicional, ya que en el etiquetado intervendrán varios filtros con periodos diferentes. Para generar una señal, bastará con que las desviaciones de la media, en la distancia de los límites cuantílicos, activen al menos uno de los filtros.
Esto permitirá crear una estructura jerárquica para etiquetar las transacciones. Por ejemplo, primero se comprueba la condición para el filtro de paso alto, luego la condición para el filtro de paso medio y, por último, la condición para el filtro de paso bajo. Las señales del filtro de paso bajo pueden considerarse más fiables, por lo que las señales anteriores serán sobrescritas por la señal del filtro de paso bajo, si se produce. Pero si el filtro de paso bajo no ha generado ninguna señal, las transacciones seguirán realizándose usando como base las señales de los filtros anteriores. Esto favorecerá los ejemplos más etiquetados y permitirá umbrales más altos para las entradas (cuantiles), ya que aumentará la probabilidad de que aparezca al menos una señal en el conjunto de filtros.
Los cuantiles se calcularán ahora en una ventana deslizante con un periodo personalizable, lo que permitirá considerar la varianza variable de las desviaciones respecto a la media, para obtener así señales más nítidas.
Por último, podemos considerar el caso de las transacciones asimétricas, suponiendo que el margen de compra y venta, debido a la asimetría de las cotizaciones medias, pueda requerir filtros con periodos de suavizado diferentes. Este enfoque se aplicará en la función get_labels_filter_bidirectional.
@njit def calc_labels_bidirectional(close, lvl1, lvl2, q1, q2): labels = np.empty(len(close), dtype=np.float64) for i in range(len(close)): curr_lvl1 = lvl1[i] curr_lvl2 = lvl2[i] if curr_lvl1 > q1[1]: labels[i] = 1.0 elif curr_lvl2 < q2[0]: labels[i] = 0.0 else: labels[i] = 2.0 return labels def get_labels_filter_bidirectional(dataset, rolling1=200, rolling2=200, quantiles=[.45, .55], polyorder=3) -> pd.DataFrame: """ Generates trading labels based on price deviation from two Savitzky-Golay filters applied in opposite directions (forward and reversed) to the closing price data. This function calculates trading signals (buy/sell) based on the price's position relative to smoothed price trends generated by two Savitzky-Golay filters with potentially different window sizes (`rolling1`, `rolling2`). Args: dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column. rolling1 (int, optional): Window size for the first Savitzky-Golay filter. Defaults to 200. rolling2 (int, optional): Window size for the second Savitzky-Golay filter. Defaults to 200. quantiles (list, optional): Quantiles to define the "reversion zones". Defaults to [.45, .55]. polyorder (int, optional): Polynomial order for both Savitzky-Golay filters. Defaults to 3. Returns: pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows: - 'labels' column: - 0: Buy - 1: Sell - Rows where 'labels' is 2 (no signal) are removed. - Rows with missing values (NaN) are removed. - Temporary 'lvl1' and 'lvl2' columns are removed. """ # Apply the first Savitzky-Golay filter (forward direction) smoothed_prices = savgol_filter(dataset['close'].values, window_length=rolling1, polyorder=polyorder) # Apply the second Savitzky-Golay filter (could be in reverse direction if rolling2 is negative) smoothed_prices2 = savgol_filter(dataset['close'].values, window_length=rolling2, polyorder=polyorder) # Calculate price deviations from both smoothed price series diff1 = dataset['close'] - smoothed_prices diff2 = dataset['close'] - smoothed_prices2 # Add price deviations as new columns to the DataFrame dataset['lvl1'] = diff1 dataset['lvl2'] = diff2 # Remove rows with NaN values dataset = dataset.dropna() # Calculate quantiles for the "reversion zones" for both price deviation series q1 = dataset['lvl1'].quantile(quantiles).to_list() q2 = dataset['lvl2'].quantile(quantiles).to_list() # Extract relevant data for label calculation close = dataset['close'].values lvl1 = dataset['lvl1'].values lvl2 = dataset['lvl2'].values # Calculate buy/sell labels using the 'calc_labels_bidirectional' function labels = calc_labels_bidirectional(close, lvl1, lvl2, q1, q2) # Process the dataset and labels dataset = dataset.iloc[:len(labels)].copy() dataset['labels'] = labels dataset = dataset.dropna() dataset = dataset.drop(dataset[dataset.labels == 2.0].index) # Remove bad signals (if any) # Return the DataFrame with temporary columns removed return dataset.drop(columns=['lvl1', 'lvl2'])
Esta función admite los periodos de suavizado rolling1 y rolling2, que se corresponden con las transacciones de venta y compra. Variando estos parámetros, podemos intentar conseguir un mejor etiquetado y una generalizabilidad de los nuevos datos de mayor de calidad. Por ejemplo, si un par de divisas tiene una tendencia alcista y resulta preferible abrir transacciones de compra, podemos aumentar la duración de la ventana roling1 para etiquetar las transacciones de venta, y estas serán cada vez menos, o se producirán solo en momentos de cambios de tendencia realmente fuertes. Y para las transacciones de compra se podrá reducir la duración de la ventana roling2, y entonces habrá más transacciones de compra que de venta.
Etiquetado con restricción de transacciones estrictamente rentables y con selección de filtro
Ya hemos mencionado anteriormente que los anotadores de transacciones propuestos permiten la presencia de transacciones etiquetadas cuyo carácter irrentable se conoce de antemano. No se trata de un error, sino más bien de una particularidad.
Podemos añadir comprobaciones para asegurarnos de que solo se etiquetan las transacciones rentables. Esto puede resultar útil si es necesario aproximar el gráfico de balance a una línea recta perfecta, sin reducciones significativas.
Además, solo hemos utilizado un filtro Savitzky-Golei, pero nos gustaría aumentar su variedad añadiendo una media móvil simple y un spline como filtros.
Vamos a echar un vistazo a las opciones de estos muestrarios de ofertas. Tomaremos como base la función get_labels_mean_reversion, que proporciona restricciones sobre la rentabilidad y la selección de filtros.
@njit def calculate_labels_mean_reversion(close, lvl, markup, min_l, max_l, q): labels = np.empty(len(close) - max_l, dtype=np.float64) for i in range(len(close) - max_l): rand = random.randint(min_l, max_l) curr_pr = close[i] curr_lvl = lvl[i] future_pr = close[i + rand] if curr_lvl > q[1] and (future_pr + markup) < curr_pr: labels[i] = 1.0 elif curr_lvl < q[0] and (future_pr - markup) > curr_pr: labels[i] = 0.0 else: labels[i] = 2.0 return labels def get_labels_mean_reversion(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=0) -> pd.DataFrame: """ Generates labels for a financial dataset based on mean reversion principles. This function calculates trading signals (buy/sell) based on the deviation of the price from a chosen moving average or smoothing method. It identifies potential buy opportunities when the price deviates significantly below its smoothed trend, anticipating a reversion to the mean. Args: dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column. markup (float): The percentage markup used to determine buy signals. min_l (int, optional): Minimum number of consecutive days the markup must hold. Defaults to 1. max_l (int, optional): Maximum number of consecutive days the markup is considered. Defaults to 15. rolling (float, optional): Rolling window size for smoothing/averaging. If method='spline', this controls the spline smoothing factor. Defaults to 0.5. quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.45, .55]. method (str, optional): Method for calculating the price deviation: - 'mean': Deviation from the rolling mean. - 'spline': Deviation from a smoothed spline. - 'savgol': Deviation from a Savitzky-Golay filter. Defaults to 'spline'. shift (int, optional): Shift the smoothed price data forward (positive) or backward (negative). Useful for creating a lag/lead effect. Defaults to 0. Returns: pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows: - 'labels' column: - 0: Buy - 1: Sell - Rows where 'labels' is 2 (no signal) are removed. - Rows with missing values (NaN) are removed. - The temporary 'lvl' column is removed. """ # Calculate the price deviation ('lvl') based on the chosen method if method == 'mean': dataset['lvl'] = (dataset['close'] - dataset['close'].rolling(rolling).mean()) elif method == 'spline': x = np.array(range(dataset.shape[0])) y = dataset['close'].values spl = UnivariateSpline(x, y, k=3, s=rolling) yHat = spl(np.linspace(min(x), max(x), num=x.shape[0])) yHat_shifted = np.roll(yHat, shift=shift) # Apply the shift dataset['lvl'] = dataset['close'] - yHat_shifted dataset = dataset.dropna() # Remove NaN values potentially introduced by spline/shift elif method == 'savgol': smoothed_prices = savgol_filter(dataset['close'].values, window_length=int(rolling), polyorder=3) dataset['lvl'] = dataset['close'] - smoothed_prices dataset = dataset.dropna() # Remove NaN values before proceeding q = dataset['lvl'].quantile(quantiles).to_list() # Calculate quantiles for the 'reversion zone' # Prepare data for label calculation close = dataset['close'].values lvl = dataset['lvl'].values # Calculate buy/sell labels labels = calculate_labels_mean_reversion(close, lvl, markup, min_l, max_l, q) # Process the dataset and labels dataset = dataset.iloc[:len(labels)].copy() dataset['labels'] = labels dataset = dataset.dropna() dataset = dataset.drop(dataset[dataset.labels == 2.0].index) # Remove sell signals (if any) return dataset.drop(columns=['lvl']) # Remove the temporary 'lvl' column
El código de la función get_labels que analizamos al principio de la sección y hemos utilizado en artículos anteriores se tomará como comprobación de la rentabilidad de las transacciones y también como su base. Este principio selecciona las transacciones que han pasado por el etiquetado usando el filtro. Solo se seleccionan las transacciones que, para un número determinado de pasos por delante, aportan beneficios; en caso contrario, se etiquetarán como 2,0 y se eliminarán del conjunto de datos. También se han añadido dos nuevos filtros: media móvil y spline.
Si el deslizamiento simple resulta ampliamente conocido en los círculos de tráders, el método de construcción del spline no es familiar para todos, y debe ser divulgado.
Las splines son una herramienta flexible para aproximar funciones. En lugar de construir un polinomio complejo para toda la función, los splines dividen el dominio de definición en intervalos y construyen polinomios independientes en cada intervalo. Estos polinomios se unen suavemente en los límites de los intervalos, creando una curva suave y continua.
Existen diferentes tipos de splines, pero todos se basan en un principio similar:
- Etiquetado del dominio de definición: el intervalo original sobre el que se define la función se particiona en subintervalos usando puntos denominados nodos.
- Selección del grado del polinomio: se define el grado del polinomio que se usará en cada subintervalo.
- Construcción de polinomios: en cada subintervalo, se construye un polinomio del grado seleccionado que pasa por los puntos de datos de ese intervalo.
- Garantía de la suavidad: los coeficientes de los polinomios se eligen de forma que se garantice la suavidad del spline en los límites del intervalo. Esto suele significar que los valores de los polinomios vecinos y sus derivadas deben coincidir en los nodos.
Los splines pueden resultar útiles en el análisis de series temporales financieras para:
- La interpolación y el suavizado de datos: los splines permiten suavizar el ruido de los datos y estimar los valores de las series temporales en los puntos en los que faltan mediciones.
- Modelización de tendencias: los splines pueden usarse para modelizar tendencias a largo plazo en los datos, separándolas de las fluctuaciones a corto plazo.
- Predicción: algunos tipos de splines pueden usarse para predecir valores futuros de una serie temporal.
- Estimación de las derivadas: los splines permiten estimar las derivadas de una serie temporal, lo cual puede ser útil para analizar la tasa de variación de los precios.
En nuestro caso, suavizaremos la serie temporal con un spline y una media móvil del mismo modo que hemos hecho con el filtro Savitzky-Golei. Podemos realizar el etiquetado usando cada filtro individualmente, y luego comparar los resultados y elegir el mejor para su situación particular.
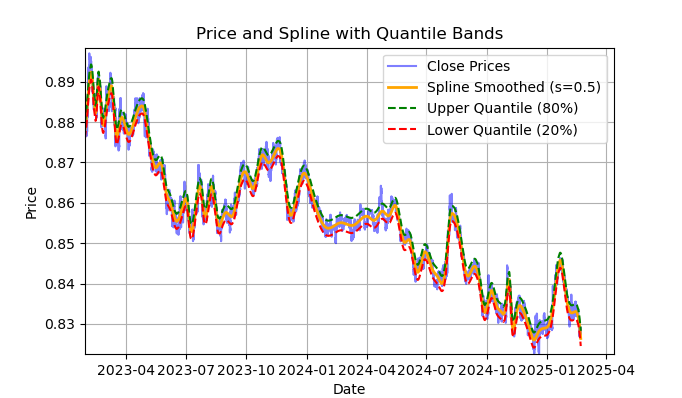
Fig. 2 visualización del filtro spline y las bandas (cuantiles)
En la fig. 2 se muestra la línea de suavizado del filtro spline y las bandas de los cuantiles 20 y 80. La principal diferencia entre el filtro spline y el filtro Savitzky-Golei es que este suaviza las series mediante funciones lineales o no lineales a trozos, dependiendo del factor de suavizado s, que se fija mejor en el intervalo 0,1;1 y del grado del polinomio, que suele fijarse en el intervalo 1 a 3. Variando estos parámetros, podemos evaluar visualmente las diferencias en el suavizado resultante. En el código, el grado del polinomio k=3 es fijo, también se puede cambiar.
El código para construir y evaluar visualmente el spline será el siguiente:
import pandas as pd from scipy.interpolate import UnivariateSpline import matplotlib.pyplot as plt def plot_close_filter_quantiles(dataset, rolling=200, quantiles=[0.2, 0.8]): """ Plots close prices with spline smoothing and quantile bands. Args: dataset (pd.DataFrame): DataFrame with 'close' column and datetime index. rolling (int, optional): Rolling window size for spline smoothing. Defaults to 200. quantiles (list, optional): Quantiles for band calculation. Defaults to [0.2, 0.8]. s (float, optional): Smoothing factor for UnivariateSpline. Adjusts the spline stiffness. Defaults to 1000. """ # Create spline smoothing # Convert datetime index to numerical values (Unix timestamps) numerical_index = pd.to_numeric(dataset.index) # Create spline smoothing using the numerical index spline = UnivariateSpline(numerical_index, dataset['close'], k=3, s=rolling) smoothed = spline(numerical_index) # Calculate difference between prices and filter lvl = dataset['close'] - smoothed # Get quantile values q_low, q_high = lvl.quantile(quantiles).tolist() # Calculate bands based on quantiles upper_band = smoothed + q_high lower_band = smoothed + q_low # Create plot plt.figure(figsize=(14, 7)) plt.plot(dataset.index, dataset['close'], label='Close Prices', color='blue', alpha=0.5) plt.plot(dataset.index, smoothed, label=f'Spline Smoothed (s={rolling})', color='orange', linewidth=2) plt.plot(dataset.index, upper_band, label=f'Upper Quantile ({quantiles[1]*100:.0f}%)', color='green', linestyle='--') plt.plot(dataset.index, lower_band, label=f'Lower Quantile ({quantiles[0]*100:.0f}%)', color='red', linestyle='--') # Configure display plt.title('Price and Spline with Quantile Bands') plt.xlabel('Date') plt.ylabel('Price') plt.legend() plt.grid(True) plt.show()
A continuación le ofrecemos una descripción detallada de toda la función calculate_labels_mean_reversion, para una comprensión completa del código de etiquetado de las transacciones.
La función calculate_labels_mean_reversion:
Datos de entrada:
- close: array de precios de cierre
- lvl: array de desviaciones de precios de la serie suavizada
- recargo: margen (en porcentaje)
- min_l: número mínimo de velas para comprobar la condición
- max_l: número máximo de velas para comprobar la condición
- array de cuantiles que definen las zonas de señales
Lógica:
1. Inicialización: Creamos un array de etiquetas vacía de longitud len(close) - max_l para almacenar las señales. Hemos acortado la longitud para tener en cuenta los futuros valores de los precios.
2. Ciclo por precios: Para cada precio close[i] con índice i de 0 a len(close) - max_l - 1:
- Definimos un número aleatorio rand entre min_l y max_l.
- Obtenemos el precio actual curr_pr, la desviación actual curr_lvl y el precio futuro future_pr para velas rand por delante.
- Señal "Sell": Si curr_lvl es mayor que el cuantil superior (q[1]) y el precio futuro future_pr incluido el margen es menor que el precio actual, estableceremos labels[i] = 1,0.
- Señal "Buy": Si curr_lvl es menor que el cuantil inferior (q[0]) y el precio futuro future_pr incluida la deducción del margen es mayor que el precio actual, establecemos labels[i] = 0,0.
- No hay señal: En los demás casos, establecemos labels[i] = 2,0.
3. Retorno del resultado: Devuelve un array labels con señales.
La función get_labels_mean_reversion:
Datos de entrada:
- dataset: DataFrame con datos financieros que contienen la columna 'close'
- recargo: margen (en porcentaje)
- min_l: número mínimo de velas para comprobar la condición
- max_l: número máximo de velas para comprobar la condición
- rolling: parámetro de suavizado (tamaño de la ventana o coeficiente)
- quantiles: cuantiles para definir zonas de las señales
- method: método de suavizado ('mean', 'spline', 'savgol')
- shift: desplazamiento de la serie suavizada
Lógica:
1. Cálculo de la desviación: Calculamos las desviaciones lvl de la serie de precios suavizada (close) según el método elegido:
- mean: desviación de la media móvil
- spline: desviación de la curva suavizada por spline
- savgol: desviación del filtro suavizado Savitzky-Golei
2. Eliminación de valores ausentes: eliminamos las filas con valores ausentes (NaN) del conjunto de datos.
3. Cálculo de cuantiles: calculamos los cuantiles q para las desviaciones lvl.
4. Preparación de los datos: extraemos los arrays de precios close y las desviaciones lvl del dataset.
5. Cálculo de señales:
- Llamamos a la función calculate_labels_mean_reversion con los datos preparados para obtener un array labels con señales.
6. Procesamiento de DataFrame:
- Recortamos el conjunto de datos a la longitud de las etiquetas.
- Añadimos labels como nueva columna 'labels' al conjunto de datos.
- Eliminamos las filas con omisiones (NaN) del conjunto de datos.
- Eliminamos las líneas en las que labels sean iguales a 2,0 (sin señal).
- Borramos la columna lvl.
Para variar, implementaremos una variante del mismo muestreador que compruebe las condiciones a través de múltiples filtros con diferentes periodos, en lugar de solo uno. Si se cumplen todas las condiciones para todos los filtros y tienen la misma dirección (compra o venta), y además la transacción es rentable para el intervalo de n barras en el futuro, entonces cumplirá las condiciones de margen, de lo contrario se ignorará y se eliminará de la muestra de entrenamiento.
@njit def calculate_labels_mean_reversion_multi(close_data, lvl_data, q, markup, min_l, max_l, windows): labels = [] for i in range(len(close_data) - max_l): rand = random.randint(min_l, max_l) curr_pr = close_data[i] future_pr = close_data[i + rand] buy_condition = True sell_condition = True qq = 0 for rolling in windows: curr_lvl = lvl_data[i, qq] if not (curr_lvl >= q[qq][1]): sell_condition = False if not (curr_lvl <= q[qq][0]): buy_condition = False qq+=1 if sell_condition and (future_pr + markup) < curr_pr: labels.append(1.0) elif buy_condition and (future_pr - markup) > curr_pr: labels.append(0.0) else: labels.append(2.0) return labels def get_labels_mean_reversion_multi(dataset, markup, min_l=1, max_l=15, windows=[0.2, 0.3, 0.5], quantiles=[.45, .55]): """ Generates labels for a financial dataset based on mean reversion principles using multiple smoothing windows. This function calculates trading signals (buy/sell) based on the deviation of the price from smoothed price trends calculated using multiple spline smoothing factors (windows). It identifies potential buy opportunities when the price deviates significantly below its smoothed trends across multiple timeframes. Args: dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column. markup (float): The percentage markup used to determine buy signals. min_l (int, optional): Minimum number of consecutive days the markup must hold. Defaults to 1. max_l (int, optional): Maximum number of consecutive days the markup is considered. Defaults to 15. windows (list, optional): List of smoothing factors (rolling window equivalents) for spline calculations. Defaults to [0.2, 0.3, 0.5]. quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.45, .55]. Returns: pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows: - 'labels' column: - 0: Buy - 1: Sell - Rows where 'labels' is 2 (sell signal) are removed. - Rows with missing values (NaN) are removed. """ q = [] # Initialize an empty list to store quantiles for each window lvl_data = np.empty((dataset.shape[0], len(windows))) # Initialize a 2D array to store price deviation data # Calculate price deviation from smoothed trends for each window for i, rolling in enumerate(windows): x = np.array(range(dataset.shape[0])) # Create an array of x-values (time index) y = dataset['close'].values # Extract closing prices spl = UnivariateSpline(x, y, k=3, s=rolling) # Create a spline smoothing function yHat = spl(np.linspace(min(x), max(x), num=x.shape[0])) # Generate smoothed price data lvl_data[:, i] = dataset['close'] - yHat # Calculate price deviation from smoothed prices q.append(np.quantile(lvl_data[:, i], quantiles).tolist()) # Calculate and store quantiles dataset = dataset.dropna() # Remove NaN values before proceeding close_data = dataset['close'].values # Extract closing prices # Calculate buy/hold labels using multiple price deviation series labels = calculate_labels_mean_reversion_multi(close_data, lvl_data, q, markup, min_l, max_l, windows) # Process the dataset and labels dataset = dataset.iloc[:len(labels)].copy() # Trim the dataset to match label length dataset['labels'] = labels # Add the calculated labels as a new column dataset = dataset.dropna() # Remove rows with NaN values dataset = dataset.drop(dataset[dataset.labels == 2.0].index) # Remove sell signals (if any) return dataset
Por último, escribiremos otra función de etiqueta comercial para volver a la media, que calculará los cuantiles en una ventana móvil con un periodo determinado en lugar de sobre toda la historia de observaciones. Esto ayudará a suavizar el impacto de la variable de volatilidad en la desviación de los precios respecto a la media.
@njit def calculate_labels_mean_reversion_v(close_data, lvl_data, volatility_group, quantile_groups, markup, min_l, max_l): labels = [] for i in range(len(close_data) - max_l): rand = random.randint(min_l, max_l) curr_pr = close_data[i] curr_lvl = lvl_data[i] curr_vol_group = volatility_group[i] future_pr = close_data[i + rand] q = quantile_groups[curr_vol_group] if curr_lvl > q[1] and (future_pr + markup) < curr_pr: labels.append(1.0) elif curr_lvl < q[0] and (future_pr - markup) > curr_pr: labels.append(0.0) else: labels.append(2.0) return labels def get_labels_mean_reversion_v(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=1, volatility_window=20) -> pd.DataFrame: """ Generates trading labels based on mean reversion principles, incorporating volatility-based adjustments to identify buy opportunities. This function calculates trading signals (buy/sell), taking into account the volatility of the asset. It groups the data into volatility bands and calculates quantiles for each band. This allows for more dynamic "reversion zones" that adjust to changing market conditions. Args: dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column. markup (float): The percentage markup used to determine buy signals. min_l (int, optional): Minimum number of consecutive days the markup must hold. Defaults to 1. max_l (int, optional): Maximum number of consecutive days the markup is considered. Defaults to 15. rolling (float, optional): Rolling window size or spline smoothing factor (see 'method'). Defaults to 0.5. quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.45, .55]. method (str, optional): Method for calculating the price deviation: - 'mean': Deviation from the rolling mean. - 'spline': Deviation from a smoothed spline. - 'savgol': Deviation from a Savitzky-Golay filter. Defaults to 'spline'. shift (int, optional): Shift the smoothed price data (lag/lead effect). Defaults to 1. volatility_window (int, optional): Window size for calculating volatility. Defaults to 20. Returns: pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows: - 'labels' column: - 0: Buy - 1: Sell - Rows where 'labels' is 2 (no signal) are removed. - Rows with missing values (NaN) are removed. - Temporary 'lvl', 'volatility', 'volatility_group' columns are removed. """ # Calculate Volatility dataset['volatility'] = dataset['close'].pct_change().rolling(window=volatility_window).std() # Divide into 20 groups by volatility dataset['volatility_group'] = pd.qcut(dataset['volatility'], q=20, labels=False) # Calculate price deviation ('lvl') based on the chosen method if method == 'mean': dataset['lvl'] = (dataset['close'] - dataset['close'].rolling(rolling).mean()) elif method == 'spline': x = np.array(range(dataset.shape[0])) y = dataset['close'].values spl = UnivariateSpline(x, y, k=3, s=rolling) yHat = spl(np.linspace(min(x), max(x), num=x.shape[0])) yHat_shifted = np.roll(yHat, shift=shift) # Apply the shift dataset['lvl'] = dataset['close'] - yHat_shifted dataset = dataset.dropna() elif method == 'savgol': smoothed_prices = savgol_filter(dataset['close'].values, window_length=rolling, polyorder=5) dataset['lvl'] = dataset['close'] - smoothed_prices dataset = dataset.dropna() # Calculate quantiles for each volatility group quantile_groups = {} for group in range(20): group_data = dataset[dataset['volatility_group'] == group]['lvl'] quantile_groups[group] = group_data.quantile(quantiles).to_list() # Prepare data for label calculation (potentially using Numba) close_data = dataset['close'].values lvl_data = dataset['lvl'].values volatility_group = dataset['volatility_group'].values # Calculate buy/sell labels labels = calculate_labels_mean_reversion_v(close_data, lvl_data, volatility_group, quantile_groups, markup, min_l, max_l) # Process dataset and labels dataset = dataset.iloc[:len(labels)].copy() dataset['labels'] = labels dataset = dataset.dropna() dataset = dataset.drop(dataset[dataset.labels == 2.0].index) # Remove sell signals # Remove temporary columns and return return dataset.drop(columns=['lvl', 'volatility', 'volatility_group'])
Así pues, ya disponemos de un cierto número de anotadores de transacciones con los que experimentar. Podemos combinar enfoques y crear otros nuevos.
A continuación le ofrecemos una lista completa de los muestreadores de transacciones anteriores de la biblioteca labelling_lib.py. Puede modificar los antiguos y crear otros nuevos basándose en ellos, dependiendo de lo bien que comprenda los patrones del mercado y del tipo de estrategia que quiera tener como resultado. El módulo contiene otros muestreadores de transacciones personalizados, pero no están relacionados con las estrategias de retorno a la media, por lo que no los describiremos en este artículo.
# FILTERING BASED LABELING W/O RESTRICTIONS def get_labels_filter(dataset, rolling=200, quantiles=[.45, .55], polyorder=3) -> pd.DataFrame def get_labels_multiple_filters(dataset, rolling_periods=[200, 400, 600], quantiles=[.45, .55], window=100, polyorder=3) -> pd.DataFrame def get_labels_filter_bidirectional(dataset, rolling1=200, rolling2=200, quantiles=[.45, .55], polyorder=3) -> pd.DataFrame: # MEAN REVERSION WITH RESTRICTIONS BASED LABELING def get_labels_mean_reversion(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=0) -> pd.DataFrame def get_labels_mean_reversion_multi(dataset, markup, min_l=1, max_l=15, windows=[0.2, 0.3, 0.5], quantiles=[.45, .55]) -> pd.DataFrame def get_labels_mean_reversion_v(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=1, volatility_window=20) -> pd.DataFrame:
Ha llegado el momento de pasar a la segunda parte del artículo: en ella, hablaremos de la clusterización de los modos de mercado y, a continuación, de la combinación de ambos enfoques para crear sistemas comerciales de rentabilidad media.
Qué clusterizar y para qué necesitamos esto
Antes de clusterizar nada, debemos decidir por qué necesitamos esto. Imaginemos un gráfico de cotizaciones donde tenemos tendencias, flat, periodos de volatilidad alta y baja, diversos patrones y otras características. Es decir, el gráfico de cotizaciones no es algo homogéneo donde se muestren los mismos patrones. Incluso podríamos decir que existen o pueden existir patrones diferentes en distintos periodos temporales que desaparecen en otros.
La clusterización permite dividir la serie temporal original en varios estados según determinadas características, de modo que cada uno de estos estados describa observaciones similares. Esto puede facilitar la construcción del sistema comercial, ya que el aprendizaje tendrá lugar sobre datos más homogéneos y similares. Al menos, así es como podemos imaginarlo. Naturalmente, el sistema comercial no funcionará en todo el periodo histórico, sino en una parte seleccionada, compuesta por diferentes momentos del tiempo cuyos valores de características caen dentro de este grupo concreto.
Tras la clusterización, solo los ejemplos seleccionados podrán dividirse, es decir, solo a estos se les podrán asignar etiquetas de clase únicas, para construir el modelo final. Si un clúster contiene datos homogéneos con observaciones similares, su etiquetado también debería ser más homogéneo y, en consecuencia, más predecible. Podemos tomar varios clústeres de datos, dividir cada clúster por separado y, a continuación, entrenar modelos de aprendizaje automático con los datos de cada clúster y validarlos con datos de entrenamiento y de prueba. Si encontramos una clusterización que permita al modelo entrenarse bien, es decir, generalizar y predecir sobre nuevos datos, la construcción del sistema comercial puede considerarse casi terminada.
Clusterización de series temporales financieras para identificar los modos de mercado
Antes de leer esta sección, le será útil familiarizarse con los diferentes tipos de algoritmos de clusterización que se describieron en el artículo anterior. Ahí también se proporciona una tabla comparativa de los distintos algoritmos de clusterización y sus resultados en las pruebas. Para este artículo, hemos elegido el algoritmo clásico de clusterización k-means, porque es el más rápido y resulta bastante eficiente.
En la fase de creación de características a través de la función get_features, deberemos prever la posibilidad de tener en el conjunto de datos exactamente aquellas características de las que se realizará el clusterización. Le sugiero considerar tres opciones básicas a partir de las cuales construir. Si tiene otras características que considere que describen bien los modos de mercado, puede utilizarlas libremente. Para ello, su cálculo deberá añadirse a la función de generación de características, y deberán contener símbolos "meta_feature" en su nombre, para separarlas aún más de las características principales.
def get_features(data: pd.DataFrame) -> pd.DataFrame: pFixed = data.copy() pFixedC = data.copy() count = 0 for i in hyper_params['periods']: pFixed[str(count)] = pFixedC.rolling(i).mean() count += 1 for i in hyper_params['periods_meta']: pFixed[str(count)+'meta_feature'] = pFixedC.rolling(i).skew() count += 1 # for i in hyper_params['periods_meta']: # pFixed[str(count)+'meta_feature'] = pFixedC.rolling(i).std() # count += 1 # for i in hyper_params['periods_meta']: # pFixed[str(count)+'meta_feature'] = pFixedC - pFixedC.rolling(i).mean() # count += 1 return pFixed.dropna()
El primer ciclo calculará todas las características especificadas en la lista "periods". Estas son las características clave que se utilizarán para entrenar el modelo de aprendizaje automático básico que predice las transacciones de compra o venta. En este caso, se trata de medias móviles simples con periodos distintos.
El segundo ciclo calculará las características especificadas en la lista "periods_meta". Estas son precisamente las características que intervendrán en el proceso de clusterización de los modos de mercado. Por defecto, la clusterización se calculará según la asimetría de las cotizaciones en la ventana deslizante. Los campos comentados corresponden al cálculo de características según la desviación estándar en una ventana deslizante, o según los incrementos de precio. La selección de características se realiza de forma empírica, mediante la enumeración de distintas opciones. Los experimentos han demostrado que la clusterización por asimetría separa bien los datos, así que la utilizaremos en el artículo.
La asimetría en las distribuciones es una característica que describe el grado en que una distribución de datos resulta asimétrica respecto a su media. Así, la asimetría indica cuánto se desvía la distribución respecto a una distribución simétrica (por ejemplo, una distribución normal). La asimetría se mide mediante el factor de asimetría (skewness). La clusterización por asimetría nos permite identificar grupos de datos con características de distribución similares, lo cual ayuda a identificar estos modos. Por ejemplo, una asimetría positiva puede indicar periodos con picos de precios raros pero intensos (por ejemplo, durante las crisis), mientras que una asimetría negativa puede indicar periodos con cambios más suaves.
Tras generar las características, el conjunto de datos final se transmite a la función que realiza la clusterización. Y le añade una nueva columna "clusters", que contiene los números de los clústeres.
def clustering(dataset, n_clusters: int) -> pd.DataFrame: data = dataset[(dataset.index < hyper_params['forward']) & (dataset.index > hyper_params['backward'])].copy() meta_X = data.loc[:, data.columns.str.contains('meta_feature')] data['clusters'] = KMeans(n_clusters=n_clusters).fit(meta_X).labels_ return data
Para eliminar el "peeking", los datos se recortan antes y después de las fechas establecidas en la configuración del algoritmo, de modo que la clusterización se realice solo en los datos que intervendrán en el proceso de formación del modelo. El código también incluye una selección de características para la clusterización seleccionadas mediante la palabra clave "meta_feature" en el nombre de la columna de características.
Todos los hiperparámetros del algoritmo se introducen en un diccionario cuyos datos se utilizarán para la composición de características, la selección del periodo de entrenamiento, etc.
hyper_params = {
'symbol': 'EURGBP_H1',
'export_path': '/Users/dmitrievsky/Library/Containers/com.isaacmarovitz.Whisky/Bottles/54CFA88F-36A3-47F7-915A-D09B24E89192/drive_c/Program Files/MetaTrader 5/MQL5/Include/Mean reversion/',
# 'export_path': '/Users/dmitrievsky/Library/Containers/com.isaacmarovitz.Whisky/Bottles/54CFA88F-36A3-47F7-915A-D09B24E89192/drive_c/Program Files (x86)/RoboForex MT4 Terminal/MQL4/Include/',
'model_number': 0,
'markup': 0.00010,
'stop_loss': 0.02000,
'take_profit': 0.00200,
'periods': [i for i in range(5, 300, 30)],
'periods_meta': [10],
'backward': datetime(2000, 1, 1),
'forward': datetime(2021, 1, 1),
'n_clusters': 10,
'rolling': 200,
} - El nombre del archivo del disco que contiene las cotizaciones del símbolo
- La ruta de exportación para exportar los modelos entrenados al directorio #include del terminal MetaTrader5.
- El número de identificación del modelo para distinguirlos tras la exportación cuando sea necesario exportar varios modelos.
- El markup, que debe tener en cuenta el spread medio y la comisión, en puntos, para etiquetar más correctamente las transacciones y comprobar posteriormente la historia.
- El stop loss respaldado por un rápido comprobador personalizado
- El take profit
- La lista de periodos para el cálculo de características clave. Cada elemento individual de la lista representa un periodo para un característica diferente. Cuantos más elementos, más características.
- Una lista de periodos para las características que intervienen en la clusterización.
- La fecha inicial de entrenamiento del modelo
- La fecha final del entrenamiento del modelo
- El número de clústeres (modos) en que se dividirán los datos
- El parámetro de ventana deslizante para el suavizado del filtro
Ahora vamos a juntarlo todo, a ver el ciclo básico de formación de modelos y a desglosar todos los pasos tanto del preprocesamiento como del entrenamiento propiamente dicho.
# LEARNING LOOP dataset = get_features(get_prices()) models = [] for i in range(1): data = clustering(dataset, n_clusters=hyper_params['n_clusters']) sorted_clusters = data['clusters'].unique() sorted_clusters.sort() for clust in sorted_clusters: clustered_data = data[data['clusters'] == clust].copy() if len(clustered_data) < 500: print('too few samples: {}'.format(len(clustered_data))) continue clustered_data = get_labels_filter(clustered_data, rolling=hyper_params['rolling'], quantiles=[0.45, 0.55], polyorder=3 ) print(f'Iteration: {i}, Cluster: {clust}') clustered_data = clustered_data.drop(['close', 'clusters'], axis=1) meta_data = data.copy() meta_data['clusters'] = meta_data['clusters'].apply(lambda x: 1 if x == clust else 0) models.append(fit_final_models(clustered_data, meta_data.drop(['close'], axis=1)))
En primer lugar, crearemos un conjunto de datos que contiene los precios y características. El proceso de creación de características se ha descrito anteriormente. A continuación, crearemos una lista de modelos para almacenar los modelos que ya han sido entrenados. Luego podremos elegir cuántas iteraciones de entrenamiento se realizarán en el ciclo. El valor predeterminado será una iteración. Si vamos a entrenar varios modelos, estableceremos el número de modelos en el iterador range().
A continuación, agruparemos el conjunto de datos de origen y le asignaremos a cada ejemplo un número de clúster. Si indicamos 10 n_clusters en los hiperparámetros, este parámetro se pasará a la función y se realizará la clusterización en 10 clústeres. Los experimentos han demostrado que 10 clústeres es el número óptimo de modos de mercado, pero por supuesto se puede experimentar con este parámetro.
A continuación, determinaremos el número total de clústeres, clasificaremos sus números ordinales en orden ascendente y, después, para cada número de clúster, solo seleccionaremos las filas del conjunto de datos que coincidan con él. No nos interesan los clústeres con muy pocas observaciones, por lo que comprobaremos que haya al menos 500 ejemplos.
El siguiente paso consistirá en llamar a la función de etiquetado de transacciones para el clúster actualmente seleccionado. En este caso, hemos tomado la primera función de etiquetado get_labels_filter, que es donde comenzó este artículo. Tras la etiquetado de las transacciones, los datos se dividirán en dos conjuntos de datos. El primer conjunto de datos contendrá las características y etiquetas principales, mientras que el segundo conjunto de datos contendrá las meta-características sobre las que se ha realizado el clusterización, así como las etiquetas 0 y 1. Una unidad indicará que los datos se corresponden con el clúster seleccionado, mientras que los ceros indicarán que se trata de cualquier otro clúster distinto del seleccionado. Al fin y al cabo, solo queremos que el sistema comercial negocie en un modo de mercado específico.
Así, el primer modelo aprenderá a predecir la dirección de una transacción, mientras que el segundo pronosticará cuándo se pueden abrir y cuándo no.
Veamos ahora la propia función fit_final_models, que toma dos conjuntos de datos para dos modelos finales y entrena el algoritmo CatBoost con ellos.
def fit_final_models(clustered, meta) -> list: # features for model\meta models. We learn main model only on filtered labels X, X_meta = clustered[clustered.columns[:-1]], meta[meta.columns[:-1]] X = X.loc[:, ~X.columns.str.contains('meta_feature')] X_meta = X_meta.loc[:, X_meta.columns.str.contains('meta_feature')] # labels for model\meta models y = clustered['labels'] y_meta = meta['clusters'] y = y.astype('int16') y_meta = y_meta.astype('int16') # train\test split train_X, test_X, train_y, test_y = train_test_split( X, y, train_size=0.7, test_size=0.3, shuffle=True) train_X_m, test_X_m, train_y_m, test_y_m = train_test_split( X_meta, y_meta, train_size=0.7, test_size=0.3, shuffle=True) # learn main model with train and validation subsets model = CatBoostClassifier(iterations=1000, custom_loss=['Accuracy'], eval_metric='Accuracy', verbose=False, use_best_model=False, task_type='CPU', thread_count=-1) model.fit(train_X, train_y, eval_set=(test_X, test_y), early_stopping_rounds=30, plot=False) # learn meta model with train and validation subsets meta_model = CatBoostClassifier(iterations=500, custom_loss=['F1'], eval_metric='F1', verbose=False, use_best_model=True, task_type='CPU', thread_count=-1) meta_model.fit(train_X_m, train_y_m, eval_set=(test_X_m, test_y_m), early_stopping_rounds=25, plot=False) R2 = test_model([model, meta_model], hyper_params['stop_loss'], hyper_params['take_profit']) if math.isnan(R2): R2 = -1.0 print('R2 is fixed to -1.0') print('R2: ' + str(R2)) return [R2, model, meta_model]
Descripción de las etapas de aprendizaje:
1. Preparación de datos:
- A partir de los marcos de datos de entrada clustered y meta, se extraen las características (X, X_meta) y etiquetas (y, y_meta).
- Los tipos de datos de las etiquetas se convierten a int16. Esto resulta necesario para convertir sin problemas el modelo al formato ONNX.
- Los datos se dividen en conjuntos de entrenamiento y de prueba usando train_test_split.
2. Entrenamiento del modelo básico:
- Se crea un objeto CatBoostClassifier con los hiperparámetros indicados.
- El modelo se entrena con datos de entrenamiento (train_X, train_y) usando un conjunto de pruebas (test_X, test_y) para detenerlo antes.
3. Entrenamiento del metamodelo:
- Se crea un objeto CatBoostClassifier para el metamodelo con los hiperparámetros indicados.
- El metamodelo se entrena de manera similar al modelo principal usando datos de entrenamiento y validación adecuados.
4. Evaluación de modelos:
- Los modelos entrenados (modelo, meta_modelo) se transmiten a la función test_model junto con los parámetros stop_loss y take_profit para evaluar su rendimiento.
- El valor retornado R2 representa la métrica de rendimiento del modelo.
5. Procesamiento de R2 y retorno del resultado:
- Si R2 es igual a NaN, se sustituirá por -1,0.
- El valor de R2 aparece en la pantalla.
- La función retorna una lista que contiene R2 y los modelos entrenados (model, meta_model).
Para cada clúster, el resultado son dos modelos de clasificador entrenados listos para la prueba visual final y la exportación al terminal MetaTrader 5. Debemos considerar que para cada iteración de entrenamiento se crearán tantos pares de modelos como clústeres se hayan indicado en los hiperparámetros. Este número deberá multiplicarse por el número de iteraciones para tener una idea de cuántos pares de modelos totales resultarán. Por ejemplo, dados 10 clústeres y 10 iteraciones, esto significará que en la salida tendremos 100 pares de modelos, excluyendo aquellos que no hayan sido filtrados para el número mínimo de ejemplos.
Entrenamiento y prueba de los modelos. Vamos a realizar las pruebas de nuestro algoritmo
Para un uso más cómodo del algoritmo, deberemos ejecutarlo en un entorno Python interactivo línea a línea. A continuación, podremos cambiar los hiperparámetros y experimentar con diferentes muestreadores. O pasar todo el código a formato .ipynb para ejecutarlo en IPython a través del portátil. Si va a ejecutar el script en su totalidad, todavía tendrá que editarlo para ajustar los parámetros.
Le propongo probar cada una de las funciones de etiquetado ejecutando 10 iteraciones para cada una. El resto de los parámetros serán los mismos que los establecidos en el script adjunto.
Tras ejecutar el ciclo de entrenamiento, se mostrarán los resultados del entrenamiento en cada iteración para cada clúster de datos.
R2: 0.9815970951474068 Iteration: 9, Cluster: 5 R2: 0.9914890771969395 Iteration: 9, Cluster: 6 R2: 0.9450681335265942 Iteration: 9, Cluster: 7 R2: 0.9631330369697314 Iteration: 9, Cluster: 8 R2: 0.9680380185183347 Iteration: 9, Cluster: 9 R2: 0.8203651933893291
A continuación, podrá ordenar todos los resultados en orden ascendente de R^2, para seleccionar el mejor. Y evaluar visualmente la curva de equilibrio en el simulador.
models.sort(key=lambda x: x[0]) test_model(models[-1][1:], hyper_params['stop_loss'], hyper_params['take_profit'], plt=True)
El valor resaltado indica que se probará el primer modelo del final. Es decir, el que tenga el R^2 más alto. Para probar el segundo a partir del modelo final, deberemos poner -2 y así sucesivamente. El simulador mostrará un gráfico de balance (azul) y un gráfico de pares de divisas (naranja), así como una línea vertical que separa el periodo de entrenamiento y los nuevos datos. Todos los modelos se entrenan desde principios de 2010 hasta principios de 2021, esto lo establecemos en los hiperparámetros. Podrá cambiar los intervalos de entrenamiento y prueba a su discreción. El periodo de prueba para todos los modelos de este artículo abarca desde principios de 2021 hasta principios de 2025.
Probando distintos muestreadores de transacciones
- get_labels_filter(dataset, rolling=200, quantiles=[.45, .55], polyorder=3)
A continuación se muestra el mejor resultado para el anotador get_labels_filter.
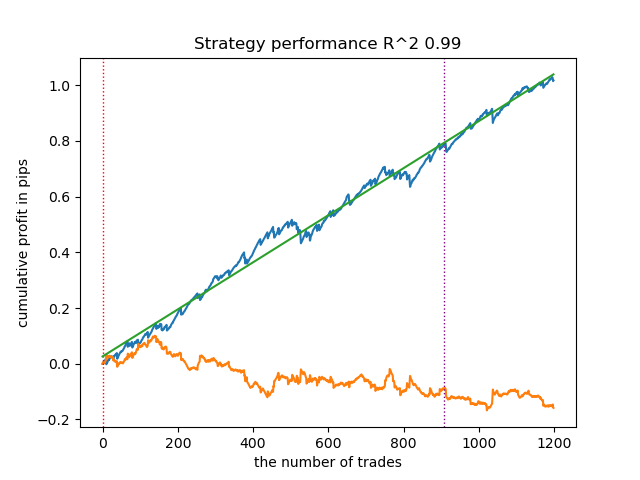
El anotador básico ha etiquetado bastante bien las transacciones y todos los modelos han sido rentables con los nuevos datos. Vamos a hacer lo mismo con el resto de los partidores y a ver los resultados.
- get_labels_multiple_filters(dataset,rolling_periods=[50,100,200],quantiles=[.45,.55],window=100,polyorder=3)
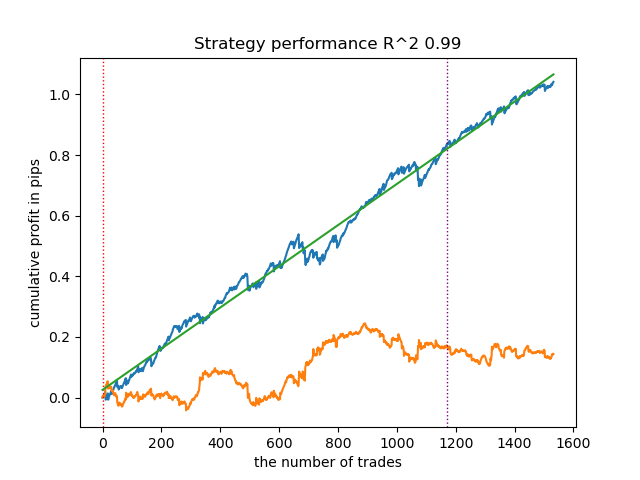
Los modelos entrenados con los datos de este anotador suelen mostrar un aumento del número de transacciones en relación con la base de referencia. Aquí no hemos experimentado con los ajustes porque el artículo sería demasiado largo.
- get_labels_filter_bidirectional(dataset, rolling1=50, rolling2=200, quantiles=[.45, .55], polyorder=3)
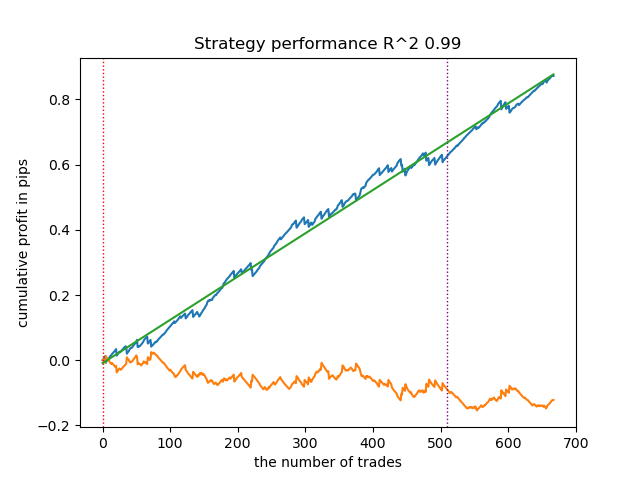
Este anotador asimétrico también ha demostrado su eficacia con datos nuevos. Seleccionando diferentes parámetros de suavizado por separado para las transacciones de compra y de venta, podemos lograr el resultado óptimo.
Ahora pasaremos a los anotadores con una restricción a las transacciones estrictamente rentables. Se ve bien que los anotadores anteriores no dan una curva de equilibrio suave ni siquiera en el periodo de entrenamiento, pero captan bien las pautas generales. Veamos qué cambia si eliminamos las transacciones perdedoras del conjunto de datos de entrenamiento.
- get_labels_mean_reversion(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=0)
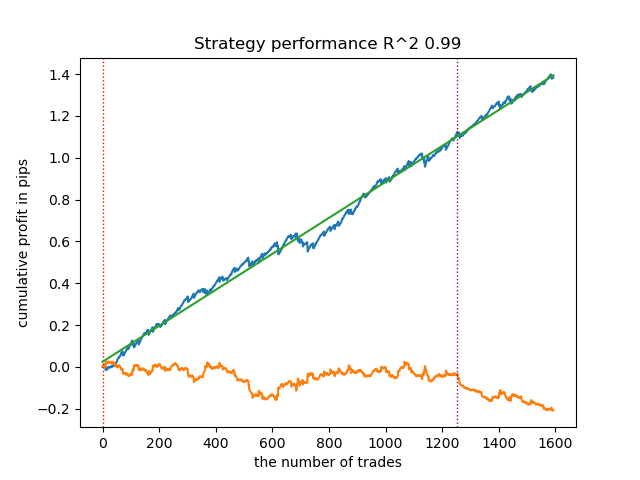
Hemos probado este anotador usando una spline como filtro y con un factor de suavizado fijo de 0,5. El artículo no incluye pruebas para el filtro Savitzky-Golei y la media móvil simple. No obstante, podemos ver que es posible conseguir curvas más suaves usando una restricción sobre la rentabilidad de las transacciones.
- get_labels_mean_reversion_multi(dataset, markup, min_l=1, max_l=15, windows=[0.2, 0.3, 0.5], quantiles=[.45, .55])
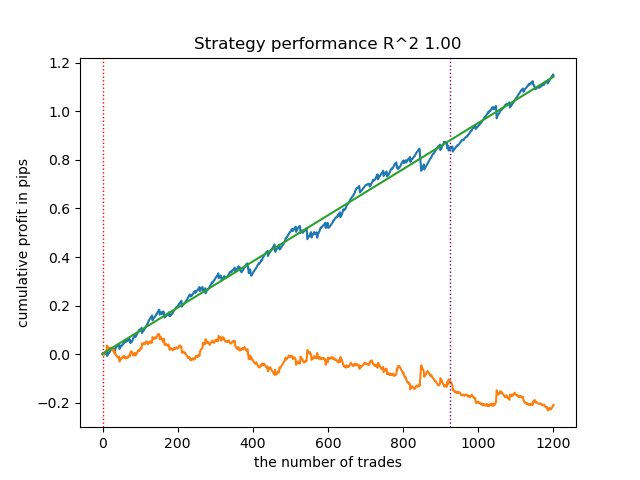
Este muestreador también es capaz de ofrecer muestras de calidad, gracias a las cuales, el modelo sigue negociando de forma rentable con nuevos datos.
- get_labels_mean_reversion_v(dataset, markup, min_l=1, max_l=15, rolling=0.2, quantiles=[.45, .55], method='spline', shift=0, volatility_window=20)
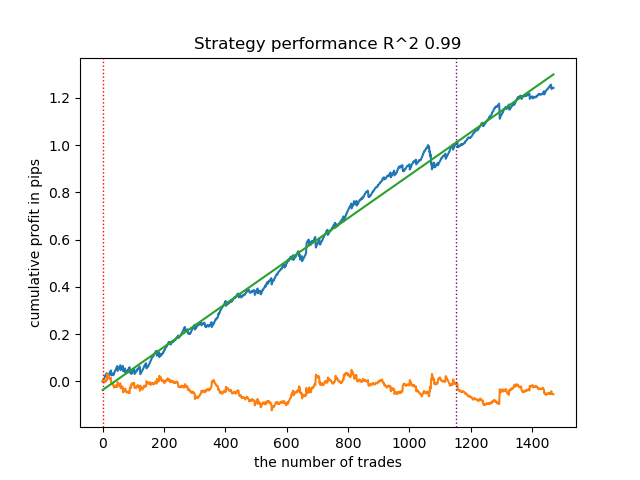
Este algoritmo también es capaz de demostrar un etiquetado aceptable y buenos modelos en la salida.
Conclusiones sobre los anotadores de transacciones:
- Cuando no sabemos por dónde empezar y todo nos parece demasiado complicado, podemos usar el muestreador más básico que pueda producir resultados aceptables.
- Si no obtenemos imágenes bonitas de inmediato, no olvide que en el etiquetado de transacciones y el entrenamiento de modelos hay componentes aleatorios. Solo tendrá que reiniciar el algoritmo varias veces.
- Todos los muestreadores con ajustes básicos pueden producir resultados aceptables. Para afinar más, deberá centrarse en uno de ellos y dedicarse a ajustar los parámetros.
Conclusiones sobre la clusterización:
- Entre bastidores, hemos realizado pruebas múltiples de los muestreadores sin utilizar la clusterización, así como de la clusterización sin utilizar los muestreadores. así, hemos visto en la práctica que por separado estos algoritmos no funcionan tan bien como en conjunto.
- No debemos crear demasiadas características sobre las que realizar la clusterización. Esto complicará el modelo y lo hará menos robusto con nuevos datos.
- El número óptimo de clústeres oscila entre 5 y 10. Menos clústeres provocan una escasa generalizabilidad y malos resultados sobre los nuevos datos, mientras que demasiados implican una fuerte reducción del número de transacciones.
Para facilitar su uso, descomente el anotador de transacciones deseado en el código.
# LEARNING LOOP dataset = get_features(get_prices()) models = [] for i in range(10): data = clustering(dataset, n_clusters=hyper_params['n_clusters']) sorted_clusters = data['clusters'].unique() sorted_clusters.sort() for clust in sorted_clusters: clustered_data = data[data['clusters'] == clust].copy() if len(clustered_data) < 500: print('too few samples: {}'.format(len(clustered_data))) continue clustered_data = get_labels_filter(clustered_data, rolling=hyper_params['rolling'], quantiles=[0.45, 0.55], polyorder=3 ) # clustered_data = get_labels_multiple_filters(clustered_data, # rolling_periods=[50, 100, 200], # quantiles=[.45, .55], # window=100, # polyorder=3) # clustered_data = get_labels_filter_bidirectional(clustered_data, # rolling1=50, # rolling2=200, # quantiles=[.45, .55], # polyorder=3) # clustered_data = get_labels_mean_reversion(clustered_data, # markup = hyper_params['markup'], # min_l=1, max_l=15, # rolling=0.5, # quantiles=[.45, .55], # method='spline', shift=0) # clustered_data = get_labels_mean_reversion_multi(clustered_data, # markup = hyper_params['markup'], # min_l=1, max_l=15, # windows=[0.2, 0.3, 0.5], # quantiles=[.45, .55]) # clustered_data = get_labels_mean_reversion_v(clustered_data, # markup = hyper_params['markup'], # min_l=1, max_l=15, # rolling=0.2, # quantiles=[.45, .55], # method='spline', # shift=0, # volatility_window=100) print(f'Iteration: {i}, Cluster: {clust}') clustered_data = clustered_data.drop(['close', 'clusters'], axis=1) meta_data = data.copy() meta_data['clusters'] = meta_data['clusters'].apply(lambda x: 1 if x == clust else 0) models.append(fit_final_models(clustered_data, meta_data.drop(['close'], axis=1))) # TESTING & EXPORT models.sort(key=lambda x: x[0]) test_model(models[-1][1:], hyper_params['stop_loss'], hyper_params['take_profit'], plt=True)
Exportación de modelos entrenados a MetaTrader 5
El penúltimo paso que queda es la exportación de los modelos entrenados y el archivo de encabezado al formato ONNX. El módulo export_lib.py adjunto al final de este artículo contiene la función export_model_to_ONNX(**kwargs). Veámosla con detalle.
def export_model_to_ONNX(**kwargs): model = kwargs.get('model') symbol = kwargs.get('symbol') periods = kwargs.get('periods') periods_meta = kwargs.get('periods_meta') model_number = kwargs.get('model_number') export_path = kwargs.get('export_path') model[1].save_model( export_path +'catmodel ' + symbol + ' ' + str(model_number) +'.onnx', format="onnx", export_parameters={ 'onnx_domain': 'ai.catboost', 'onnx_model_version': 1, 'onnx_doc_string': 'main model', 'onnx_graph_name': 'CatBoostModel_main' }, pool=None) model[2].save_model( export_path + 'catmodel_m ' + symbol + ' ' + str(model_number) +'.onnx', format="onnx", export_parameters={ 'onnx_domain': 'ai.catboost', 'onnx_model_version': 1, 'onnx_doc_string': 'meta model', 'onnx_graph_name': 'CatBoostModel_meta' }, pool=None) code = '#include <Math\Stat\Math.mqh>' code += '\n' code += '#resource "catmodel '+ symbol + ' '+str(model_number)+'.onnx" as uchar ExtModel_' + symbol + '_' + str(model_number) + '[]' code += '\n' code += '#resource "catmodel_m '+ symbol + ' '+str(model_number)+'.onnx" as uchar ExtModel2_' + symbol + '_' + str(model_number) + '[]' code += '\n\n' code += 'int Periods' + symbol + '_' + str(model_number) + '[' + str(len(periods)) + \ '] = {' + ','.join(map(str, periods)) + '};' code += '\n' code += 'int Periods_m' + symbol + '_' + str(model_number) + '[' + str(len(periods_meta)) + \ '] = {' + ','.join(map(str, periods_meta)) + '};' code += '\n\n' # get features code += 'void fill_arays' + symbol + '_' + str(model_number) + '( double &features[]) {\n' code += ' double pr[], ret[];\n' code += ' ArrayResize(ret, 1);\n' code += ' for(int i=ArraySize(Periods'+ symbol + '_' + str(model_number) + ')-1; i>=0; i--) {\n' code += ' CopyClose(NULL,PERIOD_H1,1,Periods' + symbol + '_' + str(model_number) + '[i],pr);\n' code += ' ret[0] = MathMean(pr);\n' code += ' ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n' code += ' ArraySetAsSeries(features, true);\n' code += '}\n\n' # get features code += 'void fill_arays_m' + symbol + '_' + str(model_number) + '( double &features[]) {\n' code += ' double pr[], ret[];\n' code += ' ArrayResize(ret, 1);\n' code += ' for(int i=ArraySize(Periods_m' + symbol + '_' + str(model_number) + ')-1; i>=0; i--) {\n' code += ' CopyClose(NULL,PERIOD_H1,1,Periods_m' + symbol + '_' + str(model_number) + '[i],pr);\n' code += ' ret[0] = MathSkewness(pr);\n' code += ' ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n' code += ' ArraySetAsSeries(features, true);\n' code += '}\n\n' file = open(export_path + str(symbol) + ' ONNX include' + ' ' + str(model_number) + '.mqh', "w") file.write(code) file.close() print('The file ' + 'ONNX include' + '.mqh ' + 'has been written to disk')
Deberemos transmitir una lista de argumentos a la función, tales como:
- model = models[-1]— lista de dos modelos entrenados que se ha rellenado previamente con modelos de diferentes iteraciones de entrenamiento. Usando la analogía del simulador, un índice -1 correspondería al modelo con el R^2 más alto; bajo el índice -2 estaría el segundo modelo más rápido, y así sucesivamente. Si le ha gustado un modelo concreto al realizar la prueba visual, use el mismo índice al exportar.
- symbol = hyper_params['symbol'] — nombre del símbolo, por ejemplo "EURGBP_H1", que se ha establecido en los hiperparámetros. Este nombre se añadirá al exportar los modelos para que podamos distinguir los modelos de los distintos personajes.
- periods = hyper_params['periods']— lista de periodos de las principales características del modelo.
- periods_meta = hyper_params['periods_meta'] — lista de periodos de características del modelo adicional que define el modo de mercado actual.
- model_number = hyper_params['model_number']— número de modelo, si exportamos muchos modelos y no queremos que se sobrescriban. Se añade a los nombres de los modelos.
-
export_path = hyper_params['export_path']— ruta para incluir la carpeta terminal o su subdirectorio para guardar los archivos en el disco.
La función guarda ambos modelos en formato .onnx y genera un archivo de encabezado a través del cual se llama a estos modelos y se calculan las características para ellos. Tenga en cuenta que el cálculo de los rasgos se realiza directamente en el terminal, por lo que deberá asegurarse de que sea idéntico a su cálculo en el script de Python. Podrá ver en el código que la función fill_arrays calcula medias móviles para el primer modelo, mientras que la función fill_arrays_m calcula la asimetría de precios para el segundo modelo. Si cambia las características en un script de Pyhon, cambiará su cálculo en esa función, o ya en el propio archivo de encabezado.
A continuación le mostramos un ejemplo de llamada a la propia función, para guardar modelos en el disco.
export_model_to_ONNX(model = models[-1], symbol = hyper_params['symbol'], periods = hyper_params['periods'], periods_meta = hyper_params['periods_meta'], model_number = hyper_params['model_number'], export_path = hyper_params['export_path'])
Creación de un bot comercial que utiliza modelos ONNX para realizar transacciones comerciales
Supongamos que hemos entrenado y seleccionado un modelo que nos haya gustado visualmente usando un probador personalizado como el siguiente:
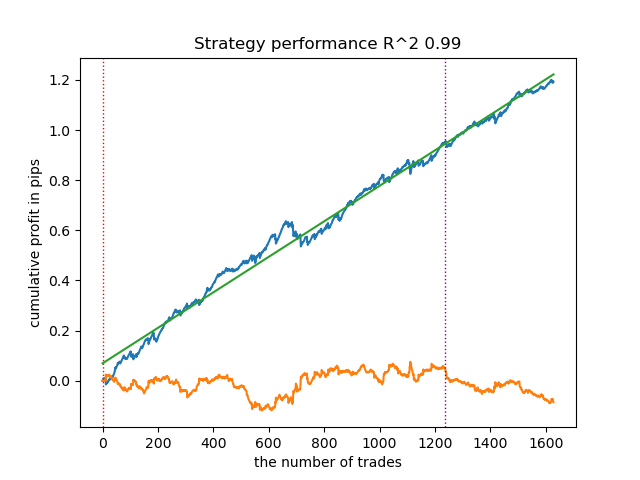
Ahora tendremos que llamar a la función de exportación en el terminal.
Después de exportar el modelo, aparecerán 3 archivos en la carpeta include/mean reversion/del terminal MetaTrader 5 (en mi caso se utiliza un subdirectorio para que no haya confusión entre otros modelos):
- catmodel EURGBP_H1 0.onnx — modelo principal que da señales de compra y venta
- catmodel_m EURGBP_H1 0.onnx — modelo adicional que permite o no la negociación
- EURGBP_H1 ONNX include 0.mqh — archivo de encabezado que importa estos modelos y calcula las características.
Los nombres de los modelos ONNX empiezan siempre por la palabra "catmodel" (que indica el modelo catboost), seguida del nombre del símbolo y el marco temporal. El modelo adicional se etiqueta con el sufijo _m de las palabras meta model. El nombre del archivo de encabezado siempre empieza por el símbolo comercial y termina con el número de modelo, que se establece durante la exportación para que los nuevos modelos exportados no se sobrescriban entre sí a menos que sea necesario.
Vamos a ver el contenido del archivo .mqh.
#include <Math\Stat\Math.mqh> #resource "catmodel EURGBP_H1 0.onnx" as uchar ExtModel_EURGBP_H1_0[] #resource "catmodel_m EURGBP_H1 0.onnx" as uchar ExtModel2_EURGBP_H1_0[] int PeriodsEURGBP_H1_0[10] = {5,35,65,95,125,155,185,215,245,275}; int Periods_mEURGBP_H1_0[1] = {10}; void fill_araysEURGBP_H1_0( double &features[]) { double pr[], ret[]; ArrayResize(ret, 1); for(int i=ArraySize(PeriodsEURGBP_H1_0)-1; i>=0; i--) { CopyClose(NULL,PERIOD_H1,1,PeriodsEURGBP_H1_0[i],pr); ret[0] = MathMean(pr); ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); } ArraySetAsSeries(features, true); } void fill_arays_mEURGBP_H1_0( double &features[]) { double pr[], ret[]; ArrayResize(ret, 1); for(int i=ArraySize(Periods_mEURGBP_H1_0)-1; i>=0; i--) { CopyClose(NULL,PERIOD_H1,1,Periods_mEURGBP_H1_0[i],pr); ret[0] = MathSkewness(pr); ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); } ArraySetAsSeries(features, true); }
Primero se conecta la biblioteca de matemáticas, que será necesaria para calcular la media y la asimetría, y potencialmente para otros momentos de distribuciones y otras matemáticas si fuera necesario cambiar el cálculo de las características. A continuación, nuestros dos modelos ONNX se cargarán como recursos que se utilizarán para generar señales comerciales. Luego se declararán los arrays con los periodos para calcular las características, que serán los datos de entrada para los modelos principal y meta.
Las dos funciones restantes rellenarán los arrays con los valores de las características. Recuerde que estos archivos se crean al exportar modelos desde un script de Python y no será necesario escribirlos desde cero cada vez. Es muy fácil conectar con un experto comercial. Esto resulta muy cómodo en los casos en que deseamos volver a entrenar el modelo después de algún tiempo; a continuación, solo tendremos que realizar una exportación a la terminal, el modelo se sobrescribirá con una más reciente, y volverá a compilar el bot sin hacer ningún cambio en el código. La abundancia de código puede intimidar al principio, pero en la práctica el aprendizaje se reduce a ejecutar un script y luego compilar el bot, lo cual puede llevar solo unos minutos de tiempo.
Ahora deberemos crear un asesor experto comercial al que se conectará este archivo de encabezado e inicializar los modelos ONNX.
#include <Mean reversion/EURGBP_H1 ONNX include 0.mqh> #include <Trade\Trade.mqh> #include <Trade\AccountInfo.mqh> #property strict #property copyright "Copyright 2025, Dmitrievsky max." #property link "https://www.mql5.com/ru/users/dmitrievsky" #property version "1.0" CTrade mytrade; CPositionInfo myposition; input bool Allow_Buy = true; //Allow BUY input bool Allow_Sell = true; //Allow SELL double main_threshold = 0.5; double meta_threshold = 0.5; sinput double MaximumRisk=0.001; //Progressive lot coefficient sinput double ManualLot=0.01; //Fixed lot, set 0 if progressive sinput ulong OrderMagic = 57633493; //Orders magic input int max_orders = 3; //Max positions number input int orders_time_delay = 5; //Time delay between positions input int max_spread = 20; //Max spread input int stoploss = 2000; //Stop loss input int takeprofit = 200; //Take profit input string comment = "mean reversion bot"; static datetime last_time = 0; #define Ask SymbolInfoDouble(_Symbol, SYMBOL_ASK) #define Bid SymbolInfoDouble(_Symbol, SYMBOL_BID) const long ExtInputShape [] = {1, ArraySize(PeriodsEURGBP_H1_0)}; const long ExtInputShape2 [] = {1, ArraySize(Periods_mEURGBP_H1_0)}; long ExtHandle = INVALID_HANDLE, ExtHandle2 = INVALID_HANDLE; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { mytrade.SetExpertMagicNumber(OrderMagic); ExtHandle = OnnxCreateFromBuffer(ExtModel_EURGBP_H1_0, ONNX_DEFAULT); ExtHandle2 = OnnxCreateFromBuffer(ExtModel2_EURGBP_H1_0, ONNX_DEFAULT); if(ExtHandle == INVALID_HANDLE || ExtHandle2 == INVALID_HANDLE) { Print("OnnxCreateFromBuffer error ", GetLastError()); return(INIT_FAILED); } if(!OnnxSetInputShape(ExtHandle, 0, ExtInputShape)) { Print("OnnxSetInputShape 1 failed, error ", GetLastError()); OnnxRelease(ExtHandle); return(-1); } if(!OnnxSetInputShape(ExtHandle2, 0, ExtInputShape2)) { Print("OnnxSetInputShape 2 failed, error ", GetLastError()); OnnxRelease(ExtHandle2); return(-1); } const long output_shape[] = {1}; if(!OnnxSetOutputShape(ExtHandle, 0, output_shape)) { Print("OnnxSetOutputShape 1 error ", GetLastError()); return(INIT_FAILED); } if(!OnnxSetOutputShape(ExtHandle2, 0, output_shape)) { Print("OnnxSetOutputShape 2 error ", GetLastError()); return(INIT_FAILED); } return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- OnnxRelease(ExtHandle); OnnxRelease(ExtHandle2); }
Lo más importante es inicializar correctamente la dimensionalidad de los arrays de entrada de cada modelo. Es igual al tamaño del array del archivo de encabezado que contiene los valores de periodo para el cálculo de características. Hay tantos valores de época como características.
La dimensionalidad de la salida para ambos modelos será igual a la unidad.
const long ExtInputShape [] = {1, ArraySize(PeriodsEURGBP_H1_0)}; const long ExtInputShape2 [] = {1, ArraySize(Periods_mEURGBP_H1_0)};
A continuación, asignamos manejadores a los modelos.
ExtHandle = OnnxCreateFromBuffer(ExtModel_EURGBP_H1_0, ONNX_DEFAULT); ExtHandle2 = OnnxCreateFromBuffer(ExtModel2_EURGBP_H1_0, ONNX_DEFAULT);
Y estableceremos la dimensionalidad correcta de las entradas y salidas en el cuerpo de la función de inicialización del bot.
if(!OnnxSetInputShape(ExtHandle, 0, ExtInputShape)) { Print("OnnxSetInputShape 1 failed, error ", GetLastError()); OnnxRelease(ExtHandle); return(-1); } if(!OnnxSetInputShape(ExtHandle2, 0, ExtInputShape2)) { Print("OnnxSetInputShape 2 failed, error ", GetLastError()); OnnxRelease(ExtHandle2); return(-1); }
Una vez eliminado el bot del gráfico, también se eliminarán los modelos.
El bot negocia en la apertura de cada nueva vela para acelerar los cálculos. Ahora tendremos que considerar la forma en que obtenemos las señales de nuestros modelos.
void OnTick() { if(!isNewBar()) return; double features[], features_m[]; fill_araysEURGBP_H1_0(features); fill_arays_mEURGBP_H1_0(features_m); double f[ArraySize(PeriodsEURGBP_H1_0)], f_m[ArraySize(Periods_mEURGBP_H1_0)]; for(int i = 0; i < ArraySize(PeriodsEURGBP_H1_0); i++) { f[i] = features[i]; } for(int i = 0; i < ArraySize(Periods_mEURGBP_H1_0); i++) { f_m[i] = features_m[i]; } static vector out(1), out_meta(1); struct output { long label[]; float proba[]; }; output out2[], out2_meta[]; OnnxRun(ExtHandle, ONNX_DEBUG_LOGS, f, out, out2); OnnxRun(ExtHandle2, ONNX_DEBUG_LOGS, f_m, out_meta, out2_meta); double sig = out2[0].proba[1]; double meta_sig = out2_meta[0].proba[1];
Orden en que se reciben las señales de los modelos ONNX:
- Se crean dos arrays features y features_m
- Se rellenan con valores de características usando las funciones fill_arrays correspondientes.
- El orden de los elementos en estos arrays se invierte en relación con el orden en que el modelo debe recibirlos. Por lo tanto, se crean los arrays f y f_m y se sobrescriben los datos en el orden deseado.
- Se crean dos vectores out y out_meta, que indican a los modelos la dimensionalidad de los vectores de salida.
- Se crea una estructura output que acepta las etiquetas y probabilidades 0;1 predichas. Las probabilidades se usan en el cálculo de las señales.
- Se crean dos instancias de la estructura output out2 y out2_meta para recibir las señales.
- Se ejecutan modelos a los que se pasan las características y dimensionalidades de los valores de salida; los modelos devuelven las predicciones.
- Las predicciones (probabilidades) se extraen de instancias de estructuras.
En conclusión, queda por analizar la lógica de la apertura de posiciones en función de las señales recibidas. Las señales de cierre funcionan con la lógica inversa.
// OPEN POSITIONS BY SIGNALS if((Ask-Bid < max_spread*_Point) && meta_sig > meta_threshold && AllowTrade(OrderMagic)) if(countOrders(OrderMagic) < max_orders && CheckMoneyForTrade(_Symbol, LotsOptimized(), ORDER_TYPE_BUY)) { double l = LotsOptimized(); if(sig < 1-main_threshold && Allow_Buy) { int res = -1; do { double stop = Bid - stoploss * _Point; double take = Ask + takeprofit * _Point; res = mytrade.PositionOpen(_Symbol, ORDER_TYPE_BUY, l, Ask, stop, take, comment); Sleep(50); } while(res == -1); } else { if(sig > main_threshold && Allow_Sell) { int res = -1; do { double stop = Ask + stoploss * _Point; double take = Bid - takeprofit * _Point; res = mytrade.PositionOpen(_Symbol, ORDER_TYPE_SELL, l, Bid, stop, take, comment); Sleep(50); } while(res == -1); } } }
En primer lugar, se comprueba la señal del segundo modelo. Si la probabilidad es superior a 0,5, esto significará que la apertura de transacciones está permitida (el mercado está en el modo correcto). A continuación, las condiciones se contrastarán con el modelo básico que predice la probabilidad de compra o venta. Una probabilidad < 0,5 indicará una compra, mientras que una probabilidad > 0,5 indicará una venta. En función de las condiciones, se abrirán las transacciones.
Ahora podremos compilar el bot y probarlo en el simulador de estrategias.
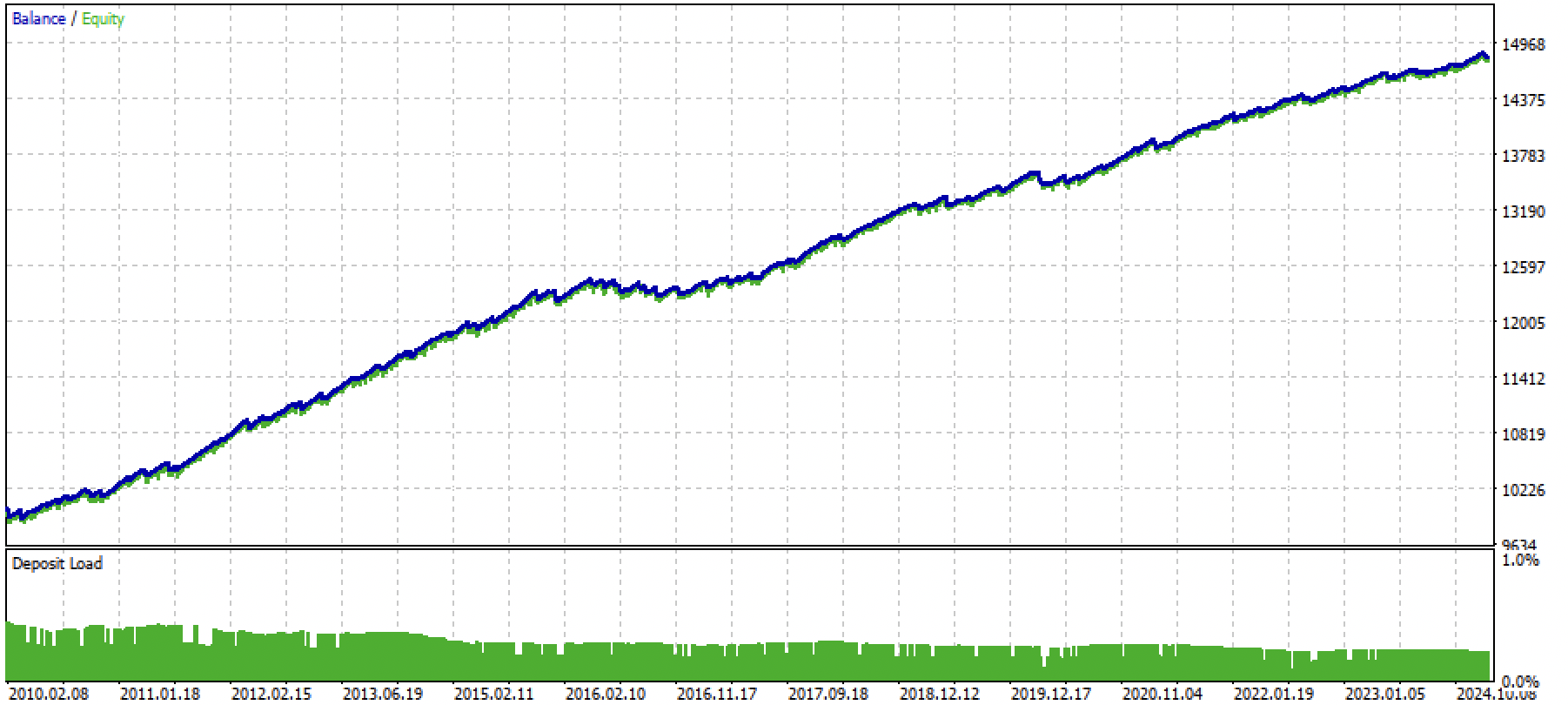
Fig. 3 prueba del modelo entrenado usando la estrategia de retorno a la media
Conclusión
Este artículo muestra todos los pasos para desarrollar una estrategia de retorno a la media usando el aprendizaje automático. Asimismo, esboza un enfoque completo: desde el etiquetado de las transacciones y la definición de los modos de mercado, hasta el entrenamiento de los modelos y la creación de un robot comercial completo.
El artículo va acompañado de todos los códigos necesarios para realizar experimentos por cuenta propia.
El fichero Python files.zip contiene los siguientes archivos para el desarrollo en el entorno Python:
| Nombre del archivo | Descripción |
|---|---|
| mean reversion.py | Script básico para el entrenamiento de modelos |
| labeling_lib.py | Módulo con anotadores de transacciones |
| tester_lib.py | Probador personalizado de estrategias basadas en el aprendizaje automático |
| export_lib.py | Biblioteca para exportar modelos al terminal MetaTrader 5 en formato ONNX |
| EURGBP_H1.csv | Archivo con las cotizaciones exportadas desde el terminal MetaTrader 5 |
El fichero MQL5 files.zip contiene archivos para el terminal MetaTrader 5:
| Nombre del archivo | Descripción |
|---|---|
| mean reversion.ex5 | Bot recopilado de este artículo |
| mean reversion.mq5 | Bot fuente del artículo |
| carpeta Include//Mean reversion | Asimismo, encontrará los modelos ONNX y el archivo de encabezado para conectarse al bot |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16457
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Creación de un Panel de administración de operaciones en MQL5 (Parte IX): Organización del código (II): Modularización
Creación de un Panel de administración de operaciones en MQL5 (Parte IX): Organización del código (II): Modularización
 Creación de un indicador canal de Keltner con gráficos personalizados en Canvas en MQL5
Creación de un indicador canal de Keltner con gráficos personalizados en Canvas en MQL5
 Redes neuronales en el trading: Integración de la teoría del caos en la previsión de series temporales (Final)
Redes neuronales en el trading: Integración de la teoría del caos en la previsión de series temporales (Final)
 Algoritmo de optimización del billar — Billiards Optimization Algorithm (BOA)
Algoritmo de optimización del billar — Billiards Optimization Algorithm (BOA)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Comprobado, todo me funciona. Adjunto los archivos de modelos entrenados del artículo y el bot actualizado arriba.
Es conveniente volver a entrenar los modelos después, porque hay modelos de demostración adjunta al artículo. Cuando usted entiende el script de python.
Sí, en esta versión el propio bot compila y funciona correctamente. Pero los modelos necesitan ser reentrenados. Y en general, según tengo entendido, debe hacerse con regularidad.
Me estoy familiarizando con python, pero todavía no lo entiendo todo. He rodado la versión principal de Rutop en mi portátil y la he actualizado a la versión actual. Instalé todos los paquetes necesarios (pandas, numba, numpy, catboost, scipy, scikit-learn). Descargué quotes. He puesto el fichero de quotes y todos los scripts en la carpeta Files del catálogo principal de MT5. He escrito las rutas en el código del script de entrenamiento del modelo. Pero algo no va al resultado.
corrijo el código del script en MetaEditore. Intento ejecutar el script desde allí. El proceso cae en un error (no encuentra el paquete bots python, y el intento de instalarlo según el esquema de instalación de otros paquetes también termina con un error). El mismo error se produce al ejecutar el script a través de la consola de python.
¿Puedes aconsejarme en qué dirección perforar el tema?
Buenos días!
Sí, en esta versión el bot compila y funciona correctamente. Pero los modelos necesitan ser reentrenados. Y en general, según tengo entendido, debe hacerse con regularidad.
Me estoy familiarizando con python, pero no todo funciona hasta ahora. Rodé la versión principal de Rutop en mi portátil y lo actualicé a la versión actual. Instalé todos los paquetes necesarios (pandas, numba, numpy, catboost, scipy, scikit-learn). Descargué quotes. He puesto el fichero de quotes y todos los scripts en la carpeta Files del catálogo principal de MT5. He escrito las rutas en el código del script de entrenamiento del modelo. Pero algo no va al resultado.
corrijo el código del script en MetaEditore. Intento ejecutar el script desde allí. El proceso cae en un error (no encuentra el paquete bots python, y el intento de instalarlo según el esquema de instalación de otros paquetes también termina con un error). El mismo error se produce al ejecutar el script a través de la consola de python.
¿Puedes aconsejarme en qué dirección perforar el tema?
Bots es sólo el directorio raíz (carpeta) donde se encuentran los módulos del artículo. Si el script no los ve al importar los módulos (archivos adicionales), entonces escribe las rutas completas a los archivos.
O ponga todos estos archivos en la misma carpeta que el script principal y haga esto en su lugar:
Esto puede ocurrir si no tenías PYTHONPATH prescrito cuando instalaste Python. Busca en internet cómo prescribirlo para tu sistema. Es decir, Python no ve los archivos del disco.
O lee un curso básico de importación de módulos en internet.
Bots es sólo un directorio raíz (carpeta) donde se encuentran los módulos del artículo. Si el script no los ve al importar módulos (archivos adicionales), escriba las rutas completas a los archivos.
O ponga todos estos archivos en la misma carpeta que el script principal y haga esto en su lugar:
Esto puede ocurrir si no tenías prescrito PYTHONPATH cuando instalaste Python. Busca en internet cómo prescribirlo para tu sistema. Es decir, python no ve los archivos en el disco.
O lee un curso básico de importación de módulos en internet.
Buenos días, Maxim. Gracias. Casi todo está resuelto. La última pregunta.
Hay líneas comentadas (154-182) en el script principal para modelos de entrenamiento. Según tengo entendido, se trata de muestreadores de reparto alternativos (marcas). Pero no puedo probarlos. Si se descomenta cualquiera de los marcadores (condicionalmente, líneas 154-158) y se comenta el original (líneas 149-153), el script no arranca.
¿Cuál puede ser la razón, dónde mirar?
Gracias )
Buenos días, Maxim. Muchas gracias. Casi todo está resuelto. La última pregunta.
Hay líneas comentadas (154-182) en el script principal para el entrenamiento de modelos. Según tengo entendido, se trata de muestreadores de reparto alternativos (marcas). Pero no puedo probarlos. Si se descomenta alguno de los marcadores (condicionalmente, líneas 154-158), y se comenta el original (líneas 149-153), el script no arranca.
¿Cuál puede ser la razón, dónde mirar?
Gracias )
Hola, necesitas logs de lo que escribe el intérprete de Python.
Buenos días, Maxim. Muchas gracias. Casi todo está resuelto. La última pregunta.
Hay líneas comentadas (154-182) en el script principal para el entrenamiento de modelos. Según tengo entendido, se trata de muestreadores de reparto alternativos (marcas). Pero no puedo probarlos. Si se descomenta alguno de los marcadores (condicionalmente, líneas 154-158), y se comenta el original (líneas 149-153), el script no arranca.
¿Cuál puede ser la razón, dónde mirar?
Gracias )
Comprueba si el texto no comentado está en la misma línea
No debería haber un subrayado como en la captura de pantalla de abajo