Optimización por herencia sanguínea — Blood inheritance optimization (BIO)
Contenido
Introducción
Un día, mientras observaba cómo una enfermera extraía sangre a los pacientes en el laboratorio, me surgió un pensamiento inesperado. Los grupos sanguíneos -este antiguo sistema de herencia, transmitido de generación en generación según estrictas leyes genéticas- adquirieron de repente una dimensión completamente nueva. ¿Y si estas cualidades naturales de la herencia pudieran usarse en el campo de los algoritmos de optimización?
Cada uno de nosotros lleva en sus venas una combinación única heredada de sus padres. Al igual que los grupos sanguíneos determinan la compatibilidad en la transfusión, estos podrían determinar los modos de transmisión y las mutaciones de los parámetros en el proceso de optimización. Me encantó la idea, así que decidí retomarla cuando tuviera tiempo para investigar. Cuando se presentó la oportunidad adecuada, me puse manos a la obra, y, tras varios experimentos, nació el algoritmo Blood Inheritance Optimisation (BIO), un método que utiliza las leyes naturales de la herencia de los grupos sanguíneos como metáfora para guiar la evolución de las soluciones. En él, los cuatro tipos de sangre han evolucionado en cuatro estrategias diferentes para mutar parámetros, mientras que las leyes de la herencia determinan cómo la descendencia adquiere y modifica las características de sus progenitores.
Al igual que en la naturaleza, el grupo sanguíneo de un niño no es una simple media de los grupos sanguíneos de los padres, sino que está sujeto a leyes genéticas; en el BIO los parámetros de las nuevas soluciones se forman igualmente a través de un sistema de herencia y mutaciones. Cada grupo sanguíneo aporta su propio enfoque para explorar el espacio de soluciones: desde la mantenimiento conservador de los mejores valores encontrados hasta mutaciones radicales que abren nuevas áreas y direcciones prometedoras para seguir explorando el espacio de soluciones.
En este artículo, queremos compartir los principios del algoritmo BIO, que combina la inspiración biológica con el rigor algorítmico, y ofrecer resultados de pruebas sobre características que ya conocemos. Bien, allá vamos.
Implementación del algoritmo
Para empezar, nos familiarizaremos con la tabla de herencia del grupo sanguíneo de la descendencia de los padres. Como podemos ver, la herencia del grupo sanguíneo no es homogénea. Existen algunas estadísticas interesantes sobre la distribución de los grupos sanguíneos en la población mundial. El grupo 1 (O) es el más común : alrededor del 40% de la población mundial es portadora de este. Le sigue el segundo grupo (A), que posee aproximadamente el 30% de la población. El tercer grupo (B) se encuentra en el 20% de la población, mientras que el cuarto grupo (AB) es el más raro, con solo un 10% de personas portadoras.
Al estudiar los mecanismos de la herencia, entendí que el primer grupo sanguíneo es recesivo con respecto a todos los demás. Esto significa que las personas con el grupo uno solo pueden transmitirlo a sus hijos. Al mismo tiempo, el segundo y el tercer grupo muestran codominancia entre sí, lo cual da lugar a un cuarto grupo cuando se combinan. Por cierto, desde un punto de vista evolutivo, el grupo sanguíneo cuatro es el más joven.
Resultan especialmente interesantes algunas de las propiedades únicas de los distintos grupos sanguíneos. Por ejemplo, el tipo 1 se considera el "donante universal" porque puede transfundirse a personas con cualquier tipo de sangre. El cuarto grupo, en cambio, convierte a sus portadores en "receptores universales": pueden admitir sangre de cualquier grupo.
Todas estas peculiaridades del sistema de grupos sanguíneos me inspiraron para crear los mecanismos correspondientes en mi algoritmo. Considerando el hecho de que el primer grupo sanguíneo es el básico y el más común, en el algoritmo se corresponderá con la estrategia de preservación de la mejor solución encontrada en el algoritmo. La tabla de herencia de grupos sanguíneos que muestra todas las combinaciones posibles de los grupos sanguíneos de los padres y los posibles grupos sanguíneos de sus hijos constituyó la base del mecanismo para determinar el "grupo sanguíneo" de una nueva solución usando como base los "grupos sanguíneos" de las soluciones parentales, lo que afecta directamente a la forma en que mutan los parámetros en el algoritmo BIO.
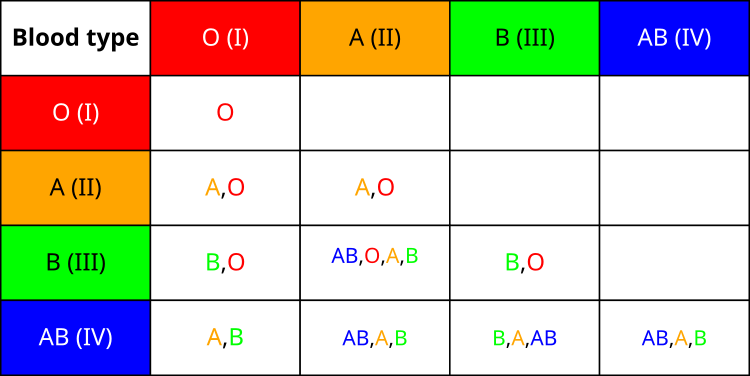
Figura 1. Tabla de herencia del grupo sanguíneo
La base del algoritmo BIO es una idea bastante simple: cada solución de la población (individuos parentales) se corresponde con su "grupo sanguíneo" (de 1 a 4), que viene determinado por su número ordinal en la población. Cuando creamos una nueva generación de soluciones, seleccionamos dos "padres" de la población actual. En este caso, la probabilidad de selección es cuadrática en lugar de lineal, lo cual significa que las mejores elecciones tienen muchas más posibilidades de convertirse en progenitores.
Y ahora viene la parte divertida. Basándonos en los grupos sanguíneos de los padres, usando una matriz especial de herencia (está escrita en el código en el método Init), determinamos los posibles grupos sanguíneos para el "hijo": la nueva solución. A continuación, para cada parámetro de esta nueva solución, si le ha tocado el primer grupo sanguíneo, tomaremos el valor de la mejor solución encontrada. Lo hemos hecho por analogía con el grupo sanguíneo 1 como donante universal. Si le toca el segundo grupo, tomaremos el valor de uno de los padres y le aplicaremos la distribución exponencial. Esto creará una tendencia a explorar los bordes del rango de parámetros. Con el tercer grupo, también tomaremos el valor de uno de los padres, pero lo moveremos hacia la mejor solución en una cantidad aleatoria. Y con el cuarto grupo, tomaremos el valor padre y lo reflejaremos en relación con los límites del rango, una especie de inversión que nos permitirá explorar nuevas áreas de búsqueda.
Tras crear una nueva generación, comprobaremos si han surgido soluciones mejores que la solución global actual y guardaremos los mejores individuos para la siguiente iteración. Así es como, usando una analogía con la herencia de grupos sanguíneos, nuestro algoritmo explorará el espacio de soluciones combinando diferentes estrategias de mutación de parámetros. A continuación presentamos el pseudocódigo del algoritmo.
Inicialización:
- Se crea una población de agentes con un tamaño popSize (por defecto es 50)
- Se crear una matriz de herencia de grupos sanguíneos que identifica los posibles grupos sanguíneos de los hijos en función de los grupos sanguíneos de los padres (1,2,3,4).
- Se inicializan los rangos de los parámetros (mín., máx., valores de paso)
Ciclo principal:
- Si se trata de la primera iteración (revisión = false):
- Se inicializan aleatoriamente las posiciones de todos los agentes dentro de los rangos de los parámetros.
- Se establece la bandera de revisión en true
- Para cada agente de la población:
- Se seleccionan los agentes parentales (padre y madre) mediante una distribución de probabilidad cuadrática
- Se determinan los grupos sanguíneos de ambos progenitores mediante la función: bloodType = 1 + (position_in_population % 4)
- Para cada parámetro de la solución hija:
- Se obtiene el posible grupo sanguíneo del hijo a partir de la matriz de herencia basada en los grupos sanguíneos de los padres.
- Si el grupo sanguíneo del hijo es 1:
- Se utiliza la mejor solución conocida para este parámetro.
- De lo contrario:
- Se selecciona aleatoriamente el valor del parámetro o bien del padre o bien de la madre
- Se aplica la mutación según el grupo sanguíneo del niño:
- Tipo 2: Se aplica la distribución exponencial con un exponente 20
- Tipo 3: Se desplaza el valor del parámetro hacia la mejor solución con un factor aleatorio
- Tipo 4: Se invierte el parámetro en todo el rango de parámetros
- Asegúrese de que el parámetro se mantiene dentro del intervalo válido y los límites del paso.
Fase de revisión:
- Se actualiza la mejor solución global si algún agente tiene mejor aptitud
- Se copia la población actual en la segunda mitad del array de población ampliada
- Se clasifica la población ampliada según la aptitud
- Se retienen los mejores agentes para la próxima generación
Vamos a escribir el código del algoritmo. La clase "C_AO_BIO", derivada de "C_AO", implementa el algoritmo BIO e implica el uso de una estructura de datos para representar individuos (agentes) en una población así como su control.
SetParams () — el método permite establecer los parámetros de la clase, en este caso se establece el tamaño de la población "popSize" a partir de un array de parámetros.
Init () — el método inicializa el algoritmo tomando los valores mínimo y máximo de los parámetros, el paso de cambio y el número de épocas.
Moving () y Revision () — los métodos son responsables del movimiento (evolución) de los agentes en la población y de su revisión (evaluación del rendimiento y selección de los mejores).
S_Papa y S_Mama:
- S_Papa — estructura que contiene un array de tipos de sangre (bTipos).
- S_Mama — contiene un array de cuatro objetos S_Papa, que sugieren "padres" para posteriores mezclas genéticas.
Esta forma de representar como estructuras obtendrá directamente el grupo sanguíneo probable del hijo a partir de los padres especificando el grupo sanguíneo de los padres, así "ma [1].pa [2].bTypes", donde "1" y "2" serán los grupos sanguíneos de la madre y el padre respectivamente.
El método GetBloodType () devuelve el tipo de sangre de un agente concreto, mientras que GetBloodMutation () implementa un mecanismo para mutar un gen en función del tipo de sangre.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BIO : public C_AO { public: //-------------------------------------------------------------------- C_AO_BIO () { ao_name = "BIO"; ao_desc = "Blood Inheritance Optimization"; ao_link = "https://www.mql5.com/es/articles/17246"; popSize = 50; // population size ArrayResize (params, 1); params [0].name = "popSize"; params [0].val = popSize; } void SetParams () { popSize = (int)params [0].val; } bool Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0); // number of epochs void Moving (); void Revision (); private: //------------------------------------------------------------------- struct S_Papa { int bTypes []; }; struct S_Mama { S_Papa pa [4]; }; S_Mama ma [4]; S_AO_Agent p []; int GetBloodType (int ind); void GetBloodMutation (double &gene, int indGene, int bloodType); }; //——————————————————————————————————————————————————————————————————————————————
El método "Init" inicializa una instancia de la clase "C_AO_BIO" y la prepara para trabajar, configurando la población de agentes y sus características: vamos a analizar la implementación de este método.
Llamada al método "StandardInit" — la primera línea comprueba el resultado de la llamada al método, que comprueba/inicializa los parámetros básicos necesarios para que el algoritmo funcione.
Inicialización de un array de agentes:
- Cambia el tamaño del array de agentes "p" al doble del tamaño de población dado "popSize".
- En un ciclo "for", se llama al método "Init" para cada agente, inicializando el agente utilizando los parámetros de coordenadas.
- A continuación, el método de tamaño establece los arrays de tipos de sangre (bTypes) para las estructuras "S_Mama" y "S_Papa".
- Para distintas combinaciones (por ejemplo, ma [0].pa [0], ma [1].pa [2], etc.), se establecen diferentes tipos de sangre según un array de herencia especial, mientras que el tamaño de los arrays se especifica mediante "ArrayResize".
Así, el método "Init" de la clase "C_AO_BIO" realiza una importante tarea de preparación del objeto para el algoritmo de optimización: crea una población de agentes, establece sus parámetros iniciales y define las reglas de vinculación para los tipos de sangre (herencia). Esto nos permitirá obtener instantáneamente el posible grupo sanguíneo de la descendencia, y utilizar sus parámetros "sanguíneos" para la evolución posterior dentro del algoritmo.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_BIO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (p, popSize * 2); for (int i = 0; i < popSize * 2; i++) p [i].Init (coords); //1-1 ArrayResize (ma [0].pa [0].bTypes, 1); ma [0].pa [0].bTypes [0] = 1; //2-2 ArrayResize (ma [1].pa [1].bTypes, 2); ma [1].pa [1].bTypes [0] = 1; ma [1].pa [1].bTypes [1] = 2; //3-3 ArrayResize (ma [2].pa [2].bTypes, 2); ma [2].pa [2].bTypes [0] = 1; ma [2].pa [2].bTypes [1] = 3; //1-2; 2-1 ArrayResize (ma [0].pa [1].bTypes, 2); ArrayResize (ma [1].pa [0].bTypes, 2); ma [0].pa [1].bTypes [0] = 1; ma [0].pa [1].bTypes [1] = 2; ma [1].pa [0].bTypes [0] = 1; ma [1].pa [0].bTypes [1] = 2; //1-3; 3-1 ArrayResize (ma [0].pa [2].bTypes, 2); ArrayResize (ma [2].pa [0].bTypes, 2); ma [0].pa [2].bTypes [0] = 1; ma [0].pa [2].bTypes [1] = 3; ma [2].pa [0].bTypes [0] = 1; ma [2].pa [0].bTypes [1] = 3; //1-4; 4-1 ArrayResize (ma [0].pa [3].bTypes, 2); ArrayResize (ma [3].pa [0].bTypes, 2); ma [0].pa [3].bTypes [0] = 2; ma [0].pa [3].bTypes [1] = 3; ma [3].pa [0].bTypes [0] = 2; ma [3].pa [0].bTypes [1] = 3; //2-3; 3-2 ArrayResize (ma [1].pa [2].bTypes, 4); ArrayResize (ma [2].pa [1].bTypes, 4); ma [1].pa [2].bTypes [0] = 1; ma [1].pa [2].bTypes [1] = 2; ma [1].pa [2].bTypes [2] = 3; ma [1].pa [2].bTypes [3] = 4; ma [2].pa [1].bTypes [0] = 1; ma [2].pa [1].bTypes [1] = 2; ma [2].pa [1].bTypes [2] = 3; ma [2].pa [1].bTypes [3] = 4; //2-4; 4-2; 3-4; 4-3; 4-4 ArrayResize (ma [1].pa [3].bTypes, 3); ArrayResize (ma [3].pa [1].bTypes, 3); ArrayResize (ma [2].pa [3].bTypes, 3); ArrayResize (ma [3].pa [2].bTypes, 3); ArrayResize (ma [3].pa [3].bTypes, 3); ma [1].pa [3].bTypes [0] = 2; ma [1].pa [3].bTypes [1] = 3; ma [1].pa [3].bTypes [2] = 4; ma [3].pa [1].bTypes [0] = 2; ma [3].pa [1].bTypes [1] = 3; ma [3].pa [1].bTypes [2] = 4; ma [2].pa [3].bTypes [0] = 2; ma [2].pa [3].bTypes [1] = 3; ma [2].pa [3].bTypes [2] = 4; ma [3].pa [2].bTypes [0] = 2; ma [3].pa [2].bTypes [1] = 3; ma [3].pa [2].bTypes [2] = 4; ma [3].pa [3].bTypes [0] = 2; ma [3].pa [3].bTypes [1] = 3; ma [3].pa [3].bTypes [2] = 4; return true; } //——————————————————————————————————————————————————————————————————————————————
El método "Moving" realiza etapas evolutivas en el proceso de optimización aplicando los conceptos de herencia y mutación a una población de agentes; vamos a analizarlos con más detalle:
Comprobación sobre la necesita de revisión — la primera parte del método comprueba si los agentes necesitan ser actualizados o "movidos" y si "revision" es "false"; se produce la inicialización (o actualización) inicial de las coordenadas de los agentes (a [i] .c [j]):
- Cada agente recibe valores aleatorios generados en el rango [rangeMin [j], rangeMax [j]] usando el método "u.RNDfromCI".
- A continuación, el valor se lleva al rango deseado mediante "u.SeInDiSp", que aplica el paso indicado en "rangeStep".
Cambiar al estado de revisión — después de la primera iteración, el parámetro "revision" se establece en "true" para cambiar al siguiente paso, y el método finaliza la ejecución (return).
Inicialización de variables — al principio del método se inicializan las variables responsables de los valores aleatorios y los tipos de sangre de los padres (papIND, mamIND, pBloodType, mBloodType, cBloodType y bloodIND).
Ciclo principal a través de la población (popSize) — el método realiza un ciclo a través de cada agente de la población:
- Se generan dos índices aleatorios para los padres (papIND y mamIND) mediante el método "u.RNDprobab ()", que genera probabilidades aleatorias.
- La función "GetBloodType" recupera los grupos sanguíneos de ambos progenitores.
Ciclo por las coordenadas (coords) — dentro del ciclo principal para cada coordenada del agente:
- Se selecciona un índice de grupo sanguíneo aleatorio del array "bTypes" de los padres seleccionados (en función del grupo sanguíneo de la madre y del padre).
- Si el tipo de sangre seleccionado es "1", el agente obtendrá el valor de "cB [c]". De lo contrario, se producirá la mezcla:
- El valor de las coordenadas de los agentes se selecciona al azar entre el padre o la madre.
- Se aplica la función "GetBloodMutation", que produce una mutación del valor elegido basada en el grupo sanguíneo.
- El valor se ajusta usando el método "u.SeInDiSp" para garantizar que se mantenga dentro de los límites aceptables.
El método Moving supone una parte clave del algoritmo que emula el proceso de evolución de la población de agentes e incluye tanto la inicialización aleatoria, como mecanismos de mutación y combinación de los parámetros de los agentes basados en los principios de la herencia de los grupos sanguíneos. El método combina aspectos de aleatoriedad y herencia para crear nuevos descendientes con valores distintos. Esto prepara a los agentes para una mayor optimización y exploración en el espacio de soluciones.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BIO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = u.RNDfromCI (rangeMin [j], rangeMax [j]); a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } revision = true; return; } //---------------------------------------------------------------------------- double rnd = 0.0; int papIND = 0; int mamIND = 0; int pBloodType = 0; int mBloodType = 0; int cBloodType = 0; int bloodIND = 0; for (int i = 0; i < popSize; i++) { rnd = u.RNDprobab (); rnd *= rnd; papIND = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1); rnd = u.RNDprobab (); rnd *= rnd; mamIND = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1); pBloodType = GetBloodType (papIND); mBloodType = GetBloodType (mamIND); for (int c = 0; c < coords; c++) { bloodIND = MathRand () % ArraySize (ma [mBloodType - 1].pa [pBloodType - 1].bTypes); cBloodType = ma [mBloodType - 1].pa [pBloodType - 1].bTypes [bloodIND]; if (cBloodType == 1) a [i].c [c] = cB [c]; else { if (u.RNDbool () < 0.5) a [i].c [c] = p [papIND].c [c]; else a [i].c [c] = p [mamIND].c [c]; GetBloodMutation (a [i].c [c], c, cBloodType); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
El método "GetBloodType" determina el grupo sanguíneo basándose en el índice "ind" transmitido: la posición actual en la población. Así, el método sirve para asignar índices a tipos sanguíneos usando una simple operación aritmética con un resto. Esto permite alternar los tipos de sangre entre los índices disponibles (0-3).
//—————————————————————————————————————————————————————————————————————————————— int C_AO_BIO::GetBloodType (int ind) { if (ind % 4 == 0) return 1; if (ind % 4 == 1) return 2; if (ind % 4 == 2) return 3; if (ind % 4 == 3) return 4; return 1; } //——————————————————————————————————————————————————————————————————————————————
El método "GetBloodMutation" está diseñado para modificar (mutación) el valor de un parámetro genético (gen) en según su grupo sanguíneo e índice.
Parámetros:
- gene — referencia al valor del gen que se modificará
- indGene — índice de genes que se utiliza para obtener rangos de mutación
- bloodType — grupo sanguíneo que determina la lógica de la mutación
Tipo de Sangre 2 — aplica una "PowerDistribution" escalonada al valor del gen, que cambia el gen basándose en un rango dado, distribuyendo probabilísticamente los valores a su alrededor.
Grupo sanguíneo 3 — el gen se incrementa en una fracción de la diferencia entre el mejor valor actual del gen en la población "cB [indGene]" y el valor actual del gen. La fracción de desplazamiento viene determinada por un número aleatorio [0,0; 1,0].
Otros tipos de sangre (por defecto) — el gen se cambia para que su nuevo valor sea simétrico al rango dado (inversión), estando entre "rangoMin [indGene]" y "rangoMax [indGene]".
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BIO::GetBloodMutation (double &gene, int indGene, int bloodType) { switch (bloodType) { case 2: gene = u.PowerDistribution (gene, rangeMin [indGene], rangeMax [indGene], 20); return; case 3: gene += (cB [indGene] - gene) * u.RNDprobab (); return; default: { gene = rangeMax [indGene] - (gene - rangeMin [indGene]); } } } //——————————————————————————————————————————————————————————————————————————————
El método "Revision" se encarga de actualizar y clasificar la población en el algoritmo BIO. En el primer ciclo "for" (de 0 a popSize), el método itera todos los miembros de la población "a[i]". Si el valor de la función de aptitud "f" del miembro actual de la población "a[i].f" supera el mejor valor actual "fB", "fB" se actualizará con el nuevo valor, y las coordenadas "c" del miembro actual de la población se copiarán en el array "cB". En el segundo ciclo "for", los miembros actuales de la población "a[i]" se copian al final del array "p", empezando por el índice "popSize". A continuación, se crea un array temporal "pT" que tiene el doble del tamaño de la población actual "popSize * 2". Luego se llama al método de clasificación "u.Sorting" para clasificar el array combinado "p", almacenando los resultados en "pT".
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BIO::Revision () { //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { // Update the best global solution if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { p [popSize + i] = a [i]; } S_AO_Agent pT []; ArrayResize (pT, popSize * 2); u.Sorting (p, pT, popSize * 2); } //——————————————————————————————————————————————————————————————————————————————
Resultados de las pruebas
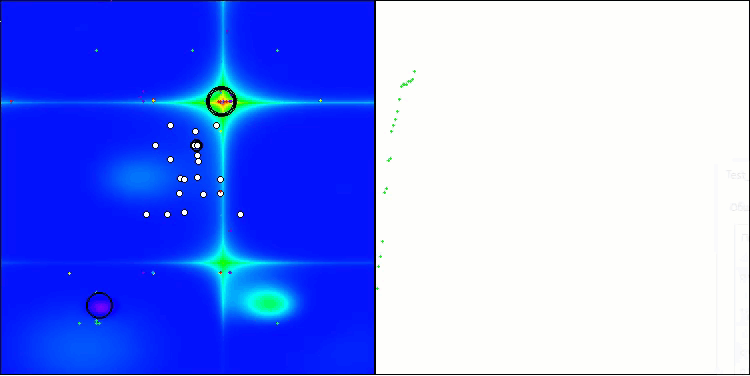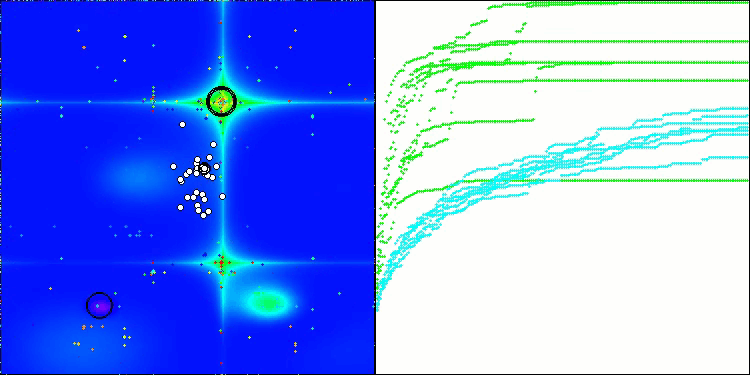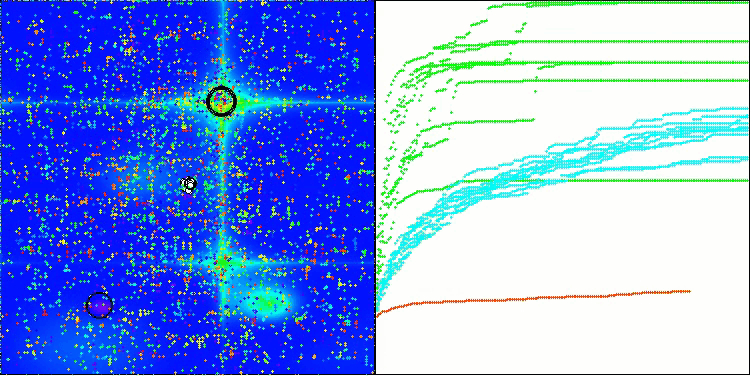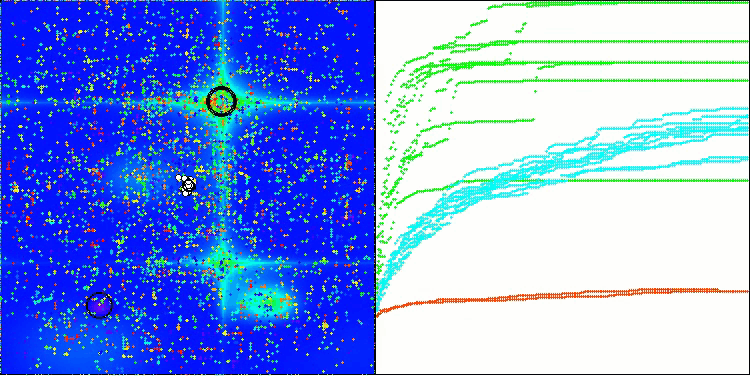
Hemos probado el algoritmo con tres funciones de prueba diferentes (Hilly, Forest y Megacity) con diferentes dimensiones del espacio de búsqueda (5*2, 25*2 y 500*2 dimensiones) con 10.000 cálculos de la función objetivo. El resultado global del 53,80% indica que el BIO se sitúa en una posición intermedia entre los algoritmos de optimización basados en la población, lo que es bastante positivo para un método nuevo.
=============================
5 Hilly's; Func runs: 10000; result: 0.8156790458423091
25 Hilly's; Func runs: 10000; result: 0.6533623929914842
500 Hilly's; Func runs: 10000; result: 0.3087659267627686
=============================
5 Forest's; Func runs: 10000; result: 0.8993708810337727
25 Forest's; Func runs: 10000; result: 0.6531872390668734
500 Forest's; Func runs: 10000; result: 0.21759965952460583
=============================
5 Megacity's; Func runs: 10000; result: 0.6784615384615384
25 Megacity's; Func runs: 10000; result: 0.4763076923076923
500 Megacity's; Func runs: 10000; result: 0.13901538461538585
=============================
All score: 4.84175 (53.80%)
El único problema que se aprecia en la visualización del algoritmo es la tendencia a estancarse en óptimos locales con problemas de pequeña dimensionalidad, algo bastante habitual en los algoritmos poblacionales.
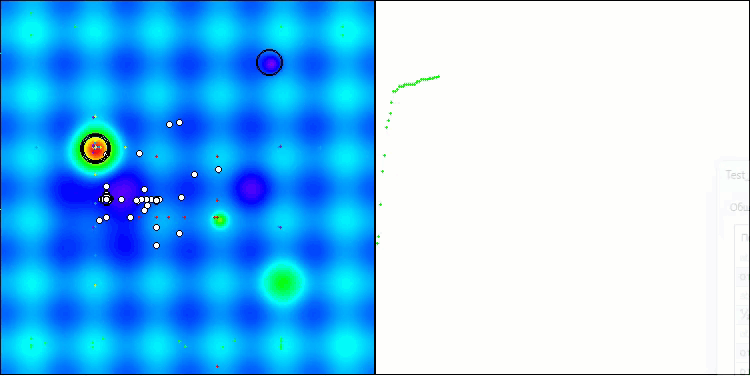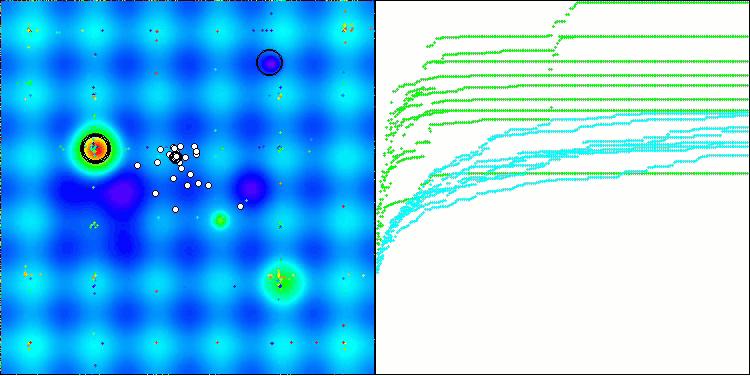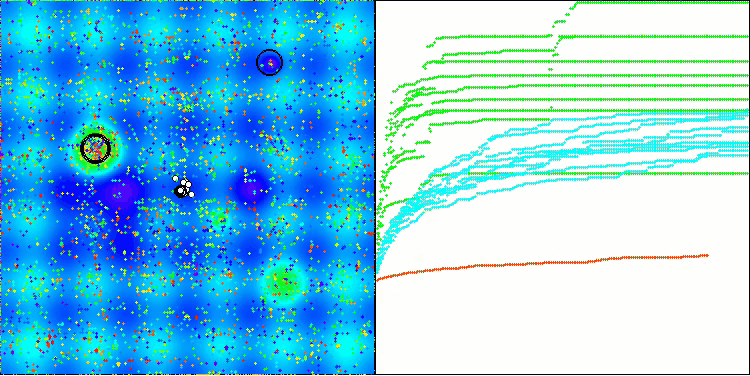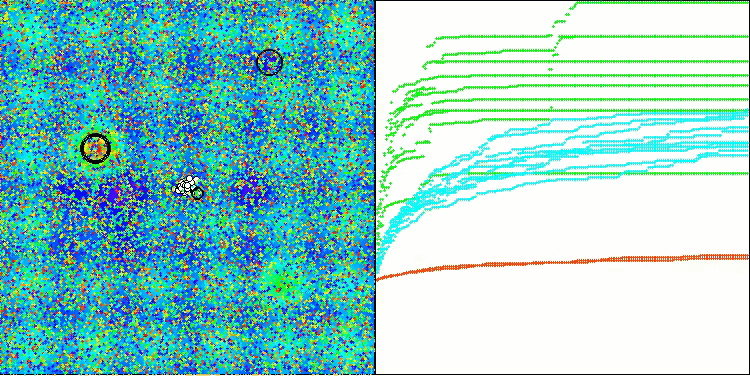
BIO en la función de prueba Hilly
BIO en la función de prueba Forest
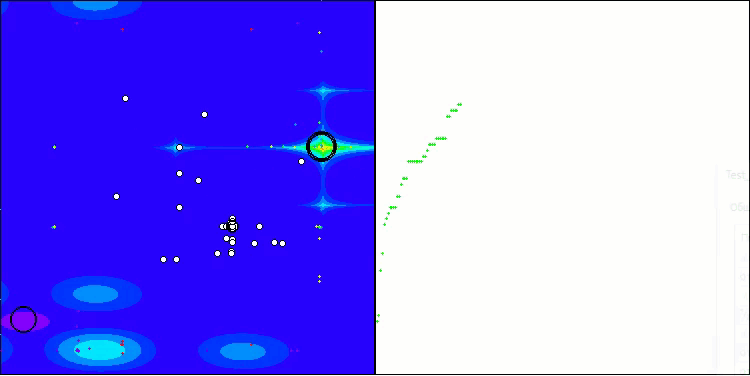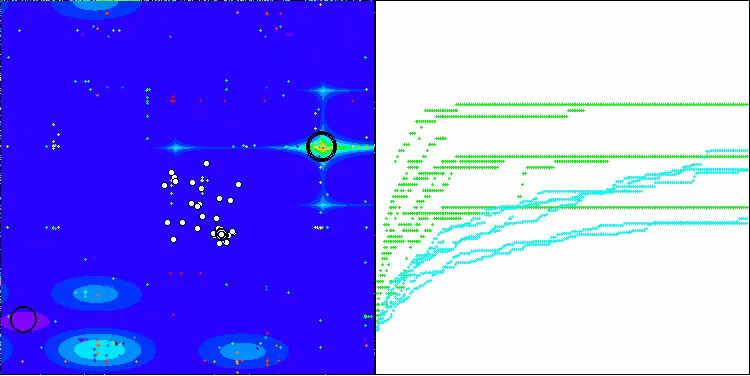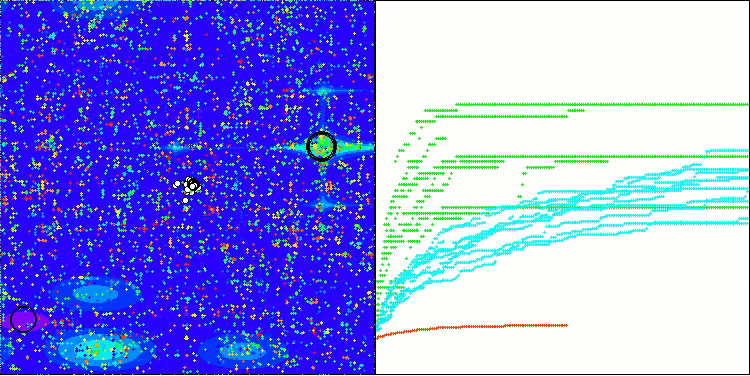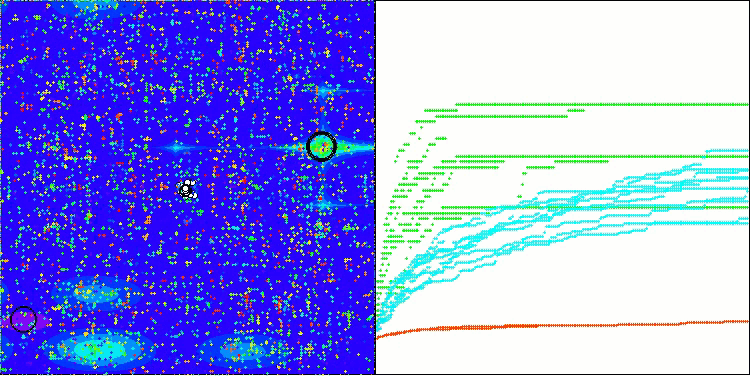
BIO en la función de prueba Megacity
Al final de la prueba, el algoritmo BIO ocupa el puesto 20 en la tabla de clasificación de algoritmos de optimización basados en la población.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration optimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 9 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 10 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 11 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 12 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 13 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0.34583 | 1,86493 | 0.93593 | 0.80152 | 0,27177 | 2,00923 | 0.65077 | 0.51646 | 0,15472 | 1,32195 | 5.196 | 57.73 |
| 14 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 15 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 16 | AOSm | búsqueda de orbitales atómicos M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 17 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 18 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 19 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 20 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 21 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 22 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 23 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 24 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 25 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 26 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 27 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 28 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 29 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 30 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 31 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 32 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 33 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 34 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1,65585 | 0.89675 | 0.37401 | 0.16984 | 1,44060 | 0.69538 | 0.28031 | 0.10852 | 1,08422 | 4.181 | 46,45 |
| 35 | ABH | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4.127 | 45,85 |
| 36 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 37 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0,26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1,39880 | 0,66154 | 0.27046 | 0.10594 | 1,03794 | 4.037 | 44.85 |
| 38 | ATAm | artificial tribe algorithm M | 0.71771 | 0.55304 | 0,25235 | 1,52310 | 0.82491 | 0.55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 39 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 40 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3.657 | 40,63 |
| 41 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 42 | CSA | circle search algorithm | 0,66560 | 0,45317 | 0,29126 | 1,41003 | 0,68797 | 0,41397 | 0,20525 | 1,30719 | 0,37538 | 0,23631 | 0,10646 | 0,71815 | 3,435 | 38,17 |
| 43 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 44 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 45 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| R.W. | random walk | 0.48754 | 0.32159 | 0.25781 | 1,06694 | 0.37554 | 0,21944 | 0,15877 | 0,75375 | 0.27969 | 0,14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Conclusiones
En el proceso de desarrollo y prueba del algoritmo Blood Inheritance Optimization (BIO), hemos llegado a varias conclusiones importantes. En primer lugar, el uso de la asociación hereditaria de grupos sanguíneos ha demostrado ser un enfoque acertado para organizar las distintas estrategias de mutación en un algoritmo de optimización basado en la población. Las pruebas realizadas con diferentes funciones y dimensionalidades han demostrado que el algoritmo es bastante versátil y puede tratar eficazmente tanto problemas sencillos de baja dimensionalidad como problemas multidimensionales más complejos.
Resulta especialmente importante señalar que la aplicación del BIO presentada es solo una versión básica que demuestra el concepto. La idea clave del algoritmo no reside tanto en los operadores de mutación específicos (que pueden sustituirse por cualquier otro operador), como en la propia estructura de herencia de las estrategias de cambio de parámetros a través de la analogía con los grupos sanguíneos. Esto abre un amplio abanico de posibilidades para modificar y ampliar el algoritmo. Cada "grupo sanguíneo" puede asociarse a cualquier otro operador de mutación tomado de otros algoritmos o creado concretamente para una tarea concreta. Además, podemos experimentar con el número de "grupos sanguíneos" añadiendo nuevas estrategias o combinando las existentes.
Los resultados de las pruebas actuales, que muestran una posición decente en el ranking de algoritmos de población (con una puntuación de alrededor del 54%), indican que el enfoque resulta viable incluso en su implementación básica. La tendencia observada a quedarse atascado en óptimos locales puede superarse modificando los operadores de mutación o añadiendo nuevas estrategias para explorar el espacio de soluciones.
En mi opinión, la dirección más prometedora del desarrollo de algoritmos es la creación de versiones adaptativas en las que los operadores de mutación de cada "grupo sanguíneo" puedan modificarse dinámicamente durante el proceso de optimización, ajustándose al paisaje de la función objetivo. También resulta interesante investigar la posibilidad de utilizar diferentes esquemas de herencia distintos del clásico sistema de grupos sanguíneos "ABO", lo cual puede conducir a la creación de toda una familia de algoritmos basados en diferentes sistemas de herencia biológica.
Así pues, el BIO representa no solo otro algoritmo de optimización, sino también un marco conceptual flexible para crear una familia de algoritmos unidos por la idea común de la herencia de las estrategias de búsqueda de soluciones a través de la metáfora de los grupos sanguíneos y abre un amplio abanico de posibilidades para nuevas investigaciones y modificaciones destinadas a mejorar la eficacia del algoritmo en distintos ámbitos de aplicación.
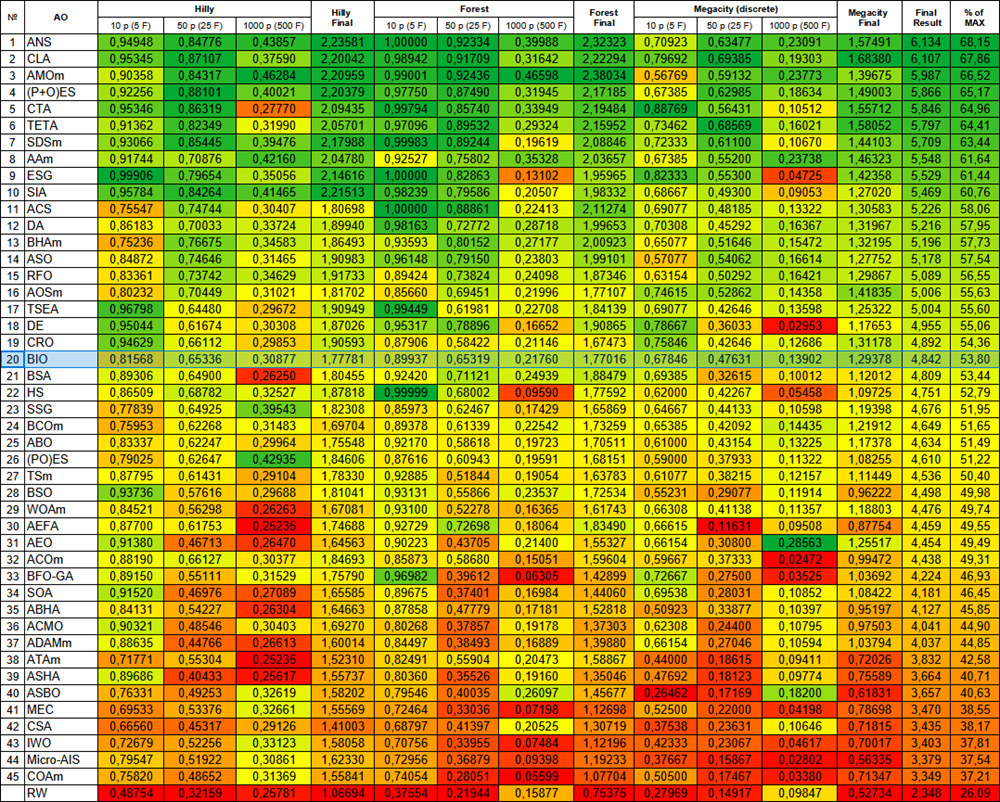
Figura 2. Clasificación por colores de los algoritmos según las pruebas respectivas
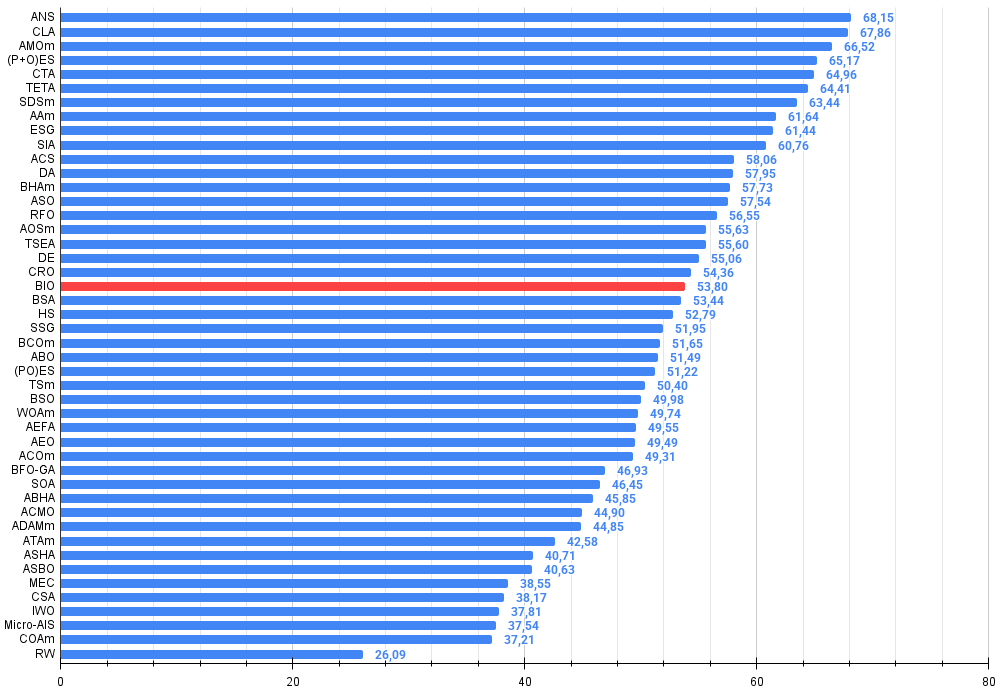
Figura 3. Histograma de los resultados de las pruebas de algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de puntuación está en el archivo)
Ventajas e inconvenientes del algoritmo BIO:
Ventajas:
- No tiene parámetros externos
- La idea de la herencia por grupo sanguíneo es interesante
- Buena convergencia en funciones de dimensionalidad alta y media
Desventajas:
- Se atasca en extremos locales en problemas de pequeña dimensionalidad.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | #C_AO.mqh | Archivo de inclusión | Clase parental de algoritmos de población optimizaciones |
| 2 | #C_AO_enum.mqh | Archivo de inclusión | Enumeración de los algoritmos de optimización basados en la población |
| 3 | TestFunctions.mqh | Archivo de inclusión | Biblioteca de funciones de prueba |
| 4 | TestStandFunctions.mqh | Archivo de inclusión | Biblioteca de funciones del banco de pruebas |
| 5 | Utilities.mqh | Archivo de inclusión | Biblioteca de funciones auxiliares |
| 6 | CalculationTestResults.mqh | Archivo de inclusión | Script para calcular los resultados en una tabla comparativa |
| 7 | Testing AOs.mq5 | Script | Banco de pruebas único para todos los algoritmos de optimización basados en la población |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización |
| 9 | Test_AO_BIO.mq5 | Script | Banco de pruebas para el BIO |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/17246
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Simulación de mercado (Parte 13): Sockets (VII)
Simulación de mercado (Parte 13): Sockets (VII)
 La estrategia de negociación de la brecha del valor razonable inverso (Inverse Fair Value Gap, IFVG)
La estrategia de negociación de la brecha del valor razonable inverso (Inverse Fair Value Gap, IFVG)
 Mecanismos de compuertas en el aprendizaje en conjuntos
Mecanismos de compuertas en el aprendizaje en conjuntos
 Simulación de mercado (Parte 12): Sockets (VI)
Simulación de mercado (Parte 12): Sockets (VI)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso