Algoritmos de optimización de la población: Búsqueda por difusión estocástica (Stochastic Diffusion Search, SDS)

Contenido:

1. Introducción
2. Descripción del algoritmo
3. Resultados de las pruebas

1. Introducción

El algoritmo de búsqueda por difusión estocástica (SDS) fue propuesto en 1989 por J. Bishop y desde entonces ha sido desarrollado activamente por su autor y S. Nasuto. El rasgo distintivo de este algoritmo es su profundo razonamiento matemático en comparación con otros algoritmos basados en la población. La SDS se desarrolló originalmente para la optimización discreta, pero no fue hasta 2011 cuando se propuso una modificación que permitía la optimización continua global.

Datos de interés:

1. La búsqueda por difusión estocástica (SDS) supuso la primera metaheurística de inteligencia de enjambre perteneciente a la familia de los algoritmos de inteligencia de enjambre y de búsqueda y optimización naturales. Otros ejemplos de este tipo de algoritmos son la optimización de colonias de hormigas, la optimización de enjambres de partículas y los algoritmos genéticos.

2. A diferencia de la optimización de colonias de hormigas basada en la comunicación estigmérgica, la SDS utiliza la comunicación directa entre agentes, de una forma similar al mecanismo de llamada en tándem utilizado por las hormigas de la especie Leptothorax Acervorum.

El algoritmo SDS se basa en la evaluación parcial barata de una hipótesis (una solución candidata al problema de búsqueda) por parte de los agentes. Después, los agentes intercambian información sobre la hipótesis mediante la comunicación directa cara a cara. Usando un mecanismo de difusión, se pueden identificar soluciones de alta calidad a partir de grupos de agentes con la misma hipótesis.

Para entender mejor cómo funciona el algoritmo SDS, podemos usar una analogía sencilla: el juego del restaurante.

En el juego del restaurante, los participantes desempeñan el papel de agentes y los restaurantes el de hipótesis. Cada agente elige el restaurante en el que quiere comer según sus preferencias y la información que recibe de otros agentes. A continuación, los agentes intercambian información sobre sus elecciones y preferencias. Como resultado de este proceso, se forman grupos de agentes que seleccionan el mismo restaurante y pueden identificarse como decisiones potencialmente buenas.

El algoritmo SDS posee varias ventajas. En primer lugar, permite a los agentes realizar evaluaciones parciales baratas de las hipótesis, lo cual reduce la complejidad computacional del algoritmo. En segundo lugar, usa la comunicación directa cara a cara entre agentes, lo cual permite una difusión eficaz de la información. En tercer lugar, la SDS tiene un fundamento matemático, lo cual la hace más fiable y predecible.

No obstante, el algoritmo SDS también tiene sus limitaciones. En primer lugar, solo puede ser eficaz en determinados tipos de tareas en las que es aplicable el concepto de hipótesis. En segundo lugar, puede sufrir el problema de la convergencia prematura, en la que los agentes convergen a una hipótesis demasiado rápido sin explorar otras posibilidades. En tercer lugar, el algoritmo requiere ajustar los parámetros, lo cual puede suponer un proceso complejo y lento. Algunos autores señalan limitaciones, vamos a comprobar si es el caso.

En general, la SDS es un algoritmo interesante y eficaz para resolver problemas de optimización. Asimismo, combina las ventajas de los algoritmos basados en la población y el razonamiento matemático, lo que lo hace atractivo para la investigación y la aplicación en diversos campos.

2. Descripción del algoritmo

Veamos el algoritmo SDS con más detalle.

La SDS es un algoritmo poblacional basado en dos ideas de estrategia de búsqueda:

1. La evaluación parcial de decisiones.
2. La difusión de soluciones prometedoras entre la población.

Hay dos juegos canónicos que describen de forma sencilla cómo funciona la SDS.
1. El juego del restaurante
2. El juego de la minería de oro.

El juego del "Restaurante"

Un grupo de delegados asiste a una larga conferencia en una ciudad desconocida. Cada noche se enfrentan al problema de elegir un restaurante para comer. La ciudad tiene un gran número de establecimientos con una gran variedad de cocinas. El objetivo del grupo es encontrar el mejor restaurante donde cada delegado pueda disfrutar de una comida agradable. No obstante, llevaría demasiado tiempo realizar una búsqueda exhaustiva de todas las combinaciones posibles de restaurantes y platos. Para resolver este problema, los delegados recurren al uso de la búsqueda de difusión estocástica.

Cada delegado actúa como un agente que adivina cuál será el mejor restaurante de la ciudad. Cada noche, los delegados ponen a prueba sus hipótesis visitando restaurantes y eligiendo al azar uno de los platos de la carta. A la mañana siguiente, durante el desayuno, cada delegado que no haya quedado satisfecho con la cena de la noche anterior pedirá a uno de sus colegas que comparta sus impresiones sobre la comida. Si las impresiones del colega son positivas, el delegado también elegirá ese restaurante. En caso contrario, seleccionará aleatoriamente otro establecimiento de la lista de restaurantes disponibles en esa ciudad.

Así, gracias a esta estrategia, se acumulará rápidamente un número importante de delegados, que se reunirán en torno al mejor restaurante de la ciudad.

Este proceso de juego de restaurante tiene algunas características interesantes. En ausencia total de control y gestión externos, un grupo de delegados se comunicará para resolver un problema que no puede resolverse rápidamente en solitario. Si la calidad del servicio o del menú del restaurante actual disminuye significativamente o el restaurante se cierra, los delegados se trasladan al siguiente mejor establecimiento. El principal requisito sería la comparabilidad de restaurantes, menús y platos individuales. Cada agente decidir por sí mismo si su experiencia ha sido buena.

Los delegados pasan muchas noches en un restaurante de alta calidad antes de que llegue a juzgarse la comida de todos los establecimientos de la ciudad.
Los críticos señalan que es probable que los delegados tengan preferencias culinarias distintas, por lo que un delegado puede encontrar un restaurante donde le guste toda la comida, pero esto podría no satisfacer al resto del grupo. Si bien solo uno o una pequeña parte de los delegados se queda permanentemente en ese restaurante, el resto continúa como de costumbre y, al final, la mayoría sigue reuniéndose en el mejor restaurante. Sin embargo, como último recurso, aunque haya un único restaurante excelente que satisfaga a la mayoría de los delegados, todos los agentes podrían encontrarse cenando solos. Este restaurante nunca se encontrará, pues todos los delegados están satisfechos con sus opciones actuales y no buscarán nuevos establecimientos.

En nuestra implementación hemos introducido un pequeño cambio en la lógica de la estrategia de búsqueda para que los delegados sigan buscando restaurantes aunque no haya ningún delegado con una mejor experiencia, de esta forma la búsqueda de restaurantes no se detendrá, a diferencia de la versión canónica, donde el cambio en la opinión actual sobre un restaurante respecto a la anterior resulta importante; si la opinión no ha cambiado a mejor para la mayoría de los delegados, estos seguirán yendo al mismo restaurante, lo cual implicará quedarse estancado en el extremo local.

Juego de "Extracción de oro"

Un grupo de amigos, formado por mineros experimentados, descubre la oportunidad de extraer oro en las colinas de una cordillera. Sin embargo, no disponen de información sobre dónde se encuentra exactamente el yacimiento de oro más rico. En sus mapas, la cordillera está dividida en varias colinas distintas, cada una de las cuales contiene un conjunto de estratos que requieren explotación minera. La probabilidad de descubrir oro a lo largo del tiempo será proporcional a su riqueza.

Para maximizar su riqueza colectiva, los mineros deberán identificar la colina con las vetas de oro más ricas para que el máximo número de mineros pueda extraer allí. Sin embargo, esta información no está previamente disponible. Para resolver el problema, los mineros deciden utilizar una sencilla búsqueda de difusión estocástica.

El proceso de minería comenzará con la asignación aleatoria de una colina a cada minero (su hipótesis de colina). Cada día, cada minero seleccionará al azar una veta de su colina para explotarla.

Al final de cada día, la probabilidad de que un minero esté contento será proporcional a la cantidad de oro que haya encontrado (valor de la función de aptitud).
Por la noche, una vez terminado el trabajo, los mineros se reunirán. Un minero descontento elegirá al azar a otro minero para hablar con él. Si el minero elegido está satisfecho, se "contentará" con decirle a su colega el nombre de la colina que está explotando. Así pues, ambos mineros apoyarán la hipótesis de la colina. Si el minero elegido no está satisfecho, no dirá nada, y el minero original se verá otra vez obligado a elegir una nueva hipótesis: la definición de la colina que explotará al día siguiente de forma aleatoria.

En el contexto de los SDS (sistemas dinámicos autoorganizados), los agentes actúan como mineros. Los agentes activos son "mineros felices", mientras que los inactivos son "mineros infelices". La hipótesis de cada agente representará la "hipótesis de la colina" del minero. Este proceso es isomorfo a SDS, lo cual permite a los mineros autoorganizarse de forma natural y reunirse rápidamente en la(s) colina(s) de una cadena montañosa con una alta concentración de oro.

La felicidad de los mineros puede medirse de forma probabilística o representarse mediante un valor lógico absoluto, dado que cada minero es feliz o infeliz al final de cada día. Si el oro se modela como un recurso finito que disminuye con el tiempo, la prospección se volverá bastante adaptativa y los mineros se desplazarán a los lugares con más oro.

Aunque el término "feliz" resulta subjetivo, como las preferencias alimentarias, en este caso se utilizará en sentido objetivo. Todos los mineros seguirán el mismo proceso: la cantidad de oro que encuentran en un día determinará la probabilidad de que se declaren "felices" al final de la jornada, al reunirse para compartir potencialmente información sobre las colinas que explotan.

No utilizaremos la división de los mineros en "felices" e "infelices", esto permitirá, al igual que sucede con el concepto del juego del "Restaurante", aumentar la actividad de los agentes en busca de nuevos lugares inexplorados.

Para formalizar el algoritmo usaremos la noción de "candidato", que equivaldrá a un delegado en el juego "Restaurante" y a un minero en el juego de extracción de oro. El candidato representará a un agente de búsqueda. Para comprender de forma más sencilla la esencia de un restaurante o una colina, podemos imaginar un espacio con dos coordenadas, aunque en realidad podemos aplicar un número ilimitado de coordenadas para resolver problemas multidimensionales. En la figura 1, las designaciones C1, C2, C3 mostrarán a los candidatos que posean los números de restaurante (espacios correspondientes en el campo de búsqueda). En el proceso de difusión del intercambio de información sobre restaurantes, los candidatos tomarán prestados los números de restaurante de los participantes en la conferencia seleccionados al azar en caso de que el valor de la función de aptitud del interlocutor sea superior. El rango de cada parámetro de optimización (coordenadas del espacio de búsqueda) se dividirá por el número de restaurantes especificado en los parámetros externos del algoritmo, por ejemplo, si especificamos un número de 100 restaurantes en los parámetros del algoritmo, significará que el rango de cada coordenada se dividirá en 100 partes.

Cada restaurante ofrecerá una lista de platos en el menú, cada plato del menú será una coordenada específica del espacio de búsqueda dentro de un único restaurante. El algoritmo aplicará un esquema en el que el candidato solo probará un plato de restaurante elegido al azar.

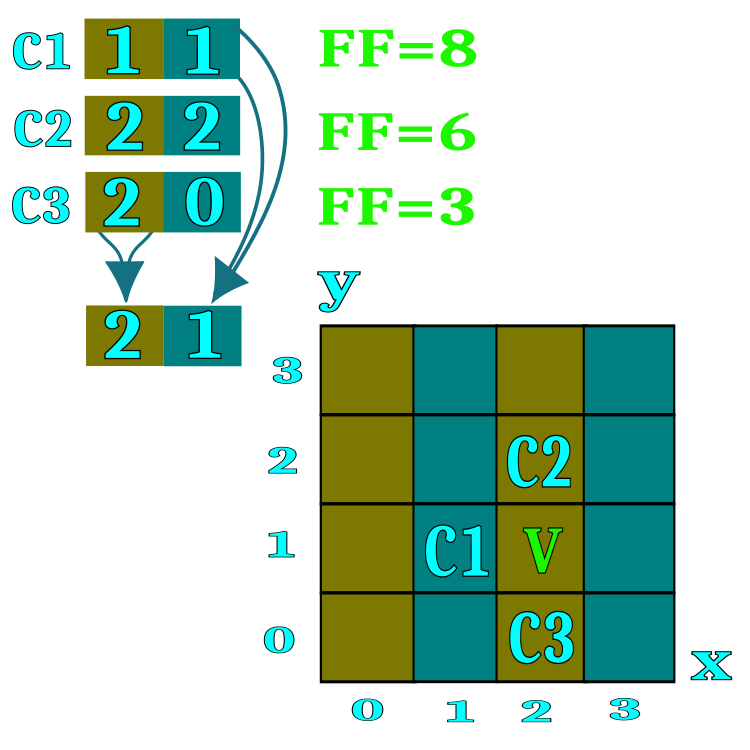
Figura 1. Representación visual del principio de difusión de la información en los restaurantes.

Echemos un vistazo a los pasos del algoritmo SDS en forma de pseudocódigo.

1. Inicialización de los candidatos (asignación aleatoria de restaurantes y comidas).

2.0. Comprobación de hipótesis e intercambio de difusión entre candidatos.

2.1. Comparación de la experiencia actual del candidato con su experiencia anterior.

2.1.1. Si la experiencia resulta mejor, asignaremos las direcciones de los restaurantes como hipótesis para la siguiente iteración.

2.1.2. Si la experiencia es peor, pediremos la opinión de un candidato seleccionado al azar.

2.1.2.1. Si la experiencia del entrevistado-candidato es mejor, entonces tomaremos las direcciones de los restaurantes prometedores (para el candidato actual).

2.1.2.2. Si la experiencia del interlocutor-candidato es peor, lo más probable es que elija la dirección de un restaurante seleccionado al azar o abandone el actual.

3.0. Luego seleccionaremos los platos, en la lista de restaurantes generada, como hipótesis para la siguiente iteración.

El marco lógico para la comprobación de hipótesis se muestra en la figura 2. La mayor parte del circuito lógico realizará la tarea de seleccionar un restaurante y, una vez completada la selección del restaurante, se elegirá un plato al azar. La selección del restaurante será la tarea principal del algoritmo; sin embargo, la elección del plato resultará completamente aleatoria e independiente de las iteraciones anteriores.

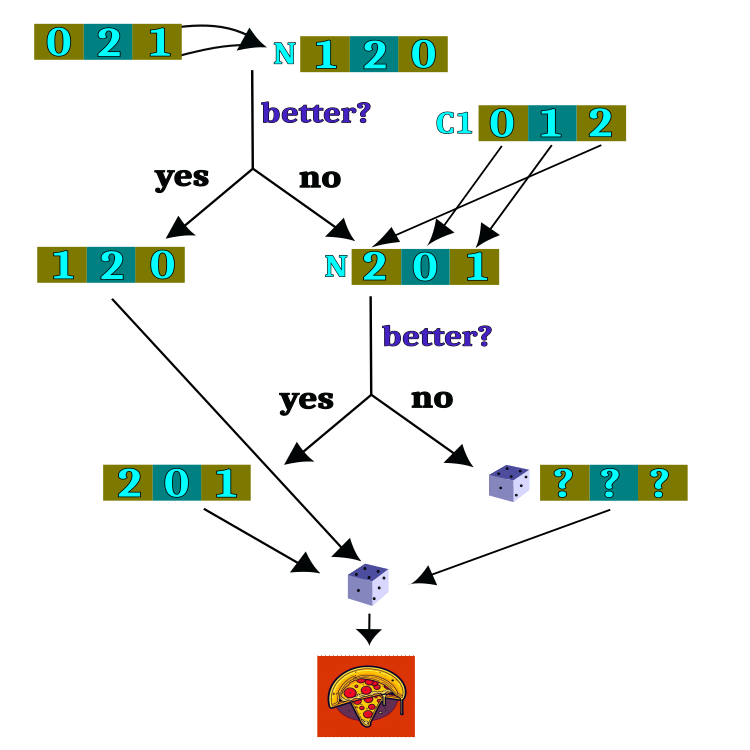
Figura 2. Marco lógico para la comprobación de hipótesis.

Es hora de echar un vistazo al código de SDS (Stochastic Diffusion Search) y profundizar en el corazón y el alma del algoritmo: el agente, también conocido como candidato, que puede ser descrito por la estructura S_Candidate. Contendrá los siguientes campos:

1. raddr: array que contiene las direcciones de los restaurantes. Cada elemento del array representa la dirección de un restaurante.
2. raddrPrev: array que contiene las direcciones anteriores de los restaurantes. Cada elemento del array representa la dirección anterior de un restaurante.
3. c: array que contiene las coordenadas (del plato). Cada elemento del array representa la coordenada de un plato.
4. cPrev: array que contiene las coordenadas anteriores (platos). Cada elemento del array representa la coordenada anterior de un plato.
5. f: valor de aptitud para el estado actual del agente.
6. fPrev: valor de aptitud para el estado anterior del agente.

La estructura S_Candidate tiene un método Init que inicializa todos los arrays de dimensionalidad coords (el número de coordenadas - los parámetros a optimizar) y establece los valores iniciales de f y fPrev a -DBL_MAX, ya que no hay nada ni nadie con quien comparar la experiencia del candidato en la primera iteración.

//——————————————————————————————————————————————————————————————————————————————
struct S_Candidate
{
  void Init (int coords)
  {
    ArrayResize (c,         coords);
    ArrayResize (cPrev,     coords);
    ArrayResize (raddr,     coords);
    ArrayResize (raddrPrev, coords);
    f        = -DBL_MAX;
    fPrev    = -DBL_MAX;
  }
  int    raddr     []; //restaurant address
  int    raddrPrev []; //previous restaurant address
  double c         []; //coordinates (dishes)
  double cPrev     []; //previous coordinates (dishes)
  double f;            //fitness
  double fPrev;        //previous fitness
};
//——————————————————————————————————————————————————————————————————————————————

Ahora declararemos una clase de algoritmo SDS que contendrá lo siguiente:

Campos de clase:
- cB: array que contiene las mejores coordenadas
- fB: valor de la función de aptitud para las mejores coordenadas
- cands: array de candidatos para encontrar las coordenadas óptimas
- rangeMax: array que contiene los valores máximos de cada coordenada
- rangeMin: array que contiene los valores mínimos de cada coordenada
- rangeStep: array que contiene los pasos de búsqueda para cada coordenada

Métodos de clase:
- Init: inicialización de los parámetros del algoritmo, como el número de coordenadas, el tamaño de la población, el número de restaurantes y la probabilidad de selección de los mismos.
- Moving: ejecución del paso del algoritmo, desplazando a los candidatos a las nuevas coordenadas.
- Revision: ejecución del paso de revisión, actualización de las mejores coordenadas y la función de aptitud.
- SeInDiSp: método para calcular una nueva coordenada en un intervalo dado con un tamaño de paso específico.
- RNDfromCI: método para generar un número aleatorio dentro de un intervalo determinado

Otros campos de clase:
- coords: número de coordenadas
- populationSize: tamaño de la población
- restNumb: número de restaurantes
- probabRest: probabilidad de seleccionar un restaurante
- restSpace: espacio de restaurantes
- revision: indicador sobre la necesidad de realizar una revisión

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SDS
{
  //----------------------------------------------------------------------------
  public: double cB   [];       //best coordinates
  public: double fB;            //FF of the best coordinates
  public: S_Candidate cands []; //candidates

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search



  public: void Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    restaurantsNumberP,   //restaurants number
                     const double probabRestP);         //probability restaurant choosing

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;            //coordinates number
  private: int    populationSize;    //population size

  private: int    restNumb;          //restaurants number
  private: double probabRest;        //probability restaurant choosing
  private: double restSpace [];      //restaurants space

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

El método de inicialización del algoritmo SDS comienza estableciendo valores iniciales para algunas variables y arrays.

Los parámetros de entrada del método serán:
- coordinatesNumberP: número de coordenadas (dimensionalidad del espacio de búsqueda)
- populationSizeP: tamaño de la población (número de candidatos)
- restaurantsNumberP: número de restaurantes
- probabRestP: probabilidad de seleccionar un restaurante

En primer lugar, se reiniciará el generador de números aleatorios utilizando la función MathSrand y transmitiéndole el valor actual de microsegundos. A continuación, las variables fB y revision se inicializarán con valores iniciales de -DBL_MAX y false, respectivamente.
A continuación, los parámetros de entrada coordinatesNumberP y populationSizeP se asignarán a las variables coords y populationSize.
Las variables restNumb y probabRest se inicializarán con los valores de restaurantsNumberP y probabRestP.
Se creará un array restSpace de coordenadas de tamaño utilizando la función ArrayResize.
A continuación se creará un array cands de populationSize utilizando la función ArrayResize. El ciclo inicializará cada elemento del array cands llamando al método Init con el parámetro coords.
Los arrays rangeMax, rangeMin, rangeStep y cB de las coordenadas de tamaño también se crearán utilizando la función ArrayResize.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDS::Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    restaurantsNumberP,   //restaurants number
                     const double probabRestP)          //probability restaurant choosing
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords         = coordinatesNumberP;
  populationSize = populationSizeP;

  restNumb   = restaurantsNumberP;
  probabRest = probabRestP;
  ArrayResize (restSpace, coords);

  ArrayResize (cands, populationSize);
  for (int i = 0; i < populationSize; i++) cands [i].Init (coords);

  ArrayResize (rangeMax,       coords);
  ArrayResize (rangeMin,       coords);
  ArrayResize (rangeStep,      coords);
  ArrayResize (cB,             coords);
}
//——————————————————————————————————————————————————————————————————————————————

El método Moving(), aunque será llamado en cada iteración, la lógica básica del método se ejecutará una sola vez, controlada por la bandera revision.

Al principio de la función se comprobará la variable de revisión, si es falsa, se inicializan las variables y arrays.
A continuación, realizaremos un ciclo a través de las coordenadas de los puntos del espacio.

Dentro de este ciclo, se calculará el valor restSpace[i], que es la longitud del intervalo para cada coordenada, definida como la diferencia entre los valores máximo y mínimo del intervalo dividido por restNumb.

Luego se declararán las variables min y max, que se utilizarán para definir el rango de valores del espacio de un restaurante concreto.

Después se inicializarán las variables n y dish, que se utilizarán para definir valores aleatorios dentro del rango del restaurante seleccionado.

A continuación se ejecutará un ciclo sobre la población populationSize, dentro del cual se ejecutará un ciclo sobre las coordenadas de los puntos del espacio. Dentro de este ciclo, se generará un número aleatorio n utilizando la función RNDfromCI(), que se utilizará para determinar el índice en el array restSpace. Si el valor resultante de n es mayor o igual que restNumb, se asignará a restNumb - 1, para asegurar una distribución uniforme de la variable aleatoria. A continuación, se calcularán los valores mínimo y máximo usando rangeMin, restSpace y n.

Luego generaremos el número aleatorio dish (plato) utilizando RNDfromCI() que va del mínimo al máximo (espacio del restaurante).

El valor dish se utilizará entonces para calcular el valor de c[i] utilizando la función SeInDiSp() que usa rangeMin, rangeMax, rangeStep para garantizar que los parámetros que se están optimizando se escalonen correctamente.

Como resultado de este algoritmo, cada punto del espacio obtendrá valores aleatorios para cada coordenada según el espacio del restaurante, simulando la selección aleatoria de un plato.

La variable revision se establecerá en true para que las variables y arrays no se inicialicen la próxima vez que se llame a Moving().

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDS::Moving ()
{
  if (!revision)
  {
    for (int i = 0; i < coords; i++)
    {
      restSpace [i] = (rangeMax [i] - rangeMin [i]) / restNumb;
    }

    double min = 0.0;
    double max = 0.0;

    int    n   = 0;
    double dish = 0.0;

    for (int i = 0; i < populationSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        n = (int)(RNDfromCI (0, restNumb));
        if (n >= restNumb) n = restNumb - 1;

        cands [i].raddr     [c] = n;
        cands [i].raddrPrev [c] = n;
        min = rangeMin [c] + restSpace [c] * n;
        max = min + restSpace [c];

        dish = RNDfromCI (min, max);

        cands [i].c [c] =  SeInDiSp (dish, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método de revisión del algoritmo SDS ejecutará la lógica básica de selección de restaurantes y platos en los restaurantes. Esto no resulta típico de los algoritmos considerados anteriormente, en los que la lógica principal del movimiento de los agentes se situaba en el método Moving, aunque el orden de acceso a los métodos del algoritmo seguirá siendo el mismo y se corresponderá con el concepto elegido en el primer artículo de la serie. El algoritmo constará de los siguientes pasos:

1. Actualización del mejor valor encontrado de la función de aptitud fB y su correspondiente conjunto de coordenadas cB. Para cada candidato i de la población, se realizará una comparación, si el valor de f (puntuación de la característica) es mayor que el valor global actual fB, entonces se actualizará fB y se copiará el mejor conjunto de coordenadas globales cB del candidato i.

2. Actualización de los valores de evaluación anteriores y los conjuntos de restaurantes para cada candidato. Para cada candidato i de la población, si el valor f es superior al valor fPrev anterior, entonces se actualizará fPrev, mientras que los conjuntos de restaurantes c y raddr del candidato i se copiarán en los correspondientes valores anteriores de cPrev y raddrPrev.

3. Selección de un nuevo conjunto de restaurantes para cada candidato. Para cada candidato i de la población y cada coordenada c, se elegirá un número aleatorio n entre 0 y populationSize. Si el valor de fPrev para el candidato n es superior al valor fPrev para el candidato i, entonces el conjunto de restaurantes raddr para el candidato i se actualizará con el valor de raddrPrev para el candidato n. En caso contrario, se generará un número aleatorio rnd comprendido entre 0,0 y 1,0. Si rnd es inferior a la probabilidad probabRest, se elegirá un número aleatorio n entre 0 y restNumb, y el conjunto de restaurantes raddr para el candidato i se actualizará con el valor de n. De lo contrario, el conjunto de restaurantes raddr para el candidato i permanecerá inalterado.

4. Generación de un nuevo conjunto de coordenadas para cada candidato. Para cada candidato i de la población y cada coordenada c, se determinarán los valores mínimo y máximo min y max basándose en el rangeMin y restSpace de la coordenada correspondiente. A continuación, se generará un número aleatorio comprendido entre el mínimo y el máximo utilizando la función SeInDiSp, y el valor resultante se asignará a la coordenada c correspondiente en el conjunto c para el candidato i.

Así, el método Revision del algoritmo SDS ejecutará cada iteración sobre la población de candidatos, actualizando el mejor valor encontrado y el conjunto de restaurantes; luego seleccionará los nuevos conjuntos de restaurantes y generará nuevos conjuntos de coordenadas para cada candidato.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDS::Revision ()
{
  //----------------------------------------------------------------------------
  for (int i = 0; i < populationSize; i++)
  {
    if (cands [i].f > fB)
    {
      fB = cands [i].f;
      ArrayCopy (cB, cands [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  double min = 0.0;
  double max = 0.0;
  double rnd = 0.0;
  int    n   = 0;

  for (int i = 0; i < populationSize; i++)
  {
    if (cands [i].f > cands [i].fPrev)
    {
      cands [i].fPrev = cands [i].f;
      ArrayCopy (cands [i].cPrev, cands [i].c, 0, 0, WHOLE_ARRAY);
      ArrayCopy (cands [i].raddrPrev, cands [i].raddr, 0, 0, WHOLE_ARRAY);
    }
  }

  for (int i = 0; i < populationSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      n = (int)(RNDfromCI (0, populationSize));
      if (n >= populationSize) n = populationSize - 1;

      if (cands [n].fPrev > cands [i].fPrev)
      {
        cands [i].raddr [c] = cands [n].raddrPrev [c];
      }
      else
      {
        rnd = RNDfromCI (0.0, 1.0);

        if (rnd < probabRest)
        {
          n = (int)(RNDfromCI (0, restNumb));
          if (n >= restNumb) n = restNumb - 1;
          cands [i].raddr [c] = n;
        }
        else
        {
          cands [i].raddr [c] = cands [i].raddrPrev [c];
        }
      }

      min = rangeMin [c] + restSpace [c] * cands [i].raddr [c];
      max = min + restSpace [c];

      cands [i].c [c] = SeInDiSp (RNDfromCI (min, max), rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Resultados de las pruebas

Impresión del rendimiento del algoritmo de búsqueda por difusión estocástica en un banco de pruebas:

C_AO_SDS:100;1000;0.1
=============================
5 Rastrigin's; Func runs 10000 result: 80.64253803557851
Score: 0.99921
25 Rastrigin's; Func runs 10000 result: 79.00996143538204
Score: 0.97898
500 Rastrigin's; Func runs 10000 result: 54.31544686388126
Score: 0.67300
=============================
5 Forest's; Func runs 10000 result: 1.677891584229713
Score: 0.94910
25 Forest's; Func runs 10000 result: 1.4089003503272384
Score: 0.79694
500 Forest's; Func runs 10000 result: 0.2437939668372883
Score: 0.13790
=============================
5 Megacity's; Func runs 10000 result: 8.6
Score: 0.71667
25 Megacity's; Func runs 10000 result: 6.448
Score: 0.53733
500 Megacity's; Func runs 10000 result: 0.9551999999999999
Score: 0.07960
=============================
All score: 5.86873

Nada más imprimir los resultados del algoritmo, notamos los resultados increíblemente altos en comparación con otros algoritmos. En el cuadro siguiente le ofrecemos una comparación detallada.

Cabe destacar el comportamiento atípico del algoritmo al visualizarse el movimiento de los agentes. Los agentes se distribuyen en número de manera uniforme y proporcional a la altura de la colina de la función de aptitud, mostrando una clusterización de alta calidad por extremos locales. Da la impresión de que el algoritmo no pasará por alto ninguna colina. También cabe destacar el crecimiento casi continuo de la convergencia del algoritmo en cada iteración, lo cual indica una pequeña tendencia a quedarse atascado en extremos locales. Incluso en la función Forest más compleja con un extremo global agudo, no se observa convergencia escalonada.

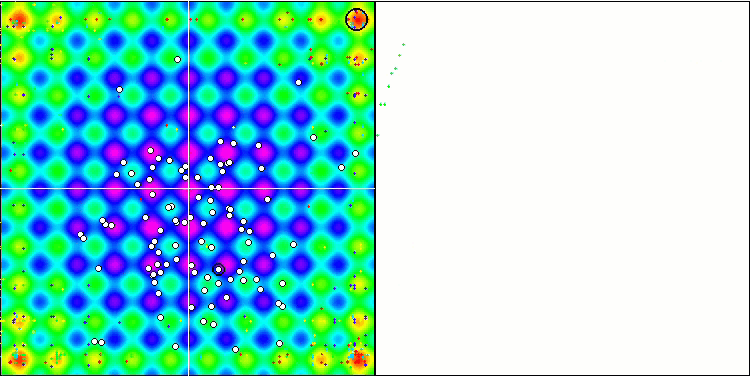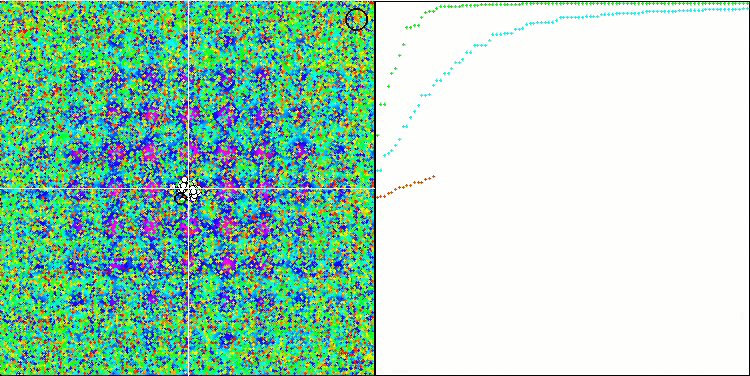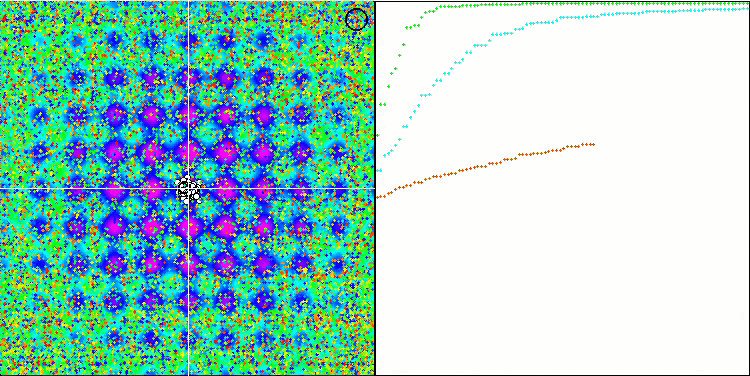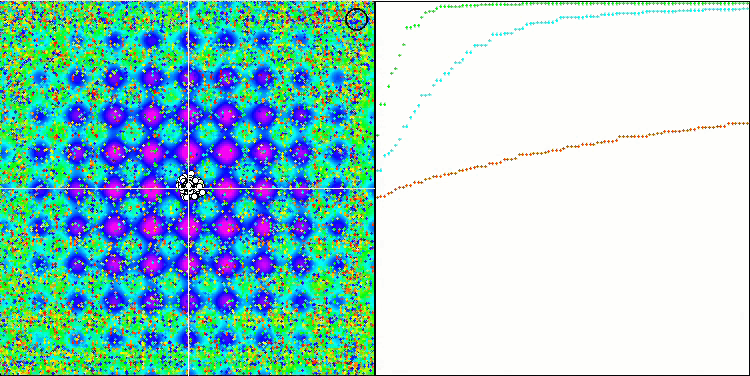
  SDS en la función de prueba Rastrigin.

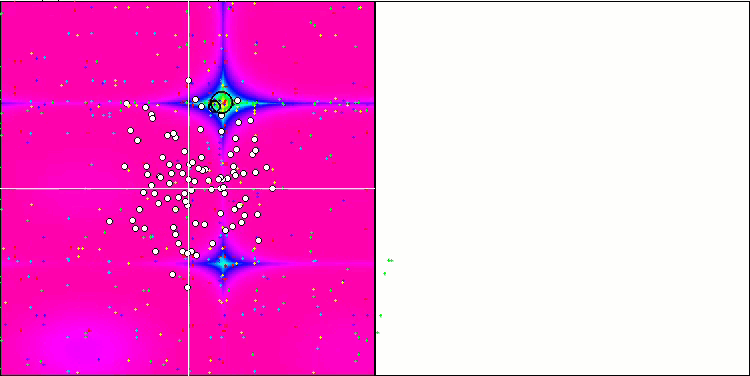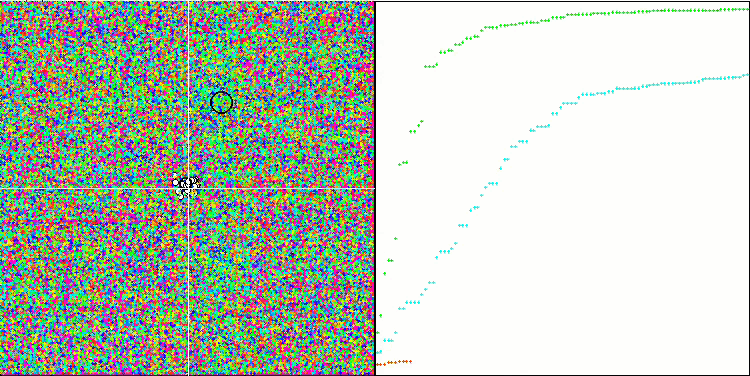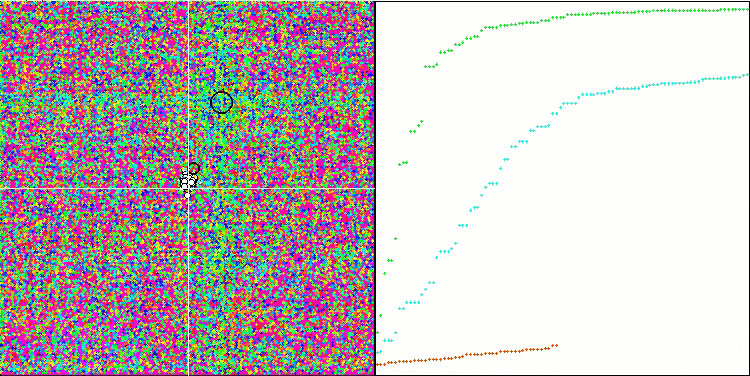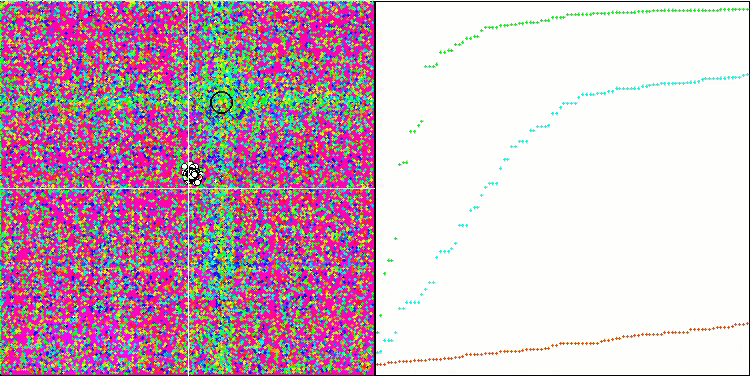
  FDS en la función de prueba Forest.

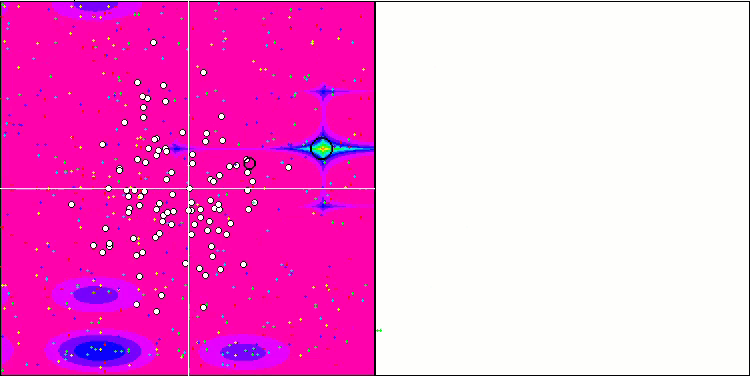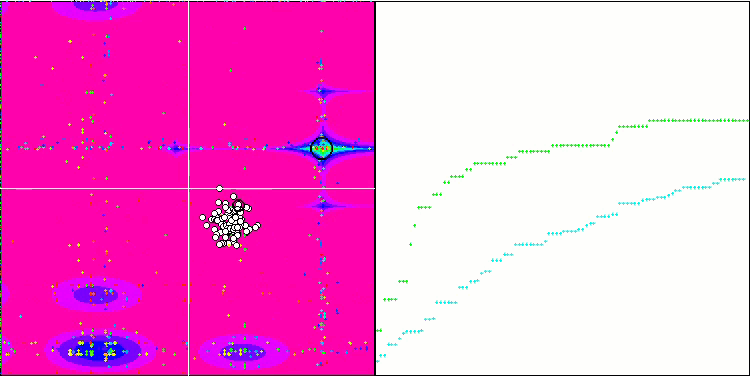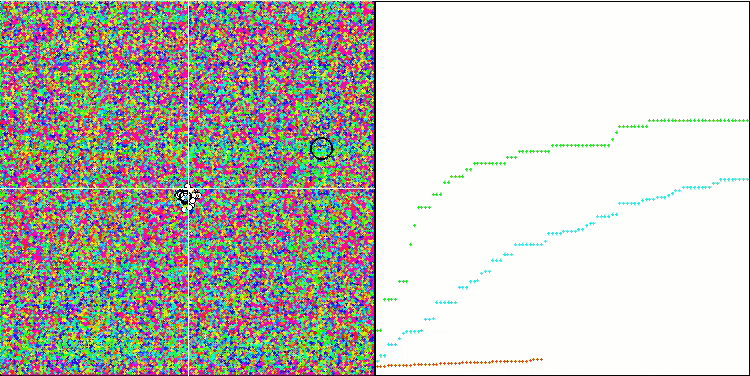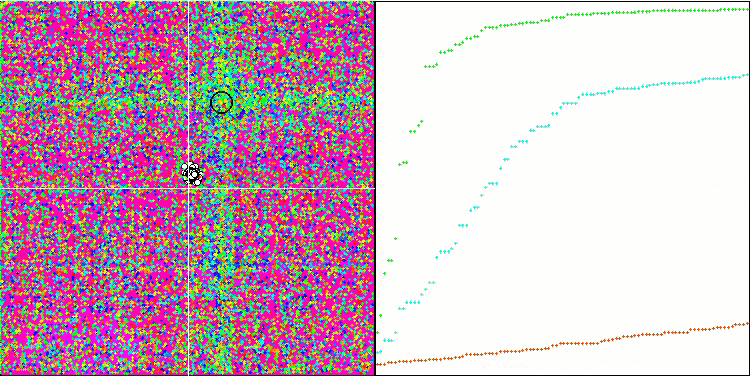
  SDS en la función de prueba Megacity.

Me gustaría señalar que no esperaba resultados asombrosos de un algoritmo tan simple basado en un paseo aleatorio puro. El algoritmo SDS ha superado a todos los algoritmos anteriormente analizados por un amplio margen, casi un 13%, mostrando mejores resultados en muchas pruebas (4 primeros puestos de 9 posibles). La única disciplina es la función multivariable Rastrigin, en la que el líder (el algoritmo EM) ha dejado a todos muy atrás.

Incluso en la extremadamente compleja función discreta Megacity, el algoritmo SDS se comporta admirablemente sin mostrar apenas interferencias; el único que supera a SDS en pruebas con 1 000 variables en Forest y Megacity es el algoritmo de árbol creciente (SSG). 

№	AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	SDS	stochastic diffusion search	0,99737	1,00000	0,63507	2,63244	0,96893	1,00000	0,95092	2,91985	1,00000	1,00000	0,72149	2,72149	100,000
2	SSG	saplings sowing and growing	1,00000	0,95313	0,55665	2,50978	0,72740	0,69680	1,00000	2,42421	0,69612	0,65726	1,00000	2,35338	87,489
3	HS	harmony search	0,99676	0,90817	0,48178	2,38670	1,00000	0,72930	0,44806	2,17736	0,91159	0,76446	0,41537	2,09142	79,474
4	ACOm	ant colony optimization M	0,34611	0,17142	0,17044	0,68797	0,86888	0,73719	0,77362	2,37968	0,91159	0,67983	0,05606	1,64749	54,863
5	IWO	invasive weed optimization	0,95828	0,63939	0,29807	1,89575	0,70773	0,34168	0,31773	1,36714	0,72927	0,32158	0,33289	1,38375	53,994
6	MEC	mind evolutionary computation	0,99270	0,48648	0,22800	1,70718	0,60762	0,29973	0,25459	1,16194	0,85083	0,31594	0,26170	1,42847	49,567
7	COAm	cuckoo optimization algorithm M	0,92400	0,44601	0,26004	1,63006	0,58378	0,25090	0,16526	0,99994	0,66298	0,25246	0,17083	1,08627	42,193
8	FAm	firefly algorithm M	0,59825	0,32387	0,17135	1,09348	0,51073	0,31182	0,49790	1,32045	0,31491	0,21438	0,35258	0,88188	36,860
9	ABC	artificial bee colony	0,78170	0,31182	0,20822	1,30174	0,53837	0,15816	0,13344	0,82998	0,51381	0,20311	0,13926	0,85617	32,954
10	BA	bat algorithm	0,40526	0,60773	0,84451	1,85750	0,20841	0,12884	0,25989	0,59714	0,27073	0,07616	0,17371	0,52060	32,794
11	GSA	gravitational search algorithm	0,70167	0,43098	0,00000	1,13265	0,31660	0,26845	0,33204	0,91710	0,54144	0,26797	0,00000	0,80941	31,322
12	BFO	bacterial foraging optimization	0,67203	0,29511	0,11813	1,08528	0,39702	0,19626	0,20652	0,79980	0,47514	0,25388	0,18932	0,91834	30,615
13	EM	electroMagnetism-like algorithm	0,12235	0,44109	1,00000	1,56344	0,00000	0,02578	0,34880	0,37458	0,00000	0,00000	0,10924	0,10924	21,024
14	SFL	shuffled frog-leaping	0,40072	0,22627	0,26548	0,89247	0,20153	0,03057	0,02652	0,25862	0,24862	0,04231	0,06639	0,35732	14,189
15	MA	monkey algorithm	0,33192	0,31883	0,14644	0,79719	0,10012	0,05817	0,08932	0,24762	0,19889	0,03243	0,10720	0,33853	12,603
16	FSS	fish school search	0,46812	0,24149	0,11302	0,82264	0,12840	0,03696	0,06516	0,23052	0,15471	0,03666	0,08283	0,27420	11,893
17	PSO	particle swarm optimisation	0,20449	0,07816	0,07160	0,35425	0,18895	0,07730	0,21738	0,48363	0,21547	0,04513	0,01957	0,28016	9,238
18	RND	random	0,16826	0,09287	0,08019	0,34132	0,13496	0,03546	0,04715	0,21757	0,15471	0,02962	0,04922	0,23354	5,108
19	GWO	grey wolf optimizer	0,00000	0,00000	0,02256	0,02256	0,06570	0,00000	0,00000	0,06570	0,29834	0,05640	0,02557	0,38031	1,000

Conclusiones

El algoritmo de búsqueda estocástica (SDS) es un método de optimización eficaz que usa muestras aleatorias para encontrar el óptimo global de una función dada.
En este artículo le hemos presentado los principios básicos del algoritmo SDS. Este se basa en la idea de seleccionar aleatoriamente puntos en un espacio de búsqueda particionado. Los resultados de las pruebas muestran que SDS es capaz de encontrar óptimos globales en funciones complejas con un gran número de extremos locales, mostrando una excelente convergencia. Una de las ventajas del algoritmo SDS es su sencillez y facilidad de aplicación. No requiere una gran cantidad de cálculos y podemos aplicarlo a distintos tipos de problemas de optimización.

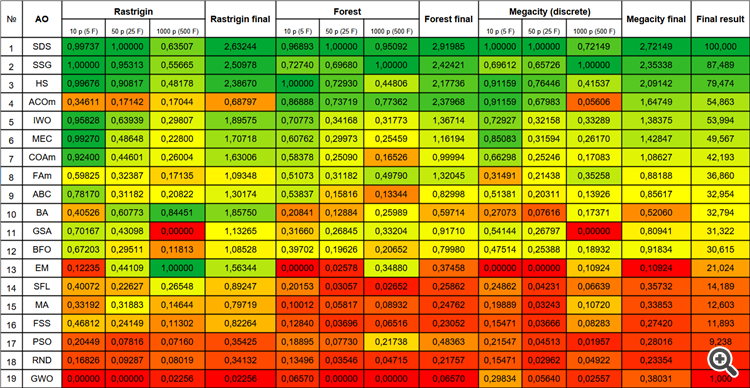
Para visualizar mejor las ventajas y desventajas de cada algoritmo en comparación con los demás, la tabla anterior puede representarse usando la escala de colores de la figura 3.

Figura 3. Gradación por colores de los algoritmos según sus respectivas pruebas.

Histograma de los resultados de los algoritmos de prueba en la figura 3 (en una escala de 0 a 100, cuanto más mejor, en el archivo hay un script para calcular la tabla de clasificación según la metodología de este artículo):

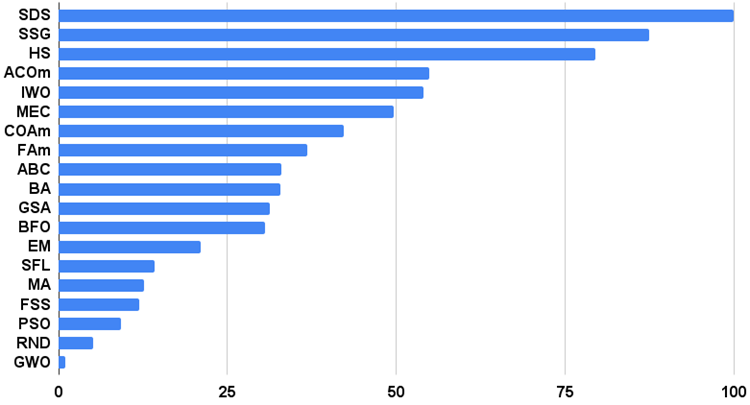
Figura 4. Histograma con los resultados finales de los algoritmos de prueba.

Ventajas e inconvenientes del algoritmo de búsqueda por difusión estocástica (SDS):

Ventajas:
1. Número mínimo de parámetros externos.
2. Alta eficiencia en una gran variedad de tareas.
3. Bajo gasto de recursos informáticos.
4. Facilidad de aplicación del algoritmo.
5. Resistencia a los atascos.
6. Buenos resultados en funciones discretas tanto suaves como complejas.
7. Alta convergencia.

Desventajas:
1. No se han detectado.

En cada artículo adjuntamos un archivo que contiene versiones reales actualizadas de los códigos de los algoritmos descritos en los artículos anteriores. No obstante, cabe señalar que no nos hacemos responsable de la exactitud absoluta en la descripción de los algoritmos canónicos. Con frecuencia también hemos añadido ideas propias y mejoras basadas en experiencias y opiniones personales. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.