
Algoritmo de optimización caótica — Chaos optimization algorithm (COA): Continuación
Contenido
Introducción
En el artículo anterior, presentamos el método de optimización caótica y analizamos algunos de los métodos incluidos en el algoritmo. En este artículo, completaremos el análisis de los métodos restantes y pasaremos directamente a probar el algoritmo en funciones de prueba.
El método de optimización caótica, en esta implementación, usa el caos determinista para explorar el espacio de soluciones. El principio clave es el uso de tres mapas caóticos diferentes (logístico, sinusoidal y de tienda) para generar secuencias con propiedades de pseudoaleatoriedad y ergodicidad. El algoritmo funciona en tres fases: la búsqueda caótica inicial, el refinamiento de la solución utilizando el método de gradiente ponderado y la búsqueda local final con estrechamiento adaptativo del dominio.
El uso de vectores de velocidad con inercia y mecanismos de detección de estancamiento permite evitar los extremos locales. La adaptación dinámica de parámetros y diversos tipos de mutaciones garantizan un equilibrio entre la exploración global y la explotación local de las soluciones halladas. Ese es el punto principal, ahora podemos continuar con los métodos restantes.
Implementación del algoritmo
El método "ApplyMutation" se usa para introducir mutaciones en el agente. Su tarea principal consiste en cambiar aleatoriamente los parámetros de un determinado agente.
El método comienza comprobando la exactitud del índice del agente especificado. Si el índice se encuentra fuera de rango, el método finaliza. A continuación, se recopila información sobre el tamaño de varios arrays asociados con el agente, como el tamaño de sus parámetros y su velocidad. Esto evita que el método vaya más allá de los límites de estos arrays.
El método calcula el número máximo de coordenadas que se pueden cambiar según los tamaños de los arrays disponibles para garantizar la seguridad de las operaciones. Luego se selecciona un número aleatorio para determinar cuántas coordenadas se mutarán. Este valor varía entre el 1 y el 30% del número máximo de coordenadas disponibles. Se forma un array de índices que representan las coordenadas que se pueden cambiar. Este array se mezcla para garantizar una selección aleatoria al aplicar mutaciones.
En el ciclo, las coordenadas para la mutación se seleccionan del array mezclado. Para cada coordenada seleccionada, se determina un tipo de mutación según un valor aleatorio. Los tipos posibles incluyen mutación aleatoria completa (donde se elige un nuevo valor aleatoriamente dentro de un rango determinado), mutación respecto a la mejor solución global y mutación con representaciones caóticas.
Tras cambiar el valor de cada coordenada, la velocidad del agente se restablece para que el nuevo valor no se vea afectado por las velocidades anteriores. Finalmente, el nuevo valor para la coordenada del agente correspondiente se establece considerando los rangos y pasos, lo que garantiza que los valores se mantengan dentro del rango aceptable.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::ApplyMutation (int agentIdx) { // Определяем количество координат для мутации (от 1 до 30% координат) int mutationCount = 1 + (int)(u.RNDprobab () * coords * 0.3); mutationCount = MathMin (mutationCount, coords); // Создаем массив индексов для мутации без повторений int mutationIndices []; ArrayResize (mutationIndices, coords); // Заполняем массив индексами for (int i = 0; i < coords; i++) { mutationIndices [i] = i; } // Перемешиваем индексы for (int i = coords - 1; i > 0; i--) { int j = (int)(u.RNDprobab () * (i + 1)); if (j <= i) // Дополнительная проверка для безопасности { int temp = mutationIndices [i]; mutationIndices [i] = mutationIndices [j]; mutationIndices [j] = temp; } } // Применяем мутации к выбранным координатам for (int m = 0; m < mutationCount; m++) { int c = mutationIndices [m]; // Различные типы мутаций для разнообразия double r = u.RNDprobab (); double x; if (r < 0.3) { // Полная случайная мутация x = rangeMin [c] + u.RNDprobab () * (rangeMax [c] - rangeMin [c]); } else if (r < 0.6) { // Мутация относительно глобального лучшего double offset = (u.RNDprobab () - 0.5) * (rangeMax [c] - rangeMin [c]) * 0.2; x = cB [c] + offset; } else { // Мутация с использованием хаотического отображения agent [agentIdx].gamma [c] = SelectChaosMap (agent [agentIdx].gamma [c], (epochNow + c) % 3); x = rangeMin [c] + agent [agentIdx].gamma [c] * (rangeMax [c] - rangeMin [c]); } // Сбрасываем скорость agent [agentIdx].velocity [c] = 0.0; // Применяем новое значение с проверкой диапазона a [agentIdx].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
El método "UpdateSigma" de la clase se encarga de adaptar dinámicamente el parámetro de penalización que se utiliza durante el proceso de optimización. Este regula el valor de la penalización en función del número de soluciones factibles en la población de agentes.
Si se llama al método por primera vez (la época es 1), el valor de penalización actual (currentSigma) se establece como igual a la mitad del valor básico (sigma). El método itera la población de agentes completa y calcula el número de soluciones factibles. Para ello, se usa una función auxiliar para determinar si el agente es válido. Aquí, se realiza una iteración sobre todos los agentes, lo cual nos permite determinar cuántos de ellos cumplen los criterios dados.
A continuación, el método calcula la proporción de soluciones factibles en la población total dividiendo el número de soluciones factibles por el número total de agentes. Esta relación ayudará a comprender cómo de bien está funcionando la estrategia actual. Basándose en la proporción calculada de soluciones factibles, el método toma decisiones sobre la corrección de la penalización: si la proporción de soluciones factibles es inferior al 30%, esto indica que el algoritmo es demasiado estricto y se aumenta la penalización para obligar a los agentes a mostrar más diversidad en sus decisiones. Si la proporción supera el 70%, esto indica que demasiados agentes encuentran soluciones factibles y se reduce la penalización para evitar una convergencia prematura.
Al final, el método garantiza que el valor de la penalización actual se mantenga dentro de límites admisibles. Si resulta demasiado pequeño (menos del 10% del valor básico), la penalización aumenta hasta ese nivel. De manera similar, si la penalización excede el 500% del valor básico, se limita a ese nivel.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::UpdateSigma () { // Динамическая адаптация параметра штрафа // Начинаем с малого значения и увеличиваем его при необходимости if (epochNow == 1) { currentSigma = sigma * 0.5; return; } // Подсчет количества допустимых решений int feasibleCount = 0; for (int i = 0; i < popSize; i++) { if (IsFeasible (i)) { feasibleCount++; } } double feasibleRatio = (double)feasibleCount / MathMax (1, popSize); // Адаптация параметра штрафа в зависимости от доли допустимых решений if (feasibleRatio < 0.3) { // Слишком мало допустимых решений - увеличиваем штраф currentSigma *= 1.2; } else if (feasibleRatio > 0.7) { // Слишком много допустимых решений - уменьшаем штраф currentSigma *= 0.9; } // Ограничиваем значение sigma if (currentSigma < sigma * 0.1) currentSigma = sigma * 0.1; else if (currentSigma > sigma * 5.0) currentSigma = sigma * 5.0; } //——————————————————————————————————————————————————————————————————————————————
El método "IsFeasible" determina si una solución particular representada por un agente con un índice "agentIdx" dado es factible con respecto a las restricciones dadas.
En primer lugar, el método verifica que el índice de agente dado (agentIdx) esté dentro del rango permitido, es decir, mayor o igual a 0 y menor que el tamaño de la población (popSize). Si el índice no es válido, el método retorna "false", lo que indica que la solución no es válida. Si el índice del agente es correcto, el método procede a verificar las restricciones para esta solución. Este itera a través de todas las coordenadas de la solución y para cada coordenada calcula el valor de infracción de la restricción utilizando la función CalculateConstraintValue.
La función CalculateConstraintValue devuelve un valor que refleja el grado de infracción de la restricción para una coordenada de solución particular. Si después de verificar todas las coordenadas no se infringe ninguna restricción, es decir, todos los valores de infracción son menores o iguales a "eps", entonces la solución se considera aceptable y el método devuelve "true".
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_COA_chaos::IsFeasible (int agentIdx) { // Проверяем, находится ли решение в допустимой области for (int c = 0; c < coords; c++) { double violation = CalculateConstraintValue (agentIdx, c); if (violation > eps) { return false; } } return true; } //——————————————————————————————————————————————————————————————————————————————
El método "UpdateBestHistory" es necesario para guardar el mejor valor actual en la historia de búsqueda. Toma el nuevo mejor valor y primero verifica si es correcto o válido. Si el valor es correcto, se almacena en el array que guarda la historia de los mejores resultados, en la posición indexada actual. Después de esto, el índice se actualiza para el próximo guardado, usando una actualización cíclica que utiliza la operación restante de división por el tamaño del array de la historia, lo que garantiza que la historia siempre se llene con los últimos 10 valores sin ir más allá de los límites del array.
Este método permite realizar un seguimiento del progreso de la búsqueda y utilizar la historia de las mejores soluciones para el análisis.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::UpdateBestHistory (double newBest) { // Защита от некорректных значений if (!MathIsValidNumber (newBest)) return; // Обновляем историю лучших значений globalBestHistory [historyIndex] = newBest; historyIndex = (historyIndex + 1) % 10; } //——————————————————————————————————————————————————————————————————————————————
El método "IsConverged" se usa para determinar si el algoritmo ha alcanzado la convergencia. Analiza la historia de las mejores soluciones globales para evaluar significativamente cómo las soluciones mejoran con el tiempo. Si las mejoras se vuelven insignificantes, se considera que el algoritmo ha convergido.
El método inicializa las variables para contar el número de valores permitidos (válidos), la suma de valores, y los valores mínimo y máximo de la historia de las mejores soluciones globales (globalBestHistory). Las variables "minVal" y "maxVal" se inicializan a los valores máximo y mínimo posibles de "double" respectivamente, para definir correctamente el mínimo y máximo en el futuro.
El método itera por el array "globalBestHistory" y para cada valor de la historia realiza comprobaciones sobre la validez, la suficiencia de los datos y su diversidad, además calcula la media y la diferencia relativa y comprueba la convergencia. En general, el método IsConverged ofrece una manera de determinar la convergencia de un algoritmo de optimización analizando la historia de las mejores soluciones y evaluando qué tan significativas son las mejoras a lo largo del tiempo.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_COA_chaos::IsConverged () { // Проверка достаточного количества данных в истории int validValues = 0; double sum = 0.0; double minVal = DBL_MAX; double maxVal = -DBL_MAX; // Находим min, max и sum значений в истории for (int i = 0; i < 10; i++) { if (globalBestHistory [i] == -DBL_MAX || !MathIsValidNumber (globalBestHistory [i])) continue; minVal = MathMin (minVal, globalBestHistory [i]); maxVal = MathMax (maxVal, globalBestHistory [i]); sum += globalBestHistory [i]; validValues++; } // Если недостаточно данных или все значения одинаковые if (validValues < 5 || minVal == maxVal) return false; // Вычисляем среднее значение double average = sum / validValues; // Проверка случая, когда среднее близко к нулю if (MathAbs (average) < eps) return MathAbs (maxVal - minVal) < eps * 10.0; // Относительная разница для проверки сходимости double relDiff = MathAbs (maxVal - minVal) / MathAbs (average); return relDiff < 0.001; // Порог сходимости - 0.1% } //——————————————————————————————————————————————————————————————————————————————
El método "ResetStagnatingAgents" está diseñado para administrar agentes durante el proceso de optimización, especialmente para gestionar casos donde los agentes dejan de mostrar mejoras en sus resultados. Así, monitorea el estado de estancamiento de los agentes y, si es necesario, aplica mutación a aquellos que se encuentran estancados en extremos locales.
Para cada agente, se comprueba si su valor de función de aptitud actual (a[i].f) ha mejorado en comparación con su valor anterior (a[i].fB). Si el valor actual no ha mejorado o ha empeorado, el "stagnationCounter" del agente se incrementa, lo cual indica que el agente se encuentra en un estado de estancamiento. Si el valor ha mejorado, el contador de estancamiento se reinicia.
Si el agente se queda estancado durante más de 5 iteraciones, el método calcula la probabilidad de reinicio (resetProb). Esta probabilidad resulta proporcional al valor actual del contador de estancamiento, lo que significa que cuanto más tiempo permanezca estancado el agente, mayor será la probabilidad de que se reinicie. La fórmula para calcular la probabilidad considera un valor fijo (0,2) y el valor relativo del contador de estancamiento. Si el valor generado aleatoriamente es menor que la probabilidad calculada "resetProb", se aplica una mutación al agente usando la función "ApplyMutation". Tras aplicar una mutación, el contador de estancamiento del agente se reinicia y el contador "resetCount" aumenta.
El método finaliza después de procesar todos los agentes, descartando aquellos que han cruzado el umbral de estancamiento y han cumplido las condiciones para la mutación.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::ResetStagnatingAgents () { int resetCount = 0; for (int i = 0; i < popSize; i++) { // Увеличиваем счетчик стагнации, если нет улучшения if (a [i].f <= a [i].fB) { agent [i].stagnationCounter++; } else { agent [i].stagnationCounter = 0; } // Сбрасываем агента, если он находится в стагнации слишком долго if (agent [i].stagnationCounter > 5) { // Сброс только части агентов с вероятностью, зависящей от стагнации double resetProb = 0.2 * (1.0 + (double)agent [i].stagnationCounter / 10.0); if (u.RNDprobab () < resetProb) { ApplyMutation (i); agent [i].stagnationCounter = 0; resetCount++; } } } } //——————————————————————————————————————————————————————————————————————————————
El método CalculateWeightedGradient se usa para valorar el gradiente de restricción para un agente y una coordenada específicos, considerando el grado en que se infringen dichas restricciones. Ayuda a determinar en qué dirección y con qué fuerza se debe ajustar la solución para eliminar la infracción, ponderando el gradiente según el nivel de la infracción.
En primer lugar, se comprueban los índices y las coordenadas del agente para garantizar que se encuentren dentro de límites aceptables. Si los índices no son válidos, se retorna un valor nulo, lo que significa que no hay dirección para el ajuste. Luego, el método recorre todas las coordenadas asociadas con el agente actual y calcula el valor de infracción para cada una. Durante este proceso, busca la máxima infracción entre ellas. Si la infracción de una coordenada determinada es mayor que el umbral "eps", se considera que vale la pena tomar medidas correctivas; de lo contrario, se retorna cero: el movimiento en esta dirección no tiene sentido o no es necesario.
Si la infracción es significativa, se calcula el gradiente de restricción para la coordenada: la medida de la dirección y la fuerza del cambio en la restricción en relación con los cambios en esa coordenada. El gradiente se multiplica por un peso que se define como la relación entre la infracción de la coordenada actual y la infracción máxima entre todas las restricciones. Esto garantiza que una mayor perturbación tenga una influencia más fuerte en la dirección del ajuste. El valor resultante es un gradiente de restricción ponderado que indica cuánto y en qué dirección debe ajustarse la solución para eliminar la infracción en una coordenada dada, proporcional a su grado.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::CalculateWeightedGradient (int agentIdx, int coordIdx) { // Вычисляем максимальное значение нарушения ограничений double maxViolation = eps; for (int c = 0; c < coords; c++) { double violation = CalculateConstraintValue (agentIdx, c); maxViolation = MathMax (maxViolation, violation); } // Нарушение для текущей координаты double violation = CalculateConstraintValue (agentIdx, coordIdx); // Если нет значительного нарушения, возвращаем 0 if (violation <= eps) return 0.0; // Вычисляем градиент double gradient = CalculateConstraintGradient (agentIdx, coordIdx); // Нормализуем влияние в зависимости от степени нарушения double weight = violation / maxViolation; return gradient * weight; } //——————————————————————————————————————————————————————————————————————————————
El método "CalculateConstraintValue" se usa para estimar el grado de infracción de la restricción para una coordenada dada de un agente determinado. Determina en qué medida el valor de la coordenada actual está fuera de los límites aceptables y retorna un valor numérico que refleja la magnitud de esta infracción.
En primer lugar, el método verifica que los índices del agente (agentIdx) y las coordenadas (coordIdx) sean correctos. El método obtiene el valor actual de la coordenada "x" del estado del agente y también determina los límites mínimos (min) y máximos (max) aceptables para esta coordenada, respectivamente. A continuación, el método comprueba si el valor "x" se encuentra dentro del rango aceptable (min. y max.). Finalmente, el método retorna un valor de "infracción" que supone la cantidad total de infracción de la restricción para la coordenada dada del agente dado.
Características principales:
- El método retorna un valor positivo si se infringe la restricción y 0 si se cumple.
- La magnitud de la infracción es proporcional al grado en que el valor de la coordenada supera los límites aceptables.
En última instancia, el método CalculateConstraintValue ofrece información importante sobre el grado en que cada agente de la población cumple las restricciones del problema. Así, mide la magnitud de la perturbación, lo que ayuda al algoritmo a comprender cuánto debe ajustarse la posición del agente.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::CalculateConstraintValue (int agentIdx, int coordIdx) { double x = a [agentIdx].c [coordIdx]; double min = rangeMin [coordIdx]; double max = rangeMax [coordIdx]; // Сглаженная функция нарушения ограничений с плавным переходом на границе double violation = 0.0; // Проверка нижней границы if (x < min) { violation += min - x; } // Проверка верхней границы else if (x > max) { violation += x - max; } return violation; } //——————————————————————————————————————————————————————————————————————————————
El método "CalculateConstraintGradient" calcula el gradiente de restricción para una coordenada dada de un agente concreto. Este método determina en qué dirección y con qué fuerza se debe cambiar el valor de la coordenada debido a la infracción de la restricción.
El método primero verifica los índices del agente de entrada (agentIdx) y las coordenadas (coordIdx) para garantizar que estos sean correctos. Si al menos uno de los índices está fuera del rango válido, el método retorna 0,0, lo que indica que no se puede calcular el gradiente. El método recupera el valor actual de la coordenada del agente, así como los límites mínimo y máximo establecidos para dicha coordenada. Estos valores son necesarios para futuras evaluaciones. A continuación, el método comprueba si el valor actual de la coordenada "x" se halla fuera de los límites establecidos.
El valor final retornado por el método refleja la dirección y la necesidad de cambiar el valor actual de la coordenada del agente, considerando las restricciones especificadas.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::CalculateConstraintGradient (int agentIdx, int coordIdx) { double x = a [agentIdx].c [coordIdx]; double min = rangeMin [coordIdx]; double max = rangeMax [coordIdx]; // Сглаженный градиент для лучшей стабильности if (x < min) return -1.0; // Нужно увеличивать значение else if (x > max) return 1.0; // Нужно уменьшать значение return 0.0; } //——————————————————————————————————————————————————————————————————————————————
El método "CalculatePenaltyFunction" calcula los valores de la función objetivo considerando la penalización por infringir las restricciones para un agente específico. Combina un valor básico de la función objetivo con una penalización basada en la magnitud de las infracciones de las restricciones.
El método comienza verificando la validez del índice del agente (agentIdx), y si el índice es válido, el método obtiene el valor básico (no penalizado) de la función objetivo de este agente (a[agentIdx].f) y lo almacena en la variable "baseValue". Luego, el método itera todas las coordenadas de cada agente. Para cada coordenada, se calcula la magnitud de la infracción de la restricción. Si la magnitud de la infracción supera un valor pequeño dado "eps", entonces el cuadrado de la magnitud de la infracción se añade a la suma de sanciones "penaltySum".
Se usa una penalización cuadrática para proporcionar una evaluación más "suave" para las infracciones menores y una evaluación más "dura" para las infracciones mayores. Después de sumar todas las multas por infringir las restricciones, se calcula la penalización total.
Finalmente, el método calcula el valor "penalizado" de la función objetivo restando la penalización "penalty" del valor básico de la función objetivo "baseValue". Luego se retorna el valor penalizado de la función objetivo.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_COA_chaos::CalculatePenaltyFunction (int agentIdx) { // Базовое значение целевой функции double baseValue = a [agentIdx].f; // Штрафной терм double penaltySum = 0.0; for (int c = 0; c < coords; c++) { double violation = CalculateConstraintValue (agentIdx, c); // Квадратичный штраф для лучшего разрешения близких к границе решений if (violation > eps) { penaltySum += violation * violation; } } // Применяем динамический коэффициент штрафа double penalty = currentSigma * penaltySum; // Для задачи максимизации: f_penalty = f - penalty return baseValue - penalty; } //——————————————————————————————————————————————————————————————————————————————
El método "Moving" es el principal procedimiento de control para mover la solución a través del proceso de optimización. Este realiza pasos secuenciales encaminados a actualizar el estado actual del sistema, adaptar los parámetros y gestionar las fases de búsqueda.
En primer lugar, se incrementa el contador de la época actual. Si esta es la primera llamada al método, se inicia la creación de la población inicial de agentes, tras lo cual finaliza esta etapa. A continuación, el parámetro de penalización (sigma) se actualiza dinámicamente, lo cual ayuda a regular la influencia de las funciones de penalización durante el proceso de búsqueda. Una tarea importante consiste en verificar y reiniciar periódicamente los agentes que están bloqueados o no muestran progreso, lo que ayuda a prevenir el estancamiento en las trampas locales.
La fase actual de la búsqueda está determinada entonces por el valor del contador de épocas: en las etapas iniciales, se realiza una búsqueda global y luego se pasa a una búsqueda local más estrecha. Dependiendo de la fase se llaman las estrategias de búsqueda correspondientes, que controlan el movimiento de los agentes.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::Moving () { epochNow++; if (!revision) { InitialPopulation (); revision = true; return; } // Динамическое обновление параметра штрафа UpdateSigma (); // Сброс агентов, находящихся в стагнации if (epochNow % 5 == 0) { ResetStagnatingAgents (); } // Определяем фазу поиска if (epochNow <= S1) { FirstCarrierWaveSearch (); } else if (epochNow <= S1 + S2) { SecondCarrierWaveSearch (); } } //——————————————————————————————————————————————————————————————————————————————
El método “Revision” se encarga de mejorar las soluciones y adaptar los parámetros de búsqueda durante el proceso de optimización iterativa. Este reevalúa el estado actual de la población, actualiza las mejores soluciones y ajusta los parámetros de búsqueda en función del rendimiento de los últimos pasos.
El método itera a través de todas las soluciones de la población, calculando su nuevo valor de "penalización" usando la función de penalización, que permite tener en cuenta las infracciones de las restricciones. Se comprueba que el valor recibido sea correcto y, si es válido, se almacena como el valor actual de la función. Para cada agente cuyo nuevo valor de función sea mejor que el anterior, se actualizan sus datos personales: se guarda el nuevo valor y también se copian las coordenadas actuales. Con esto garantiza que se recuerde la mejor solución local para cada agente. Si el agente encuentra una solución mejor que la global actual, se actualiza el mejor resultado global y se recuerdan las coordenadas correspondientes. También se actualiza la historia de las mejores soluciones.
Tras el primer nivel de iteraciones (epochNow > 1), se evalúa el éxito de la búsqueda: se determina la proporción de mejoras entre todos los agentes. En base a esta evaluación se adaptan los parámetros, especialmente “alfa” (el área de búsqueda para cada coordenada). Dependiendo de la fase de búsqueda actual (global o local), las reglas para ajustar "alfa" pueden diferir: en la fase de búsqueda global, con un bajo nivel de mejora, el área de búsqueda aumenta para ampliar las posibilidades; en la fase de búsqueda local, con una mejora insuficiente, el área de búsqueda también aumenta; y con un éxito significativo, el área de búsqueda se reduce, lo que ayuda a localizar la solución óptima. En este caso, el parámetro "alfa" se ve limitado por valores máximos y mínimos en función del rango de valores aceptables para la coordenada.
Este enfoque permite un equilibrio dinámico entre la exploración de nuevas soluciones y la localización de las óptimas, usando información sobre el rendimiento de iteraciones pasadas.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA_chaos::Revision () { int improvementCount = 0; double bestImprovement = 0.0; // Оценка всех решений for (int i = 0; i < popSize; i++) { double newValue = CalculatePenaltyFunction (i); // Проверка на валидность нового значения if (!MathIsValidNumber (newValue)) continue; // Сохраняем текущее значение для следующей итерации a [i].f = newValue; // Обновление личного лучшего решения (перед глобальным для эффективности) if (newValue > a [i].fB) { a [i].fB = newValue; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); improvementCount++; } // Обновление глобального лучшего решения if (newValue > fB) { double improvement = newValue - fB; fB = newValue; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); // Обновляем историю лучших значений UpdateBestHistory (fB); bestImprovement = MathMax (bestImprovement, improvement); improvementCount++; } } // Адаптация параметров поиска в зависимости от фазы и успешности if (epochNow > 1) { // Коэффициент успешности поиска (предотвращение деления на ноль) double successRate = (double)improvementCount / MathMax (1, 2 * popSize); // Адаптация параметра alpha for (int c = 0; c < coords; c++) { double oldAlpha = alpha [c]; if (epochNow <= S1) { // В фазе глобального поиска if (successRate < 0.1) { // Очень мало улучшений - увеличиваем область поиска alpha [c] *= t3; } else if (successRate < 0.3) { // Мало улучшений - слегка увеличиваем область alpha [c] *= 1.2; } else if (successRate > 0.7) { // Много улучшений - сужаем область alpha [c] *= 0.9; } } else { // В фазе локального поиска if (successRate < 0.05) { // Очень мало улучшений - увеличиваем область поиска alpha [c] *= t3; } else if (successRate > 0.2) { // Достаточно улучшений - сужаем область alpha [c] *= 0.8; } } // Ограничения на диапазон alpha с безопасной проверкой границ if (c < ArraySize (rangeMax) && c < ArraySize (rangeMin)) { double maxAlpha = 0.2 * (rangeMax [c] - rangeMin [c]); double minAlpha = 0.0001 * (rangeMax [c] - rangeMin [c]); if (alpha [c] > maxAlpha) { alpha [c] = maxAlpha; } else if (alpha [c] < minAlpha) { alpha [c] = minAlpha; } } } } } //——————————————————————————————————————————————————————————————————————————————
Ahora que hemos examinado todos los métodos, podemos pasar directamente a probar el algoritmo.
Resultados de las pruebas
De hecho, el resultado habla por sí solo: los parámetros externos se han optimizado ligeramente, mientras que los internos se han mantenido sin cambios y se presentan como describimos anteriormente en los métodos.COA(CHAOS)|Chaos Optimization Algorithm|50.0|10.0|40.0|2.0|1.2|0.0001|
=============================
5 Hilly's; Func runs: 10000; result: 0.6083668756744218
25 Hilly's; Func runs: 10000; result: 0.4079413401686229
500 Hilly's; Func runs: 10000; result: 0,2678056430575926
=============================
5 Forest's; Func runs: 10000; result: 0.668343763134901
25 Forest's; Func runs: 10000; result: 0.38894787694645416
500 Forest's; Func runs: 10000; result: 0,2198998763835145
=============================
5 Megacity's; Func runs: 10000; result: 0.32307692307692304
25 Megacity's; Func runs: 10000; result: 0.1987692307692308
500 Megacity's; Func runs: 10000; result: 0.10598461538461638
=============================
All score: 3.18914 (35.43%)
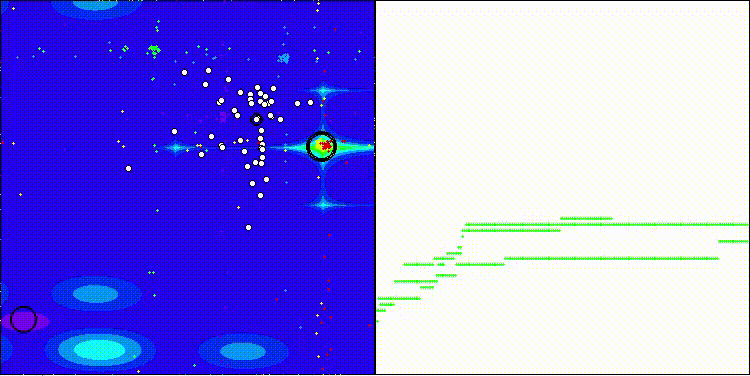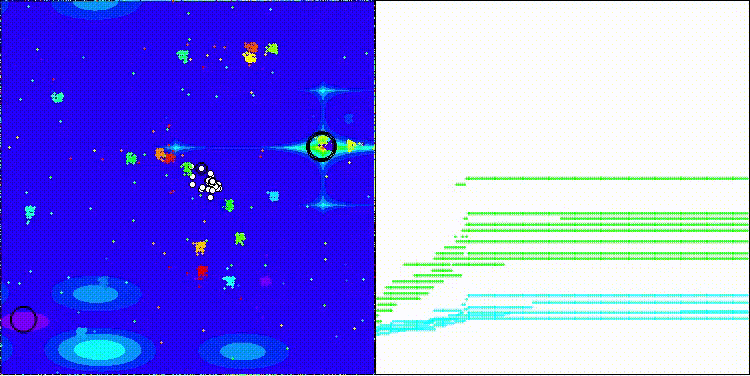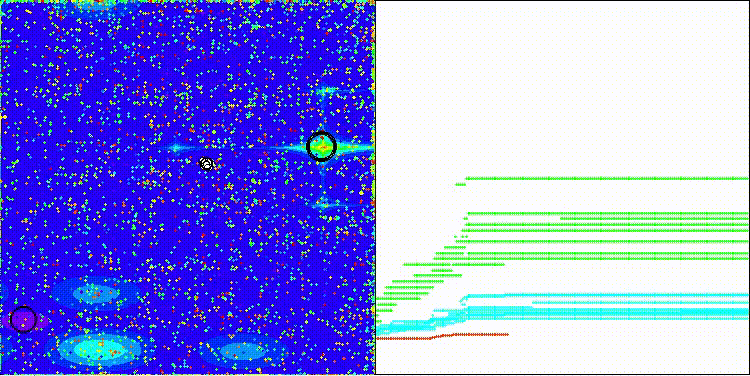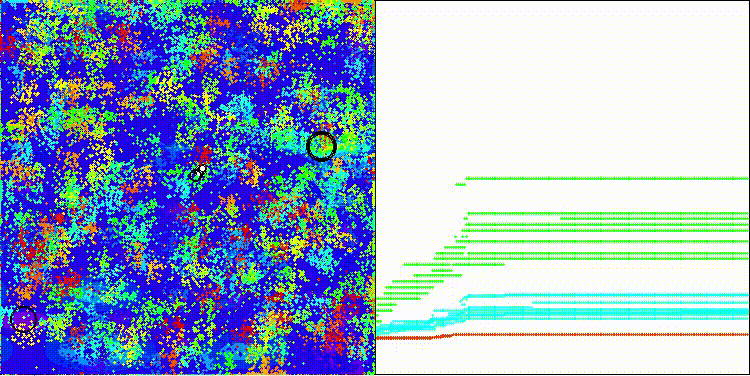
Me gustaría llamar la atención sobre la visualización del funcionamiento del algoritmo: la combinación de la variedad de métodos de búsqueda usados produce un efecto visual inusual.
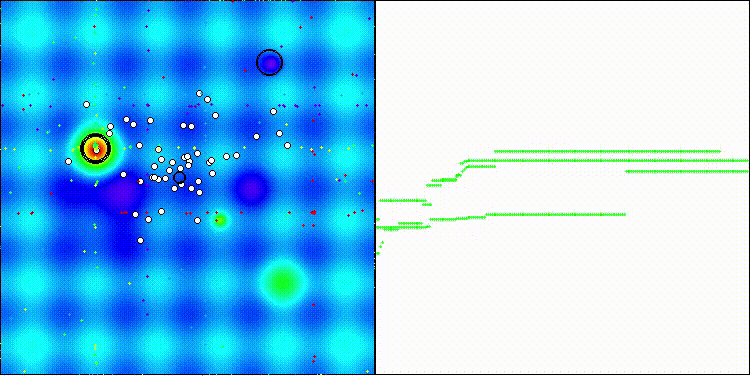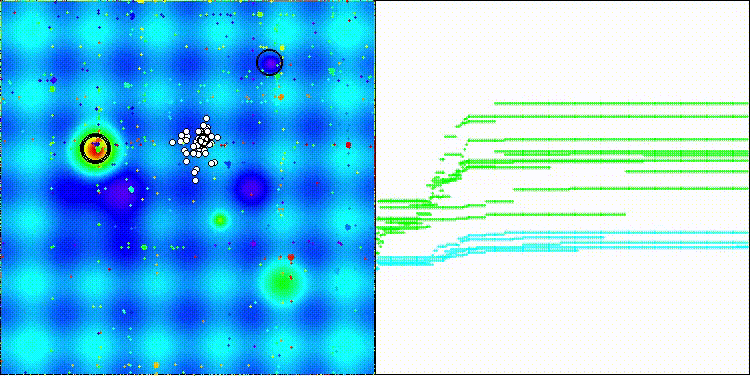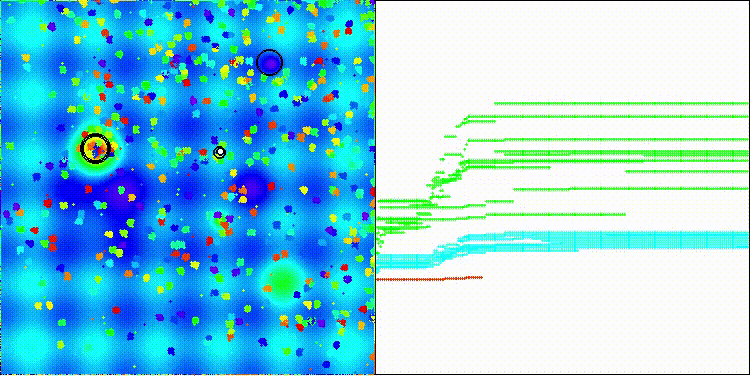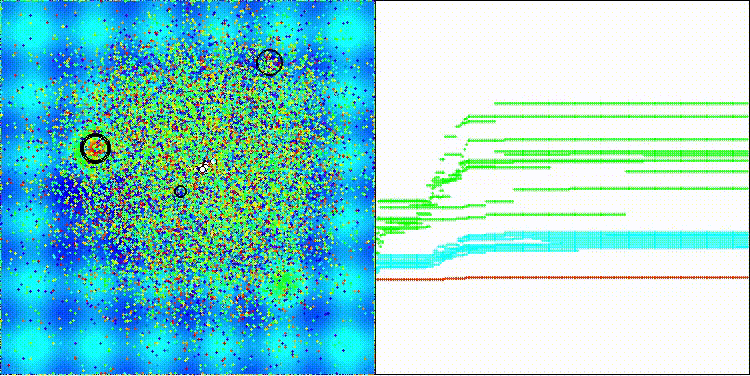
COA(CHAOS) en la función de prueba de Hilly
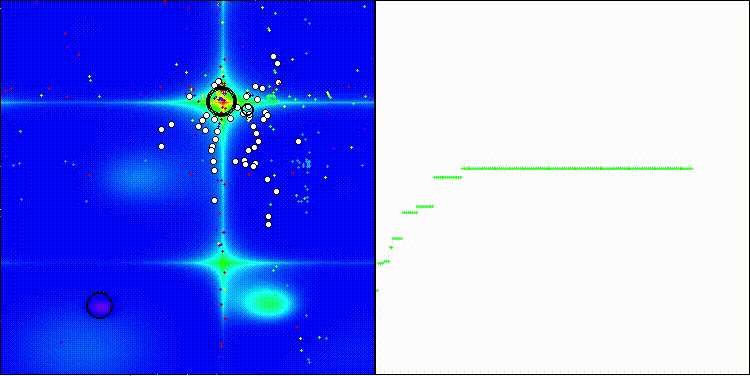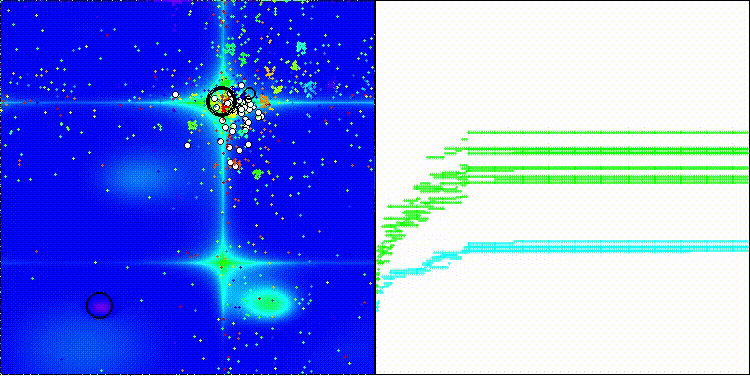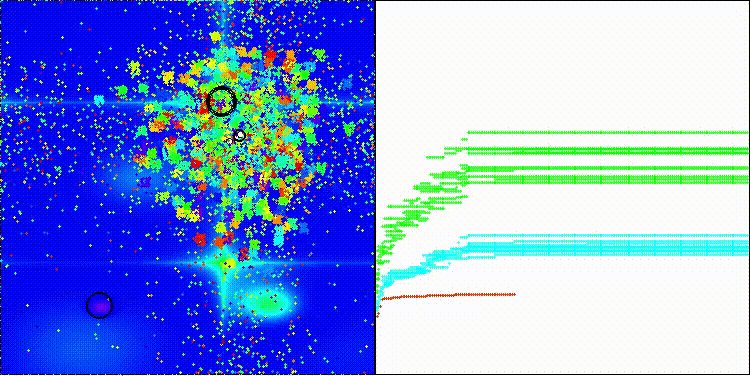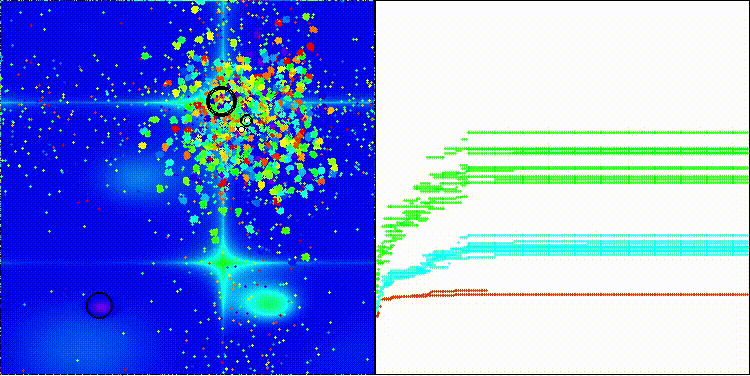
COA(CHAOS) en la función de prueba Forest
COA(CHAOS) en la función de prueba Megacity
Con base en los resultados de las pruebas, el algoritmo COA(CHAOS) se presenta en nuestra tabla de calificación.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Resultado | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration optimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 13 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 14 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0.34583 | 1,86493 | 0.93593 | 0.80152 | 0,27177 | 2,00923 | 0.65077 | 0.51646 | 0,15472 | 1,32195 | 5.196 | 57.73 |
| 15 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 16 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 17 | AOSm | búsqueda de orbitales atómicos M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 18 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 19 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 20 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 21 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 22 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 23 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 24 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 25 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 26 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 27 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 28 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 29 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 30 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 31 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 32 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 33 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 34 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 35 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 36 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1,65585 | 0.89675 | 0.37401 | 0.16984 | 1,44060 | 0.69538 | 0.28031 | 0.10852 | 1,08422 | 4.181 | 46,45 |
| 37 | ABH | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4.127 | 45,85 |
| 38 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 39 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0,26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1,39880 | 0,66154 | 0.27046 | 0.10594 | 1,03794 | 4.037 | 44.85 |
| 40 | CGO | chaos game optimization | 0,57256 | 0,37158 | 0,32018 | 1,26432 | 0,61176 | 0,61931 | 0,62161 | 1,85267 | 0,37538 | 0,21923 | 0,19028 | 0,78490 | 3,902 | 43,35 |
| 41 | ATAm | artificial tribe algorithm M | 0.71771 | 0.55304 | 0,25235 | 1,52310 | 0.82491 | 0.55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 42 | CROm | coral reefs optimization M | 0,78512 | 0,46032 | 0,25958 | 1,50502 | 0,86688 | 0,35297 | 0,16267 | 1,38252 | 0,63231 | 0,26738 | 0,10734 | 1,00703 | 3,895 | 43,27 |
| 43 | CFO | central force optimization | 0,60961 | 0,54958 | 0,27831 | 1,43750 | 0,63418 | 0,46833 | 0,22541 | 1,32792 | 0,57231 | 0,23477 | 0,09586 | 0,90294 | 3,668 | 40,76 |
| 44 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 45 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3.657 | 40,63 |
| CAOS | chaos optimization algorithm | 0.60837 | 0.40794 | 0,26781 | 1,28412 | 0.66834 | 0.38895 | 0,21990 | 1,27719 | 0.32308 | 0,19877 | 0,10598 | 0.62783 | 3.189 | 35.43 | |
| R.W. | neuroboids optimization algorithm 2(joo) | 0.48754 | 0.32159 | 0.25781 | 1,06694 | 0.37554 | 0,21944 | 0,15877 | 0,75375 | 0.27969 | 0,14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Conclusiones
El resultado del 35% después de la prueba muestra un buen potencial del algoritmo COA(CHAOS), especialmente considerando su complejidad y la cantidad de parámetros externos configurables, incluidos los internos que no fueron optimizados. El algoritmo simplemente aún no ha demostrado su máximo rendimiento.
Los aspectos más interesantes y prometedores del algoritmo son: el uso de tres mapeos diferentes (logístico, sinusoidal y tipo tienda) para las capacidades de búsqueda del algoritmo; la adición de inercia ayuda al algoritmo a mantener el impulso mientras supera los obstáculos locales; los cambios dinámicos de parámetros, dependiendo del éxito y la fase de optimización, aumentan su flexibilidad; el seguimiento de la historia de decisiones y el reinicio de los agentes "atascados" permiten que el algoritmo evite desperdiciar recursos computacionales en áreas poco prometedoras. Además, el uso del hipercubo latino y diferentes enfoques para la colocación inicial del agente garantizan una buena cobertura del espacio de búsqueda desde el principio. Para mejorar aún más el algoritmo, merecería la pena realizar una optimización más exhaustiva de los parámetros internos.
Este algoritmo ofrece una rica fuente de ideas para mejorar otros métodos de optimización, especialmente sus mecanismos adaptativos y métodos de manejo del estancamiento que podrían transferirse con éxito a otros algoritmos de aprendizaje automático y optimización para los mercados financieros.
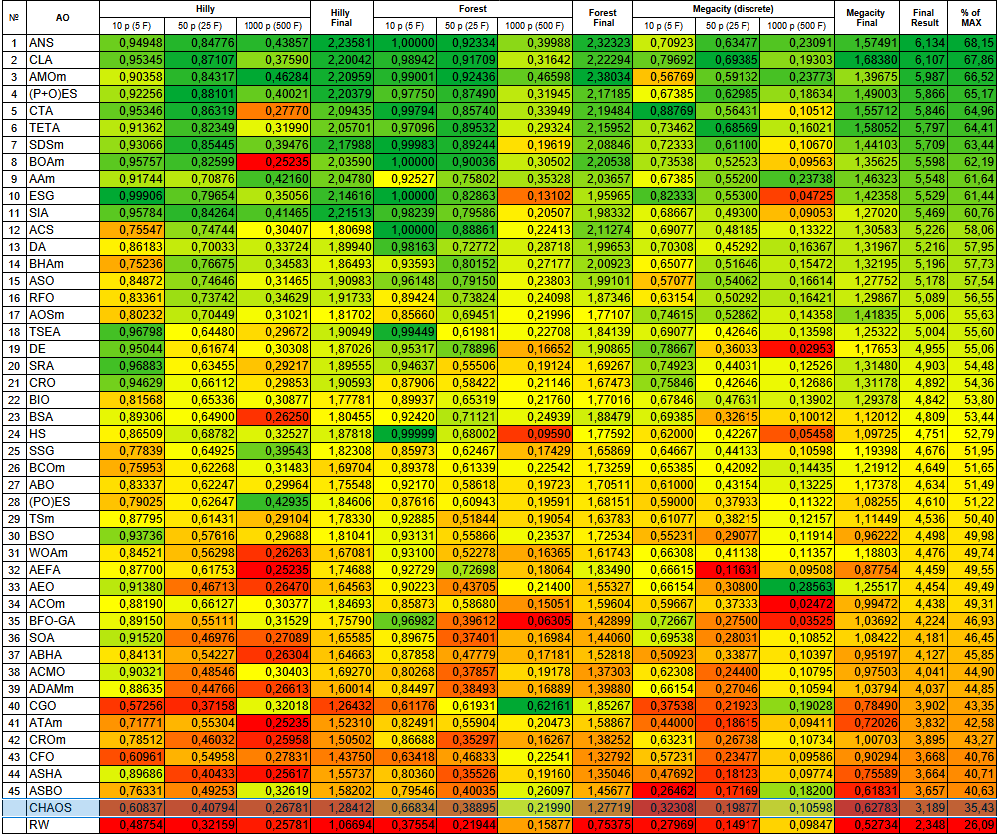
Figura 1. Clasificación por colores de los algoritmos según las pruebas respectivas
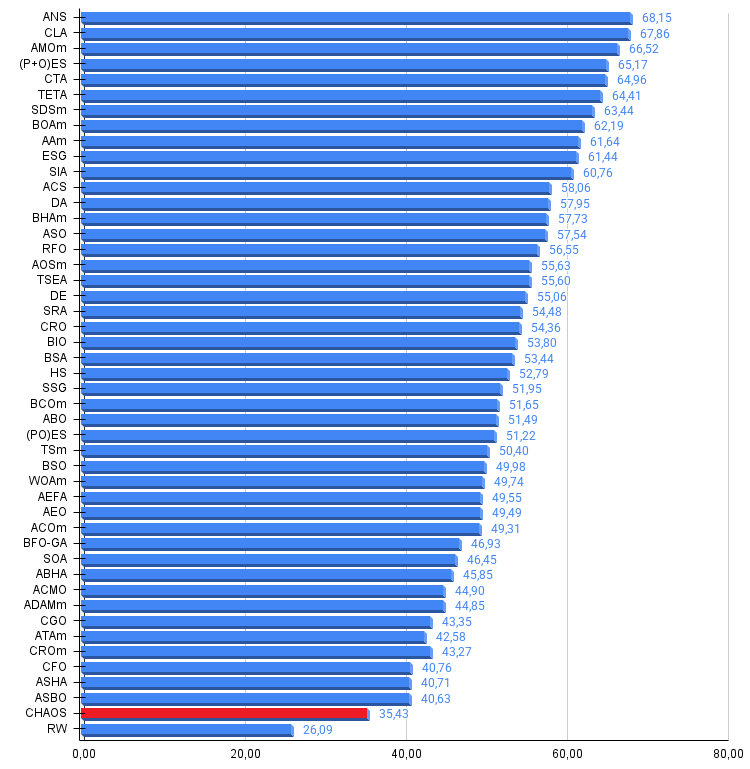
Figura 2. Histograma de los resultados de las pruebas de algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de puntuación está en el archivo)
Ventajas y desventajas del algoritmo COA(CHAOS):
Ventajas:
- Variedad de métodos de búsqueda.
- Desarrollo prometedor.
- Resultados estables.
Desventajas:
- Gran número de parámetros externos.
- Gran cantidad de parámetros internos no optimizables.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | #C_AO.mqh | Archivo de inclusión | Clase padre de algoritmos de optimización basados en la población |
| 2 | #C_AO_enum.mqh | Archivo de inclusión | Enumeración de los algoritmos de optimización basados en la población |
| 3 | TestFunctions.mqh | Archivo de inclusión | Biblioteca de funciones de prueba |
| 4 | TestStandFunctions.mqh | Archivo de inclusión | Biblioteca de funciones del banco de pruebas |
| 5 | Utilities.mqh | Archivo de inclusión | Biblioteca de funciones auxiliares |
| 6 | CalculationTestResults.mqh | Archivo de inclusión | Script para calcular los resultados en una tabla comparativa |
| 7 | Testing AOs.mq5 | Script | Banco de pruebas único para todos los algoritmos de optimización basados en la población |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización |
| 9 | Test_AO_COA_chaos.mq5 | Script | Banco de pruebas COA (CHAOS) |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/17874
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Superando las limitaciones del aprendizaje automático (Parte 1): Falta de métricas interoperables
Superando las limitaciones del aprendizaje automático (Parte 1): Falta de métricas interoperables
 Del básico al intermedio: Objetos (I)
Del básico al intermedio: Objetos (I)
 Particularidades del trabajo con números del tipo double en MQL4
Particularidades del trabajo con números del tipo double en MQL4
 Simulación de mercado (Parte 21): Iniciando SQL (IV)
Simulación de mercado (Parte 21): Iniciando SQL (IV)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso