Algoritmo de campo eléctrico artificial (AEFA) — Artificial Electric Field Algorithm (AEFA)
112
0
Introducción
El algoritmo del campo eléctrico artificial es una creación asombrosa que personifica la armonía de la tecnología y la naturaleza. Inspirado en la ley de Coulomb de la fuerza electrostática, este algoritmo ha llamado la atención por su capacidad única de modelar fenómenos eléctricos para resolver complejos problemas de optimización. En el contexto de los algoritmos ya conocidos y descritos previamente en artículos relacionados con las leyes de la naturaleza, como Charged System Search (CSS), ElectroMagnetism-like algorithm (ЕМ), Gravitational Search Algorithm (GSA) y otros, el campo eléctrico artificial supone una innovación apasionante que no dejará indiferente a ningún investigador. Y bueno, yo no he podido pasarlo por alto....
El algoritmo del campo eléctrico artificial se inspira en la ley de Coulomb, según la cual la fuerza electrostática (atracción o repulsión) entre dos partículas cargadas resulta directamente proporcional al producto de sus cargas e inversamente proporcional al cuadrado de la distancia que las separa. En el algoritmo propuesto, los agentes se tratan como partículas cargadas y su fuerza se mide por sus cargas. Todas estas partículas pueden atraerse o repelerse por fuerza electrostática y, debido a esta fuerza, los objetos se desplazan en el espacio de búsqueda. Por tanto, las cargas se usan como forma directa de comunicación a través de la fuerza electrostática, y la posición de la carga se corresponde con la solución del problema. Las cargas se definen según la adaptación de la solución candidata y de la adaptación de la población. En el algoritmo propuesto, solo consideramos la fuerza de atracción electrostática, de modo que la partícula cargada con mayor carga (el "mejor" individuo) atrae a todas las demás partículas con menor carga y se mueve lentamente en el espacio de búsqueda.
Así, el AEFA puede considerarse como un sistema aislado de cargas que obedecen a la primera ley de Coulomb de la electrostática de la fuerza electrostática y a la ley del movimiento: las partículas cargadas homónimas se repelen, mientras que las partículas cargadas de nombre distinto se atraen, y a la segunda ley de Coulomb de la electrostática: la fuerza de atracción entre partículas cargadas de nombre distinto o la fuerza de repulsión entre partículas cargadas homónimas es directamente proporcional al producto de sus cargas e inversamente proporcional al cuadrado de la distancia entre los centros de las cargas: la velocidad actual de cualquier carga es igual a la suma de las fracciones de su velocidad anterior y de los cambios de velocidad. El cambio de velocidad o aceleración de cualquier carga es igual a la fuerza que actúa sobre el sistema dividida por la masa de la partícula.
Los autores del AEFA son:
1. Anita - pertenece al Departamento de Ciencias y Humanidades del Instituto Nacional de Tecnología de Uttarakhand, Srinagar, India.
2. Anupam Yadav - pertenece al Departamento de Matemáticas del Instituto Nacional de Tecnología Dr. B.R. Ambedkar, Jalandhar, India.
El algoritmo AEFA se expuso en 2019 y se publicó en la revista Swarm and Evolutionary Computation. Los autores del artículo señalan que el concepto de campo eléctrico y partículas cargadas nos ofrece una teoría sólida del funcionamiento de la fuerza de atracción o repulsión entre dos partículas cargadas. Así, el AEFA utiliza los principios de la fuerza electrostática para desarrollar un algoritmo de optimización basado en la población.
Implementación del algoritmo
El algoritmo AEFA tiene diversas fórmulas y, antes de pasar a examinarlas, deberemos tomar nota de sus puntos clave:
- Los agentes del algoritmo (soluciones) se representan como partículas cargadas que se desplazan bajo la acción de una fuerza electrostática.
- La carga de una partícula depende de su mejor resultado personal y de los mejores y peores resultados actuales de la población (no los mejores resultados obtenidos durante la optimización, sino concretamente los resultados actuales de la población).
- La fuerza que actúa sobre una partícula depende de las cargas de las partículas y de la distancia entre las mismas.
- La constante de Coulomb K(t) disminuye al aumentar las iteraciones, controlando el equilibrio entre la búsqueda global y la optimización local.
Vamos ahora a ver la formalización del algoritmo y a analizar más de cerca las fórmulas utilizadas en él.
Digamos que la posición de la partícula i-ésima en el espacio de búsqueda d-dimensional se denota como X_i = (x_1, x_2, ..., x_d), donde i = 1, 2, ..., N, donde N es el tamaño de la población.
La mejor posición encontrada por la partícula i-ésima se denota como P_i, mientras que la mejor posición global se denota como P_best.
1. Fórmula de Coulomb para la fuerza electrostática: F_ij = K * Q_i * Q_j / R^2, donde:
- F_ij - valor de la fuerza electrostática entre dos objetos cargadosi-ésimo y j-ésimo
- K - constante de Coulomb
- Q_i y Q_j - cargas de los objetos i-ésimo y j-ésimo, respectivamente
- R - distancia entre dos cargas Q_i y Q_j
2. Fórmula para el campo eléctrico alrededor de una carga Q_i: E_i = F_ij / Q_i , donde:
- E_i - campo eléctrico alrededor de la carga Q_i
- F_ij - fuerza que actúa sobre la carga Q_i
3. Fórmula de la aceleración de una partícula según la segunda ley de Newton: a_i = F_ij / M, donde:
- a_i - aceleración de la partícula i-ésima
- F_ij - fuerza que actúa sobre la partícula
- M - masa de la partícula
4. Fórmula para la aceleración de una partícula a través de un campo eléctrico: a_i = E_i * Q_i / M, donde:
- a_i - aceleración de la partícula i-ésima
- E_i - campo eléctrico alrededor de la partícula
- Q_i - carga de la partícula
- M - masa de la partícula
5. Fórmula para actualizar la mejor posición de una partícula: p_di (t+1) = {p_di (t) y X_i (t+1) = X_i (t)}, si f (X_i (t+1)) > f (X_i (t)), donde:
- p_di (t) - valor de aptitud de la partícula i-ésima en el momento t
- p_di (t+1) - valor de aptitud de la i-ésima partícula en el momento del tiempo (t+1)
- X_i (t) - posición de la partícula i-ésima en el momento t
- X_i (t+1) - nueva posición de la partícula i-ésima en el momento (t+1)
- f(X_i (t)) - valor de la función objetivo en la posición anterior de la partícula i-ésima en el tiempo t
- f(X_i (t+1)) - valor de la función objetivo en la nueva posición de la partícula i-ésima en el tiempo (t+1)
6. Fórmula de la fuerza que actúa sobre la partícula i-ésima por la partícula j-ésima: F_dij (t) = K (t) * (Q_i (t) * Q_j (t) * (p_dj (t) - X_di (t))) / (R_ij (t)^2 + ε), donde:
- F_dij (t) - fuerza que actúa sobre la partícula i desde la partícula j en el tiempo t
- K (t) - constante de Coulomb en el tiempo t
- Q_i (t) y Q_j (t) - cargas de las partículas i-ésima y j-ésima en el tiempo t
- p_dj (t) - mejor posición de la j-ésima partícula en el tiempo t
- X_di (t) - posición de la partícula i-ésima en el momento t
- R_ij (t) - distancia euclidiana entre las partículas i-ésima y j-ésima en el tiempo t
- ε - pequeña constante positiva utilizada para evitar la división por 0.
7. Fórmula para la distancia euclidiana entre las partículas i-ésima y j-ésima: R_ij (t) = (X_i (t) - X_j (t))^2
8. Fórmula de la constante de Coulomb: K (t) = K_0 * exp (-α * t / maxiter), donde:
- K_0 - valor inicial de la constante de Coulomb
- α - parámetro externo
- t - momento actual del tiempo (época)
- maxiter - número máximo de iteraciones
9. Fórmula de la fuerza total que actúa sobre la i-ésima partícula: F_di (t) = Σ (rand () * F_dij (t)), j=(de 1 a N), j≠i, donde:
- F_di (t) - fuerza total que actúa sobre la partícula i-ésima en el tiempo t
- rand () - número aleatorio en el intervalo [0, 1]
- N - número de partículas en el espacio de búsqueda
10. Fórmula del campo eléctrico que actúa sobre la partícula i-ésima: E_di (t) = F_di (t) / Q_i (t), donde:
- E_di (t) - campo eléctrico que actúa sobre la partícula i-ésima en el tiempo t
- F_di (t) - fuerza total que actúa sobre la partícula i-ésima
- Q_i (t) - carga de la partícula i-ésima en el tiempo t
11. Fórmula actualiza la velocidad de la partícula i en el tiempo t+1: V_i (t+1) = rand () * V_i (t) + a_i (t), donde:
- V_i(t) - velocidad anterior
- a_i(t) - aceleración que actúa sobre la partícula
- rand () - número aleatorio en el intervalo [0, 1]
12. La fórmula actualiza la posición de la partícula i en el tiempo t+1: X_i (t+1) = X_i (t) + V_i (t+1) , donde:
- V_i (t+1) - nueva velocidad
13. La fórmula indica que la carga de todas las partículas de la población es la misma e igual a Q_i (t) = Q_j (t) para todas las i, j = 1, 2,..., N
14. La fórmula calcula la carga relativa q_i (t) de cada partícula i en el tiempo t: q_i (t) = exp ((fit_p_i (t) - worst (t)) / (best (t) - worst (t))), donde:
- fit_p_i (t) - valor de aptitud de la mejor posición personal de la partícula
- fit_best (t) - valor de aptitud de la mejor posición global
- fit_worst(t) - valor de aptitud de la peor partícula de la población
15. Fórmula: Q_i (t) = q_i (t) / Σ_j=1...N q_j (t).
Esta fórmula normaliza las cargas relativas q_i (t) de todas las partículas para que su suma sea igual a 1. Así se obtienen las cargas normalizadas Q_i (t) de cada partícula.
16. Fórmula: best (t) = max (fit_j (t)) para j = 1, 2,..., N
Esta fórmula calcula el mejor valor de aptitud actual best (t) de la población en el tiempo t como el máximo de los valores de aptitud de todas las partículas.
17. Fórmula: worst (t) = min (fit_j (t)) para j = 1, 2,..., N
Esta fórmula calcula el peor valor de aptitud actual worst (t) de la población en el tiempo t como el mínimo de los valores de aptitud de todas las partículas.
Ahora que conocemos las fórmulas de las leyes de movimiento de las partículas en el algoritmo, podemos componer un pseudocódigo que nos ayudará a escribir en el futuro el código del algoritmo AEFA en MQL5.
Pseudocódigo del algoritmo AEFA:
Paso 1: Inicialización
- Inicializamos aleatoriamente las posiciones de las partículas.
- Calculamos los valores de la función objetivo para cada partícula.
- Establecemos la iteración actual t = 0.
Paso 2: Actualizamos las posiciones de las partículas hasta que se cumpla la condición de parada:
1. Calculamos la constante de Coulomb K(t) mediante la fórmula (8)
2. Calculamos el mejor fit_best (t) y peor fit_worst(t) valor de la función objetivo en la iteración actual.
3. Para cada partícula i = 1, 2, ..., N:
a. Calculamos la carga de la partícula Q_i (t) mediante la fórmula (14)
b. Calculamos la fuerza que actúa sobre la partícula i desde el lado de la partícula j según la fórmula (6)
c. Calculamos la fuerza total que actúa sobre la partícula i usando la fórmula (9)
d. Calculamos la aceleración de la partícula i mediante la fórmula (4)
e. Actualizamos la velocidad mediante la fórmula (11) y la posición de la partícula i mediante la fórmula (12)
4. Aumentamos el contador de iteraciones t = t + 1
Paso 3: Condición de parada. Comprobamos la condición de parada (por ejemplo, alcanzar el número máximo de iteraciones). Si no se cumple la condición, iremos al paso 2.
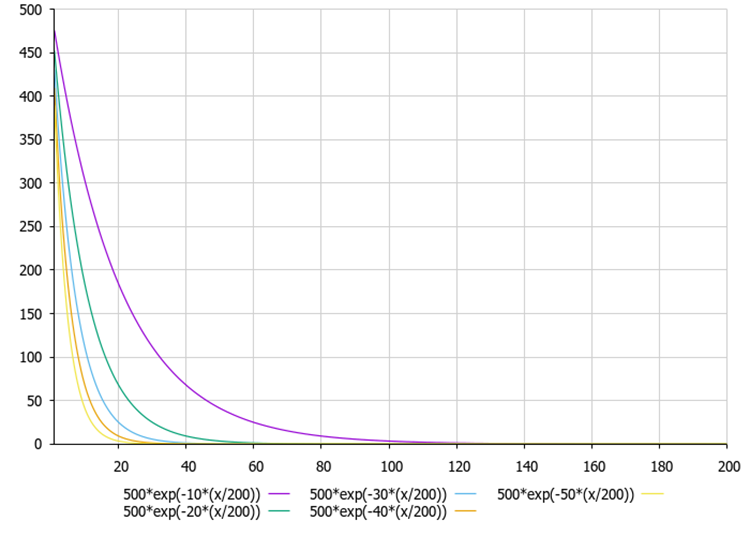
Figura 1. Dependencia de la fuerza electrostática según la fórmula de Coulomb del coeficiente α (parámetro externo).
Bien, por fin tenemos la descripción, las fórmulas y el pseudocódigo del algoritmo ordenados. Ahora tendremos que pasar a la generación del código.
Para ello, escribiremos la estructura "S_AEFA_Agent", que se utilizará para describir los agentes en el algoritmo. Esta estructura contendrá los siguientes campos:
- best_fitness - la variable representa la mejor aptitud del agente.
- best_position[] - array de coordenadas de la mejor posición del agente en el espacio de búsqueda.
- velocity[] - array que representa el vector de velocidad del movimiento de la partícula.
- charge - carga del agente.
- relative_charge - carga relativa de la partícula.
También se define en la estructura la función "Init", que inicializará la partícula (agente). Tomará el parámetro "coords", que indicará el número de coordenadas del agente, y redimensionará los arrays "best_position" y "velocity" en consecuencia. A continuación, estableceremos "best_fitness" en el valor mínimo posible de tipo double "DBL_MAX", y "charge" y "relative_charge" en 0.
Este código presenta un marco para describir a los agentes en el algoritmo del campo eléctrico artificial y los preparará para seguir trabajando en este contexto.
//—————————————————————————————————————————————————————————————————————————————— struct S_AEFA_Agent { double best_fitness; double best_position []; double velocity []; double charge; double relative_charge; void Init (int coords) { ArrayResize (best_position, coords); ArrayResize (velocity, coords); best_fitness = -DBL_MAX; charge = 0; relative_charge = 0; } }; //——————————————————————————————————————————————————————————————————————————————
Ahora describiremos la clase "C_AO_AEFA", que heredará de la clase "C_AO". Dentro de la clase se definirán los siguientes métodos y variables:
- C_AO_AEFA - constructor donde se establecen los valores de variables y parámetros.
- SetParams - el método establece los parámetros basándose en los valores almacenados en el array "params".
- Init - el método aceptará un conjunto de valores y realiza la inicialización.
- "Moving" y "Revision" - los métodos ejecutan la lógica básica del algoritmo.
- Diversas variables de tipo "double", como "K0", "alpha", "particleMass", "epsilon", así como el array "agent" y otras variables privadas.
- Los métodos privados "CalculateK", "UpdateCharges", "CalculateForces", "CalculateDistance", "UpdateVelocityAndPosition" realizan operaciones para desplazar las partículas en el espacio de búsqueda.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_AEFA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_AEFA () { } C_AO_AEFA () { ao_name = "AEFA"; ao_desc = "Artificial Electric Field Algorithm"; ao_link = ""; //"https://www.mql5.com/es/articles/15162"; popSize = 50; K0 = 500.0; alpha = 20.0; particleMass = 1.0; ArrayResize (params, 4); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "K0"; params [1].val = K0; params [2].name = "alpha"; params [2].val = alpha; params [3].name = "particleMass"; params [3].val = particleMass; } void SetParams () { popSize = (int)params [0].val; K0 = params [1].val; alpha = params [2].val; particleMass = params [3].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0); void Moving (); void Revision (); //---------------------------------------------------------------------------- double K0; double alpha; double particleMass; double epsilon; S_AEFA_Agent agent []; private: //------------------------------------------------------------------- int epochs; int epochNow; double K; double CalculateK (int t); void UpdateCharges (double best, double worst); void CalculateForces (); double CalculateDistance (const double &x1 [], const double &x2 []); void UpdateVelocityAndPosition (int i); }; //——————————————————————————————————————————————————————————————————————————————
A continuación procederemos a la implementación del método "Init" de la clase "C_AO_AEFA". Este método inicializará el algoritmo AEFA con los parámetros especificados.
Parámetros de entrada del método "Init":
- rangeMinP - array de valores de los límites mínimos del rango.
- rangeMaxP - array de valores de los límites máximos del rango.
- rangeStepP - array de valores de paso del rango.
- epochsP - número de épocas (por defecto es 0).
Acciones realizadas en el método "Init":
1. Primero llamaremos al método "StandardInit" y le transmitiremos los arrays "rangeMinP", "rangeMaxP" y "rangeStepP". Si el método "StandardInit" retorna "false", el método "Init" devolverá "false".
2. Luego estableceremos los valores de las variables "epochs" y "epochNow" iguales a los valores de los parámetros "epochsP" y "0", respectivamente.
3. Después realizaremos el redimensionamiento del array "agent" al valor "popSize".
4. En un ciclo, inicializaremos cada elemento del array "agent" llamando al método "Init" y transmitiéndole el array "coords".
5. Luego estableceremos el valor de la variable "epsilon" en "1e-10".
6. El método retornará "true".
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_AEFA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; ArrayResize (agent, popSize); for (int i = 0; i < popSize; i++) agent [i].Init (coords); epsilon = 1e-10; return true; } //——————————————————————————————————————————————————————————————————————————————
Iremos al método "Moving()" de la clase C_AO_AEFA. En este método, se actualizarán las posiciones de las partículas en el algoritmo de optimización. Aquí tenemos una breve descripción de lo que ocurrirá:
1. Se incrementará el valor de la variable "epochNow".
2. Si la variable "revision" es "false", se inicializarán las posiciones iniciales de las partículas. Cada coordenada de partícula se fijará en un valor aleatorio dentro de un rango determinado y, a continuación, se realizará una transformación de ese valor según un paso determinado.
3. Si la variable "revision" es "true", se calcularán el valor "K" y las estimaciones de la mejor y la peor función para cada partícula, se actualizarán las cargas, se calcularán las fuerzas y se actualizarán la velocidad y la posición de cada partícula.
El sentido general de este método consistirá en actualizar las posiciones de las partículas en el algoritmo de optimización utilizando métodos especiales para calcular las fórmulas de las leyes de movimiento de las partículas.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEFA::Moving () { epochNow++; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- K = CalculateK (epochNow); double best = -DBL_MAX; double worst = DBL_MAX; for (int i = 0; i < popSize; i++) { if (a [i].f > best) best = a [i].f; if (a [i].f < worst) worst = a [i].f; } UpdateCharges (best, worst); CalculateForces (); for (int i = 0; i < popSize; i++) { UpdateVelocityAndPosition (i); } } //——————————————————————————————————————————————————————————————————————————————
El método "CalculateK()" de la clase "C_AO_AEFA" calculará el valor del parámetro "K" basándose en el tiempo "t" (el número de la época actual) y otros parámetros "K0", "alpha" y "epochs". Eso es lo que ocurrirá con este método:
1. El método tomará como entrada el parámetro"t", que representará el número de la época actual del algoritmo.
2. A continuación se calculará el valor "K".
3. El resultado del cálculo de la fórmula se devolverá como valor del método.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_AEFA::CalculateK (int t) { return K0 * MathExp (-alpha * t / epochs); } //——————————————————————————————————————————————————————————————————————————————
El método "UpdateCharges()" de la clase "C_AO_AEFA" actualizará las cargas de las partículas basándose en el mejor y peor valor de aptitud. Breve descripción de las acciones del método:
1. Primero crearemos la variable "sum_q" y la estableceremos en "0".
2. A continuación, realizaremos un ciclo a través de todas las partículas entre "0" y "popSize".
3. Dentro del ciclo, la carga relativa se calculará para cada partícula utilizando la fórmula.
4. El valor de la carga relativa se añadirá a la variable "sum_q".
5. A continuación, se realizará un segundo ciclo a través de todas las partículas, en el que a cada partícula se le asignará un valor de carga igual a la carga relativa dividida por "sum_q".
Así, este método actualizará las cargas de las partículas según su aptitud para reflejar su calidad relativa frente a valores de aptitud mejores y peores.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEFA::UpdateCharges (double best, double worst) { double sum_q = 0; for (int i = 0; i < popSize; i++) { agent [i].relative_charge = MathExp ((a [i].f - worst) / (best - worst)); sum_q += agent [i].relative_charge; } for (int i = 0; i < popSize; i++) { agent [i].charge = agent [i].relative_charge / sum_q; } } //——————————————————————————————————————————————————————————————————————————————
Ahora le presentaremos los métodos "CalculateForces()" y "CalculateDistance()" de la clase "C_AO_AEFA".
El método "CalculateDistance()" tomará dos arrays "x1[]" y "x2[]" que representarán las coordenadas de dos partículas, y calculará la distancia entre ellas en el espacio. Para ello, iteraremos sobre todas las coordenadas del array y, para cada coordenada, calcularemos el cuadrado de la diferencia de los elementos correspondientes del array y, a continuación, sumaremos estos cuadrados. Luego extraeremos la raíz de la suma obtenida y retornaremos este valor como distancia entre dos puntos en el espacio (distancia euclidiana).
El método "CalculateForces()" calculará las fuerzas que actúan sobre cada partícula. Para cada partícula, calcularemos el vector de fuerzas con respecto a todas las demás partículas. Para cada par de partículas, salvo para las partículas idénticas (i != j), calcularemos la distancia entre ellas usando el método "CalculateDistance()". A continuación, para cada coordenada del espacio, calcularemos la fuerza que actúa sobre la partícula mediante una fórmula en la que intervienen las cargas de las partículas, sus posiciones y la distancia entre ellas. Los resultados se sumarán para cada coordenada, y las fuerzas resultantes se dividirán por la carga de la partícula para considerar su efecto sobre la velocidad de la partícula.
Así, los métodos realizarán cálculos de las fuerzas que actúan entre las partículas en el algoritmo y de las distancias entre ellas en el espacio, respectivamente.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEFA::CalculateForces () { double force []; ArrayResize (force, coords); for (int i = 0; i < popSize; i++) { ArrayInitialize (force, 0); for (int j = 0; j < popSize; j++) { if (i != j) { double R = CalculateDistance (a [i].c, a [j].c); for (int d = 0; d < coords; d++) { force [d] += u.RNDprobab () * K * (agent [i].charge * agent [j].charge * (agent [j].best_position [d] - a [i].c [d])) / (R * R + epsilon); } } } for (int d = 0; d < coords; d++) { agent [i].velocity [d] = force [d] / agent [i].charge; } } } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— double C_AO_AEFA::CalculateDistance (const double &x1 [], const double &x2 []) { double sum = 0; for (int d = 0; d < coords; d++) { sum += (x1 [d] - x2 [d]) * (x1 [d] - x2 [d]); } return MathSqrt (sum); } //——————————————————————————————————————————————————————————————————————————————
A continuación, presentaremos el método "UpdateVelocityAndPosition()" de la clase "C_AO_AEFA". Este método actualizará la velocidad y la posición de la partícula con el índice "i". Para cada coordenada de la partícula en el espacio, ocurrirá lo siguiente:
1. Se calculará la aceleración, que depende de la carga de la partícula, de su velocidad actual y de la masa de la partícula.
2. La velocidad de la partícula se actualizará añadiendo un componente aleatorio multiplicado por la velocidad actual y la aceleración.
3. Se actualizará la posición de la partícula, añadiendo una nueva velocidad a la posición actual. A continuación, la nueva posición se restringirá dentro de los valores mínimo y máximo especificados para cada coordenada mediante el método "u.SeInDiSp()".
Así, el método "UpdateVelocityAndPosition()" actualizará la velocidad y la posición de la partícula en el algoritmo de optimización, teniendo en cuenta la aceleración, los factores aleatorios y las restricciones de posición en el espacio.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEFA::UpdateVelocityAndPosition (int i) { for (int d = 0; d < coords; d++) { double acceleration = (agent [i].charge * agent [i].velocity [d]) / particleMass; agent [i].velocity [d] = (u.RNDfromCI (0, 1)) * agent [i].velocity [d] + acceleration; a [i].c [d] += agent [i].velocity [d]; a [i].c [d] = u.SeInDiSp (a [i].c [d], rangeMin [d], rangeMax [d], rangeStep [d]); } } //——————————————————————————————————————————————————————————————————————————————
Y por último, veremos el método "Revision()" de la clase C_AO_AEFA. En este método, se actualizarán las mejores posiciones de las partículas y sus mejores valores de aptitud, así como la mejor solución global "fB". El método hará lo siguiente:
1. Creará una variable "ind" como bandera e índice de la posición en el array de la mejor solución y lo establecerá en "-1".
2. A continuación, realizaremos un ciclo a través de todas las partículas entre "0" y "popSize".
3. Dentro de un ciclo se comprobará si el valor de la función de aptitud de la partícula supera el valor "fB". En caso afirmativo, "fB" se actualizará y la variable "ind" se fijará en "i".
4. A continuación, se comprobará si la aptitud de una partícula supera la mejor aptitud de esa partícula en todas las épocas (almacenada en agent[i].best_fitness). En caso afirmativo, se actualizará la mejor puntuación y la mejor posición.
5. Por último, si "ind" no es igual a "-1", la posición de "cB" se actualizará copiando la posición de la partícula con el índice "ind".
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AEFA::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } if (a [i].f > agent [i].best_fitness) { agent [i].best_fitness = a [i].f; ArrayCopy (agent [i].best_position, a [i].c, 0, 0, WHOLE_ARRAY); } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
3. Resultados de las pruebas
Impresión del rendimiento del algoritmo AEFA en el banco de pruebas con las funciones de prueba:
AEFA|Artificial Electric Field Algorithm|20.0|1000.0|10.0|100.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8769988087850553
25 Hilly's; Func runs: 10000; result: 0.617530930198765
500 Hilly's; Func runs: 10000; result: 0.2523539056281608
=============================
5 Forest's; Func runs: 10000; result: 0.927287032866128
25 Forest's; Func runs: 10000; result: 0.7269761843712702
500 Forest's; Func runs: 10000; result: 0.18063577020760296
=============================
5 Megacity's; Func runs: 10000; result: 0.6661538461538462
25 Megacity's; Func runs: 10000; result: 0.11630769230769236
500 Megacity's; Func runs: 10000; result: 0.0950769230769239
=============================
All score: 4.45932 (49.55%)
Una vez analizada la visualización del funcionamiento del algoritmo, podemos extraer las siguientes conclusiones: existe una importante dispersión de resultados de una prueba a otra. Además, el algoritmo muestra una capacidad de búsqueda muy pobre cuando se trata de funciones de alta dimensionalidad, lo que también se confirma en la impresión de sus resultados. Asimismo, hemos detectado problemas particulares cuando se trata de funciones discretas.
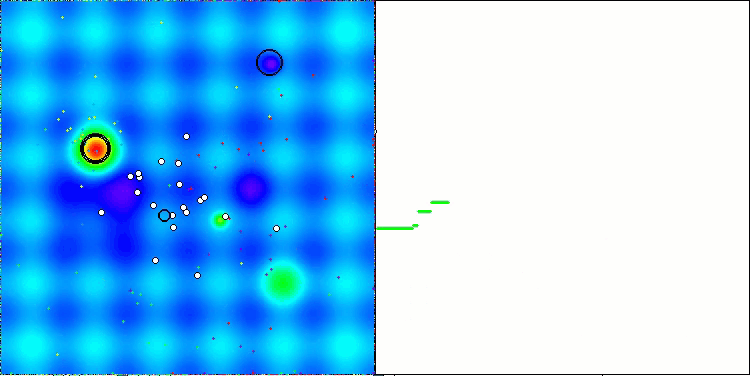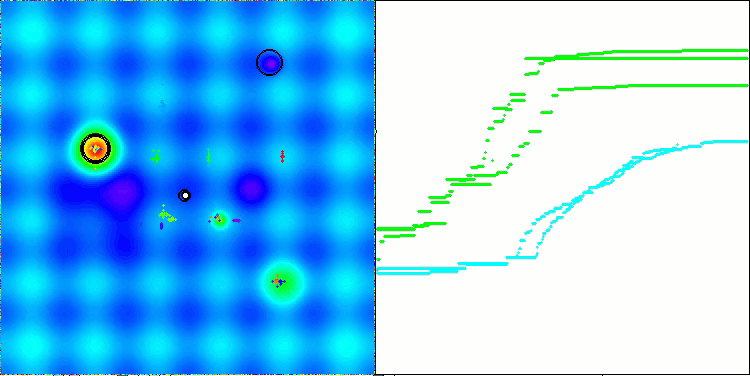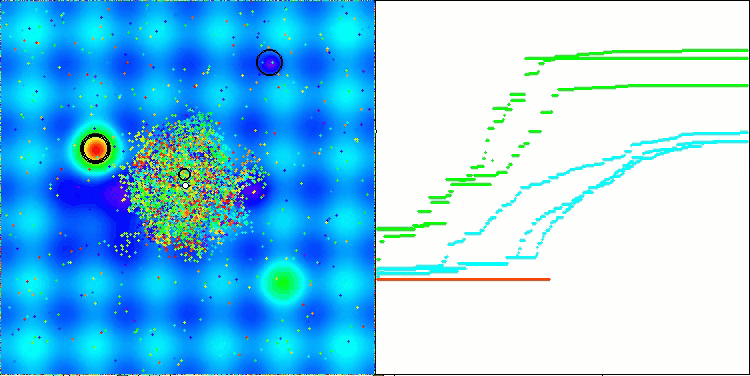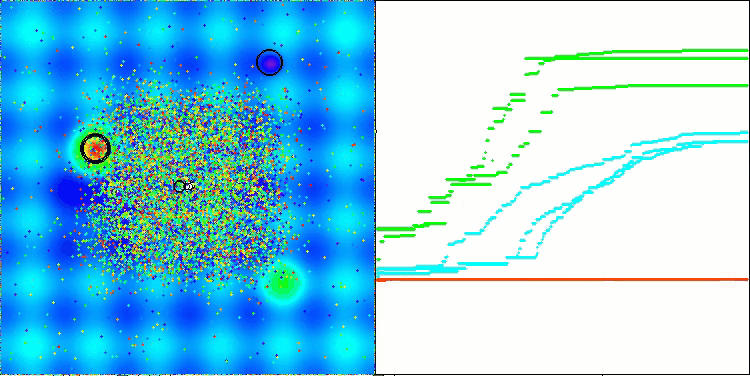
AEFA en la función de prueba Hilly.
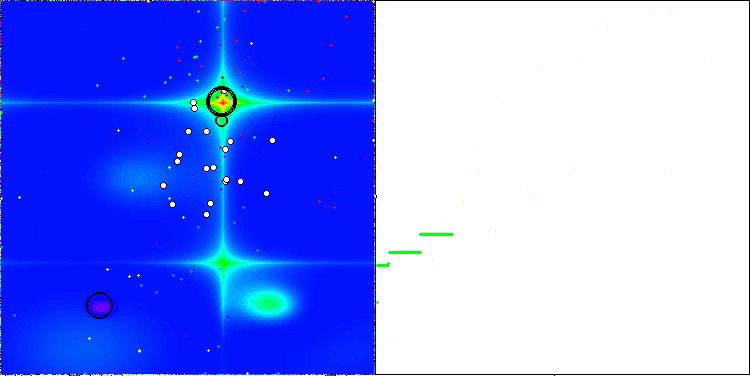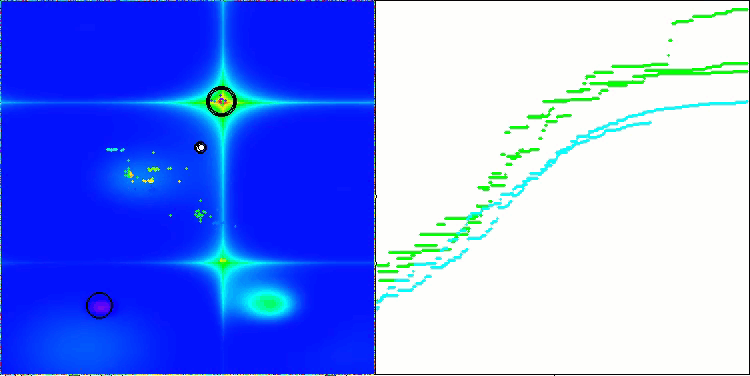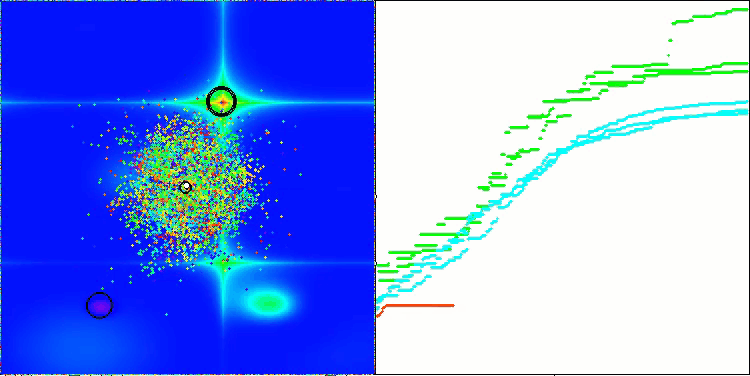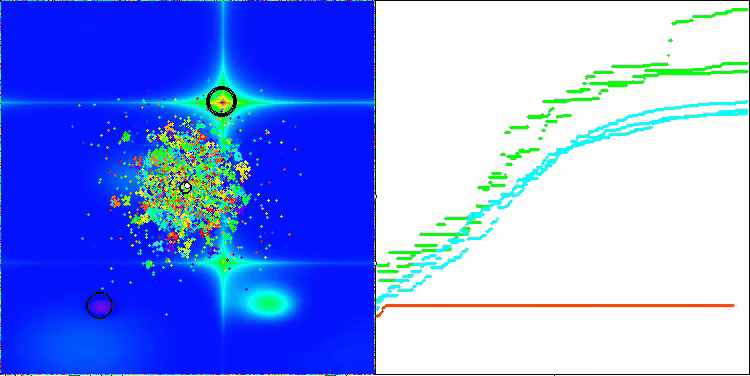
AEFA en la función de prueba Forest.
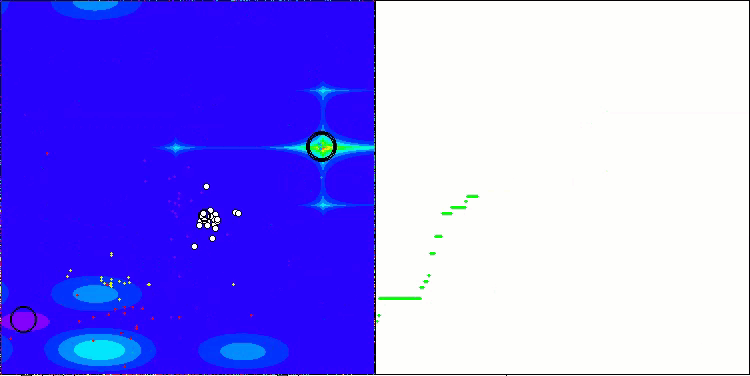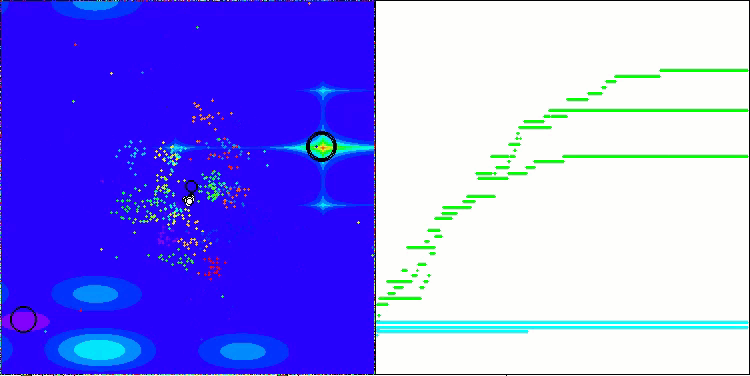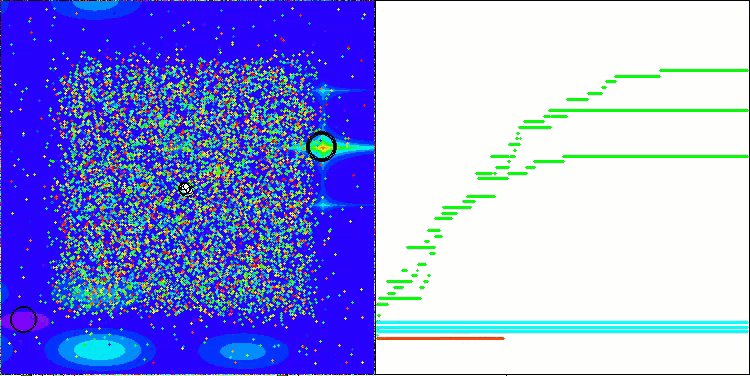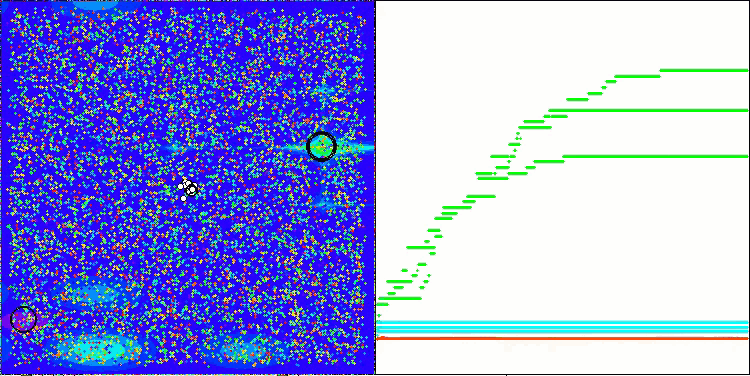
AEFA en la función de prueba Megacity.
Me gustaría destacar un aspecto importante del algoritmo de AEFA. Tras realizar una investigación estándar con 10 000 ejecuciones de la función de aptitud, hemos decidido realizar experimento adicional aumentando el número de ejecuciones a 100 000 y el resultado ha superado mis expectativas. En muchas funciones con un número reducido de parámetros, el algoritmo ha alcanzado el 100% de convergencia al aumentarse el número de ejecuciones de la función de aptitud. Debemos señalar que no todos los algoritmos de la tabla de clasificación, ni siquiera los mejor clasificados, pueden alcanzar el 100% de convergencia cuando se aumenta el número de ejecuciones porque se quedan atascados en extremos locales. En este caso, el algoritmo demuestra bastante robustez frente a las interferencias. Sin embargo, el algoritmo se enfrenta a las mismas dificultades al realizar la búsqueda en espacios multidimensionales, especialmente en funciones discretas.
Impresión del rendimiento del algoritmo AEFA en un banco de pruebas con 100 000 funciones de prueba:
SDSm|Stochastic Diffusion Search M|100.0|100.0|0.05|
=============================
5 Hilly's; Func runs: 100000; result: 0.9874670077970368
25 Hilly's; Func runs: 100000; result: 0.9355482229513405
500 Hilly's; Func runs: 100000; result: 0.5943074120378588
=============================
5 Forest's; Func runs: 100000; result: 0.994126703499673
25 Forest's; Func runs: 100000; result: 0.9627011069578397
500 Forest's; Func runs: 100000; result: 0.5628894538341265
=============================
5 Megacity's; Func runs: 100000; result: 0.9015384615384615
25 Megacity's; Func runs: 100000; result: 0.7264615384615385
500 Megacity's; Func runs: 100000; result: 0.37464615384615396
=============================
All score: 7.03969 (78.22%)
Podemos observar esta característica de la convergencia del algoritmo en las imágenes siguientes para las funciones correspondientes.
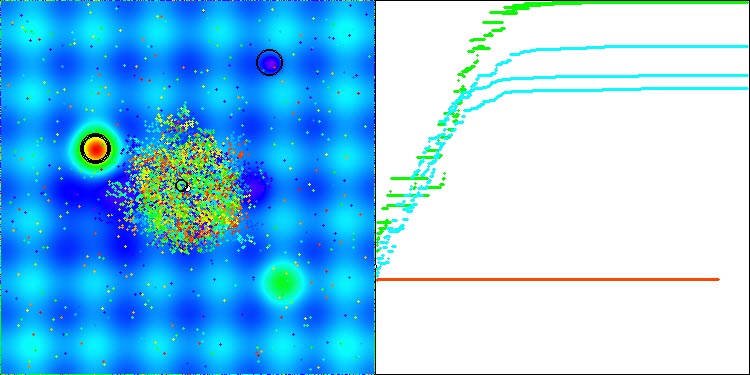
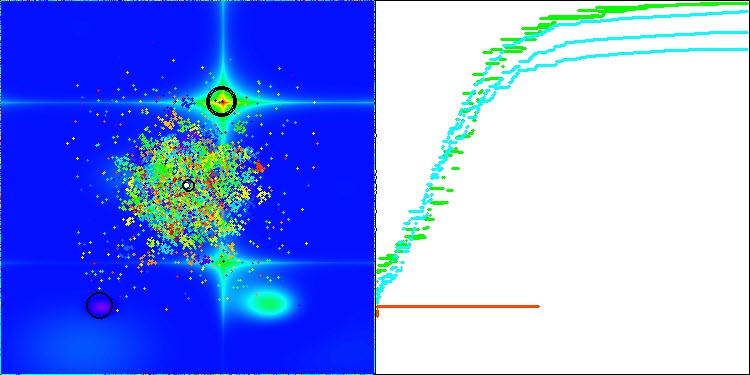
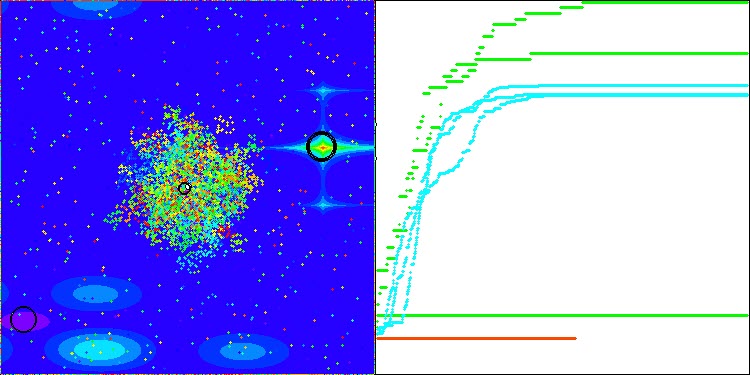
Tabla de clasificación de algoritmos de optimización basados en la población:
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | BGA | binary genetic algorithm | 0,99989 | 0,99518 | 0,42835 | 2,42341 | 0,96153 | 0,96181 | 0,32027 | 2,24360 | 0,91385 | 0,95908 | 0,24220 | 2,11512 | 6,782 | 75,36 |
| 2 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 3 | CLA | code lock algorithm | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | ESG | evolution of social groups | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 8 | SIA | simulated isotropic annealing | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 9 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 10 | TSEA | turtle shell evolution algorithm | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 11 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 12 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 13 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 14 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 15 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 16 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 17 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 18 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 19 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 20 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 21 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 22 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 23 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 24 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 25 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 26 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 27 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 28 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 29 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 30 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 31 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 32 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 33 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 34 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
| 35 | PSO | particle swarm Optimization | 0,59726 | 0,36923 | 0,29928 | 1,26577 | 0,37237 | 0,16324 | 0,07010 | 0,60572 | 0,25667 | 0,08000 | 0,02157 | 0,35823 | 2,230 | 24,77 |
| 36 | Boids | boids algorithm | 0,43340 | 0,30581 | 0,25425 | 0,99346 | 0,35718 | 0,20160 | 0,15708 | 0,71586 | 0,27846 | 0,14277 | 0,09834 | 0,51957 | 2,229 | 24,77 |
| 37 | MA | monkey algorithm | 0,59107 | 0,42681 | 0,31816 | 1,33604 | 0,31138 | 0,14069 | 0,06612 | 0,51819 | 0,22833 | 0,08567 | 0,02790 | 0,34190 | 2,196 | 24,40 |
| 38 | SFL | shuffled frog-leaping | 0,53925 | 0,35816 | 0,29809 | 1,19551 | 0,37141 | 0,11427 | 0,04051 | 0,52618 | 0,27167 | 0,08667 | 0,02402 | 0,38235 | 2,104 | 23,38 |
| 39 | FSS | fish school search | 0,55669 | 0,39992 | 0,31172 | 1,26833 | 0,31009 | 0,11889 | 0,04569 | 0,47467 | 0,21167 | 0,07633 | 0,02488 | 0,31288 | 2,056 | 22,84 |
| 40 | RND | random | 0,52033 | 0,36068 | 0,30133 | 1,18234 | 0,31335 | 0,11787 | 0,04354 | 0,47476 | 0,25333 | 0,07933 | 0,02382 | 0,35648 | 2,014 | 22,37 |
| 41 | GWO | grey wolf optimizer | 0,59169 | 0,36561 | 0,29595 | 1,25326 | 0,24499 | 0,09047 | 0,03612 | 0,37158 | 0,27667 | 0,08567 | 0,02170 | 0,38403 | 2,009 | 22,32 |
| 42 | CSS | charged system search | 0,44252 | 0,35454 | 0,35201 | 1,14907 | 0,24140 | 0,11345 | 0,06814 | 0,42299 | 0,18333 | 0,06300 | 0,02322 | 0,26955 | 1,842 | 20,46 |
| 43 | EM | electroMagnetism-like algorithm | 0,46250 | 0,34594 | 0,32285 | 1,13129 | 0,21245 | 0,09783 | 0,10057 | 0,41085 | 0,15667 | 0,06033 | 0,02712 | 0,24412 | 1,786 | 19,85 |
Conclusiones
Basándonos en los resultados del algoritmo de campo eléctrico artificial (AEFA) en funciones de prueba de diferente dimensionalidad, podemos extraer las siguientes conclusiones:
1. El AEFA se comporta satisfactoriamente en ciertas pruebas, como Hill, Forest y Megacity. Sin embargo, los resultados de la función Megacity discreta son inferiores a los de las demás funciones.
2. El algoritmo muestra un buen rendimiento con un gran número de ejecuciones de la función (100 000), lo cual mejora la precisión de la convergencia hasta el 100% en dimensionalidades pequeñas.
3. El AEFA muestra una puntuación global de 4,45932 (49,55%) y ocupa el puesto 19 en la tabla de clasificación, situándose en la mitad de la lista entre los algoritmos de optimización basados en poblaciones.
Aunque el algoritmo AEFA no obtiene los mejores resultados en funciones de prueba de diferente dimensionalidad en nuestras pruebas estándar, tiene una ventaja añadida: con el aumento de las ejecuciones, la función de aptitud logra un impresionante resultado global de 7,03969 (78,22%), lo cual hace que resulte útil para tareas de pequeña dimensionalidad, especialmente aquellas con superficie lisa.
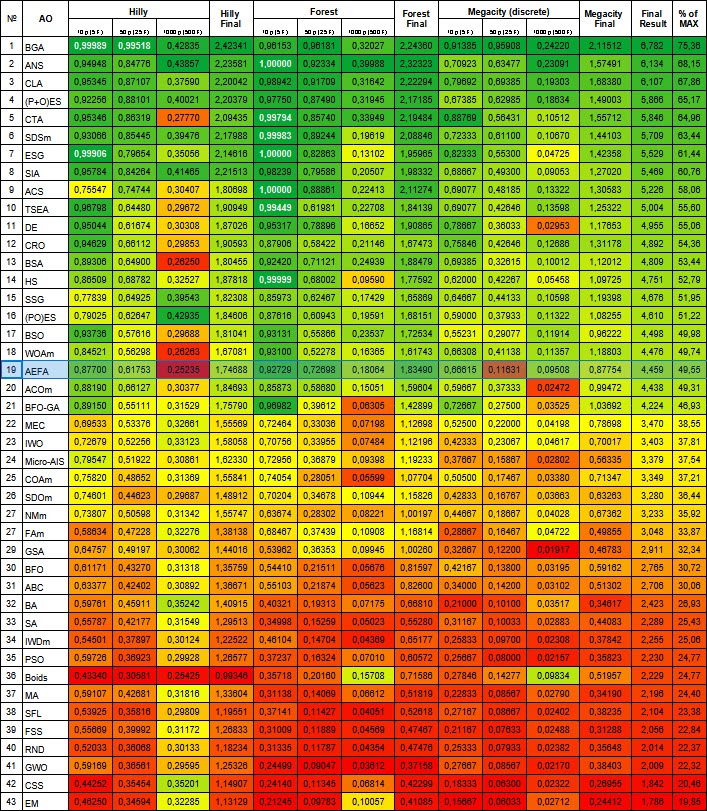
Figura 2. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0,99 aparecen resaltados en blanco.
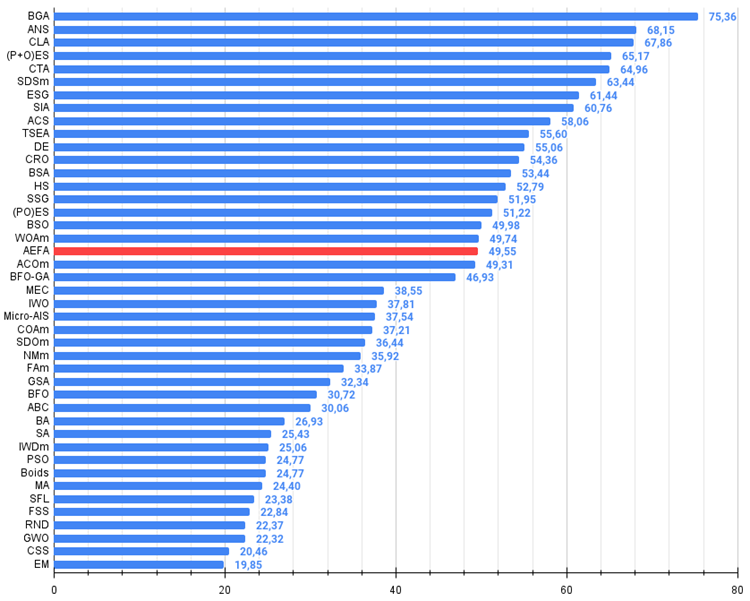
Figura 3. Histograma de los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor),
donde 100 es el máximo resultado teórico posible; el script para calcular la tabla de clasificación está en el archivo)
Ventajas y desventajas del algoritmo de campo eléctrico artificial (AEFA):
Ventajas:
- Excelente convergencia en funciones suaves de pequeña dimensionalidad con un número suficiente de ejecuciones de la función de aptitud.
- Número relativamente pequeño de parámetros externos.
Desventajas:
- Gran variación en los resultados sobre las características de nuestra prueba estándar.
- Resultados débiles sobre funciones discretas.
- Muy baja escalabilidad.
- Difícil implementación.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15162
Del básico al intermedio: Comando FOR
Características del Wizard MQL5 que debe conocer (Parte 28): Revisión de las GAN con una introducción a las tasas de aprendizaje
Del básico al intermedio: Precedencia de operadores
Redes neuronales en el trading: Modelo de doble atención para la previsión de tendencias
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso