Algoritmo de optimización basado en la migración animal (Animal Migration Optimization, AMO)

Contenido

1. Introducción
2. Implementación del algoritmo
3. Resultados de la prueba

Introducción

Migración animal: armonía y estrategia natural de la naturaleza. Los animales suelen migrar entre zonas de invernada y de reproducción, siguiendo rutas bien establecidas desarrolladas a lo largo de siglos de evolución. Estos viajes estacionales no son vagabundeos aleatorios, sino rutas cuidadosamente planificadas que conducen a áreas más favorables para su supervivencia y reproducción. Dependiendo de la estación del año, los animales se desplazan en busca de alimento, refugio y condiciones adecuadas para la reproducción, guiados por las necesidades naturales de su manada y sus instintos. Cada uno de estos viajes no es sólo una lucha por la existencia, sino también una manifestación de armonía con la naturaleza, donde cada individuo desempeña un papel único en el ecosistema general.

Por ejemplo, los renos migran grandes distancias en busca de mejores tierras de pastoreo, y las aves, como las grullas y los gansos, realizan largos vuelos entre las zonas de invernada y de nidificación, utilizando rutas específicas que se transmiten de generación en generación. Estas migraciones no sólo aseguran la supervivencia de especies individuales, sino que también apoyan al ecosistema en su conjunto, facilitando la polinización de las plantas y la dispersión de semillas.

Inspiración de la naturaleza. El algoritmo AMO (Animal Migration Optimization) fue propuesto en 2013 por el investigador Xiantao Li. La idea principal de este algoritmo es modelar el proceso de migración estacional de los animales en busca de condiciones óptimas para la vida y la reproducción en la naturaleza. El algoritmo se inspiró en la observación del comportamiento de animales migratorios como aves, peces y mamíferos. Estos animales realizan movimientos estacionales entre las zonas de invernada y de reproducción, siguiendo ciertas reglas de interacción desarrolladas por la naturaleza durante la migración.

El algoritmo AMO simula tres componentes principales del movimiento de animales a largas distancias: evitar colisiones con individuos vecinos, moverse en la misma dirección que la bandada (grupo) y mantener una distancia suficiente entre ellos. Estos principios no sólo ayudan a evitar conflictos, sino también a mantener el comportamiento colectivo, que es fundamental para la supervivencia en la naturaleza.

Etapas de optimización en el algoritmo AMO. El algoritmo incluye dos etapas clave de optimización en una iteración:

• Migración: Durante esta etapa se actualiza la posición del individuo teniendo en cuenta a sus vecinos.
  
• Renovación poblacional: en esta etapa los individuos son reemplazados parcialmente por otros nuevos, con una probabilidad que depende de la posición del individuo en la bandada.

Modelar el comportamiento colectivo de los animales migratorios puede ser un enfoque eficaz para resolver problemas de optimización complejos. El algoritmo intenta equilibrar la exploración del espacio de búsqueda y la explotación de las mejores soluciones encontradas, imitando los procesos naturales.

2. Implementaciones de algoritmos

En este modelo algorítmico de migración animal, el concepto básico es crear "zonas" concéntricas alrededor de cada animal. En la zona de repulsión, el animal tiende a alejarse de sus vecinos para evitar colisiones. El algoritmo de la migración animal, según el autor, se divide en dos procesos principales:

1. Migración animal. Un anillo topológico se utiliza para describir un vecindario limitado de individuos. Para mayor comodidad, la longitud del vecindario se establece en cinco para cada dimensión. La topología del vecindario permanece estacionaria y se determina en función de los índices de un individuo en la población. Si el índice del animal es "j", entonces sus vecinos tienen índices [j - 2, j - 1, j, j + 1 y j + 2]. Si el índice de un animal es "1", sus vecinos tendrán índices [N - 1, N, 1, 2, 3] y así sucesivamente. Una vez formada la topología del vecindario, se selecciona un vecino al azar y la posición del individuo se actualiza para reflejar la posición de este vecino. Esta descripción es dada por los autores del algoritmo original. En este caso, la limitación en el número de vecinos se puede pasar a los parámetros del algoritmo para encontrar, mediante experimentos, el mejor número de vecinos para asegurar la mayor eficiencia posible del algoritmo.

2. Renovación poblacional. Durante la renovación de la población, el algoritmo modela cómo algunos animales abandonan el grupo y otros se unen a la población. Los individuos pueden ser reemplazados por nuevos animales con una probabilidad de "p" determinada en función de la calidad de la función de aptitud. Ordenamos la población en orden descendente de los valores de la función de aptitud, lo que significa que la probabilidad de cambiar a un individuo con la mejor aptitud es 1/N, mientras que la probabilidad de cambiar a un individuo con la peor aptitud es 1.

La migración animal y la renovación poblacional, según la versión del autor, pueden describirse algorítmicamente, como se muestra a continuación.

Migración animal:

1. Para cada animal: a. Determinar la vecindad topológica de un animal (5 vecinos más cercanos).
   b. Seleccionar un vecino aleatorio de la lista de vecinos.
   c. Actualizar la posición del animal en la dirección del vecino seleccionado utilizando la siguiente ecuación:
      x_j_new = x_j_old + r * (x_neighbor - x_j_old), donde:

• x_j_new — nueva posición del j animal,
  
• x_j_old — posición actual,
• x_neighbor — posición del vecino seleccionado,
• r — número aleatorio de una distribución normal.
  

   d. Evaluación de la nueva posición del animal mediante la función objetivo.

Renovación poblacional:

1. Ordenar los animales según el valor de la función objetivo en orden descendente. 2. Para cada animal: a. Calcular la probabilidad de reemplazar un animal por un nuevo animal aleatorio:

      p = 1,0 - (1,0 / (x + 1)), donde x es el rango (índice) del i tercer animal de la lista ordenada.

   b. Si un número aleatorio es menor que p, reemplaza el animal (cambia la coordenada al valor promedio de las coordenadas de dos animales seleccionados al azar de la población).    c. De lo contrario, deje el animal sin cambios.

3. Estimación de una nueva población utilizando una función objetivo.

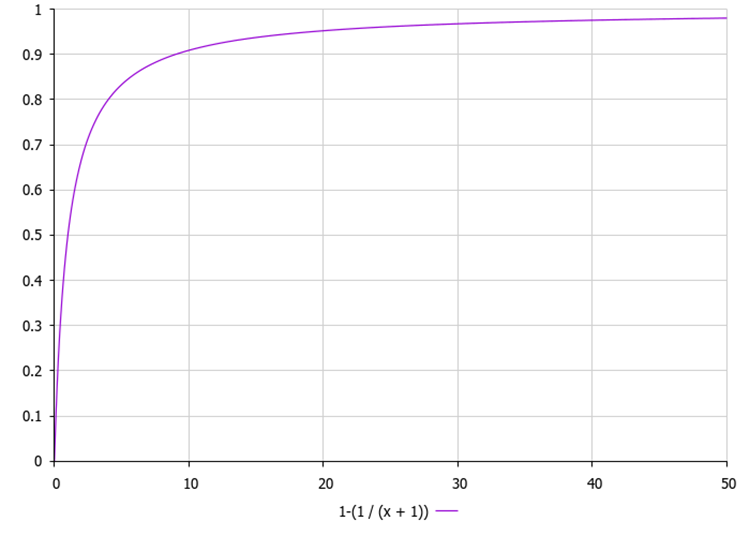
Figura 1. Cambiar la probabilidad de un individuo en función de su posición en la población, donde «x» es el índice del individuo en la población.

Escribamos un pseudocódigo para el algoritmo de migración animal AMO.

1. Inicialización de la población animal con posiciones aleatorias.

2. Bucle principal:

   a. Para cada animal:

      Definición de un vecindario topológico.
      Seleccionar un vecino al azar.
      Actualización de la posición del animal en la dirección de su vecino.
      Evaluar un nuevo puesto.

   b. Ordenar la población por los valores de la función objetivo.

   c. Reemplazo probabilístico de animales inferiores por nuevos.

   d. Estimación de la población actualizada.

   e. Actualizando la mejor solución.

3. Repita desde el paso 2 hasta que se cumpla el criterio de detención.

Ahora que estamos familiarizados con el algoritmo, podemos pasar a escribir el código. Echemos un vistazo más de cerca al código de la clase C_AO_AMO:

1. La clase C_AO_AMO se hereda de la clase base C_AO, lo que permite utilizar su funcionalidad y ampliarla.

2. El constructor especifica las características básicas del algoritmo, como el nombre, la descripción y el enlace al artículo. También se inicializan los parámetros del algoritmo, incluido el tamaño de la población, el sesgo y el número de vecinos.

3. popSize, deviation, neighborsNumberOnSide- las variables determinan el tamaño de la población, la desviación estándar y el número de vecinos de un lado que se tendrán en cuenta durante la migración.

4. SetParams — el método se encarga de actualizar los parámetros del algoritmo en función de los valores almacenados en la matriz params.

5. Init — método de inicialización que acepta matrices para los valores de rango mínimo y máximo, pasos y número de épocas. 

6. Moving () — el método se encarga de mover los agentes en el espacio de búsqueda, Revisión () - el método comprueba y actualiza el estado de los agentes en la población.

7. S_AO_Agent population [] — el array almacena la población actual de agentes (animales), S_AO_Agent pTemp [] - array temporal para usar al ordenar la población.

8. GetNeighborsIndex — método privado utilizado para obtener índices de vecinos para un agente específico.

La clase C_AO_AMO implementa un algoritmo de optimización basado en la migración animal, proporcionando los métodos y parámetros necesarios para configurar y ejecutar el algoritmo. Hereda la funcionalidad de la clase base, lo que nos permite extender y modificar su comportamiento dependiendo de los requerimientos de la tarea.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AMOm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AMOm () { }
  C_AO_AMOm ()
  {
    ao_name = "AMOm";
    ao_desc = "Animal Migration Optimization M";
    ao_link = "https://www.mql5.com/en/articles/15543";

    popSize               = 50;   // Population size
    deviation             = 8;
    neighborsNumberOnSide = 10;

    ArrayResize (params, 3);

    params [0].name = "popSize";               params [0].val = popSize;

    params [1].name = "deviation";             params [1].val = deviation;
    params [2].name = "neighborsNumberOnSide"; params [2].val = neighborsNumberOnSide;
  }

  void SetParams ()
  {
    popSize               = (int)params [0].val;

    deviation             = params      [1].val;
    neighborsNumberOnSide = (int)params [2].val;
  }

  bool Init (const double &rangeMinP  [],
             const double &rangeMaxP  [],
             const double &rangeStepP [],
             const int     epochsP = 0);

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double deviation;
  int    neighborsNumberOnSide;

  S_AO_Agent population []; // Animal population
  S_AO_Agent pTemp      []; // Temporary animal population

  private: //-------------------------------------------------------------------
  int   GetNeighborsIndex (int i);
};
//——————————————————————————————————————————————————————————————————————————————

A continuación, consideremos el código del método Init de la clase C_AO_AMO. Descripción de cada parte del método:

1. rangeMinP[], rangeMaxP[], rangeStepP[] - matrices para determinar los rangos mínimo y máximo de los parámetros optimizados y sus pasos.

2. El método StandardInit realiza una inicialización estándar basada en los rangos pasados.

3. Cambio de tamaño de las matrices population y pTemp en popSize.

4. La inicialización de los agentes se realiza sobre todos los elementos del array population e inicializa cada agente mediante el método Init pasándole el número de coordenadas coords. 

5. Si todas las operaciones se realizan correctamente, el método devuelve true.

El método Init de la clase C_AO_AMO se encarga de inicializar la población de agentes teniendo en cuenta los rangos y parámetros dados.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AMO::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (population, popSize);
  ArrayResize (pTemp,      popSize);

  for (int i = 0; i < popSize; i++) population [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

A continuación veremos el método Moving de la clase C_AO_AMO responsable del movimiento de los agentes en la población. Principales partes del código:

1. Comprueba el estado de revision:

• Si revision es igual a false, se llama al método por primera vez o después de un reinicio. En este caso, se inicializa la población.
• Para cada individuo de la población (de 0 a popSize) y para cada coordenada (de 0 a coords), se generan valores aleatorios en el rango especificado (rangeMin y rangeMax).
• Estos valores son tratados por la función "SeInDiSp", que los ajusta teniendo en cuenta el paso especificado (rangeStep).

2. Establecer la bandera revision:

• Después de la inicialización, revision se establece en true, y el método termina.

3. Ciclo básico de migración:

• Si revision es igual a true, el método pasa a la lógica de migración principal.
• Para cada individuo, se vuelve a iterar sobre las coordenadas.
• GetNeighborsIndex(i) se utiliza para obtener el índice del vecino con el que se comparará el individuo actual.
• Se calcula la distancia dist entre las coordenadas del vecino y el individuo actual.
• A partir de esta distancia, se determinan los límites mínimo y máximo (min y max), en los que se encuentra la nueva coordenada.

4. Ajuste de los valores:

• Si los límites calculados están fuera del rango aceptable, se ajustan para tener en cuenta rangeMin y rangeMax.
• A continuación, se calcula el nuevo valor de coordenadas utilizando la distribución normal (función GaussDistribution), que permite tener en cuenta la desviación estándar (deviation).
• Como en el primer caso, el nuevo valor también se gestiona mediante SeInDiSp.

El método Moving se encarga de actualizar las posiciones de los agentes en función de sus vecinos y de factores aleatorios. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AMO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  int    ind1    = 0;
  double dist    = 0.0;
  double x       = 0.0;
  double min     = 0.0;
  double max     = 0.0;

  for (int i = 0; i < popSize; i++)
  { 
    for (int c = 0; c < coords; c++)
    {
      //------------------------------------------------------------------------
      ind1 = GetNeighborsIndex (i);

      dist = fabs (population [ind1].c [c] - a [i].c [c]);

      x    = a [i].c [c];
      min  = x - dist;
      max  = x + dist;

      if (min < rangeMin [c]) min = rangeMin [c];
      if (max > rangeMax [c]) max = rangeMax [c];

      a [i].c [c] = u.GaussDistribution (x, min, max, deviation);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

El siguiente código es el método revision del C_AO_AMO. Veámoslo pieza por pieza:

1. Encontrar al mejor individuo:

• La variable ind se utiliza para almacenar el índice del individuo con la mejor función (f).
• Pasando por toda la población (de 0 a popSize), el código actualiza el valor de fB si el individuo actual tiene el mejor valor de la función.
• Si se encuentra el mejor individuo, sus características (coordenadas) se copian en la matriz cB.

2. El ciclo básico del cambio demográfico:

• Para cada individuo de la población (de 0 a popSize), se calcula la probabilidad prob, que depende del índice i.
• Para cada coordenada (de 0 a coordenadas), se realiza una comparación aleatoria con la probabilidad prob.
• Si el número aleatorio es menor que prob, se seleccionan dos individuos aleatorios ind1 y ind2.
• Si ambos individuos coinciden, ind2 se incrementa para evitar seleccionar al mismo individuo.
• El nuevo valor de las coordenadas del individuo actual se calcula como la media de las coordenadas de dos individuos aleatorios y, a continuación, se ajusta mediante la función "SeInDiSp", que limita el valor a un rango determinado.

3. Actualización de la población:

•    Una vez completados los cambios, se actualiza toda la población copiando los valores de la matriz a.
•    A continuación se llama a la función Sorting. Ordena la población mediante la función f.

El uso de condiciones probabilísticas y la selección aleatoria de individuos para actualizar los valores de las coordenadas sugiere que el método pretende encontrar una solución óptima basada en la interacción entre vecinos.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AMO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB  = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  int    ind1 = 0;
  int    ind2 = 0;
  double dist = 0.0;
  double x    = 0.0;
  double min  = 0.0;
  double max  = 0.0;
  double prob = 0.0;
  
  for (int i = 0; i < popSize; i++)
  {
    prob = 1.0 - (1.0 / (i + 1));
    
    for (int c = 0; c < coords; c++)
    {  
      if (u.RNDprobab() < prob)
      {
        ind1 = u.RNDminusOne (popSize);
        ind2 = u.RNDminusOne (popSize);

        if (ind1 == ind2)
        {
          ind2++;
          if (ind2 > popSize - 1) ind2 = 0;
        }

        a [i].c [c] = (population [ind1].c [c] + population [ind2].c [c]) * 0.5;
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
  
  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++) population [i] = a [i];

  u.Sorting (population, pTemp, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

Por último, consideremos el código del método GetNeighborsIndex de la clase C_AO_AMO encargado de obtener el índice de un vecino aleatorio para el índice i especificado teniendo en cuenta los límites del array.

1. Inicialización de variables:

• Ncount — número de vecinos determinado por la variable neighborsNumberOnSide.
• N — número total de vecinos, incluido el propio elemento, se define como Ncount * 2 + 1.

2. El método utiliza sentencias condicionales para comprobar la posición del índice i respecto a los límites de la matriz.

3. Manejo de los primeros elementos Ncount (bordes a la izquierda). Si el índice i es menor que Ncount, significa que está al principio de la matriz. Si el índice i es menor que Ncount, significa que está al principio de la matriz.

4. Manejo de los últimos elementos Ncount (bordes a la derecha). Si el índice i es mayor o igual que popSize - Ncount, significa que se encuentra al final de la matriz. El método genera un índice de vecinos a partir de popSize - N para tener en cuenta los límites.

5. Manejo de todos los demás elementos. Si el índice de i está en algún lugar en el medio de la matriz, el método genera un índice vecino que está desplazado por Ncount a la izquierda y añade un valor aleatorio de 0 a N-1.

6. Al final, el método devuelve el índice de vecinos generado.

El método GetNeighborsIndex permite obtener el índice de un vecino aleatorio para un índice dado de i considerando los límites del array.

//——————————————————————————————————————————————————————————————————————————————
int C_AO_AMO::GetNeighborsIndex (int i)
{
  int Ncount = neighborsNumberOnSide;
  int N = Ncount * 2 + 1;
  int neighborIndex;

  // Select a random neighbor given the array boundaries
  if (i < Ncount)
  {
    // For the first Ncount elements
    neighborIndex = MathRand () % N;
  }
  else
  {
    if (i >= popSize - Ncount)
    {
      // For the last Ncount elements
      neighborIndex = (popSize - N) + MathRand () % N;
    }
    else
    {
      // For all other elements
      neighborIndex = i - Ncount + MathRand () % N;
    }
  }

  return neighborIndex;
}
//——————————————————————————————————————————————————————————————————————————————

Ahora, una vez que hemos terminado de escribir el algoritmo, vamos a comprobar cómo funciona. Resultados de la versión original del algoritmo:

AMO|Animal Migration Optimization|50.0|1.0|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.43676335174918435
25 Hilly's; Func runs: 10000; result: 0.28370099295372453
500 Hilly's; Func runs: 10000; result: 0.25169663266864406
=============================
5 Forest's; Func runs: 10000; result: 0.312993148861033
25 Forest's; Func runs: 10000; result: 0.23960515885149344
500 Forest's; Func runs: 10000; result: 0.18938496103401775
=============================
5 Megacity's; Func runs: 10000; result: 0.18461538461538463
25 Megacity's; Func runs: 10000; result: 0.12246153846153851
500 Megacity's; Func runs: 10000; result: 0.10223076923076994
=============================
All score: 2.12345 (23.59%)

Desafortunadamente, la versión original muestra cualidades de búsqueda débiles. Dichos indicadores no se incluirán en la tabla de calificación. El análisis de los resultados reveló una brecha significativa entre el algoritmo y los demás participantes, lo que me llevó a repensarlo profundamente.

Al examinar la estrategia más de cerca, se descubrió un fallo clave: la clasificación de la población no contribuía a la acumulación de material genético de los mejores individuos. Sólo cambió su disposición topológica sin afectar su esencia. La influencia de la clasificación se limitó únicamente a ajustar la probabilidad de cambiar las coordenadas de los individuos en el espacio de búsqueda, y esta probabilidad es inversamente proporcional a su aptitud.

Es de destacar que las nuevas coordenadas se formaron exclusivamente sobre la base de las ya existentes en la población, promediando los valores de dos individuos seleccionados al azar. El reconocimiento de estos matices condujo a la idea de ampliar la población para integrar a las crías en el grupo parental antes de realizar la clasificación. Este enfoque no sólo preservará las mejores combinaciones genéticas, sino que también desplazará naturalmente a los individuos menos adaptados. Sin duda, el problema de la actualización del acervo genético de la población sigue siendo relevante, pero la modificación propuesta debería incrementar significativamente la dinámica del proceso evolutivo. Para implementar esta idea, comenzamos cambiando el método de inicialización duplicando el tamaño de la población principal.

Presentemos el código de inicialización completo, donde podemos ver la duplicación de la población padre.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AMOm::Init (const double &rangeMinP  [],
                      const double &rangeMaxP  [],
                      const double &rangeStepP [],
                      const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (population, popSize * 2);
  ArrayResize (pTemp,      popSize * 2);

  for (int i = 0; i < popSize * 2; i++) population [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

En consecuencia, es necesario corregir el método Revision:

//----------------------------------------------------------------------------
for (int i = 0; i < popSize; i++) population [i + popSize] = a [i];

u.Sorting (population, pTemp, popSize * 2);

Después de los ajustes apropiados, probaremos nuevamente el algoritmo y compararemos los resultados:

AMOm|Animal Migration Optimization M|50.0|1.0|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.4759595972704031
25 Hilly's; Func runs: 10000; result: 0.31711543296080447
500 Hilly's; Func runs: 10000; result: 0.2540492181444619
=============================
5 Forest's; Func runs: 10000; result: 0.40387880560608347
25 Forest's; Func runs: 10000; result: 0.27049305409901064
500 Forest's; Func runs: 10000; result: 0.19135802944407254
=============================
5 Megacity's; Func runs: 10000; result: 0.23692307692307696
25 Megacity's; Func runs: 10000; result: 0.14461538461538465
500 Megacity's; Func runs: 10000; result: 0.10109230769230851
=============================
All score: 2.39548 (26.62%)

En este caso, vemos una mejora en el resultado general del 3%, lo que indica las posibilidades de éxito en el camino elegido.

A continuación, intentaremos transferir el cambio probabilístico de los individuos en función del rango al método Moving. Esto permitirá realizar cambios en las coordenadas de las personas inmediatamente después de recibir nuevas coordenadas de sus vecinos más cercanos.

//----------------------------------------------------------------------------
int    ind1 = 0;
int    ind2 = 0;
double dist = 0.0;
double x    = 0.0;
double min  = 0.0;
double max  = 0.0;
double prob = 0.0;

for (int i = 0; i < popSize; i++)
{
  prob = 1.0 - (1.0 / (i + 1));
    
  for (int c = 0; c < coords; c++)
  {
    //------------------------------------------------------------------------
    ind1 = GetNeighborsIndex (i);

    dist = fabs (population [ind1].c [c] - a [i].c [c]);

    x    = a [i].c [c];
    min  = x - dist;
    max  = x + dist;

    if (min < rangeMin [c]) min = rangeMin [c];
    if (max > rangeMax [c]) max = rangeMax [c];

    a [i].c [c] = u.GaussDistribution (x, min, max, deviation);
      
    //----------------------------------------------------------------------------
    if (u.RNDprobab() < prob)
    {
      ind1 = u.RNDminusOne (popSize);
      ind2 = u.RNDminusOne (popSize);

      if (ind1 == ind2)
      {
        ind2++;
        if (ind2 > popSize - 1) ind2 = 0;
      }

      a [i].c [c] = (population [ind1].c [c] + population [ind2].c [c]) * 0.5;
    }
      
    a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Revisemos nuevamente los resultados:

AMO|Animal Migration Optimization|50.0|1.0|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.7204154413083147
25 Hilly's; Func runs: 10000; result: 0.4480389094268583
500 Hilly's; Func runs: 10000; result: 0.25286213277651365
=============================
5 Forest's; Func runs: 10000; result: 0.7097109421461968
25 Forest's; Func runs: 10000; result: 0.3299544372347476
500 Forest's; Func runs: 10000; result: 0.18667655927410348
=============================
5 Megacity's; Func runs: 10000; result: 0.41076923076923083
25 Megacity's; Func runs: 10000; result: 0.20400000000000001
500 Megacity's; Func runs: 10000; result: 0.09586153846153929
=============================
All score: 3.35829 (37.31%)

Esto es mucho mejor y vale la pena continuar. Después de algunos experimentos con el código, obtuvimos la versión final del método Moving:

//----------------------------------------------------------------------------
  int    ind1    = 0;
  int    ind2    = 0;
  double dist    = 0.0;
  double x       = 0.0;
  double min     = 0.0;
  double max     = 0.0;
  double prob    = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    prob = 1.0 - (1.0 / (i + 1));
    
    for (int c = 0; c < coords; c++)
    {
      //------------------------------------------------------------------------
      ind1 = GetNeighborsIndex (i);

      dist = fabs (population [ind1].c [c] - a [i].c [c]);

      x    = population [ind1].c [c];
      min  = x - dist;
      max  = x + dist;

      if (min < rangeMin [c]) min = rangeMin [c];
      if (max > rangeMax [c]) max = rangeMax [c];

      a [i].c [c] = u.GaussDistribution (x, min, max, deviation);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);


      //------------------------------------------------------------------------
      if (u.RNDprobab() < prob)
      {
        if (u.RNDprobab() <= 0.01)
        {
          ind1 = u.RNDminusOne (popSize);
          ind2 = u.RNDminusOne (popSize);

          //if (ind1 == ind2)
          {
            //ind2++;
            //if (ind2 > popSize - 1) ind2 = 0;

            a [i].c [c] = (population [ind1].c [c] + population [ind2].c [c]) * 0.5;
            a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
          }
        }
        //ind1 = u.RNDminusOne (popSize);
        //a [i].c [c] = population [ind1].c [c];
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Pasemos del método Moving a la versión final del método Revision del C_AO_AMO encargado de actualizar y ordenar la población de agentes.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AMO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB  = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  
  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++) population [popSize + i] = a [i];

  u.Sorting (population, pTemp, popSize * 2);
}
//——————————————————————————————————————————————————————————————————————————————

Una vez que el código está finalmente formado, pasamos a realizar pruebas nuevamente.

3. Resultados de la prueba

Resultados del banco de pruebas AMO:

AMOm|Animal Migration Optimization|50.0|8.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9627642143272663
25 Hilly's; Func runs: 10000; result: 0.8703754433240446
500 Hilly's; Func runs: 10000; result: 0.467183248460726
=============================
5 Forest's; Func runs: 10000; result: 0.9681183408862706
25 Forest's; Func runs: 10000; result: 0.9109372988714968
500 Forest's; Func runs: 10000; result: 0.4719026790932256
=============================
5 Megacity's; Func runs: 10000; result: 0.6676923076923076
25 Megacity's; Func runs: 10000; result: 0.5886153846153845
500 Megacity's; Func runs: 10000; result: 0.23546153846153978
=============================
All score: 6.14305 (68.26%)

Podemos ver resultados elevados en la tabla de clasificación. Sin embargo, el precio es una gran diferencia de valores finales en funciones de pequeñas dimensiones. Realicemos 50 pruebas en lugar de las 10 habituales.

AMOm|Animal Migration Optimization|50.0|8.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.903577388020872
25 Hilly's; Func runs: 10000; result: 0.8431723262743616
500 Hilly's; Func runs: 10000; result: 0.46284266807030283
=============================
5 Forest's; Func runs: 10000; result: 0.9900061169785055
25 Forest's; Func runs: 10000; result: 0.9243600311397848
500 Forest's; Func runs: 10000; result: 0.4659761237381695
=============================
5 Megacity's; Func runs: 10000; result: 0.5676923076923077
25 Megacity's; Func runs: 10000; result: 0.5913230769230771
500 Megacity's; Func runs: 10000; result: 0.23773230769230896
=============================
All score: 5.98668 (66.52%)

Ahora los resultados son más realistas, pero la eficiencia también ha disminuido ligeramente.

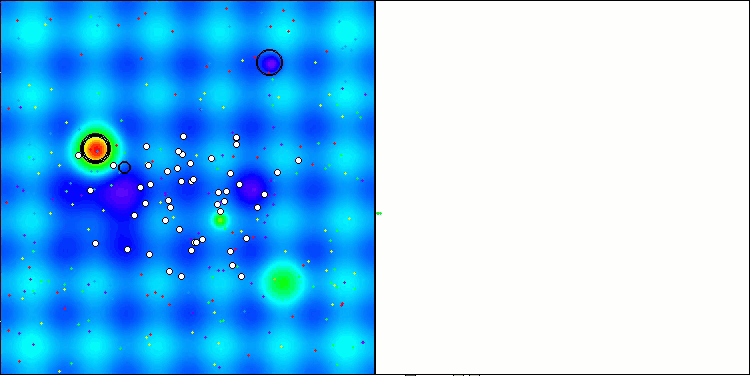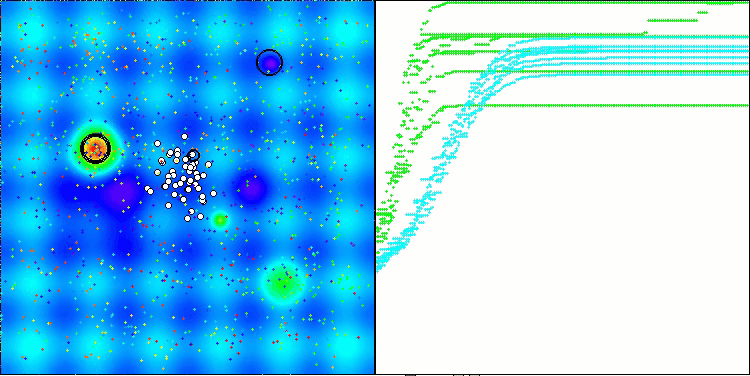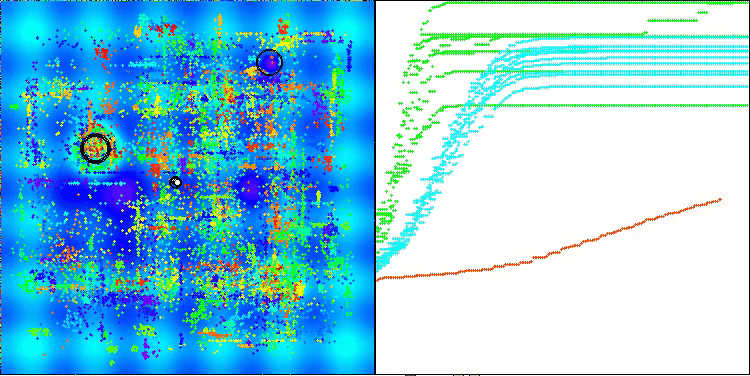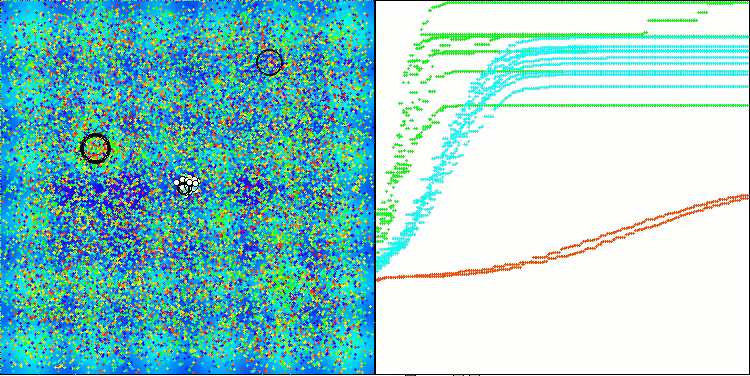
 AMOm sobre la función Hilly.

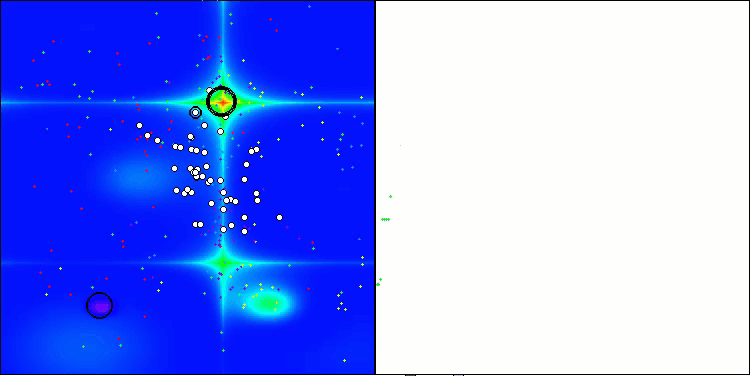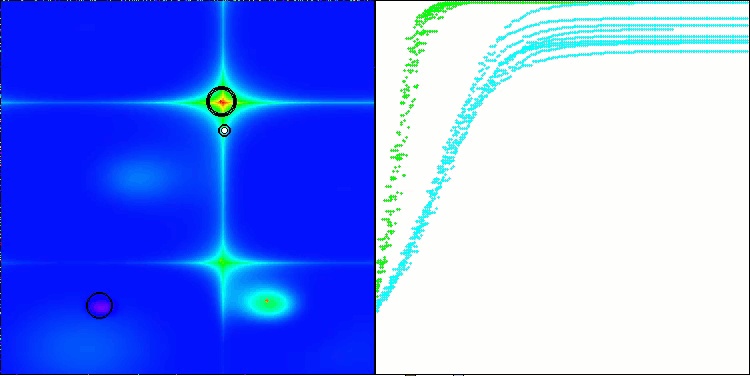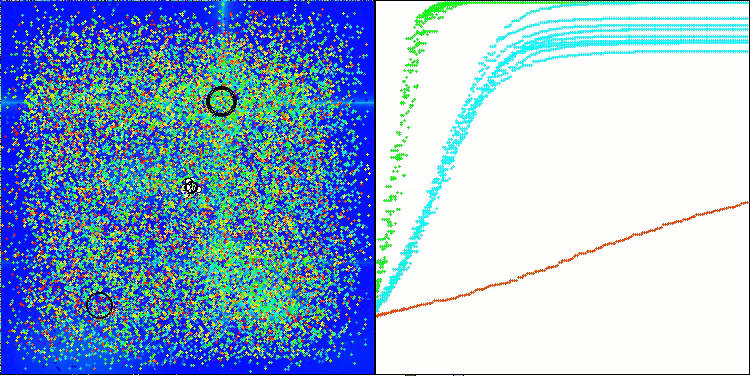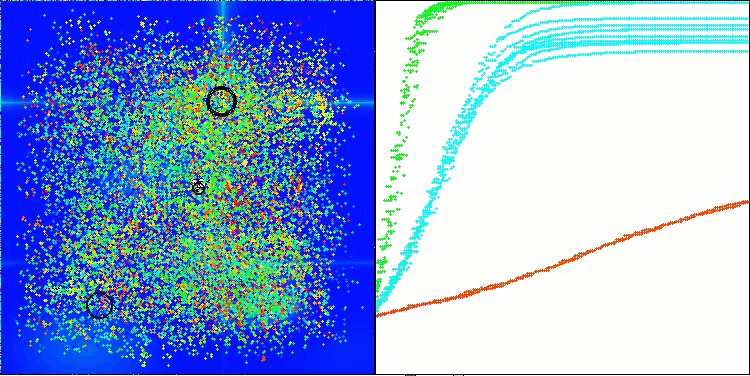
AMOm sobre la función Forest

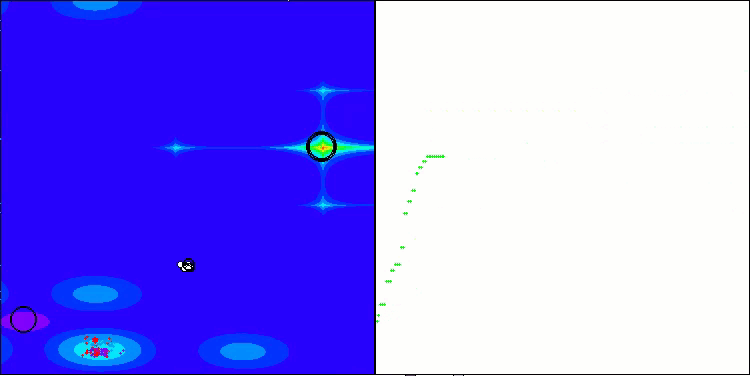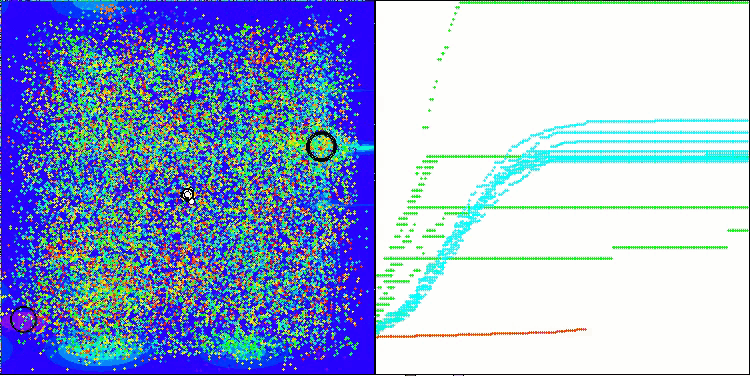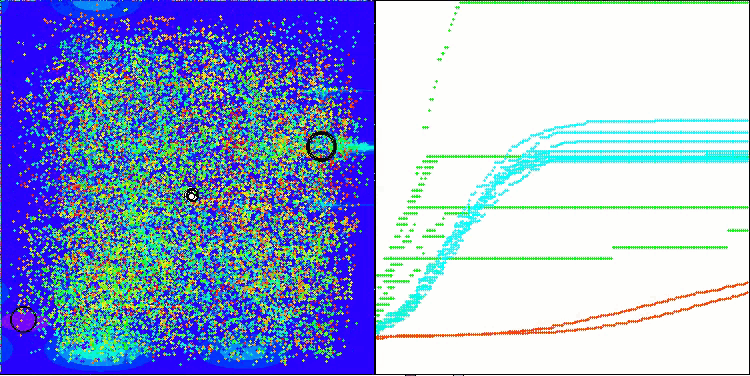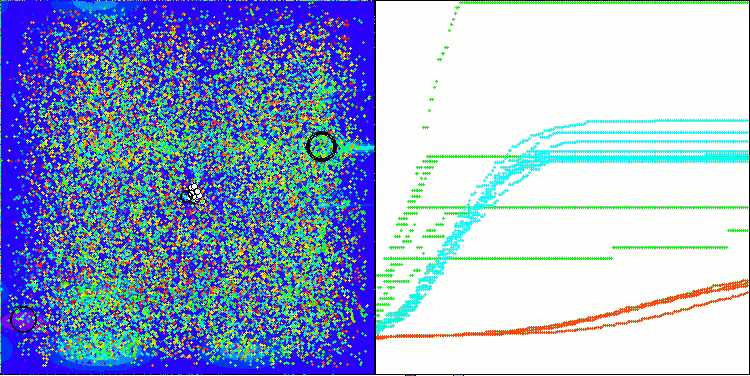
AMOm sobre la función Megacity

Después de algunas transformaciones sorprendentes, el algoritmo ocupa con confianza el tercer lugar en la tabla de clasificación.

#	AO	Descripción	Hilly			Hilly final	Forest			Forest final	Megaciudad (discreto)			Megacity final	Resultado final	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	búsqueda en todo el vecindario	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	algoritmo de bloqueo de código	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	Optimización de la migración animal M	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	Estrategias de evolución (P+O)	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	algoritmo de cola de cometa	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	búsqueda por difusión estocástica M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	ESG	evolución de los grupos sociales	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
8	SIA	recocido isotrópico simulado	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
9	ACS	búsqueda cooperativa artificial	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
10	ASO	anarquía sociedad optimización	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
11	TSEA	algoritmo de evolución del caparazón de tortuga	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
12	DE	evolución diferencial	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
13	CRO	optimización de reacciones químicas	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
14	BSA	algoritmo de enjambre de aves	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
15	HS	búsqueda de armonías	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
16	SSG	árboles, siembra y crecimiento	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
17	(PO)ES	(PO) estrategias de evolución	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
18	BSO	optimización brain storm	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
19	WOAm	algoritmo de optimización de wale M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
20	AEFA	algoritmo de campo eléctrico artificial	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
21	ACOm	optimización de colonias de hormigas M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
22	BFO-GA	Optimización de la alimentación bacteriana - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
23	ABHA	algoritmo de colmena artificial	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
24	ASBO	optimización del comportamiento social adaptativo	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
25	MEC	computación evolutiva de la mente	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
26	IWO	optimización de malezas invasoras	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
27	Micro-AIS	microsistema inmunológico artificial	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
28	COAm	algoritmo de optimización de cuco M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
29	SDOm	Optimización de la dinámica espiral M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
30	NMm	Método de Nelder-Mead M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
31	FAm	algoritmo de luciérnaga M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
32	GSA	algoritmo de búsqueda gravitacional	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
33	BFO	optimización de la búsqueda de alimento bacteriano	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
34	ABC	colonia de abejas artificial	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
35	BA	algoritmo de murciélago	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
36	SA	recocido simulado	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
37	IWDm	Gotas de agua inteligentes M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
38	PSO	optimización del enjambre de partículas	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
39	Boids	algoritmo de boids	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
40	MA	algoritmo del mono	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
41	SFL	Salto de rana barajado	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
42	FSS	búsqueda de bancos de peces	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
43	RND	aleatorio	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
44	GWO	optimizador de lobo gris	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32
45	CSS	búsqueda de sistema cargado	0.44252	0.35454	0.35201	1.14907	0.24140	0.11345	0.06814	0.42299	0.18333	0.06300	0.02322	0.26955	1.842	20.46

Resumen

Con base en los resultados del algoritmo AMOm en funciones de prueba, se pueden extraer las siguientes conclusiones: a pesar de la dispersión de valores en funciones de pequeña dimensión, el algoritmo muestra una excelente escalabilidad en funciones de gran dimensión. Los principales cambios realizados a la versión original del algoritmo mejoraron significativamente su rendimiento. En este caso, duplicar la población principal (para ordenar junto con los individuos hija) y cambiar la secuencia de ejecución de las etapas del algoritmo hicieron posible obtener una gama más amplia de soluciones diversas. Este algoritmo se convirtió en un claro ejemplo de las posibilidades de utilizar técnicas adicionales para su modificación, lo que condujo a mejoras significativas. Esto fue posible gracias a la mejora de la propia lógica del algoritmo, que no siempre funciona en relación con otros algoritmos de optimización. 

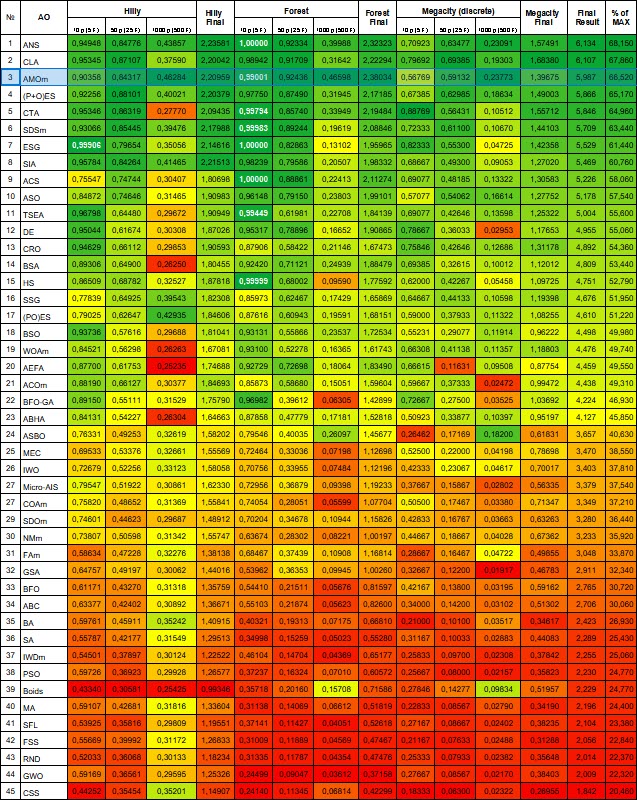
Figura 2. Gradación por colores de los algoritmos según las pruebas pertinentes Los resultados superiores o iguales a 0,99 se resaltan en blanco

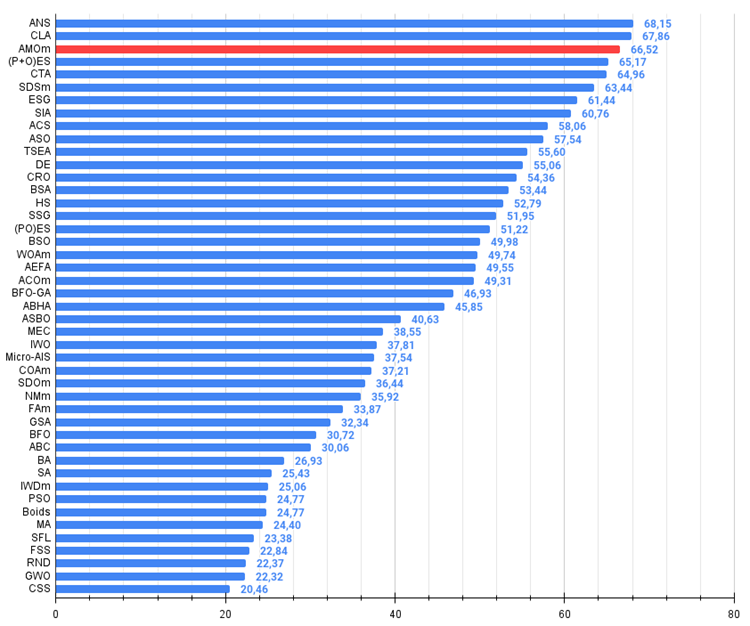
Figura 3. El histograma de los resultados de la prueba del algoritmo (en una escala de 0 a 100, cuanto más, mejor).

Donde 100 es el resultado teórico máximo posible, el archivo incluye un script para calcular la tabla de calificación)

Pros y contras de AMOm:

Ventajas:

1. Excelente convergencia.
2. Alta escalabilidad.
3. Pocos parámetros.
4. Implementación sencilla.

Desventajas:

1. Dispersión de resultados en funciones de baja dimensión.

El artículo se acompaña de un archivo con las versiones actuales de los códigos del algoritmo. El autor del artículo no es responsable de la exactitud absoluta en la descripción de los algoritmos canónicos. Se han realizado cambios en muchos de ellos para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/es/code/49355