
Optimización con el juego del caos — Game Optimization (CGO)
Contenido
Introducción
Los algoritmos de optimización desempeñan un papel estratégico en la resolución de problemas complejos no solo en diversos campos de la ciencia moderna, sino también en el trading. Con el rápido desarrollo de la tecnología, estas tareas se hacen aún más complejas y la búsqueda de la mejor solución consume cada vez más energía, por lo que también aumentan los requisitos de los algoritmos de optimización, y su rendimiento con una alta rentabilidad. Uno de los métodos más recientes y prometedores es el algoritmo Chaos Game Optimisation (CGO), desarrollado por Siamak Talatahari y Mehdi Azizi en 2020. Este algoritmo se basa en los principios de la teoría del caos y usa secuencias caóticas para generar y mejorar las soluciones.
La idea básica del algoritmo consiste en utilizar secuencias caóticas para encontrar óptimos globales en espacios multidimensionales complejos. Las secuencias caóticas poseen ciertas propiedades que, teóricamente, les permiten evitar las trampas locales y encontrar soluciones de alta calidad. En este artículo, analizaremos los principios esenciales y las etapas del algoritmo de Chaos Game Optimization, lo implementaremos en código y realizaremos pruebas estándar en funciones de prueba para sacar conclusiones sobre su funcionamiento.
Implementación del algoritmo
Imaginemos un grupo de investigadores, cada uno de los cuales trata de encontrar un extremo en un laberinto multidimensional. Al principio del viaje, nuestros buscadores se dispersan aleatoriamente por el laberinto y encuentran su primer refugio dentro de los límites estrictamente definidos del espacio. Ese supone su punto de referencia. Cada buscador no actúa solo: observa a sus compañeros y, en cada momento, selecciona un grupo de compañeros al azar y calcula el centro de su ubicación, como si encontrara un punto de equilibrio entre sus posiciones.
Se trata de la sabiduría colectiva promediada por la experiencia del grupo. Y entonces comienza la verdadera magia del caos. El buscador puede seleccionar uno de los cuatro caminos para dar el siguiente paso. Cada trayectoria supone una fórmula de movimiento específica en la que se entrelazan tres puntos clave: su posición actual, el mejor lugar encontrado por todo el grupo y el centro del subgrupo elegido. Estos puntos se mezclan, y la fuerza de su influencia en el movimiento posterior viene definida por el coeficiente α, el conductor del caos.
El propio coeficiente α adopta diferentes formas, y cada buscador, siguiendo las reglas, se puede impulsar desde su posición, apuntando a la media áurea entre el mejor resultado y el centro del grupo, o comenzar desde el mejor punto, explorando el espacio que lo rodea, y también puede impulsarse desde el centro del grupo, o dar un salto completamente aleatorio hacia lo desconocido.
Al final de cada acción, se comparan los resultados. Si uno de los buscadores encuentra un lugar mejor que el récord anterior, se convertirá en un nuevo faro para todo el grupo en su búsqueda continua.
Ahí reside la verdadera belleza del algoritmo: en su capacidad para convertir el caos en orden, el azar en movimiento intencionado, la incertidumbre en progreso, y cada paso, cada movimiento está sujeto a la búsqueda de soluciones entre lo conocido y lo desconocido, entre la estabilidad y el riesgo, entre el orden y el caos.
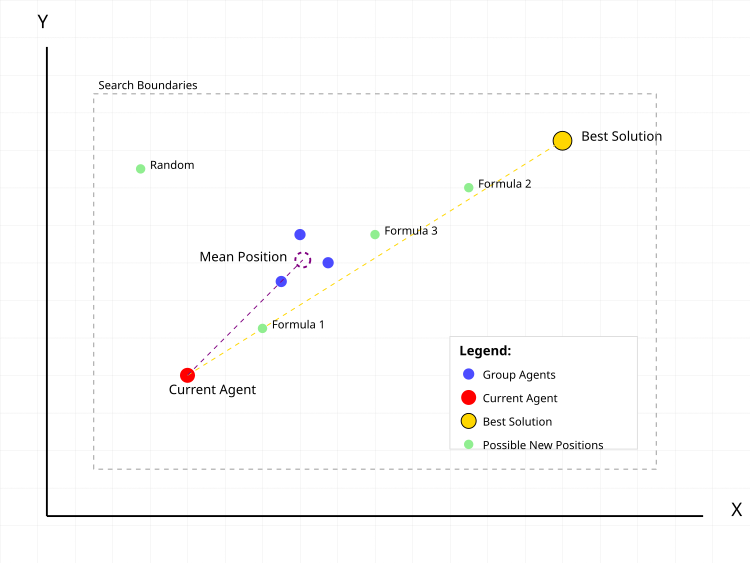
Figura 1. Acciones típicas de un agente de búsqueda en el algoritmo CGO
En la figura 1, el punto rojo es el agente actual para el que calculamos la nueva posición. Los puntos azules suponen un grupo de agentes seleccionados aleatoriamente en la población en un número elegido al azar. El círculo de puntos violetas es la posición central del grupo. El punto dorado es la mejor solución encontrada. Los puntos verdes son posibles nuevas posiciones del agente según distintas fórmulas:- Fórmula 1: actual + α(β×mejor - γ×media)
- Fórmula 2: mejor + α(β×media - γ×actual)
- Fórmula 3: media + α(β×mejor - γ×actual)
- Random: posición aleatoria
Las líneas de puntos muestran los vectores de influencia de la mejor solución y la posición media del grupo dentro del movimiento del agente actual. El rectángulo gris punteado indica los límites de la zona de búsqueda.
Vamos a escribir ahora el pseudocódigo del algoritmo.
- Establecemos el tamaño de la población (por defecto es de 50 agentes)
- Definimos los límites de búsqueda para cada coordenada:
- valores mínimos (rangeMin)
- valores máximos (rangeMax)
- cambio de paso (rangeStep)
- Para cada agente de la población:
- generamos coordenadas iniciales aleatorias dentro de los límites dados
- redondeamos las coordenadas para ajustarlas al paso
- calculamos el valor de la función objetivo
- Determinamos la mejor solución inicial entre todos los agentes
- Para cada agente de la población:
- tamaño del subgrupo = número aleatorio entre 1 y el tamaño de la población
- seleccionamos aleatoriamente a los agentes en un subgrupo
- para cada coordenada: coordenada_media = suma_grupo_coordenadas / tamaño_grupo
- α (alfa) = elegir al azar uno de los métodos:
- método 1: número aleatorio de 0 a 1
- método 2: 2 × aleatorio(0,1) - 1 [obtenemos un número de -1 a 1]
- método 3: Ir × aleatorio(0,1) + 1
- método 4: Ir × aleatorio(0,1) + (1-Ir) donde Ir = aleatorio 0 ó 1
- β (beta) = aleatoriamente 1 o 2
- γ (gamma) = aleatoriamente 1 o 2
- Fórmula 1: nueva_posición = actual + α(β×mejor - γ×media)
- Fórmula 2: nueva_posición = mejor + α(β×media - γ×actual)
- Fórmula 3: nueva_posición = media + α(β×mejor - γ×actual)
- Fórmula 4: nueva_posición = posición aleatoria dentro de los límites de búsqueda
- para cada coordenada:
- calculamos el nuevo valor mediante la fórmula
- comprobamos si la búsqueda está fuera de los límites
- si está fuera de los límites, corregimos a los límites más cercanos
- redondeamos el valor considerando el paso de cambio
- Para cada agente:
- si el valor de la función objetivo del agente es mejor que el mejor actual:
- actualizamos el mejor valor
- guardamos las coordenadas de la nueva mejor solución
- si el valor de la función objetivo del agente es mejor que el mejor actual:
- Repetimos los pasos 2-3 hasta que se cumpla la condición de parada:
- se ha alcanzado el número máximo de iteraciones
- o se ha encontrado una solución de la calidad necesaria
- u otro criterio de parada
Pasemos ahora a la aplicación del algoritmo en sí. La clase "C_AO_CGO" implementa el algoritmo CGO y deriva de la clase "C_AO"; hereda propiedades y métodos de la clase básica.
Métodos:
- SetParams () — establece el valor de "popSize" basándose en los datos del array de parámetros "params". Esto resulta importante para afinar el algoritmo antes de utilizarlo.
- Init () — método de inicialización, admite valores de rango mínimo y máximo, paso de cambio y número de épocas. Su objetivo consiste en preparar el algoritmo para su ejecución estableciendo los límites de búsqueda y otros parámetros.
- Moving () — describe los pasos necesarios para desplazar a los individuos durante el proceso de optimización. Su aplicación proporciona una lógica para las soluciones alternativas y su mejora.
- Revision () — se encarga de revisar tanto las soluciones actuales de la población como la mejor solución global.
Métodos privados:
- GetAlpha () — para obtener el parámetro alpha, que se utiliza para controlar la estrategia, la "intensidad" y la "diversidad" de la búsqueda.
- GenerateNewSolution () — para generar una nueva solución basada en el índice (seedIndex) y el valor medio del grupo (meanGroup).
class C_AO_CGO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_CGO () { } C_AO_CGO () { ao_name = "CGO"; ao_desc = "Chaos Game Optimization"; ao_link = "https://www.mql5.com/es/articles/17047"; popSize = 25; ArrayResize (params, 1); params [0].name = "popSize"; params [0].val = popSize; } void SetParams () { popSize = (int)params [0].val; } bool Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0); // number of epochs void Moving (); void Revision (); private: //------------------------------------------------------------------- double GetAlpha (); void GenerateNewSolution (int seedIndex, double &meanGroup []); }; //——————————————————————————————————————————————————————————————————————————————
El método "Init" de la clase "C_AO_CGO" se encarga de inicializar los parámetros del algoritmo de optimización antes de su inicio. Toma los siguientes argumentos: los arrays que contienen los valores mínimo y máximo para cada variable de búsqueda, el cambio de paso para cada variable y el número de épocas (iteraciones) del algoritmo.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_CGO::Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0) // number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; return true; } //——————————————————————————————————————————————————————————————————————————————
El método Moving ejecuta la lógica básica de desplazamiento de los individuos de la población de soluciones en el algoritmo CGO. El objetivo principal de este método consiste en actualizar las soluciones de la población basándose en reglas, lo que incluye generar nuevas soluciones y promediar los resultados. Veamos con detalle sus partes principales.
Primera parte, inicialización en la primera llamada (si la variable "revision" es "false"):
- Se ejecuta un ciclo externo sobre todos los elementos de la población (popSize) y para cada elemento (individuo i):
- Se inicia un ciclo interno sobre las coordenadas (coords):
- Se genera un valor aleatorio para cada coordenada usando el método u.RNDfromCI (), que retorna un valor aleatorio dentro del rango especificado.
- A continuación, este valor se ajusta mediante u.SeInDiSp (), que garantiza que el valor se mantenga dentro del intervalo, y redondea al paso más próximo.
- Establece la bandera "revision" en "true" para la siguiente llamada al método y sale del método.
- Para cada individuo de la población:
- Se genera un tamaño de grupo aleatorio "randGroupSize" de "1" a "popSize".
- Se crea un array "meanGroup" para almacenar el valor medio de las coordenadas, cuyo tamaño corresponde al número de coordenadas establecidas en "coords".
- El array "randIndices" se rellena con índices aleatorios (individuos) que se utilizarán para formar el grupo.
- En cada iteración, se añaden índices aleatorios a "randIndices", con los índices seleccionados al azar.
- A continuación, para cada grupo, se suman los valores de las coordenadas de cada individuo a partir de índices seleccionados al azar y el resultado se guarda en "meanGroup".
- Después de la suma, el valor de "meanGroup" se divide por el número de individuos del grupo para obtener el valor medio.
- Luego se genera una nueva solución para el individuo "i" basada en la media del grupo utilizando el método "GenerateNewSolution ()".
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { int randGroupSize = u.RNDminusOne (popSize) + 1; double meanGroup []; ArrayResize (meanGroup, coords); ArrayInitialize (meanGroup, 0); int randIndices []; ArrayResize (randIndices, randGroupSize); for (int j = 0; j < randGroupSize; j++) randIndices [j] = u.RNDminusOne (popSize); for (int j = 0; j < randGroupSize; j++) { for (int c = 0; c < coords; c++) { meanGroup [c] += a [randIndices [j]].c [c]; } } for (int c = 0; c < coords; c++) meanGroup [c] /= randGroupSize; GenerateNewSolution (i, meanGroup); } } //——————————————————————————————————————————————————————————————————————————————
Acto seguido, el método de revisión actualiza las mejores soluciones de la población. Itera por todos los individuos de la población y comprueba si el valor "f" de su función de aptitud es mayor que el mejor valor actual "fB". En caso afirmativo, actualiza "fB" con el nuevo valor "f" y copia las coordenadas c del individuo actual en el array "cB". Así, el método Revision encuentra y actualiza la mejor solución conocida en la población basándose en los valores de la función de aptitud.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::Revision () { for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
El método "GetAlpha" genera y retorna un valor "alpha" aleatorio según unas condiciones de selección aleatorias.
- Ir — valor aleatorio igual a "0" o "1".
- Hay cuatro casos posibles (disponibles en "case"), cada uno de los cuales genera un valor "alpha" utilizando la fórmula correspondiente:
- Caso 0: Genera un valor de 0 a 1.
- Caso 1: Genera un valor entre -1 y 1.
- Caso 2: Genera un valor de 1 a 2 multiplicándolo por "Ir" (0 ó 1).
- Caso 3: Genera un valor que depende de "Ir" y tiene un rango de 0 a 1, o 1, dependiendo del valor "Ir".
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CGO::GetAlpha () { int Ir = u.RNDminusOne (2); switch (u.RNDminusOne (4)) { case 0: return u.RNDfromCI (0, 1); case 1: return 2 * u.RNDfromCI (0, 1) - 1; case 2: return Ir * u.RNDfromCI (0, 1) + 1; case 3: return Ir * u.RNDfromCI (0, 1) + (1 - Ir); } return 0; } //——————————————————————————————————————————————————————————————————————————————
El método "GenerateNewSolution" se encarga de generar una nueva solución para un agente concreto de la población en función de varios parámetros aleatorios.
Inicialización de parámetros:- alpha — valor obtenido llamando al método "GetAlpha ()", utilizado para influir en la nueva posición.
- beta y gamma son valores aleatorios (1 ó 2).
- formula — selecciona aleatoriamente una de las cuatro ecuaciones posibles mediante las que se calculará la nueva posición.
- newPos — variable para almacenar la nueva posición utilizando la fórmula seleccionada.
- Dependiendo del valor de "formula":
- Caso 0: la nueva posición se calcula como la posición actual del agente añadiendo la combinación de coordenadas de "cB" (mejor solución poblacional) y "meanGroup".
- Caso 1: la nueva posición se calcula usando la coordenada de "cB" y el valor medio "meanGroup".
- Caso 2: la nueva posición se determina partiendo del valor medio y la coordenada del agente actual.
- Caso 3: la nueva posición se establece aleatoriamente dentro del rango especificado (rangoMin [c] y rangoMax [c]).
- a [seedIndex].c [c] — la coordenada del agente correspondiente se actualiza mediante el método "u.SeInDiSp ()", que considera los valores mínimos, los valores máximos y los pasos para garantizar que el nuevo valor se encuentra dentro de los límites aceptables.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::GenerateNewSolution (int seedIndex, double &meanGroup []) { double alpha = GetAlpha (); int beta = u.RNDminusOne (2) + 1; int gamma = u.RNDminusOne (2) + 1; int formula = u.RNDminusOne (4); for (int c = 0; c < coords; c++) { double newPos = 0; switch (formula) { case 0: newPos = a [seedIndex].c [c] + alpha * (beta * cB [c] - gamma * meanGroup [c]); break; case 1: newPos = cB [c] + alpha * (beta * meanGroup [c] - gamma * a [seedIndex].c [c]); break; case 2: newPos = meanGroup [c] + alpha * (beta * cB [c] - gamma * a [seedIndex].c [c]); break; case 3: newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); break; } a [seedIndex].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
Tras las pruebas, intentamos mejorar la convergencia del algoritmo y decidimos hacer un añadido respecto a la versión básica del algoritmo CGO. La principal diferencia se halla al principio del procesamiento de cada coordenada, antes de aplicar las fórmulas básicas de movimiento:
double rnd = u.RNDprobab(); // Get a random number from 0.0 to 1.0 rnd *= rnd; // Squate it int ind = (int)u.Scale(rnd, 0.0, 1.0, 0, popSize - 1); // Scale to index a[seedIndex].c [c] = a[ind].c [c]; // Copy the coordinate from another agent with the received index
La coordenada se copia de un agente seleccionado aleatoriamente, y la selección del agente no es uniforme sino con una distribución de probabilidad cuadrática (rnd *= rnd). Esto crea un "desplazamiento" hacia la selección de agentes con índices más pequeños (las mejores soluciones tienen una mayor probabilidad de ser seleccionadas). Luego elevamos al cuadrado el número aleatorio, creando así una distribución desigual, escalamos al rango del índice de población y, a continuación, copiamos, antes de aplicar las fórmulas básicas de movimiento. Lamentablemente, nuestro empeño a la hora de acelerar la convergencia en áreas prometedoras no ha tenido el efecto esperado.
Probablemente como consecuencia de la convergencia prematura, debido al efecto de amplificación, la diversidad en la población disminuye rápidamente, lo que en este algoritmo provoca un atasco aún mayor; es posible que la propia lógica del algoritmo impida que esto ocurra. A continuación le mostramos la sección de código donde se introdujimos los cambios; además hicimos algunos otros intentos de mejora, sin embargo, no hubo ningún progreso notable y decidimos quedarnos con la versión original del algoritmo.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CGO::GenerateNewSolution (int seedIndex, double &meanGroup []) { double alpha = GetAlpha (); int beta = u.RNDminusOne (2) + 1; int gamma = u.RNDminusOne (2) + 1; int formula = u.RNDminusOne (4); for (int c = 0; c < coords; c++) { double rnd = u.RNDprobab (); rnd *= rnd; int ind = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1); a [seedIndex].c [c] = a [ind].c [c]; double newPos = 0; switch (formula) { case 0: newPos = a [seedIndex].c [c] + alpha * (beta * cB [c] - gamma * meanGroup [c]); break; case 1: newPos = cB [c] + alpha * (beta * meanGroup [c] - gamma * a [seedIndex].c [c]); break; case 2: newPos = meanGroup [c] + alpha * (beta * cB [c] - gamma * a [seedIndex].c [c]); break; case 3: newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]); break; } a [seedIndex].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]); } } //——————————————————————————————————————————————————————————————————————————————
Resultados de las pruebas
Como podemos ver a continuación por los resultados de las pruebas, el número total de porcentajes anotados por el algoritmo resulta bastante modesto, sin embargo, si miramos más de cerca, podemos notar una característica interesante de este algoritmo, que vamos a describir a continuación.
CGO|Chaos Game Optimization|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.5725597668122144
25 Hilly's; Func runs: 10000; result: 0.3715760642098293
500 Hilly's; Func runs: 10000; result: 0.32017971142744234
=============================
5 Forest's; Func runs: 10000; result: 0.6117551660766816
25 Forest's; Func runs: 10000; result: 0.619308424855028
500 Forest's; Func runs: 10000; result: 0.6216109945434442
=============================
5 Megacity's; Func runs: 10000; result: 0.3753846153846153
25 Megacity's; Func runs: 10000; result: 0.2192307692307692
500 Megacity's; Func runs: 10000; result: 0.19028461538461647
=============================
All score: 3.90189 (43.35%)
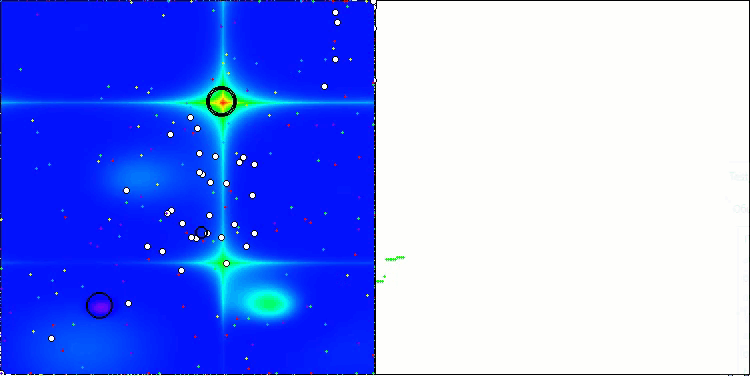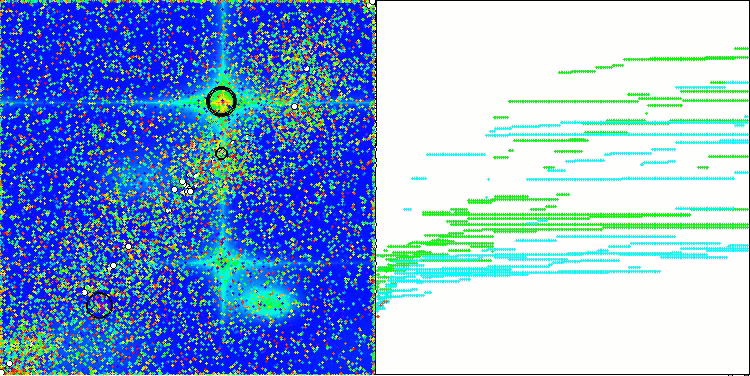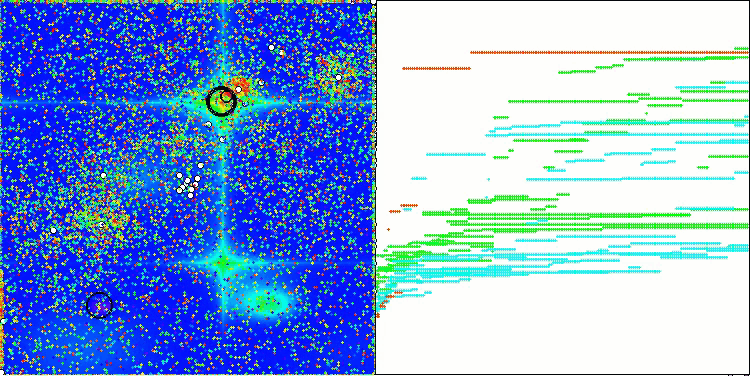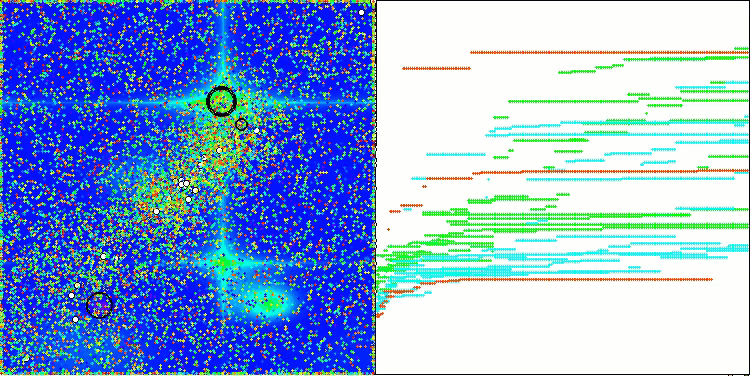
La visualización del funcionamiento del algoritmo con las funciones de prueba muestra claramente la formación de estructuras en la agrupación de agentes, y estas estructuras son diferentes en las distintas tareas. Pero lo que resulta común en la naturaleza del algoritmo es la enorme variación de los resultados de la optimización.

CGO en la función de prueba Hilly
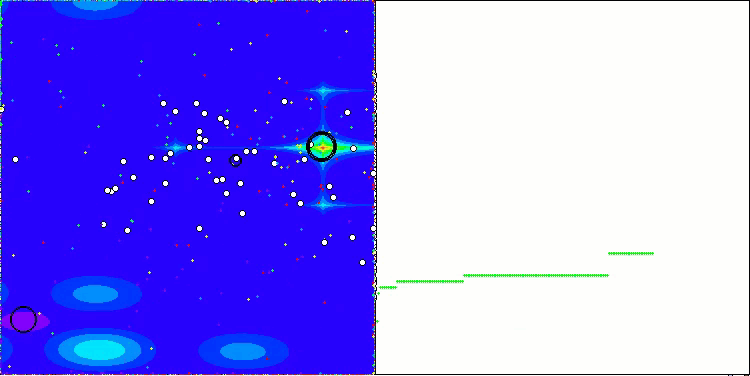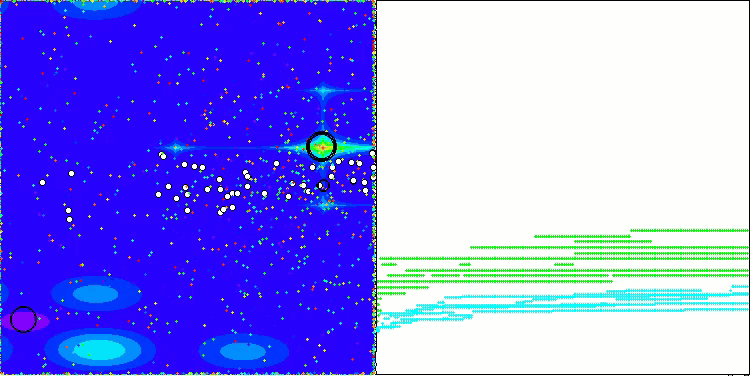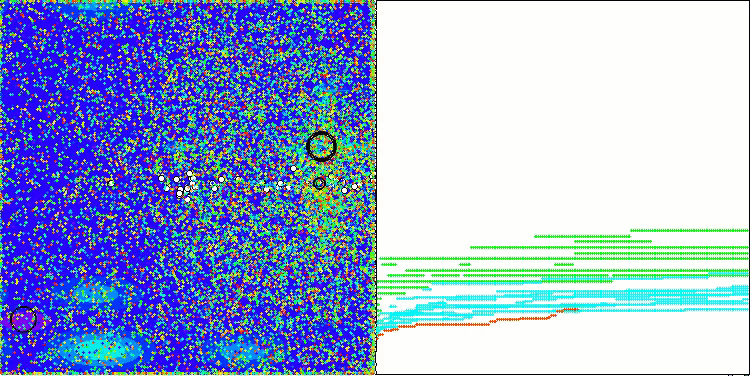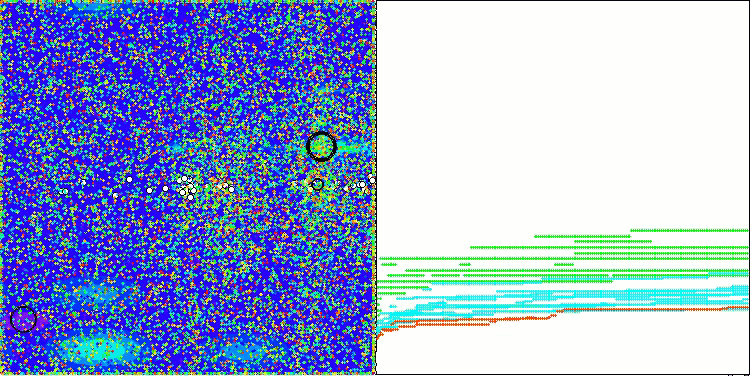
CGO en la función de prueba Forest
CGO en la función de prueba Forest
Al final de la prueba, el algoritmo CGO ocupa el puesto 38 en la tabla de clasificación de algoritmos de optimización basados en poblaciones.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration optimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0.91362 | 0.82349 | 0.31990 | 2.05701 | 0.97096 | 0.89532 | 0.29324 | 2.15952 | 0.73462 | 0.68569 | 0.16021 | 1.58052 | 5.797 | 64.41 |
| 7 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 8 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 9 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 10 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 11 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 12 | DA | dialectical algorithm | 0.86183 | 0.70033 | 0.33724 | 1.89940 | 0.98163 | 0.72772 | 0.28718 | 1.99653 | 0.70308 | 0.45292 | 0.16367 | 1.31967 | 5.216 | 57.95 |
| 13 | BHAm | black hole algorithm M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 14 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 15 | RFO | royal flush optimization (joo) | 0.83361 | 0.73742 | 0.34629 | 1.91733 | 0.89424 | 0.73824 | 0.24098 | 1.87346 | 0.63154 | 0.50292 | 0.16421 | 1.29867 | 5.089 | 56.55 |
| 16 | AOSm | búsqueda de orbitales atómicos M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 17 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 18 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 19 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 20 | BIO | blood inheritance optimization (joo) | 0.81568 | 0.65336 | 0.30877 | 1.77781 | 0.89937 | 0.65319 | 0.21760 | 1.77016 | 0.67846 | 0.47631 | 0.13902 | 1.29378 | 4.842 | 53.80 |
| 21 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 22 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 23 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 24 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 25 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 26 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 27 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 28 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 29 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 30 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 31 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 32 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 33 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 34 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 35 | ABH | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 36 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 37 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 38 | CGO | chaos game optimization | 0.57256 | 0.37158 | 0.32018 | 1.26432 | 0.61176 | 0.61931 | 0.62161 | 1.85267 | 0.37538 | 0.21923 | 0.19028 | 0.78490 | 3.902 | 43.35 |
| 39 | ATAm | artificial tribe algorithm M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 40 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 41 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 42 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 43 | CSA | circle search algorithm | 0.66560 | 0.45317 | 0.29126 | 1.41003 | 0.68797 | 0.41397 | 0.20525 | 1.30719 | 0.37538 | 0.23631 | 0.10646 | 0.71815 | 3.435 | 38.17 |
| 44 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 45 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| R.W. | random walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Conclusiones
Tras analizar los resultados del algoritmo CGO, hemos llegado a conclusiones importantes. El algoritmo de Chaos Game Optimization muestra un comportamiento extremadamente interesante. En conjunto, su rendimiento puede calificarse de inferior a la media, como demuestra una puntuación global del 43,35%. Sin embargo, lo más destacable es su comportamiento al escalar la tarea, pues el CGO muestra una alta eficiencia exactamente en tareas multivariantes, en las pruebas con una dimensionalidad de 1000 variables. Se trata de una propiedad atípica para la mayoría de los algoritmos metaheurísticos, que suelen sufrir la "maldición de la dimensionalidad" y pierden eficacia con el aumento del número de variables. En cambio, el CGO a veces incluso supera sus resultados en tareas de 10 y 50 dimensiones al trabajar con tareas de 1000 dimensiones. Esto resulta especialmente evidente en la función de prueba Forest, que tiene un extremo global en un punto "agudo".
Creo que este fenómeno se debe a la propia naturaleza del algoritmo. La base caótica del CGO y la variedad de fórmulas de movimiento proporcionan un mecanismo eficaz para explorar espacios de alta dimensionalidad. Las cuatro estrategias diferentes de actualización de la posición, la selección aleatoria entre ellas y un coeficiente α impredecible, permiten al algoritmo resolver problemas en paisajes multidimensionales complejos. El algoritmo funciona especialmente bien con características de tipo Forest, con resultados de 0,61-0,62, muy por encima de su rendimiento medio.
Analizando el dispositivo del algoritmo, podemos ver que su fuerza en la alta dimensionalidad se relaciona con el procesamiento de las coordenadas. En lugar de trabajar con el vector soluciones completo, el CGO actualiza cada coordenada de forma independiente, lo que le ofrece una ventaja al aumentar la dimensionalidad. Además, el uso de grupos aleatorios y sus posiciones medias garantiza un intercambio eficaz de información entre los agentes, incluso en espacios de alta dimensionalidad.
Hemos intentado rotado la superficie de la función Forest en diferentes ángulos para asegurarnos de que los interesantes resultados obtenidos no suponen una coincidencia aleatoria derivada de las peculiaridades de la lógica del algoritmo y la función de prueba correspondiente. Esto era necesario para eliminar la posibilidad de alcanzar accidentalmente el extremo global. Los experimentos con rotación de funciones solo han confirmado que esos resultados no son aleatorios. Dada esta peculiaridad del trabajo del CGO con funciones con extremos agudos, recomiendo múltiples ejecuciones de optimización si se utiliza este algoritmo. Esta recomendación resulta especialmente relevante para este algoritmo en particular.
En general, a pesar de su rendimiento global medio, la capacidad única del CGO para mantener e incluso mejorar la eficiencia a medida que aumenta la dimensionalidad del problema lo convierte en un algoritmo extremadamente interesante para su posterior estudio y aplicación a problemas de optimización complejos.
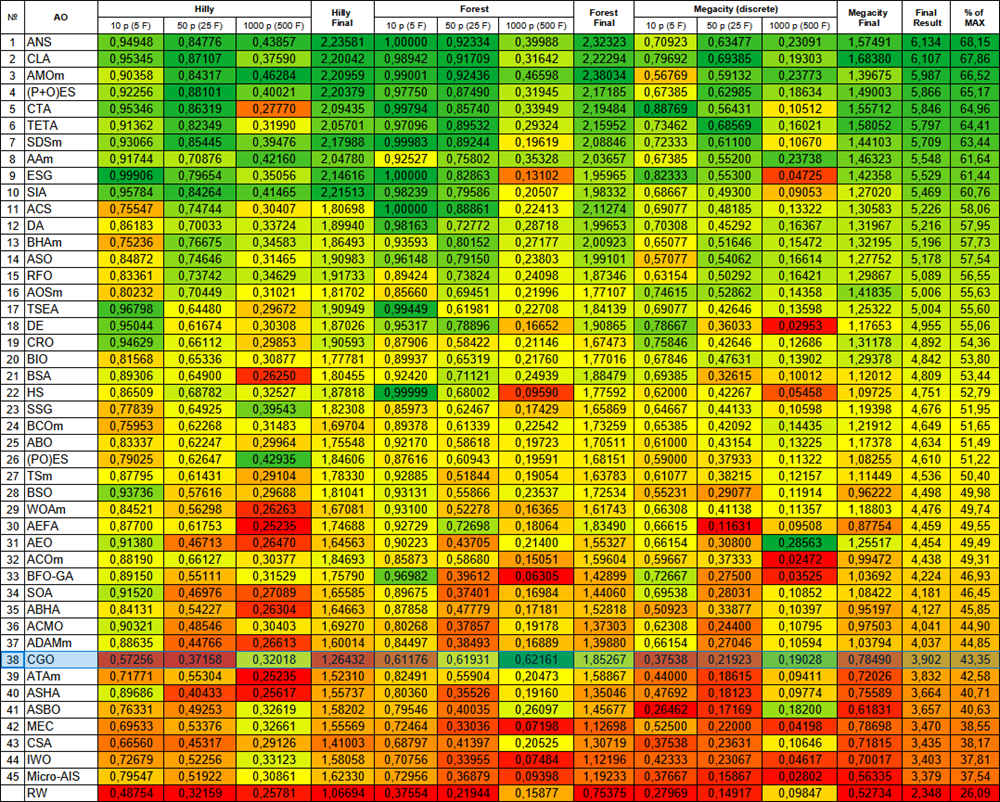
Figura 2. Clasificación por colores de los algoritmos según las pruebas respectivas
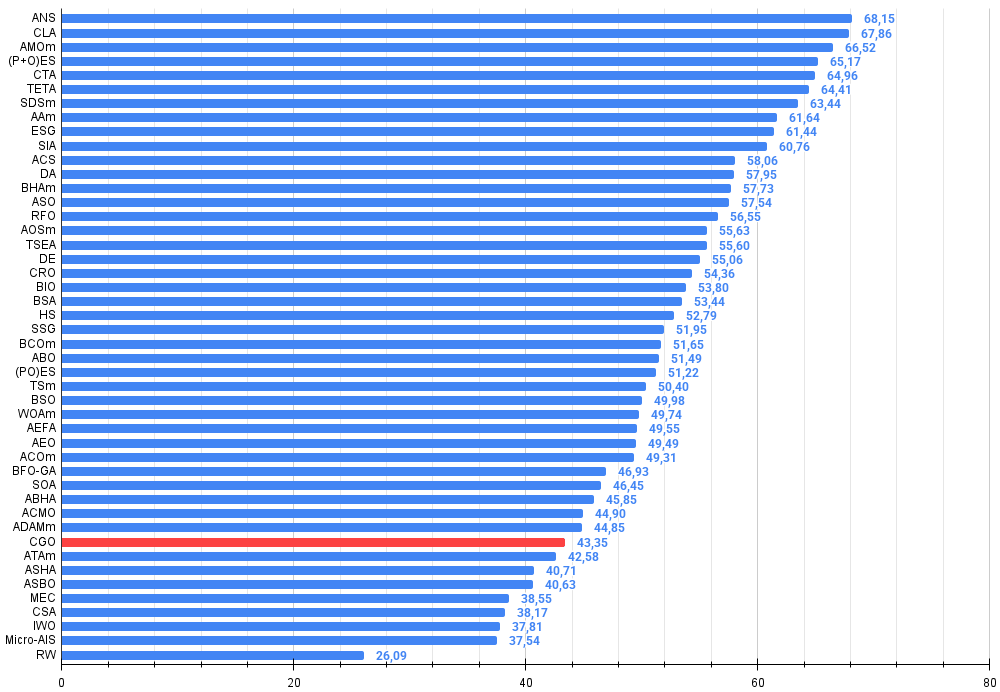
Figura 3. Histograma de los resultados de las pruebas de algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de puntuación está en el archivo)
Ventajas e inconvenientes del algoritmo CGO:
Ventajas:
- Sin parámetros externos
- Buena convergencia en funciones de dimensionalidad alta y media
Desventajas:
- Se atasca en extremos locales en problemas de pequeña dimensionalidad.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | #C_AO.mqh | Archivo de inclusión | Clase padre de algoritmos de población optimizaciones |
| 2 | #C_AO_enum.mqh | Archivo de inclusión | Enumeración de los algoritmos de optimización basados en la población |
| 3 | TestFunctions.mqh | Archivo de inclusión | Biblioteca de funciones de prueba |
| 4 | TestStandFunctions.mqh | Archivo de inclusión | Biblioteca de funciones del banco de pruebas |
| 5 | Utilities.mqh | Archivo de inclusión | Biblioteca de funciones auxiliares |
| 6 | CalculationTestResults.mqh | Archivo de inclusión | Script para calcular los resultados en una tabla comparativa |
| 7 | Testing AOs.mq5 | Script | Banco de pruebas único para todos los algoritmos de optimización basados en la población |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización |
| 9 | Test_AO_CGO.mq5 | Script | Banco de pruebas para el CGO |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/17047
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Desarrollo de asesores expertos autooptimizables en MQL5 (Parte 5): Reglas de negociación autoadaptativas
Desarrollo de asesores expertos autooptimizables en MQL5 (Parte 5): Reglas de negociación autoadaptativas
 Desarrollo de un kit de herramientas para el análisis de la acción del precio (Parte 10): Flujo externo (II) VWAP
Desarrollo de un kit de herramientas para el análisis de la acción del precio (Parte 10): Flujo externo (II) VWAP
 Aprendizaje automático y Data Science (Parte 33): Pandas Dataframe en MQL5, recopilación de datos para facilitar el uso de ML
Aprendizaje automático y Data Science (Parte 33): Pandas Dataframe en MQL5, recopilación de datos para facilitar el uso de ML
 Redes neuronales en el trading: Modelos híbridos de secuencias de grafos (Final)
Redes neuronales en el trading: Modelos híbridos de secuencias de grafos (Final)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso