
Algoritmo de búsqueda por vecindad — Across Neighbourhood Search (ANS)
1. Introducción
En el mundo actual, el desarrollo de métodos de optimización eficientes desempeña un papel importante en la resolución de una serie de problemas que van desde las aplicaciones de ingeniería hasta la investigación en el aprendizaje automático y la inteligencia artificial. En este contexto, los algoritmos evolutivos metaheurísticos suponen potentes herramientas para resolver problemas de optimización complejos. No obstante, para mejorar aún más su rendimiento y eficacia, resulta necesario seguir desarrollando y modificando los métodos existentes, así como desarrollar nuevos algoritmos.
En el presente artículo, nos familiarizaremos con un algoritmo de optimización conocido como Across Neighborhood Search (ANS), propuesto por Guohua Wu en 2014 y basado en la búsqueda poblacional para la optimización numérica. El algoritmo ANS desarrollado representa un avance significativo en el campo de la optimización, y promete resolver una amplia variedad de problemas del mundo real con alta eficiencia y precisión. Hoy confirmaremos si es esto cierto o no. La idea básica de ANS consiste en modelar el comportamiento de un sistema multiagente en el que cada agente se mueve por el espacio de decisión, interactuando con sus vecinos e intercambiando información. Este enfoque ofrece una excelente exploración del espacio de búsqueda, pues combina la optimización local y global.
Así, veremos una descripción detallada de la estructura del algoritmo ANS y sus principios de funcionamiento, además de un análisis comparativo con los métodos de optimización ya existentes. El algoritmo ANS desarrollado nos descubre un nuevo camino en el campo de la optimización, permitiéndonos resolver una amplia gama de problemas con un alto rendimiento. Asimismo, en el contexto del desarrollo de la inteligencia artificial, cabe señalar que el algoritmo ANS supone un paso importante hacia métodos de optimización más flexibles e inteligentes, capaces de considerar la especificidad del problema y la dinámica del entorno.
2. Aplicación del algoritmo
El algoritmo Across Neighborhood Search (ANS) es un método de optimización que usa ideas del campo de los algoritmos evolutivos y la metaheurística y está diseñado para encontrar soluciones óptimas en el espacio de parámetros de un problema.
Vamos a destacar las principales características del ANS:
- Búsqueda de vecindad: los agentes exploran la vecindad de las soluciones actuales, lo cual les permite encontrar óptimos locales de forma más eficiente.
- Uso de la distribución normal: El ANS utiliza la distribución normal para generar nuevos valores de los parámetros.
- Colecciones de soluciones: el ANS utiliza colecciones de las mejores soluciones para ayudar a guiar al algoritmo en varias direcciones prometedoras a la vez.
En el ANS, un grupo de individuos realiza una búsqueda conjunta en el espacio de soluciones para ejecutar de forma óptima el problema de optimización considerado. La idea básica del algoritmo es mantener y actualizar de forma dinámica la colección de soluciones superiores encontradas por los individuos hasta el momento. En cada generación, un individuo busca directamente en la vecindad varias soluciones distintas según una distribución de probabilidad normal. De esta forma, se explota la idea de que existen varias soluciones potencialmente buenas a la vez, ya que no se sabe de antemano cuál será la mejor.
A continuación analizaremos una descripción completa del algoritmo ANS con sus fórmulas y pasos, según el concepto del autor. El ANS realiza los siguientes pasos:
1. Inicialización de parámetros:
- Tamaño de la población m
- Recopilación de un conjunto de las mejores soluciones c
- Desviación típica de la distribución gaussiana sigma
- Dimensionalidad del espacio de búsqueda D
- Número máximo de generaciones MaxG
2. Inicialización de la población. Inicialización aleatoria de la posición de cada individuo de la población en el espacio de búsqueda.
3. Actualización de las mejores soluciones. Cada individuo de la población actualiza su posición actual explorando la vecindad de las mejores soluciones de la colección usando una distribución normal.
4. Selección de la coordenada a buscar. Selección de un número aleatorio n (across-search degree) para determinar la coordenada actual de la posición de un individuo en el espacio de soluciones.
5. Actualización de la posición del individuo. Actualización de la posición del individuo i según el paso anterior.
Fórmulas y operaciones:
1. Actualización de la posición pos_i del individuo i (exploración de la vecindad de la solución a partir de la colección):
- La posición del individuo i se actualiza usando una distribución gaussiana: pos_i = r_g + G (r_g - pos_i), donde:
- G - valor aleatorio de la distribución gaussiana
- r_g - posición de la mejor solución de la colección
2. Actualización de la posición pos_i del individuo i (exploración de la vecindad de la mejor solución propia del individuo):
- La posición del individuo i se actualiza usando una distribución gaussiana: pos_i = r_i + G (r_i - pos_i), donde:
- G - valor aleatorio de la distribución gaussiana
- r_i - posición de la mejor decisión del individuo
3. Actualización de un conjunto de mejores soluciones:
- La recopilación de las mejores soluciones se actualiza según las nuevas posiciones de los individuos.
De esta forma, las fórmulas reflejarán el mecanismo de búsqueda de un individuo i en la vecindad de su mejor solución r_i, así como en la vecindad de otras mejores soluciones r_g de la colección R. Los pasos mencionados del algoritmo representan la lógica básica del método ANS para resolver problemas de optimización. Esta incluye la inicialización de los parámetros, la inicialización aleatoria de las posiciones de los individuos, la actualización de las posiciones de los individuos dada la vecindad de las mejores soluciones y la actualización de la colección de mejores soluciones. El algoritmo seguirá funcionando hasta que se cumple la condición de parada.
La búsqueda basada en las mejores soluciones o individuos es una técnica de búsqueda común y frecuentemente usada en los algoritmos basados en estrategias poblacionales, aunque los procesos que implementan este mecanismo de búsqueda pueden diferir para distintos algoritmos de optimización. De hecho, en este caso, además de la población principal de agentes, se introducirá una población adicional: una colección de las mejores soluciones (direcciones potenciales de búsqueda). El tamaño de la colección se define en los parámetros externos del algoritmo y puede ser mayor o menor que el tamaño de la población principal.
La estrategia de búsqueda en el algoritmo ANS empieza poblando la colección de mejores soluciones, y luego procede a buscar en la vecindad de las mejores soluciones de la colección y las mejores soluciones individuales de cada agente. El tamaño de la desviación estándar sigma desempeñará un papel clave en el algoritmo. Los valores pequeños de sigma ofrecen una exploración más amplia del espacio de búsqueda, mientras que los valores más altos permiten refinar las soluciones estrechando sus vecindades. Este parámetro del algoritmo es responsable del equilibrio entre intensificación y diversificación de la búsqueda. En algunos algoritmos, este equilibrio está vinculado con el número de época actual para permitir cambios dinámicos de equilibrio entre exploración y refinamiento, pero en este caso los autores definieron el ajuste de equilibrio como un parámetro ANS externo.
Así, el algoritmo ANS combina la explotación de las mejores soluciones encontradas (mediante la búsqueda en sus vecindades) y la exploración del espacio de soluciones (mediante la búsqueda en las vecindades de las mejores soluciones de los propios individuos). En teoría, esto debería proporcionar un buen equilibrio entre la intensificación y la diversificación de la búsqueda.
Ahora vamos a escribir y analizar el código del algoritmo ANS. Primero definiremos la estructura "S_ANS_Agent" que se utilizará para representar a los agentes en el algoritmo ANS. Campos de la estructura:
- c: array para almacenar las coordenadas del agente.
- cBest: array para almacenar las mejores coordenadas del agente.
- f: valor de aptitud (fitness) del agente.
- fBest: mejor valor de adaptación del agente.
- Init(int coords): método de inicialización, establece los tamaños de los arrays "c" y "cBest" y establece los valores iniciales de "f" y "fBest".
Esta parte del código representa la estructura básica de un agente, un array de los cuales (agentes) representará la población básica en el algoritmo ANS.
//—————————————————————————————————————————————————————————————————————————————— struct S_ANS_Agent { double c []; //coordinates double cBest []; //best coordinates double f; //fitness double fBest; //best fitness void Init (int coords) { ArrayResize (c, coords); ArrayResize (cBest, coords); f = -DBL_MAX; fBest = -DBL_MAX; } }; //—————————————————————————————————————————————————————————————————————————————
Para describir la colección de mejores soluciones, escribiremos la estructura "S_Collection", que se utilizará para almacenar información sobre las mejores coordenadas en el espacio de búsqueda y su correspondiente valor de aptitud. La estructura contendrá los campos siguientes:
- c: array para almacenar coordenadas.
- f: valor de aptitud para una solución dada a un problema de la colección.
- Init(int coords): método de inicialización; establece el tamaño del array "c" y el valor inicial "f" al mínimo valor posible de tipo "double".
//—————————————————————————————————————————————————————————————————————————————— struct S_Collection { double c []; //coordinates double f; //fitness void Init (int coords) { ArrayResize (c, coords); f = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Luego declararemos una clase "C_AO_ANS", que será heredera de la clase básica "C_AO" y supondrá una implementación del algoritmo Across Neighbourhood Search (ANS). He aquí algunos puntos clave:
- ao_name, ao_desc, ao_link: propiedades que describen el algoritmo ANS.
- popSize: tamaño de la población.
- collectionSize, sigma, range, collChoiceProbab: parámetros del algoritmo ANS.
- SetParams(): método de parametrización.
- Init(), Moving(), Revision(): métodos para inicializar, mover agentes y actualizar la población y la colección de soluciones.
- S_ANS_Agent, S_Collection: estructuras para guardar los datos del agente y la colección.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ANS : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ANS () { } C_AO_ANS () { ao_name = "ANS"; ao_desc = "Across Neighbourhood Search"; ao_link = "https://www.mql5.com/es/articles/15049"; popSize = 50; //population size collectionSize = 20; //Best solutions collection sigma = 3.0; //Form of normal distribution range = 0.5; //Range of values dispersed collChoiceProbab = 0.8; //Collection choice probab ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "collectionSize"; params [1].val = collectionSize; params [2].name = "sigma"; params [2].val = sigma; params [3].name = "range"; params [3].val = range; params [4].name = "collChoiceProbab"; params [4].val = collChoiceProbab; } void SetParams () { popSize = (int)params [0].val; collectionSize = (int)params [1].val; sigma = params [2].val; range = params [3].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- int collectionSize; //Best solutions collection double sigma; //Form of normal distribution double range; //Range of values dispersed double collChoiceProbab; //Collection choice probab S_ANS_Agent agent []; private: //------------------------------------------------------------------- S_Collection coll []; S_Collection collTemp []; }; //——————————————————————————————————————————————————————————————————————————————
El método "Init" inicializa los parámetros del algoritmo ANS (Across Neighbourhood Search).
- rangeMinP, rangeMaxP, rangeStepP: arrays que representan el mínimo, el máximo y el paso del rango de búsqueda.
- epochsP: número de épocas (generaciones).
Método interior:
- Comprobamos que se hayan inicializado correctamente los parámetros estándar con "StandardInit".
- Creamos los arrays de agentes "agent" y colecciones "coll" (una segunda población para almacenar las mejores soluciones) y "collTemp" (un array temporal para clasificación de la colección).
- Para cada agente y colección, se llama al método "Init" para establecer los valores iniciales.
Este método desempeña un papel esencial en la preparación del algoritmo ANS para realizar la optimización. Debemos considerar que los arrays "coll" y "collTemp" se inicializan con un tamaño doble con respecto al parámetro "collectionSize". Así se garantizará que los nuevos agentes añadidos a la colección se sitúen en la segunda mitad del array. A continuación, se clasificará toda la colección y solo la primera mitad, que contiene los mejores agentes, se utilizará para el trabajo posterior.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ANS::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) //number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (agent, popSize); for (int i = 0; i < popSize; i++) agent [i].Init (coords); ArrayResize (coll, collectionSize * 2); ArrayResize (collTemp, collectionSize * 2); for (int i = 0; i < collectionSize * 2; i++) { coll [i].Init (coords); collTemp [i].Init (coords); } return true; } //——————————————————————————————————————————————————————————————————————————————
El método "Moving" realizará el movimiento (desplazamiento) de los agentes en el algoritmo ANS. Vamos a desglosar este código con detalle:
1. Inicialización (si "revision" es igual a "false"):
- Si es el primer paso (primera época), entonces para cada agente:
- Se generará un valor aleatorio "val" en un rango comprendido entre "rangeMin[c]" y "rangeMax[c]".
- El operador "SeInDiSp" se aplica para considerar el paso "rangeStep[c]".
- El valor "val" se asigna a las coordenadas del agente "agent[i].c[c]".
- El valor "val" también se asigna a las mejores coordenadas del agente "agent[i].cBest[c]" (en esta fase se desconocen los valores de adaptación de los agentes, por lo que las mejores coordenadas serán iguales a las coordenadas iniciales actuales).
- El valor "val" se asigna al array de agentes "a[i].c[c]".
2. Desplazamiento de agentes (si "revisión" es igual a "true"):
- Para cada agente y cada coordenada:
- Si el número aleatorio es menor que "collChoiceProbab", se selecciona una solución aleatoria de la colección:
- Se selecciona un índice aleatorio "ind" de la colección (hasta que se encuentre una solución no vacía).
- El valor "p" se toma de las coordenadas actuales del agente.
- El valor "r" se toma de la solución seleccionada en la colección.
- En caso contrario, se usan las mejores coordenadas del agente:
- El valor "p" se toma de las coordenadas actuales del agente.
- El valor "r" se toma de las mejores coordenadas del agente.
- Se calculan la distancia "dist" y el alcance ("min" y "max") del desplazamiento.
- Los valores "min" y "max" se limitan a los rangos "rangeMin[c]" y "rangeMax[c]".
- Se aplica una distribución normal con los parámetros "r", "min", "max" y "sigma".
- El valor "val" se asigna a las coordenadas del agente "agent[i].c[c]".
- El valor "val" también se asigna al array de agentes "a[i].c[c]".
Este código actualiza las coordenadas de los agentes en el algoritmo ANS, dadas las coordenadas propias de los mejores agentes y las soluciones de la colección.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ANS::Moving () { double val = 0.0; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { val = u.RNDfromCI (rangeMin [c], rangeMax [c]); val = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); agent [i].c [c] = val; agent [i].cBest [c] = val; a [i].c [c] = val; } } revision = true; return; } //---------------------------------------------------------------------------- double min = 0.0; double max = 0.0; double dist = 0.0; int ind = 0; double r = 0.0; double p = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { if (u.RNDprobab () < collChoiceProbab) { do ind = u.RNDminusOne (collectionSize); while (coll [ind].f == -DBL_MAX); p = agent [i].c [c]; r = coll [ind].c [c]; } else { p = agent [i].c [c]; r = agent [i].cBest [c]; } dist = fabs (p - r) * range; min = r - dist; max = r + dist; if (min < rangeMin [c]) min = rangeMin [c]; if (max > rangeMax [c]) max = rangeMax [c]; val = u.GaussDistribution (r, min, max, sigma); val = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); agent [i].c [c] = val; a [i].c [c] = val; } } } //——————————————————————————————————————————————————————————————————————————————
El método "Revision" realiza una revisión (actualización) de los agentes y de la colección en el algoritmo ANS. Aquí tenemos lo más destacado:
- Primera parte del método: busca un agente cuya aptitud resulte mejor que la solución global con aptitud "fB" y almacena sus coordenadas en el array "cB".
- Segunda parte del método: actualiza las mejores coordenadas de los agentes "agent[i].cBest" según su aptitud actual "a[i].f".
- Tercera parte del método: actualiza la colección "coll" basándose en las mejores coordenadas de los agentes.
- Clasifica la colección.
Este método desempeña un papel importante en la actualización de los agentes y la colección de soluciones durante la ejecución del algoritmo. La población de agentes se coloca en la segunda parte de la colección; luego se realiza la clasificación de la colección y se utiliza la primera mitad de la colección que contiene las mejores soluciones.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ANS::Revision () { //---------------------------------------------------------------------------- int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > agent [i].fBest) { agent [i].fBest = a [i].f; ArrayCopy (agent [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY); } } //---------------------------------------------------------------------------- int cnt = 0; for (int i = collectionSize; i < collectionSize * 2; i++) { if (cnt < popSize) { coll [i].f = agent [cnt].fBest; ArrayCopy (coll [i].c, agent [cnt].cBest, 0, 0, WHOLE_ARRAY); cnt++; } else break; } u.Sorting (coll, collTemp, collectionSize * 2); } //——————————————————————————————————————————————————————————————————————————————
3. Resultados de las pruebas
Impresión del rendimiento del algoritmo ANS en un banco de pruebas con funciones de prueba:
ANS|Across Neighbourhood Search|50.0|100.0|8.0|1.0|0.6|
=============================
5 Hilly's; Func runs: 10000; result: 0.9494753644543816
25 Hilly's; Func runs: 10000; result: 0.8477633752716718
500 Hilly's; Func runs: 10000; result: 0.43857039929159747
=============================
5 Forest's; Func runs: 10000; result: 0.9999999999988883
25 Forest's; Func runs: 10000; result: 0.9233446583489741
500 Forest's; Func runs: 10000; result: 0.3998822848099108
=============================
5 Megacity's; Func runs: 10000; result: 0.709230769230769
25 Megacity's; Func runs: 10000; result: 0.6347692307692309
500 Megacity's; Func runs: 10000; result: 0.2309076923076936
=============================
All score: 6.13394 (68.15%)
El ANS muestra unos resultados impresionantes en todas las funciones de prueba. Bien, ahora podemos disfrutar de la visualización del funcionamiento de este algoritmo en el banco de pruebas. Los resultados del ANS son realmente asombrosos, pero surgen algunos problemas a la hora de visualizarlos. En particular, llama la atención el comportamiento de la población, que parece desaparecer del campo visual. Podemos observar que el espacio de soluciones se despeja y el paisaje de características queda sin agentes. Esto solo puede significar una cosa: a pesar de los excelentes resultados del algoritmo, la población resulta propensa a la degeneración. La colección de soluciones excelentes está plagada de soluciones muy similares, y simplemente no se pueden crear nuevas soluciones porque todas ellas se derivan de las ya existentes.
Semejante dinámica de la población puede indicar la necesidad de perfeccionar los mecanismos para mantener la diversidad en la población. Puede que merezca la pena plantearse añadir un operador de mutación o introducir otros mecanismos que mantengan una mayor diversidad de soluciones durante la optimización. Esto servirá para evitar la degeneración de la población y proporcionará un algoritmo más estable.
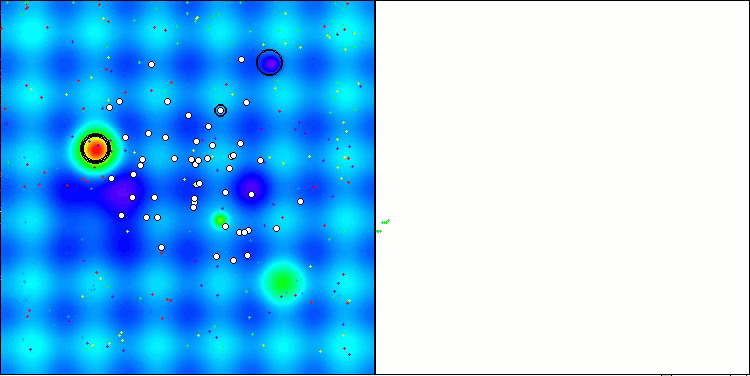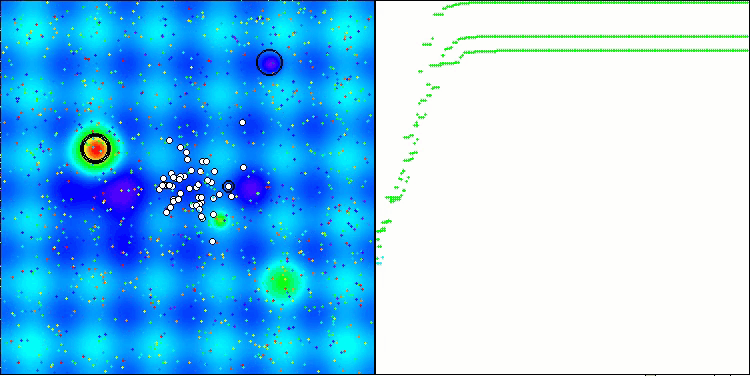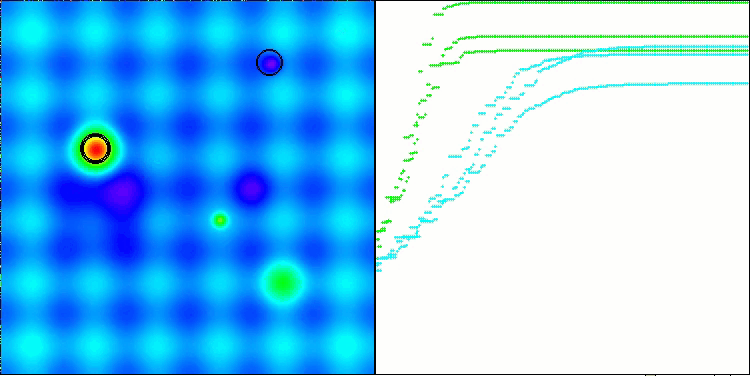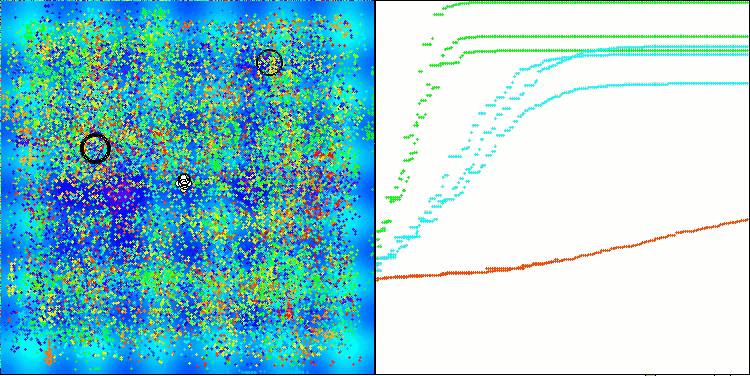
ANS en la función de prueba Hilly.
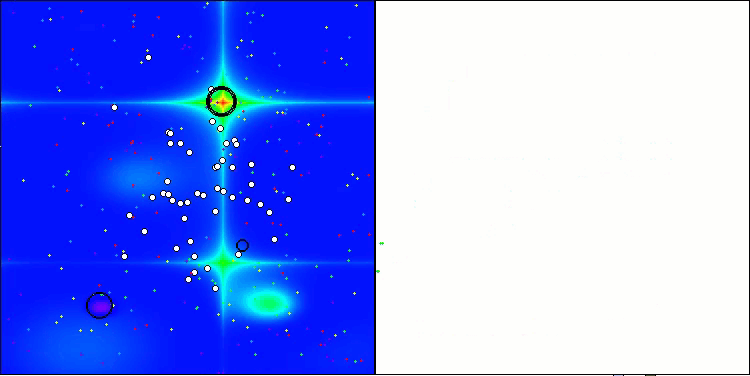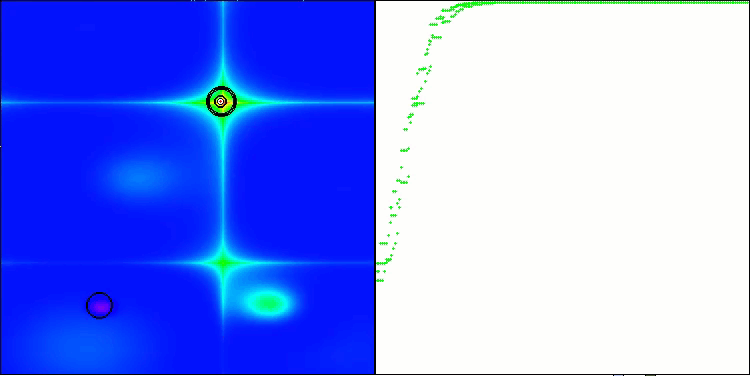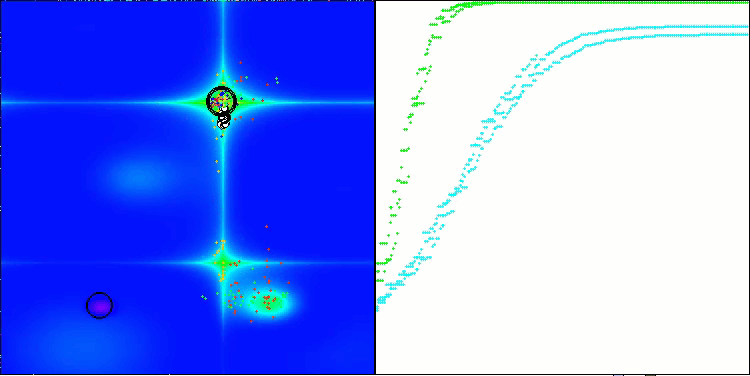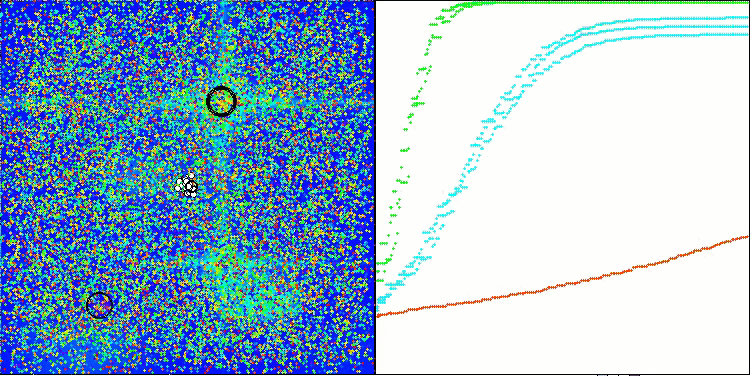
ANS en la función de prueba Forest.
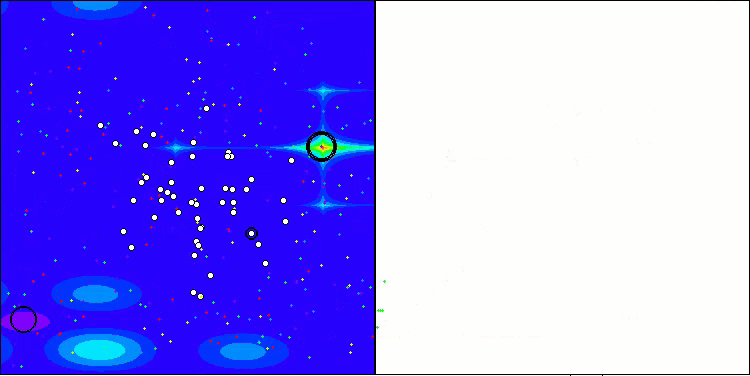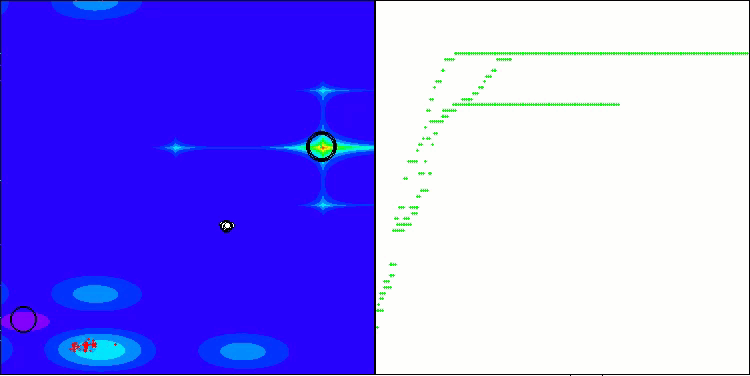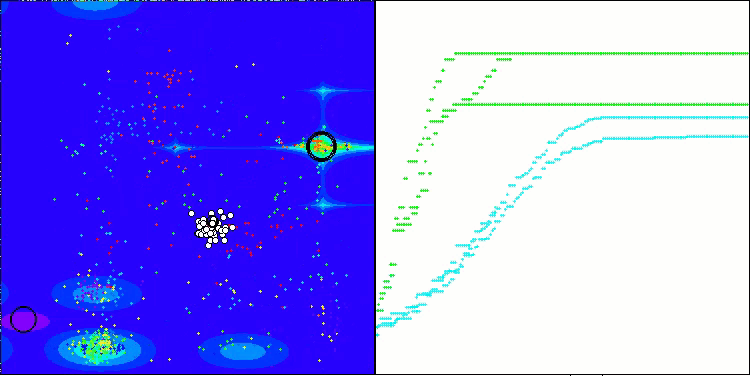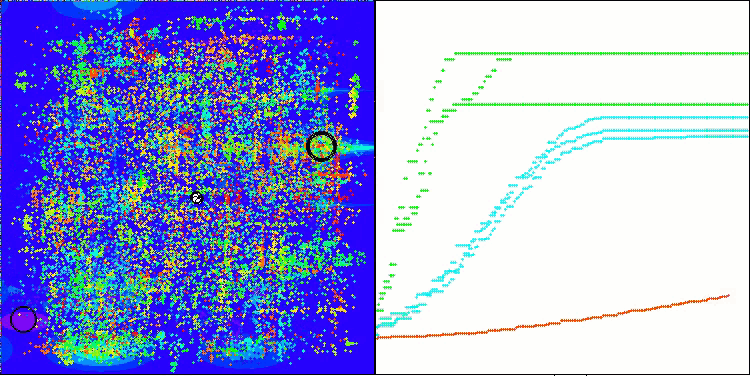
ANS en la función de prueba Megacity.
El algoritmo analizado en este artículo se sitúa con seguridad en la segunda línea de la tabla de clasificación. Los comentarios resultan innecesarios, pero podemos destacar ciertos puntos esenciales: el algoritmo muestra una escalabilidad impresionante, manteniendo su capacidad de búsqueda incluso con problemas de grandes dimensionalidad.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | BGA | binary genetic algorithm | 0,99989 | 0,99518 | 0,42835 | 2,42341 | 0,96153 | 0,96181 | 0,32027 | 2,24360 | 0,91385 | 0,95908 | 0,24220 | 2,11512 | 6,782 | 75,36 |
| 2 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 3 | CLA | code lock algorithm | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | ESG | evolution of social groups | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 8 | SIA | simulated isotropic annealing | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 9 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 10 | TSEA | turtle shell evolution algorithm | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 11 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 12 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 13 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 14 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 15 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 16 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 17 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 18 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 19 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 20 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 21 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 22 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 23 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 24 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 25 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 26 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 27 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 28 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 29 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 30 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 31 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 32 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 33 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
| 34 | PSO | particle swarm Optimization | 0,59726 | 0,36923 | 0,29928 | 1,26577 | 0,37237 | 0,16324 | 0,07010 | 0,60572 | 0,25667 | 0,08000 | 0,02157 | 0,35823 | 2,230 | 24,77 |
| 35 | Boids | boids algorithm | 0,43340 | 0,30581 | 0,25425 | 0,99346 | 0,35718 | 0,20160 | 0,15708 | 0,71586 | 0,27846 | 0,14277 | 0,09834 | 0,51957 | 2,229 | 24,77 |
| 36 | MA | monkey algorithm | 0,59107 | 0,42681 | 0,31816 | 1,33604 | 0,31138 | 0,14069 | 0,06612 | 0,51819 | 0,22833 | 0,08567 | 0,02790 | 0,34190 | 2,196 | 24,40 |
| 37 | SFL | shuffled frog-leaping | 0,53925 | 0,35816 | 0,29809 | 1,19551 | 0,37141 | 0,11427 | 0,04051 | 0,52618 | 0,27167 | 0,08667 | 0,02402 | 0,38235 | 2,104 | 23,38 |
| 38 | FSS | fish school search | 0,55669 | 0,39992 | 0,31172 | 1,26833 | 0,31009 | 0,11889 | 0,04569 | 0,47467 | 0,21167 | 0,07633 | 0,02488 | 0,31288 | 2,056 | 22,84 |
| 39 | RND | random | 0,52033 | 0,36068 | 0,30133 | 1,18234 | 0,31335 | 0,11787 | 0,04354 | 0,47476 | 0,25333 | 0,07933 | 0,02382 | 0,35648 | 2,014 | 22,37 |
| 40 | GWO | grey wolf optimizer | 0,59169 | 0,36561 | 0,29595 | 1,25326 | 0,24499 | 0,09047 | 0,03612 | 0,37158 | 0,27667 | 0,08567 | 0,02170 | 0,38403 | 2,009 | 22,32 |
| 41 | CSS | charged system search | 0,44252 | 0,35454 | 0,35201 | 1,14907 | 0,24140 | 0,11345 | 0,06814 | 0,42299 | 0,18333 | 0,06300 | 0,02322 | 0,26955 | 1,842 | 20,46 |
| 42 | EM | electroMagnetism-like algorithm | 0,46250 | 0,34594 | 0,32285 | 1,13129 | 0,21245 | 0,09783 | 0,10057 | 0,41085 | 0,15667 | 0,06033 | 0,02712 | 0,24412 | 1,786 | 19,85 |
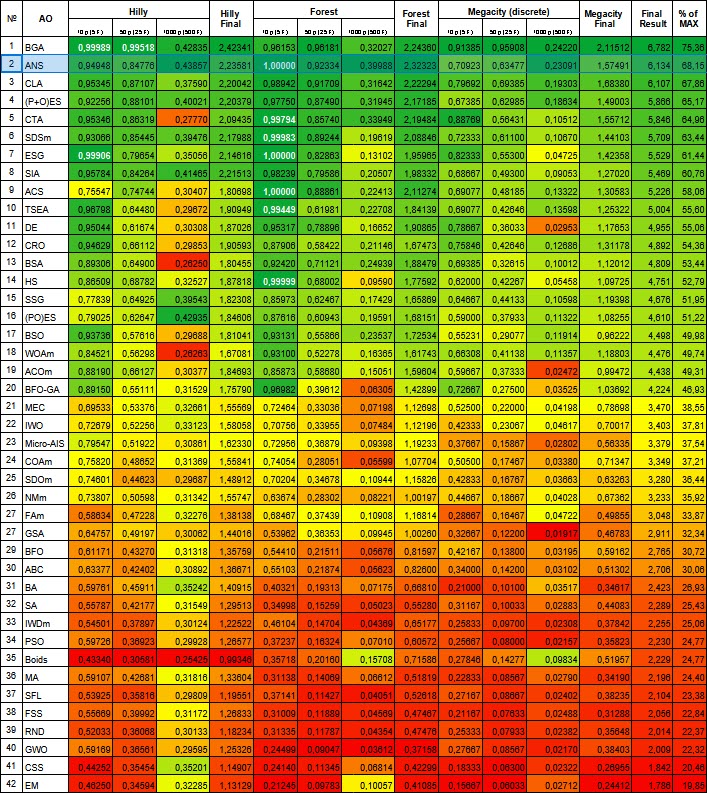
Figura 1. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0,99 aparecen resaltados en blanco.
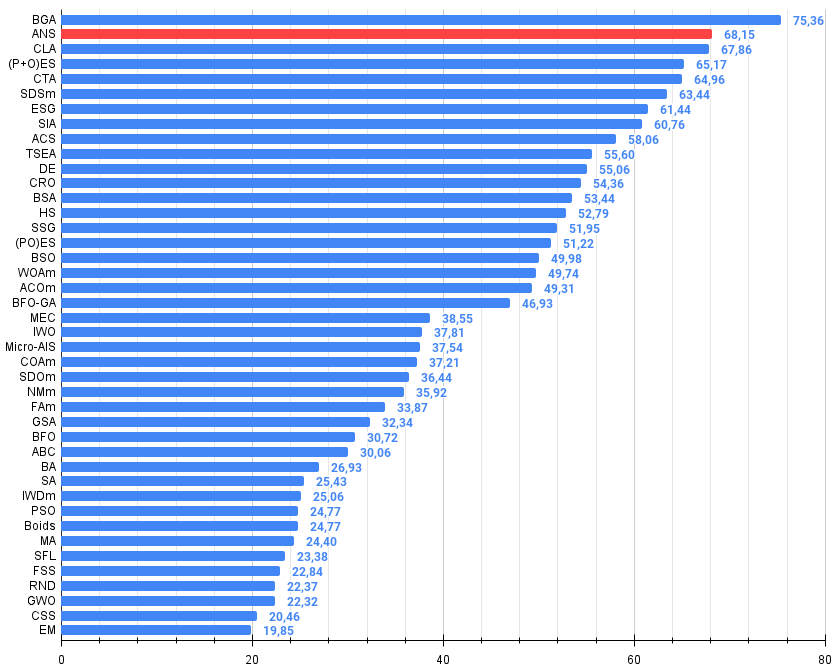
Figura 2. Histograma de los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor),
donde 100 es el máximo resultado teórico posible; el script para calcular la tabla de clasificación está en el archivo)
Más arriba en el artículo, hemos señalado la tendencia de la población del algoritmo ANS a degenerar. Para solventar esta importante deficiencia, hemos decidido modificar el algoritmo añadiendo un operador de mutación. En este caso, la mutación sería la probabilidad gaussiana de obtener una nueva coordenada en la vecindad de la mejor solución del agente, pero oscilando entre el valor mínimo aceptable y el máximo para la coordenada correspondiente. Para ello, tendremos que hacer algunos cambios en el método Moving.
Ahora veremos qué cambios hemos realizado en el código y describiremos brevemente la lógica del método:
- Si el número aleatorio es inferior a 0,005, la mutación se producirá utilizando una distribución normal.
- En caso contrario, elegiremos una solución aleatoria de la colección o utilizaremos las mejores coordenadas del agente.
- Para una distribución normal se calcularán la distancia y el rango.
- Luego aplicaremos la distribución normal para obtener nuevos valores de coordenadas.
//---------------------------------------------------------------------------- double min = 0.0; double max = 0.0; double dist = 0.0; int ind = 0; double r = 0.0; double p = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { if (u.RNDprobab () < 0.005) { val = u.GaussDistribution (agent [i].cBest [c], rangeMin [c], rangeMax [c], sigma); val = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); } else { if (u.RNDprobab () < collChoiceProbab) { do ind = u.RNDminusOne (collectionSize); while (coll [ind].f == -DBL_MAX); p = agent [i].c [c]; r = coll [ind].c [c]; } else { p = agent [i].c [c]; r = agent [i].cBest [c]; } dist = fabs (p - r) * range; min = r - dist; max = r + dist; if (min < rangeMin [c]) min = rangeMin [c]; if (max > rangeMax [c]) max = rangeMax [c]; val = u.GaussDistribution (r, min, max, sigma); val = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); } agent [i].c [c] = val; a [i].c [c] = val; } }
Tras añadir el operador de mutación, el algoritmo continúa explorando el espacio de búsqueda en cualquier número de épocas, como se demuestra en la figura 3 (captura de pantalla de la visualización del funcionamiento del algoritmo).
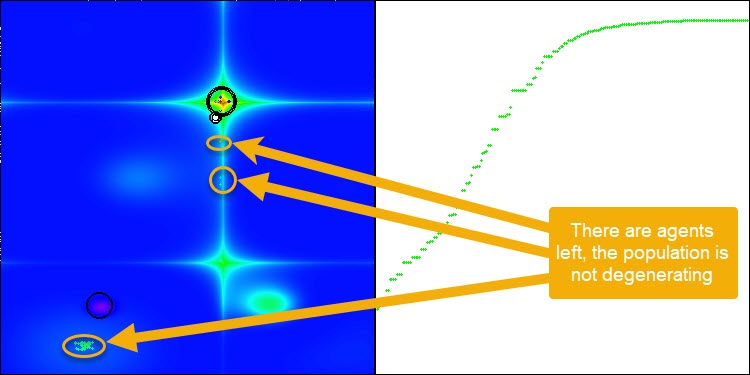
Figura 3. Los agentes permanecen, la población no degenera (parámetro mut = 0,005)
- El operador de mutación con el parámetro "mut 0,1" tiene un efecto negativo en el resultado global. Cuando el factor de mutación es tan significativo (10% del número total de operaciones en cada coordenada), se observa un deterioro de los resultados del algoritmo. Por ello, hemos decidido reducir sistemáticamente este parámetro. Reduciendo el valor del parámetro hemos obtenido mejores resultados; nos hemos decidido por un valor de 0,005. Este coeficiente ha sido suficiente para evitar la degeneración de la población y, al mismo tiempo, proporcionar una mejora en el rendimiento del algoritmo, como se refleja en las impresiones siguientes.
Resultados del algoritmo con una probabilidad de mutación mut = 0,1:
=============================
All score: 6.05103 (67.23%)
ANS|Across Neighbourhood Search|50.0|100.0|8.0|1.0|0.6|
=============================
5 Hilly's; Func runs: 10000; result: 0.9534829314854332
25 Hilly's; Func runs: 10000; result: 0.8136803288623282
500 Hilly's; Func runs: 10000; result: 0.31144979106165716
=============================
5 Forest's; Func runs: 10000; result: 0.9996561274415626
25 Forest's; Func runs: 10000; result: 0.81670393859872
500 Forest's; Func runs: 10000; result: 0.25620559379918284
=============================
5 Megacity's; Func runs: 10000; result: 0.8753846153846153
25 Megacity's; Func runs: 10000; result: 0.5778461538461539
500 Megacity's; Func runs: 10000; result: 0.13375384615384744
=============================
All score: 5.73816 (63.76%)
Resultados del algoritmo con una probabilidad de mutación mut = 0,01:
=============================
5 Hilly's; Func runs: 10000; result: 0.9073657389037575
25 Hilly's; Func runs: 10000; result: 0.871278233418226
500 Hilly's; Func runs: 10000; result: 0.3960769225373809
=============================
5 Forest's; Func runs: 10000; result: 0.989394440004635
25 Forest's; Func runs: 10000; result: 0.9513150500729907
500 Forest's; Func runs: 10000; result: 0.35407610928209116
=============================
5 Megacity's; Func runs: 10000; result: 0.7492307692307691
25 Megacity's; Func runs: 10000; result: 0.6387692307692309
500 Megacity's; Func runs: 10000; result: 0.19352307692307838
=============================
All score: 6.05103 (67.23%)
Resultados del algoritmo con una probabilidad de mutación mut = 0,005:
ANS|Across Neighbourhood Search|50.0|100.0|8.0|1.0|0.6|
=============================
5 Hilly's; Func runs: 10000; result: 0.949632264944664
25 Hilly's; Func runs: 10000; result: 0.871206955779846
500 Hilly's; Func runs: 10000; result: 0.40738389742274217
=============================
5 Forest's; Func runs: 10000; result: 0.9924803131691761
25 Forest's; Func runs: 10000; result: 0.9493489251290264
500 Forest's; Func runs: 10000; result: 0.3666276564633121
=============================
5 Megacity's; Func runs: 10000; result: 0.8061538461538461
25 Megacity's; Func runs: 10000; result: 0.6732307692307691
500 Megacity's; Func runs: 10000; result: 0.20844615384615534
=============================
All score: 6.22451 (69.16%)
Conclusiones
Ahora que hemos analizado los resultados junto con el operador de mutación, podemos sacar las siguientes conclusiones:
1. Simplicidad y facilidad de aplicación.
2. Equilibrio entre exploración y explotación.
3. Eficacia en la resolución de distintos tipos de problemas.
4. Adaptabilidad a diferentes tareas.
5. Potencial de mejora.
Así pues, el ANS es un algoritmo de optimización sencillo pero eficiente que muestra resultados competitivos en una amplia gama de problemas y tiene potencial para seguir desarrollándose.
Ventajas e inconvenientes generales del algoritmo de búsqueda por vecindad (ANS):
Ventajas:
- Buena convergencia en varios tipos de funciones.
- Muy rápido.
- Implementación sencilla.
- Excelente escalabilidad.
Desventajas:
- A veces se atasca en los extremos locales.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15049
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Redes neuronales en el trading: Representación lineal por partes de series temporales
Redes neuronales en el trading: Representación lineal por partes de series temporales
 Creación de un modelo de restricción de tendencia de velas (Parte 6): Integración todo en uno
Creación de un modelo de restricción de tendencia de velas (Parte 6): Integración todo en uno
 Combinación de estrategias de análisis técnico y fundamental en MQL5 para principiantes
Combinación de estrategias de análisis técnico y fundamental en MQL5 para principiantes
 Redes neuronales: así de sencillo (Parte 97): Entrenamiento de un modelo con el MSFformer
Redes neuronales: así de sencillo (Parte 97): Entrenamiento de un modelo con el MSFformer
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso