MetaTrader 5 / Probador
English Русский Deutsch Português
preview
Optimización del modelo de nubes atmosféricas — Atmosphere Clouds Model Optimization (ACMO): Práctica

Optimización del modelo de nubes atmosféricas — Atmosphere Clouds Model Optimization (ACMO): Práctica

MetaTrader 5 — Probador | 13 mayo 2025, 08:18
130 0
Andrey Dik
Andrey Dik

Contenido

  1. Introducción
  2. Implementación del algoritmo
  3. Resultados de las pruebas


Introducción

En el mundo de la ciencia, donde la tecnología y la naturaleza se entrecruzan, surgió hace una década la idea única del algoritmo metaheurístico ACMO (Atmospheric Cloud Model Optimisation) para la optimización de problemas complejos. En el artículo anterior, deconstruimos técnicamente la implementación de un algoritmo que modela el proceso de formación y movimiento de las nubes en la atmósfera en función de diversos parámetros meteorológicos. Qué se hizo en la primera parte: creamos una clase para gestionar el modelado de las nubes que contiene métodos para la inicialización, el movimiento de las nubes, la actualización de las propiedades de las regiones y otros procesos.

Dividimos el espacio de búsqueda en regiones. Asimismo, establecimos los valores de humedad y presión iniciales en estas regiones, y fijamos los parámetros del modelo como: entropía inicial, hiperentropía, umbral de humedad para la formación de nubes y otros. El siguiente paso consistió en generar nubes seleccionando una zona con mucha humedad. Calculamos el centro de la nube, la entropía y la hiperentropía. Luego realizamos una actualización de los parámetros meteorológicos de humedad y presión en las regiones tras la generación de nubes. Después implementamos el movimiento de nubes hacia regiones de bajas presiones y actualizamos posteriormente las características de las nubes según su movimiento entre regiones, además de la dispersión de las nubes. 

¿Qué queda por hacer? Pues implementar las funciones para aleatorizar la colocación de las gotas y su distribución entre las nubes; finalizar el proceso de lluvia y actualizar la solución global; probar el modelo de nuestras funciones de prueba con distintos parámetros para evaluar su rendimiento y precisión; y modificar el proceso de formación de lluvia y gotas para realizar un intercambio de información más completo en la población sobre las regiones prometedoras.


Implementación del algoritmo

Describiremos el proceso meteorológico completo en forma de pseudocódigo; esto nos permitirá construir la versión final del algoritmo basándonos en él:

1. En la primera época, la colocación aleatoria de las nubes:
   EnCk = EnM0;
   HeCk = HeM0;
//------------------------------------------------------------------------------
1.1 Desplazamiento de las nubes hacia regiones con menor presión:
   β = deltaP / normP
   d = Tck.x - Cck.c
   VC = β * d;
   Ck = Ck + VC

   cambio en el número de gotas después del movimiento:
   nk = nk × (1 - γ)

   cambio de entropía e hiperentropía:
   α = ΔP / ΔPmax;
   EnCk = EnCk * (1 + α)
   HeCk = HeCk * (1 - α)
//------------------------------------------------------------------------------
2. Proceso de la lluvia, caída de las gotas:
   la distribución de las gotas entre las nubes es proporcional a la humedad de la región
   aumento del número de gotas a las existentes en las nubes
//------------------------------------------------------------------------------
3. Cálculo de la función de aptitud para las gotas
//------------------------------------------------------------------------------
4. Actualización de la solución global y la presión mínima en las regiones donde se han producido caídas
//------------------------------------------------------------------------------
5. Comprobación de la disipación de nubes y creación de nuevas nubes en las regiones para sustituir a las que se han desintegrado, superiores al umbral:
   aquí tenemos la regla de decadencia debida a una expansión superior al valor admisible (estallido de nubes):
   En > 5 * EnM0_t
   regla de decaimiento con un contenido de humedad inferior al valor crítico (secado de la nube):
   dCk < dMin

   valor umbral por encima del cual las regiones pueden formar nubes:
   HT = H_min + λ * (H_max - H_min);
//------------------------------------------------------------------------------
6. Entropía e hiperentropía para el cálculo de nuevas nubes:
   En = EnM0 / (1 + 2.72 ^ (-(8 - 16 * (t / maxT))))
   He = HeM0 / (1 + 2.72 ^ ((8 - 16 * (t / maxT))))

Bien, vamos a continuar. Ahora analizaremos el método "Moving" de la clase "C_AO_ACMO". El método realiza dos operaciones: "MoveClouds (revision)" es responsable de mover las nubes, "RainProcess (revision)" gestiona el proceso de la lluvia, que depende del estado de las nubes así como del parámetro "revision". El métodoMoving efectúa dos acciones principales relacionadas con la dinámica de las nubes y el proceso de lluvia. Este encapsula la lógica del movimiento de las nubes y su interacción con el proceso de lluvia. Así, el métodoMoving se usa para actualizar las condiciones de nubes y la lluvia dentro de una simulación meteorológica.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::Moving ()
{
  MoveClouds       (revision);
  RainProcess      (revision);
}
//——————————————————————————————————————————————————————————————————————————————

Vamos a analizar con detalle el siguiente método "MoveClouds" de la clase "C_AO_ACMO":

1. Primer bloque (si "rev" es "false"), el método crea nubes con centros aleatorios. Para cada nube y cada coordenada:

  • Se genera un valor aleatorio del centro de la nube dentro de los rangos indicados (función "RNDfromCI").
  • El centro se corrige con "SeInDiSp" para normalizar los valores.
  • El índice de la región en la que se encuentra la nube se determina con ayuda de "GetRegionIndex".
  • Luego se establecen los valores de entropía y entropía inicial de la nube.
  • Y se establece el valor inicial de hiperentropía "hyperEntropy".
El método finaliza su ejecución.

2. Segundo bloque (si "rev" es "true"):

  • Si "rev" es "true", el método empezará a buscar regiones con la presión más baja.
  • Luego se crean arrays para almacenar los índices de las regiones con menor humedad "lHind" y para la normalización de la presión "normP".

3. Ciclo para encontrar la región con la presión más baja:

  • Para cada coordenada "c", determinamos la presión mínima y máxima entre todas las regiones.
  • El índice de la región con la presión más baja se almacena en el array "lHind".
  • La presión normalizada para cada coordenada se guarda en "normP".

5. Nubes móviles para cada uno de ellas y cada coordenada:

  • Si la nube ya se encuentra en la región de presión más baja, se saltará una iteración.
  • Luego se selecciona una región objetivo aleatoria con menor presión.
  • Y se calcula la diferencia de presión entre la región actual y la región objetivo.
  • El valor de la presión se normaliza y se calcula la velocidad de desplazamiento de la nube "VC".
  • El centro de la nube se actualiza con la velocidad de movimiento.
  • Y se actualiza el índice de la región.
  • La entropía de la nube se actualiza considerando el cambio de presión.
  • Después se reduce la cantidad de humedad en la nube y se actualiza la hiperentropía, limitando su valor a un valor máximo de 8.

El método "MoveClouds" se encarga de desplazar las nubes a regiones con menor presión, actualizando sus parámetros como la entropía y la hiperentropía. El método aplica un modelo dinámico que muestra los cambios en la atmósfera.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::MoveClouds (bool &rev)
{
  //----------------------------------------------------------------------------
  if (!rev)
  {
    //creating clouds with random centers---------------------------------------
    for (int i = 0; i < cloudsNumber; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        clouds [i].center [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        clouds [i].center [c] = u.SeInDiSp  (clouds [i].center [c], rangeMin [c], rangeMax [c], rangeStep [c]);

        clouds [i].regionIndex [c] = GetRegionIndex (clouds [i].center [c], c);

        clouds [i].entropy      [c] = entropy [c] * EnM0;
        clouds [i].entropyStart [c] = clouds [i].entropy [c];
      }

      clouds [i].hyperEntropy = HeM0;
    }

    return;
  }

  //search for the region with the lowest pressure------------------------------
  int targetRegion = 0;

  int lHind []; //lowest humidity index
  ArrayResize     (lHind, coords);
  ArrayInitialize (lHind, 0);

  double normP [];
  ArrayResize (normP, coords);
  double minP;
  double maxP;

  for (int c = 0; c < coords; c++)
  {
    minP =  DBL_MAX;
    maxP = -DBL_MAX;

    for (int r = 0; r < regionsNumber; r++)
    {
      if (areas [c].regions [r].pressure < areas [c].regions [lHind [c]].pressure)
      {
        lHind [c] = r;
      }

      if (areas [c].regions [r].pressure < minP) minP = areas [c].regions [r].pressure;
      if (areas [c].regions [r].pressure > maxP) maxP = areas [c].regions [r].pressure;
    }

    normP [c] = maxP - minP;
  }

  //moving the cloud to a region with less pressure-----------------------------
  int    clRegIND = 0;
  double deltaP   = 0.0;
  double α        = 0.0; // Entropy factor
  double β        = 0.0; // Atmospheric pressure factor
  double VC       = 0.0; // Cloud velocity
  double d        = 0.0; // Cloud direction

  for (int i = 0; i < cloudsNumber; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      //find a region with lower pressure---------------------------------------
      if (clouds [i].regionIndex [c] == lHind [c]) continue;

      clRegIND = clouds [i].regionIndex [c];

      do targetRegion = u.RNDminusOne (regionsNumber);
      while (areas [c].regions [clRegIND].pressure < areas [c].regions [targetRegion].pressure);

      //------------------------------------------------------------------------
      deltaP = areas [c].regions [clRegIND].pressure - areas [c].regions [targetRegion].pressure;

      β = deltaP / normP [c];
      d = areas [c].regions [targetRegion].x - areas [c].regions [clRegIND].centre;

      VC = β * d;

      clouds [i].center      [c] += VC;
      clouds [i].center      [c] = u.SeInDiSp (clouds [i].center [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      clouds [i].regionIndex [c] = GetRegionIndex (clouds [i].center [c], c);

      α = β;
      clouds [i].entropy [c] *=(1 + α);
    }

    clouds [i].droplets     *=(1 - γ);
    clouds [i].hyperEntropy *=(1 + α);
    if (clouds [i].hyperEntropy > 8) clouds [i].hyperEntropy = 8;
  }
}
//——————————————————————————————————————————————————————————————————————————————

A continuación, analizaremos el método "GetRegionIndex" de la clase "C_AO_ACMO". Descripción del método:

1. Cálculo de la posición de la región. Se realiza el cálculo del índice de la región "regPos" donde se encuentra el punto dado "point" y se redondea hacia abajo al entero más cercano utilizando la función "floor".
2. Comprobación de los límites. Este bloque comprueba si el índice calculado "regPos" no supera los valores permitidos (es decir, no debe superar el número de regiones permitido).
3. El método retorna el índice de la región en la que se encuentra el punto.

El método "GetRegionIndex" está diseñado para determinar el índice de la región en la que se encuentra el punto indicado dentro de un rango determinado. Este tiene en cuenta el número de regiones y procesa correctamente los casos en los que un punto se encuentra en el límite del intervalo. 

//——————————————————————————————————————————————————————————————————————————————
int C_AO_ACMO::GetRegionIndex (double point, int ind)
{
  int regPos = (int)floor ((point - rangeMin [ind]) / ((rangeMax [ind] - rangeMin [ind]) / regionsNumber));

  if (regPos >= regionsNumber) regPos = regionsNumber - 1;

  return regPos;
}
//——————————————————————————————————————————————————————————————————————————————

Vamos a describir ahora el siguiente método "RainProcess" de la clase "C_AO_ACMO":

2. Inicialización de arrays:

  • Se crean dos arrays: "cloud" para almacenar los valores de las nubes y "drops" para almacenar el número de gotas de lluvia de cada nube.
  • Ambos arrays varían de tamaño en función del número de nubes "cloudsNumber".

3. Inicialización del array "cloud":

  • Si "rev" es "false", todos los elementos del array "cloud" se inicializarán con el valor "1.0".
  • En caso contrario, el array "cloud" se inicializará con el valor "0,0" y, a continuación, se calculará la humedad de cada nube.

4. Cálculo de la humedad:

  • Para cada nube y cada coordenada, se calcula la humedad concreta de la región.
  • Si la humedad no es igual a "-DBL_MAX", se añadirá al elemento correspondiente del array "cloud". En caso contrario, se añadirá el valor mínimo de caída "minGp".

5. Distribución de las gotas:

  • Llamada del método "DropletsDistribution" para distribuir las gotas en función de los valores del array "cloud".

6. Ciclo básico de procesamiento de gotas, para cada nube y cada gota:

  • Se calculan los valores "dist", "centre", "xMin", "xMax".
  • Se genera un valor "x" utilizando una distribución normal (gaussiana).
  • Si "x" está fuera de rango, se corregirá con el método "RNDdeCI".
  • El valor de "x" se normaliza usando el método "SeInDiSp" y se almacena en el array "a".

Una vez procesados todos las gotas de una nube, se actualizará el número total de gotas de la nube. Así, el método "RainProcess" modela el proceso de la lluvia que cae de las nubes considerando la humedad y la distribución de las gotas. Inicializa los arrays, calcula la humedad de cada nube, distribuye las gotas de lluvia y genera valores para cada gota dada una distribución normal. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::RainProcess (bool &rev)
{
  //to shed drops from every cloud----------------------------------------------
  double cloud [];
  int    drops [];
  ArrayResize (cloud, cloudsNumber);
  ArrayResize (drops, cloudsNumber);

  if (!rev)
  {
    ArrayInitialize (cloud, 1.0);
  }
  else
  {
    ArrayInitialize (cloud, 0.0);

    double humidity;

    for (int i = 0; i < cloudsNumber; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        for (int r = 0; r < regionsNumber; r++)
        {
          humidity = areas [c].regions [clouds [i].regionIndex [r]].humidity;
          if (humidity != -DBL_MAX) cloud [i] += humidity;
          else                      cloud [i] += minGp;
        }
      }
    }
  }

  DropletsDistribution (cloud, drops);

  double dist   = 0.0;
  double centre = 0.0;
  double xMin   = 0.0;
  double xMax   = 0.0;
  double x      = 0.0;
  int    dCNT   = 0;

  for (int i = 0; i < cloudsNumber; i++)
  {
    for (int dr = 0; dr < drops [i]; dr++)
    {
      for (int c = 0; c < coords; c++)
      {
        dist   = clouds [i].entropy [c];
        centre = clouds [i].center  [c];
        xMin   = centre - dist;
        xMax   = centre + dist;

        x = u.GaussDistribution (centre, xMin, xMax, clouds [i].hyperEntropy);

        if (x < rangeMin [c]) x = u.RNDfromCI (rangeMin [c], centre);
        if (x > rangeMax [c]) x = u.RNDfromCI (centre, rangeMax [c]);

        x = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);

        a [dCNT].c [c] = x;
      }

      dCNT++;
    }

    clouds [i].droplets += drops [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————

El siguiente método "DropletsDistribution" de la clase "C_AO_ACMO" está diseñado para distribuir las gotas de lluvia entre las nubes según su humedad. Veámoslo paso a paso.

2. Inicialización de variables:

  • minHumidity- se inicializa con el valor máximo para poder encontrar la humedad mínima.
  • indMinHumidity- almacena el índice de la nube con humedad mínima.
  • totalHumidity- se utiliza para almacenar la suma de la humedad de todas las nubes.

3. Suma de humedad: este ciclo suma la humedad de todas las nubes e identifica la nube con la humedad mínima.

4. Distribución proporcional de las gotas: para cada nube, se calcula un número de gotas proporcional a su humedad en relación con la humedad total. Este valor se almacena en el array "droplets".

5. Distribución de las gotas restantes:

  • En primer lugar, se calcula el número total de gotas distribuidas "totalDrops".
  • Luego se calcula el número de gotas restantes "remainingDrops".
  • Si quedan gotas, se añaden a la nube con un mínimo de humedad.

El método "DropletsDistribution" distribuye de forma eficaz las gotas de lluvia entre las nubes según su contenido de humedad. Primero distribuye las gotas de manera proporcional y luego corrige la distribución añadiendo las gotas restantes a la nube con la humedad más baja. Esto permite una simulación más realista del proceso de precipitación, manteniendo un número constante de gotas que se corresponda con el tamaño de la población en los parámetros externos del algoritmo.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::DropletsDistribution (double &cloud [], int &droplets [])
{
  double minHumidity    = DBL_MAX;
  int    indMinHumidity = -1;
  double totalHumidity  = 0; //total amount of humidity in all clouds

  for (int i = 0; i < ArraySize (cloud); i++)
  {
    totalHumidity += cloud [i];

    if (cloud [i] < minHumidity)
    {
      minHumidity = cloud [i];
      indMinHumidity = i;
    }
  }

  // Filling the droplets array in proportion to the value in clouds
  for (int i = 0; i < ArraySize (clouds); i++)
  {
    droplets [i] = int((cloud [i] / totalHumidity)*popSize); //proportional distribution of droplets
  }

  // Distribute the remaining drops, if any
  int totalDrops = 0;

  for (int i = 0; i < ArraySize (droplets); i++)
  {
    totalDrops += droplets [i];
  }

  // If not all drops are distributed, add the remaining drops to the element with the lowest humidity
  int remainingDrops = popSize - totalDrops;

  if (remainingDrops > 0)
  {
    droplets [indMinHumidity] += remainingDrops; //add the remaining drops to the lightest cloud
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "Revision" de la clase "C_AO_ACMO" realiza la actualización del estado del sistema. Echemos un vistazo al método más de cerca:

1. Ciclo por los elementos del array "a" (población de agentes de optimización). Este ciclo itera a través de todos los elementos del array "a" de tamaño "popSize":

  • Si el valor de adaptación "f" del elemento actual es mayor que el valor de adaptación máximo actual "fB", "fB" se actualizará y el índice "ind" se establecerá en el índice actual.
  • También se realiza la búsqueda del valor mínimo de adaptabilidad "f" entre todos los elementos del array, y si el valor actual es inferior a "minGp", entonces se actualizará "minGp".

2. Copiado de datos: si se ha encontrado un elemento con el máximo valor de aptitud "f" (es decir, "ind" no es igual a -1), los datos se copiarán del array "c" del elemento "a [ind]" al array "cB".

3. Actualización de las propiedades de la región: se llama al método "UpdateRegionProperties", que actualiza los parámetros de humedad y presión de las distintas regiones.

4. Generación de nubes: se llama al método "GenerateClouds", que hace desaparecer nubes antiguas y crea otras nuevas.

5. Actualización de la situación:

  • La bandera "revision" se establece en "true", indicando que el estado inicial del sistema ha pasado.
  • Se aumenta el contador "epochNow" para registrar el número de épocas.

El método "Revision" se encarga de actualizar el estado del sistema relacionado con la nube. Encuentra el valor máximo de adaptación "f", actualiza los parámetros pertinentes, inicializa nuevas nubes y actualiza las propiedades de las regiones. Este método es clave para mantener actualizados los datos del modelo, lo cual permite al sistema adaptarse a los cambios.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }

    if (a [i].f < minGp) minGp = a [i].f;
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  UpdateRegionProperties (); //updating humidity and pressure in the regions
  GenerateClouds         (); //disappearance of clouds and the creation of new ones

  revision = true;
  epochNow++;
}
//——————————————————————————————————————————————————————————————————————————————

El método "GenerateClouds" de la clase "C_AO_ACMO" crea nubes y gestiona su estado según diversos factores como la humedad y la entropía. Descripción del método:

1. Cálculo del umbral de humedad: se llama a la función "CalculateHumidityThreshold", que retorna el valor del umbral de humedad necesario para la formación de nubes.

2. Estructura para almacenar los índices de las regiones:

  • Se define una estructura "S_Areas" que contiene un array con los índices de las regiones capaces de formar nubes. 
  • El array "ar" se inicializa con un tamaño igual al número de coordenadas "coords".

3. Recopilación de información de la región: en este doble ciclo, cada región se compara con el umbral de humedad. Si la humedad de una región es superior al umbral, el índice de esa región se añadirá al array "regsIND" de la estructura "S_Areas" correspondiente.

4. Verificación de las condiciones de ruptura de las nubes:

  • Para cada nube, se comprueba si su entropía no supera un determinado límite (5 veces la entropía inicial). De ser así, se considerará que la nube se ha desintegrado.
  • A continuación, se comprueba si la cantidad de humedad en la nube es inferior al valor mínimo "dMin", lo cual también puede provocar la disipación de la nube.

5. Creación de una nueva nube en las regiones más húmedas:

  • Si la nube ha desaparecido, se creará una nueva nube en una de las regiones más húmedas. Para cada coordenada, se selecciona aleatoriamente un índice de región y la nube obtiene las nuevas coordenadas centrales y el índice de la región.
  • A continuación, se llama a la función "CalculateNewEntropy", que recalcula la entropía basada en la época actual para la nueva nube.

El método GenerateClouds gestiona la creación y disipación de las nubes en función de la humedad y la entropía. Recopila información sobre las regiones susceptibles de formar nubes, comprueba que las nubes existentes no se disipen y crea nuevas nubes en las regiones adecuadas. Este método resulta clave para controlar dinámicamente el estado de las nubes en el modelo.                                                                                                                                                    

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::GenerateClouds ()
{
  //Collecting statistics of regions capable of creating clouds-----------------
  double Ht = CalculateHumidityThreshold ();

  struct S_Areas
  {
      int regsIND []; //index of the potential region
  };

  S_Areas ar [];
  ArrayResize (ar, coords);

  int sizePr = 0;

  for (int i = 0; i < coords; i++)
  {
    for (int r = 0; r < regionsNumber; r++)
    {
      if (areas [i].regions [r].humidity > Ht)
      {
        sizePr = ArraySize (ar [i].regsIND);
        sizePr++;
        ArrayResize (ar [i].regsIND, sizePr, coords);
        ar [i].regsIND [sizePr - 1] = r;
      }
    }
  }

  //Check the conditions for cloud decay----------------------------------------
  bool   cloudDecay = false;

  for (int i = 0; i < cloudsNumber; i++)
  {
    cloudDecay = false;

    //checking the cloud for too much entropy-----------------------------------
    for (int c = 0; c < coords; c++)
    {
      if (clouds [i].entropy [c] > 5.0 * clouds [i].entropyStart [c])
      {
        //Print ("Disintegration of cloud #", i, " - tore at epoch ", epochNow);
        cloudDecay = true;
        break;
      }
    }

    //checking the cloud for decay----------------------------------------------
    if (!cloudDecay)
    {
      if (clouds [i].droplets < dMin)
      {
        //Print ("Disintegration of cloud #", i, " - dried up at epoch ", epochNow);
        cloudDecay = true;
      }
    }

    //if the cloud has decayed--------------------------------------------------
    int regIND = 0;

    if (cloudDecay)
    {
      //creating a cloud in a very humid region---------------------------------
      for (int c = 0; c < coords; c++)
      {
        regIND = u.RNDminusOne (ArraySize (ar [c].regsIND));
        regIND = ar [c].regsIND [regIND];

        clouds [i].center      [c] = areas [c].regions [regIND].x;
        clouds [i].regionIndex [c] = regIND;
      }

      CalculateNewEntropy (clouds [i], epochNow);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "CalculateHumidityThreshold" de la clase "C_AO_ACMO" se ocupa de calcular el umbral de humedad necesario para la formación de nubes. Aquí tenemos los pasos con mayor detalle:

1. Doble ciclo para encontrar la humedad mínima. El ciclo exterior itera todas las coordenadas "coords", mientras que el ciclo interior itera todas las regiones "regionsNumber" de cada coordenada. Si la humedad de la región no es igual a "-DBL_MAX", se realizará una comprobación: si la humedad actual es inferior a "H_min" actual, se actualizará "H_min".

2. El método retorna un valor que representa "H_min" incrementado por el producto de "λ" y la diferencia entre "H_max" y "H_min", que es el umbral de humedad necesario para la formación de nubes.

El método "CalculateHumidityThreshold" calcula el umbral de humedad a partir de la humedad mínima entre todas las regiones y lo ajusta considerando la humedad máxima y el coeficiente "λ". Esto permite determinar en qué condiciones resulta posible la formación de nubes según las condiciones ambientales.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_ACMO::CalculateHumidityThreshold ()
{
  double H_max = fB;
  double H_min = DBL_MAX;

  for (int c = 0; c < coords; c++)
  {
    for (int r = 0; r < regionsNumber; r++)
    {
      if (areas [c].regions [r].humidity != -DBL_MAX)
      {
        if (areas [c].regions [r].humidity < H_min)
        {
          H_min = areas [c].regions [r].humidity;
        }
      }
    }
  }

  return H_min + λ * (H_max - H_min);
}
//——————————————————————————————————————————————————————————————————————————————

El método "CalculateNewEntropy" de la clase "C_AO_ACMO" calcula la nueva entropía e hiperentropía de las nubes representadas por la estructura "S_ACMO_Cloud". Vamos a analizarlo:

1. Cálculo de la entropía:

  • El ciclo itera por todas las coordenadas "coords".
  • Para cada coordenada, se calcula un nuevo valor de entropía "cl.entropy [c]" mediante la fórmula: En = (entropy [c] * EnM0) / (1 + e ^ (-(8 - 16 * (t / epochs)))).
  • cl.entropyStart [c] y cl.entropy [c] se inicializan con el valor "entropy [c]", que sirve para almacenar el valor inicial de entropía.

2. Cálculo de la hiperentropía: He = 1 / (1 + e ^ (8 - 16 * (t / epochs))).

3. La hiperentropía se escala usando el método "Scale" del objeto "u", que escala el valor de la hiperentropía a un rango determinado (0 a 8) utilizando los parámetros "HeM0" y 8.0.

El método "CalculateNewEntropy" actualiza los valores de entropía e hiperentropía de las nubes según el tiempo actual "t" y los parámetros dados. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::CalculateNewEntropy (S_ACMO_Cloud &cl, int t)
{
  //----------------------------------------------------------------------------
  //En: 1/(1+2.72^(-(8-16*(t/maxT))))
  for (int c = 0; c < coords; c++)
  {
    cl.entropy      [c] = entropy [c] * EnM0 / (1.0 + pow (M_E, (-(8.0 - 16.0 * (t / epochs)))));
    cl.entropyStart [c] = cl.entropy [c] = entropy [c];
  }

  //----------------------------------------------------------------------------
  //He: 1/(1+2.72^((8-16*(t/maxT))))
  cl.hyperEntropy = 1.0 / (1.0 + pow (M_E, ((8.0 - 16.0 * (t / epochs)))));

  cl.hyperEntropy = u.Scale (cl.hyperEntropy, 0.0, 8.0, HeM0, 8.0);
}
//——————————————————————————————————————————————————————————————————————————————

En and He 2

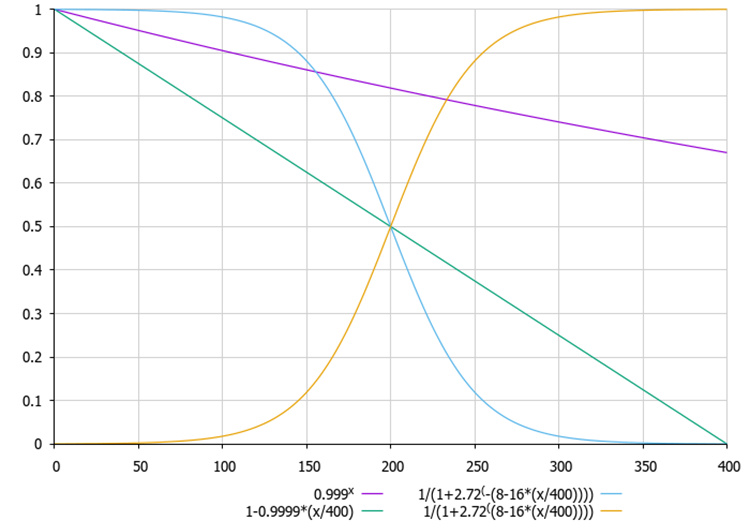
Figura 1. Opciones de fórmula para calcular el coeficiente ζ según la época actual. Podemos seleccionar una fórmula y probar el algoritmo con cada una de ellas (las líneas están comentadas en el código).


Resultados de las pruebas

Vamos a probar el algoritmo. El modelo meteorológico de formación de nubes concebido por los autores funciona de la forma que sigue:

//original version
ACMO|Atmospheric Cloud Model Optimization|50.0|5.0|10.0|0.2|5.0|5.0|0.9|0.2|
=============================
5 Hilly's; Func runs: 10000; result: 0.6017884495404766
25 Hilly's; Func runs: 10000; result: 0.3426222382089618
500 Hilly's; Func runs: 10000; result: 0.2526410178225118
=============================
5 Forest's; Func runs: 10000; result: 0.4780554376190664
25 Forest's; Func runs: 10000; result: 0.261057831391174
500 Forest's; Func runs: 10000; result: 0.17318135866144563
=============================
5 Megacity's; Func runs: 10000; result: 0.3507692307692307
25 Megacity's; Func runs: 10000; result: 0.16153846153846158
500 Megacity's; Func runs: 10000; result: 0.09632307692307775
=============================
All score: 2.71798 (30.20%)

Por desgracia, los resultados son mucho más bajos de lo esperado. Creo que a pesar del hermoso modelo del principio de formación de nubes con tantas fórmulas diferentes y acciones lógicas para evitar quedarse atascado en los extremos, la convergencia del algoritmo muestra una baja convergencia. El algoritmo carece de interacción directa e intercambio de información entre los agentes de las mejores soluciones, cuya presencia suele suponer una mejora en el rendimiento de la búsqueda de cualquier algoritmo. Como resultado, he decidido añadir el intercambio de información mediante la transferencia probabilística de información de las mejores gotas a las peores. Ahora veamos cómo ha resultado:

ACMOm|Atmospheric Cloud Model Optimization|50.0|4.0|10.0|0.2|0.2|2.0|0.9|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.9032099148349984
25 Hilly's; Func runs: 10000; result: 0.48545807643133143
500 Hilly's; Func runs: 10000; result: 0.30403284557071203
=============================
5 Forest's; Func runs: 10000; result: 0.8026793420899985
25 Forest's; Func runs: 10000; result: 0.3785708322859447
500 Forest's; Func runs: 10000; result: 0.1917777390119122
=============================
5 Megacity's; Func runs: 10000; result: 0.6230769230769231
25 Megacity's; Func runs: 10000; result: 0.244
500 Megacity's; Func runs: 10000; result: 0.10795384615384714
=============================
All score: 4.04076 (44.90%)

Los resultados han mejorado espectacularmente. Así que la idea ha tenido éxito. La idea consiste en transferir información sobre la mejor solución con cierta probabilidad a gotas de nubes desde otras gotas si tienen mayor humedad (en el contexto del algoritmo, esto significa adaptabilidad). 

Al final, para cada nube, se actualiza el número total de gotas (para una nube, se trata de una medida de humedad) caídas desde ella añadiendo el valor correspondiente del array "drops". El método "RainProcess" implementa un mecanismo que modela el proceso de lluvia considerando la humedad, la distribución de las gotas y la interacción de la población. La ubicación de los cambios de código aparece resaltada en verde.

Para cada valor generado "x", se selecciona un índice aleatorio "p" de la población. Según la probabilidad (95%), se produce una actualización de los valores del array "a", que supone una población o conjunto de soluciones. Al final, para cada nube, se actualiza el número total de gotas arrojadas desde ella añadiendo el valor correspondiente del array "drops".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::RainProcess (bool &rev)
{
  //to shed drops from every cloud----------------------------------------------
  double cloud [];
  int    drops [];
  ArrayResize (cloud, cloudsNumber);
  ArrayResize (drops, cloudsNumber);

  if (!rev)
  {
    ArrayInitialize (cloud, 1.0);
  }
  else
  {
    ArrayInitialize (cloud, 0.0);

    double humidity;

    for (int i = 0; i < cloudsNumber; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        humidity = areas [c].regions [clouds [i].regionIndex [c]].humidity;
       
        if (humidity != -DBL_MAX) cloud [i] += humidity;

        else                      cloud [i] += minGp;
      }
    }
  }

  DropletsDistribution (cloud, drops);
  //ArrayPrint (drops);

  double dist   = 0.0;
  double centre = 0.0;
  double xMin   = 0.0;
  double xMax   = 0.0;
  double x      = 0.0;

  int    dCNT   = 0;


  for (int i = 0; i < cloudsNumber; i++)
  {
    for (int dr = 0; dr < drops [i]; dr++)
    {
      for (int c = 0; c < coords; c++)
      {
        dist   = clouds [i].entropy [c];
        centre = clouds [i].center  [c];
        xMin   = centre - dist;
        xMax   = centre + dist;

        x = u.GaussDistribution (centre, xMin, xMax, clouds [i].hyperEntropy);

        if (x < rangeMin [c]) x = u.RNDfromCI (rangeMin [c], centre);
        
        if (x > rangeMax [c]) x = u.RNDfromCI (centre, rangeMax [c]);

        x = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);

        int p = u.RNDminusOne (popSize);

        if (a [p].f > a [dCNT].f)
        {
          if (u.RNDprobab () < 0.95) a [dCNT].c [c] = a [p].c [c];
        }

        else
        {
          a [dCNT].c [c] = x;
        }
      }
      dCNT++;
    }

    clouds [i].droplets += drops [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————

En la visualización del funcionamiento del algoritmo podemos ver lo siguiente: buena convergencia del algoritmo; las largas áreas suaves en el gráfico de convergencia con un pequeño número de parámetros optimizados indican cierta tendencia a quedarse atascado en extremos locales, pero con un aumento en el número de parámetros esta desventaja quedará en nada.

Las nubes de la visualización aparecen como cúmulos densos, pero seleccionando otros ajustes de los parámetros externos (número de regiones, nubes, entropía inicial y umbral de secado), podemos imitar el aspecto de nubes flotantes en el cielo, como en la naturaleza viva.

Hilly

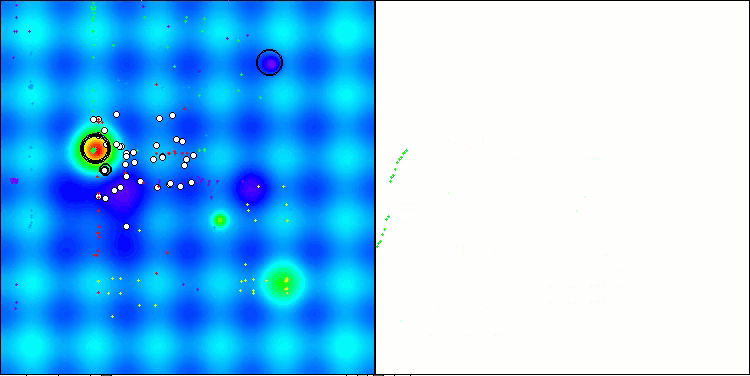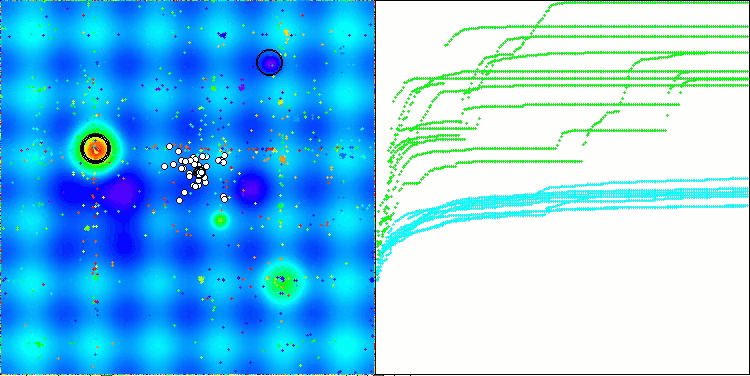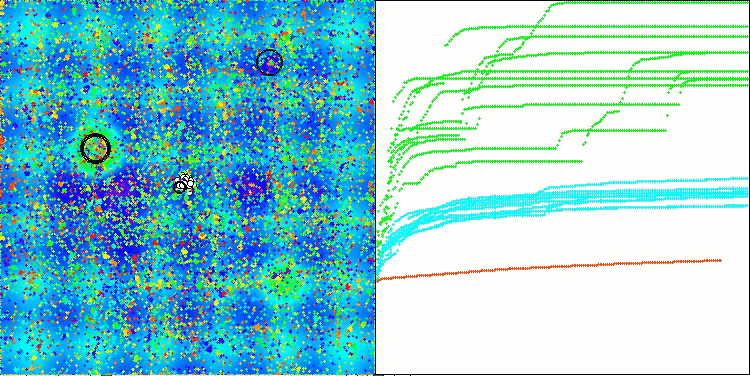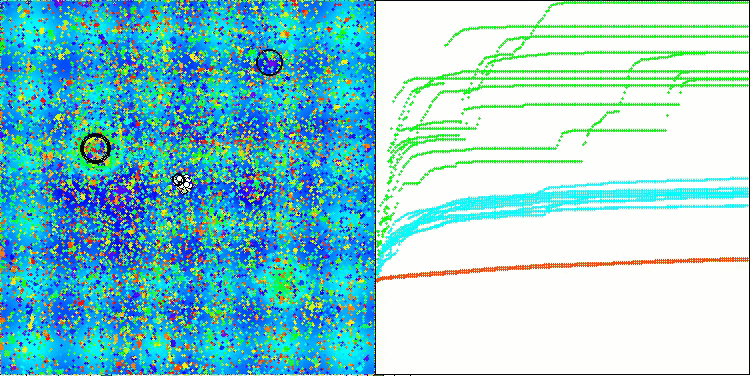
OMAPE en la función de prueba Hilly

Forest

ACMO en la función de prueba Forest

Megacity

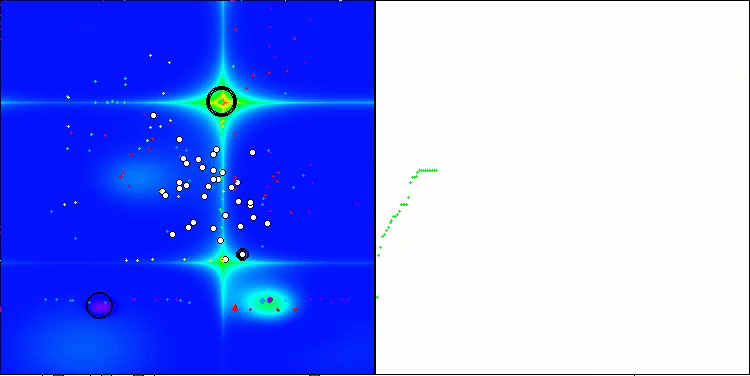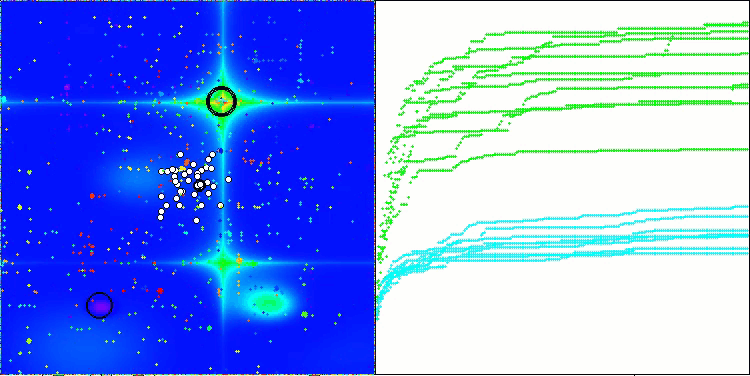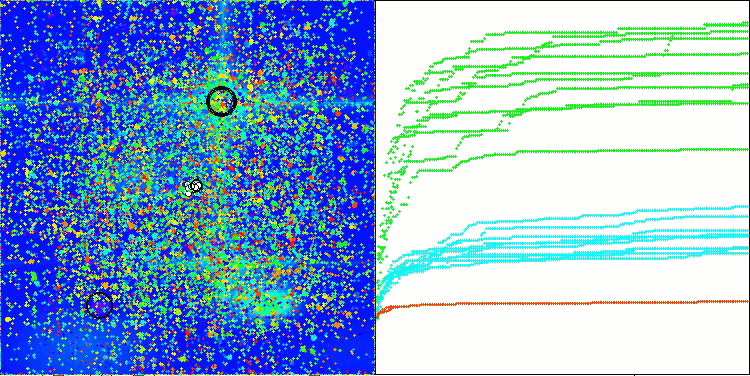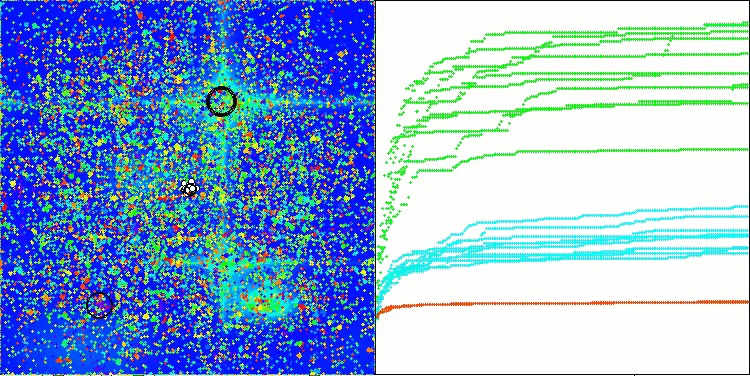
ACMO en la función de prueba Megacity

Según los resultados de las pruebas de la versión modificada, el algoritmo ocupa el puesto 27, lo cual supone un indicador bastante estable. Me gustaría destacar que la tabla contiene ahora siempre 45 algoritmos y, en realidad, con cada nuevo algoritmo la diferencia entre el anterior y el siguiente disminuirá gradualmente, por lo que podemos decir que la tabla representa la cima de lo mejor de todos los algoritmos conocidos. 

№ AO Description Hilly Hilly final Forest Forest final Megacity (discrete) Megacity final Final result % de MAX
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 ANS across neighbourhood search 0,94948 0,84776 0,43857 2,23581 1,00000 0,92334 0,39988 2,32323 0,70923 0,63477 0,23091 1,57491 6,134 68,15
2 CLA code lock algorithm 0,95345 0,87107 0,37590 2,20042 0,98942 0,91709 0,31642 2,22294 0,79692 0,69385 0,19303 1,68380 6,107 67,86
3 AMOm animal migration optimization M 0,90358 0,84317 0,46284 2,20959 0,99001 0,92436 0,46598 2,38034 0,56769 0,59132 0,23773 1,39675 5,987 66,52
4 (P+O)ES (P+O) evolution strategies 0,92256 0,88101 0,40021 2,20379 0,97750 0,87490 0,31945 2,17185 0,67385 0,62985 0,18634 1,49003 5,866 65,17
5 CTA comet tail algorithm 0,95346 0,86319 0,27770 2,09435 0,99794 0,85740 0,33949 2,19484 0,88769 0,56431 0,10512 1,55712 5,846 64,96
6 SDSm stochastic diffusion search M 0,93066 0,85445 0,39476 2,17988 0,99983 0,89244 0,19619 2,08846 0,72333 0,61100 0,10670 1,44103 5,709 63,44
7 AAm archery algorithm M 0,91744 0,70876 0,42160 2,04780 0,92527 0,75802 0,35328 2,03657 0,67385 0,55200 0,23738 1,46323 5,548 61,64
8 ESG evolution of social groups 0,99906 0,79654 0,35056 2,14616 1,00000 0,82863 0,13102 1,95965 0,82333 0,55300 0,04725 1,42358 5,529 61,44
9 SIA simulated isotropic annealing 0,95784 0,84264 0,41465 2,21513 0,98239 0,79586 0,20507 1,98332 0,68667 0,49300 0,09053 1,27020 5,469 60,76
10 ACS artificial cooperative search 0,75547 0,74744 0,30407 1,80698 1,00000 0,88861 0,22413 2,11274 0,69077 0,48185 0,13322 1,30583 5,226 58,06
11 ASO anarchy society optimization 0,84872 0,74646 0,31465 1,90983 0,96148 0,79150 0,23803 1,99101 0,57077 0,54062 0,16614 1,27752 5,178 57,54
12 TSEA turtle shell evolution algorithm 0,96798 0,64480 0,29672 1,90949 0,99449 0,61981 0,22708 1,84139 0,69077 0,42646 0,13598 1,25322 5,004 55,60
13 DE differential evolution 0,95044 0,61674 0,30308 1,87026 0,95317 0,78896 0,16652 1,90865 0,78667 0,36033 0,02953 1,17653 4,955 55,06
14 CRO chemical reaction optimisation 0,94629 0,66112 0,29853 1,90593 0,87906 0,58422 0,21146 1,67473 0,75846 0,42646 0,12686 1,31178 4,892 54,36
15 BSA bird swarm algorithm 0,89306 0,64900 0,26250 1,80455 0,92420 0,71121 0,24939 1,88479 0,69385 0,32615 0,10012 1,12012 4,809 53,44
16 HS harmony search 0,86509 0,68782 0,32527 1,87818 0,99999 0,68002 0,09590 1,77592 0,62000 0,42267 0,05458 1,09725 4,751 52,79
17 SSG saplings sowing and growing 0,77839 0,64925 0,39543 1,82308 0,85973 0,62467 0,17429 1,65869 0,64667 0,44133 0,10598 1,19398 4,676 51,95
18 BCOm bacterial chemotaxis optimization M 0,75953 0,62268 0,31483 1,69704 0,89378 0,61339 0,22542 1,73259 0,65385 0,42092 0,14435 1,21912 4,649 51,65
19 (PO)ES (PO) evolution strategies 0,79025 0,62647 0,42935 1,84606 0,87616 0,60943 0,19591 1,68151 0,59000 0,37933 0,11322 1,08255 4,610 51,22
20 TSm tabu search M 0,87795 0,61431 0,29104 1,78330 0,92885 0,51844 0,19054 1,63783 0,61077 0,38215 0,12157 1,11449 4,536 50,40
21 BSO brain storm optimization 0,93736 0,57616 0,29688 1,81041 0,93131 0,55866 0,23537 1,72534 0,55231 0,29077 0,11914 0,96222 4,498 49,98
22 WOAm wale optimization algorithm M 0,84521 0,56298 0,26263 1,67081 0,93100 0,52278 0,16365 1,61743 0,66308 0,41138 0,11357 1,18803 4,476 49,74
23 AEFA artificial electric field algorithm 0,87700 0,61753 0,25235 1,74688 0,92729 0,72698 0,18064 1,83490 0,66615 0,11631 0,09508 0,87754 4,459 49,55
24 ACOm ant colony optimization M 0,88190 0,66127 0,30377 1,84693 0,85873 0,58680 0,15051 1,59604 0,59667 0,37333 0,02472 0,99472 4,438 49,31
25 BFO-GA bacterial foraging optimization - ga 0,89150 0,55111 0,31529 1,75790 0,96982 0,39612 0,06305 1,42899 0,72667 0,27500 0,03525 1,03692 4,224 46,93
26 ABH artificial bee hive algorithm 0,84131 0,54227 0,26304 1,64663 0,87858 0,47779 0,17181 1,52818 0,50923 0,33877 0,10397 0,95197 4.127 45,85
27 ACMO atmospheric cloud model optimization 0,90321 0,48546 0,30403 1,69270 0,80268 0,37857 0,19178 1,37303 0,62308 0,24400 0,10795 0,97503 4,041 44,90
28 ASBO adaptive social behavior optimization 0,76331 0,49253 0,32619 1,58202 0,79546 0,40035 0,26097 1,45677 0,26462 0,17169 0,18200 0,61831 3.657 40,63
29 MEC mind evolutionary computation 0,69533 0,53376 0,32661 1,55569 0,72464 0,33036 0,07198 1,12698 0,52500 0,22000 0,04198 0,78698 3,470 38,55
30 IWO invasive weed optimization 0,72679 0,52256 0,33123 1,58058 0,70756 0,33955 0,07484 1,12196 0,42333 0,23067 0,04617 0,70017 3,403 37,81
31 Micro-AIS micro artificial immune system 0,79547 0,51922 0,30861 1,62330 0,72956 0,36879 0,09398 1,19233 0,37667 0,15867 0,02802 0,56335 3,379 37,54
32 COAm cuckoo optimization algorithm M 0,75820 0,48652 0,31369 1,55841 0,74054 0,28051 0,05599 1,07704 0,50500 0,17467 0,03380 0,71347 3,349 37,21
33 SDOm spiral dynamics optimization M 0,74601 0,44623 0,29687 1,48912 0,70204 0,34678 0,10944 1,15826 0,42833 0,16767 0,03663 0,63263 3,280 36,44
34 NMm Nelder-Mead method M 0,73807 0,50598 0,31342 1,55747 0,63674 0,28302 0,08221 1,00197 0,44667 0,18667 0,04028 0,67362 3,233 35,92
35 FAm firefly algorithm M 0,58634 0,47228 0,32276 1,38138 0,68467 0,37439 0,10908 1,16814 0,28667 0,16467 0,04722 0,49855 3,048 33,87
36 GSA gravitational search algorithm 0,64757 0,49197 0,30062 1,44016 0,53962 0,36353 0,09945 1,00260 0,32667 0,12200 0,01917 0,46783 2,911 32,34
37 BFO bacterial foraging optimization 0,61171 0,43270 0,31318 1,35759 0,54410 0,21511 0,05676 0,81597 0,42167 0,13800 0,03195 0,59162 2,765 30,72
38 ABC artificial bee colony 0,63377 0,42402 0,30892 1,36671 0,55103 0,21874 0,05623 0,82600 0,34000 0,14200 0,03102 0,51302 2,706 30,06
39 BA bat algorithm 0,59761 0,45911 0,35242 1,40915 0,40321 0,19313 0,07175 0,66810 0,21000 0,10100 0,03517 0,34617 2,423 26,93
40 AAA algae adaptive algorithm 0,50007 0,32040 0,25525 1,07572 0,37021 0,22284 0,16785 0,76089 0,27846 0,14800 0,09755 0,52402 2,361 26,23
41 SA simulated annealing 0,55787 0,42177 0,31549 1,29513 0,34998 0,15259 0,05023 0,55280 0,31167 0,10033 0,02883 0,44083 2,289 25,43
42 IWDm intelligent water drops M 0,54501 0,37897 0,30124 1,22522 0,46104 0,14704 0,04369 0,65177 0,25833 0,09700 0,02308 0,37842 2,255 25,06
43 PSO particle swarm Optimization 0,59726 0,36923 0,29928 1,26577 0,37237 0,16324 0,07010 0,60572 0,25667 0,08000 0,02157 0,35823 2,230 24,77
44 Boids boids algorithm 0,43340 0,30581 0,25425 0,99346 0,35718 0,20160 0,15708 0,71586 0,27846 0,14277 0,09834 0,51957 2,229 24,77
45 MA monkey algorithm 0,59107 0,42681 0,31816 1,33604 0,31138 0,14069 0,06612 0,51819 0,22833 0,08567 0,02790 0,34190 2,196 24,40


Conclusiones

Hoy hemos presentado dos versiones del algoritmo: la original y la modificada. Esta última implica pequeños cambios, pero mejora significativamente el rendimiento gracias a la información compartida en la población. Esto demuestra que incluso pequeños ajustes en la lógica del algoritmo pueden dar lugar a un notable aumento de la eficiencia en diversas tareas.

Me ha gustado mucho la idea del algoritmo, ya que pretende evitar el estancamiento en los extremos. El algoritmo usa una lógica compleja de varias etapas para desplazar las nubes de las zonas de alta presión a las de baja presión y precipitación. Sin embargo, esto no resulta suficiente para lograr una alta convergencia. Como resultado, he intentado incluir una modificación introduciendo información compartida en la población, lo que ha ayudado a mejorar la convergencia, uno de los aspectos clave de cualquier algoritmo de optimización.

La peculiaridad del algoritmo reside en que ninguna nube permanece demasiado tiempo en su sitio. El continuo aumento de la presión en la región empuja inevitablemente la nube hacia una nueva zona inexplorada. Dicho mecanismo fue concebido por los autores como un medio para contrarrestar el estancamiento en extremos locales. Sin embargo, si intentamos aumentar la convergencia del algoritmo aumenta la probabilidad de atascarse, lo que desgraciadamente anula en parte la característica clave que me ha inspirado para permitir que el enfoque se aplique a otros algoritmos de optimización. En el diseño de cualquier algoritmo de optimización siempre se intenta encontrar un equilibrio entre la robustez frente a las interferencias y la búsqueda de una solución exacta. Si se desea, la probabilidad de compartir información puede reducirse en el código; actualmente es del 95%, lo cual mejorará la resistencia.

El algoritmo supone una base notable y un conjunto de técnicas interesantes (reglas para la formación de humedad en regiones y distribución de presión entre ellas, y además se pueden aplicar leyes físicas de aceleración e inercia dependientes de la masa de las nubes y muchas otras ideas) y es una bendición para los investigadores.

Tab

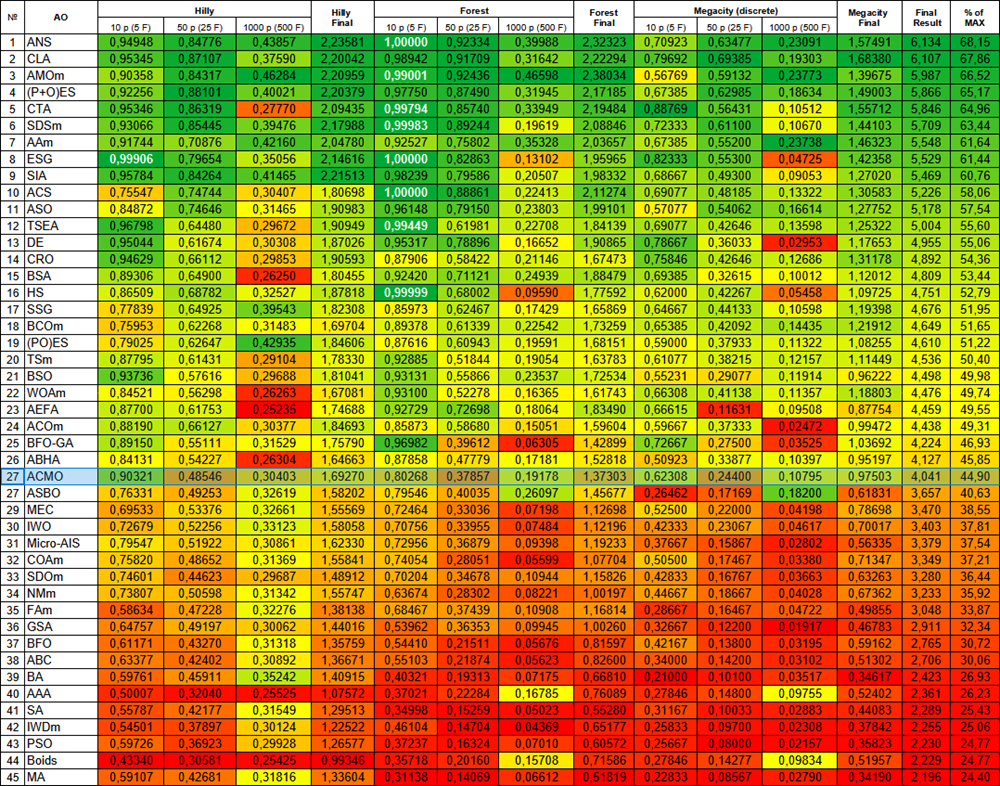
Figura 2. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de puntuación está en el archivo)

chart

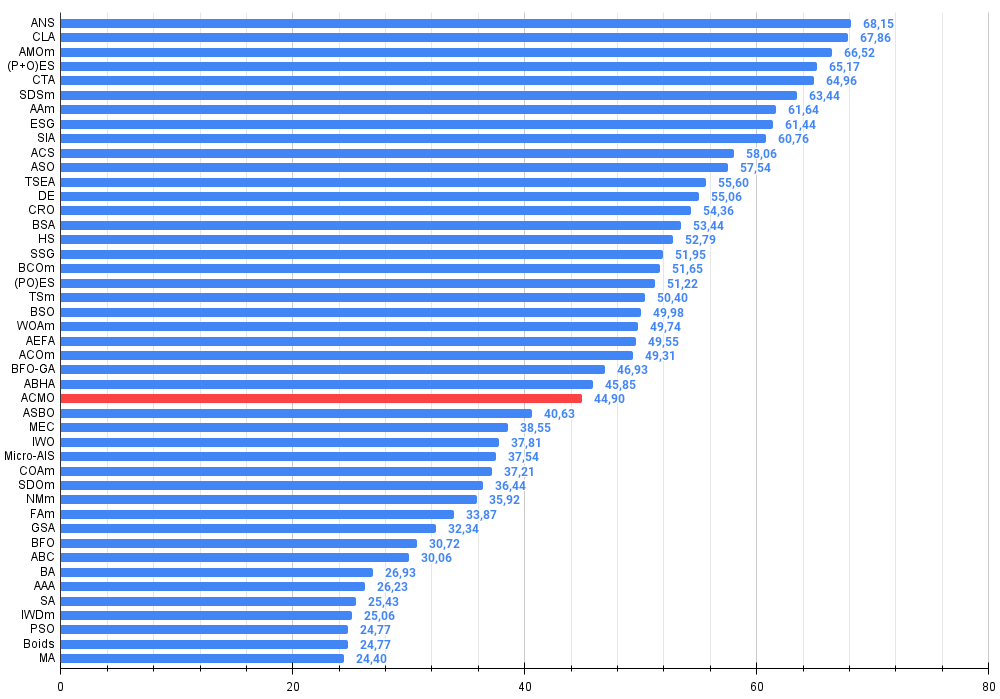
Figura 3. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0,99 aparecen resaltados en blanco.

Ventajas e inconvenientes del algoritmo ACMO:

Ventajas:

  1. Mecanismos anti-interferencias incorporados.
  2. No tiene mala convergencia.
  3. La escalabilidad no está mal.

Desventajas:

  1. Un gran número de parámetros externos.
  2. Difícil implementación.
  3. Resulta difícil encontrar el equilibrio entre la interferencia y la convergencia con los parámetros.

Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15921

Archivos adjuntos |
Descargar ZIP
ACMO.zip (39.7 KB)
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores
Redes neuronales en el trading: Enfoque sin máscara para la predicción del movimiento de precios Redes neuronales en el trading: Enfoque sin máscara para la predicción del movimiento de precios
En este artículo nos familiarizaremos con el método Mask-Attention-Free Transformer (MAFT) y su aplicación en el ámbito del trading. A diferencia de los Transformers tradicionales, que requieren el enmascaramiento de los datos durante el procesamiento de la secuencia, el MAFT optimiza el proceso de atención eliminando la necesidad de enmascaramiento, lo que mejora significativamente la eficiencia computacional.
HTTP y Connexus (Parte 2): Comprensión de la arquitectura HTTP y el diseño de bibliotecas HTTP y Connexus (Parte 2): Comprensión de la arquitectura HTTP y el diseño de bibliotecas
Este artículo explora los fundamentos del protocolo HTTP, cubriendo los métodos principales (GET, POST, PUT, DELETE), los códigos de estado y la estructura de las URL. Además, presenta el inicio de la construcción de la librería Conexus con las clases CQueryParam y CURL, que facilitan la manipulación de URLs y parámetros de consulta en peticiones HTTP.
Scalping Orderflow en MQL5 Scalping Orderflow en MQL5
Este Asesor Experto de MetaTrader 5 implementa una estrategia Scalping Orderflow con gestión avanzada de riesgos. Utiliza múltiples indicadores técnicos para identificar oportunidades de negociación basadas en los desequilibrios del flujo de órdenes (Orderflow). Las pruebas retrospectivas muestran una rentabilidad potencial, pero resaltan la necesidad de una mayor optimización, especialmente en la gestión de riesgos y en los ratios de resultados comerciales. Adecuado para operadores experimentados, requiere pruebas y comprensión exhaustivas antes de la implementación en vivo.
Redes neuronales en el trading: Superpoint Transformer (SPFormer) Redes neuronales en el trading: Superpoint Transformer (SPFormer)
En este artículo, nos familiarizaremos con un método de segmentación de objetos 3D basado en el Superpoint Transformer (SPFormer), que elimina la necesidad de agregar datos intermedios, lo cual acelera el proceso de segmentación y mejora el rendimiento del modelo.