
ADAM poblacional (Estimación Adaptativa de Momentos)
Contenido
Introducción
En el mundo del aprendizaje automático, donde los datos se multiplican rápidamente y los algoritmos son cada vez más complejos, la optimización juega un papel fundamental para lograr un alto rendimiento. Entre los numerosos métodos que intentan abordar esta tarea, el algoritmo ADAM (Adaptive Moment Estimation) destaca por su elegancia y eficacia.
En 2014, dos mentes prominentes - D.P. Kingma y J. Ba propusieron el algoritmo ADAM, que combina las mejores características de sus predecesores, como AdaGrad y RMSProp. El algoritmo se diseñó específicamente para optimizar los pesos de las redes neuronales usando los gradientes de las funciones de activación de las neuronas. Se basa en las estimaciones adaptativas del primer y segundo momento, lo cual hace que sea fácil de aplicar y muy eficiente desde el punto de vista computacional. El algoritmo necesita unos recursos de memoria mínimos y no depende del escalado diagonal de los gradientes, lo que lo hace especialmente adecuado para problemas intensivos en datos y parámetros.
ADAM también funciona bien con objetivos no estacionarios y en situaciones en las que los gradientes pueden ser ruidosos o dispersos. Los hiperparámetros del algoritmo son fáciles de interpretar y no suelen requerir un ajuste complejo.
Sin embargo, a pesar de su eficacia en el campo de las redes neuronales, ADAM se limita al uso de gradientes analíticos, lo cual reduce su gama de aplicaciones. En este trabajo, le proponemos un enfoque innovador para modificar el algoritmo ADAM, transformándolo en un algoritmo de optimización poblacional capaz de manejar gradientes numéricos. Esta modificación no solo amplía el alcance de ADAM más allá de las redes neuronales, sino que también descubre nuevas posibilidades para resolver una amplia gama de problemas generales de optimización.
Nuestra investigación pretende desarrollar un optimizador universal que mantenga las ventajas del ADAM original, pero que sea capaz de funcionar eficazmente en entornos en los que no se disponga de gradientes analíticos. Esto permitirá aplicar el ADAM modificado en ámbitos como la optimización global y la optimización multicriterio, ampliando enormemente su potencial y su valor práctico.
Implementación del algoritmo
El algoritmo ADAM suele clasificarse como un método de optimización basado en gradientes estocásticos. Sin embargo, debemos señalar que el propio ADAM no contiene elementos estocásticos internos en su lógica básica. En realidad, la estocasticidad asociada a ADAM se debe a la forma en que se preparan y suministran los datos al algoritmo, más que a su mecánica interna. Debemos distinguir entre la estocasticidad en la preparación de los datos y el determinismo en el propio algoritmo de optimización.
El propio algoritmo ADAM es completamente determinista. Dados los mismos datos de entrada y las mismas condiciones iniciales, siempre producirá resultados idénticos. Las actualizaciones de los parámetros en ADAM se basan en fórmulas bien definidas que no incluyen elementos de aleatoriedad.
Esta distinción entre la naturaleza determinista del algoritmo ADAM y la naturaleza estocástica de la preparación de los datos para él, resulta importante para comprender correctamente su funcionamiento y su potencial de modificación. Reconocer este hecho abre la puerta a la adaptación de ADAM a tareas en las que la preparación estocástica de datos puede no ser aplicable o deseable, manteniendo al mismo tiempo sus potentes propiedades de optimización.
Veamos el pseudocódigo con fórmulas:
1. Inicialización:
m₀ = 0 (inicialización del primer momento)
v₀ = 0 (inicialización del segundo momento).
t = 0 (contador de pasos)
2. En cada paso t:
t = t + 1
gₜ = ∇ₜf(θₜ₋₁) (cálculo del gradiente)
3. Actualización de los momentos primero y segundo ajustados:
mₜ = β₁ · mₜ₋₁ + (1 - β₁) · gₜ
vₜ = β₂ · vₜ₋₁ + (1 - β₂) · gₜ²
m̂ₜ = mₜ / (1 - β₁ᵗ)
v̂ₜ = vₜ / (1 - β₂ᵗ)
4. Actualización de parámetros:
θₜ = θₜ₋₁ - α · m̂ₜ / (√v̂ₜ + ε)
Donde:
θₜ - parámetros del modelo en el paso t
f(θ) - función objetivo
α - tasa de aprendizaje (normalmente α = 0,001)
β₁, β₂ - coeficientes de decaimiento de los momentos (normalmente β₁ = 0,9, β₂ = 0,999).
ε - constante menor para evitar la división por cero (normalmente 10-⁸).
mₜ, vₜ - estimaciones del primer y segundo momento del gradiente.
m̂ₜ, v̂ₜ - estimaciones de momentos ajustadas.
Estas fórmulas capturan la esencia del algoritmo ADAM mostrando cómo ajusta adaptativamente la tasa de aprendizaje para cada parámetro basándose en las estimaciones del primer y segundo momento de los gradientes. Como podemos ver, no existe en absoluto estocasticidad en el algoritmo. Normalmente, el algoritmo ADAM, en sus numerosas implementaciones programáticas, está firmemente entrelazado con el tejido de la arquitectura de redes neuronales. En este artículo, sin embargo, haremos un poco de magia: no solo lo convertiremos en una entidad independiente y autosuficiente, sino que lo convertiremos, atención, en un método basado en la población y verdaderamente estocástico.
Para empezar, tendremos que implementar ADAM en un formato poblacional, conservando sus fórmulas originales, pero añadiendo un elemento de aleatoriedad solo durante la fase inicial de inicialización de los parámetros a optimizar. Pero eso será solo el principio. A continuación, introduciremos la aleatoriedad en el comportamiento dinámico de este método de gradiente y veremos a qué resultados puede conducir.
Luego definiremos una estructura "S_Gradients" que almacenará los gradientes y dos vectores de momento (primero y segundo). El método "Init (int coords)" establecerá el tamaño de los arrays y los inicializará con ceros.
//—————————————————————————————————————————————————————————————————————————————— // Structure for storing gradients and moments struct S_Gradients { double g []; // Gradients double m []; // Vectors of the first moment double v []; // Vectors of the second moment // Method for initializing gradients void Init (int coords) { ArrayResize (g, coords); ArrayResize (m, coords); ArrayResize (v, coords); ArrayInitialize (g, 0.0); // Initialize gradients to zeros ArrayInitialize (m, 0.0); // Initialize the first moment with zeros ArrayInitialize (v, 0.0); // Initialize the second moment with zeros } }; //——————————————————————————————————————————————————————————————————————————————
La clase "C_AO_ADAM" implementará el algoritmo de optimización ADAM. Funciones básicas de la clase:
- Constructor — inicializa los parámetros del algoritmo, como el tamaño de la población y los coeficientes de aprendizaje y decaimiento.
- SetParams () — establece los valores de los parámetros del array "params", lo cual permite cambiarlos después de la inicialización.
- Init () — prepara el algoritmo para su funcionamiento aceptando los rangos de los parámetros y el número de épocas.
- Moving() y Revision () — han sido diseñados para ejecutar los pasos de optimización, actualizar los parámetros del modelo y comprobar el estado del algoritmo.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ADAM : public C_AO { public: //-------------------------------------------------------------------- // Class destructor ~C_AO_ADAM () { } // Class constructor C_AO_ADAM () { ao_name = "ADAM"; // Algorithm name ao_desc = "Adaptive Moment Estimation"; // Algorithm description ao_link = "https://www.mql5.com/en/articles/16443"; // Link to the article popSize = 50; // Population size alpha = 0.001; // Learning ratio beta1 = 0.9; // Exponential decay ratio for the first moment beta2 = 0.999; // Exponential decay ratio for the second moment epsilon = 1e-8; // Small constant to prevent division by zero // Initialize the parameter array ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "alpha"; params [1].val = alpha; params [2].name = "beta1"; params [2].val = beta1; params [3].name = "beta2"; params [3].val = beta2; params [4].name = "epsilon"; params [4].val = epsilon; } // Method for setting parameters void SetParams () { popSize = (int)params [0].val; // Set population size alpha = params [1].val; // Set the learning ratio beta1 = params [2].val; // Set beta1 beta2 = params [3].val; // Set beta2 epsilon = params [4].val; // Set epsilon } // Initialization method bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // Moving method void Revision (); // Revision method //---------------------------------------------------------------------------- double alpha; // Learning ratio double beta1; // Exponential decay ratio for the first moment double beta2; // Exponential decay ratio for the second moment double epsilon; // Small constant S_Gradients grad []; // Array of gradients private: //------------------------------------------------------------------- int step; // Iteration step int t; // Iteration counter }; //——————————————————————————————————————————————————————————————————————————————
El método "Init" de la clase "C_AO_ADAM" ejecuta la inicialización del algoritmo:
- Llama a "StandardInit ()" para normalizar los parámetros; si no lo consigue, retorna "false".
- Pone a cero los contadores de pasos step" y las iteraciones "t".
- Cambia el tamaño del array de gradientes "grad" para que coincida con el tamaño de la población "popSize".
- Inicializa los gradientes para cada individuo de la población usando las coordenadas "coords".
Si todas las operaciones se realizan correctamente, el método retorna "true".
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ADAM::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Standard initialization if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- step = 0; // Reset step counter t = 1; // Reset iteration counter ArrayResize (grad, popSize); // Resize the gradient array for (int i = 0; i < popSize; i++) grad [i].Init (coords); // Initialize gradients for each individual return true; } //——————————————————————————————————————————————————————————————————————————————
El método "Moving" de la clase "C_AO_ADAM" implementa el paso de optimización en el algoritmo ADAM:
1. Comprobación del paso, si el paso es inferior a 2:
- Para cada individuo de la población, se almacenan el valor anterior de la función y las coordenadas.
- Luego se generan nuevas coordenadas aleatorias dentro del rango especificado y se corrigen a valores aceptables.
- Después el contador de pasos se incrementa y el método finaliza su ejecución.
2. Cálculo de los gradientes: si el paso es 2 o más, para cada individuo se calcula el cambio en el valor de la función objetivo y las coordenadas.
- Luego se añade un pequeño valor "epsilon" para evitar la división por cero que, además, supone un parámetro externo del algoritmo que afecta a las propiedades de búsqueda.
- Acto seguido, se calcula el gradiente de cada parámetro.
3. Actualización de los parámetros de cada individuo:
- Se conservan los valores anteriores de la función y las coordenadas.
- Se actualizan las estimaciones desplazadas de los momentos del primer y segundo gradiente.
- Se calculan las estimaciones de momento ajustadas y se actualizan las coordenadas usando la fórmula ADAM.
- Las coordenadas se ajustan para permanecer dentro de los límites aceptables.
4. Se incrementa el contador de iteraciones "t".
Así, el método se encarga de actualizar las posiciones de los individuos durante la optimización explotando los momentos adaptativos del gradiente. Los dos primeros pasos del algoritmo son necesarios para calcular el gradiente del cambio en el valor de la función de aptitud, dado que el gradiente se calcula numéricamente, sin conocimiento de la fórmula analítica del problema de optimización a resolver. Requiere al menos dos puntos para su cálculo, y las soluciones obtenidas en los dos pasos anteriores pueden usarse en los pasos posteriores.
La lógica del algoritmo ADAM realmente no sugiere una manera específica de calcular el gradiente. El gradiente puede calcularse analítica o numéricamente, y su cómputo se realiza fuera del propio algoritmo. La abstracción del algoritmo respecto a la forma en que se aplica resulta realmente importante para comprender el papel de los componentes individuales en el proyecto global de aprendizaje automático. Esto permite evaluar mejor la influencia de cada elemento en el resultado final y facilita la adaptación del algoritmo a distintas tareas.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAM::Moving () { //---------------------------------------------------------------------------- if (step < 2) // If step is less than 2 { for (int i = 0; i < popSize; i++) { a [i].fP = a [i].f; // Save the previous value of the function for (int c = 0; c < coords; c++) { a [i].cP [c] = a [i].c [c]; // Save the previous coordinate value // Generate new coordinates randomly a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Bringing new coordinates to acceptable values a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } step++; // Increase the step counter return; // Exit the method } //---------------------------------------------------------------------------- double ΔF, ΔX; // Changes in function and coordinates for (int i = 0; i < popSize; i++) { ΔF = a [i].f - a [i].fP; // Calculate the change of the function for (int c = 0; c < coords; c++) { ΔX = a [i].c [c] - a [i].cP [c]; // Calculate the change in coordinates if (ΔX == 0.0) ΔX = epsilon; // If change is zero, set it to epsilon grad [i].g [c] = ΔF / ΔX; // Calculate the gradient } } // Update parameters using ADAM algorithm for (int i = 0; i < popSize; i++) { // Save the previous value of the function a [i].fP = a [i].f; for (int c = 0; c < coords; c++) { // Save the previous coordinate value a [i].cP [c] = a [i].c [c]; // Update the biased first moment estimate grad [i].m [c] = beta1 * grad [i].m [c] + (1.0 - beta1) * grad [i].g [c]; // Update the biased second moment estimate grad [i].v [c] = beta2 * grad [i].v [c] + (1.0 - beta2) * grad [i].g [c] * grad [i].g [c]; // Calculate the adjusted first moment estimate double m_hat = grad [i].m [c] / (1.0 - MathPow (beta1, t)); // Calculate the adjusted estimate of the second moment double v_hat = grad [i].v [c] / (1.0 - MathPow (beta2, t)); // Update coordinates a [i].c [c] = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); // Make sure the coordinates stay within the allowed range a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } t++; // Increase the iteration counter } //——————————————————————————————————————————————————————————————————————————————
El método "Revision" de la clase "C_AO_ADAM" realiza las siguientes acciones:
- Inicializa el índice del mejor individuo "ind" como -1.
- Itera todos los individuos de la población y si el valor de la función del individuo actual es mayor que el mejor valor encontrado "fB", actualiza la mejor solución global y almacena el índice del mejor individuo.
- Si se ha encontrado el mejor individuo, copia sus coordenadas en el array "cB".
Así, el método encuentra y guarda las coordenadas del mejor individuo basándose en los valores de la función de aptitud.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAM::Revision () { int ind = -1; // Best individual index for (int i = 0; i < popSize; i++) { if (a [i].f > fB) // If the current value of the function is greater than the best one { fB = a [i].f; // Update the best value of the function ind = i; // Store the index of the best individual } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best individual } //——————————————————————————————————————————————————————————————————————————————
Como podemos ver, el algoritmo ADAM está ahora basado en la población, y si establecemos el parámetro del tamaño de la población externa en 1, el algoritmo se comportará completamente como un ADAM normal no basado en la población. Ahora también podremos probar el algoritmo en nuestras funciones de prueba. Veamos los resultados:
ADAM|Adaptive Moment Estimation|50.0|0.001|0.9|0.999|0.00000001|
=============================
5 Hilly's; Func runs: 10000; result: 0.3857584301959297
25 Hilly's; Func runs: 10000; result: 0.29733109680042824
500 Hilly's; Func runs: 10000; result: 0.25390478702062613
=============================
5 Forest's; Func runs: 10000; result: 0.30772687797850234
25 Forest's; Func runs: 10000; result: 0.1982664040653052
500 Forest's; Func runs: 10000; result: 0.15554626746207786
=============================
5 Megacity's; Func runs: 10000; result: 0.18153846153846154
25 Megacity's; Func runs: 10000; result: 0.12430769230769231
500 Megacity's; Func runs: 10000; result: 0.09503076923077
=============================
All score: 1.99941 (22.22%)
Desgraciadamente, los resultados no son los mejores, pero esto nos descubre ciertas posibilidades de crecimiento y ofreciéndonos margen para realizar mejoras, en particular introduciendo un verdadero componente estocástico en el algoritmo.
En la implementación anterior del algoritmo ADAM poblacional, cada agente representa un "hilo" independiente de ejecución de la lógica original de los autores, como serpientes que se arrastran por las colinas del espacio de búsqueda, distribuidas por el campo gracias a una inicialización aleatoria inicial. Estas serpientes no interactúan entre sí ni comparten información sobre las mejores soluciones. Como el algoritmo se basa en el gradiente, resulta esencial que considere los cambios en el nivel de la superficie en puntos lo más cercanos posible. Disminuyendo el paso de la diferenciación numérica, podemos encontrarnos con una convergencia lenta, mientras que aumentando el paso se producen grandes saltos en el espacio, lo cual dificulta la obtención de información sobre la superficie entre puntos.
Para resolver estos problemas, haremos que parte de la población sean individuos híbridos que estén compuestos por elementos de las soluciones de otros agentes. La idea es la siguiente: clasificar la población según la adaptabilidad de los individuos, y al final de la lista, donde estén los más débiles, crear híbridos. Para estos individuos, las soluciones se generarán formando un nuevo punto en el espacio basado en elementos de las soluciones de los individuos mejor adaptados. Cuanto mayor sea la adaptabilidad de un individuo, más probable será que transmita información sobre su posición a los híbridos.
Así, parte de los individuos de la población representarán soluciones según la lógica original del algoritmo, mientras que la otra parte serán los llamados híbridos, que son una combinación de elementos de solución de la población. El híbrido resultante no se copiará simplemente de partes de otros individuos; cada una de estas partes variará según una ley escalonada de distribución de probabilidades. Llamaremos "estabilidad del híbrido" al grado de esta ley: cuanto mayor sea el grado, menos cambios sufrirá el híbrido y más se parecerá a los elementos de las mejores soluciones de la población.
Pasemos ahora a la versión actualizada del algoritmo. La clase "C_AO_ADAMm" implementa varios cambios en comparación con la clase "C_AO_ADAMm" que, en teoría, pueden influir positivamente en su funcionalidad y comportamiento. Estos son los principales cambios:
1. Nuevos parámetros:
- hybridsPercentage - parámetro que define el porcentaje de híbridos en la población.
- hybridsResistance - parámetro que ajusta la resistencia de los híbridos a los cambios.
2. En el constructor de la clase "C_AO_ADAMm" se inicializan los nuevos parámetros "hybridsPercentage" e "hybridsResistance" y sus valores se añaden al array "params".
3. SetParams - este método añade las líneas para establecer los nuevos parámetros "hybridsPercentage" e "hybridsResistance", lo cual permite cambiar dinámicamente sus valores.
Si ajustamos el parámetro de porcentaje híbrido a "1", la lógica ADAM quedará efectivamente desactivada. Si establecemos este valor en "0", el algoritmo no tendrá propiedades combinatorias. Como resultado, hemos seleccionado de forma experimental un valor óptimo igual a "0,5", que ha resultado ser el mejor.
El segundo parámetro es el responsable de la resistencia de los híbridos al cambio. Cuando se fijan valores bajos, los híbridos cambian sustancialmente tras la herencia de la característica y pueden abarcar toda la gama de valores aceptables de los parámetros optimizados. Al mismo tiempo, si fijamos valores demasiado altos, por ejemplo "20" o más, la variabilidad de los híbridos tenderá a "0" y se convertirán solo en portadores de las mejores cualidades de los individuos parentales. El valor óptimo de este parámetro se ha hallado de forma experimental: "10".
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ADAMm : public C_AO { public: //-------------------------------------------------------------------- // Class destructor ~C_AO_ADAMm () { } // Class constructor C_AO_ADAMm () { ao_name = "ADAMm"; // Algorithm name ao_desc = "Adaptive Moment Estimation M"; // Algorithm description ao_link = "https://www.mql5.com/en/articles/16443"; // Link to the article popSize = 100; // Population size hybridsPercentage = 0.5; // Percentage of hybrids in the population hybridsResistance = 10; // Resistance of hybrids to changes alpha = 0.001; // Learning ratio beta1 = 0.9; // Exponential decay ratio for the first moment beta2 = 0.999; // Exponential decay ratio for the second moment epsilon = 0.1; // Small constant to prevent division by zero // Initialize the parameter array ArrayResize (params, 7); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "hybridsPercentage"; params [1].val = hybridsPercentage; params [2].name = "hybridsResistance"; params [2].val = hybridsResistance; params [3].name = "alpha"; params [3].val = alpha; params [4].name = "beta1"; params [4].val = beta1; params [5].name = "beta2"; params [5].val = beta2; params [6].name = "epsilon"; params [6].val = epsilon; } // Method for setting parameters void SetParams () { popSize = (int)params [0].val; // Set population size hybridsPercentage = params [1].val; // Set the percentage of hybrids in the population hybridsResistance = params [2].val; // Set hybrids' resistance to change alpha = params [3].val; // Set the learning ratio beta1 = params [4].val; // Set beta1 beta2 = params [5].val; // Set beta2 epsilon = params [6].val; // Set epsilon } // Initialization method bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // Moving method void Revision (); // Revision method //---------------------------------------------------------------------------- double hybridsPercentage; // Percentage of hybrids in the population double hybridsResistance; // Resistance of hybrids to changes double alpha; // Learning ratio double beta1; // Exponential decay ratio for the first moment double beta2; // Exponential decay ratio for the second moment double epsilon; // Small constant S_Gradients grad []; // Array of gradients private: //------------------------------------------------------------------- int step; // Iteration step int t; // Iteration counter int hybridsNumber; // Number of hybrids in the population }; //——————————————————————————————————————————————————————————————————————————————
El método "Init" de la clase "C_AO_ADAMm" tiene los siguientes cambios en comparación con el método similar de la clase anterior:
- Se calcula el número de híbridos en la población usando como base el porcentaje "hybridsPercentage". Este nuevo valor "hybridsNumber" se usa para controlar la composición de la población.
- Hemos añadido una comprobación para garantizar que el número de híbridos no supere el tamaño de la población "popSize". De este modo se evitan los errores asociados a la salida del array.
Estos cambios hacen que el método "Init" se adapte mejor a las características del algoritmo asociadas a los híbridos, y garantizan que el estado y la inicialización de los individuos de la población se gestionen correctamente.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ADAMm::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Standard initialization if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- step = 0; // Reset step counter t = 1; // Reset iteration counter hybridsNumber = int(popSize * hybridsPercentage); // Calculation of the number of hybrids in the population if (hybridsNumber > popSize) hybridsNumber = popSize; // Correction ArrayResize (grad, popSize); // Resize the gradient array for (int i = 0; i < popSize; i++) grad [i].Init (coords); // Initialize gradients for each individual return true; } //——————————————————————————————————————————————————————————————————————————————
El método "Moving" también presenta algunos cambios con respecto a la versión anterior de este método.
Actualización de parámetros mediante el algoritmo ADAM. En este bloque se han añadido las condiciones para procesar híbridos. Si el índice del individuo "i" es mayor o igual que "popSize - hybridsNumber", se generarán nuevas coordenadas utilizando una distribución aleatoria y el parámetro "hybridsResistance". Esto permitirá que los híbridos presenten pequeñas desviaciones en las características heredadas con respecto a los individuos parentales (algo análogo a la mutación de características). En caso contrario, para los individuos que no son híbridos, se actualizarán las estimaciones desplazadas del primer y segundo momento y, a continuación, se calcularán las estimaciones ajustadas.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAMm::Moving () { //---------------------------------------------------------------------------- if (step < 2) // If step is less than 2 { for (int i = 0; i < popSize; i++) { a [i].fP = a [i].f; // Save the previous value of the function for (int c = 0; c < coords; c++) { a [i].cP [c] = a [i].c [c]; // Save the previous coordinate value // Generate new coordinates randomly a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Bringing new coordinates to acceptable values a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } step++; // Increase the step counter return; // Exit the method } //---------------------------------------------------------------------------- double ΔF, ΔX; // Changes in function and coordinates double cNew; for (int i = 0; i < popSize; i++) { ΔF = a [i].f - a [i].fP; // Calculate the change of the function for (int c = 0; c < coords; c++) { ΔX = a [i].c [c] - a [i].cP [c]; // Calculate the change in coordinates if (ΔX == 0.0) ΔX = epsilon; // If change is zero, set it to epsilon grad [i].g [c] = ΔF / ΔX; // Calculate the gradient } } // Update parameters using ADAM algorithm for (int i = 0; i < popSize; i++) { // Save the previous value of the function a [i].fP = a [i].f; for (int c = 0; c < coords; c++) { // Save the previous coordinate value a [i].cP [c] = a [i].c [c]; if (i >= popSize - hybridsNumber) { double pr = u.RNDprobab (); pr *= pr; int ind = (int)u.Scale (pr, 0, 1, 0, popSize - 1); cNew = u.PowerDistribution (a [ind].c [c], rangeMin [c], rangeMax [c], hybridsResistance); } else { // Update the biased first moment estimate grad [i].m [c] = beta1 * grad [i].m [c] + (1.0 - beta1) * grad [i].g [c]; // Update the biased second moment estimate grad [i].v [c] = beta2 * grad [i].v [c] + (1.0 - beta2) * grad [i].g [c] * grad [i].g [c]; // Calculate the adjusted first moment estimate double m_hat = grad [i].m [c] / (1.0 - MathPow (beta1, t)); // Calculate the adjusted estimate of the second moment double v_hat = grad [i].v [c] / (1.0 - MathPow (beta2, t)); // Update coordinates //a [i].c [c] = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); cNew = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); } // Make sure the coordinates stay within the allowed range a [i].c [c] = u.SeInDiSp (cNew, rangeMin [c], rangeMax [c], rangeStep [c]); } } t++; // Increase the iteration counter } //——————————————————————————————————————————————————————————————————————————————
El método "Revision" presenta los siguientes cambios con respecto a la versión anterior de este método.
Preparación del array para la clasificación: se crea un array temporal "aT" de tamaño poblacional y a continuación se llama al método de clasificación "u.Sorting ()". El array de población clasificado permite que los híbridos implementen la herencia de características con una mayor probabilidad a partir de individuos mejor adaptados. El array de población temporal podría trasladarse a los campos de clase, pero en este caso se hace así por claridad.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAMm::Revision () { int ind = -1; // Best individual index for (int i = 0; i < popSize; i++) { if (a [i].f > fB) // If the current value of the function is greater than the best one { fB = a [i].f; // Update the best value of the function ind = i; // Store the index of the best individual } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best individual //---------------------------------------------------------------------------- S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Resultados de las pruebas
Veamos los resultados de la versión modificada del ADAMm poblacional verdaderamente estocástico:
ADAMm|Adaptive Moment Estimation M|100.0|0.5|10.0|0.001|0.9|0.999|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.8863499654810468
25 Hilly's; Func runs: 10000; result: 0.4476644542595641
500 Hilly's; Func runs: 10000; result: 0.2661291031673467
=============================
5 Forest's; Func runs: 10000; result: 0.8449728914068644
25 Forest's; Func runs: 10000; result: 0.3849320103361983
500 Forest's; Func runs: 10000; result: 0.16889385703816007
=============================
5 Megacity's; Func runs: 10000; result: 0.6615384615384616
25 Megacity's; Func runs: 10000; result: 0.2704615384615384
500 Megacity's; Func runs: 10000; result: 0.10593846153846247
=============================
All score: 4.03688 (44.85%)
Los resultados obtenidos han mejorado notablemente. A continuación le mostramos una visualización del algoritmo ADAM basado en una población simple, que muestra el peculiar movimiento de las "serpientes" individuales que se dispersan en todas direcciones mientras exploran el espacio de búsqueda. También se presentan visualizaciones de la población estocástica ADAMm que muestran un movimiento más activo de los agentes de búsqueda hacia el óptimo global, pero se pierde el aspecto característico de las "serpientes".
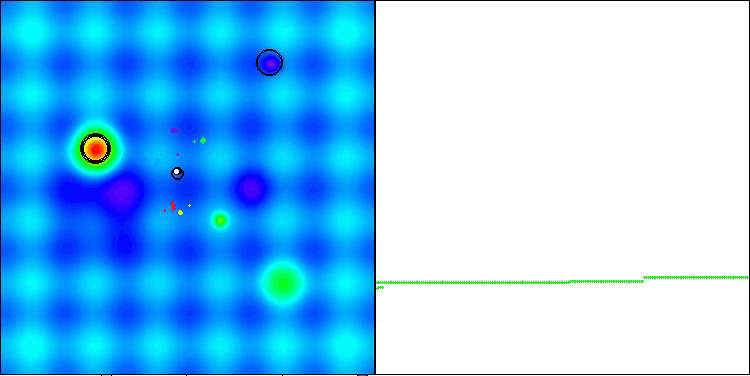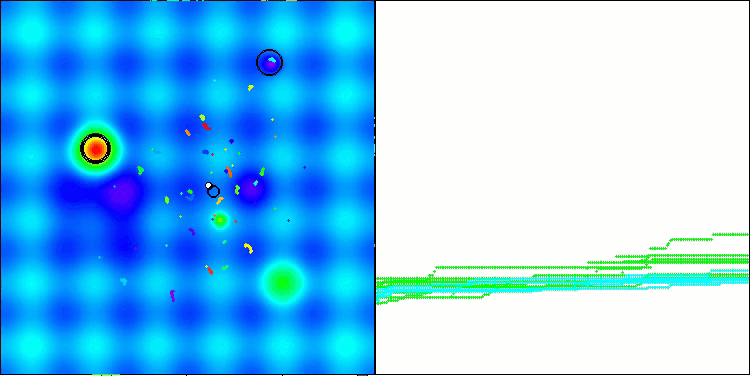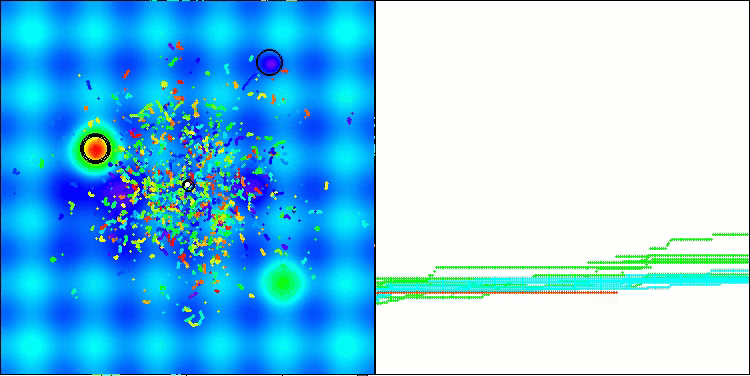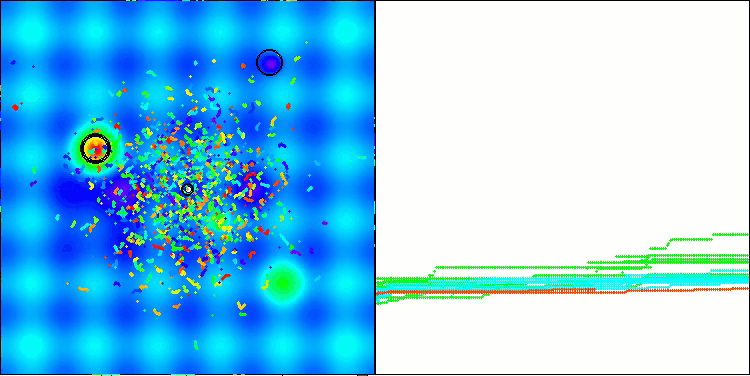
ADAM en la función de prueba Hilly

ADAMm en la función de prueba Hilly

ADAMm en la función de prueba Forest

ADAMm en la función de prueba Megacity
Al final de las pruebas, la versión poblacional estocástica de ADAM ocupa el puesto 32 en la tabla de clasificación, un resultado bastante bueno. La versión original no ha podido entrar en la tabla.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration optimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 12 | AOSm | búsqueda de orbitales atómicos M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 13 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 14 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 15 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 16 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 17 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 18 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 19 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 20 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 21 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 22 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 23 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 24 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 25 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 26 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 27 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 28 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 29 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1,65585 | 0.89675 | 0.37401 | 0.16984 | 1,44060 | 0.69538 | 0.28031 | 0.10852 | 1,08422 | 4.181 | 46,45 |
| 30 | ABH | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4.127 | 45,85 |
| 31 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 32 | ADÁN | adaptive moment estimation M | 0.88635 | 0.44766 | 0,26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1,39880 | 0,66154 | 0.27046 | 0.10594 | 1,03794 | 4.037 | 44.85 |
| 33 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 34 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3.657 | 40,63 |
| 35 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 36 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 37 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 38 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 39 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 40 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 41 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 42 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 43 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 44 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 45 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
Conclusiones
El artículo presenta un intento de adaptar el conocido método de gradiente ADAM, tradicionalmente usado en las redes neuronales, para resolver problemas de optimización de forma general. Este intento ha tenido éxito, ya que el ADAMm poblacional verdaderamente estocástico resultante es capaz de competir con los algoritmos más potentes para problemas de optimización global. El artículo demuestra que los enfoques deterministas en los problemas de búsqueda de soluciones óptimas no suelen resultar tan eficaces en los espacios de búsqueda multidimensionales como los métodos estocásticos, y solo elementos adicionales de aleatoriedad pueden ampliar la capacidad de búsqueda de cada algoritmo de optimización.
Sin embargo, debemos señalar que el uso de métodos de gradiente integrado en la red, como el ADAM clásico, en el entrenamiento de redes neuronales sigue estando casi fuera de la competencia, ya que utilizan el valor exacto del gradiente mientras retropropagan el error. No obstante, cuando las redes neuronales se entrenan utilizando criterios de evaluación más complejos que la función de minimización del error, los métodos basados en gradientes pueden encontrar dificultades y quedarse atascados en óptimos locales, como han señalado muchos autores de artículos sobre el aprendizaje automático.
El enfoque presentado en este trabajo puede ser útil en la aplicación clásica de métodos integrados a redes neuronales, manteniendo una excelente precisión y velocidad de convergencia, explotando la forma analítica de la función de activación neuronal y multiplicando la capacidad de resistencia al atascamiento en el entrenamiento de redes neuronales. Esto permitirá usar los métodos clásicos también en problemas con métricas y criterios muy complejos en el entrenamiento. Espero que este artículo ayude a investigadores y profesionales a contemplar desde una nueva perspectiva los problemas de optimización en general y las técnicas de aprendizaje automático en particular.
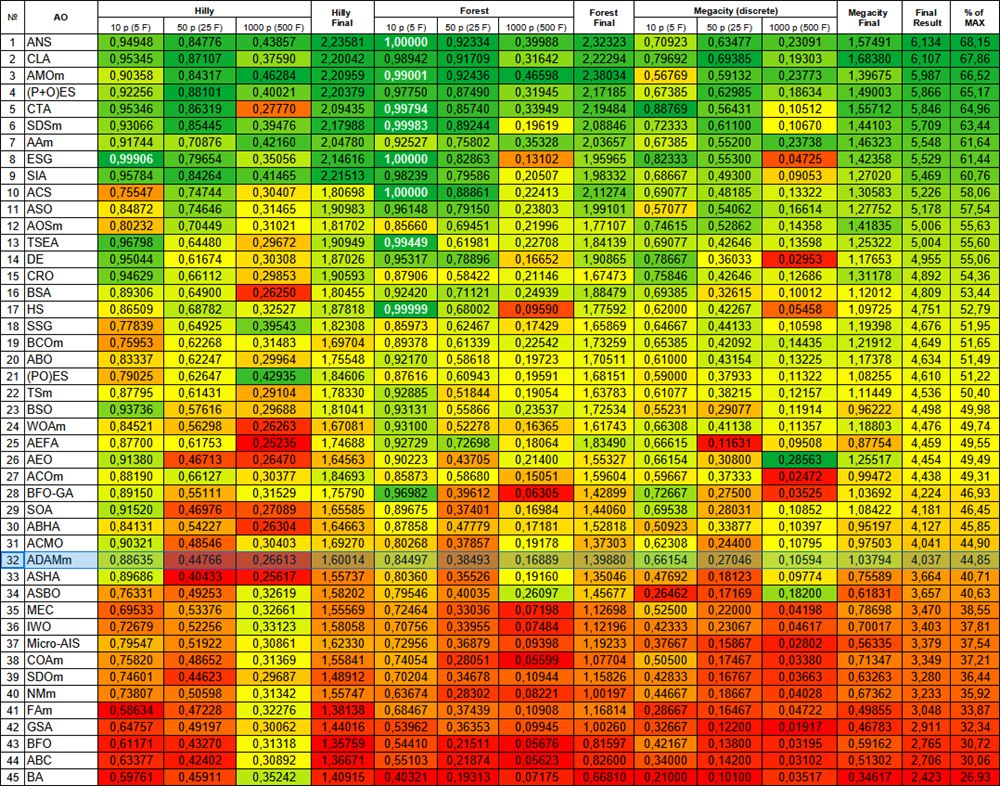
Figura 1. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0.99 se resaltan en blanco.
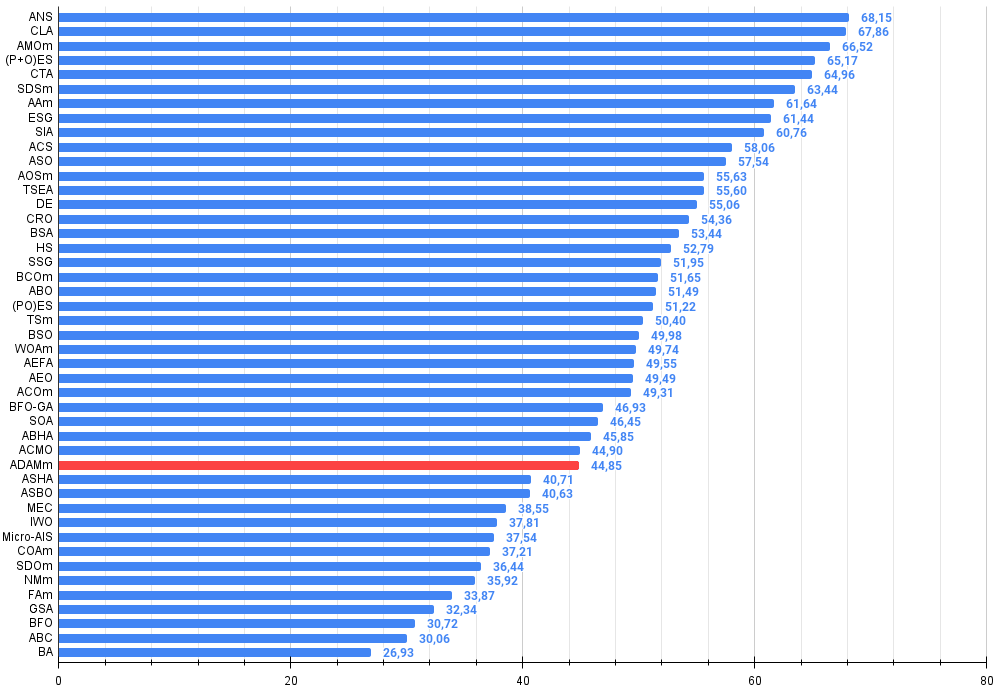
Figura 2. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor,
donde 100 es el máximo resultado teórico posible; el script para calcular la tabla de clasificación está en el archivo)
Ventajas e inconvenientes del algoritmo ADAMm:
Ventajas:
- Buenos resultados con problemas de baja dimensionalidad.
- Los resultados varían poco.
Desventajas:
- Muchos parámetros externos.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | #C_AO.mqh | Archivo de inclusión | Clase padre de algoritmos de optimización basados en la población |
| 2 | #C_AO_enum.mqh | Archivo de inclusión | Enumeración de los algoritmos de optimización basados en la población |
| 3 | TestFunctions.mqh | Archivo de inclusión | Biblioteca de funciones de prueba |
| 4 | TestStandFunctions.mqh | Archivo de inclusión | Biblioteca de funciones del banco de pruebas |
| 5 | Utilities.mqh | Archivo de inclusión | Biblioteca de funciones auxiliares |
| 6 | CalculationTestResults.mqh | Archivo de inclusión | Script para calcular los resultados en una tabla comparativa |
| 7 | Testing AOs.mq5 | Script | Banco de pruebas único para todos los algoritmos de optimización basados en la población |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización |
| 9 | Test_AO_ADAM.mq5 | Script | Banco de pruebas para ADAM y ADAMm |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16443
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Creación de un Panel de administración de operaciones en MQL5 (Parte VIII): Panel de análisis
Creación de un Panel de administración de operaciones en MQL5 (Parte VIII): Panel de análisis
 Introducción a MQL5 (Parte 10): Guía de trabajo con indicadores incorporados en MQL5 para principiantes
Introducción a MQL5 (Parte 10): Guía de trabajo con indicadores incorporados en MQL5 para principiantes
 Creamos y optimizamos un sistema comercial basado en los volúmenes negociados (Chaikin Money Flow (CMF))
Creamos y optimizamos un sistema comercial basado en los volúmenes negociados (Chaikin Money Flow (CMF))
 Kit de herramientas de negociación MQL5 (Parte 4): Desarrollo de una biblioteca EX5 para la gestión del historial
Kit de herramientas de negociación MQL5 (Parte 4): Desarrollo de una biblioteca EX5 para la gestión del historial
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso