
Algoritmo de optimización de sociedad anárquica (Anarchic Society Optimization, ASO)
Contenido
1. Introducción
Siempre me ha atraído el tema de las relaciones sociales y la posibilidad de construir un algoritmo en el concepto de conexiones sociales, ya que éste es el fenómeno más interesante en el desarrollo de la sociedad, y sugiere un amplio campo de actividad para la posibilidad de describir algorítmicamente la estructura del sistema de relaciones e implementar un algoritmo de optimización adecuado.
En los artículos anteriores, ya hemos considerado algoritmos de comportamiento social como la evolución de grupos sociales y la búsqueda cooperativa artificial. En este artículo, trataremos de entender el concepto de sociedad anárquica, un sistema de interacción social sin un poder centralizado y estructuras jerárquicas, donde se supone que las personas pueden organizar sus vidas e interactuar sobre la base de acuerdos voluntarios.
La sociedad anarquista se basa en los principios de autonomía y libertad, en los que cada persona puede tomar de forma independiente y autónoma decisiones relativas a su vida, sin interferencias externas, los principios de cooperación voluntaria, en la que las personas interactúan sobre la base del consentimiento de todos los participantes sin coacción, la igualdad de derechos y oportunidades, así como los principios de solidaridad, asistencia mutua y cooperación. La idea es muy interesante desde el punto de vista de su aplicación en el algoritmo. Se ha intentado implementar dicha construcción social en el algoritmo de optimización Anarchic Society Optimization (ASO). El algoritmo fue propuesto por Ahmadi-Javid y publicado en 2011.
La idea principal es el desarrollo de un método de optimización inspirado en el comportamiento de los individuos en las sociedades anárquicas. A diferencia de los métodos de inteligencia de enjambre existentes desarrollados a partir de enjambres de insectos o animales, como PSO y ACO, desarrollar un algoritmo basado en el estudio de la construcción de una sociedad humana estándar sólo puede tener un éxito limitado, ya que una sociedad bien organizada no tiene la capacidad de alcanzar sus deseos a través de decisiones individuales. Además, ningún miembro de la sociedad es verdaderamente independiente y autónomo, y no puede mejorar radicalmente su situación en un periodo de tiempo determinado. Esta constatación llevó al creador del algoritmo a la idea de tomar prestado el concepto básico para el desarrollo de una sociedad basada en una estructura anómala.
El núcleo del ASO es un grupo de individuos volubles, aventureros, a quienes no les gusta la estabilidad y a menudo se comportan de manera irracional, moviéndose a las peores posiciones que visitaron en la fase de exploración. El nivel de comportamiento anárquico entre los miembros aumenta a medida que aumentan las diferencias en sus situaciones. Utilizando estos participantes, ASO explora el espacio de soluciones y trata de evitar caer en trampas de óptimos locales. De esta forma, el creador de ASO intenta transmitir la idea de que el estudio y la aplicación de principios basados en el comportamiento anómalo de comunidades pueden conducir a la creación de algoritmos eficientes capaces de resolver problemas de optimización complejos. Consideraremos un marco unificado para ASO que pueda usarse fácilmente tanto para problemas continuos como discretos.
2. Implementación del algoritmo
Antes de escribir el código del algoritmo, necesitamos entender cómo está estructurado y qué mecanismos básicos ha puesto el autor en él. El algoritmo ASO es un método de optimización que combina las ventajas del algoritmo Particle Swarm Optimization (PSO) con nuevos mecanismos característicos del comportamiento social anárquico. La naturaleza adaptativa y la capacidad de equilibrar entre diferentes estrategias de movimiento es la principal característica del algoritmo.
Empecemos con una descripción detallada del algoritmo ASO:
1. Inicialización:
- Se crea una población (popSize) a partir de los miembros de la sociedad.
- Cada miembro se inicializa en una posición aleatoria en el espacio de búsqueda.
- Cada miembro conserva su mejor marca personal y sus posiciones anteriores.
2. Bucle básico de optimización:
En cada iteración, el algoritmo realiza los siguientes pasos para cada miembro de la sociedad:
a) Cálculo de índices:
- Fickleness Index (FI) — el índice refleja la inestabilidad de un miembro de la sociedad y mide su insatisfacción en comparación con otros individuos.
- External Irregularity Index (EI) — el índice evalúa la diversidad de posiciones en la sociedad y muestra la desviación respecto a la mejor solución global.
- Internal Irregularity Index (II) — el índice evalúa los cambios en la posición del individuo durante la iteración y refleja la desviación de la mejor solución personal.
b) Selección de la política de movimiento:
Basándose en la comparación de los índices FI, EI y II , se selecciona una de las tres políticas de movimientos:
- Current Movement Policy (CurrentMP) utiliza la ecuación PSO con relaciones de inercia y aceleración.
- Society Movement Policy (SocietyMP) aplica un cruce con un miembro de la sociedad elegido al azar.
- Past Movement Policy (PastMP) utiliza información sobre el puesto anterior del individuo.
c) Comportamiento anárquico: la posición del individuo puede ser completamente aleatoria con la probabilidad anarchyprob.
d) Actualización de la posición: la nueva posición se compara con las restricciones del espacio de búsqueda.
e) Actualizar las primeras posiciones:
- La posición de mejor rendimiento personal, pBest, se actualiza si la posición actual es superior.
- La posición de mejor rendimiento global, gBest, se actualiza si se encuentra una nueva solución superior.
3. Adaptación de los parámetros:
- La probabilidad anarchyProb de comportamiento anárquico disminuye gradualmente.
- El parámetro alfa para calcular FI aumenta gradualmente.
- El peso inercial omega disminuye gradualmente.
4. Parámetros del algoritmo:
- popSize — tamaño de la población.
- omega, lambda1, lambda2 - parámetros para calcular la velocidad en CurrentMP (como en PSO).
- anarchyProb — probabilidad de comportamiento anárquico.
- alpha, theta, delta - parámetros para calcular los índices FI, EI y II según corresponda.
El algoritmo es bastante complejo. Intentaré describir su mecanismo de funcionamiento de forma muy clara y estructurada para facilitar su comprensión. El siguiente paso es analizar las ecuaciones utilizadas en el algoritmo.
La ecuación básica del algoritmo ASO se hereda del algoritmo PSO. Realiza el cálculo de la actualización de la velocidad: V_i (k+1) = ω * V_i (k) + λ1 * r1 * (P_i (k) - X_i (k)) + λ2 * r2 * (G (k) - X_i (k)), donde:
- V_i (k) — i velocidad de la partícula en k iteración.
- X_i (k) — i posición de la partícula en k iteración.
- P_i (k) — mejor posición encontrada por i partícula antes de k iteración.
- G (k) — globalmente la mejor posición encontrada por todas las partículas antes de k iteración.
- ω — relación de inercia.
- λ1, λ2 — ratios de aceleración.
- r1, r2 — números aleatorios del intervalo (0, 1).
El autor señala que la ecuación PSO es un caso especial de la estructura general ASO cuando se definen las políticas de movimiento y la regla de combinación correspondientes. En la versión original, la velocidad anterior del agente se incluyó en los cálculos. Cambié el enfoque dejando solo el valor de velocidad actual, lo que resultó en una mejora notable en el rendimiento del algoritmo.
Las ecuaciones (1) y (2) definen el índice de inconstancia y FI para i miembros de la comunidad en k iteraciónes en el algoritmo ASO. Estas ecuaciones ayudan a evaluar el grado de insatisfacción de un individuo con su puesto actual en comparación con otros puestos. Vamos a verlos en detalle:
1. Ecuación (1) para calcular el índice de inconstancia: (kFI)i = α - α (f (Xi (k)) - f (Pi (k))) / (f (Xi (k*)) - f (Xi (k))).
Esta ecuación muestra cuánto difiere la posición actual de un individuo i de su mejor posición personal y de su mejor posición global ponderada por el parámetro α (alfa).
2. Ecuación (2) para calcular el índice de i inconstancia individual en k iteración: (kFI)i = α - α (f (Xi (k)) - f (Pi (k))) / (f (G (k)) - f (Xi (k))).
Esta ecuación es similar a la primera, pero se utiliza para propósitos diferentes, donde se compara la posición actual, la mejor posición personal y la mejor posición global.
Ambas ecuaciones sirven para evaluar el grado de insatisfacción de los miembros de la sociedad, lo que les permite tomar decisiones más informadas sobre cómo cambiar sus posiciones en busca de una solución óptima.
Las ecuaciones (3) y (4) describen el índice de irregularidad externa y el índice de irregularidad interna para los miembros de la sociedad en el algoritmo.
3. Equation (3) — índice de irregularidad externa de i individuo en k iteración: (kEI)i = exp (-(θi) (f (G) - f (Xi (k)))).
4. Equation (4) — índice de irregularidad interna de i individuo en k iteración: (kEI)i = 1 - exp (-δi (kD)).
Donde:
- (kFI)i — índice de inconstancia de i individuo en k iteración.
- α — número «alfa» no negativo en el intervalo [0,1].
- f (Xi (k)) — valor de la función objetivo para i individuo en k iteración.
- f (Pi (k)) — valor de la función objetivo para la mejor posición visitada previamente por el individuo i.
- f (Xi (k)) — valor de la función objetivo para la posición del mejor individuo en k iteración.
- f (G (k)) — valor de la función objetivo para la mejor posición global visitada por la sociedad antes de la iteración k.
- (kEI)i — índice de irregularidad externa del individuo i en la iteración k.
- θi — número theta positivo.
- kD — medida adecuada de la diversidad en la sociedad, por ejemplo, la proporción de variación de los valores de la función objetivo de los individuos.
- δi — número delta positivo.
Estas ecuaciones muestran que si aumenta la diversidad en una sociedad (es decir, los individuos tienen más valores diferentes de la función objetivo), será más probable que los individuos se comporten de forma irregular. Las ecuaciones se utilizan para evaluar la variabilidad del comportamiento de los miembros de la sociedad en el algoritmo ASO, lo que les permite tomar decisiones más diversas y adaptativas mientras buscan la solución óptima.
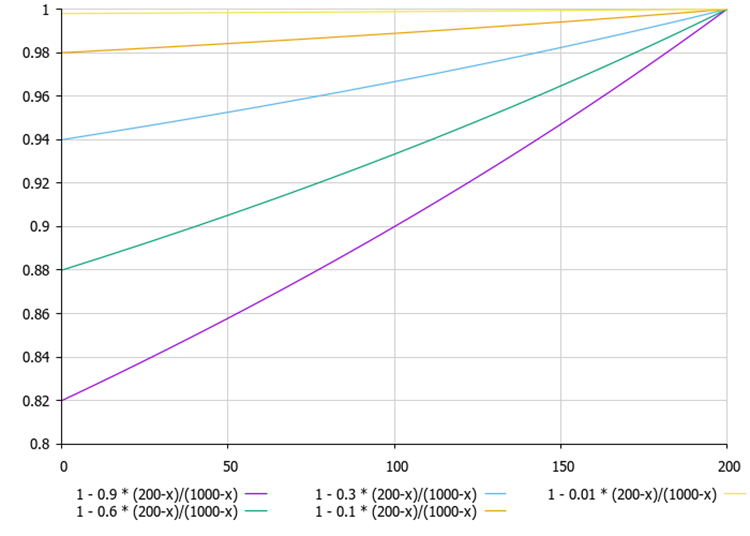
Figura 1. Si la mejor solución actual del agente (200) tiene un valor mucho menor que la mejor solución para la población de agentes (1000), entonces la línea del gráfico cambia casi linealmente.
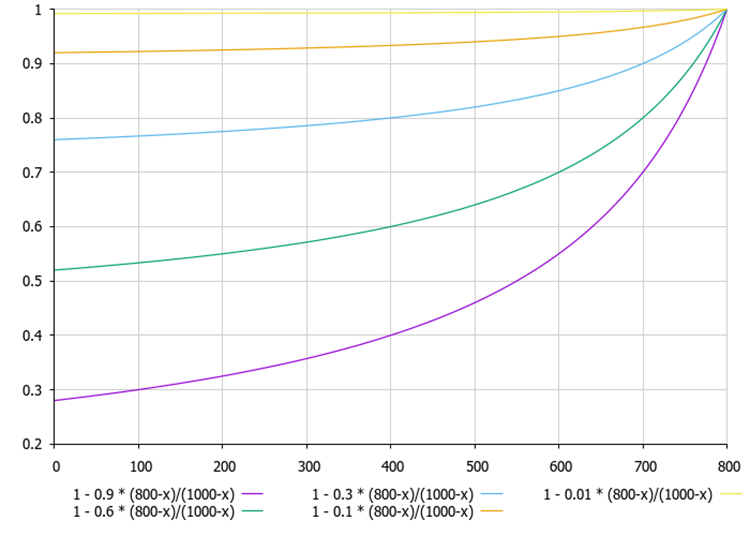
Figura 2. Cuanto menor es la diferencia entre la mejor solución actual del agente por la población de agentes (1000), más no lineal es la línea en el gráfico.
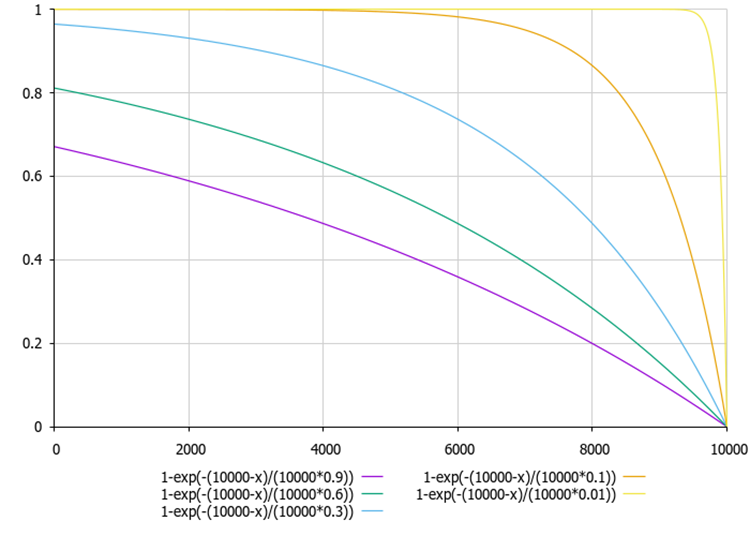
Figura 3. El gráfico de dependencia de los índices externos e internos de irregularidades en función de las relaciones «theta» y «delta» (utilizando como ejemplo valores de 0,01 a 0,9).
Así, los miembros de una sociedad pueden utilizar la información sobre los demás miembros para tomar decisiones sobre sus movimientos, así como sobre la forma en que su comportamiento puede variar en función del nivel de diversidad de la sociedad.
Ahora sabemos un poco más sobre el algoritmo ASO y, en base a la teoría que hemos obtenido, podemos pasar a la parte práctica. Compondremos un pseudocódigo del algoritmo para su implementación en código. Pseudocódigo del algoritmo ASO:
Inicialización:
1. Establecer parámetros: popSize, omega, lambda1, lambda2, anarchyProb, alfa, theta, delta, rangeMin [], rangeMax [], rangeStep []
2. Crear una población de miembros popSize: para cada miembro i de 0 a popSize-1: para cada coordenada c de 0 a coords-1:
position [i].[c] = número aleatorio entre rangeMin [c] y rangeMax [c]
pBest [i].[c] = position [i].[c]
prevPosition [i].[c] = position [i].[c]
pBestFitness [i] = -infinito
3. Set gBest = mejor posición de la población inicial
4. Establecer gBestFitness = gBest fitness
Bucle principal:
5. Hasta que se alcance el criterio de parada: para cada miembro i de 0 a popSize-1:
5.1 Calcular índices
FI = CalculateFI (i)
EI = CalculateEI (i)
II = CalculateII (i)
5.2 Seleccionar la política de movimientos
Si FI > EI y FI > II: newPosition = CurrentMP (i)
En caso contrario, si EI > FI y EI > II: newPosition = SocietyMP (i)
En caso contrario, newPosition = PastMP (i)
5.3 Aplicar un comportamiento anárquico
Si número aleatorio < anarchyProb: para cada coordenada c de 0 a coords-1:
newPosition [c] = número aleatorio entre rangeMin [c] y rangeMax [c]
5.4 Actualiza la posición de cada coordenada c de 0 a coords-1:
prevPosition [i].[c] = position [i].[c]
position [i].[c] = límite (newPosition [c], rangeMin [c], rangeMax [c], rangeStep [c])
5.5 Califica la nueva posición 'fitness' = rate_fitness (posición [i])
5.6 Actualiza el 'mejor' personal si 'fitness' > pBestFitness [i]:
pBestFitness [i] = fitness
pBest [i] = position [i]
5.7 Actualizar global 'mejor' si 'fitness' > gBestFitness:
gBestFitness = fitness
gBest = position [i]
5.8 Adaptar el parámetro AdaptParameters()
5.9 Función CalculateFI (i): devuelve 1 - alpha * (fitness [i] - pBestFitness [i]) / (gBestFitness - fitness [i])
5.10 Función CalculateEI (i): devuelve 1 - exp(-(gBestFitness - fitness [i]) / theta)
5.11 Función CalculateII (i): devuelve 1 - exp(-(pBestFitness [i] - fitness [i]) / delta)
5.12 Función CurrentMP (i): para cada coordenada c de 0 a coords-1:
r1 = número aleatorio entre 0 y 1
r2 = número aleatorio entre 0 y 1
velocity = omega * (position [i].[c] - pBest [i].[c]) + lambda1 * r1 * (pBest [i].[c] - position [i].[c]) + lambda2 * r2 * (gBest [c] - position [i].[c])
newPosition [c] = position [i].[c] + velocity
return newPosition
5.13 Función SocietyMP (i): j = miembro aleatorio de la población, no igual a i, para cada coordenada c de 0 a coords - 1:
Si el número aleatorio < 0.5:
newPosition [c] = position [i].[c]
En caso contrario, newPosition[c] = position [j].[c]
return newPosition
5.14 Función PastMP (i): para cada coordenada c de 0 a coords - 1:
Si el número aleatorio < 0.5:
newPosition [c] = position [i].[c]
En caso contrario, newPosition [c] = prevPosition [i].[c]
return newPosition
Ahora que tenemos el pseudocódigo, podemos empezar a escribir el código del algoritmo basándonos en él. Vamos a describir la estructura S_ASO_Member utilizada para representar a un participante (agente) en el algoritmo.
1. Campos de estructura:
- pPrev [] - matriz de posiciones anteriores de los participantes.
- pBest [] - matriz de las mejores posiciones conocidas de los participantes (mejores personales).
- pBestFitness - la variable almacena el valor de conveniencia (calidad) de la mejor posición conocida.
2. El método Init inicializa las matrices pPrev y pBest estableciendo su tamaño en función del número de coordenadas (o de la dimensionalidad del espacio de búsqueda) pasadas como parámetro coords. ArrayResize(pBest, coords) y ArrayResize(pPrev, coords) - estas llamadas redimensionan arrays al valor de coords. pBestFitness = -DBL_MAX - establece el valor inicial para la mejor adecuación de la posición para asegurar que cualquier valor encontrado será mejor que este.
La estructura S_ASO_Member está diseñada para almacenar información sobre cada participante en el algoritmo de optimización. Nos permite hacer un seguimiento tanto de la posición actual como de la mejor posición del participante, así como de su forma física.
//—————————————————————————————————————————————————————————————————————————————— struct S_ASO_Member { double pPrev []; // Previous position double pBest []; // Personal best position double pBestFitness; // Personal best fitness void Init (int coords) { ArrayResize (pBest, coords); ArrayResize (pPrev, coords); pBestFitness = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Define la clase C_AO_ASO heredada de la clase base C_AO. Veámoslo con más detalle:
1. Los parámetros son:
- popSize - tamaño de la población (número de miembros de la sociedad).
- anarchyProb - posibilidad de comportamiento anárquico, algunos participantes pueden actuar independientemente de los demás.
- omega, lambda1, lambda2 - parámetros relacionados con la inercia y la aceleración utilizados para controlar el comportamiento de los participantes.
- alpha, theta, delta - parámetros utilizados para calcular los indicadores (FI, EI, II).
2. params - matriz de parámetros, donde cada elemento contiene un nombre y un valor.
3. SetParams () - el método actualiza los valores de los parámetros de la matriz params, lo que permite cambiar los parámetros del algoritmo después de su inicialización.
4. Init () - el método inicializa el algoritmo con los rangos y pasos dados. Acepta las matrices rangeMinP, rangeMaxP y rangeStepP, así como el número de épocas epochsP.
5. Moving () y Revision () - métodos implementan la lógica básica del movimiento de los participantes y su revisión (actualización) en la optimización.
6. Campos de clase:
S_ASO_Member member [] - array de miembros de la sociedad almacena información sobre cada participante en el algoritmo.
7. Métodos privados:
- CalculateFI - el método para calcular el valor FI (Indicador de condición física) para un participante específico.
- CalculateEI - el método para calcular el EI (Indicador de Exploración).
- CalculateII - el método para calcular el valor de II (Indicador de Inercia).
- CurrentMP, SocietyMP, PastMP - los métodos implementan la lógica de interacción de los participantes con sus posiciones actuales, sociales y pasadas.
La clase C_AO_ASO es una implementación del concepto de «sociedad anárquica» en la que los participantes pueden actuar tanto de forma conjunta como independiente unos de otros, e incluye parámetros que controlan el comportamiento de los participantes y métodos para su inicialización y actualización.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ASO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ASO () { } C_AO_ASO () { ao_name = "ASO"; ao_desc = "Anarchy Society Optimization"; ao_link = "https://www.mql5.com/en/articles/15511"; popSize = 50; // Population size anarchyProb = 0.1; // Probability of anarchic behavior omega = 0.7; // Inertia weight lambda1 = 1.5; // Acceleration coefficient for P-best lambda2 = 1.5; // Acceleration coefficient for G-best alpha = 0.5; // Parameter for FI calculation theta = 1.0; // Parameter for EI calculation delta = 1.0; // Parameter for II calculation ArrayResize (params, 8); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "anarchyProb"; params [1].val = anarchyProb; params [2].name = "omega"; params [2].val = omega; params [3].name = "lambda1"; params [3].val = lambda1; params [4].name = "lambda2"; params [4].val = lambda2; params [5].name = "alpha"; params [5].val = alpha; params [6].name = "theta"; params [6].val = theta; params [7].name = "delta"; params [7].val = delta; } void SetParams () { popSize = (int)params [0].val; anarchyProb = params [1].val; omega = params [2].val; lambda1 = params [3].val; lambda2 = params [4].val; alpha = params [5].val; theta = params [6].val; delta = params [7].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0); void Moving (); void Revision (); //---------------------------------------------------------------------------- double anarchyProb; // Probability of anarchic behavior double omega; // Inertia weight double lambda1; // Acceleration coefficient for P-best double lambda2; // Acceleration coefficient for G-best double alpha; // Parameter for FI calculation double theta; // Parameter for EI calculation double delta; // Parameter for II calculation S_ASO_Member member []; // Vector of society members private: //------------------------------------------------------------------- double CalculateFI (int memberIndex); double CalculateEI (int memberIndex); double CalculateII (int memberIndex); void CurrentMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd); void SocietyMP (S_AO_Agent &agent, int coordInd); void PastMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd); }; //——————————————————————————————————————————————————————————————————————————————
Veamos el siguiente método Init de la clase C_AO_ASO. Lógica del método:
- StandardInit - se llama al método para realizar la inicialización estándar utilizando los rangos pasados. Si este método devuelve false, se ha producido un error.
- ArrayResize - el método redimensiona la matriz member a popSize, que determina el número de participantes (miembros de la sociedad) en el algoritmo.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ASO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (member, popSize); for (int i = 0; i < popSize; i++) member [i].Init (coords); return true; } //——————————————————————————————————————————————————————————————————————————————
Veamos el código del método Moving de la clase C_AO_ASO. Estructura y lógica del método:
1. Comprobación de la primera llamada:
- Si revision es false, el método inicializa la matriz a con valores aleatorios dentro de los rangos especificados rangeMin y rangeMax.
- Para cada coordenada c de cada miembro de la población i, se llama al método u.RNDfromCI. Genera un valor aleatorio y, a continuación, este valor se normaliza utilizando u.SeInDiSp.
- Los valores se guardan en member [i].pPrev[c] para su uso posterior.
- Después de eso, revision se establece en true, y el método completa la ejecución.
2. Lógica básica del movimiento:
- Para cada miembro de la población i, se calculan tres índices: fi, ei y ii. Son métricas que caracterizan el estado de un miembro de la población.
- Para cada coordenada c se ejecuta lo siguiente:
- El valor actual se guarda en member [i].pPrev[c].
- rnd - número aleatorio se genera utilizando u.RNDprobab ().
- Si el número aleatorio es menor que anarchyProb (que significa el cumplimiento de la probabilidad de manifestación de anarquía en el comportamiento), la coordenada c para el miembro i se inicializará aleatoriamente del rango.
- En caso contrario, dependiendo de los valores fi, ei y ii, se llama a los métodos CurrentMP, SocietyMP y PastMP.
- Después de todos los cambios, el valor de cada coordenada c se ajusta utilizando u.SeInDiSp.
El método Moving implementa la lógica de mover miembros de la población en el espacio de soluciones basándose en sus estados y métricas actuales.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); member [i].pPrev [c] = a [i].c [c]; } } revision = true; return; } //---------------------------------------------------------------------------- double fi = 0.0; //fickleness index double ei = 0.0; //external irregularity index double ii = 0.0; //internal irregularity index double rnd = 0.0; for (int i = 0; i < popSize; i++) { fi = CalculateFI (i); ei = CalculateEI (i); ii = CalculateII (i); for (int c = 0; c < coords; c++) { member [i].pPrev [c] = a [i].c [c]; rnd = u.RNDprobab (); if (u.RNDprobab () < anarchyProb) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); else { if (rnd > fi) CurrentMP (a [i], member [i], c); else { if (rnd < ei) SocietyMP (a [i], c); else { if (rnd < ii) PastMP (a [i], member [i], c); } } } } for (int c = 0; c < coords; c++) { a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Pasemos del método Moving al método Revision. Estructura general y lógica:
1. La variable ind se inicializa con el valor -1. Se utilizará para almacenar el índice del miembro de la población que tenga el mejor valor de la función f.
2. El método recorre todos los miembros de la población desde 0 hasta popSize - 1.
3. Encontrar el mejor valor de función: para cada miembro de la población, se comprueba a[i], es decir, si su valor de función f es superado por el mejor valor actual de fB. Si este es el caso, fB se actualiza por a[i].f, mientras que el índice ind se establece en i.
4. Actualizar el mejor valor personal: el método también comprueba si el valor de la función a[i].f es mayor que el valor del miembro de la población member [i].pBestFitness. En caso afirmativo, el valor se actualiza y las coordenadas actuales a[i].c se copian en member[i].pBest mediante la función ArrayCopy.
5. Copia de la mejor solución: una vez finalizado el bucle, si se encuentra el índice ind (es decir, al menos un miembro de la población tenía un valor de función mayor que fB), las coordenadas de este miembro de la población se copian en cB utilizando ArrayCopy.
El método Revision se encarga de actualizar la mejor solución encontrada en la población, así como de actualizar los mejores valores personales de cada miembro de la población. Utiliza una lógica sencilla para comparar los valores de las funciones y determinar qué soluciones son las mejores, y las almacena para su uso posterior.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } if (a [i].f > member [i].pBestFitness) { member [i].pBestFitness = a [i].f; ArrayCopy (member [i].pBest, a [i].c, 0, 0, WHOLE_ARRAY); } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
A continuación, el método CalculateFI de la clase C_AO_ASO. Descripción del método:
1. El método toma el índice del miembro de la población memberIndex para el que se va a calcular la aptitud (fitness).
2. Obtención de valores de fitness:
- currentFitness - obtiene el valor de fitness actual de un miembro de la población de la matriz a por el índice memberIndex..
- personalBestFitness - obtiene el valor de mejor fitness personal de este miembro de la matriz member.
- globalBestFitness - obtiene el mejor valor de condición física global almacenado en la variable fB.
3. Cálculo del índice de aptitud (Fitness Index, FI): el método devuelve el valor calculado mediante la ecuación.
La ecuación normaliza la diferencia entre la forma física personal y la actual dividiéndola por la diferencia entre la forma física global y la actual. El método CalculateFI calcula un índice de aptitud para un miembro de la población, que se utiliza para evaluar su calidad en comparación con sus mejores valores de aptitud personal y global.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ASO::CalculateFI (int memberIndex) { double currentFitness = a [memberIndex].f; double personalBestFitness = member [memberIndex].pBestFitness; double globalBestFitness = fB; //1 - 0.9 * (800-x)/(1000-x) return 1 - alpha * (personalBestFitness - currentFitness) / (globalBestFitness - currentFitness); } //——————————————————————————————————————————————————————————————————————————————
El método CalculateEI de la clase C_AO_ASO viene a continuación. El método hace casi lo mismo que el anterior, pero utiliza la mejor aptitud global y personal actual para calcularlo.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ASO::CalculateEI (int memberIndex) { double currentFitness = a [memberIndex].f; double globalBestFitness = fB; //1-exp(-(10000-x)/(10000*0.9)) return 1 - MathExp (-(globalBestFitness - currentFitness) / (globalBestFitness * theta)); } //——————————————————————————————————————————————————————————————————————————————
El método CalculateII de la clase C_AO_ASO es completamente similar al anterior, pero utiliza la mejor y actual aptitud propia.
La función exponencial ayuda a suavizar los cambios y proporciona una transición suave entre valores. El método CalculateII calcula un índice de mejora para un miembro de la población que tiene en cuenta lo bien que se compara el estado de forma actual con los logros personales.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ASO::CalculateII (int memberIndex) { double currentFitness = a [memberIndex].f; double personalBestFitness = member [memberIndex].pBestFitness; //1-exp(-(10000-x)/(10000*0.9)) return 1 - MathExp (-(personalBestFitness - currentFitness) / (personalBestFitness * delta)); } //——————————————————————————————————————————————————————————————————————————————
Pasemos al método CurrentMP de la clase C_AO_ASO. Descripción:
1. Generación de números aleatorios:
- r1 = u.RNDprobab () - generar un número aleatorio r1 en el rango [0, 1].
- r2 = u.RNDprobab () - generar un número aleatorio r2 en el rango [0, 1].
2. Calcular velocity: la ecuación incluye tres componentes:
- omega * (agent.c [coordInd] - memb.pBest [coordInd]) - componente inercial, el movimiento del agente teniendo en cuenta su posición anterior.
- lambda1 * r1 * (memb.pBest[coordInd] - agent.c[coordInd]) - dirigir al agente teniendo en cuenta su mejor posición personal.
- lambda2 * r2 * (cB[coordInd] - agent.c[coordInd]) - dirige al agente teniendo en cuenta la mejor posición de la población.
3. Actualización de la posición del agente añadiendo la velocidad al valor de la coordenada actual.
El método CurrentMP implementa la actualización de la posición del agente en el espacio basándose en su posición actual, su mejor posición personal y la mejor posición de la población.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::CurrentMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd) { double r1 = u.RNDprobab (); double r2 = u.RNDprobab (); double velocity = omega * (agent.c [coordInd] - memb.pBest [coordInd]) + lambda1 * r1 * (memb.pBest [coordInd] - agent.c [coordInd]) + lambda2 * r2 * (cB [coordInd] - agent.c [coordInd]); agent.c [coordInd] += velocity; } //——————————————————————————————————————————————————————————————————————————————
El método SocietyMP de la clase C_AO_ASO actualiza las coordenadas del agente basándose en una elección aleatoria entre información grupal y personal. Esto permite al agente adaptarse al estado tanto de toda la población como de un agente individual.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::SocietyMP (S_AO_Agent &agent, int coordInd) { int otherMember = u.RNDminusOne (popSize); agent.c [coordInd] = u.RNDprobab () < 0.5 ? cB [coordInd] : member [otherMember].pBest [coordInd]; } //——————————————————————————————————————————————————————————————————————————————
El método PastMP de la clase C_AO_ASO actualiza la coordenada del agente basándose en una elección aleatoria entre el mejor estado actual del miembro de la población y su estado anterior. Esto permite al agente tener en cuenta tanto los logros actuales de un miembro de la población como sus resultados pasados. Este enfoque mejora las propiedades combinatorias del algoritmo.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::PastMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd) { agent.c [coordInd] = u.RNDprobab () < 0.5 ? memb.pBest [coordInd] : memb.pPrev [coordInd]; } //——————————————————————————————————————————————————————————————————————————————
3. Resultados de las pruebas
Resultados del banco de pruebas ASO:
ASO|Anarchy Society Optimization|50.0|0.01|0.7|1.5|1.5|0.5|0.1|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.8487202680440514
25 Hilly's; Func runs: 10000; result: 0.746458607174428
500 Hilly's; Func runs: 10000; result: 0.31465494017509904
=============================
5 Forest's; Func runs: 10000; result: 0.9614752193694915
25 Forest's; Func runs: 10000; result: 0.7915027321897546
500 Forest's; Func runs: 10000; result: 0.23802894131144553
=============================
5 Megacity's; Func runs: 10000; result: 0.5707692307692309
25 Megacity's; Func runs: 10000; result: 0.5406153846153848
500 Megacity's; Func runs: 10000; result: 0.16613846153846298
=============================
All score: 5.17836 (57.54%)
Si observamos la visualización del funcionamiento del algoritmo, podemos sacar algunas conclusiones: hay una dispersión de resultados. Sin embargo, el algoritmo demuestra una buena capacidad de búsqueda cuando trabaja con funciones de grandes dimensiones, lo que también confirman sus resultados.
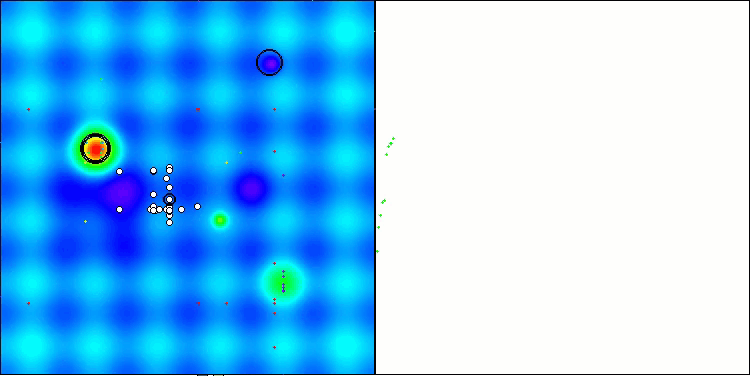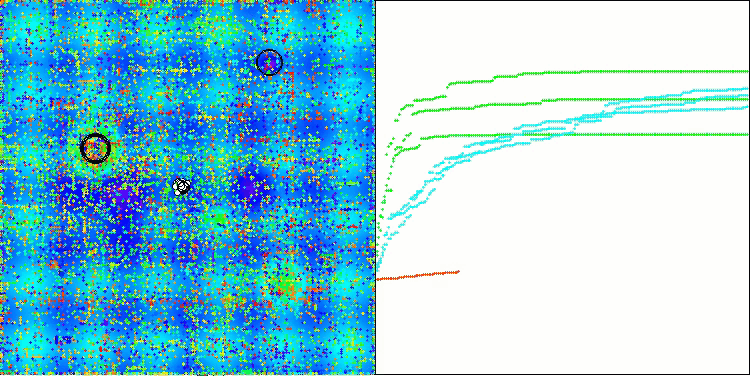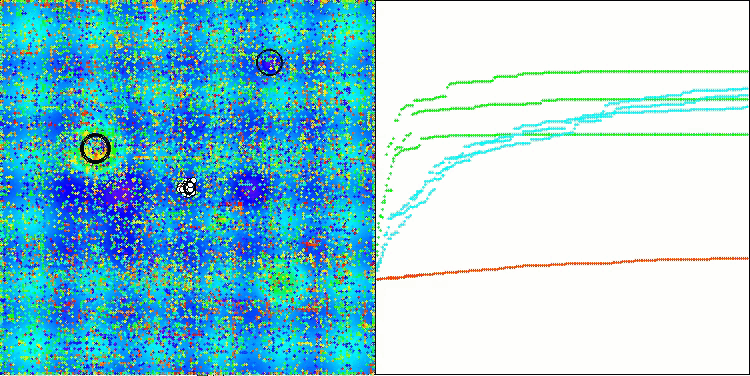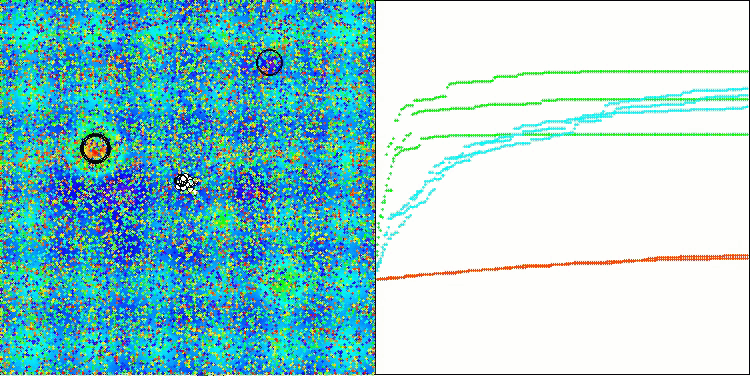
ASO en la función Hilly.
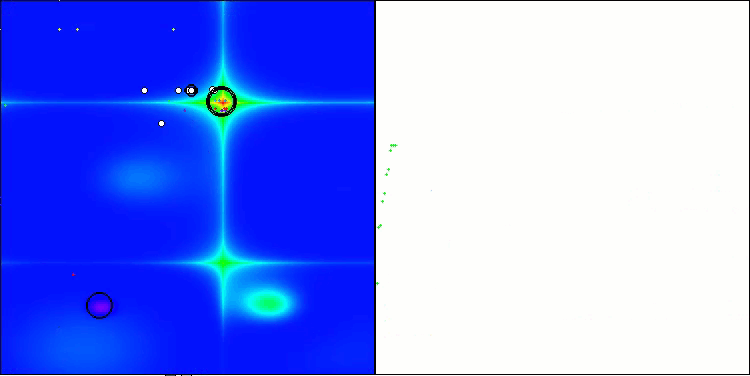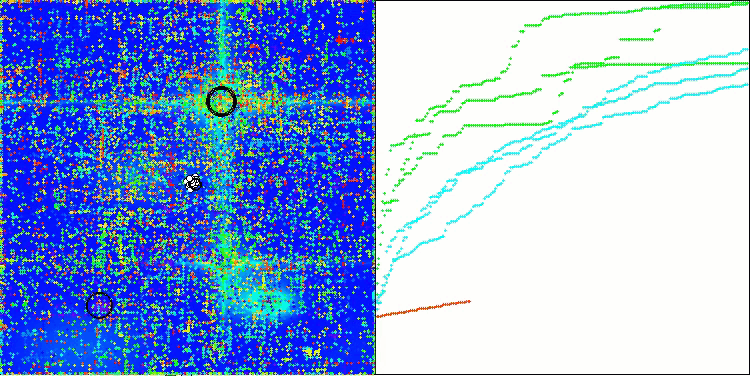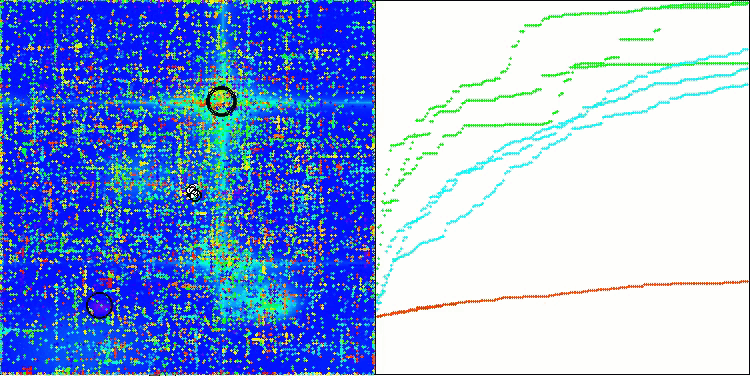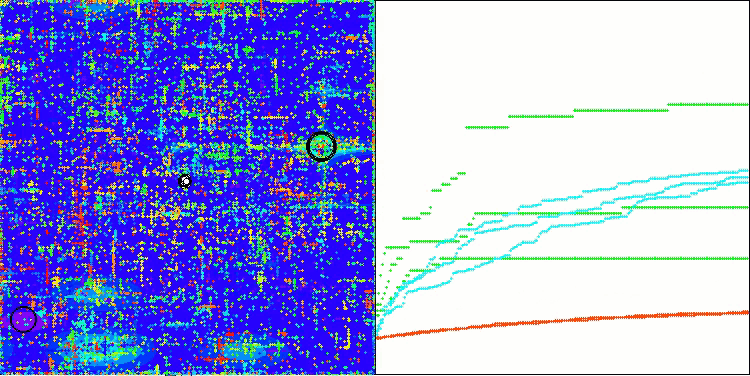
ASO sobre la función Forest.
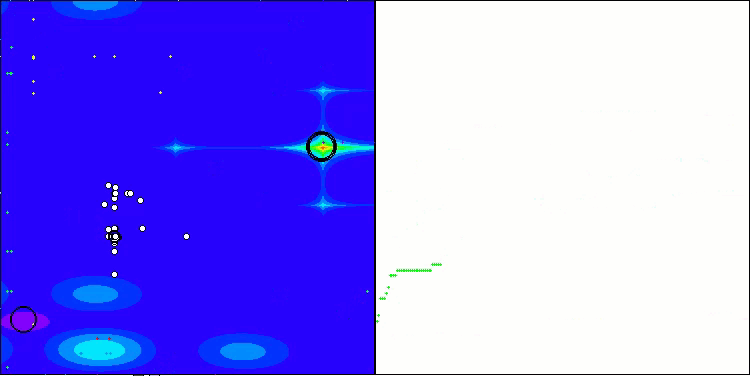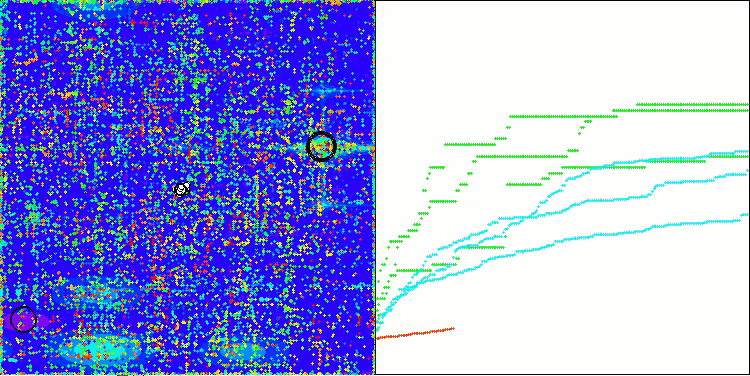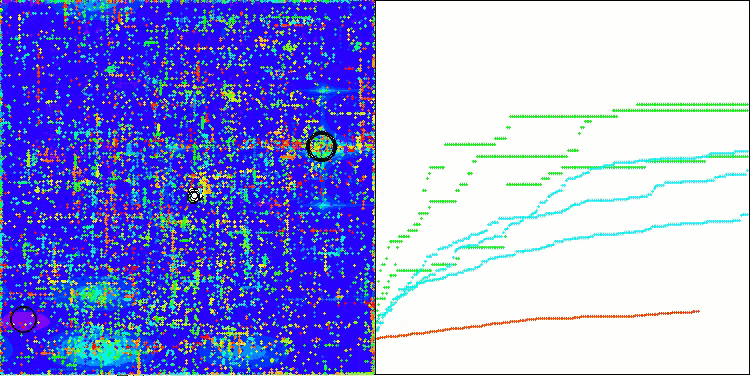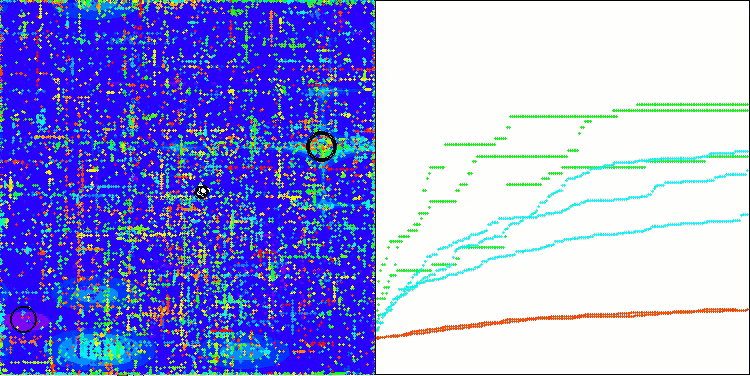
ASO sobre la función Megacity.
Tabla de clasificación de los algoritmos de optimización de la población: El algoritmo ASO se situó entre los diez primeros tras la prueba y ocupó el noveno puesto en la tabla de clasificación.
| # | AO | Descripción | Hilly | Hilly final | Forest | Forest final | Megacity (discreto) | Megacity final | Resultado final | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | A través de la búsqueda de vecinos | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Algoritmo de bloqueo de código | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | (P+O)ES | (P+O) estrategias de evolución | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 4 | CTA | Algoritmo de cola de cometa | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 5 | SDSm | Búsqueda por difusión estocástica M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 6 | ESG | Evolución de los grupos sociales | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 7 | SIA | Recocido isotrópico simulado | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 8 | ACS | Búsqueda cooperativa artificial | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 9 | ASO | Optimización de la sociedad anárquica | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 10 | TSEA | Algoritmo de evolución del caparazón de tortuga | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 11 | DE | Evolución diferencial | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 12 | CRO | Optimización de reacciones químicas | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 13 | BSA | Algoritmo de enjambre de aves | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 14 | HS | Búsqueda de armonía | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 15 | SSG | Siembra y crecimiento de plantones | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 16 | (PO)ES | (PO) Estrategias de evolución | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 17 | BSO | Optimización de la lluvia de ideas | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 18 | WOAm | Algoritmo de optimización de Wale M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 19 | AEFA | Algoritmo de campo eléctrico artificial | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 20 | ACOm | Optimización de colonias de hormigas M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 21 | BFO-GA | Optimización de la alimentación bacteriana - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 22 | ABHA | Algoritmo de colmena artificial | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 23 | ASBO | Optimización del comportamiento social adaptativo | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 24 | MEC | Computación evolutiva de la mente | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 25 | IWO | Optimización de malezas invasoras | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 26 | Micro-AIS | Microsistema inmunológico artificial | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 27 | COAm | Algoritmo de optimización de cuco M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 28 | SDOm | Optimización de la dinámica espiral M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 29 | NMm | Método de Nelder-Mead M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 30 | FAm | Algoritmo de luciérnaga M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 31 | GSA | Algoritmo de búsqueda gravitacional | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 32 | BFO | Optimización de la búsqueda de alimento bacteriano | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 33 | ABC | Colonia de abejas artificial | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 34 | BA | Algoritmo de murciélago | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 35 | SA | Recocido simulado | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 36 | IWDm | Gotas de agua inteligentes M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 37 | PSO | Optimización del enjambre de partículas | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 38 | Boids | Algoritmo de boids | 0.43340 | 0.30581 | 0.25425 | 0.99346 | 0.35718 | 0.20160 | 0.15708 | 0.71586 | 0.27846 | 0.14277 | 0.09834 | 0.51957 | 2.229 | 24.77 |
| 39 | MA | Algoritmo del mono | 0.59107 | 0.42681 | 0.31816 | 1.33604 | 0.31138 | 0.14069 | 0.06612 | 0.51819 | 0.22833 | 0.08567 | 0.02790 | 0.34190 | 2.196 | 24.40 |
| 40 | SFL | Algoritmo de salto de rana barajado | 0.53925 | 0.35816 | 0.29809 | 1.19551 | 0.37141 | 0.11427 | 0.04051 | 0.52618 | 0.27167 | 0.08667 | 0.02402 | 0.38235 | 2.104 | 23.38 |
| 41 | FSS | Búsqueda de bancos de peces | 0.55669 | 0.39992 | 0.31172 | 1.26833 | 0.31009 | 0.11889 | 0.04569 | 0.47467 | 0.21167 | 0.07633 | 0.02488 | 0.31288 | 2.056 | 22.84 |
| 42 | RND | Aleatorio | 0.52033 | 0.36068 | 0.30133 | 1.18234 | 0.31335 | 0.11787 | 0.04354 | 0.47476 | 0.25333 | 0.07933 | 0.02382 | 0.35648 | 2.014 | 22.37 |
| 43 | GWO | Optimizador de lobo gris | 0.59169 | 0.36561 | 0.29595 | 1.25326 | 0.24499 | 0.09047 | 0.03612 | 0.37158 | 0.27667 | 0.08567 | 0.02170 | 0.38403 | 2.009 | 22.32 |
| 44 | CSS | Búsqueda de sistema cargado | 0.44252 | 0.35454 | 0.35201 | 1.14907 | 0.24140 | 0.11345 | 0.06814 | 0.42299 | 0.18333 | 0.06300 | 0.02322 | 0.26955 | 1.842 | 20.46 |
| 45 | EM | Algoritmo similar al electromagnetismo | 0.46250 | 0.34594 | 0.32285 | 1.13129 | 0.21245 | 0.09783 | 0.10057 | 0.41085 | 0.15667 | 0.06033 | 0.02712 | 0.24412 | 1.786 | 19.85 |
Resumen
Con base en los resultados de la operación del algoritmo en las funciones de prueba de diferentes dimensiones, se pueden sacar las siguientes conclusiones: ASO muestra resultados promedio en la función Hilly suave en comparación con sus vecinos más cercanos en la tabla, pero resultados muy decentes en la función Forest "aguda" y especialmente en la Megacity discreta. La puntuación final global es 5,17836 (57,54%). El algoritmo demuestra buenas capacidades de búsqueda, especialmente cuando se trabaja con funciones de gran dimensión. En otras palabras, escala bien. El algoritmo puede recomendarse para resolver problemas de optimización discreta, lo cual es una prioridad para los traders.
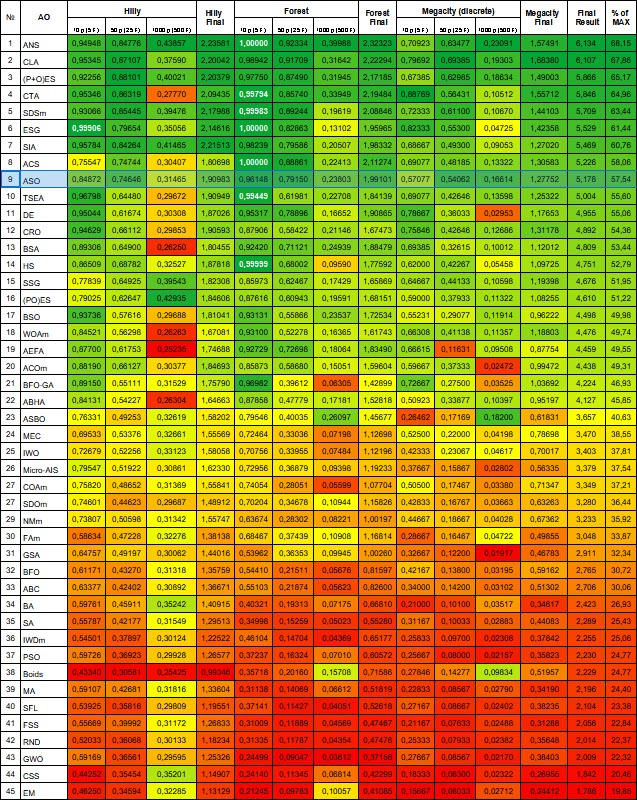
Figura 4. Gradación por colores de los algoritmos según las pruebas pertinentes. Los resultados superiores o iguales a 0,99 se resaltan en blanco.
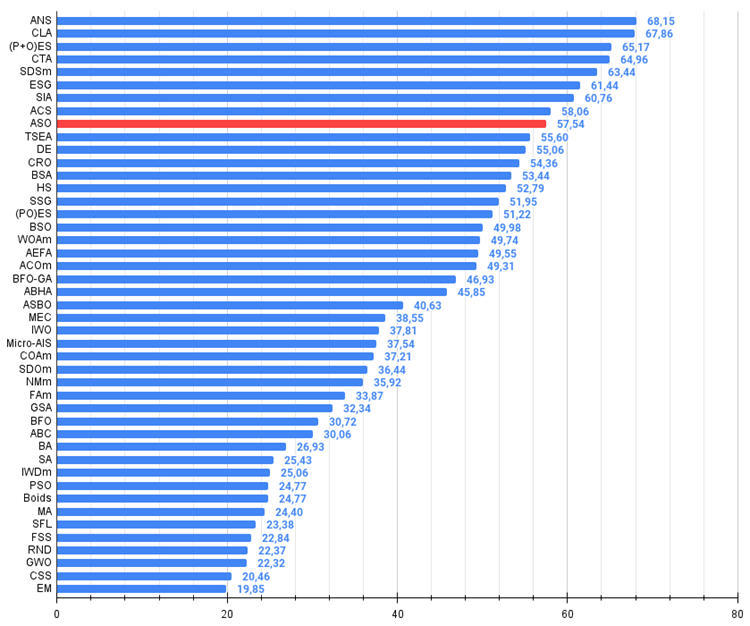
Figura 5. El histograma de los resultados de las pruebas de algoritmos (en una escala de 0 a 100, cuanto más, mejor,
donde 100 es el máximo resultado teórico posible, el archivo contiene un script para calcular la tabla de clasificación).
Ventajas e inconvenientes del algoritmo ASO:
Ventajas:
- Buena convergencia en varias funciones.
- Excelentes resultados en funciones discretas.
Desventajas:
- Gran cantidad de parámetros (muy difícil de configurar).
- Dispersión de resultados en funciones de baja dimensión.
- Implementación compleja.
El artículo se acompaña de un archivo con las versiones actuales de los códigos del algoritmo. El autor del artículo no es responsable de la exactitud absoluta en la descripción de los algoritmos canónicos. Se han realizado cambios en muchos de ellos para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15511
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Búsqueda con restricciones — Tabu Search (TS).
Búsqueda con restricciones — Tabu Search (TS).
 Redes neuronales en el trading: Transformador vectorial jerárquico (HiVT)
Redes neuronales en el trading: Transformador vectorial jerárquico (HiVT)
 Gráficos del índice del dólar y del índice del euro — ejemplo de servicio en MetaTrader 5
Gráficos del índice del dólar y del índice del euro — ejemplo de servicio en MetaTrader 5
 Del básico al intermedio: Array (IV)
Del básico al intermedio: Array (IV)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso