Algoritmo de optimización de neuroboides 2 — Neuroboids Optimization Algorithm 2 (NOA2)

Contenido

1. Introducción
2. Implementación del algoritmo
3. Resultados de las pruebas

Introducción

Al sumergirme cada vez más en los algoritmos de optimización a lo largo de los años, con frecuencia me atraían dos inspiraciones paralelas, como la autoorganización de los enjambres biológicos y la capacidad de aprendizaje adaptativo de las redes neuronales. La síntesis de estos dos paradigmas me llevó a desarrollar un algoritmo de enfoque híbrido que combina la inteligencia espacial de los Boids de Craig Reynolds con la capacidad de aprendizaje adaptativo que poseen las redes neuronales.

Mi viaje comenzó con la observación de que los algoritmos de enjambre tradicionales, aunque adecuados para explorar espacios de búsqueda complejos a través de un comportamiento colectivo, a menudo carecen de la capacidad de aprender de la historia de sus exploraciones. Y al contrario, las redes neuronales son excelentes en el aprendizaje de patrones complejos, pero pueden tener dificultades con la exploración espacial eficiente cuando se aplican directamente a problemas de optimización. La pregunta que impulsó mi investigación resultaba aparentemente sencilla: ¿y si cada agente del enjambre pudiera aprender a mejorar sus estrategias de movimiento usando una red neuronal específica?

El algoritmo resultante utiliza agentes que siguen las reglas boid clásicas de cohesión, separación y alineación, lo cual les permite autoorganizarse y explorar el espacio de búsqueda con eficacia. No obstante, a diferencia de las implementaciones boid tradicionales, cada agente está equipado con una red neuronal multicapa que aprende continuamente de la experiencia del agente adaptando sus estrategias de movimiento a las características específicas del paisaje de adaptabilidad. Este nivel de control neuronal influye gradualmente en el comportamiento de los boids, pasando de estrategias dominadas por la exploración en las primeras iteraciones a movimientos impulsados por la explotación a medida que se identifican regiones prometedoras.

Lo que más me fascinó durante el desarrollo fue observar cómo las redes neuronales evolucionaban con estrategias distintas según su posición en el espacio de búsqueda. Los agentes situados cerca de zonas prometedoras desarrollaron patrones neuronales que potenciaron la explotación local, mientras que los situados en zonas poco pobladas favorecieron el comportamiento exploratorio. Dicha especialización emergente surgió de forma natural a partir de procesos de aprendizaje individuales, creando un enjambre con un comportamiento heterogéneo y dependiente del contexto, sin coordinación global aparente.

En este artículo, presentaremos la arquitectura, los detalles de implementación y el análisis de rendimiento del algoritmo NOA2, así como una demostración de sus capacidades en varios parámetros de referencia. 

Implementación del algoritmo

Puede que me esté repitiendo, la idea básica del algoritmo de neuroboids consiste en combinar dos paradigmas: la inteligencia colectiva de los algoritmos de enjambre y el aprendizaje adaptativo de las redes neuronales.

En el algoritmo tradicional de boids que propuso Craig Reynolds, los agentes siguen tres reglas sencillas: convergencia (moverse hacia el centro del grupo), separación (evitar colisiones) y alineación (igualar la velocidad con los vecinos). Estas reglas crean un comportamiento de grupo realista, similar al de los pájaros en bandada. Los neuroboids amplían este concepto dotando a cada agente de una red neuronal individual que aprende de la experiencia del agente conforme explora el espacio de búsqueda. Esta red neuronal realiza dos funciones clave:

1. Control de movimiento adaptativo: ajusta la velocidad del agente según el estado actual y la historia de movimientos.
2. Modificación de las reglas estándar de boids: ajusta dinámicamente el impacto de las reglas de convergencia, separación y alineación en función del contexto.

El resultado es un algoritmo híbrido en el que cada agente mantiene el comportamiento social necesario para explorar el espacio de forma eficiente, pero se adapta individualmente al paisaje de la función de aptitud mediante el aprendizaje. Esto crea un equilibrio autorregulado entre exploración y explotación.

Las principales ventajas de este enfoque son que los agentes aprenden de manera autónoma estrategias de movimiento óptimas, como consecuencia de lo cual el algoritmo se adapta automáticamente a distintos tipos de paisajes de optimización, al tiempo que se preserva la exploración del espacio mediante un comportamiento colectivo sin control centralizado. Por poner una analogía sencilla: imagine una bandada de pájaros volando por el cielo. Se mueven con coherencia: ninguno choca, se mantienen unidos y vuelan en la misma dirección. Este comportamiento puede describirse con tres sencillas reglas: permanecer cerca de los vecinos (no separarse de la bandada), no chocar con ellos (mantener la distancia) y volar en la misma dirección (mantener un rumbo común).

Esta es la base del algoritmo llamado "boids" (de "bird-oid", "semejante a un pájaro"). Cada ave de la bandada no se limita a seguir estas reglas, sino que es capaz de aprender de sus experiencias. El pájaro recuerda qué acciones le llevaron al éxito (por ejemplo, encontrar más comida) y cuáles de ellas no. Con el tiempo, se vuelve más inteligente y toma mejores decisiones sobre cómo volar. Esta es la esencia del algoritmo de neuroboids: combinar las sencillas reglas del movimiento en grupo con la capacidad de cada participante para aprender de su propia experiencia. El "neuro" del nombre se refiere exactamente a la capacidad de aprender. Este enfoque resulta especialmente interesante porque combina el poder de la investigación colaborativa (nadie se pierde un área importante) con los beneficios del aprendizaje individualizado (cada uno se convierte en el mejor en su área de búsqueda).

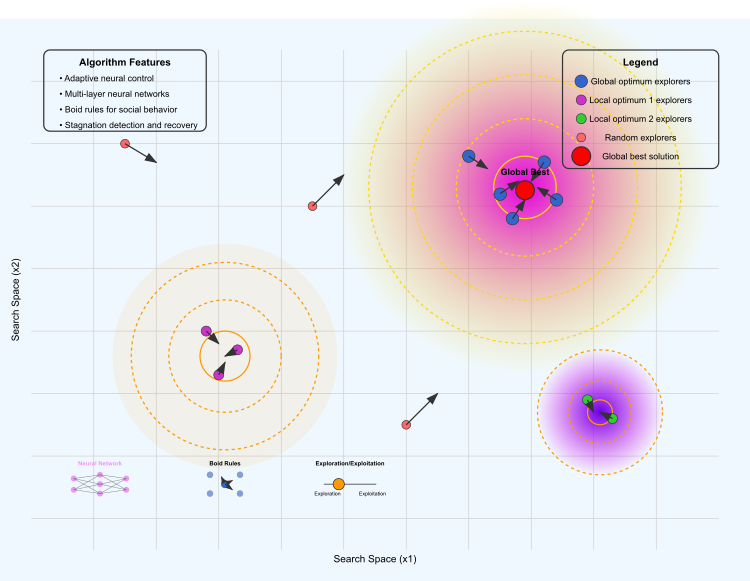
Figura 1. Ilustración del funcionamiento del algoritmo NOA2  

La ilustración muestra los siguientes elementos clave: el paisaje de optimización, en el que la región amarilla y morada representa el óptimo global, las regiones naranja y morada representan los óptimos locales, y las curvas de nivel muestran la "altura" del paisaje de la función de aptitud. 

Diferentes grupos de agentes: los agentes azules exploran la región del óptimo global, los agentes morados se concentran en torno al primer óptimo local, los agentes verdes exploran el segundo óptimo local y los agentes rojos exploran el espacio de forma aleatoria. Las flechas muestran la dirección de movimiento de los boids. El punto rojo marca la mejor solución encontrada actualmente.

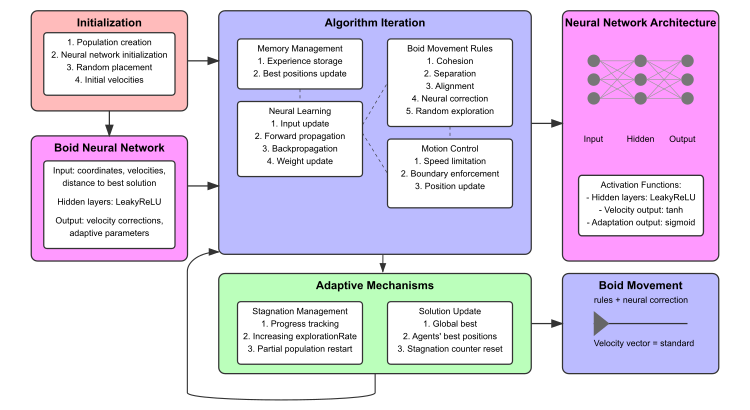
Figura 2. Esquema de funcionamiento del algoritmo NOA2  

El esquema incluye: un bloque de inicialización (rojo), una red neuronal de boid (rosa), iteraciones del algoritmo con subbloques (azul), mecanismos adaptativos (verde) y visualización de la arquitectura de la red neuronal con conexiones de ejemplo. La parte inferior muestra esquemas en miniatura en forma de estructura de red neuronal, la visualización de las reglas de movimiento de los boids y el entre investigación y explotación.

Una vez entendido el concepto básico, podemos empezar a describir el pseudocódigo del algoritmo.

INICIALIZACIÓN:

• Establecemos los parámetros de búsqueda y creamos una población de agentes.
• Para cada agente: inicializamos una posición aleatoria, una velocidad pequeña, una red neuronal (entrada → oculta → capas de salida) y una memoria de experiencia vacía.
• Establecemos la mejor adaptabilidad global en infinito negativo y el contador de estancamiento en cero.

CICLO GENERAL:

• Para cada iteración:

  EVALUACIÓN:

  • Calculamos la adaptabilidad de todos los agentes.
  • Actualizamos las primeras posiciones personales y globales.
  • Guardamos los experimentos en los búferes de memoria.

  GESTIÓN DEL ESTANCAMIENTO:

  • Si no hay mejora: aumentamos la investigación, reiniciamos los agentes débiles de vez en cuando.
  • En caso contrario: reducimos gradualmente el nivel de investigación.

  PROCESAMIENTO NEURONAL:

  • Para cada agente:
    • Pasada directa: entradas (posición, velocidad, distancia al mejor, adaptabilidad) → capas ocultas → salidas.
    • Si se acumula suficiente experiencia y se detecta una mejora: actualizamos los pesos neuronales.

  ACTUALIZACIÓN DEL MOVIMIENTO:

  • Para cada agente:
    • Calculamos las fuerzas estándar de boids (cohesión, separación, nivelación).
    • Aplicamos fuerzas modificadas por neuronas y correcciones neuronales directas.
    • Añadimos un componente de investigación aleatoria con probabilidad.
    • Hacemos cumplir los límites de velocidad y consideramos los límites.
    • Actualizamos la posición según la velocidad final.

CÁLCULOS DE SOPORTE:

• Cálculo de la masa: normalizamos los valores de adaptabilidad para asignar una masa a cada agente.
• Cohesión: nos desplazamos hacia el centro de masa ponderado de los agentes más próximos.
• Separación: evitamos la aglomeración de vecinos.
• Alineación: coordinamos la velocidad con los agentes cercanos.
• Actualización neuronal: retropropagación simplificada basada en la mejora de la adaptabilidad.

RETORNO: mejor posición global y adaptabilidad.

Ahora todo está preparado para escribir el código del algoritmo. Asignaremos la estructura "S_NeuroBoids_Agent", que será un agente neuroboid basado en una arquitectura de red neuronal para realizar tareas de optimización. En esta implementación, el agente tendrá los siguientes componentes y funciones clave:

Coordenadas y velocidades:

• x [] — coordenadas actuales del agente.
• dx [] — velocidades actuales del agente.

Red neuronal:

• inputs [] — valores de entrada para las neuronas (coordenadas, velocidades, distancia a la mejor posición conocida, etc.).
• outputs [] — valores de salida de la red neuronal (corrección de velocidad y parámetros de adaptación).
• steps [] — pesos de los enlaces en la red neuronal.
• biases [] — sesgos para las neuronas.

Memoria:

• memory [] — array para almacenar las posiciones anteriores y sus valores de aptitud.
• memory_size — tamaño máximo de la memoria para el almacenamiento.
• memory_index — índice actual en la memoria.

Aptitud y masa:

• best_local_fitness — mejor agente local de aptitud.
• m — masa del agente.
• cB [] — coordenadas de la mejor posición encontrada por el agente.
• fB — valor de la función de aptitud para la mejor posición.

Inicialización: (Init) todas los arrays y variables se inicializan con ceros o valores aleatorios. Se fijan los tamaños de los arrays y se inicializan las influencias (pesos y desplazamientos) con pequeños valores aleatorios.

Funciones de activación — Tanh, ReLU, Sigmoid; diferentes funciones de activación que se aplican en la red neuronal.

Activación de los datos de entrada (UpdateInputs) — rellena un array con las coordenadas actuales, las velocidades, la distancia a la mejor posición conocida y el valor de aptitud actual.

Pasada directa (ForwardPass) — calcula las salidas de la red neuronal basándose en las entradas, los pesos y los desplazamientos aplicando funciones de activación.

Aprendizaje basado en la experiencia (Learn) — actualiza los pesos y desplazamientos según la experiencia si la experiencia actual es mejor que la anterior.

Memorización de la experiencia (MemorizeExperience) — guarda en la memoria las coordenadas actuales y la forma física del agente.

Actualización de la mejor posición (UpdateBestPosition) — si el valor de aptitud actual es mejor que el encontrado anteriormente, actualiza la mejor posición.

//——————————————————————————————————————————————————————————————————————————————
// Neuro-boid agent structure
//——————————————————————————————————————————————————————————————————————————————
struct S_NeuroBoids_Agent
{
    double x       [];            // current coordinates
    double dx      [];            // current speeds
    double inputs  [];            // neuron inputs
    double outputs [];            // neuron outputs
    double weights [];            // neuron weights
    double biases  [];            // neuron biases
    double memory  [];            // memory of previous positions and their fitnesses
    int    memory_size;           // memory size for accumulating experience
    int    memory_index;          // current index in memory
    double best_local_fitness;    // best local agent fitness
    double m;                     // boid mass
    double cB [];                 // best position coordinates
    double fB;                    // fitness function value

    // Agent initialization
    void Init (int coords, int neuron_size)
    {
      ArrayResize (x, coords);
      ArrayResize (dx, coords);
      ArrayInitialize (x, 0.0);
      ArrayInitialize (dx, 0.0);

      // Initialize the best position structure
      ArrayResize     (cB, coords);
      ArrayInitialize (cB, 0.0);
      fB = -DBL_MAX;

      // Inputs: coordinates, speeds, distance to best, etc.
      int input_size = coords * 2 + 2; // x, dx, dist_to_best, current_fitness
      ArrayResize (inputs, input_size);
      ArrayInitialize (inputs, 0.0);

      // Outputs: Speed correction and adaptive factors for flock rules
      int output_size = coords + 3; // dx_correction + 3 adaptive parameters
      ArrayResize (outputs, output_size);
      ArrayInitialize (outputs, 0.0);

      // Weights and biases for each output
      ArrayResize (weights, input_size * output_size);
      ArrayInitialize (weights, 0.0);
      ArrayResize (biases, output_size);
      ArrayInitialize (biases, 0.0);

      // Initialize weights and biases with small random values
      for (int i = 0; i < ArraySize (weights); i++)
      {
        weights [i] = 0.01 * (MathRand () / 32767.0 * 2.0 - 1.0);
      }

      for (int i = 0; i < ArraySize (biases); i++)
      {
        biases [i] = 0.01 * (MathRand () / 32767.0 * 2.0 - 1.0);
      }

      // Initialize memory for accumulating experience
      memory_size = 10;
      ArrayResize (memory, memory_size * (coords + 1)); // coordinates + fitness
      ArrayInitialize (memory, 0.0);
      memory_index = 0;
      best_local_fitness = -DBL_MAX;

      // Initialize mass
      m = 0.5;
    }

    // Activation function - hyperbolic tangent
    double Tanh (double input_val)
    {
      return MathTanh (input_val);
    }

    // ReLU activation function
    double ReLU (double input_val)
    {
      return (input_val > 0.0) ? input_val : 0.0;
    }

    // Sigmoid activation function
    double Sigmoid (double input_val)
    {
      return 1.0 / (1.0 + MathExp (-input_val));
    }

    // Updating neural network inputs - Corrected version
    void UpdateInputs (double &global_best [], double current_fitness, int coords_count)
    {
      int input_index = 0;

      // Coordinates
      for (int c = 0; c < coords_count; c++)
      {
        inputs [input_index++] = x [c];
      }

      // Speeds
      for (int c = 0; c < coords_count; c++)
      {
        inputs [input_index++] = dx [c];
      }

      // Distance to the best global solution
      double dist_to_best = 0;
      for (int c = 0; c < coords_count; c++)
      {
        dist_to_best += MathPow (x [c] - global_best [c], 2);
      }
      dist_to_best = MathSqrt (dist_to_best);
      inputs [input_index++] = dist_to_best;

      // Current fitness function
      inputs [input_index++] = current_fitness;
    }

    // Direct distribution over the network
    void ForwardPass (int coords_count)
    {
      int input_size = ArraySize (inputs);
      int output_size = ArraySize (outputs);

      // For each output, calculate the weighted sum of the inputs + bias
      for (int o = 0; o < output_size; o++)
      {
        double sum = biases [o];

        for (int i = 0; i < input_size; i++)
        {
          sum += inputs [i] * weights [o * input_size + i];
        }

        // Apply different activation functions depending on the output
        if (o < coords_count) // Use the hyperbolic tangent to correct the speed
        {
          outputs [o] = Tanh (sum);
        }
        else // Use sigmoid for adaptive parameters
        {
          outputs [o] = Sigmoid (sum);
        }
      }
    }

    // Learning from accumulated experience
    void Learn (double learning_rate, int coords_count)
    {
      if (memory_index < memory_size) return; // Insufficient experience

      // Find the best experience in memory
      int best_index = 0;
      double best_fitness = memory [coords_count]; // The first fitness function in memory

      for (int i = 1; i < memory_size; i++)
      {
        double fitness = memory [i * (coords_count + 1) + coords_count];
        if (fitness > best_fitness)
        {
          best_fitness = fitness;
          best_index = i;
        }
      }

      // If the current experience is not better than the previous one, do not update the weights
      if (best_fitness <= best_local_fitness) return;

      best_local_fitness = best_fitness;

      // Simple method for updating weights
      int input_size = ArraySize (inputs);
      int output_size = ArraySize (outputs);

      // Simple form of gradient update
      for (int o = 0; o < output_size; o++)
      {
        for (int i = 0; i < input_size; i++)
        {
          int weight_index = o * input_size + i;
          if (weight_index < ArraySize (weights))
          {
            weights [weight_index] += learning_rate * outputs [o] * inputs [i];
          }
        }

        // Update offsets
        biases [o] += learning_rate * outputs [o];
      }
    }

    // Save current experience (coordinates and fitness)
    void MemorizeExperience (double fitness, int coords_count)
    {
      int offset = memory_index * (coords_count + 1);

      // Save the coordinates
      for (int c = 0; c < coords_count; c++)
      {
        memory [offset + c] = x [c];
      }

      // Save the fitness function
      memory [offset + coords_count] = fitness;

      // Update the memory index
      memory_index = (memory_index + 1) % memory_size;
    }

    // Update the agent's best position
    void UpdateBestPosition (double current_fitness, int coords_count)
    {
      if (current_fitness > fB)
      {
        fB = current_fitness;
        ArrayCopy (cB, x, 0, 0, WHOLE_ARRAY);
      }
    }
};

La clase "C_AO_NOA2" es una implementación del algoritmo NOA2 y se hereda de la clase básica "C_AO". Veamos más de cerca la estructura y los aspectos clave de esta clase.

Parámetros clave:

• popSize — tamaño de la población de agentes (boids).
• cohesionWeight, cohesionDist — peso y distancia de la regla de cohesión.
• separationWeight, separationDist — peso y distancia de la regla de separación.
• alignmentWeight, alignmentDist — peso y distancia de la regla de alineación.
• maxSpeed y minSpeed — velocidades máxima y mínima de los agentes.
• learningRate — velocidad de aprendizaje de la red neuronal.
• neuralInfluence — influencia de la red neuronal en el movimiento de los agentes.
• ExplorationRate — probabilidad de exploración aleatoria del espacio de soluciones.
• m_stagnationCounter y m_prevBestFitness — contador de estancamiento y valor anterior de mejor valor de aptitud.

Métodos de clase:

• SetParams () — método que establece los parámetros del algoritmo basándose en los valores almacenados en el array "params".
• Init () — inicialización, acepta los parámetros para definir los rangos de valores para los agentes. Este método establece las condiciones iniciales para que se ejecute el algoritmo.
• Moving () — se encarga del movimiento de los agentes usando como base varias reglas de interacción.
• Revision () — se utiliza para revisar el estado de los agentes durante la ejecución del algoritmo.

Agentes: S_NeuroBoids_Agent agent [] — array de agentes que representan los boids en la población.

Métodos privados (para el uso dentro de una clase):

• CalculateMass () — calcula la masa de los agentes.
• Cohesión () — implementa la regla de convergencia.
• Separation () — implementa la regla de separación.
• Alignment () — implementa la regla de alineación.
• LimitSpeed () — limita la velocidad del agente.
• KeepWithinBounds () — mantiene a los agentes dentro de los límites dados.
• Distance () — calcula la distancia entre dos agentes.
• ApplyNeuralControl () — aplica el control de la red neuronal al agente.
• AdaptiveExploration() — implementa la exploración adaptativa.

//——————————————————————————————————————————————————————————————————————————————
// Class of neuron-like optimization algorithm inherited from C_AO
//——————————————————————————————————————————————————————————————————————————————
class C_AO_NOA2 : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_NOA2 () { }
  C_AO_NOA2 ()
  {
    ao_name = "NOA2";
    ao_desc = "Neuroboids Optimization Algorithm 2 (joo)";
    ao_link = "https://www.mql5.com/es/articles/17497";

    popSize          = 50;     // population size

    cohesionWeight   = 0.6;    // cohesion weight
    cohesionDist     = 0.001;  // cohesion distance

    separationWeight = 0.005;  // separation weight
    separationDist   = 0.03;   // separation distance

    alignmentWeight  = 0.1;    // alignment weight
    alignmentDist    = 0.1;    // alignment distance

    maxSpeed         = 0.001;  // maximum speed
    minSpeed         = 0.0001; // minimum speed 

    learningRate     = 0.01;   // neural network learning speed
    neuralInfluence  = 0.3;    // influence of the neural network on movement
    explorationRate  = 0.1;    // random exploration probability

    ArrayResize (params, 12);

    params [0].name  = "popSize";          params [0].val = popSize;

    params [1].name  = "cohesionWeight";   params [1].val  = cohesionWeight;
    params [2].name  = "cohesionDist";     params [2].val  = cohesionDist;

    params [3].name  = "separationWeight"; params [3].val  = separationWeight;
    params [4].name  = "separationDist";   params [4].val  = separationDist;

    params [5].name  = "alignmentWeight";  params [5].val  = alignmentWeight;
    params [6].name  = "alignmentDist";    params [6].val  = alignmentDist;

    params [7].name  = "maxSpeed";         params [7].val  = maxSpeed;
    params [8].name  = "minSpeed";         params [8].val  = minSpeed;

    params [9].name  = "learningRate";     params [9].val  = learningRate;
    params [10].name = "neuralInfluence";  params [10].val = neuralInfluence;
    params [11].name = "explorationRate";  params [11].val = explorationRate;

    // Initialize the stagnation counter and the previous best fitness value
    m_stagnationCounter = 0;
    m_prevBestFitness   = -DBL_MAX;
  }

  void SetParams ()
  {
    popSize          = (int)params [0].val;

    cohesionWeight   = params [1].val;
    cohesionDist     = params [2].val;

    separationWeight = params [3].val;
    separationDist   = params [4].val;

    alignmentWeight  = params [5].val;
    alignmentDist    = params [6].val;

    maxSpeed         = params [7].val;
    minSpeed         = params [8].val;

    learningRate     = params [9].val;
    neuralInfluence  = params [10].val;
    explorationRate  = params [11].val;
  }

  bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0);
  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double cohesionWeight;     // cohesion weight
  double cohesionDist;       // cohesion distance

  double separationWeight;   // separation weight
  double separationDist;     // separation distance

  double alignmentWeight;    // alignment weight
  double alignmentDist;      // alignment distance

  double minSpeed;           // minimum speed
  double maxSpeed;           // maximum speed

  double learningRate;       // neural network learning speed
  double neuralInfluence;    // influence of the neural network on movement
  double explorationRate;    // random exploration probability

  int m_stagnationCounter;   // stagnation counter
  double m_prevBestFitness;  // previous best fitness value

  S_NeuroBoids_Agent agent []; // agents (boids)

  private: //-------------------------------------------------------------------
  double distanceMax;     // maximum distance
  double speedMax [];     // maximum speeds by measurements

  int neuron_size;        // neuron size (number of inputs)

  void   CalculateMass       ();                                  // calculation of agent masses 
  void   Cohesion            (S_NeuroBoids_Agent &boid, int pos); // cohesion rule
  void   Separation          (S_NeuroBoids_Agent &boid, int pos); // separation rule
  void   Alignment           (S_NeuroBoids_Agent &boid, int pos); // alignment rule
  void   LimitSpeed          (S_NeuroBoids_Agent &boid);          // speed limit
  void   KeepWithinBounds    (S_NeuroBoids_Agent &boid);          // keep within bounds
  double Distance            (S_NeuroBoids_Agent &boid1, S_NeuroBoids_Agent &boid2); // calculate distance
  void   ApplyNeuralControl  (S_NeuroBoids_Agent &boid, int pos); // apply neural control
  void   AdaptiveExploration ();                                  // adaptive research
};
//——————————————————————————————————————————————————————————————————————————————

El método "Init" se encarga de inicializar el algoritmo y los parámetros del agente e inicia su trabajo con la llamada "StandardInit", transmitiéndole los arrays de valores mínimo y máximo del rango y los pasos de búsqueda. Si falla la inicialización estándar, el método retornará inmediatamente "false". Luego se establecerá el tamaño de la neurona que se utilizará en la red neuronal agente.

En este caso, el tamaño se calculará como el número de coordenadas multiplicado por 2, y se añadirán dos valores adicionales: "dist_to_best" y "current_fitness". El tamaño del array de agentes se redimensionará según el tamaño de población especificado "popSize". A continuación, para cada agente, se llamará al método "Init ", que inicializará sus parámetros, incluida la red neuronal.

Cálculo de la distancia y la velocidad máximas:

• La variable "distanceMax" se inicializará con cero.
• Para cada coordenada, el valor máximo de velocidad se calculará partiendo de la diferencia entre los valores máximo y mínimo del intervalo.
• La distancia máxima también se calculará como la raíz cuadrada de la suma de los cuadrados de las velocidades máximas.

El contador de estancamiento (m_stagnationCounter) se pondrá a cero, y la variable que almacenará el valor anterior de mejor forma física (m_prevBestFitness) se establecerá en el valor más bajo posible. El método establecerá diversas variables globales, como la convergencia, los pesos de separación y alineación, las velocidades máxima y mínima, la tasa de aprendizaje, la influencia de la red neuronal y la probabilidad de exploración. Si todos los pasos se han realizado correctamente, el método retornará "true", lo cual confirmará que la inicialización se ha realizado correctamente.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_NOA2::Init (const double &rangeMinP  [],  // minimum search range
                      const double &rangeMaxP  [],  // maximum search range
                      const double &rangeStepP [],  // search step
                      const int    epochsP)         // number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  // Determine the size of a neuron
  neuron_size = coords * 2 + 2; // x, dx, dist_to_best, current_fitness

  // Initialize the agents
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++)
  {
    agent [i].Init (coords, neuron_size);
  }

  distanceMax = 0;
  ArrayResize (speedMax, coords);

  for (int c = 0; c < coords; c++)
  {
    speedMax [c] = rangeMax [c] - rangeMin [c];
    distanceMax += MathPow (speedMax [c], 2);
  }

  distanceMax = MathSqrt (distanceMax);

  // Reset the stagnation counter and the previous best fitness value
  m_stagnationCounter = 0;
  m_prevBestFitness   = -DBL_MAX;

  GlobalVariableSet ("#reset", 1.0);

  GlobalVariableSet ("1cohesionWeight",   params [1].val);
  GlobalVariableSet ("2cohesionDist",     params [2].val);

  GlobalVariableSet ("3separationWeight", params [3].val);
  GlobalVariableSet ("4separationDist",   params [4].val);

  GlobalVariableSet ("5alignmentWeight",  params [5].val);
  GlobalVariableSet ("6alignmentDist",    params [6].val);

  GlobalVariableSet ("7maxSpeed",         params [7].val);
  GlobalVariableSet ("8minSpeed",         params [8].val);

  GlobalVariableSet ("9learningRate",     params [9].val);
  GlobalVariableSet ("10neuralInfluence", params [10].val);
  GlobalVariableSet ("11explorationRate", params [11].val);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

El método Moving se encargará de desplazar a los agentes en el entorno según los datos obtenidos y las interacciones entre ellos. En primer lugar, el método comprobará el valor de la variable global "#reset", si es igual a 1,0, se restablecerán los parámetros (la variable "revision" se pondrá en "false" y luego volverá a "0,0"). De las variables globales se extraerán los valores de diversos parámetros, como la convergencia, los pesos de separación y alineación, las velocidades mínima y máxima, la tasa de aprendizaje, la influencia de la red neuronal y la relación de exploración. Estos parámetros pueden configurarse para modificar el comportamiento de los agentes.

Si la variable "revisión" es "false", se inicializarán las posiciones "x" y velocidades "dx" de los agentes. Luego se aplicarán valores aleatorios de un rango determinado a cada coordenada, y las velocidades se fijarán en pequeños valores aleatorios. Cada coordenada almacenará igualmente el estado del agente según su posición actual. El método "AdaptiveExploration ()" se llamará para la exploración adaptativa, que puede cambiar el comportamiento de los agentes según el estado de estancamiento.

Ciclo de movimiento básico de los agentes (para cada uno):

• Primero se guardará la experiencia actual del agente.
• Luego se actualizará la mejor posición que haya encontrado el agente.
• Después se actualizarán los datos de entrada de la red neuronal del agente.
• Y se realizará una propagación directa de los datos a través de la red neuronal.
• Los agentes se entrenarán a través de la experiencia.

Cálculo de masas: se llamará al método "CalculateMass ()", para evaluar las interacciones entre los agentes con respecto a su masa.

Aplicación de reglas y movimiento: el ciclo comenzará de nuevo en los agentes, con las reglas estándar del algoritmo de boids aplicadas a cada uno:

• Cohesión: los agentes buscarán estar más cerca unos de otros.
• Separación: los agentes evitarán acercarse unos a otros para no colisionar.
• Alineación: los agentes intentarán moverse en la misma dirección que sus vecinos.

Luego se llamará al método "ApplyNeuralControl ()" para el control basado en redes neuronales. Se limitará la velocidad de los agentes mediante "LimitSpeed ()" y se comprobará que los agentes se mantengan dentro de los límites de un área determinada mediante KeepWithinBounds (). Las posiciones de los agentes en cada coordenada se actualizarán, añadiendo la velocidad actual a la posición actual, y el estado.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA2::Moving ()
{
  double reset = GlobalVariableGet ("#reset");
  if (reset == 1.0)
  {
    revision = false;
    GlobalVariableSet ("#reset", 0.0);
  }

  // Get parameters from global variables for interactive configuration
  cohesionWeight   = GlobalVariableGet ("1cohesionWeight");
  cohesionDist     = GlobalVariableGet ("2cohesionDist");

  separationWeight = GlobalVariableGet ("3separationWeight");
  separationDist   = GlobalVariableGet ("4separationDist");

  alignmentWeight  = GlobalVariableGet ("5alignmentWeight");
  alignmentDist    = GlobalVariableGet ("6alignmentDist");

  maxSpeed         = GlobalVariableGet ("7maxSpeed");
  minSpeed         = GlobalVariableGet ("8minSpeed");

  learningRate     = GlobalVariableGet ("9learningRate");
  neuralInfluence  = GlobalVariableGet ("10neuralInfluence");
  explorationRate  = GlobalVariableGet ("11explorationRate");

  // Initialization of initial positions and speeds
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        agent [i].x [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        agent [i].dx [c] = (rangeMax [c] - rangeMin [c]) * u.RNDfromCI (-1.0, 1.0) * 0.001;

        a [i].c [c] = u.SeInDiSp (agent [i].x [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  // Adaptive research depending on stagnation
  AdaptiveExploration ();

  //----------------------------------------------------------------------------
  // Main loop of boid movement
  for (int i = 0; i < popSize; i++)
  {
    // Save the current experience
    agent [i].MemorizeExperience (a [i].f, coords);

    // Update the agent's best position
    agent [i].UpdateBestPosition (a [i].f, coords);

    // Update the neural network inputs
    agent [i].UpdateInputs (cB, a [i].f, coords);

    // Forward propagation through the neural network
    agent [i].ForwardPass (coords);

    // Learning from accumulated experience
    agent [i].Learn (learningRate, coords);
  }

  // Calculate masses
  CalculateMass ();

  // Application of rules and movement
  for (int i = 0; i < popSize; i++)
  {
    // Standard rules of the boid algorithm
    Cohesion (agent [i], i);
    Separation (agent [i], i);
    Alignment (agent [i], i);

    // Apply neural control
    ApplyNeuralControl (agent [i], i);

    // Speed limit and keeping within bounds
    LimitSpeed (agent [i]);
    KeepWithinBounds (agent [i]);

    // Update positions
    for (int c = 0; c < coords; c++)
    {
      agent [i].x [c] += agent [i].dx [c];
      a [i].c [c] = u.SeInDiSp (agent [i].x [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "CalculateMass" calculará la "masa" de los agentes según su aptitud (productividad) y normalizará estos valores. Las variables "maxMass" y "minMass" se inicializarán con los valores -DBL_MAX y DBL_MAX respectivamente. Estas variables se utilizarán para encontrar los valores de aptitud más altos y más bajos entre toda la población de agentes. El método comprobará si hay al menos un agente, verificando que el "popSize" (tamaño de la población) sea mayor que cero. Si no hay agentes, el método finalizará la ejecución. El primer ciclo probará todos los agentes (de 0 a popSize), y para cada uno comprobará si su aptitud (el valor de a[i].f) es mayor que "maxMass" actual o menor que "minMass".

Como resultado de este ciclo se determinarán los valores de aptitud máximo y mínimo entre todos los agentes. En el segundo ciclo, se enumerarán de nuevo todos los agentes y, para cada uno de ellos, se calculará su "masa" (variable "m") mediante la función "u.Scale", que normalizará los valores de aptitud. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA2::CalculateMass ()
{
  double maxMass = -DBL_MAX;
  double minMass = DBL_MAX;

  // Check for data presence before calculations
  if (popSize <= 0) return;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > maxMass) maxMass = a [i].f;
    if (a [i].f < minMass) minMass = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    agent [i].m = u.Scale (a [i].f, minMass, maxMass, 0.1, 1.0);
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "ApplyNeuralControl" se encargará de aplicar el control basado en las salidas de la red neuronal a un agente de tipo "boid". El método iterará todas las coordenadas del agente "coords". Para cada coordenada "c", se comprobará que el índice actual no supere los límites del array de salidas "boid.outputs". Si el índice es correcto, se realizará una corrección de la velocidad "dx[c]" del agente basada en el valor correspondiente de las salidas de la red neuronal multiplicado por su influencia "neuralInfluence".

El tamaño del array "boid.outputs" se extraerá para simplificar las comprobaciones posteriores. Para los coeficientes de cohesión, separación y alineación "cohesion_factor", "separation_factor", "alignment_factor", se comprobará si los índices correspondientes están dentro del array de salidas. Si el índice está fuera de los límites, se asignará un valor por defecto de 0,5. Estos coeficientes se utilizarán para escalar los pesos básicos a fin de considerar el impacto de la red neuronal. Estos influirán en el comportamiento de los agentes modificando los pesos de convergencia, separación y alineación:

• local_cohesion establece el peso de convergencia.
• local_separation establece el peso de la separación.
• local_alignment establece el peso de la alineación.

El método comprobará si debe realizarse una exploración aleatoria utilizando la probabilidad dada "xplorationRate", si se cumple la condición, se seleccionará una coordenada aleatoria "c" para la perturbación. El tamaño de la perturbación "perturbation_size" se calculará según la masa del agente (que es una medida de su aptitud) y del rango de valores posibles para esa coordenada. Esto permitirá controlar la magnitud de la variación aleatoria a pesar de la masa del agente. A la velocidad "dx[c]" se le añadirá una perturbación aleatoria seleccionada desde "perturbation_size" hasta "perturbation_size". El método "ApplyNeuralControl" integrará los resultados de la red neuronal en el proceso de control del movimiento del agente. Asimismo, ajustará su tasa según los datos; el método también considerará la necesidad de una investigación aleatorio.

//——————————————————————————————————————————————————————————————————————————————
// Apply neural control to a boid
void C_AO_NOA2::ApplyNeuralControl (S_NeuroBoids_Agent &boid, int pos)
{
  // Use the neural network outputs to correct the speed
  for (int c = 0; c < coords; c++)
  {
    // Make sure the index is not outside the array bounds 
    if (c < ArraySize (boid.outputs))
    {
      // Apply neural speed correction with a given influence
      boid.dx [c] += boid.outputs [c] * neuralInfluence;
    }
  }

  // Use the neural network outputs to adapt the flock parameters
  // Check that the indices do not go beyond the array bounds
  int output_size = ArraySize (boid.outputs);

  double cohesion_factor   = (coords < output_size) ? boid.outputs [coords] : 0.5;
  double separation_factor = (coords + 1 < output_size) ? boid.outputs [coords + 1] : 0.5;
  double alignment_factor  = (coords + 2 < output_size) ? boid.outputs [coords + 2] : 0.5;

  // Scale the base weights considering neural adaptation
  // These variables are local and do not change global parameters
  double local_cohesion   = cohesionWeight * (0.5 + cohesion_factor);
  double local_separation = separationWeight * (0.5 + separation_factor);
  double local_alignment  = alignmentWeight * (0.5 + alignment_factor);

  // Random study with a given probability
  if (u.RNDprobab () < explorationRate)
  {
    // Select a random coordinate for perturbation
    int c = (int)u.RNDfromCI (0, coords - 1);

    // Adaptive perturbation size depending on mass (fitness)
    double perturbation_size = (1.0 - boid.m) * (rangeMax [c] - rangeMin [c]) * 0.01;

    // Add random perturbation
    boid.dx [c] += u.RNDfromCI (-perturbation_size, perturbation_size);
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "AdaptiveExploration" de la clase "C_AO_NOA2" implementará la exploración adaptativa según la fase de estancamiento en el proceso de optimización. El método comenzará comprobando si el valor de la función objetivo "fB" ha cambiado con respecto al mejor valor anterior "m_prevBestFitness". Si la diferencia entre ellos es inferior a 0,000001, se considerará que no hay progreso y se incrementará el contador de estancamiento "m_stagnationCounter". De lo contrario, el estancamiento se detendrá, el contador se pondrá a cero y el valor actual de "fB" se almacenará como el nuevo mejor valor.

Si el número de estancamientos es superior a 20, aumentará la probabilidad de exploración aleatoria "explorationRate", pero se limitará a un valor de "0,5" para evitar una probabilidad demasiado alta de variación aleatoria. Cada 50 iteraciones de estancamiento, se producirá un reinicio parcial: El 70% de los agentes de la población se reiniciarán con nuevos valores aleatorios dentro de los rangos especificados "rangeMin" y "rangeMax". De este modo, el resto de los agentes de primera línea mantendrán sus posiciones actuales. Tras el reinicio, se reiniciará el contador de estancamiento.

Si hay progreso y el número de parámetros "params" es superior a 11, se establecerá la probabilidad de exploración "explorationRate" del array de parámetros. Si hay menos parámetros, se establecerá un valor por defecto de 0,1.

//——————————————————————————————————————————————————————————————————————————————
// Adaptive research depending on stagnation
void C_AO_NOA2::AdaptiveExploration ()
{
  // Determine if there is progress in the search
  if (MathAbs (fB - m_prevBestFitness) < 0.000001)
  {
    m_stagnationCounter++;
  }
  else
  {
    m_stagnationCounter = 0;
    m_prevBestFitness = fB;
  }

  // Increase research during stagnation
  if (m_stagnationCounter > 20)
  {
    // Increase the probability of random exploration
    explorationRate = MathMin (0.5, explorationRate * 1.5);

    // Perform a partial restart every 50 stagnation iterations
    if (m_stagnationCounter % 50 == 0)
    {
      // Restart 70% of the population leaving the best agents
      int restart_count = (int)(popSize * 0.7);

      for (int i = popSize - restart_count; i < popSize; i++)
      {
        for (int c = 0; c < coords; c++)
        {
          agent [i].x [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
          agent [i].dx [c] = (rangeMax [c] - rangeMin [c]) * u.RNDfromCI (-1.0, 1.0) * 0.001;
        }
      }

      // Reset the stagnation counter
      m_stagnationCounter = 0;
    }
  }
  else
  {
    // If progress is good enough, use the normal research level 
    if (11 < ArraySize (params))
    {
      explorationRate = params [11].val;
    }
    else
    {
      explorationRate = 0.1; // default value
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "Cohesion" de la clase "C_AO_NOA2" se encargará de implementar el comportamiento de convergencia "cohesion" para el modelo boid basado en los agentes. Declaración de variables:

• centerX — el array se utilizará para almacenar las coordenadas del centro de masa de los agentes vecinos. El tamaño del array se corresponderá con el número de coordenadas "coords".
• numNeighbors — el contador Neighbours llevará la cuenta del número de agentes dentro de una distancia dada (considerando la masa).
• sumMass — la suma de las masas de los agentes vecinos se utilizará para normalizar las coordenadas del centro de masa.

El primer ciclo (de 0 a popSize) sumará las masas de todos los agentes de la población, excluyendo el boid (agente) actual en el índice "pos". El segundo ciclo iterará todos los agentes y comprobará si se encuentran a una distancia máxima multiplicada por el factor "cohesionDist" del boid actual. Si la distancia a un agente es inferior al máximo especificado, las coordenadas de ese agente (teniendo en cuenta su masa) se añadirán a "centreX" y el contador "numNeighbors" se incrementará.

Una vez calculadas las sumas de coordenadas y las masas de los vecinos, se comprobará si hay vecinos (es decir, numNeighbors > 0) y la suma de las masas (sumMass > 0,0), y si se encuentran vecinos, se normalizarán las coordenadas del centro de masas (dividiendo por la suma de masas). Entonces la velocidad actual "dx" del boid se incrementará hacia el centro de masa con un peso dado "cohesionWeight", esto significará que el boid se desplazará hacia el centro de masa de sus vecinos dadas sus masas.

El método "Cohesion" calculará el centro de masa y ajustará la velocidad del boid actual para que "converja" hacia ese centro. Este comportamiento será uno de los aspectos clave de la simulación del comportamiento de manada o grupo. Parámetros como "cohesionDist" y "cohesionWeight" permitirán controlar la distancia a la que se aplica este comportamiento y el grado en que el centro de masa influirá en el movimiento de los boids.

//——————————————————————————————————————————————————————————————————————————————
// Find the center of mass of other boids and adjust the speed towards the center of mass
void C_AO_NOA2::Cohesion (S_NeuroBoids_Agent &boid, int pos)
{
  double centerX [];
  ArrayResize (centerX, coords);
  ArrayInitialize (centerX, 0.0);

  int numNeighbors = 0;
  double sumMass = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i) sumMass += agent [i].m;
  }

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * cohesionDist)
      {
        for (int c = 0; c < coords; c++)
        {
          centerX [c] += agent [i].x [c] * agent [i].m;
        }

        numNeighbors++;
      }
    }
  }

  if (numNeighbors > 0 && sumMass > 0.0)
  {
    for (int c = 0; c < coords; c++)
    {
      centerX [c] /= sumMass;
      boid.dx [c] += (centerX [c] - boid.x [c]) * cohesionWeight;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "Separation" de la clase "C_AO_NOA2" implementará un comportamiento de repulsión (separación) para agentes modelo que está diseñado para prevenir colisiones entre un boid y los agentes vecinos. "moveX" — parámetros como el array "cohesionDist" se usarán para almacenar vectores de desplazamiento para alejar al boid de otros agentes.

El tamaño del array se corresponderá con el número de coordenadas "coords". El array "moveX" se inicializará con ceros para evitar la acumulación de valores aleatorios, luego se realizará la iteración sobre todos los agentes de la población (de 0 a popSize). A continuación, se comprobará si el agente está cerca del boid actual. Esto se logrará utilizando la función "Distance", y si la distancia entre el boid y el agente es menor que un máximo dado (multiplicado por el factor "separationDist"), entonces para cada coordenada, las coordenadas del agente se restarán de las coordenadas del boid actual para crear efectivamente un vector que apunte hacia el boid actual (es decir, lejos del agente).

Una vez completado el ciclo del agente, la velocidad actual "dx" del boid se incrementará con el vector de desplazamiento calculado "moveX" multiplicado por el factor "separationWeight". Esto permitirá controlar la fuerza de la repulsión: cuanto mayor sea el valor de "separationWeight", más con mayor intensidad evitará el boid las colisiones.

El método "Separation" implementará un comportamiento que hará que el boid repela a sus vecinos más cercanos, evitando colisiones. Se trata de un aspecto importante en el modelado del comportamiento de la manada, que ayuda a mantener el espacio personal de cada agente y favorece interacciones más naturales entre ellos. Parámetros como "separationDist" y "separationWeight" permiten ajustar con flexibilidad el alcance y la fuerza del efecto de repulsión, respectivamente.

//——————————————————————————————————————————————————————————————————————————————
// Pushing away from other boids to avoid collisions
void C_AO_NOA2::Separation (S_NeuroBoids_Agent &boid, int pos)
{
  double moveX [];
  ArrayResize (moveX, coords);
  ArrayInitialize (moveX, 0.0);

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * separationDist)
      {
        for (int c = 0; c < coords; c++)
        {
          moveX [c] += boid.x [c] - agent [i].x [c];
        }
      }
    }
  }

  for (int c = 0; c < coords; c++)
  {
    boid.dx [c] += moveX [c] * separationWeight;
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "Alignment" de la clase "C_AO_NOA2" implementará el comportamiento de alineación para los agentes del modelo. Este comportamiento hace que los boids coordinen sus velocidades con los agentes vecinos para crear un movimiento de grupo más armonioso y coordinado. "avgDX" es un array que se utilizará para almacenar el vector de velocidad media de los agentes vecinos. El tamaño del array se corresponde con el número de coordenadas "coords"; "numNeighbors" es un contador que llevará la cuenta del número de vecinos que se encuentran a una distancia determinada.

El ciclo iterará todos los agentes de la población. Dentro del ciclo se comprobará si el agente actual es el mismo que el boid. Si la distancia a otro agente es menor que el máximo especificado multiplicado por el factor "alignmentDist", la velocidad actual "dx" de ese agente se añadirá a "avgDX". El contador "numNeighbors" se incrementará en 1. Una vez finalizado el ciclo, si se han encontrado vecinos (es decir, numNeighbors > 0), se calculará la velocidad media (avgDX) dividiendo el vector de velocidad sumado por el número de vecinos. La velocidad actual "dx" del boid se ajustará entonces a la velocidad media de sus vecinos teniendo en cuenta el factor "alignmentWeight". 

El método de "Alignment" permitirá a un boid adaptar su velocidad a la de sus vecinos. Este comportamiento ayudará a los grupos de boids a moverse de forma más coherente y reducirá la probabilidad de conflictos o cambios bruscos de dirección. Parámetros como "alignmentDist" y "alignmentWeight" establecerán, respectivamente, el radio del efecto de alineación y el grado en que la velocidad media de los vecinos afectará a la velocidad del boid actual. 

//——————————————————————————————————————————————————————————————————————————————
// Align speed with other boids
void C_AO_NOA2::Alignment (S_NeuroBoids_Agent &boid, int pos)
{
  double avgDX [];
  ArrayResize (avgDX, coords);
  ArrayInitialize (avgDX, 0.0);

  int numNeighbors = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * alignmentDist)
      {
        for (int c = 0; c < coords; c++)
        {
          avgDX [c] += agent [i].dx [c];
        }

        numNeighbors++;
      }
    }
  }

  if (numNeighbors > 0)
  {
    for (int c = 0; c < coords; c++)
    {
      avgDX [c] /= numNeighbors;
      boid.dx [c] += (avgDX [c] - boid.dx [c]) * alignmentWeight;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "LimitSpeed" de la clase "C_AO_NOA2" está diseñado para controlar la velocidad de los agentes (boids) en el modelo para asegurarse de que las velocidades de los boids estén dentro del rango especificado, y "speed" es una variable para almacenar la velocidad actual de los boids, que será calculada como la longitud del vector de velocidad. El ciclo por coordenadas (coords) calculará el cuadrado de la velocidad para cada coordenada (sumando boid.dx [c] * boid.dx [c]) y las sumará. Esto nos permitirá calcular el cuadrado de la longitud del vector velocidad. La longitud (o velocidad real) se obtendrá entonces mediante la función "MathSqrt", que calculará la raíz cuadrada de la suma de cuadrados. Si la velocidad es mayor que un valor pequeño (1e-10), el programa continuará la ejecución, si la velocidad actual es menor que la velocidad mínima permitida (definida como speedMax[0] * minSpeed), entonces el vector de velocidad "boid.dx" será normalizado (dividido por su longitud actual) e incrementado a un valor igual al valor mínimo permitido.

Si la velocidad actual es mayor que la velocidad máxima permitida (speedMax[0] * maxSpeed), entonces, de forma similar, el vector de velocidad se normalizará y se establecerá en el valor de la velocidad máxima, mientras que si la velocidad es casi cero (cero o muy cercana a cero), en este caso, cada coordenada del vector de velocidad se sustituirá por un pequeño valor aleatorio obtenido mediante la función "u.RNDfromCI (-1.0, 1.0)" multiplicado por la velocidad máxima.

El método "LimitSpeed" garantizará que la velocidad de los boids se mantenga dentro de unos límites aceptables, evitando movimientos demasiado lentos o demasiado rápidos. Este comportamiento permitirá una simulación más realista de los agentes, ya que no permitirá grandes desviaciones de velocidad que podrían dar lugar a movimientos poco naturales. Los parámetros "minSpeed" y "maxSpeed" pueden configurarse para ajustar el comportamiento y la velocidad de los agentes según los objetivos de la simulación.

//——————————————————————————————————————————————————————————————————————————————
// Speed limit
void C_AO_NOA2::LimitSpeed (S_NeuroBoids_Agent &boid)
{
  double speed = 0;

  for (int c = 0; c < coords; c++)
  {
    speed += boid.dx [c] * boid.dx [c];
  }

  speed = MathSqrt (speed);

  // If the speed is not zero (prevent division by zero)
  if (speed > 1e-10)
  {
    // If the speed is too low, increase it
    if (speed < speedMax [0] * minSpeed)
    {
      for (int c = 0; c < coords; c++)
      {
        boid.dx [c] = boid.dx [c] / speed * speedMax [c] * minSpeed;
      }
    }
    // If the speed is too high, reduce it
    else
      if (speed > speedMax [0] * maxSpeed)
      {
        for (int c = 0; c < coords; c++)
        {
          boid.dx [c] = boid.dx [c] / speed * speedMax [c] * maxSpeed;
        }
      }
  }
  else
  {
    // If the speed is almost zero, set a small random speed
    for (int c = 0; c < coords; c++)
    {
      boid.dx [c] = u.RNDfromCI (-1.0, 1.0) * speedMax [c] * minSpeed;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "KeepWithinBounds" de la clase "C_AO_NOA2" está diseñado para mantener al agente (boid) dentro de los límites especificados. Si el boid se acerca demasiado a los bordes de la zona, este método invertirá su dirección y proporcionará un empujón definitivo hacia los límites. El método comenzará con un ciclo a través de todas las coordenadas, lo que permitirá trabajar con un espacio multidimensional.

Para cada coordenada, comprobará si la posición del boid (boid.x[c]) está por debajo del límite mínimo (rangeMin[c]), si es así, la dirección de la velocidad (boid.dx[c]) se invertirá con "boid.dx [c] *= -1.0". Esto significará que el boid se moverá en la dirección opuesta. A continuación, se añadirá un pequeño empujón desde el límite: (rangeMax[c] - rangeMin[c]) * 0,001, que ayudará a empujar el boid hacia el interior de la región.

Luego se realizará una comprobación similar para el límite máximo (rangeMax[c]): si la posición del boid sobrepasa el máximo, su velocidad también se invertirá y se corregirá, pero restándole algún valor, de forma similar al caso anterior.

El método "KeepWithinBounds" restringirá eficazmente los movimientos de los boids en un área determinada, impidiendo que salgan de los límites y garantizando que vuelvan al interior. 

//——————————————————————————————————————————————————————————————————————————————
// Keep the boid within the boundaries. If it gets too close to the edge,
// push it back and change direction.
void C_AO_NOA2::KeepWithinBounds (S_NeuroBoids_Agent &boid)
{
  for (int c = 0; c < coords; c++)
  {
    if (boid.x [c] < rangeMin [c])
    {
      boid.dx [c] *= -1.0;
      // Add a small push from the border
      boid.dx [c] += (rangeMax [c] - rangeMin [c]) * 0.001;
    }
    if (boid.x [c] > rangeMax [c])
    {
      boid.dx [c] *= -1.0;
      // Add a small push from the border
      boid.dx [c] -= (rangeMax [c] - rangeMin [c]) * 0.001;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "Distance" de la clase "C_AO_NOA2" está diseñado para calcular la distancia entre dos agentes (boids) en un espacio multidimensional. Este utilizará una fórmula para calcular la distancia euclidiana; "dist" es una variable que almacenará la suma de los cuadrados de las diferencias de las coordenadas de los dos boids.

El método iniciará un ciclo que iterará todas las coordenadas, lo que permitirá calcular la distancia en un espacio de cualquier dimensionalidad. Para cada coordenada "c", se calculará el cuadrado de la diferencia entre las coordenadas correspondientes de ambos boids: boid1.x[c] - boid2.x[c].

Los resultados ((boid1.x[c] - boid2.x[c])^2) se añadirán a la variable "dist". Una vez finalizado el ciclo, la variable "dist" contendrá la suma de cuadrados de las diferencias de coordenadas. Para obtener la distancia real, el método usará "MathSqrt" para calcular la raíz cuadrada de la suma de cuadrados, que se corresponderá con la fórmula de la distancia euclidiana.

//——————————————————————————————————————————————————————————————————————————————
// Calculate the distance between two boids
double C_AO_NOA2::Distance (S_NeuroBoids_Agent &boid1, S_NeuroBoids_Agent &boid2)
{
  double dist = 0;

  for (int c = 0; c < coords; c++)
  {
    dist += MathPow (boid1.x [c] - boid2.x [c], 2);
  }

  return MathSqrt (dist);
}
//——————————————————————————————————————————————————————————————————————————————

El método "Revision" de la clase "C_AO_NOA2" se encargará de actualizar la información sobre la mejor solución encontrada durante el proceso de optimización. Este proceso implicará la actualización del valor de la función de aptitud, así como de las coordenadas correspondientes a dicho valor. El método también supervisará los progresos y adaptará los parámetros del algoritmo si se producen mejoras significativas. El método iterará toda la población representada por el array "a", que contiene "popSize" (número de agentes).

Dentro del ciclo, se comprobará si el valor de aptitud de cada agente (a[i].f) es mayor que el mejor valor actual (fB). Si el agente actual muestra el mejor valor de aptitud, se actualizará el mejor valor de aptitud global asignando a "fB" un nuevo valor "a[i].f", luego se actualizarán las coordenadas de la mejor solución. Para cada coordenada "c", el array "cB" (que contiene las coordenadas de la mejor solución) se actualizará con los valores del agente actual. El contador de estancamiento (m_stagnationCounter) se pondrá a cero porque se ha encontrado una mejora en la solución.

El método utilizará la variable "hasProgress" para determinar si se ha avanzado. Para ello, se calculará la diferencia absoluta entre los valores actual y anterior de la mejor función de aptitud (MathAbs(fB - m_prevBestFitness)), y si esta diferencia es superior a 0,000001, se considerará que se está avanzando. Si hay progreso, "m_prevBestFitness" se actualizará al mejor valor actual "fB".
La tasa de exploración "explorationRate" también se adaptará: esta disminuirá si se encuentra una mejora, teniendo en cuenta algún parámetro del array "params" y el valor actual de "explorationRate".

//——————————————————————————————————————————————————————————————————————————————
// Update the best solution found
void C_AO_NOA2::Revision ()
{
  // Update the best coordinates and fitness function value
  for (int i = 0; i < popSize; i++)
  {
    // Update the global best solution
    if (a [i].f > fB)
    {
      fB = a [i].f;
      for (int c = 0; c < coords; c++)
      {
        cB [c] = a [i].c [c];
      }

      // Reset the stagnation counter when a better solution is found
      m_stagnationCounter = 0;
    }
  }

  // Check for progress to adapt the algorithm parameters
  bool hasProgress = MathAbs (fB - m_prevBestFitness) > 0.000001;
  if (hasProgress)
  {
    m_prevBestFitness = fB;
    explorationRate = MathMax (params [11].val * 0.5, explorationRate * 0.9);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Resultados de las pruebas

Los resultados de las pruebas son bastante flojos.

NOA2|Neuroboids Optimization Algorithm 2 (joo)|50.0|0.6|0.001|0.005|0.03|0.1|0.1|0.1|0.01|0.01|0.3|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.47680799582735267
25 Hilly's; Func runs: 10000; result: 0.30763714006051013
500 Hilly's; Func runs: 10000; result: 0.2544737238936433
=============================
5 Forest's; Func runs: 10000; result: 0.3238017030688524
25 Forest's; Func runs: 10000; result: 0.20976876473929068
500 Forest's; Func runs: 10000; result: 0.15740101965732595
=============================
5 Megacity's; Func runs: 10000; result: 0.27076923076923076
25 Megacity's; Func runs: 10000; result: 0.14676923076923082
500 Megacity's; Func runs: 10000; result: 0.09729230769230844
=============================
All score: 2.24472 (24.94%)

En la visualización podemos apreciar la modesta capacidad de búsqueda. La posibilidad de modificar los parámetros externos del algoritmo mediante variables globales permite experimentar con el comportamiento de los boids, revelando comportamientos interesantes. A continuación le mostramos algunos de los posibles comportamientos.

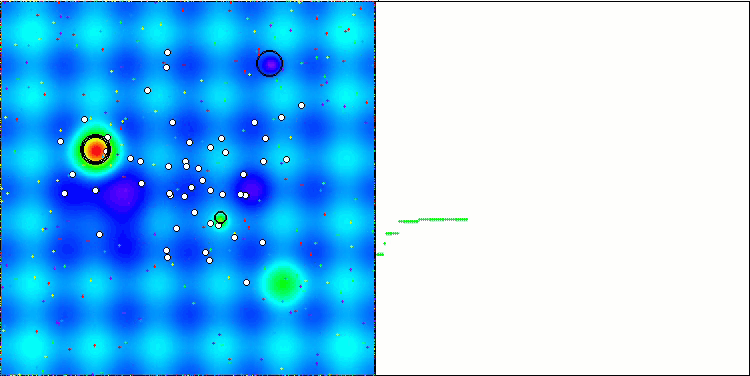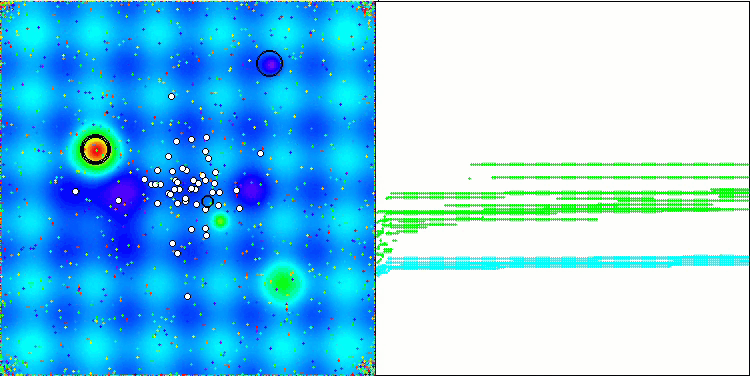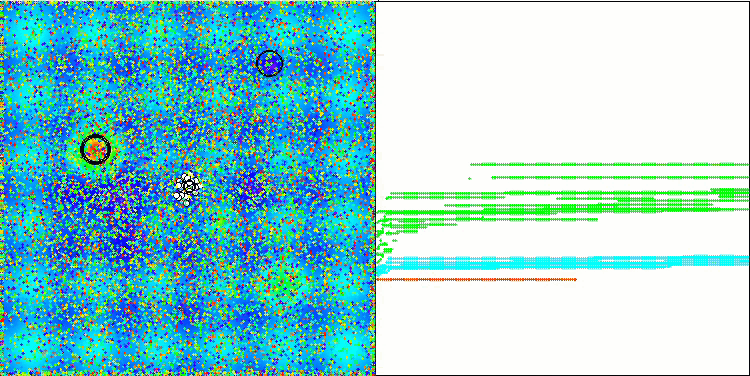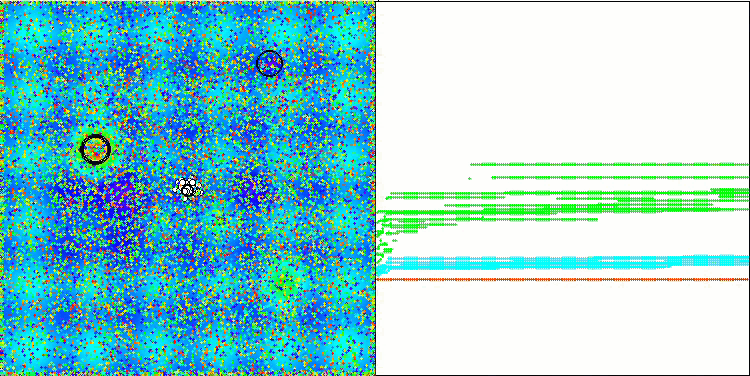
NOA2 en la función de prueba Hilly

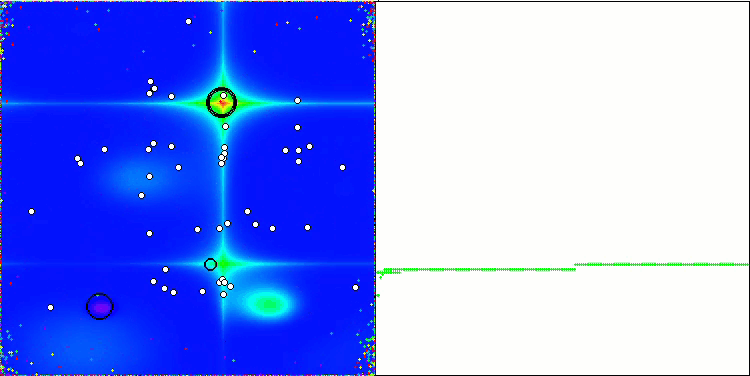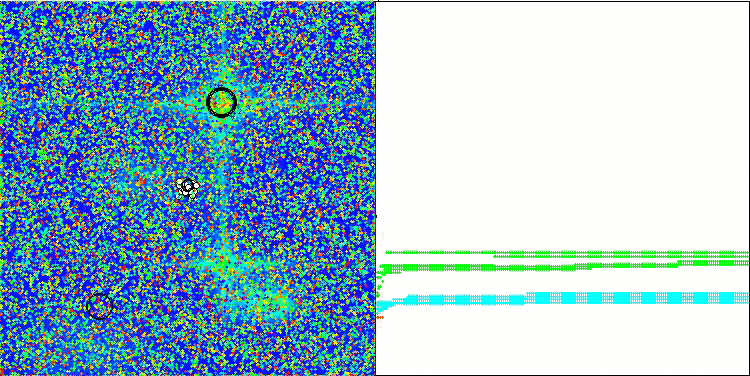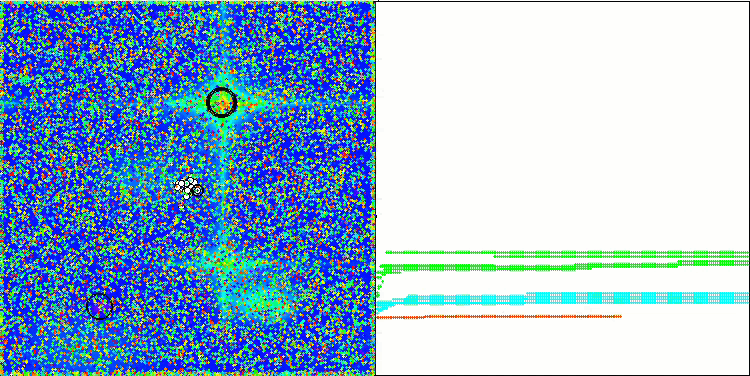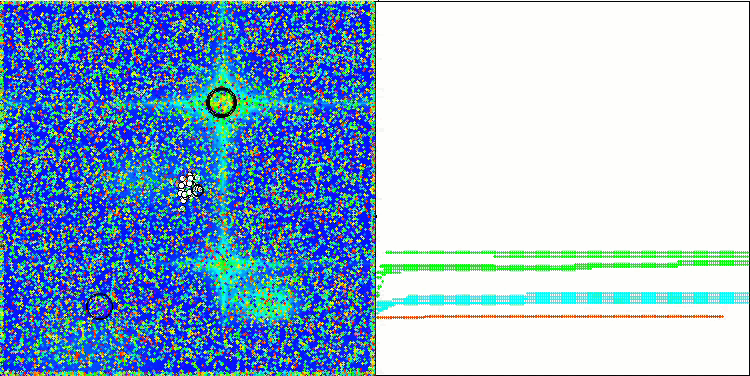
NOA2 en la función de prueba Forest

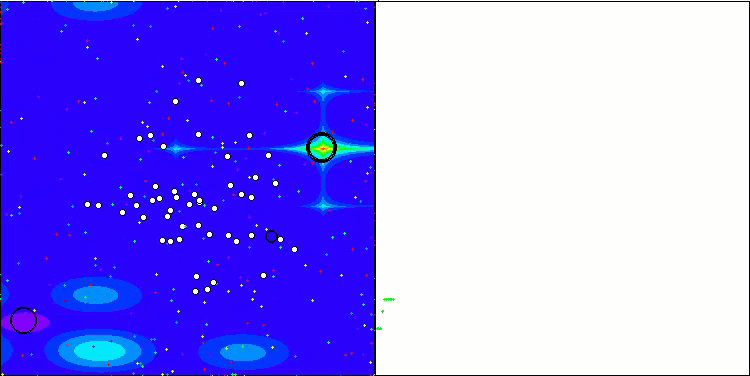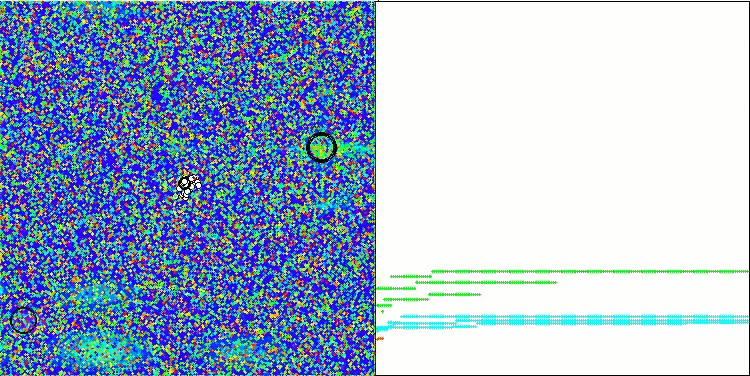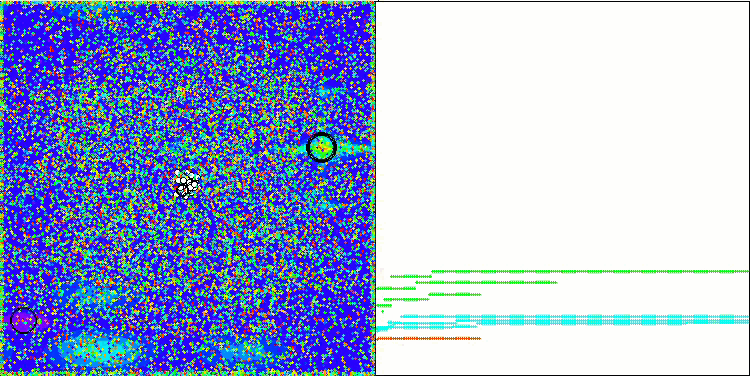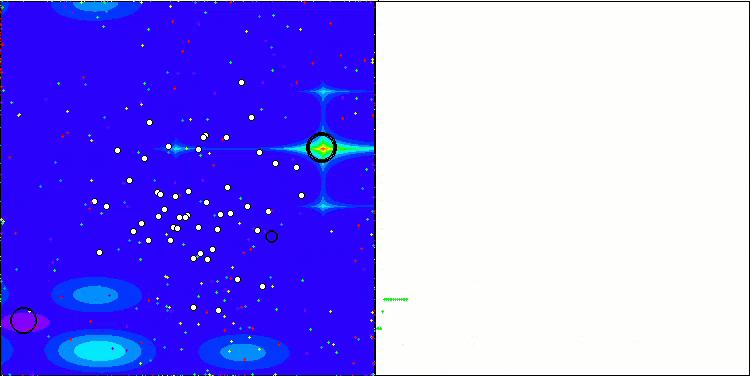
NOA2 en la función de prueba Megacity

Basándonos en los resultados de las pruebas, el algoritmo NOA2 en su versión de referencia se incluye en nuestra tabla de clasificación de algoritmos de optimización de poblaciones únicamente con fines ilustrativos.

#	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% de MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	code lock algorithm (joo)	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	animal migration optimization M	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O) evolution strategies	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	comet tail algorithm (joo)	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	TETA	time evolution travel algorithm (joo)	0.91362	0.82349	0.31990	2.05701	0.97096	0.89532	0.29324	2.15952	0.73462	0.68569	0.16021	1.58052	5.797	64.41
7	SDSm	stochastic diffusion search M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
8	BOAm	billiards optimization algorithm M	0.95757	0.82599	0.25235	2.03590	1.00000	0.90036	0.30502	2.20538	0.73538	0.52523	0.09563	1.35625	5.598	62.19
9	AAm	archery algorithm M	0.91744	0.70876	0.42160	2.04780	0.92527	0.75802	0.35328	2.03657	0.67385	0.55200	0.23738	1.46323	5.548	61.64
10	ESG	evolution of social groups (joo)	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
11	SIA	simulated isotropic annealing (joo)	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
12	ACS	artificial cooperative search	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
13	DA	dialectical algorithm	0.86183	0.70033	0.33724	1.89940	0.98163	0.72772	0.28718	1.99653	0.70308	0.45292	0.16367	1.31967	5.216	57.95
14	BHAm	black hole algorithm M	0.75236	0.76675	0.34583	1.86493	0.93593	0.80152	0.27177	2.00923	0.65077	0.51646	0.15472	1.32195	5.196	57.73
15	ASO	anarchy society optimization	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
16	RFO	royal flush optimization (joo)	0.83361	0.73742	0.34629	1.91733	0.89424	0.73824	0.24098	1.87346	0.63154	0.50292	0.16421	1.29867	5.089	56.55
17	AOSm	búsqueda de orbitales atómicos M	0.80232	0.70449	0.31021	1.81702	0.85660	0.69451	0.21996	1.77107	0.74615	0.52862	0.14358	1.41835	5.006	55.63
18	TSEA	turtle shell evolution algorithm (joo)	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
19	DE	differential evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
20	SRA	successful restaurateur algorithm (joo)	0.96883	0.63455	0.29217	1.89555	0.94637	0.55506	0.19124	1.69267	0.74923	0.44031	0.12526	1.31480	4.903	54.48
21	CRO	chemical reaction optimization	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
22	BIO	blood inheritance optimization (joo)	0.81568	0.65336	0.30877	1.77781	0.89937	0.65319	0.21760	1.77016	0.67846	0.47631	0.13902	1.29378	4.842	53.80
23	BSA	bird swarm algorithm	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
24	HS	harmony search	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
25	SSG	saplings sowing and growing	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
26	BCOm	bacterial chemotaxis optimization M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
27	ABO	african buffalo optimization	0.83337	0.62247	0.29964	1.75548	0.92170	0.58618	0.19723	1.70511	0.61000	0.43154	0.13225	1.17378	4.634	51.49
28	(PO)ES	(PO) evolution strategies	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
29	TSm	tabu search M	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
30	BSO	brain storm optimization	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
31	WOAm	wale optimization algorithm M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
32	AEFA	artificial electric field algorithm	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
33	AEO	artificial ecosystem-based optimization algorithm	0.91380	0.46713	0.26470	1.64563	0.90223	0.43705	0.21400	1.55327	0.66154	0.30800	0.28563	1.25517	4.454	49.49
34	ACOm	ant colony optimization M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
35	BFO-GA	bacterial foraging optimization — ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
36	SOA	simple optimization algorithm	0.91520	0.46976	0.27089	1.65585	0.89675	0.37401	0.16984	1.44060	0.69538	0.28031	0.10852	1.08422	4.181	46.45
37	ABH	artificial bee hive algorithm	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
38	ACMO	atmospheric cloud model optimization	0.90321	0.48546	0.30403	1.69270	0.80268	0.37857	0.19178	1.37303	0.62308	0.24400	0.10795	0.97503	4.041	44.90
39	ADAMm	adaptive moment estimation M	0.88635	0.44766	0.26613	1.60014	0.84497	0.38493	0.16889	1.39880	0.66154	0.27046	0.10594	1.03794	4.037	44.85
40	CGO	chaos game optimization	0.57256	0.37158	0.32018	1.26432	0.61176	0.61931	0.62161	1.85267	0.37538	0.21923	0.19028	0.78490	3.902	43.35
41	ATAm	artificial tribe algorithm M	0.71771	0.55304	0.25235	1.52310	0.82491	0.55904	0.20473	1.58867	0.44000	0.18615	0.09411	0.72026	3.832	42.58
42	CFO	central force optimization	0.60961	0.54958	0.27831	1.43750	0.63418	0.46833	0.22541	1.32792	0.57231	0.23477	0.09586	0.90294	3.668	40.76
43	ASHA	artificial showering algorithm	0.89686	0.40433	0.25617	1.55737	0.80360	0.35526	0.19160	1.35046	0.47692	0.18123	0.09774	0.75589	3.664	40.71
44	ASBO	adaptive social behavior optimization	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
45	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
	NOA2	neuroboids optimization algorithm 2(joo)	0.47681	0.30764	0.25447	1.03892	0.32380	0.20977	0.15740	0.69097	0.27077	0.14677	0.09729	0.51483	2.245	24.94

Conclusiones

El Algoritmo de Optimización Neuroboidal (NOA2) que hemos desarrollado es un enfoque híbrido que combina los principios de la inteligencia de enjambre (algoritmo boid) con el control neuronal. La idea clave consiste en aplicar una red neuronal para controlar de forma adaptativa los parámetros de comportamiento de los agentes boid. La aplicación actual usa una red neuronal simple de una sola capa sin capas ocultas. Consta de una capa de entrada que admite las coordenadas actuales, las velocidades, la distancia a la mejor solución y el valor de la función de aptitud, y una capa de salida que determina las correcciones de velocidad y los parámetros adaptativos de las reglas de comportamiento del enjambre boid.

En esta versión no hay capas intermedias. El número de entradas se define como (coords * 2 + 2), donde "coords" será el número de dimensiones del espacio de búsqueda. Los resultados incluyen una corrección para cada coordenada y tres parámetros adicionales para adaptar las reglas del enjambre. El algoritmo tiene un gran número de parámetros ajustables, lo cual hace difícil encontrar el mejor; hemos probado varias combinaciones, pero no hemos encontrado la combinación ideal que muestre los mejores resultados en las funciones de prueba.

En su forma actual, el algoritmo sirve claramente para demostrar el concepto y, en general, supone un experimento interesante en métodos de optimización híbridos, pero no demuestra un rendimiento suficiente para ser calificado. Ha obtenido el número mínimo de puntos en las pruebas realizadas y solo puede considerarse como una ilustración del enfoque de hibridación de algoritmos. Para los investigadores y desarrolladores interesados, el código NOA2 puede servir como punto de partida para experimentar con diferentes configuraciones y parámetros, así como para crear mejores algoritmos de optimización híbridos que aprovechen tanto los métodos de población como los de aprendizaje automático.

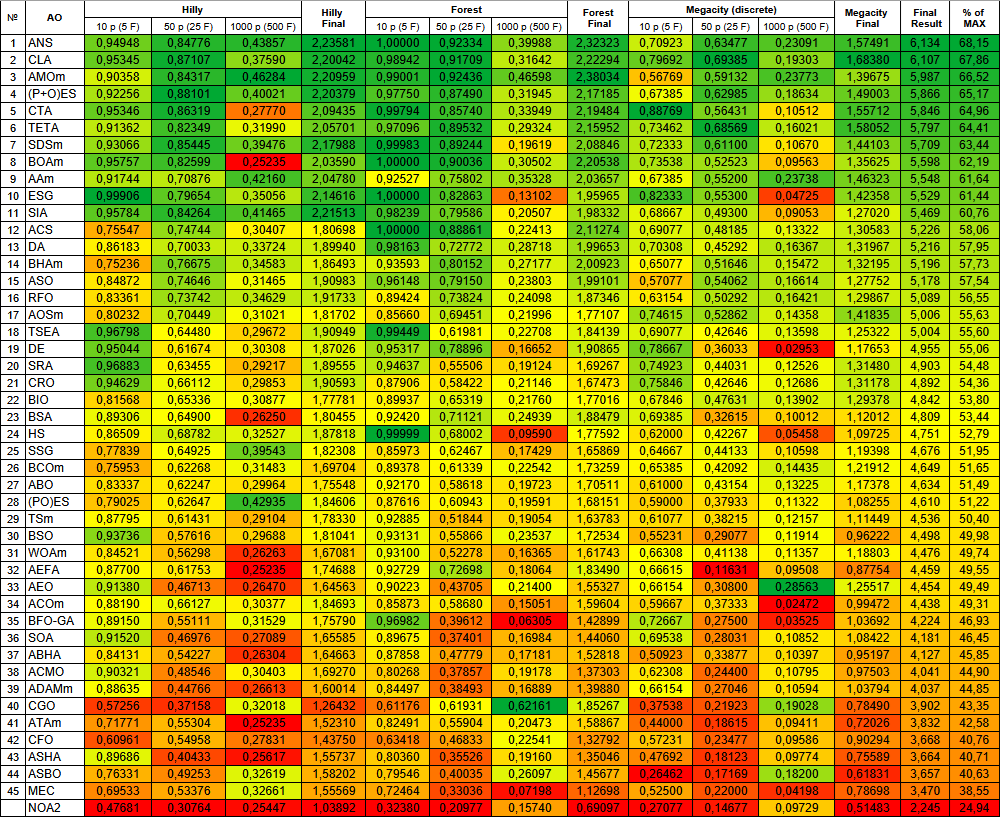
Figura 3. Clasificación por colores de los algoritmos según las pruebas respectivas

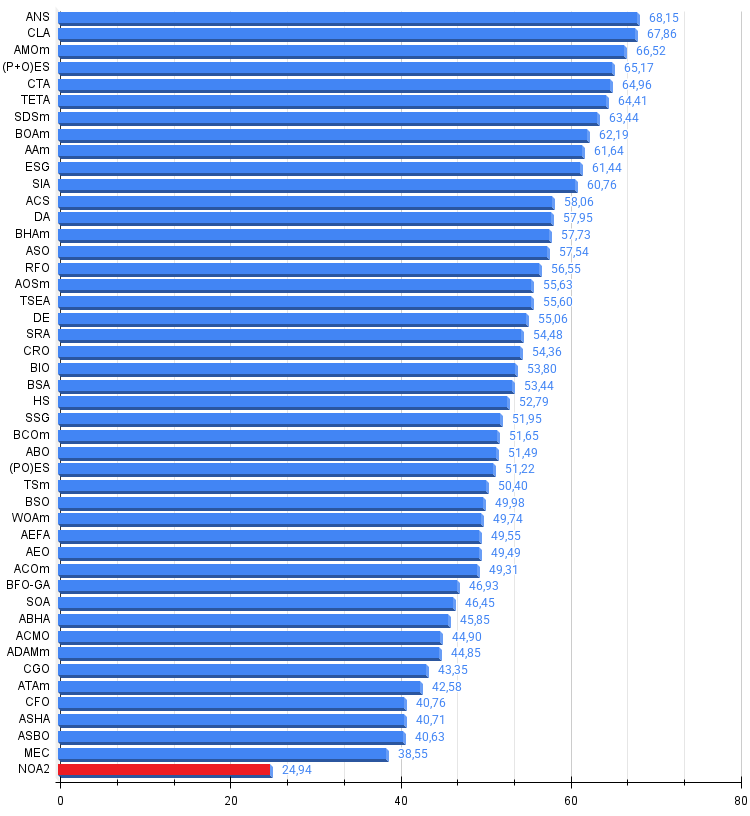
Figura 4. Histograma de los resultados de las pruebas de algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de puntuación está en el archivo)

Ventajas y desventajas del algoritmo NOA2:

Ventajas:

1. Supone una idea interesante para poner en práctica.

Desventajas:

1. Resultados muy flojos.
   

Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	#C_AO.mqh	Archivo de inclusión	Clase padre de algoritmos de optimización basados en la población
2	#C_AO_enum.mqh	Archivo de inclusión	Enumeración de los algoritmos de optimización basados en la población
3	TestFunctions.mqh	Archivo de inclusión	Biblioteca de funciones de prueba
4	TestStandFunctions.mqh	Archivo de inclusión	Biblioteca de funciones del banco de pruebas
5	Utilities.mqh	Archivo de inclusión	Biblioteca de funciones auxiliares
6	CalculationTestResults.mqh	Archivo de inclusión	Script para calcular los resultados en una tabla comparativa
7	Testing AOs.mq5	Script	Banco de pruebas único para todos los algoritmos de optimización basados en la población
8	Simple use of population optimization algorithms.mq5	Script	Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización
9	Test_AO_NOA2.mq5	Script	Banco de pruebas para NOA2