Optimización de Battle Royale — Battle Royale Optimizer (BRO)
41
1
Contenido
Introducción
En la optimización metaheurística, donde los algoritmos suelen inspirarse en procesos naturales, fenómenos físicos y mecanismos evolutivos, ha surgido una fuente de inspiración fundamentalmente nueva: los juegos de computadora. Battle Royale Optimizer (BRO), desarrollado por Taymaz Rahkar Farshi, es un innovador algoritmo de optimización basado en la mecánica de populares juegos "Battle Royale" como PlayerUnknown's Battlegrounds (PUBG).
El algoritmo BRO descubre una nueva categoría de métodos de optimización: los métodos basados en juegos ("game-based"), que complementan el trío de enfoques bien establecido de algoritmos de optimización, incluidos los algoritmos evolutivos, los algoritmos de inteligencia de enjambre y los algoritmos basados en fenómenos físicos, pertenecientes al amplio grupo de algoritmos de optimización basados en poblaciones. A diferencia de los algoritmos de inteligencia de enjambre, en los que los agentes cooperan para lograr un objetivo común, en el BRO los individuos compiten entre sí en un intento de sobrevivir y ocupar la mejor posición en el espacio de búsqueda.
Una característica clave del BRO es su mecanismo único para competir y "dañar" soluciones. Cada solución se compara con la de su vecino más próximo y el perdedor sufre un "daño", mientras que el ganador comienza de cero. Las soluciones que han acumulado demasiado daño se eliminan de la población y son sustituidas por nuevas soluciones aleatorias, del mismo modo que los jugadores de PUBG son eliminados de una partida tras recibir daño crítico. Y esto ofrece un mecanismo para explorar el espacio de búsqueda.
Implementación del algoritmo
El algoritmo Battle Royale Optimiser (BRO) imagina figuradamente un mundo virtual en el que varios jugadores se lanzan a un campo de batalla y solo uno tiene que seguir con vida, y esta es la esencia del prototipo de juego. Vamos a trasladar ahora este concepto a la resolución de problemas de optimización.
Al principio del algoritmo, crearemos una población de soluciones distribuidas aleatoriamente por el espacio de búsqueda. Cada solución será una especie de "jugador" que tendrá una posición determinada y la calidad (aptitud) de esa posición. A continuación comenzará el ciclo principal de la competición, en el que cada solución se comparará con su vecina más próxima, más o menos como los jugadores de una batalla que se enfrentan entre sí.
Cuando dos soluciones "se encuentran", se compararán en términos de calidad. La mejor solución se declarará vencedora y recibirá cero daños, mientras que la peor será la perdedora y recibirá un daño. Este contador de daños es una característica clave del algoritmo. La solución perdedora no solo sufre daños, sino que intenta mejorar su posición aproximándose a la solución más conocida de la población. Este movimiento imita el impulso de sobrevivir buscando un lugar más seguro y rentable.
Si una solución acumula demasiados daños (supera un umbral determinado), quedará "eliminada del juego", es decir, se retirará de la población y será sustituida por una nueva solución aleatoria. Esto resulta similar a la expulsión definitiva de un jugador en battle royale y la aparición de uno nuevo en la siguiente partida. Este mecanismo garantiza la renovación constante de la población y favorece la diversidad de soluciones.
Periódicamente, el algoritmo reduce el espacio de búsqueda, de forma análoga a la reducción del área de juego en el battle royale, lo que obliga a los jugadores a acercarse unos a otros. Los límites de la búsqueda se estrechan en torno a la mejor solución encontrada, lo cual hace que la población se concentre en las zonas más prometedoras.
Con este enfoque, el algoritmo BRO se equilibra entre la exploración de nuevas áreas y el uso de las buenas soluciones ya encontradas. Las soluciones perdedoras tienden a ser mejores, manteniendo una tendencia hacia la mejora, mientras que las completamente perdedoras son sustituidas por otras nuevas, ofreciendo una nueva perspectiva del espacio de búsqueda. Al mismo tiempo, el estrechamiento periódico de los límites refuerza la búsqueda localizada en torno a soluciones prometedoras.
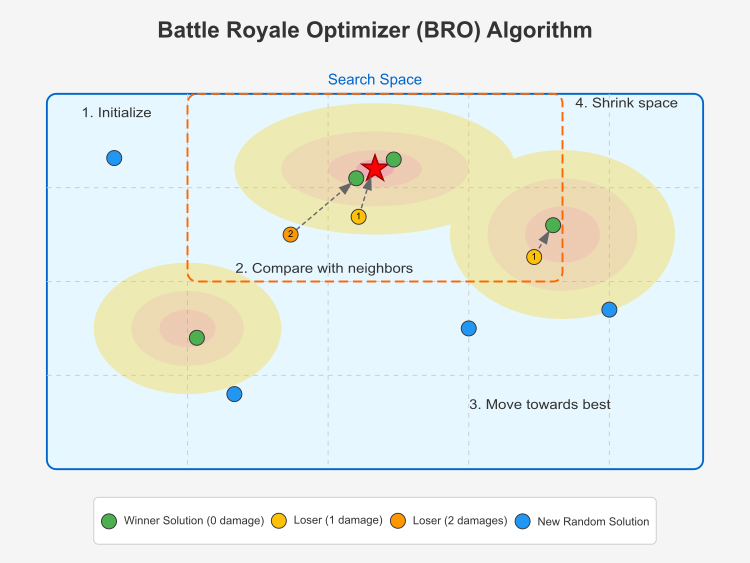
Figura 1. Ilustración del funcionamiento del algoritmo BRO.
Esta ilustración muestra los principales componentes del algoritmo de Battle Royale Optimizer (BRO). El espacio de búsqueda se representa como un área 2D con contornos que simbolizan la función de optimización (las áreas más brillantes representan las mejores soluciones). La mejor solución global está marcada con una estrella roja en el centro del "montículo" más alto. Las soluciones ganadoras están marcadas con puntos verdes: son las soluciones de daño cero (ganadoras en comparación con sus vecinas). Las soluciones perdedoras son puntos amarillos (con 1 daño) y naranjas (con 2 daños). Las nuevas soluciones aleatorias son puntos azules que aparecen cuando una solución acumula demasiados daños. Las soluciones perdedoras se desplazan hacia la mejor solución (mostrada por flechas punteadas). El estrechamiento del espacio de búsqueda se representa mediante un recuadro naranja discontinuo que se centra alrededor de la mejor solución.
Los pasos clave del algoritmo son: inicialización, comparación con los vecinos, avance hacia una solución mejor y reducción del espacio de búsqueda.Las soluciones del algoritmo BRO compiten entre sí, y las perdedoras reciben "daño". Las soluciones con demasiados daños son sustituidas por nuevas soluciones aleatorias. Ahora que entendemos cómo funciona el algoritmo, podemos escribir el pseudocódigo.
Inicialización:
- Creamos una población de soluciones con un tamaño popSize
- Para cada solución ponemos el contador de daños a 0
- Establecemos el umbral máximo de daño maxDamage
- Determinamos el número de épocas epochs
- Calculamos el valor delta inicial para el estrechamiento periódico del espacio de búsqueda
Algoritmo básico:
- Establecimiento de una población inicial:
- Para cada decisión de la población:
- Generamos coordenadas aleatorias en un espacio de búsqueda dado
- Para cada decisión de la población:
- Para cada época se cumple:
- Actualizamos la mejor solución global si se encuentra una mejor
- Se realizan "batallas" entre decisiones:
- Para cada decisión de la población:
- Encontramos el vecino más próximo (solución de distancia mínima)
- Comparamos la calidad de la solución actual con la de su vecino:
- Si la solución actual es mejor:
- Reiniciamos el contador de daños de la solución actual
- Aumentamos el contador de daño del vecino
- El perdedor (vecino) se desplaza hacia la mejor solución
- De lo contrario:
- Aumentamos el contador de daños de la solución actual
- Reiniciamos el contador de daños del vecino
- El perdedor (solución actual) se desplaza hacia la mejor solución
- Si la solución actual es mejor:
- Para cada decisión de la población:
- Procesamiento de soluciones gravemente dañadas:
- Para cada decisión de la población:
- Si el contador de daño ≥ maxDamage :
- Reiniciamos el contador de daños
- Sustituimos la solución por una nueva solución aleatoria
- Si el contador de daño ≥ maxDamage :
- Para cada decisión de la población:
- Reducción periódica del espacio de búsqueda:
- Si el número de época actual es divisible por delta :
- Calculamos las desviaciones típicas de las coordenadas en toda la población
- Reducimos el espacio de búsqueda en torno a la mejor solución
- Actualizamos el valor delta
- Si el número de época actual es divisible por delta :
- Retorno de la mejor solución encontrada
En el algoritmo intervienen las siguientes fórmulas:
- Cálculo del valor delta inicial para acotar el espacio de búsqueda: delta = ⌊epochs / log₁₀(epochs)⌋
- Cálculo de la distancia euclidiana entre soluciones: distance = √(∑(a[idx1][c] - a[idx2][c])²)
- Desplazamiento de la solución perdedora hacia la mejor solución global: a[i][c] = a[i][c] + r × (cB[c] - a[i][c])
- Cálculo del valor medio de cada coordenada: mean[c] = (∑a[i][c]) / popSize
- Cálculo de la desviación estándar de cada coordenada: sdValues[c] = √(∑(a[i][c] - mean[c])² / popSize)
- Fórmulas para reducir el espacio de búsqueda: newMin[c] = cB[c] - sdValues[c] newMax[c] = cB[c] + sdValues[c]
- Actualización del parámetro delta tras la contracción espacial: delta = delta + ⌊delta / 2⌉
Para acotar periódicamente el espacio de búsqueda, el autor propone la siguiente fórmula: Δ (delta) = maxEpochs / log₁₀(maxEpochs), cuya gráfica se muestra a continuación:
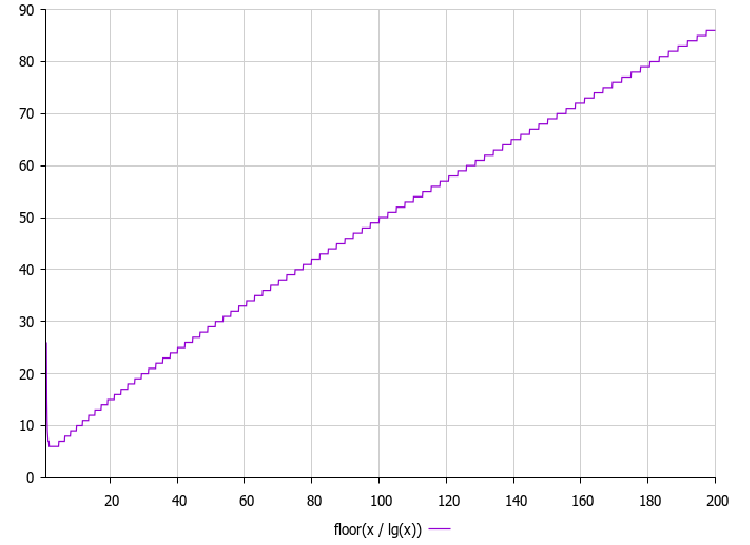
Figura 2. Gráfico de la función de dependencia del parámetro delta respecto al número de épocas
La gráfica de la función delta = epochs/log₁₀(epochs) es importante en el algoritmo BRO, ya que determina tras cuántas iteraciones se reducirá el espacio de búsqueda. Como podemos ver en el gráfico, el valor delta aumenta con el número de épocas, pero no tan rápido como las propias épocas, debido a la división por el logaritmo. Esto crea una dependencia no lineal que ofrece las siguientes ventajas: en las primeras fases de la optimización (cuando el número de épocas es pequeño), el estrechamiento se produce con relativa frecuencia, lo que ayuda al algoritmo a centrarse más rápidamente en las zonas prometedoras, mientras que en las últimas fases (cuando el número de épocas es grande), el estrechamiento se produce con menos frecuencia, lo que permite una exploración más exhaustiva de las zonas prometedoras ya encontradas.
En nuestros experimentos, hemos convertido la fórmula de dependencia del parámetro delta; cambia dos veces con el logaritmo, y el algoritmo funciona mejor.
// Вычисление начального delta для сужения пространства поиска delta = (int)MathFloor(epochs / MathLog(MathLog(epochs)));
Vamos a pasar ahora a la generación del código; para ello, escribiremos una clase personalizada "C_AO_BRO", que heredará de la clase básica "C_AO", es decir, heredará todos los miembros públicos y protegidos de la clase "C_AO" y podrá sobreescribir su comportamiento. Esta clase consistirá en la aplicación de un algoritmo de optimización basado en el concepto "Battle Royale".
1. Miembros públicos de la clase:
- popSize — establece el tamaño de la población.
- maxDamage — establece el umbral máximo de daño, cuántos "derrotas" puede sufrir la solución antes de ser eliminada.
- SetParams () — el método actualiza los valores "popSize" y "maxDamage" basándose en los valores almacenados en el array "params", lo que permite cambiar los parámetros del algoritmo durante la ejecución.
- Init () — método de inicialización del algoritmo. Admite los siguientes parámetros:
- rangeMinP [] — valores mínimos del rango de búsqueda para cada variable.
- rangeMaxP [] — valores máximos del rango de búsqueda.
- rangeStepP [] — paso de búsqueda para cada variable.
- epochsP — número de épocas (iteraciones) del algoritmo. El valor por defecto es 0.
- Moving () — el método implementa la lógica básica de desplazamiento o actualización de soluciones en el espacio de búsqueda.
- Revision () — el método implementa la lógica de revisión de las decisiones actuales, aquí se evalúa el "daño" recibido por cada decisión.
- maxDamage — miembro público que almacena el umbral máximo de daño.
2. Campos privados de la clase:
- delta — intervalo para reducir el espacio de búsqueda. Permite adaptar el tamaño del paso de búsqueda durante la optimización.
- daños [] — el array almacena el número de "daños" de cada solución de la población.
- epoch — época actual (número de iteración) del algoritmo.
- epoch — número máximo de épocas (iteraciones) del algoritmo.
3. Métodos auxiliares:
- FindNearestNeighbor () — encuentra el vecino más cercano para una solución en un índice dado utilizado para la interacción entre soluciones.
- CalculateDistance () — calcula la distancia entre dos soluciones identificadas por sus índices.
- CalculateStandardDeviations () — calcula las desviaciones estándar de los valores de solución de la población utilizados para estimar la diversidad de la población y adaptar los parámetros de búsqueda.
- ShrinkSearchSpace () — método que reduce el espacio de búsqueda. Se trata de una técnica estándar para la convergencia de un algoritmo a una solución óptima.
Introducción general:
C_AO_BRO es la clase para el algoritmo de optimización Battle Royale y la idea básica del algoritmo, en resumen, es la siguiente:
- Inicialización: creamos una población de soluciones aleatorias en un espacio de búsqueda definido.
- Evaluación: cada solución se evalúa con una función de aptitud.
- Battle Royale: las soluciones "luchan" entre sí (se comparan según los valores de la función objetivo).
- Daños: algunas soluciones reciben "daños" según los resultados de las "batallas".
- Expulsión: las soluciones que han recibido una cantidad de "daño" superior a "maxDamage" se eliminan de la población.
- Reproducción/sustitución: las soluciones eliminadas se sustituyen por nuevas soluciones aleatorias.
- Reducción del espacio de búsqueda: el espacio de búsqueda puede reducirse para centrarse en las áreas más prometedoras.
- Repetición: las etapas 2-7 se repiten durante un número determinado de épocas.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BRO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_BRO () { } C_AO_BRO () { ao_name = "BRO"; ao_desc = "Battle Royale Optimizer"; ao_link = "https://www.mql5.com/es/articles/17688"; popSize = 100; // размер популяции maxDamage = 3; // максимальный порог повреждений ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "maxDamage"; params [1].val = maxDamage; } void SetParams () { popSize = (int)params [0].val; maxDamage = (int)params [1].val; } bool Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0); // количество эпох void Moving (); void Revision (); //---------------------------------------------------------------------------- int maxDamage; // максимальный порог повреждений private: //------------------------------------------------------------------- int delta; // интервал для сужения пространства поиска int damages []; // количество повреждений для каждого решения int epoch; // текущая эпоха int epochs; // максимальное количество эпох // Вспомогательные методы int FindNearestNeighbor (int index); double CalculateDistance (int idx1, int idx2); void CalculateStandardDeviations (double &sdValues []); void ShrinkSearchSpace (); }; //——————————————————————————————————————————————————————————————————————————————
El método "Init ()" inicializa el algoritmo BRO, llama a "StandardInit ()" para una inicialización estándar usando los rangos y pasos de búsqueda transmitidos. Si "StandardInit" retorna "false", el método "Init ()" también devolverá "false", señalando un error de inicialización. Inicializa el array "damages" asignando memoria para cada solución de la población "popSize" y estableciendo el número inicial de "daños" de cada solución en 0. Establece el número total de épocas "epochs" y restablece la época actual "epoch" a 0.
El valor "delta" se calcula según el número total de épocas, de modo que el espacio de búsqueda se reduce gradualmente. Si "delta" resulta ser menor o igual que 0, se pone a 1. En general, este método prepara el algoritmo para su funcionamiento inicializando sus parámetros básicos y sus estructuras de datos.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_BRO::Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0) // количество эпох { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- // Инициализация счетчиков повреждений для каждого решения ArrayResize (damages, popSize); ArrayInitialize (damages, 0); // Установка эпох epochs = epochsP; epoch = 0; // Вычисление начального delta для сужения пространства поиска delta = (int)MathFloor (epochs / MathLog10 (epochs)); if (delta <= 0) delta = 1; return true; } //——————————————————————————————————————————————————————————————————————————————
El método "Moving ()" implementa la lógica de inicialización de una población de soluciones, con cada coordenada de cada solución generada aleatoriamente entre los rangos mínimo y máximo dados "rangeMin" y "rangeMax" y muestreada en un determinado paso "rangeStep". Este método garantiza que la población se inicialice solo una vez.
/—————————————————————————————————————————————————————————————————————————————— void C_AO_BRO::Moving () { if (!revision) { // Инициализация популяции случайными решениями for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double coordinate = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; } } //——————————————————————————————————————————————————————————————————————————————
El método "Revision ()" supone un paso clave en el algoritmo de optimización BRO. Cada iteración del método actualiza la mejor solución: si alguna solución de la población actual es mejor que la mejor solución global actual, entonces se actualizará la mejor solución global.
El método compara las soluciones con sus vecinas: para cada solución de la población, se encuentra la vecina más próxima. A continuación, se comparan los valores de sus funciones. La mejor solución de la pareja es "recompensada" reiniciando el contador de daños, mientras que el contador de daños de la peor solución se aumenta. La peor solución del par se desplaza hacia la mejor solución global.
Luego se sustituyen las soluciones "dañadas": si una solución ha acumulado suficiente "daño" (ha alcanzado el valor "maxDamage"), se sustituirá por una nueva generada aleatoriamente. Periódicamente, según la variable "delta", se reduce la zona de búsqueda. Este proceso se repite en varias iteraciones del algoritmo. Usando la comparación con los vecinos, las soluciones se desplazan a zonas más favorables para la búsqueda.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BRO::Revision () { epoch++; // Обновление глобального наилучшего решения for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } // Сравнение каждого решения с его ближайшим соседом и обновление счетчиков повреждений for (int i = 0; i < popSize; i++) { int neighbor = FindNearestNeighbor (i); if (neighbor != -1) { if (a [i].f >= a [neighbor].f) { // Решение i побеждает damages [i] = 0; damages [neighbor]++; // Проигравший (сосед) движется к наилучшему решению for (int c = 0; c < coords; c++) { double r = u.RNDfromCI (0, 1); a [neighbor].c [c] = a [neighbor].c [c] + r * (cB [c] - a [neighbor].c [c]); a [neighbor].c [c] = u.SeInDiSp (a [neighbor].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } else { // Решение i проигрывает damages [i]++; damages [neighbor] = 0; // Проигравший (i) движется к наилучшему решению for (int c = 0; c < coords; c++) { double r = u.RNDfromCI (0, 1); a [i].c [c] = a [i].c [c] + r * (cB [c] - a [i].c [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } // Проверка, достигло ли какое-либо решение максимального повреждения, и его замена for (int i = 0; i < popSize; i++) { if (damages [i] >= maxDamage) { // Сброс счетчика повреждений damages [i] = 0; // Генерация нового случайного решения for (int c = 0; c < coords; c++) { double coordinate = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]); } } } // Периодическое сужение пространства поиска if (epochs > 0 && epoch % delta == 0) { ShrinkSearchSpace (); // Обновление delta delta = delta + (int)MathRound (delta / 2); } } //——————————————————————————————————————————————————————————————————————————————
El método "FindNearestNeighbor ()" encuentra el índice del vecino más próximo para una solución con índice "index" en la población. Prueba todas las soluciones, calcula la distancia a cada una de ellas (salvo el propio "index" de la solución) y devuelve el índice de la solución con la distancia mínima. Si no se ha podido encontrar ningún vecino más cercano (por ejemplo, solo hay una solución en la población), retornará -1. En pocas palabras, el método encuentra el vecino más próximo para una solución dada.
//—————————————————————————————————————————————————————————————————————————————— int C_AO_BRO::FindNearestNeighbor (int index) { double minDistance = DBL_MAX; int nearestIndex = -1; for (int i = 0; i < popSize; i++) { if (i == index) continue; double distance = CalculateDistance (index, i); if (distance < minDistance) { minDistance = distance; nearestIndex = i; } } return nearestIndex; } //——————————————————————————————————————————————————————————————————————————————
El método "CalculateDistance ()" calcula la distancia euclidiana entre dos soluciones de una población dada según sus índices "idx1" e "idx2". Comienza inicializando la variable "distanceSum" con cero. Esta variable acumulará la suma de los cuadrados de las diferencias de las coordenadas. El ciclo for itera todas las coordenadas de la solución. En cada iteración del ciclo, se calcula la diferencia entre las coordenadas correspondientes de las soluciones "idx1" e "idx2". El cuadrado de esta diferencia se añade a la "distanceSum".
Una vez finalizado el ciclo, el método retornará la raíz cuadrada de "distanceSum", es decir, la distancia euclidiana entre las dos soluciones. Como resultado, el método retorna un valor numérico que refleja la "distancia" entre dos soluciones en el espacio de búsqueda. Cuanto mayor sea este valor, más alejadas se encontrarán las soluciones entre sí.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_BRO::CalculateDistance (int idx1, int idx2) { double distanceSum = 0.0; for (int c = 0; c < coords; c++) { double diff = a [idx1].c [c] - a [idx2].c [c]; distanceSum += diff * diff; } return MathSqrt (distanceSum); } //——————————————————————————————————————————————————————————————————————————————
El método "CalculateStandardDeviations ()" calcula la desviación estándar para cada coordenada de la solución en la población y almacena los resultados en el array "sdValues". Redimensiona el array de entrada "sdValues" para que pueda almacenar la desviación estándar de cada una de las coordenadas "coords". Luego el ciclo prueba cada coordenada de la solución y se calcula la desviación estándar. El método pone a cero la suma de cuadrados de las desviaciones de la coordenada actual y después también pone a cero su valor medio. El ciclo suma los valores de la coordenada actual "c" para todas las soluciones de la población. A continuación, calcula el valor medio de esta coordenada.
En el cálculo de la suma de los cuadrados de las desviaciones: el ciclo prueba todas las soluciones de la población y calcula la suma de cuadrados de las desviaciones del valor medio para la coordenada actual. Calcula la diferencia entre el valor de la coordenada "c" para la solución "i" y su valor medio. Luego suma el cuadrado de la diferencia respecto a la suma de los cuadrados de las desviaciones. Y calcula la desviación estándar como la raíz cuadrada de la suma de los cuadrados de las varianzas dividida por el tamaño de la población. El resultado se almacena en el elemento correspondiente del array "sdValues".
Como resultado, el método calcula una medida de la dispersión de los valores para cada coordenada de la solución en la población y la almacena en el array "sdValues" transmitido, mientras que la desviación estándar muestra cuánto varían los valores de las coordenadas alrededor del valor medio.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BRO::CalculateStandardDeviations (double &sdValues []) { ArrayResize (sdValues, coords); for (int c = 0; c < coords; c++) { double sum = 0.0; double mean = 0.0; // Вычисление среднего for (int i = 0; i < popSize; i++) mean += a [i].c [c]; mean /= popSize; // Вычисление суммы квадратов отклонений for (int i = 0; i < popSize; i++) { double diff = a [i].c [c] - mean; sum += diff * diff; } sdValues [c] = MathSqrt (sum / popSize); } } //——————————————————————————————————————————————————————————————————————————————
El método "ShrinkSearchSpace ()" reduce el espacio de búsqueda según las desviaciones estándar de las coordenadas y la ubicación de la mejor solución encontrada. En cierto modo, centra la búsqueda en un área más prometedora en la que ya existe una buena solución.
Primero viene el cálculo de las desviaciones estándar; esto se hace llamando al método "CalculateStandardDeviations ()", que calcula las desviaciones estándar para cada coordenada de la solución en la población y las almacena en el array "sdValues", o en otras palabras, se calcula cuánto difieren los valores de cada coordenada en la población. Cálculo de nuevos límites: los nuevos límites se centran alrededor de la mejor solución encontrada y su anchura viene definida por la desviación estándar. Si la desviación estándar es pequeña, la búsqueda se estrechará en torno a la mejor solución. Si la desviación estándar es elevada, la búsqueda seguirá siendo más amplia. Comprobación de admisibilidad: la búsqueda no irá más allá del espacio de soluciones inicial admisible.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BRO::ShrinkSearchSpace () { double sdValues []; CalculateStandardDeviations (sdValues); for (int c = 0; c < coords; c++) { // Новые границы центрированы вокруг наилучшего решения с шириной стандартного отклонения double newMin = cB [c] - sdValues [c]; double newMax = cB [c] + sdValues [c]; // Убедитесь, что новые границы находятся в пределах исходных ограничений if (newMin < rangeMin [c]) newMin = rangeMin [c]; if (newMax > rangeMax [c]) newMax = rangeMax [c]; // Обновление границ rangeMin [c] = newMin; rangeMax [c] = newMax; } } //——————————————————————————————————————————————————————————————————————————————
Resultados de las pruebas
Tras ejecutar las pruebas, podemos ver que el algoritmo funciona razonablemente bien en las funciones Hilly y Forest, sin embargo, el rendimiento de convergencia es mucho más débil en la Megacity discreta.
BRO|Battle Royale Optimizer|50.0|3.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.7494493002235458
25 Hilly's; Func runs: 10000; result: 0.4983307394255448
500 Hilly's; Func runs: 10000; result: 0.27994639979348446
=============================
5 Forest's; Func runs: 10000; result: 0.6962444245506945
25 Forest's; Func runs: 10000; result: 0.3845619185097379
500 Forest's; Func runs: 10000; result: 0.20427058729050862
=============================
5 Megacity's; Func runs: 10000; result: 0.3815384615384616
25 Megacity's; Func runs: 10000; result: 0.21107692307692308
500 Megacity's; Func runs: 10000; result: 0.10607692307692404
=============================
All score: 3.51150 (39.02%)
En la visualización se aprecia la dispersión de los valores resultantes y una menor capacidad de búsqueda en la última función Megacity discreta.
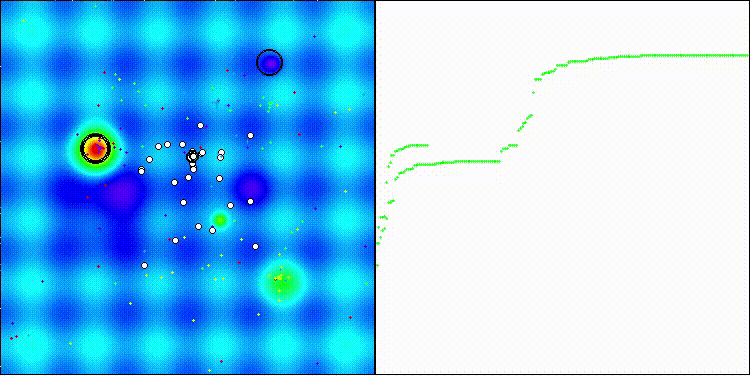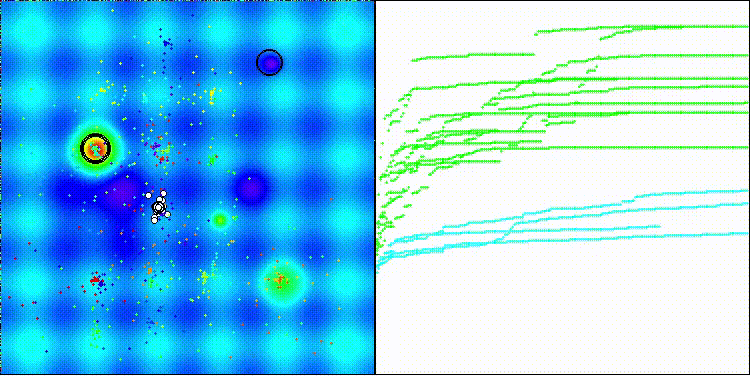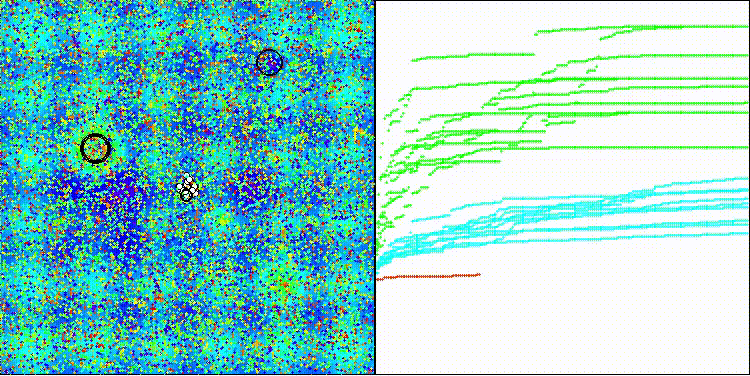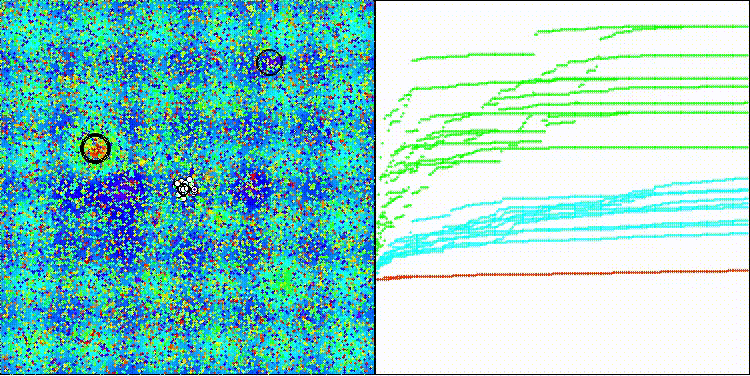
BRO en la función de prueba Hilly
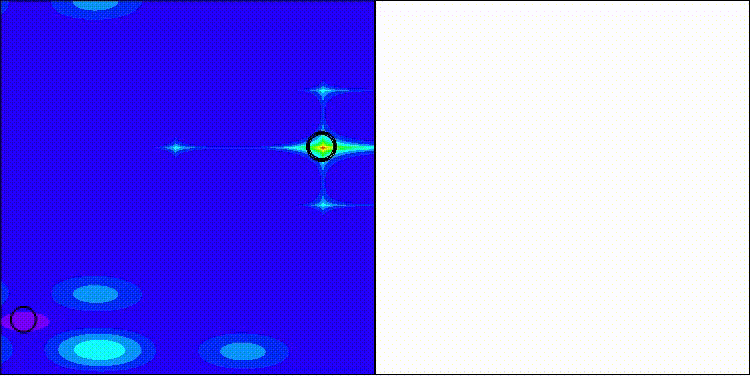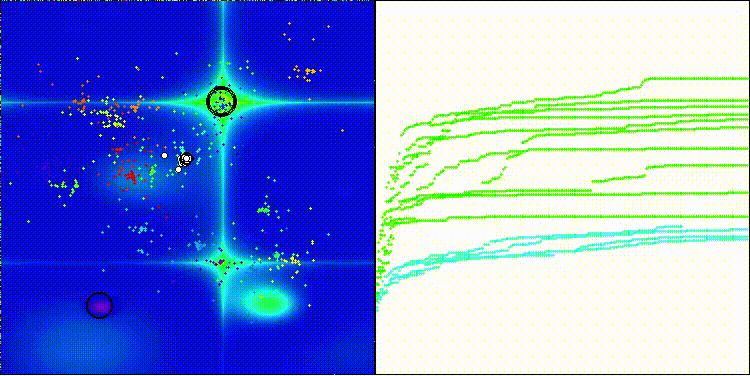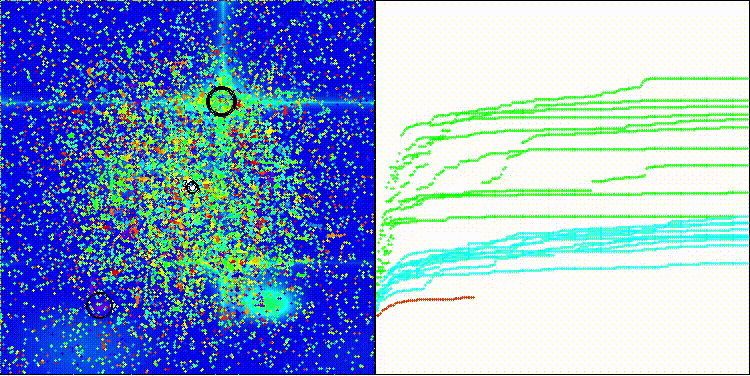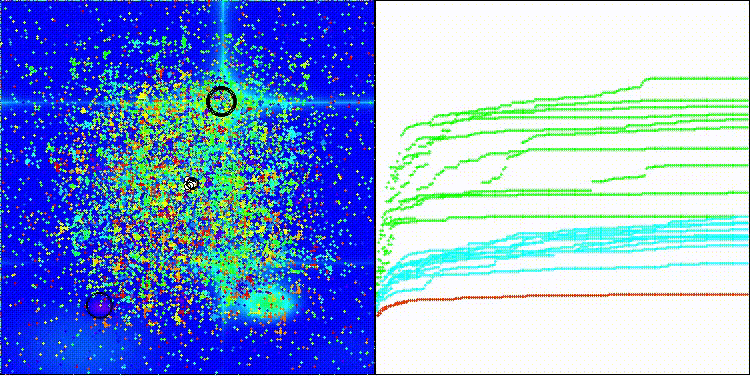
BRO en la función de prueba Forest
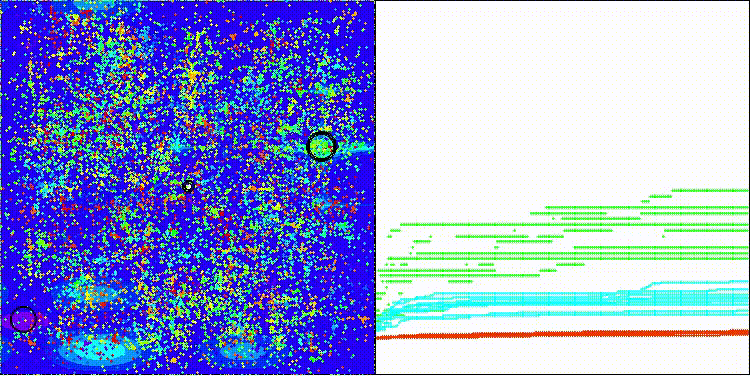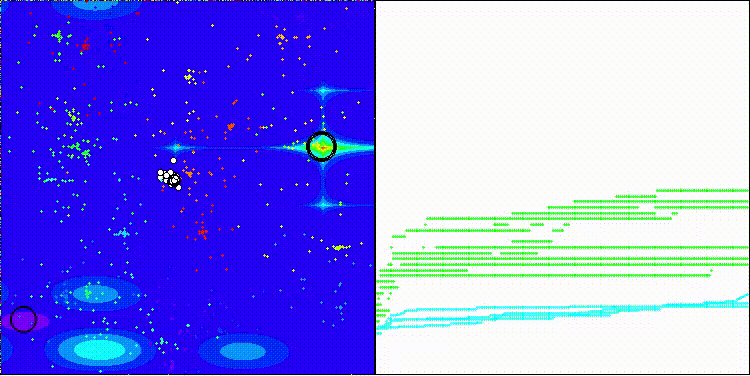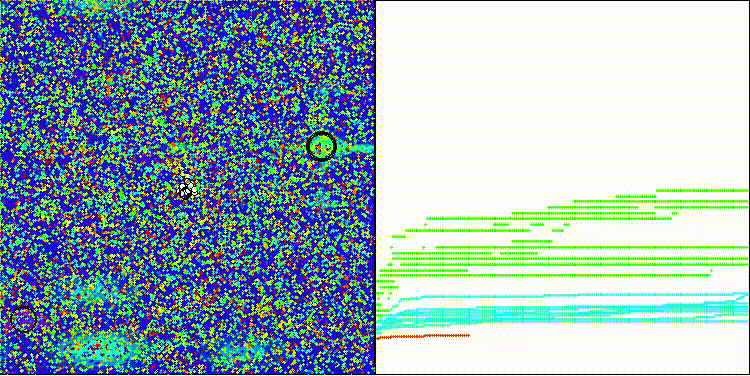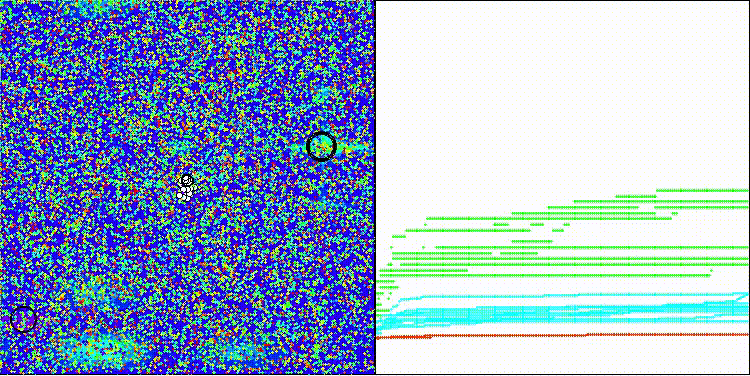
BRO en la función de prueba Megacity
Según los resultados, el algoritmo BRO cierra la tabla de clasificación de los algoritmos de optimización basados en la población.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Resultado | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration optimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 13 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 14 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0.34583 | 1,86493 | 0.93593 | 0.80152 | 0,27177 | 2,00923 | 0.65077 | 0.51646 | 0,15472 | 1,32195 | 5.196 | 57.73 |
| 15 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 16 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 17 | AOSm | búsqueda de orbitales atómicos M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 18 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 19 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 20 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 21 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 22 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 23 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 24 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 25 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 26 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 27 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 28 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 29 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 30 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 31 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 32 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 33 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 34 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 35 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 36 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1,65585 | 0.89675 | 0.37401 | 0.16984 | 1,44060 | 0.69538 | 0.28031 | 0.10852 | 1,08422 | 4.181 | 46,45 |
| 37 | ABH | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4.127 | 45,85 |
| 38 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 39 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0,26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1,39880 | 0,66154 | 0.27046 | 0.10594 | 1,03794 | 4.037 | 44.85 |
| 40 | CGO | chaos game optimization | 0,57256 | 0,37158 | 0,32018 | 1,26432 | 0,61176 | 0,61931 | 0,62161 | 1,85267 | 0,37538 | 0,21923 | 0,19028 | 0,78490 | 3,902 | 43,35 |
| 41 | ATAm | artificial tribe algorithm M | 0.71771 | 0.55304 | 0,25235 | 1,52310 | 0.82491 | 0.55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 42 | DIRECTOR FINANCIERO | central force optimization | 0,60961 | 0,54958 | 0,27831 | 1,43750 | 0,63418 | 0,46833 | 0,22541 | 1,32792 | 0,57231 | 0,23477 | 0,09586 | 0,90294 | 3,668 | 40,76 |
| 43 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 44 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3.657 | 40,63 |
| 45 | BRO | battle royale optimizer | 0,74945 | 0,49833 | 0,27995 | 1,52773 | 0,69624 | 0,38456 | 0,20427 | 1,28507 | 0,38154 | 0,21108 | 0,10608 | 0,69870 | 3,512 | 39,02 |
| R.W. | neuroboids optimization algorithm 2(joo) | 0.48754 | 0.32159 | 0.25781 | 1,06694 | 0.37554 | 0,21944 | 0,15877 | 0,75375 | 0.27969 | 0,14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Conclusiones
El algoritmo BRO muestra un enfoque interesante de la optimización metaheurística abriendo el camino a métodos de "juego", utilizando una metáfora de "Battle Royale" en la que las soluciones compiten entre sí. Los puntos fuertes del algoritmo son su simplicidad conceptual (el algoritmo es intuitivo y relativamente fácil de aplicar), el estrechamiento automático del espacio de búsqueda basado en las características estadísticas de la población y el uso del concepto de vecinos más próximos para las competiciones locales. El algoritmo BRO es un método de optimización muy prometedor cuyo potencial está aún por explotar.
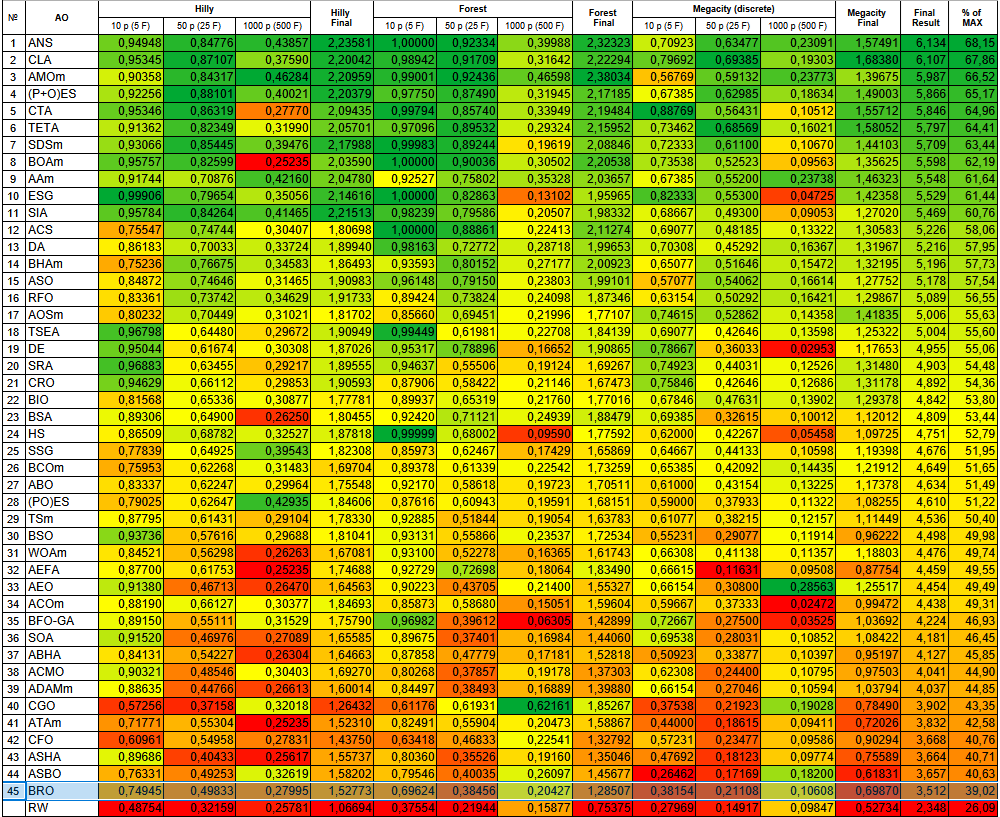
Figura 3. Clasificación por colores de los algoritmos según las pruebas respectivas
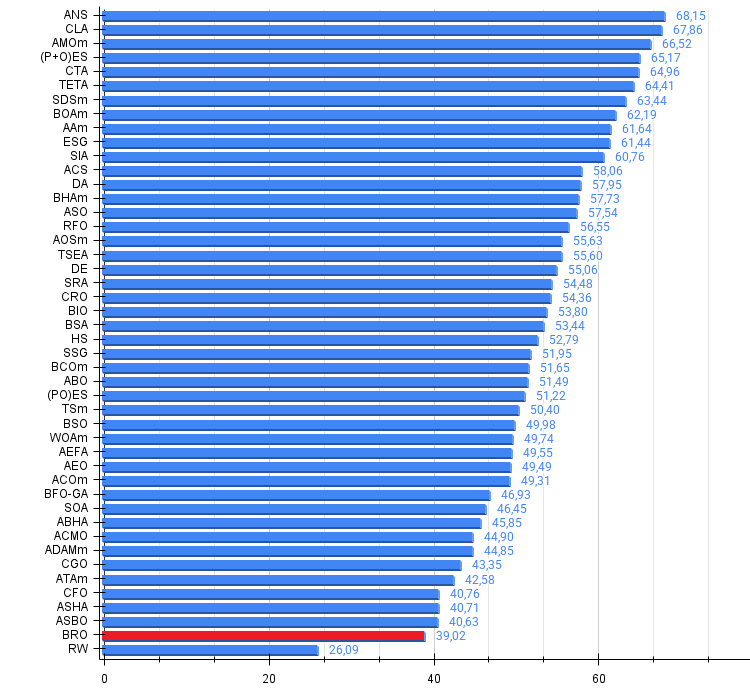
Figura 4. Histograma de los resultados de las pruebas de algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de puntuación está en el archivo)
Ventajas e inconvenientes del algoritmo BRO:
Ventajas:
- Supone una idea interesante.
- Implementación sencilla.
- Desarrollo prometedor.
Desventajas:
- Resultados débiles sobre funciones discretas.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | #C_AO.mqh | Archivo de inclusión | Clase padre de algoritmos de optimización basados en la población |
| 2 | #C_AO_enum.mqh | Archivo de inclusión | Enumeración de los algoritmos de optimización basados en la población |
| 3 | TestFunctions.mqh | Archivo de inclusión | Biblioteca de funciones de prueba |
| 4 | TestStandFunctions.mqh | Archivo de inclusión | Biblioteca de funciones del banco de pruebas |
| 5 | Utilities.mqh | Archivo de inclusión | Biblioteca de funciones auxiliares |
| 6 | CalculationTestResults.mqh | Archivo de inclusión | Script para calcular los resultados en una tabla comparativa |
| 7 | Testing AOs.mq5 | Script | Banco de pruebas único para todos los algoritmos de optimización basados en la población |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización |
| 9 | Test_AO_BRO.mq5 | Script | Banco de pruebas para BRO |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/17688
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
Utilizando redes neuronales en MetaTrader
Aprendizaje automático en la negociación de tendencias unidireccionales tomando el oro como ejemplo
Particularidades del trabajo con números del tipo double en MQL4
Técnicas avanzadas de gestión y optimización de la memoria en MQL5
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso