MetaTrader 5 / 测试者
English Русский Español Português
preview
血液遗传优化算法（BIO）

血液遗传优化算法（BIO）

MetaTrader 5 — 测试者 |
645 0
Andrey Dik
Andrey Dik

内容

  1. 概述
  2. 算法实现
  3. 测试结果


概述

有一天，我在实验室里看着护士给患者采集血样，一个突如其来的想法闪过我的脑海。血型，这一遵循严格遗传规律代代相传的古老遗传体系，突然以一种全新的视角呈现在我眼前。倘若这些自然的遗传特性能够应用于优化算法领域呢？

我们每个人的血管里都流淌着从父母那里遗传而来的独特组合。正如血型决定了输血时的兼容性，它们同样可以决定在优化过程中参数如何传递和变异。我很喜欢这个理念，决定等有时间时再进行深入探究。经过一系列实验，BIO应运而生——这是一种利用血型遗传自然规律作为管理决策进化隐喻的方法。在该算法中，四种血型演变成了四种不同的参数变异策略，而遗传规律则决定了后代如何获取并修改其父母的特征。

正如自然界中，孩子的血型并非父母血型的简单平均值，而是遵循遗传规律。在BIO算法中，新解的参数是通过一套遗传和变异体系形成的。每种血型都带来了探索解空间的独特方式：从保守地保留已找到的最优值，到激进地变异以开拓新的有前景的区域和方向，从而进一步深入研究解空间。

在本文中，我想分享一下结合了生物灵感与算法严谨性的BIO算法原理，并提供一些在已熟悉函数上的测试结果。那么，我们行动吧。


算法实现

首先，让我们来了解一下子女从父母那里继承血型的对照表。由您所见，血型的遗传并非一成不变。关于世界人口中血型分布的统计数据十分有趣。最常见的是第一类血型（O型） —— 约40%的地球人口拥有这种血型。其次是第二类血型（A型），大约30%的人属于这一血型。第三类血型（B型）出现在20%的人口中，而第四类血型（AB型）则最为罕见——只有约10%的人携带这种血型。

在研究遗传机制的过程中，我了解到第一类血型相对于其他所有血型都是隐性的。这意味着，O型血的人只能将O型血遗传给子女。同时，第二类和第三类血型彼此间表现出共显性，当它们结合时，就会产生第四类血型。从进化角度来看，第四类血型是最晚出现的。

我对不同血型的一些独特特性特别感兴趣。例如，O型血被认为是“万能供血者”，因为它可以输给任何血型的人。相反，AB型血则使其携带者成为“万能受血者”——他们可以接受任何血型的血液。 

血型系统的所有这些特性启发我在算法中创建了相应的机制。由于第一类血型是最基础且最常见的，因此它对应于算法中保留所找到最优解决方案的策略。血型遗传对照表展示了父母血型的所有可能组合及其子女可能拥有的血型，这构成了根据父母血型确定新解“血型”的基础，而这直接影响着BIO算法中参数的变异方式。

血型

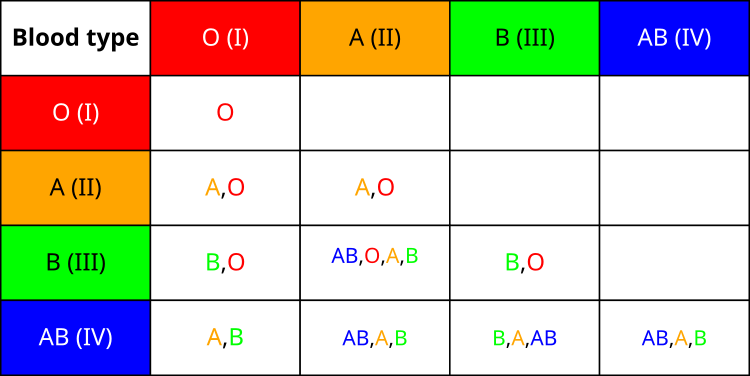
图例1. 血型遗传对照表 

BIO算法基于一个相当简单的理念：种群中的每个解（父代个体）都有其自身的“血型”（1至4型），这由其在种群中的序号决定。当我们创建新一代解时，会从当前种群中选出两个“双亲”。选择的概率并非线性，而是二次方的——这意味着最优决策成为双亲的机会显著更高。

现在，最有趣的部分开始了。根据双亲的血型，利用一个特殊的遗传矩阵（该矩阵在代码的Init方法中编写），我们确定“子代”——新解可能的血型。然后，对于这个新解的每个参数，如果发现是第一类血型，我们就采用已找到的最优解中的值。我是以第一类血型作为万能供血者为类比这样做的。如果选择的是第二类血型，我们就从其中一个双亲取值，并对其应用幂分布。这样会产生一种探索参数范围边缘的趋势。对于第三类血型，我们也从其中一个双亲取值，但将其向最优解随机移动一定量。而对于第四类血型，我们取父代值，并相对于范围边界进行反射，这是一种类似反转的操作，使我们能够探索新的搜索区域。

创建新一代后，我们检查是否出现了比当前全局解更优的解，并将最优个体保存下来供下一次迭代使用。因此，利用血型遗传做类比，我的算法通过结合不同的参数变异策略来探索解空间。以下是该算法的伪代码。

初始化：

  1. 创建一个大小为popSize（默认50）的智能体种群
  2. 创建一个血型遗传矩阵，该矩阵根据双亲的血型（1、2、3、4）确定子代可能的血型
  3. 初始化参数的范围（最小值、最大值、步长值）

主循环：

  1. 若当前为首次迭代（revision = false）：
    • 在参数范围内随机初始化所有智能体的位置
    • 将revision标识设为'true'
  2. 对于种群中的每个个体：
    • 使用二次概率分布选择父代智能体（父亲和母亲）
    • 使用函数确定双亲的血型：bloodType = 1 + (population_position % 4)
    • 对于子代解的每个参数：
      • 根据双亲的血型，从遗传矩阵中获取子代可能的血型
      • 若子代血型为1：
        • 对该参数使用已知的最优解
      • 否则：
        • 从父亲或母亲中随机选择一个参数值
        • 根据子代的血型进行变异：
          • 血型2：应用指数为20的幂律分布
          • 血型3：以随机因子将参数值向最优解移动
          • 血型4：将参数值在整个参数范围内进行镜像反射
      • 确保参数保持在可接受的范围和步长内

修订阶段：

  1. 如果存在适应度更优的智能体，则更新全局最优解
  2. 将当前种群复制到扩展种群数组的后半部分
  3. 按适应度对扩展种群进行排序
  4. 保留最优智能体以供下一代使用

让我们开始编写算法代码。从C_AO派生的C_AO_BIO类实现了BIO算法，并假设使用一种数据结构来表示种群中的个体（智能体）及其控制。

    C_AO_BIO () —— 构造函数，用于初始化外部BIO参数：将种群大小popSize设置为50，将params参数数组的大小设置为一个元素，该元素代表popSize。
    SetParams()     —— 该方法允许设置类参数，在此情况下，从参数数组中设置种群大小popSize。
    Init()     —— 该方法通过接受参数的最小值和最大值、变化步长以及迭代次数来初始化算法。
    Moving()和Revision () —— 这两种方法分别负责种群中智能体的移动（进化）和修订（性能评估与最优个体的选择）。S_Papa 和S_Mama：
    • S_Papa是一个结构体，包含一个血型数组（bTypes）。
    • S_Mama包含一个由四个S_Papa对象组成的数组，这表明存在“双亲”以便进行进一步的基因混合。

    这种以结构体形式表示的方法将使我们能够通过指定双亲的血型，直接从双亲获取子代可能的血型，例如“ma[1].pa[2].bTypes”，其中1和2分别是母亲和父亲的血型。

    GetBloodType ()方法返回给定智能体的血型，而GetBloodMutation ()则根据血型实现基因变异机制。 

    //——————————————————————————————————————————————————————————————————————————————
class C_AO_BIO : public C_AO
{
  public: //--------------------------------------------------------------------
  C_AO_BIO ()
  {
    ao_name = "BIO";
    ao_desc = "Blood Inheritance Optimization";
    ao_link = "https://www.mql5.com/en/articles/17246";

    popSize = 50; // population size

    ArrayResize (params, 1);
    params [0].name = "popSize"; params [0].val = popSize;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum values
             const double &rangeMaxP  [],  // maximum values
             const double &rangeStepP [],  // step change
             const int     epochsP = 0);   // number of epochs

  void Moving   ();
  void Revision ();

  private: //-------------------------------------------------------------------
  struct S_Papa
  {
      int bTypes [];
  };
  struct S_Mama
  {
      S_Papa pa [4];
  };
  S_Mama ma [4];

  S_AO_Agent p [];

  int  GetBloodType     (int ind);
  void GetBloodMutation (double &gene, int indGene, int bloodType);
};
//——————————————————————————————————————————————————————————————————————————————

    Init方法会对C_AO_BIO类的实例进行初始化，并通过设置智能体种群及其特征，为后续工作做好准备。让我们来看一下该方法的实现。

    调用StandardInit方法—— 第一行代码检查调用此方法的结果，该用于检查/初始化算法运行所需的基本参数。

    初始化智能体数组：

    • 将“p”智能体数组的大小调整为给定种群大小（popSize）的两倍。
    • 在for循环中，为每个智能体调用Init方法，使用坐标参数初始化智能体。
    初始化血型：
    • 接下来，该方法为S_Mama和S_Papa结构体的血型数组（bTypes）指定大小。
    • 对于不同的组合（例如，ma[0].pa[0]、ma[1].pa[2]等），根据特殊的遗传矩阵设置不同的血型，并通过ArrayResize指定数组的大小。

    因此，C_AO_BIO类中的Init方法承担着为优化算法的执行准备对象的重要任务：它创建一个智能体种群，设置其初始参数，并定义血型的关联规则（遗传）。这样使得我们能够立即获取子代可能的血型，并利用其“血型”参数在算法中实现进一步的进化。

    //——————————————————————————————————————————————————————————————————————————————
bool C_AO_BIO::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (p, popSize * 2);
  for (int i = 0; i < popSize * 2; i++) p [i].Init (coords);

  //1-1
  ArrayResize (ma [0].pa [0].bTypes, 1);

  ma [0].pa [0].bTypes [0] = 1;

  //2-2
  ArrayResize (ma [1].pa [1].bTypes, 2);

  ma [1].pa [1].bTypes [0] = 1;
  ma [1].pa [1].bTypes [1] = 2;

  //3-3
  ArrayResize (ma [2].pa [2].bTypes, 2);

  ma [2].pa [2].bTypes [0] = 1;
  ma [2].pa [2].bTypes [1] = 3;

  //1-2; 2-1
  ArrayResize (ma [0].pa [1].bTypes, 2);
  ArrayResize (ma [1].pa [0].bTypes, 2);

  ma [0].pa [1].bTypes [0] = 1;
  ma [0].pa [1].bTypes [1] = 2;

  ma [1].pa [0].bTypes [0] = 1;
  ma [1].pa [0].bTypes [1] = 2;

  //1-3; 3-1
  ArrayResize (ma [0].pa [2].bTypes, 2);
  ArrayResize (ma [2].pa [0].bTypes, 2);

  ma [0].pa [2].bTypes [0] = 1;
  ma [0].pa [2].bTypes [1] = 3;

  ma [2].pa [0].bTypes [0] = 1;
  ma [2].pa [0].bTypes [1] = 3;

  //1-4; 4-1
  ArrayResize (ma [0].pa [3].bTypes, 2);
  ArrayResize (ma [3].pa [0].bTypes, 2);

  ma [0].pa [3].bTypes [0] = 2;
  ma [0].pa [3].bTypes [1] = 3;

  ma [3].pa [0].bTypes [0] = 2;
  ma [3].pa [0].bTypes [1] = 3;

  //2-3; 3-2
  ArrayResize (ma [1].pa [2].bTypes, 4);
  ArrayResize (ma [2].pa [1].bTypes, 4);

  ma [1].pa [2].bTypes [0] = 1;
  ma [1].pa [2].bTypes [1] = 2;
  ma [1].pa [2].bTypes [2] = 3;
  ma [1].pa [2].bTypes [3] = 4;

  ma [2].pa [1].bTypes [0] = 1;
  ma [2].pa [1].bTypes [1] = 2;
  ma [2].pa [1].bTypes [2] = 3;
  ma [2].pa [1].bTypes [3] = 4;

  //2-4; 4-2; 3-4; 4-3; 4-4
  ArrayResize (ma [1].pa [3].bTypes, 3);
  ArrayResize (ma [3].pa [1].bTypes, 3);
  ArrayResize (ma [2].pa [3].bTypes, 3);
  ArrayResize (ma [3].pa [2].bTypes, 3);
  ArrayResize (ma [3].pa [3].bTypes, 3);

  ma [1].pa [3].bTypes [0] = 2;
  ma [1].pa [3].bTypes [1] = 3;
  ma [1].pa [3].bTypes [2] = 4;

  ma [3].pa [1].bTypes [0] = 2;
  ma [3].pa [1].bTypes [1] = 3;
  ma [3].pa [1].bTypes [2] = 4;

  ma [2].pa [3].bTypes [0] = 2;
  ma [2].pa [3].bTypes [1] = 3;
  ma [2].pa [3].bTypes [2] = 4;

  ma [3].pa [2].bTypes [0] = 2;
  ma [3].pa [2].bTypes [1] = 3;
  ma [3].pa [2].bTypes [2] = 4;

  ma [3].pa [3].bTypes [0] = 2;
  ma [3].pa [3].bTypes [1] = 3;
  ma [3].pa [3].bTypes [2] = 4;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

    Moving方法在优化过程中完成进化步骤，将遗传和变异的概念应用于智能体种群。让我们更详细地审视它：

    检查是否需要修订 —— 该方法的第一部分检查智能体是否需要更新或“移动”，如果“revision”为“false”，则对智能体的坐标（a[i].c[j]）进行初始初始化（或更新）：

    • 每个智能体使用u.RNDfromCI方法，在[rangeMin[j], rangeMax[j]]范围内生成随机值。
    • 然后，使用u.SeInDiSp将该值调整到所需范围，该方法应用rangeStep中指定的步长。

    切换到修订状态 —— 在首次迭代后，“revision”参数被设置为“true”，以切换到下一阶段，然后方法完成执行（返回）。

    变量初始化 —— 在方法开始时，初始化负责随机值和双亲血型的变量（papIND、mamIND、pBloodType、mBloodType、cBloodType和bloodIND）。

    基本种群循环（popSize） —— 该方法针对种群中的每个智能体运行循环：

    • 使用u.RNDprobab()方法生成两个随机索引，用于选择双亲（papIND和mamIND），该方法生成随机概率。
    • GetBloodType函数检索双亲的血型。

    坐标循环（coords） —— 在针对每个智能体坐标的主循环内部：

    • 从所选双亲的bTypes数组中随机选择一个血型索引（基于母亲和父亲的血型）。
    • 如果所选血型为1，则智能体从cB[c]获取值。否则，要进行混合：
      • 智能体的坐标值随机选择自父亲或母亲。
      • 使用GetBloodMutation函数，根据血型对所选值进行变异。
      • 使用u.SeInDiSp方法调整该值，以确保其仍然处于可接受的范围内。

    Moving方法是算法的关键部分，它模拟了智能体种群的进化过程，既包括随机初始化，也包括基于血型遗传原理的智能体参数变异和组合机制。该方法结合了随机性和遗传性，以创建具有不同值的新子代。这就为智能体在解空间中的进一步优化和搜索做好了准备。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_BIO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int j = 0; j < coords; j++)
      {
        a [i].c [j] = u.RNDfromCI (rangeMin [j], rangeMax [j]);
        a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
      }
    }
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd        = 0.0;
  int    papIND     = 0;
  int    mamIND     = 0;
  int    pBloodType = 0;
  int    mBloodType = 0;
  int    cBloodType = 0;
  int    bloodIND   = 0;

  for (int i = 0; i < popSize; i++)
  {
    rnd = u.RNDprobab ();
    rnd *= rnd;
    papIND = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1);

    rnd = u.RNDprobab ();
    rnd *= rnd;
    mamIND = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1);

    pBloodType = GetBloodType (papIND);
    mBloodType = GetBloodType (mamIND);

    for (int c = 0; c < coords; c++)
    {
      bloodIND   = MathRand () % ArraySize (ma [mBloodType - 1].pa [pBloodType - 1].bTypes);
      cBloodType = ma [mBloodType - 1].pa [pBloodType - 1].bTypes [bloodIND];

      if (cBloodType == 1) a [i].c [c] = cB [c];
      else
      {
        if (u.RNDbool () < 0.5) a [i].c [c] = p [papIND].c [c];
        else                    a [i].c [c] = p [mamIND].c [c];

        GetBloodMutation (a [i].c [c], c, cBloodType);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    GetBloodType方法根据传入的“ind”索引（即种群中的当前位置）确定血型。因此，该方法通过简单的取余算术运算，将索引与血型进行匹配。这样能够在可用的索引（0-3）范围内实现血型的循环分配。

    //——————————————————————————————————————————————————————————————————————————————
int C_AO_BIO::GetBloodType (int ind)
{
  if (ind % 4 == 0) return 1;
  if (ind % 4 == 1) return 2;
  if (ind % 4 == 2) return 3;
  if (ind % 4 == 3) return 4;

  return 1;
}
//——————————————————————————————————————————————————————————————————————————————

    GetBloodMutation方法旨在根据基因的血型和索引，对遗传参数（基因）的值进行修改（变异）。

    参数：

    • gene —— 关于将被修改的基因值
    • indGene —— 用于获取变异范围的基因索引
    • bloodType —— 血型，决定变异逻辑

    血型2 —— 对基因值应用PowerDistribution，该方法根据给定范围对基因进行改变，以概率方式在其周围分布值。

    血型3 —— 基因值增加的量，为当前cB[indGene]种群中该基因的最优值与当前基因值之差的分数。偏移分数由一个[0.0; 1.0]范围内的随机数确定。

    其他血型（默认） —— 基因的修改方式为，使其新值相对于给定范围（反向）呈对称分布，处于rangeMin[indGene]和rangeMax[indGene]之间。 

    //——————————————————————————————————————————————————————————————————————————————
void  C_AO_BIO::GetBloodMutation (double &gene, int indGene, int bloodType)
{
  switch (bloodType)
  {
    case 2:
      gene = u.PowerDistribution (gene, rangeMin [indGene], rangeMax [indGene], 20);
      return;
    case 3:
      gene += (cB [indGene] - gene) * u.RNDprobab ();
      return;
    default:
    {
      gene = rangeMax [indGene] - (gene - rangeMin [indGene]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    Revision方法负责在BIO算法中对种群进行更新和排序。在第一个for循环（从0到popSize）中，该方法遍历a[i]种群的所有成员。如果当前a[i].f种群成员的适应度函数值“f”超过当前fB的最优值，则用新值更新fB，并将当前种群成员的坐标“c”复制到cB数组中。在第二个for循环中，将a[i]种群的当前成员从popSize索引开始，复制到“p”数组的末尾。接下来创建pT数组。其大小为当前种群的两倍，即“popSize * 2”。调用u.Sorting排序方法对合并后的“p”数组进行排序，同时将结果存储在pT中。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_BIO::Revision ()
{
  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    // Update the best global solution
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    p [popSize + i] = a [i];
  }

  S_AO_Agent pT []; ArrayResize (pT, popSize * 2);
  u.Sorting (p, pT, popSize * 2);
}
//——————————————————————————————————————————————————————————————————————————————


    测试结果

    该算法在三个不同的测试函数（Hilly、Forest和Megacity）上进行了测试，这些测试函数的搜索空间维度各不相同（分别为5×2、25×2和500×2维），且均进行了10,000次目标函数评估。总体结果为53.80%，这表明在基于种群的优化算法中，BIO算法处于平均水平，对于一种新方法而言，这一表现已经相当不错。 

    BIO|Blood Inheritance Optimization|50.0|
    =============================
    5 Hilly's; Func runs: 10000; result: 0.8156790458423091
    25 Hilly's; Func runs: 10000; result: 0.6533623929914842
    500 Hilly's; Func runs: 10000; result: 0.3087659267627686
    =============================
    5 Forest's; Func runs: 10000; result: 0.8993708810337727
    25 Forest's; Func runs: 10000; result: 0.6531872390668734
    500 Forest's; Func runs: 10000; result: 0.21759965952460583
    =============================
    5 Megacity's; Func runs: 10000; result: 0.6784615384615384
    25 Megacity's; Func runs: 10000; result: 0.4763076923076923
    500 Megacity's; Func runs: 10000; result: 0.13901538461538585
    =============================
    总分：4.84175 (53.80%)

    从算法运行过程的可视化结果中，能够观察到的唯一问题是，该算法在处理低维度问题时存在陷入局部最优解的倾向，而这一情况在基于种群的算法中颇为常见。

    Hilly值

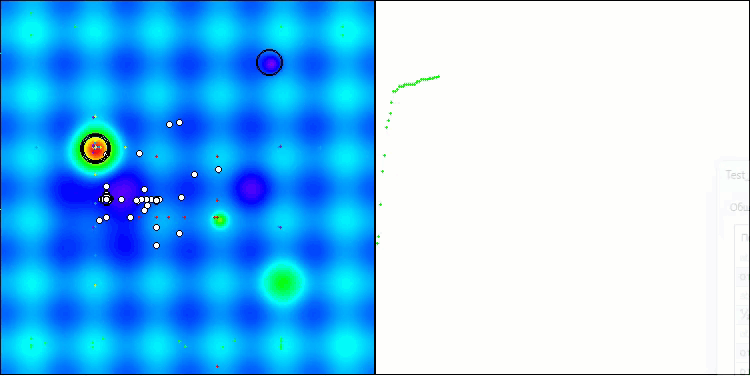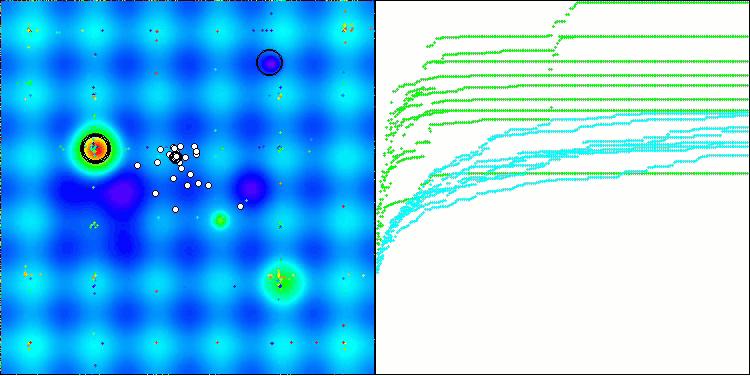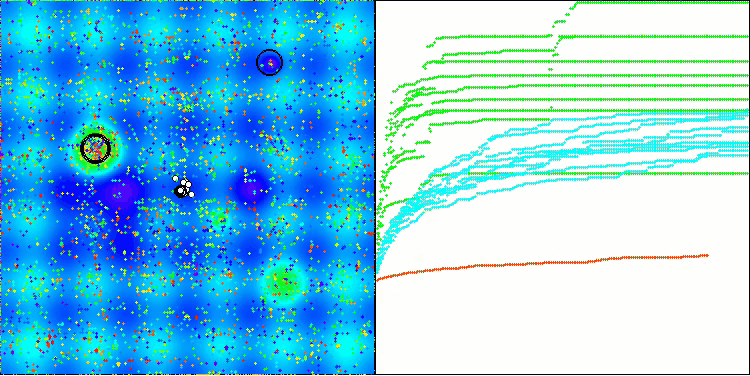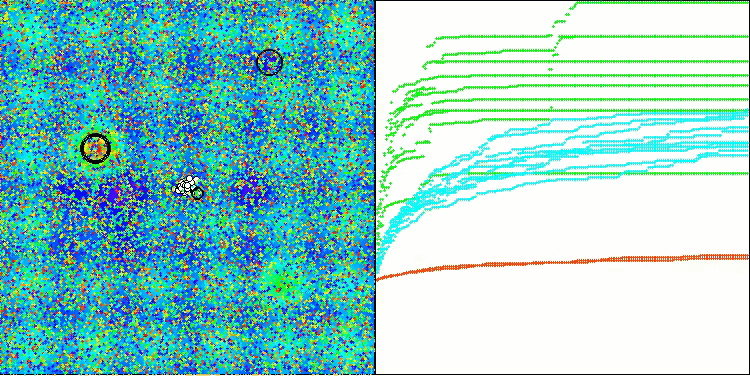
    BIO在Hilly测试函数上

    Forest值

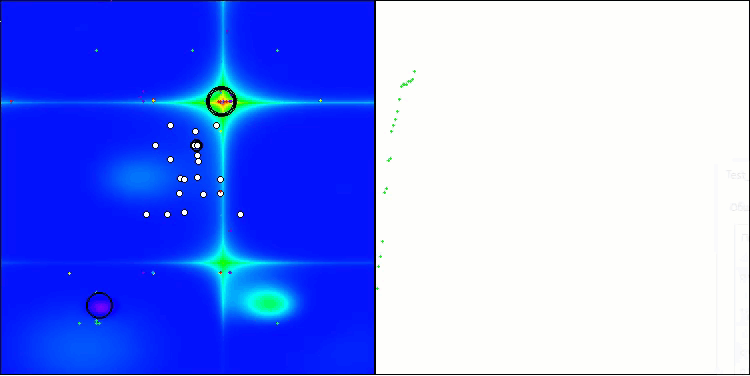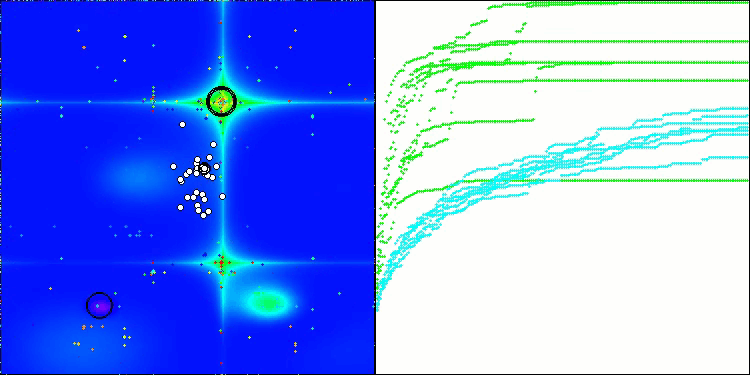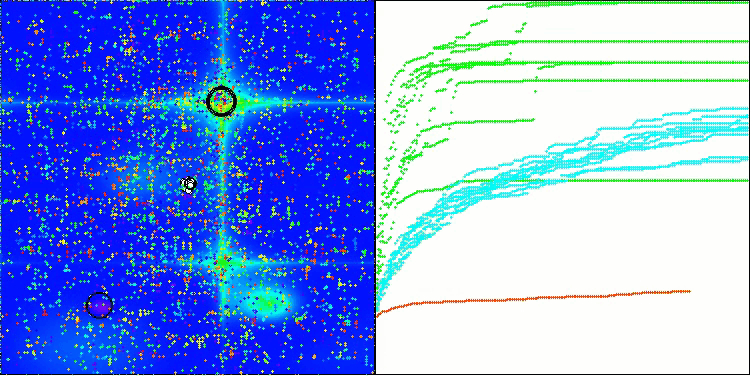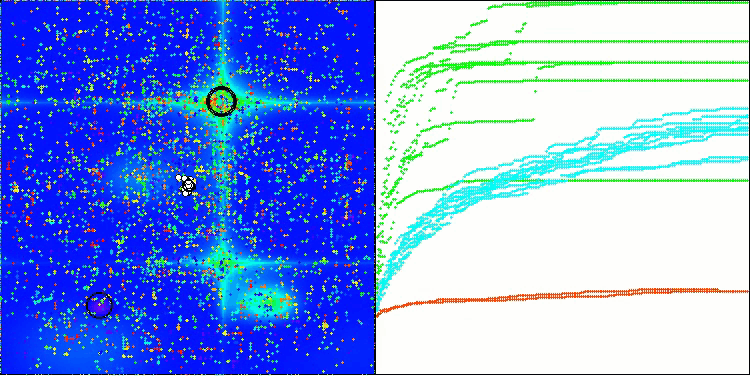
    BIO在Forest测试函数上

    Megacity值

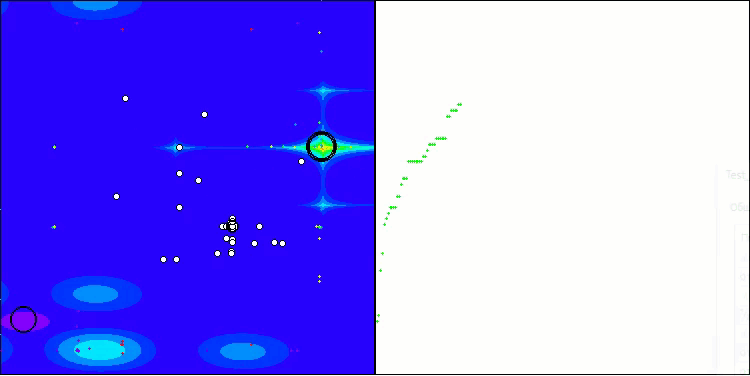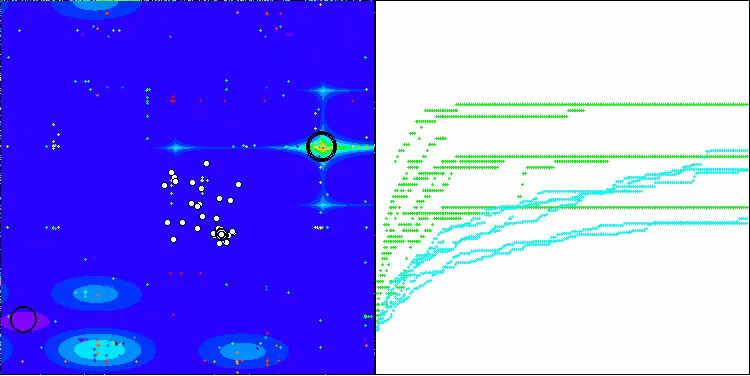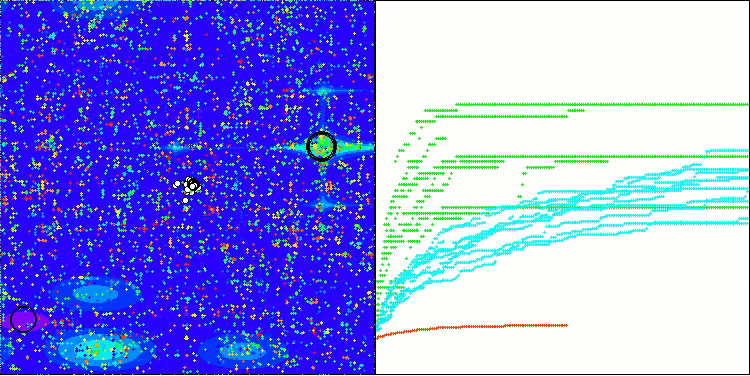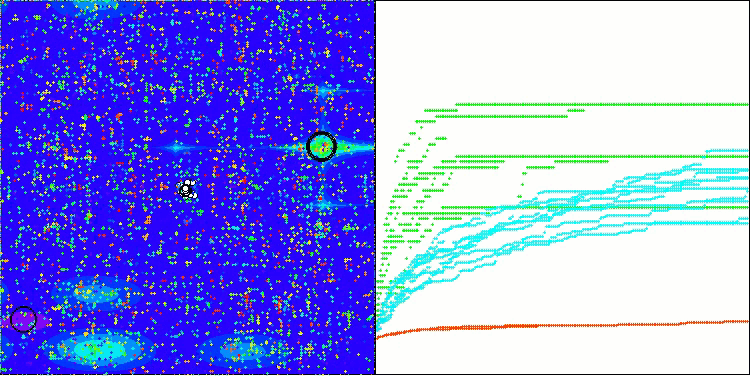
    BIO在Megacity测试函数上

    根据测试结果，BIO算法在种群优化算法排名表中位列第20。

    # AO 描述 Hilly值 Hilly最终值 Forest值 Forest最终值 Megacity (离散) Megacity最终值 最终结果 最大百分比
    10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
    1 ANS 跨邻域搜索 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
    2 CLA 密码锁算法（joo） 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
    3 AMOm 动物迁徙优化M 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
    4 (P+O)ES (P+O) 进化策略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
    5 CTA 彗星尾算法（joo） 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
    6 TETA 时间演化旅行算法（joo） 0.91362 0.82349 0.31990 2.05701 0.97096 0.89532 0.29324 2.15952 0.73462 0.68569 0.16021 1.58052 5.797 64.41
    7 SDSm 随机扩散搜索 M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
    8 AAm 射箭算法M 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
    9 ESG 社会群体的进化（joo） 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
    10 SIA 模拟各向同性退火（joo） 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
    11 ACS 人工协同搜索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
    12 DA 辩证算法 0.86183 0.70033 0.33724 1.89940 0.98163 0.72772 0.28718 1.99653 0.70308 0.45292 0.16367 1.31967 5.216 57.95
    13 BHAm 黑洞算法M 0.75236 0.76675 0.34583 1.86493 0.93593 0.80152 0.27177 2.00923 0.65077 0.51646 0.15472 1.32195 5.196 57.73
    14 ASO 无序社会优化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
    15 RFO 皇家同花顺优化（joo） 0.83361 0.73742 0.34629 1.91733 0.89424 0.73824 0.24098 1.87346 0.63154 0.50292 0.16421 1.29867 5.089 56.55
    16 AOSm 原子轨道搜索M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
    17 TSEA 龟壳演化算法（joo） 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
    18 DE 差分进化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
    19 CRO 化学反应优化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
    20 BIO 血液遗传优化算法（joo） 0.81568 0.65336 0.30877 1.77781 0.89937 0.65319 0.21760 1.77016 0.67846 0.47631 0.13902 1.29378 4.842 53.80
    21 BSA 鸟群算法 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
    22 HS 和声搜索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
    23 SSG 树苗播种和生长 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
    24 BCOm 细菌趋化性优化算法M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
    25 ABO 非洲水牛优化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
    26 (PO)ES (PO) 进化策略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
    27 TSm 禁忌搜索M 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
    28 BSO 头脑风暴优化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
    29 WOAm 鲸鱼优化算法M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
    30 AEFA 人工电场算法 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
    31 AEO 基于人工生态系统的优化算法 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
    32 ACOm 蚁群优化 M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
    33 BFO-GA 细菌觅食优化 - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
    34 SOA 简单优化算法 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
    35 ABHA 人工蜂巢算法 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
    36 ACMO 大气云模型优化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
    37 ADAMm 群体自适应矩估计M 0.88635 0.44766 0.26613 1.60014 0.84497 0.38493 0.16889 1.39880 0.66154 0.27046 0.10594 1.03794 4.037 44.85
    38 ATAm 人工部落算法M 0.71771 0.55304 0.25235 1.52310 0.82491 0.55904 0.20473 1.58867 0.44000 0.18615 0.09411 0.72026 3.832 42.58
    39 ASHA 人工淋浴算法 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
    40 ASBO 适应性社会行为优化 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
    41 MEC 思维进化计算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
    42 CSA 圆搜索算法 0.66560 0.45317 0.29126 1.41003 0.68797 0.41397 0.20525 1.30719 0.37538 0.23631 0.10646 0.71815 3.435 38.17
    43 IWO 入侵杂草优化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
    44 Micro-AIS 微型人工免疫系统 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
    45 COAm 布谷鸟优化算法 M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21

    		RW 随机游走 0.48754 0.32159 0.25781 1.06694 0.37554 0.21944 0.15877 0.75375 0.27969 0.14917 0.09847 0.52734 2.348 26.09


    总结

    在开发与测试血液遗传优化（BIO）算法的过程中，我得出了几项重要结论。首先，引入血型遗传关联机制被证明是一种成功的方法，它能够为种群优化算法中的不同变异策略提供有效的组织架构。在不同函数和维度上的测试表明，该算法具有高度的通用性，既能有效处理简单的低维问题，也能应对更复杂的多维问题。

    需要特别指出的是，此处展示的BIO算法仅为基础版本，旨在演示其核心概念。该算法的关键不在于具体的变异算子（这些算子可替换为其他任意算子），而在于通过类比血型来构建参数调整策略的继承结构。这就为算法的修改与扩展提供了广阔的空间。每个“血型”均可关联其他变异算子，这些算子既可以借鉴自其他算法，也可以针对特定任务专门设计。此外，我们还可以尝试调整“血型”数量，引入新策略或融合现有策略。

    当前测试结果显示，BIO算法在种群算法的排名中名次不错（得分约54%），这表明即使在其基础版本中，该算法也具备高效性。针对算法易陷入局部最优的问题，可通过修改变异算子或引入新的解空间探索策略加以改善。

    我认为，该算法最具潜力的发展方向是构建自适应版本，使每种“血型”的变异算子能在优化过程中动态调整，以适应目标函数的特性。此外，探索非经典ABO血型系统以外的其他遗传模式也颇具意义，这样有望催生一系列基于不同生物遗传系统的算法家族。

    因此，BIO算法不仅是一种优化算法，更是一个灵活的概念框架，它以血型隐喻为策略继承的共同理念，将多种算法统一起来，并为进一步研究及旨在提升算法在各应用领域效率的修改提供了广阔空间。

    标签

    图例2. 算法在相应测试中的颜色渐变表示

    图表

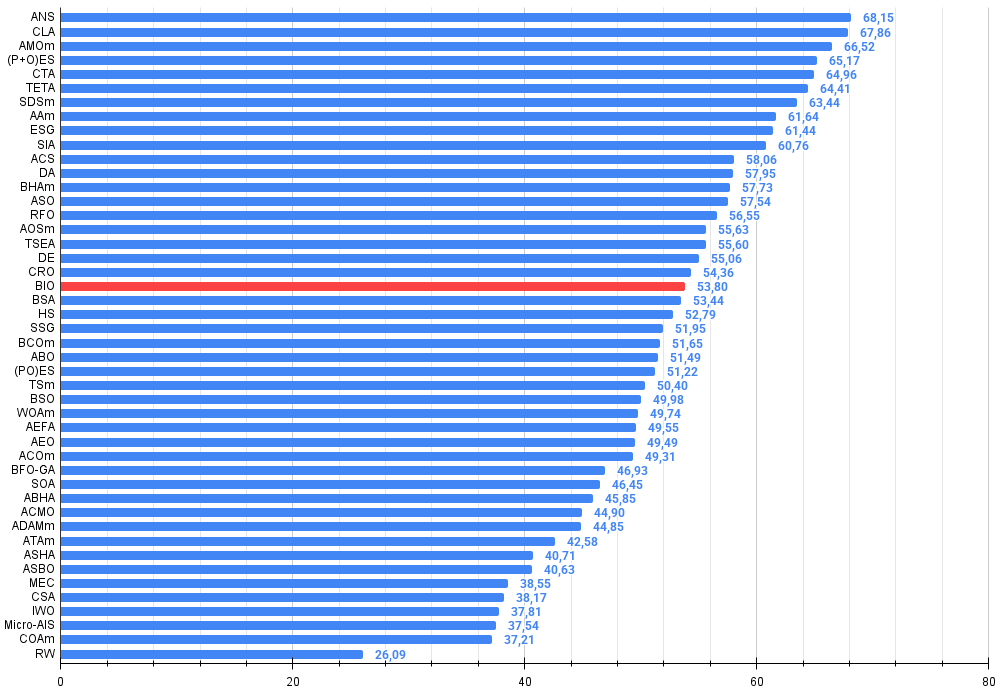
    图例3. 算法测试结果的直方图（评分范围为0到100，越高越好，其中100为理论上的最高可能得分，档案中附有计算排名表的脚本）

    BIO的优缺点：

    优点：

    1. 无外部参数。
    2. 关于基于血型遗传的理念很有意思。
    3. 在高维和中维函数上具有良好的收敛性。

    缺点：

    1. 在低维问题上易陷入局部最优。


    文章附有一个包含当前版本算法代码的归档文件。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力，已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。



    文中所用的程序

    # 名称 类型 描述
    1 #C_AO.mqh
    		 库
    		 种群优化父类
    算法
    2 #C_AO_enum.mqh
    		 库
    		 种群优化算法的枚举说明
    3 TestFunctions.mqh
    		 库
    		 测试函数库
    4
    		 TestStandFunctions.mqh
    		 库
    		 测试台函数库
    5
    		 Utilities.mqh
    		 库
    		 辅助函数库
    6
    		 CalculationTestResults.mqh
    		 库
    		 用于计算比较表结果的脚本
    7
    		 Testing AOs.mq5
    		 脚本 面向所有种群优化算法的统一测试平台
    8
    		 Simple use of population optimization algorithms.mq5
    		 脚本
    		 种群优化算法非可视化简易使用案例
    9
    		 Test_AO_BIO.mq5
    		 脚本 BIO测试台

    本文由MetaQuotes Ltd译自俄文
    原文地址： https://www.mql5.com/ru/articles/17246

    附加的文件 |
    下载ZIP
    BIO.zip (166.57 KB)

    注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

    本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

    该作者的其他文章

    前往讨论
    辩证搜索（DA） 辩证搜索（DA）
    本文介绍了辩证算法（DA），这是一种受辩证法哲学概念启发的新的全局优化方法。该算法利用了人口中独特的划分，将其分为投机思想者和实践思想者。测试表明，在低维问题上，性能令人印象深刻，高达 98%，整体效率为 57.95%。本文解释了这些度量，并详细描述了算法和不同类型函数的实验结果。
    用于预测金融时间序列的生物神经元 用于预测金融时间序列的生物神经元
    我们将为时间序列预测建立一个生物学上正确的神经元系统。在神经网络架构中引入类似等离子体的环境创造了一种“集体智能”，其中每个神经元不仅通过直接连接，还通过长距离电磁相互作用影响系统的运行。让我们看看神经大脑建模系统在市场上的表现。
    交易中的神经网络：配备注意力机制（MASAAT）的智代融汇 交易中的神经网络：配备注意力机制（MASAAT）的智代融汇
    我们概述多智代自适应投资组合优化框架（MASAAT），其结合了注意力机制和时间序列分析。MASAAT 生成一组智代，分析价格序列和方向变化，能够在不同细节层次识别资产价格的明显波动。
    使用 Python 创建波动率预测指标 使用 Python 创建波动率预测指标
    在本文中，我们将使用二元分类来预测未来的极端波动。此外，我们将利用机器学习开发极端波动预测指标。