Otimização por herança sanguínea — Blood Inheritance Optimization (BIO)

Conteúdo

1. Introdução
2. Implementação do algoritmo
3. Resultados dos testes

Introdução

Certa vez, enquanto observava uma enfermeira coletando sangue de pacientes em um laboratório, fui tomado por um pensamento inesperado. Os tipos sanguíneos, esse sistema ancestral de herança transmitido de geração em geração por leis genéticas rigorosas, se revelaram para mim sob uma nova perspectiva. E se essas propriedades naturais de herança pudessem ser aplicadas no campo dos algoritmos de otimização?

Cada um de nós carrega em suas veias uma combinação única recebida dos pais. Da mesma forma que os tipos sanguíneos determinam a compatibilidade em transfusões, eles poderiam definir modos de transmissão e mutação de parâmetros dentro do processo de otimização. Gostei dessa ideia e decidi voltar a ela quando tivesse tempo para pesquisas. A oportunidade surgiu, e após uma série de experimentos nasceu o algoritmo Blood Inheritance Optimization (BIO), que é um método que utiliza as leis naturais da herança sanguínea como metáfora para guiar a evolução das soluções. Nele, os quatro tipos sanguíneos se transformaram em quatro diferentes estratégias de mutação de parâmetros, e as leis de herança definem como os descendentes recebem e modificam as características de seus pais.

Assim como na natureza, o tipo sanguíneo de uma criança não é apenas uma média entre os tipos dos pais, mas segue regras genéticas específicas. No BIO, os parâmetros das novas soluções são formados através de um sistema de herança e mutações. Cada tipo sanguíneo traz sua própria abordagem única para explorar o espaço de soluções: desde a preservação conservadora dos melhores valores encontrados, até mutações radicais que revelam novas regiões promissoras e direções para aprofundar a exploração do espaço.

Neste artigo quero compartilhar os princípios de funcionamento do algoritmo BIO, que une inspiração biológica com rigor algorítmico, além de apresentar os resultados de testes em funções já conhecidas. Então, vamos começar.

Implementação do algoritmo

Para começar, vejamos a tabela de herança do tipo sanguíneo de um descendente a partir de seus pais. Como pode ser observado, a herança do tipo sanguíneo não é homogênea. Existe no mundo uma estatística interessante sobre a distribuição dos tipos sanguíneos entre a população. O mais comum é o primeiro tipo (O), cerca de 40% da população mundial o possui. Em seguida vem o segundo tipo (A), presente em aproximadamente 30% das pessoas. O terceiro tipo (B) aparece em 20% da população, e o quarto (AB) é o mais raro, encontrado em apenas cerca de 10% das pessoas.

Ao estudar os mecanismos de herança, descobri que o primeiro tipo sanguíneo é recessivo em relação a todos os outros. Isso significa que pessoas com o primeiro tipo só podem transmitir esse mesmo tipo aos seus filhos. Já o segundo e o terceiro tipos demonstram codominância entre si, o que leva ao surgimento do quarto tipo quando combinados. Aliás, do ponto de vista evolutivo, o quarto tipo sanguíneo é o mais recente.

Chamaram especialmente minha atenção algumas propriedades únicas dos diferentes tipos sanguíneos. Por exemplo, o primeiro tipo é considerado "doador universal", pois pode ser transfundido em pessoas de qualquer outro tipo sanguíneo. Já o quarto tipo, ao contrário, torna seus portadores "receptores universais", eles podem receber sangue de qualquer tipo. 

Todas essas particularidades do sistema de tipos sanguíneos me inspiraram a criar mecanismos correspondentes em meu algoritmo. Como o primeiro tipo sanguíneo é a base e o mais comum, no algoritmo ele corresponde à estratégia de preservação da melhor solução encontrada. A tabela de herança sanguínea, que mostra todas as possíveis combinações dos tipos sanguíneos dos pais e os tipos sanguíneos potenciais de seus filhos, serviu de fundamento para o mecanismo que define o "tipo sanguíneo" de uma nova solução com base nos "tipos sanguíneos" das soluções parentais, o que influencia diretamente a forma de mutação dos parâmetros no algoritmo BIO.

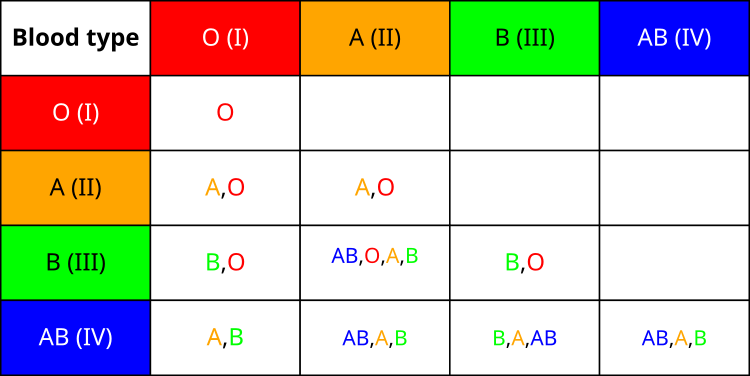
Figura 1. Tabela de herança do tipo sanguíneo

A base do algoritmo BIO é uma ideia relativamente simples: cada solução na população (indivíduos parentais) tem seu próprio "tipo sanguíneo" (de 1 a 4), determinado por sua posição na população. Quando criamos uma nova geração de soluções, escolhemos dois "pais" da população atual. Porém, a probabilidade de escolha não é linear, e sim quadrática, o que significa que as melhores soluções têm consideravelmente mais chances de se tornarem pais.

Agora começa a parte mais interessante. Com base nos tipos sanguíneos dos pais, usando uma matriz especial de herança (definida no código no método Init), determinamos os possíveis tipos sanguíneos do "filho", a nova solução. Em seguida, para cada parâmetro dessa nova solução, se for atribuído o primeiro tipo sanguíneo, pegamos o valor do melhor resultado encontrado. Fiz isso por analogia ao primeiro tipo sanguíneo como doador universal. Se sair o segundo tipo, pegamos o valor de um dos pais e aplicamos a ele uma distribuição exponencial. Isso cria uma tendência a explorar as extremidades do intervalo dos parâmetros. Para o terceiro tipo, também pegamos o valor de um dos pais, mas o deslocamos em direção ao melhor resultado por um valor aleatório. Já para o quarto tipo, usamos o valor do pai e o refletimos em relação às bordas do intervalo, uma espécie de inversão, que permite explorar novas regiões de busca.

Após criar a nova geração, verificamos se surgiram soluções melhores do que a solução global atual e preservamos os melhores indivíduos para a próxima iteração. Assim, usando a analogia com a herança dos tipos sanguíneos, meu algoritmo explora o espaço de soluções combinando diferentes estratégias de mutação de parâmetros. Abaixo apresento o pseudocódigo do algoritmo.

Inicialização:

1. Criar uma população de agentes com tamanho popSize (por padrão 50)
2. Criar a matriz de herança dos tipos sanguíneos, que define os tipos sanguíneos possíveis dos filhos com base nos tipos dos pais (1,2,3,4)
3. Inicializar intervalos para os parâmetros (mín., máx., valores de passo)

Ciclo principal:

1. Se for a primeira iteração (revisão = falso):
   • Inicializar aleatoriamente as posições de todos os agentes dentro dos intervalos dos parâmetros
   • Definir o sinalizador revisão como verdadeiro
2. Para cada agente da população:
   • Selecionar agentes pais (pai e mãe) usando distribuição de probabilidades quadrática
   • Definir os tipos sanguíneos de ambos os pais com a função: bloodType = 1 + (posição_na_população % 4)
   • Para cada parâmetro da solução filha:
     • Obter o possível tipo sanguíneo do filho a partir da matriz de herança com base nos tipos sanguíneos dos pais
     • Se o filho tiver tipo sanguíneo 1:
       • - Usar o melhor resultado conhecido para esse parâmetro.
     • Caso contrário:
       • - Selecionar aleatoriamente o valor do parâmetro do pai ou da mãe
       • - Aplicar mutação baseada no tipo sanguíneo do filho:
         • Tipo 2: Aplicar distribuição exponencial com expoente 20
         • Tipo 3: Deslocar o valor do parâmetro em direção ao melhor resultado com um fator aleatório
         • Tipo 4: Refletir o valor do parâmetro em relação a todo o intervalo permitido
     • Garantir que o parâmetro permaneça dentro do intervalo válido e respeite o passo definido

Fase de revisão:

1. Atualizar a melhor solução global, caso algum agente apresente melhor adaptabilidade
2. Copiar a população atual para a segunda metade do array expandido da população
3. Ordenar a população expandida pela adaptabilidade
4. Salvar os melhores agentes para a próxima geração

Vamos então escrever o código do algoritmo. A classe "C_AO_BIO", derivada de "C_AO", implementa o algoritmo BIO e prevê o uso de uma estrutura de dados para representar os indivíduos (agentes) da população, bem como seu controle.

C_AO_BIO () — construtorinicializa por padrão os parâmetros externos do BIO: o tamanho da população "popSize" é definido como 50, e o tamanho do array de parâmetros "params" é configurado com um único elemento representando "popSize".
SetParams () — método que permite configurar os parâmetros da classe, neste caso definindo o tamanho da população "popSize" a partir do array de parâmetros.
Init () — método que inicializa o algoritmo, recebendo valores mínimos e máximos dos parâmetros, passo de variação e número de épocas.
Moving () e Revision () — métodos responsáveis pelo movimento (evolução) dos agentes na população e pela revisão (avaliação de desempenho e seleção dos melhores).
S_Papa e S_Mama:

• S_Papa — representa uma estrutura que contém um array de tipos sanguíneos (bTypes).
• S_Mama — contém um array de quatro objetos S_Papa, o que implica a existência de "pais" para posterior combinação genética.

Esse tipo de representação em estruturas permite obter diretamente o provável tipo sanguíneo de um descendente a partir dos pais, especificando os tipos sanguíneos parentais, como em "ma [1].pa [2].bTypes", onde "1" e "2" são os tipos sanguíneos da mãe e do pai, respectivamente.

O método GetBloodType () retorna o tipo sanguíneo de um determinado agente, enquanto GetBloodMutation () implementa o mecanismo de mutação do gene conforme o tipo sanguíneo.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BIO : public C_AO
{
  public: //--------------------------------------------------------------------
  C_AO_BIO ()
  {
    ao_name = "BIO";
    ao_desc = "Blood Inheritance Optimization";
    ao_link = "https://www.mql5.com/ru/articles/17246";

    popSize = 50; // размер популяции

    ArrayResize (params, 1);
    params [0].name = "popSize"; params [0].val = popSize;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
  }

  bool Init (const double &rangeMinP  [],  // минимальные значения
             const double &rangeMaxP  [],  // максимальные значения
             const double &rangeStepP [],  // шаг изменения
             const int     epochsP = 0);   // количество эпох

  void Moving   ();
  void Revision ();

  private: //-------------------------------------------------------------------
  struct S_Papa
  {
      int bTypes [];
  };
  struct S_Mama
  {
      S_Papa pa [4];
  };
  S_Mama ma [4];

  S_AO_Agent p [];

  int  GetBloodType     (int ind);
  void GetBloodMutation (double &gene, int indGene, int bloodType);
};
//——————————————————————————————————————————————————————————————————————————————

O método "Init" inicializa a instância da classe "C_AO_BIO" e a prepara para funcionamento, configurando a população de agentes e suas características. Vamos analisar a implementação deste método.

A primeira linha verifica o resultado da chamada do método "StandardInit", que checa e inicializa os parâmetros básicos necessários para o funcionamento do algoritmo.

Inicialização do array de agentes:

• Altera o tamanho do array de agentes "p" para o dobro do tamanho definido da população "popSize".
• No laço "for", para cada agente é chamado o método "Init", que inicializa o agente com os parâmetros de coordenadas.

Inicialização dos tipos sanguíneos:

• Em seguida, o método define o tamanho dos arrays de tipos sanguíneos (bTypes) para as estruturas "S_Mama" e "S_Papa".
• Para diferentes combinações (por exemplo, ma [0].pa [0], ma [1].pa [2] etc.) são atribuídos diferentes tipos sanguíneos de acordo com a matriz especial de herança, e o tamanho dos arrays é definido através de "ArrayResize".

Assim, o método "Init" na classe "C_AO_BIO" desempenha a tarefa crucial de preparar o objeto para a execução do algoritmo de otimização: cria a população de agentes, configura seus parâmetros iniciais e define as regras de ligação para os tipos sanguíneos (herança). Isso permite obter instantaneamente o possível tipo sanguíneo de um descendente, além de usar os parâmetros de sua "sangue" para a evolução posterior dentro do algoritmo.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BIO::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (p, popSize * 2);
  for (int i = 0; i < popSize * 2; i++) p [i].Init (coords);

  //1-1
  ArrayResize (ma [0].pa [0].bTypes, 1);

  ma [0].pa [0].bTypes [0] = 1;

  //2-2
  ArrayResize (ma [1].pa [1].bTypes, 2);

  ma [1].pa [1].bTypes [0] = 1;
  ma [1].pa [1].bTypes [1] = 2;

  //3-3
  ArrayResize (ma [2].pa [2].bTypes, 2);

  ma [2].pa [2].bTypes [0] = 1;
  ma [2].pa [2].bTypes [1] = 3;

  //1-2; 2-1
  ArrayResize (ma [0].pa [1].bTypes, 2);
  ArrayResize (ma [1].pa [0].bTypes, 2);

  ma [0].pa [1].bTypes [0] = 1;
  ma [0].pa [1].bTypes [1] = 2;

  ma [1].pa [0].bTypes [0] = 1;
  ma [1].pa [0].bTypes [1] = 2;

  //1-3; 3-1
  ArrayResize (ma [0].pa [2].bTypes, 2);
  ArrayResize (ma [2].pa [0].bTypes, 2);

  ma [0].pa [2].bTypes [0] = 1;
  ma [0].pa [2].bTypes [1] = 3;

  ma [2].pa [0].bTypes [0] = 1;
  ma [2].pa [0].bTypes [1] = 3;

  //1-4; 4-1
  ArrayResize (ma [0].pa [3].bTypes, 2);
  ArrayResize (ma [3].pa [0].bTypes, 2);

  ma [0].pa [3].bTypes [0] = 2;
  ma [0].pa [3].bTypes [1] = 3;

  ma [3].pa [0].bTypes [0] = 2;
  ma [3].pa [0].bTypes [1] = 3;

  //2-3; 3-2
  ArrayResize (ma [1].pa [2].bTypes, 4);
  ArrayResize (ma [2].pa [1].bTypes, 4);

  ma [1].pa [2].bTypes [0] = 1;
  ma [1].pa [2].bTypes [1] = 2;
  ma [1].pa [2].bTypes [2] = 3;
  ma [1].pa [2].bTypes [3] = 4;

  ma [2].pa [1].bTypes [0] = 1;
  ma [2].pa [1].bTypes [1] = 2;
  ma [2].pa [1].bTypes [2] = 3;
  ma [2].pa [1].bTypes [3] = 4;

  //2-4; 4-2; 3-4; 4-3; 4-4
  ArrayResize (ma [1].pa [3].bTypes, 3);
  ArrayResize (ma [3].pa [1].bTypes, 3);
  ArrayResize (ma [2].pa [3].bTypes, 3);
  ArrayResize (ma [3].pa [2].bTypes, 3);
  ArrayResize (ma [3].pa [3].bTypes, 3);

  ma [1].pa [3].bTypes [0] = 2;
  ma [1].pa [3].bTypes [1] = 3;
  ma [1].pa [3].bTypes [2] = 4;

  ma [3].pa [1].bTypes [0] = 2;
  ma [3].pa [1].bTypes [1] = 3;
  ma [3].pa [1].bTypes [2] = 4;

  ma [2].pa [3].bTypes [0] = 2;
  ma [2].pa [3].bTypes [1] = 3;
  ma [2].pa [3].bTypes [2] = 4;

  ma [3].pa [2].bTypes [0] = 2;
  ma [3].pa [2].bTypes [1] = 3;
  ma [3].pa [2].bTypes [2] = 4;

  ma [3].pa [3].bTypes [0] = 2;
  ma [3].pa [3].bTypes [1] = 3;
  ma [3].pa [3].bTypes [2] = 4;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

O método "Moving" executa os passos evolutivos no processo de otimização, aplicando os conceitos de herança e mutação à população de agentes. Vamos analisá-lo em detalhe:

Verificação da necessidade de revisão (revision) — a primeira parte do método verifica se é preciso atualizar os agentes ou "movê-los". Se "revision" for igual a "false", ocorre a inicialização (ou atualização) das coordenadas dos agentes (a [i].c [j]):

• Cada agente recebe valores aleatórios gerados dentro do intervalo [rangeMin [j], rangeMax [j]] usando o método "u.RNDfromCI".
• Em seguida, o valor é ajustado ao intervalo adequado utilizando "u.SeInDiSp", que aplica o passo definido em "rangeStep".

Troca para o estado de revisão — após a primeira iteração, o parâmetro "revision" é definido como "true", para que o algoritmo avance para a próxima etapa, e o método encerra sua execução (return).

Inicialização de variáveis — no início do método são inicializadas as variáveis responsáveis pelos valores aleatórios e tipos sanguíneos dos pais (papIND, mamIND, pBloodType, mBloodType, cBloodType e bloodIND).

Laço principal sobre a população (popSize) — o método percorre em laço cada agente da população:

• Dois índices aleatórios para os pais (papIND e mamIND) são gerados com o método "u.RNDprobab ()", que cria probabilidades aleatórias.
• Com a função "GetBloodType" são obtidos os tipos sanguíneos de ambos os pais.

Laço sobre as coordenadas (coords) — dentro do laço principal, para cada coordenada do agente:

• Seleciona-se um índice aleatório do tipo sanguíneo a partir do array "bTypes" dos pais escolhidos (com base no tipo sanguíneo da mãe e do pai).
• Se o tipo sanguíneo selecionado for "1", o agente recebe o valor de "cB [c]". Caso contrário, ocorre a mistura:
• O valor da coordenada do agente é escolhido aleatoriamente do pai ou da mãe.
• Aplica-se a função "GetBloodMutation", que realiza a mutação do valor selecionado de acordo com o tipo sanguíneo.
• O valor é corrigido usando o método "u.SeInDiSp", garantindo que permaneça dentro dos limites permitidos.

O método "Moving" é uma parte fundamental do algoritmo, pois emula o processo de evolução da população de agentes e inclui tanto a inicialização aleatória quanto os mecanismos de mutação e combinação dos parâmetros dos agentes com base nos princípios de herança dos tipos sanguíneos. O método combina elementos de aleatoriedade e hereditariedade para criar novos descendentes com diferentes valores. Isso prepara os agentes para a otimização subsequente e para a exploração do espaço de soluções.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BIO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int j = 0; j < coords; j++)
      {
        a [i].c [j] = u.RNDfromCI (rangeMin [j], rangeMax [j]);
        a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
      }
    }
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd        = 0.0;
  int    papIND     = 0;
  int    mamIND     = 0;
  int    pBloodType = 0;
  int    mBloodType = 0;
  int    cBloodType = 0;
  int    bloodIND   = 0;

  for (int i = 0; i < popSize; i++)
  {
    rnd = u.RNDprobab ();
    rnd *= rnd;
    papIND = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1);

    rnd = u.RNDprobab ();
    rnd *= rnd;
    mamIND = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1);

    pBloodType = GetBloodType (papIND);
    mBloodType = GetBloodType (mamIND);

    for (int c = 0; c < coords; c++)
    {
      bloodIND   = MathRand () % ArraySize (ma [mBloodType - 1].pa [pBloodType - 1].bTypes);
      cBloodType = ma [mBloodType - 1].pa [pBloodType - 1].bTypes [bloodIND];

      if (cBloodType == 1) a [i].c [c] = cB [c];
      else
      {
        if (u.RNDbool () < 0.5) a [i].c [c] = p [papIND].c [c];
        else                    a [i].c [c] = p [mamIND].c [c];

        GetBloodMutation (a [i].c [c], c, cBloodType);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "GetBloodType" define o tipo sanguíneo com base no índice "ind", que é a posição atual na população. Assim, o método serve para associar índices a tipos sanguíneos utilizando uma simples operação aritmética com resto. Isso permite distribuir ciclicamente os tipos sanguíneos entre os índices disponíveis (0-3).

//——————————————————————————————————————————————————————————————————————————————
int C_AO_BIO::GetBloodType (int ind)
{
  if (ind % 4 == 0) return 1;
  if (ind % 4 == 1) return 2;
  if (ind % 4 == 2) return 3;
  if (ind % 4 == 3) return 4;

  return 1;
}
//——————————————————————————————————————————————————————————————————————————————

O método "GetBloodMutation" é responsável por modificar (mutar) o valor de um parâmetro genético (gene) de acordo com seu tipo sanguíneo e índice.

Parâmetros:

• gene — referência ao valor do gene que será modificado
• indGene — índice do gene usado para obter os intervalos de mutação
• bloodType — tipo sanguíneo que determina a lógica da mutação

Tipo sanguíneo 2 — aplica-se a distribuição exponencial "PowerDistribution" ao valor do gene, o que altera o gene com base no intervalo definido, distribuindo probabilisticamente os valores ao redor dele.

Tipo sanguíneo 3 — o gene é incrementado por uma fração da diferença entre o melhor valor atual do gene na população "cB [indGene]" e o valor atual do gene. A fração de deslocamento é definida por um número aleatório [0.0; 1.0].

Outros tipos sanguíneos (padrão) — o gene é alterado de forma que seu novo valor se torne simétrico em relação ao intervalo definido (inversão), estando compreendido entre "rangeMin [indGene]" e "rangeMax [indGene]".

//——————————————————————————————————————————————————————————————————————————————
void  C_AO_BIO::GetBloodMutation (double &gene, int indGene, int bloodType)
{
  switch (bloodType)
  {
    case 2:
      gene = u.PowerDistribution (gene, rangeMin [indGene], rangeMax [indGene], 20);
      return;
    case 3:
      gene += (cB [indGene] - gene) * u.RNDprobab ();
      return;
    default:
    {
      gene = rangeMax [indGene] - (gene - rangeMin [indGene]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "Revision" é responsável por atualizar e ordenar a população no algoritmo BIO. No primeiro laço "for" (de 0 até popSize), o método percorre todos os membros da população "a [i]". Se o valor da função de adaptabilidade "f" do membro atual "a[i].f" for maior que o melhor valor atual "fB", então "fB" é atualizado com o novo valor, e as coordenadas "c" do membro atual são copiadas para o array "cB". No segundo laço "for", os membros atuais da população "a [i]" são copiados para o final do array "p", a partir do índice "popSize". Em seguida, é criado um array temporário "pT", com tamanho duas vezes maior que a população atual "popSize * 2". O método de ordenação "u.Sorting" é chamado para ordenar o array combinado "p", armazenando os resultados em "pT".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BIO::Revision ()
{
  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    // Обновляем лучшее глобальное решение
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    p [popSize + i] = a [i];
  }

  S_AO_Agent pT []; ArrayResize (pT, popSize * 2);
  u.Sorting (p, pT, popSize * 2);
}
//——————————————————————————————————————————————————————————————————————————————

Resultados dos testes

O algoritmo foi testado em três funções de teste diferentes (Hilly, Forest e Megacity) com diferentes dimensionalidades do espaço de busca (5*2, 25*2 e 500*2 dimensões), com 10 000 avaliações da função objetivo. O resultado geral de 53,80% mostra que o BIO ocupa uma posição intermediária entre os algoritmos populacionais de otimização, o que é bastante bom para um método novo. 

BIO|Blood Inheritance Optimization|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8156790458423091
25 Hilly's; Func runs: 10000; result: 0.6533623929914842
500 Hilly's; Func runs: 10000; result: 0.3087659267627686
=============================
5 Forest's; Func runs: 10000; result: 0.8993708810337727
25 Forest's; Func runs: 10000; result: 0.6531872390668734
500 Forest's; Func runs: 10000; result: 0.21759965952460583
=============================
5 Megacity's; Func runs: 10000; result: 0.6784615384615384
25 Megacity's; Func runs: 10000; result: 0.4763076923076923
500 Megacity's; Func runs: 10000; result: 0.13901538461538585
=============================
All score: 4.84175 (53.80%)

A única dificuldade que pode ser observada na visualização do funcionamento do algoritmo é a tendência a ficar preso em ótimos locais em problemas de baixa dimensionalidade, algo relativamente comum em algoritmos populacionais.

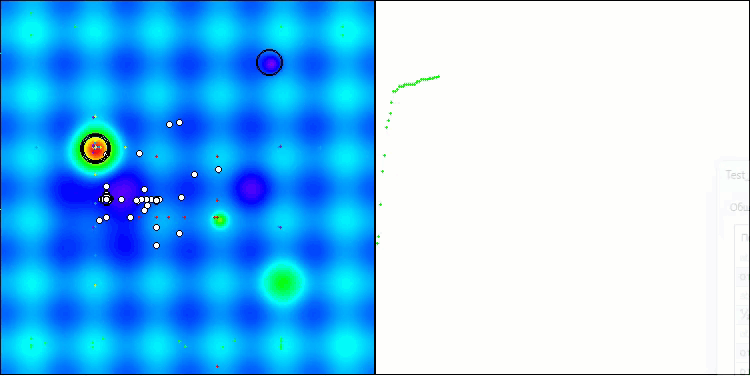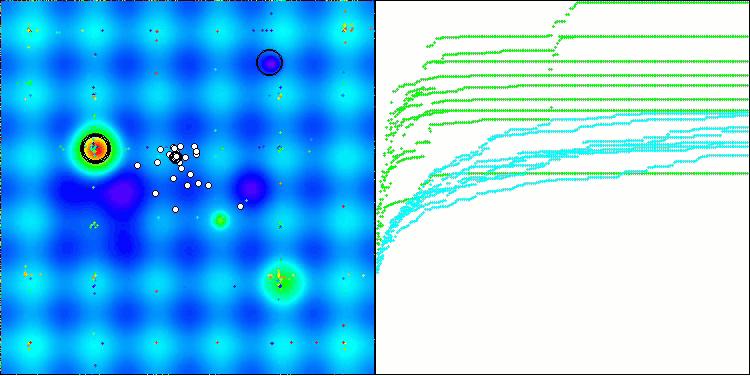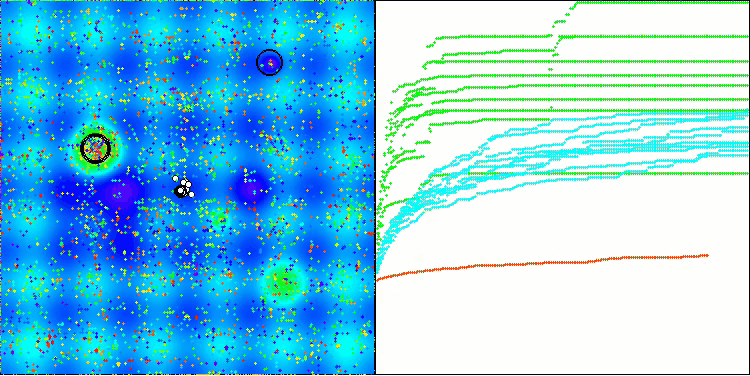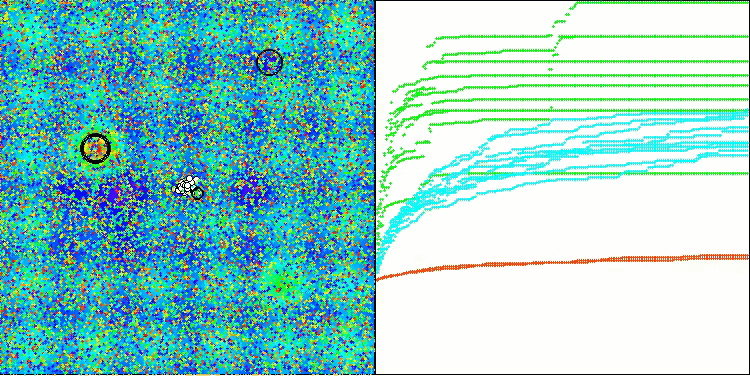
BIO na função de teste Hilly

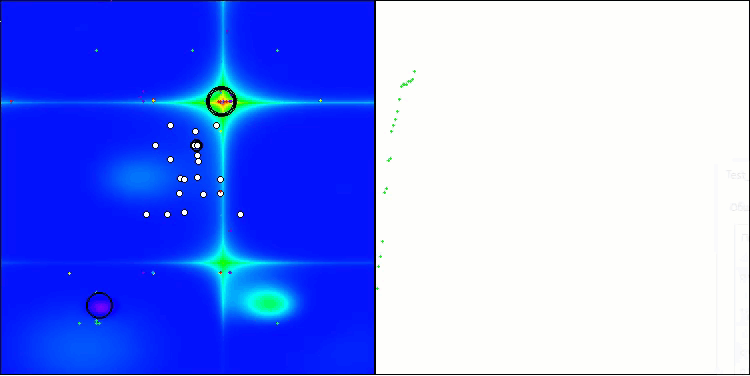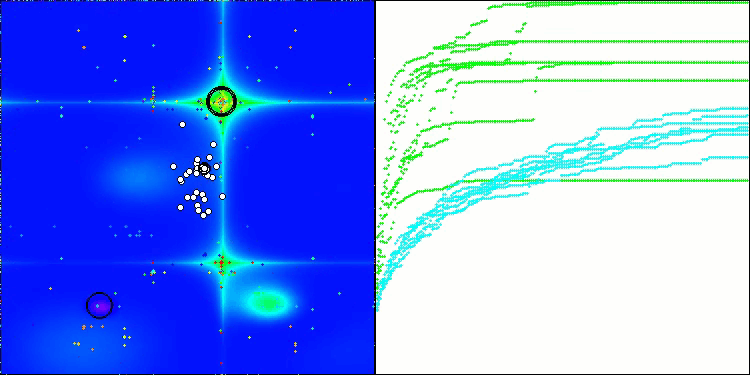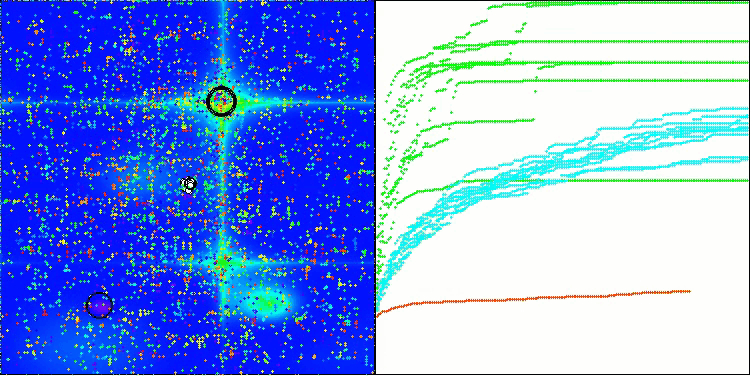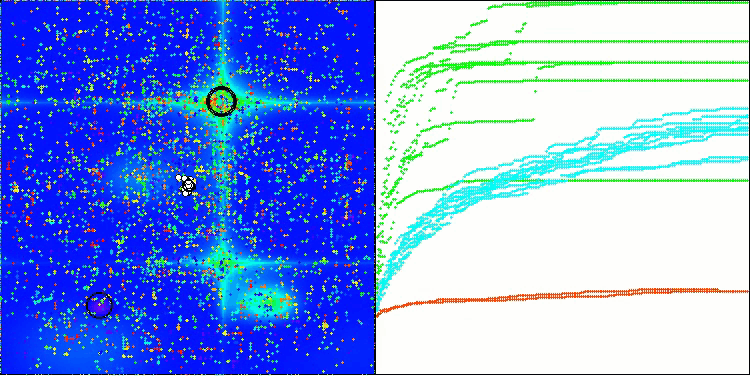
BIO na função de teste Forest

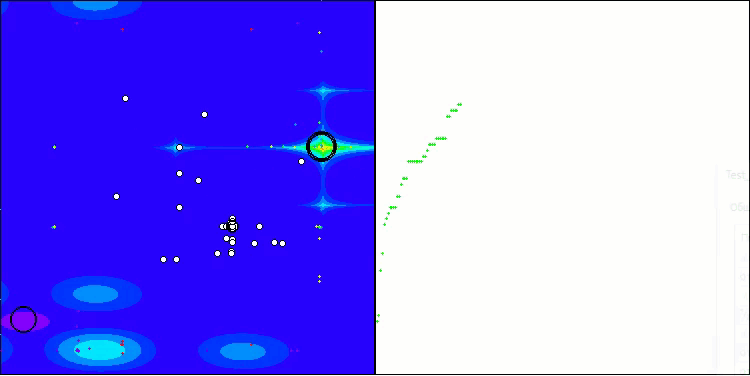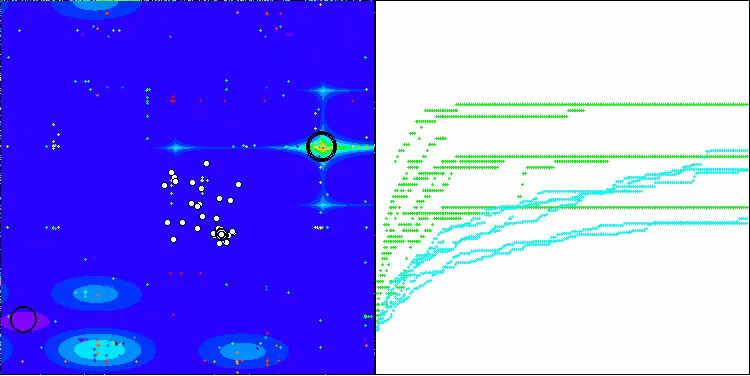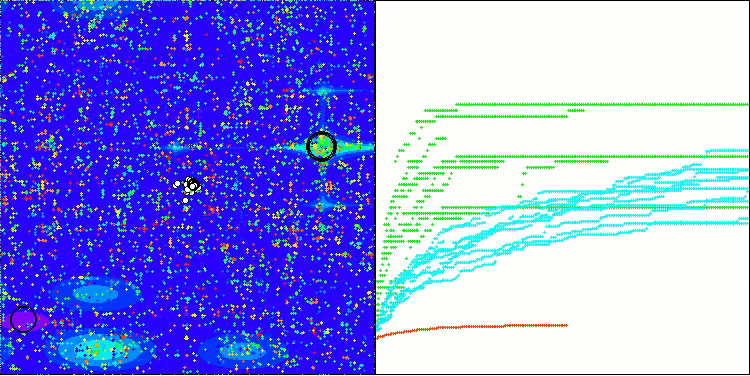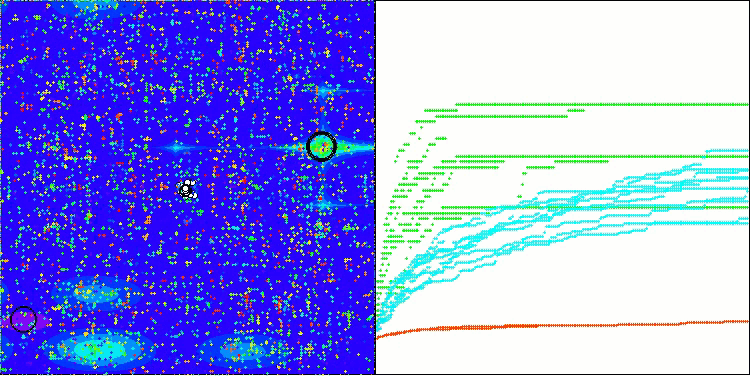
BIO na função de teste Megacity

De acordo com os testes, o algoritmo BIO ocupa a 20ª posição no ranking de algoritmos populacionais de otimização.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
2	CLA	code lock algorithm (joo)	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	AMOm	animal migration ptimization M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5,987	66,52
4	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
5	CTA	comet tail algorithm (joo)	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
6	TETA	time evolution travel algorithm (joo)	0,91362	0,82349	0,31990	2,05701	0,97096	0,89532	0,29324	2,15952	0,73462	0,68569	0,16021	1,58052	5,797	64,41
7	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
8	AAm	archery algorithm M	0,91744	0,70876	0,42160	2,04780	0,92527	0,75802	0,35328	2,03657	0,67385	0,55200	0,23738	1,46323	5,548	61,64
9	ESG	evolution of social groups (joo)	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
10	SIA	simulated isotropic annealing (joo)	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
11	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
12	DA	dialectical algorithm	0,86183	0,70033	0,33724	1,89940	0,98163	0,72772	0,28718	1,99653	0,70308	0,45292	0,16367	1,31967	5,216	57,95
13	BHAm	black hole algorithm M	0,75236	0,76675	0,34583	1,86493	0,93593	0,80152	0,27177	2,00923	0,65077	0,51646	0,15472	1,32195	5,196	57,73
14	ASO	anarchy society optimization	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5,178	57,54
15	RFO	royal flush optimization (joo)	0,83361	0,73742	0,34629	1,91733	0,89424	0,73824	0,24098	1,87346	0,63154	0,50292	0,16421	1,29867	5,089	56,55
16	AOSm	atomic orbital search M	0,80232	0,70449	0,31021	1,81702	0,85660	0,69451	0,21996	1,77107	0,74615	0,52862	0,14358	1,41835	5,006	55,63
17	TSEA	turtle shell evolution algorithm (joo)	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
18	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
19	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
20	BIO	blood inheritance optimization (joo)	0,81568	0,65336	0,30877	1,77781	0,89937	0,65319	0,21760	1,77016	0,67846	0,47631	0,13902	1,29378	4,842	53,80
21	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
22	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
23	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
24	BCOm	bacterial chemotaxis optimization M	0,75953	0,62268	0,31483	1,69704	0,89378	0,61339	0,22542	1,73259	0,65385	0,42092	0,14435	1,21912	4,649	51,65
25	ABO	african buffalo optimization	0,83337	0,62247	0,29964	1,75548	0,92170	0,58618	0,19723	1,70511	0,61000	0,43154	0,13225	1,17378	4,634	51,49
26	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
27	TSm	tabu search M	0,87795	0,61431	0,29104	1,78330	0,92885	0,51844	0,19054	1,63783	0,61077	0,38215	0,12157	1,11449	4,536	50,40
28	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
29	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
30	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
31	AEO	artificial ecosystem-based optimization algorithm	0,91380	0,46713	0,26470	1,64563	0,90223	0,43705	0,21400	1,55327	0,66154	0,30800	0,28563	1,25517	4,454	49,49
32	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
33	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
34	SOA	simple optimization algorithm	0,91520	0,46976	0,27089	1,65585	0,89675	0,37401	0,16984	1,44060	0,69538	0,28031	0,10852	1,08422	4,181	46,45
35	ABHA	artificial bee hive algorithm	0,84131	0,54227	0,26304	1,64663	0,87858	0,47779	0,17181	1,52818	0,50923	0,33877	0,10397	0,95197	4,127	45,85
36	ACMO	atmospheric cloud model optimization	0,90321	0,48546	0,30403	1,69270	0,80268	0,37857	0,19178	1,37303	0,62308	0,24400	0,10795	0,97503	4,041	44,90
37	ADAMm	adaptive moment estimation M	0,88635	0,44766	0,26613	1,60014	0,84497	0,38493	0,16889	1,39880	0,66154	0,27046	0,10594	1,03794	4,037	44,85
38	ATAm	artificial tribe algorithm M	0,71771	0,55304	0,25235	1,52310	0,82491	0,55904	0,20473	1,58867	0,44000	0,18615	0,09411	0,72026	3,832	42,58
39	ASHA	artificial showering algorithm	0,89686	0,40433	0,25617	1,55737	0,80360	0,35526	0,19160	1,35046	0,47692	0,18123	0,09774	0,75589	3,664	40,71
40	ASBO	adaptive social behavior optimization	0,76331	0,49253	0,32619	1,58202	0,79546	0,40035	0,26097	1,45677	0,26462	0,17169	0,18200	0,61831	3,657	40,63
41	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
42	CSA	circle search algorithm	0,66560	0,45317	0,29126	1,41003	0,68797	0,41397	0,20525	1,30719	0,37538	0,23631	0,10646	0,71815	3,435	38,17
43	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
44	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
45	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
	RW	random walk	0,48754	0,32159	0,25781	1,06694	0,37554	0,21944	0,15877	0,75375	0,27969	0,14917	0,09847	0,52734	2,348	26,09

Considerações finais

No processo de desenvolvimento e teste do algoritmo Blood Inheritance Optimization (BIO), cheguei a algumas conclusões importantes. Em primeiro lugar, o uso da associação com a herança dos tipos sanguíneos mostrou-se uma abordagem eficiente para organizar diferentes estratégias de mutação em um algoritmo populacional de otimização. Os testes em várias funções e dimensionalidades mostraram que o algoritmo é bastante versátil e capaz de trabalhar de forma eficaz tanto com tarefas simples de baixa dimensionalidade quanto com problemas mais complexos e multidimensionais.

É especialmente importante destacar que a implementação apresentada do BIO é apenas uma versão básica, que tem como objetivo demonstrar o conceito. A ideia central do algoritmo não está nos operadores de mutação em si (que podem ser substituídos por quaisquer outros), mas sim na estrutura de herança das estratégias de modificação de parâmetros através da analogia com os tipos sanguíneos. Isso abre amplas possibilidades de modificação e expansão do algoritmo. Cada "tipo sanguíneo" pode ser associado a quaisquer outros operadores de mutação, emprestados de outros algoritmos ou criados especificamente para um determinado problema. Além disso, é possível experimentar com a quantidade de "tipos sanguíneos", adicionando novas estratégias ou combinando as existentes.

Os resultados atuais dos testes, que mostram uma posição respeitável no ranking dos algoritmos populacionais (com desempenho em torno de 54%), confirmam a viabilidade da abordagem mesmo em sua implementação básica. Ao mesmo tempo, a tendência observada de aprisionamento em ótimos locais pode ser superada por meio da modificação dos operadores de mutação ou pela adição de novas estratégias de exploração do espaço de soluções.

A direção mais promissora para o desenvolvimento do algoritmo, na minha visão, está na criação de versões adaptativas, em que os operadores de mutação para cada "tipo sanguíneo" possam mudar dinamicamente durante o processo de otimização, ajustando-se ao formato da função objetivo. Também considero interessante investigar a aplicação de diferentes esquemas de herança, distintos do sistema clássico de tipos sanguíneos "ABO", o que pode levar à criação de uma família inteira de algoritmos baseados em diferentes sistemas biológicos de herança.

Assim, o BIO não representa apenas mais um algoritmo de otimização, mas sim uma base conceitual flexível para a criação de uma família de algoritmos, unificada pela ideia de herança de estratégias de busca de soluções através da metáfora dos tipos sanguíneos. Ele abre amplas possibilidades para pesquisas e modificações futuras, voltadas ao aumento da eficiência do algoritmo em diferentes áreas de aplicação.

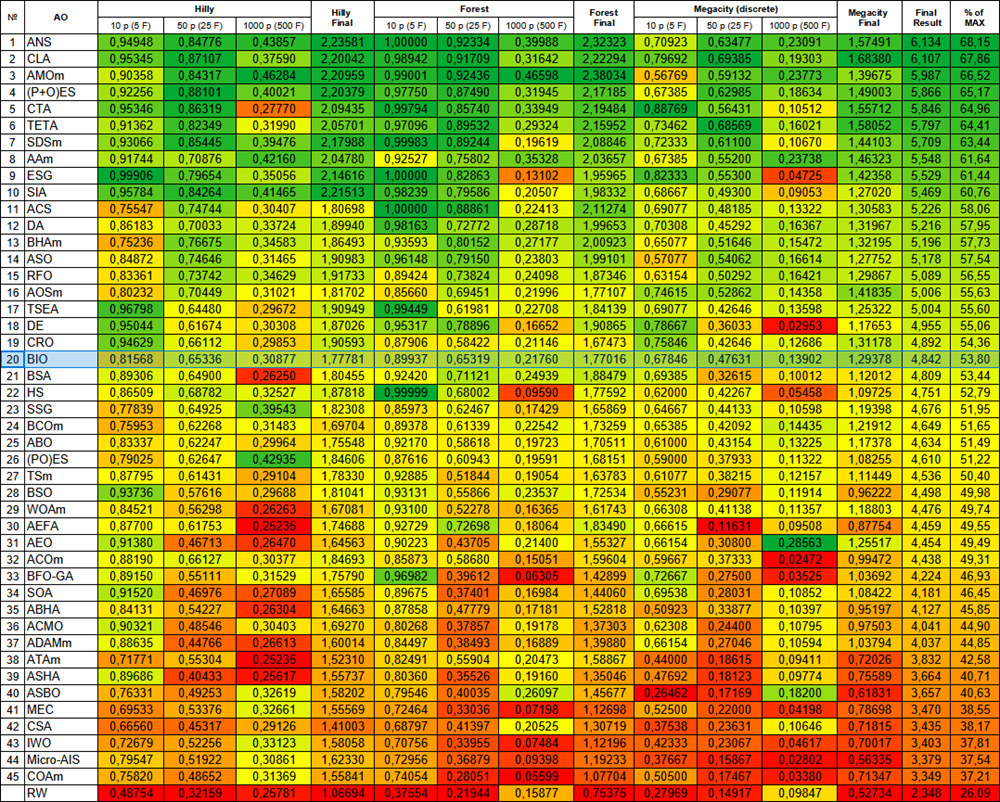
Figura 2. Gradação de cores dos algoritmos conforme os respectivos testes

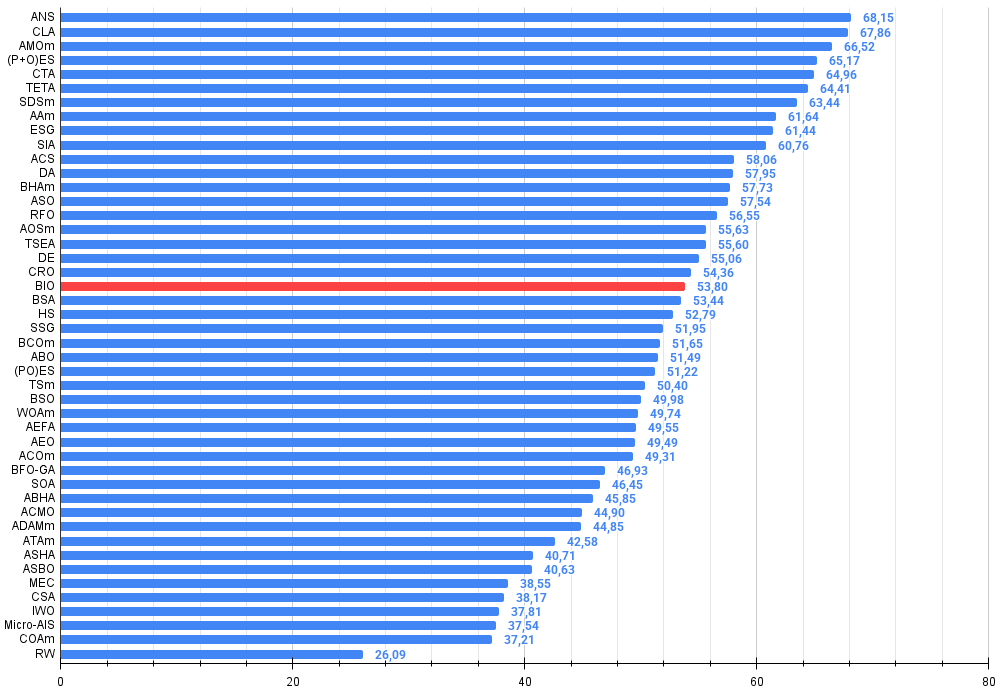
Figura 3. Histograma dos resultados dos testes dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor, onde 100 é o resultado teórico máximo possível, no arquivo está o script para cálculo da tabela de ranking)

Prós e contras do algoritmo BIO:

Prós:

1. Não possui parâmetros externos
2. Ideia interessante de herança baseada nos tipos sanguíneos
   
3. Boa convergência em funções de alta e média dimensionalidade

Contras:

1. Tende a ficar preso em extremos locais em tarefas de baixa dimensionalidade.
   

Ao artigo está anexado um arquivo compactado com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, já que em muitos deles foram feitas modificações para melhorar as capacidades de busca. As conclusões e julgamentos apresentados nos artigos baseiam-se nos resultados dos experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	C_AO.mqh	Arquivo incluído	Classe principal dos algoritmos populacionais de otimização Otimização
2	C_AO_enum.mqh	Arquivo incluído	Enumeração dos algoritmos populacionais de otimização
3	TestFunctions.mqh	Arquivo incluído	Biblioteca de funções de teste
4	TestStandFunctions.mqh	Arquivo incluído	Biblioteca de funções do test stand
5	Utilities.mqh	Arquivo incluído	Biblioteca de funções auxiliares
6	CalculationTestResults.mqh	Arquivo incluído	Script para cálculo de resultados em tabela comparativa
7	Testing AOs.mq5	Script	Ambiente de teste unificado para todos os algoritmos populacionais de otimização
8	Simple use of population optimization algorithms.mq5	Script	Exemplo simples de uso de algoritmos populacionais de otimização sem visualização
9	Test_AO_BIO.mq5	Script	Ambiente de teste para o BIO