
Royal-Flush-Optimierung (RFO)
Inhalt
Einführung
Es gibt viele Ansätze zur Lösung von Optimierungsproblemen, unter denen genetische Algorithmen einen besonderen Platz einnehmen, da sie in der Lage sind, den Suchraum effektiv zu erkunden, indem sie die Prozesse der natürlichen Evolution simulieren. Der herkömmliche genetische Algorithmus verwendet eine binäre Kodierung der Lösungen, was eine Umwandlung von reellen Zahlen in ein binäres Format erfordert. Diese Umwandlung führt nicht nur zu zusätzlicher Komplexität, sondern belastet auch den Algorithmus erheblich. In der modernen Welt spielt die Minimierung des Rechenaufwands eine entscheidende Rolle, und die Produktivität einer Methode ist in der Regel direkt proportional zu ihrer Geschwindigkeit. Bei der Lösung dieses Problems kam mir die Idee, wie man die genetischen Operatoren beibehalten und gleichzeitig die schwierigsten Berechnungen bei der Umwandlung von reellen Zahlen durch einfachere und weniger energieaufwändige Operationen ersetzen kann.
Mein Algorithmus, die Royal Flush Optimierung (RFO), ist ein neuer Ansatz zur Lösung von Optimierungsproblemen, der die wichtigsten Vorteile genetischer Algorithmen beibehält, aber eine direktere Art der Darstellung von Lösungen verwendet. Der Grundgedanke besteht darin, jede Koordinate des Suchraums in Sektoren zu unterteilen, ähnlich wie ein Pokerblatt aus einzelnen Spielkarten eines bestimmten Ranges besteht. Anstatt mit Bitstrings zu arbeiten, verwaltet der Algorithmus Spielkartenränge (Sektornummern), wodurch die Topologie des Suchraums auf natürliche Weise erhalten werden kann.
Meiner Meinung nach liegen die Hauptvorteile des vorgeschlagenen Ansatzes in der Einfachheit der Implementierung und der intuitiven Klarheit (die Arbeit mit „Spielkarten“ ist visueller als mit Bit-Strings) sowie in der Tatsache, dass keine reellen Zahlen kodiert und dekodiert werden müssen, während die kombinatorischen Eigenschaften des genetischen Algorithmus erhalten bleiben. In diesem Artikel werden wir die Implementierung des Algorithmus und die Merkmale der Entscheidungsänderungsoperatoren im Detail betrachten.
Die Poker-Metapher gibt dem Algorithmus nicht nur seinen Namen, sondern beschreibt auch sein Wesen gut: So wie beim Poker ein Spieler danach strebt, die beste Kombination von Spielkarten zu sammeln, kombiniert der Algorithmus Sektoren verschiedener Lösungen und bildet so nach und nach optimale „Hände“. So wie beim Poker jede Spielkarte ihren eigenen Rang und ihre eigene Farbe hat, so hat beim Algorithmus jeder Sektor seinen eigenen Wert und seine eigene Position im Suchraum. In diesem Fall ist, wie in einem echten Spiel, nicht nur der Wert der einzelnen Spielkarten wichtig, sondern auch ihr Zusammenspiel in der Gesamtkombination.
Es ist erwähnenswert, dass dieser Ansatz als eine Verallgemeinerung der Ideen der diskreten Optimierung auf den Fall der kontinuierlichen Räume betrachtet werden kann, was interessante Perspektiven für die theoretische Analyse und praktische Anwendung eröffnet. So wie Poker Elemente des Zufalls und der Strategie kombiniert, verbindet RFO die zufällige Suche mit gerichteter Optimierung, was es für komplexe multivariate Probleme effektiv macht.
Implementierung des Algorithmus
Der Algorithmus der Royal Flush Optimierung (RFO) basiert auf der Idee, den Suchraum als diskrete Sektoren darzustellen, ähnlich wie die Spielkarten beim Poker bestimmte Ränge haben. Bei einem herkömmlichen genetischen Algorithmus werden die Werte (optimierte Parameter) für alle Koordinaten in Binärcode umgewandelt und in eine chromosomenähnliche Sequenz gefaltet, was zusätzliche Rechenkosten verursacht. In der RFO wird dieser Ansatz zugunsten einer einfacheren und intuitiveren Darstellung aufgegeben.
Anstelle einer binären Kodierung unterteilen wir jede Koordinate des Suchraums in Sektoren und weisen ihnen Werte zu, die denen von Pokerkarten entsprechen – von Bube bis Ass (J, Q, K, A). Die Anzahl der Ränge (Sektoren) wird in den externen Parametern des Algorithmus angegeben und kann ein beliebiger ganzzahliger Wert sein. So kann jeder Punkt im Suchraum als eine Kombination von Spielkarten dargestellt werden, wobei jede Spielkarte entsprechend ihrer Koordinate einem bestimmten Sektor entspricht. Dieser Ansatz vereinfacht nicht nur die Berechnungen, sondern bewahrt auch die kombinatorischen Eigenschaften des genetischen Algorithmus.
Während der Optimierung arbeitet der Algorithmus mit „Blättern“, d. h. mit Spielkartensätzen, die verschiedene Lösungen darstellen. Crossover- und Mutations-Operatoren werden direkt auf „Hände“ (Spielkartensätze) angewandt, wobei jede Hand einem Chromosom entspricht, was die Erkundung des Suchraums ohne binäre Umwandlung ermöglicht.
Die folgende Abbildung (Abbildung 1) verdeutlicht dieses Prinzip. Sie zeigt einen dreidimensionalen Suchraum mit X-, Y- und Z-Koordinaten, wobei jede Koordinate in Sektoren unterteilt ist, die den Rängen der Spielkarten entsprechen. Auf der rechten Seite sind Beispiele für „Hände“ zu sehen – verschiedene Kombinationen von Spielkarten, die der Algorithmus bei der Suche nach der optimalen Lösung bildet.
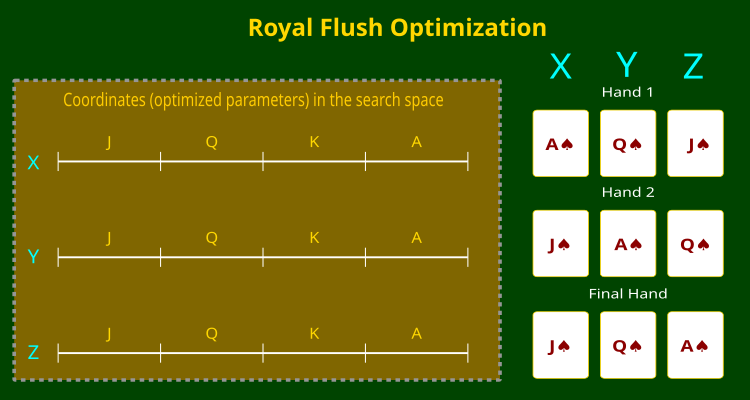
Abbildung 1. Der RFO-Algorithmus und die Aufteilung der Koordinaten in Spielkartenspielränge
Gehen wir nun dazu über, den Pseudocode für den Algorithmus der Royal Flush Optimierung (RFO) zu schreiben:
- Lege die Anzahl der Spieler am „Pokertisch“ fest (Populationsgröße).
- Bestimme die Größe des „Decks“ (die Anzahl der Sektoren für jede Dimension).
- Lege die Wahrscheinlichkeit des „Bluffens“ (Mutation) fest.
- Erstelle eine erste „Hand“ – zufällige Generierung von Spielkartenrängen für jede Koordinate.
- Wandle die Ränge in reale Werte mit einem zufälligen Offset innerhalb des Sektors.
- Für jede Position am Tisch:
- Wähle den „Gegner“ durch quadratische Auswahl (stärkere „Hände“ haben eine höhere Chance, ausgewählt zu werden).
- Kopiere die aktuelle „Hand“ (Lösung).
- Führe einen Drei-Punkte-Spielkartentausch durch:
- Wähle nach dem Zufallsprinzip drei „Schnittpunkte“ aus.
- Sortiere die Schnittpunkte.
- Wähle zufällig einen Startpunkt (0 oder 1).
- Tausche die Spielkarten zwischen der aktuellen Hand und der Hand des Gegners.
- Ein „Bluff“ (Mutationswahrscheinlichkeit) ist möglich – eine zufällige Änderung des Ranges einer Spielkarte mit einer bestimmten Wahrscheinlichkeit.
- Wandle die erhaltenen Spielkartenränge in reale Koordinatenwerte.
- Berechne den Wert jeder „Hand“ (den Wert der Zielfunktion).
- Erinnere Dich an die beste gefundene Kombination (global beste Lösung).
- Kombiniere die aktuellen Hände mit dem vorherigen Deck.
- Sortiere alle „Hände“ nach ihrem Wert.
- Gib die besten „Hände“ an die nächste Generation weiter.
Fahren wir mit dem Schreiben des Algorithmus-Codes fort. Wir schreiben die Struktur S_RFO_Agent, die ein Objekt darstellt, das Informationen über die „Hand“ im Kontext des Spiels enthält.
Die Felder der Struktur:
- card [] – Array zum Speichern des tatsächlichen Wertes der Spielkarte.
- f – Handwert (Wert der Fitnessfunktion).
- cardRanks [] – Array von Ganzzahlen, die die „Spielkartenränge“ (Sektornummern) darstellen.
Die Methode Init () initialisiert die Struktur und nimmt einen einzelnen Parameter „coords“, der die Anzahl der Spielkarten in der „Hand“ angibt.
//—————————————————————————————————————————————————————————————————————————————— // Structure for representing a single "hand" struct S_RFO_Agent { double card []; // cards double f; // value of the fitness function ("hand value") int cardRanks []; // sector numbers ("map ranks") void Init (int coords) { ArrayResize (cardRanks, coords); ArrayResize (card, coords); f = -DBL_MAX; // initialization with minimum value } }; //——————————————————————————————————————————————————————————————————————————————
Die Klasse C_AO_RFO implementiert den Algorithmus und erbt Eigenschaften und Methoden von der Basisklasse C_AO. Schauen wir uns das genauer an.
Der Konstruktor C_AO_RFO () setzt Werte für Klassenvariablen und initialisiert Parameter:- popSize – Die Populationsgröße (Pokertisch) wird auf 50 gesetzt.
- deckSize – Anzahl der Spielkarten im Deck (oder Sektoren) – 1000.
- dealerBluff – Die Wahrscheinlichkeit eines Bluffs (Mutation) wird auf 3% (0,03) gesetzt.
- Das Array „params“ dient zum Speichern von Parametern, wird auf 3 verkleinert und mit den Werten für popSize, deckSize und dealerBluff gefüllt.
Die Methode SetParams () – die Methode extrahiert Werte aus dem Array „params“ und weist sie den entsprechenden Klassenvariablen zu.
Die Methode Init () dient dazu, die Klasse mit den übergebenen Parametern zu initialisieren, z. B. mit den Minimal- und Maximalwerten der zu optimierenden Parameter und deren Schritt.
Die Methoden Moving() und Revision() werden verwendet, um Operationen auszuführen, die mit dem Mischen von Spielkarten in Ihrer Hand und der Überprüfung ihrer besten Kombination zusammenhängen.
Felder der Klasse:- deckSize – Anzahl der Sektoren in der Dimension.
- dealerBluff – Mutationswahrscheinlichkeit.
- deck [], tempDeck [], hand [] – Arrays vom Typ S_RFO_Agent, die das Hauptdeck, das temporäre Deck zum Sortieren bzw. die aktuelle Hand (Nachkommen) repräsentieren.
- cutPoints – Anzahl der „Schnittpunkte“ des vorliegenden Spielkartensatzes, die zum Kombinieren von Spielkartensatzvarianten verwendet werden.
- tempCuts [] und finalCuts [] – Arrays zum Speichern von temporären und endgültigen „Schnittpunktindizes“.
- Die verwendeten Methoden sind Evolution() – verantwortlich für die Durchführung der grundlegenden Entwicklung von Spielkarten-Permutationen, und DealCard() – verantwortlich für die Umwandlung eines Sektors in seinen realen Wert. Die Methode ShuffleRanks () ist für die Mutation der Ränge zuständig (zufällige Auswahl unter den verfügbaren Rängen).
//—————————————————————————————————————————————————————————————————————————————— class C_AO_RFO : public C_AO { public: C_AO_RFO () { ao_name = "RFO"; ao_desc = "Royal Flush Optimization"; ao_link = "https://www.mql5.com/en/articles/17063"; popSize = 50; // "poker table" (population) size deckSize = 1000; // number of "cards" in the deck (sectors) dealerBluff = 0.03; // "bluff" (mutation) probability ArrayResize (params, 3); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "deckSize"; params [1].val = deckSize; params [2].name = "dealerBluff"; params [2].val = dealerBluff; } void SetParams () { popSize = (int)params [0].val; deckSize = (int)params [1].val; dealerBluff = params [2].val; } bool Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0); // number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- int deckSize; // number of sectors in the dimension double dealerBluff; // mutation probability S_RFO_Agent deck []; // main deck (population) S_RFO_Agent tempDeck []; // temporary deck for sorting S_RFO_Agent hand []; // current hand (descendants) private: //------------------------------------------------------------------- int cutPoints; // number of cutting points int tempCuts []; // temporary indices of cutting points int finalCuts []; // final indices taking the beginning and end into account void Evolution (); // main process of evolution double DealCard (int rank, int suit); // convert sector to real value void ShuffleRanks (int &ranks []); // rank mutation }; //——————————————————————————————————————————————————————————————————————————————
Die Methode Init dient der Initialisierung eines Objekts der Klasse C_AO_RFO.
Die Methode beginnt mit dem Aufruf einer Funktion, die die Standardinitialisierung der gegebenen Parameter, wie z. B. Mindest- und Höchstwerte, sowie Parameteränderungsschritte durchführt. Schlägt diese Initialisierung fehl, bricht die Methode ab und gibt „false“ zurück. Nach erfolgreicher Initialisierung der Parameter bereitet die Methode Datenstrukturen für die Speicherung von Informationen über „Hände“ und „Decks“ vor. Dazu müssen die Arrays für die Speicherung von „Händen“ und „Decks“ an die Größe der Population angepasst werden.
Die Methode initialisiert dann jedes Element des Arrays „hands“ mit einer speziellen Methode, die sie auf der Grundlage der angegebenen Koordinaten konfiguriert. In ähnlicher Weise werden auch die Arrays „deck“ und „temp deck“ vorbereitet und initialisiert. Die Methode legt die Anzahl der Schnittpunkte fest, die für den Crossover-Algorithmus erforderlich sind. In diesem Fall werden drei Schnittpunkte festgelegt (dies ist der beste Wert, der bei Versuchen ermittelt wurde). Dann werden Arrays eingerichtet, um temporäre und endgültige Schnittpunkte zu speichern. Am Ende gibt die Methode den Wert „true“ zurück, der bestätigt, dass die Initialisierung erfolgreich abgeschlossen wurde.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_RFO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- // Initialize structures for storing "hands" and "decks" ArrayResize (hand, popSize); for (int i = 0; i < popSize; i++) hand [i].Init (coords); ArrayResize (deck, popSize * 2); ArrayResize (tempDeck, popSize * 2); for (int i = 0; i < popSize * 2; i++) { deck [i].Init (coords); tempDeck [i].Init (coords); } // Initialize arrays for cutting points cutPoints = 3; // three cutting points for a "three-card" crossover ArrayResize (tempCuts, cutPoints); ArrayResize (finalCuts, cutPoints + 2); return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode „Moving“ ist für den Prozess des „Verschiebens“ oder der Aktualisierung des Zustands der Population innerhalb des RFO-Algorithmus verantwortlich.
Überprüfung des Status – Die Methode beginnt die Ausführung mit der Überprüfung der Bedingung, die bestimmt, ob die anfängliche Initialisierung „Austeilen“ der Spielkarten abgeschlossen ist. Wenn dies nicht der Fall ist (Revision == false), führt die Methode eine Initialisierung durch.
Initialisierung der anfänglichen Verteilung – die Methode iteriert durch alle Elemente der Grundgesamtheit, für jedes Element der Grundgesamtheit (jede „Hand“) wird ein Satz von Spielkarten erstellt. Die innere Schleife durchläuft jede erforderliche Anzahl von Spielkarten und führt die folgenden Aktionen aus:
- Ein Spielkartenrang wird zufällig aus dem Stapel ausgewählt.
- Die Methode wird dann aufgerufen, um die Spielkarte auf der Grundlage des erzeugten Ranges zu verteilen.
- Die resultierende Spielkarte wird mit Hilfe einer Funktion angepasst, die prüft, ob sie innerhalb eines bestimmten Bereichs liegt, und je nach den angegebenen Parametern die erforderlichen Änderungen vornimmt.
- Schließlich wird der Wert der empfangenen Spielkarte auf das Array „a“ gesetzt.
Aktualisieren des Status – nach Abschluss der Initialisierung wird „revision“ auf „true“ gesetzt, was bedeutet, dass die ursprüngliche Verteilung abgeschlossen ist und keine weitere Neuinitialisierung erforderlich ist.
Aufruf der Methode Evolution () – wenn die erste Ausgabe bereits erfolgt ist, führt die Methode den evolutionären Prozess des Mischens und Verteilens der Spielkarten auf die Hände durch.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RFO::Moving () { //---------------------------------------------------------------------------- if (!revision) { // Initialize the initial "distribution" for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { hand [i].cardRanks [c] = u.RNDminusOne (deckSize); hand [i].card [c] = DealCard (hand [i].cardRanks [c], c); hand [i].card [c] = u.SeInDiSp (hand [i].card [c], rangeMin [c], rangeMax [c], rangeStep [c]); a [i].c [c] = hand [i].card [c]; } } revision = true; return; } //---------------------------------------------------------------------------- Evolution (); } //——————————————————————————————————————————————————————————————————————————————
Die Revisionsmethode ist dafür verantwortlich, die beste „Kombination“ von „Händen“ zu finden, ihre Eignung zu bewerten und das Gesamtdeck zu aktualisieren.
Suche nach der besten Kombination:
- Die Methode beginnt mit der Initialisierung der Variablen bestHand, die den Index des besten Blatts aller Mitglieder der Population speichert.
- Dann wird eine Schleife ausgeführt, die alle Elemente der Grundgesamtheit durchläuft (von 0 bis popSize). Innerhalb der Schleife vergleicht die Methode den Fitnesswert jeder Hand „a“ mit dem aktuell besten Wert von fB.
- Wenn der Fitnesswert der aktuellen Hand größer als fB ist, wird eine Aktualisierung mit dem neuen besten Wert vorgenommen und der Index dieser „Hand“ wird der Variablen bestHand zugewiesen.
Wenn die beste Hand gefunden wird, werden die Spielkarten in das cB-Array kopiert, wodurch der Zustand der besten Kombination (die beste globale Lösung) gespeichert werden kann. Die Methode aktualisiert dann die Fitnesswerte für jede Hand im Array „hand“ so, dass sie gleich den entsprechenden Werten im Array „a“ sind. Dies ist notwendig, um sicherzustellen, dass die Eignungsdaten für jede Hand auf dem neuesten Stand sind. Nach der Aktualisierung der Fitnesswerte werden die aktuellen Hände aus dem Array „hand“ dem allgemeinen Array „deck“ hinzugefügt, beginnend an der Position popSize (d.h. am Ende der Population, ihrer zweiten Hälfte).
Schließlich sortiert die Methode das „Deck“-Array mit Hilfe eines separaten temporären tempDeck-Arrays, um das Deck nach Kombinationswert zu ordnen. So können wir die erhöhte Wahrscheinlichkeit der Auswahl wertvoller Spielkartenkombinationen bei der Auswahl mit ihrer nachfolgenden Kombination nutzen.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RFO::Revision () { // Search for the best "combination" int bestHand = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; bestHand = i; } } if (bestHand != -1) ArrayCopy (cB, a [bestHand].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- // Update fitness values for (int i = 0; i < popSize; i++) { hand [i].f = a [i].f; } // Add current hands to the general deck for (int i = 0; i < popSize; i++) { deck [popSize + i] = hand [i]; } // Sort the deck by combination value u.Sorting (deck, tempDeck, popSize * 2); } //——————————————————————————————————————————————————————————————————————————————
Die Evolutionsmethode ist für die Hauptlogik des Algorithmus verantwortlich, bei der Spielkarten zwischen den „Händen“ der Spieler am Tisch ausgetauscht werden, „Bluffing“ stattfindet und die tatsächlichen Werte der Spielkarten aktualisiert werden.
Die Methode beginnt mit einer Schleife, die alle Elemente der Grundgesamtheit durchläuft. Die folgenden Aktionen werden durchgeführt:
Auswählen eines Gegners:
- Um einen Gegner auszuwählen, wird eine Zufallszahl generiert, die dann quadriert wird, um die Auswahl zu erhöhen (die Wahrscheinlichkeit, einen Gegner auszuwählen, wird mit seiner Bewertung gekreuzt). Dadurch wird es wahrscheinlicher, dass Sie die beste Kombination von Händen wählen.
- Die Zufallszahl wird mit der Funktion u.Scale skaliert, um den Index des Gegners zu erhalten.
Das aktuelle Blatt (aus dem Array „deck“) wird in das Array „hand“ kopiert. Die Methode erzeugt zufällige „Schnittpunkte“ für das Spielkartenblatt. Diese Punkte bestimmen, welche Spielkarten zwischen den beiden Händen ausgetauscht werden. Die Schnittpunkte werden sortiert und mit Begrenzungen versehen; die erste Begrenzung wird auf „0“ und die letzte Begrenzung auf „coords – 1“ gesetzt. Die Methode wählt einen zufälligen Startpunkt, um mit dem Spielkartentausch zu beginnen, indem sie u.RNDbool () verwendet. Nachdem der Spielkartentausch abgeschlossen ist, wird eine Chance zum „Bluffen“ gegeben.
Umrechnung von Rängen in reale Werte:- In der letzten Schleife werden die Spielkartenränge mit der Methode DealCard in ihre Werte umgerechnet und auf die Einhaltung der festgelegten Grenzen überprüft.
- Danach werden die Werte im Array „a“, das die letzten Spielkarten enthält, aktualisiert.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RFO::Evolution () { // For each position at the table for (int i = 0; i < popSize; i++) { // Select an opponent based on their rating (probability squared to enhance selection) double rnd = u.RNDprobab (); rnd *= rnd; int opponent = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1); // Copy the current hand hand [i] = deck [i]; // Define cutting points for card exchange for (int j = 0; j < cutPoints; j++) { tempCuts [j] = u.RNDminusOne (coords); } // Sort cutting points and add borders ArraySort (tempCuts); ArrayCopy (finalCuts, tempCuts, 1, 0, WHOLE_ARRAY); finalCuts [0] = 0; finalCuts [cutPoints + 1] = coords - 1; // Random selection of a starting point for exchange int startPoint = u.RNDbool (); // Exchange cards between hands for (int j = startPoint; j < cutPoints + 2; j += 2) { if (j < cutPoints + 1) { for (int len = finalCuts [j]; len < finalCuts [j + 1]; len++) hand [i].cardRanks [len] = deck [opponent].cardRanks [len]; } } // Possibility of "bluffing" (mutation) ShuffleRanks (hand [i].cardRanks); // Convert ranks to real values for (int c = 0; c < coords; c++) { hand [i].card [c] = DealCard (hand [i].cardRanks [c], c); hand [i].card [c] = u.SeInDiSp (hand [i].card [c], rangeMin [c], rangeMax [c], rangeStep [c]); a [i].c [c] = hand [i].card [c]; } } } //——————————————————————————————————————————————————————————————————————————————
Die DealCard-Methode ist ein Schlüsselelement des Royal-Flush-Optimierungsalgorithmus, der diskrete Sektoren des Suchraums in kontinuierliche Koordinatenwerte umwandelt. Die Methode benötigt zwei Parameter als Eingabe: „Rang“ – den Rang der Spielkarte und „Farbe“ – den Koordinatenindex (Farbe).
Die Umwandlung besteht aus zwei Stufen. Zunächst wird die Größe eines Sektors (suitRange) berechnet, indem der gesamte Suchbereich durch die Anzahl der Sektoren geteilt wird. Dann wird ein bestimmter Wert innerhalb des ausgewählten Sektors erzeugt. Der Zufallsabstand u.RNDprobab() gewährleistet eine gleichmäßige Erkundung des Raums innerhalb jedes Sektors, und „rank“ definiert die Basisposition im Suchraum.
Dieser Ansatz ermöglicht es, eine diskrete Darstellung von Lösungen durch Sektoren mit einem kontinuierlichen Suchraum zu kombinieren und so ein Gleichgewicht zwischen globaler und lokaler Suche herzustellen.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_RFO::DealCard (int rank, int suit) { // Convert the map rank to a real value with a random offset within the sector double suitRange = (rangeMax [suit] - rangeMin [suit]) / deckSize; return rangeMin [suit] + (u.RNDprobab () + rank) * suitRange; } //——————————————————————————————————————————————————————————————————————————————
Die Methode ShuffleRanks implementiert den Mutationsmechanismus im Royal-Flush-Optimierungsalgorithmus und fungiert als „Bluff“ bei der Arbeit mit Spielkartenrängen. Bei einem Array von Rängen als Referenz durchläuft die Methode jede Koordinate und ersetzt mit der Wahrscheinlichkeit dealerBluff den aktuellen Rang durch einen Zufallswert aus dem Bereich der gültigen Ränge im Deck. Dieser Prozess kann mit einer Situation beim Poker verglichen werden, wenn ein Spieler unerwartet die Spielkarte in seiner Hand ändert und damit ein Element der Unvorhersehbarkeit in das Spiel einbringt. Dieser Mutationsmechanismus soll dem Algorithmus helfen, nicht in lokalen Optima stecken zu bleiben und eine Vielfalt möglicher Lösungen während der Optimierung zu erhalten.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RFO::ShuffleRanks (int &ranks []) { // Rank shuffle (mutation) for (int i = 0; i < coords; i++) { if (u.RNDprobab () < dealerBluff) ranks [i] = (int)MathRand () % deckSize; } } //——————————————————————————————————————————————————————————————————————————————
Testergebnisse
RFO algorithm test results:
RFO|Royal Flush Optimization|50.0|1000.0|0.03|
=============================
5 Hilly's; Func runs: 10000; result: 0.8336125672709654
25 Hilly's; Func runs: 10000; result: 0.7374210861383783
500 Hilly's; Func runs: 10000; result: 0.34629436610445113
=============================
5 Forest's; Func runs: 10000; result: 0.8942431024645086
25 Forest's; Func runs: 10000; result: 0.7382367793268382
500 Forest's; Func runs: 10000; result: 0.24097956383750824
=============================
5 Megacity's; Func runs: 10000; result: 0.6315384615384616
25 Megacity's; Func runs: 10000; result: 0.5029230769230771
500 Megacity's; Func runs: 10000; result: 0.16420769230769366
=============================
All score: 5.08946 (56.55%)
Das Endergebnis von 56,55 % ist ein sehr respektables Ergebnis. In der Visualisierung zeigt der Algorithmus kein spezifisches Verhalten; es sieht aus wie ein chaotisches Wandern einzelner Punkte.
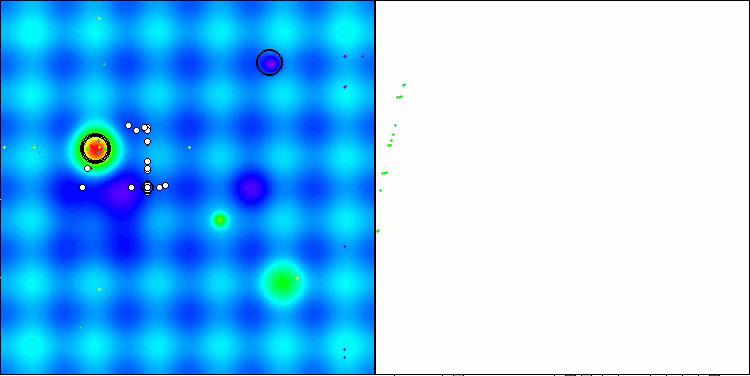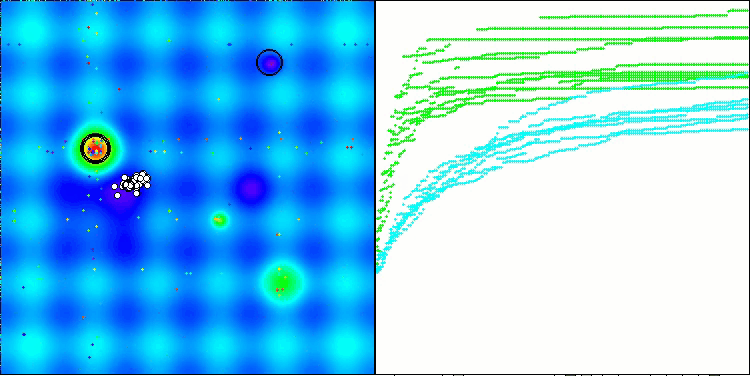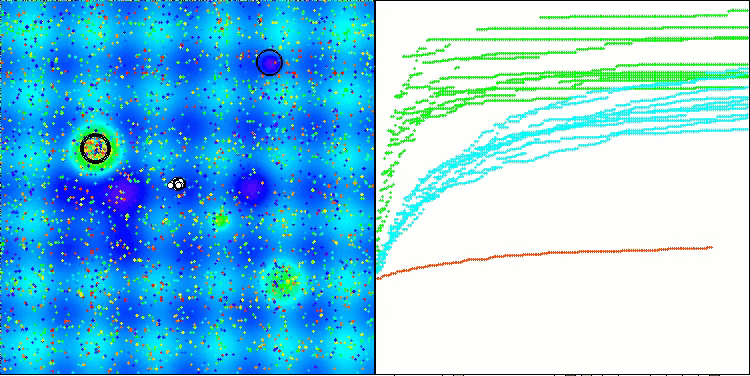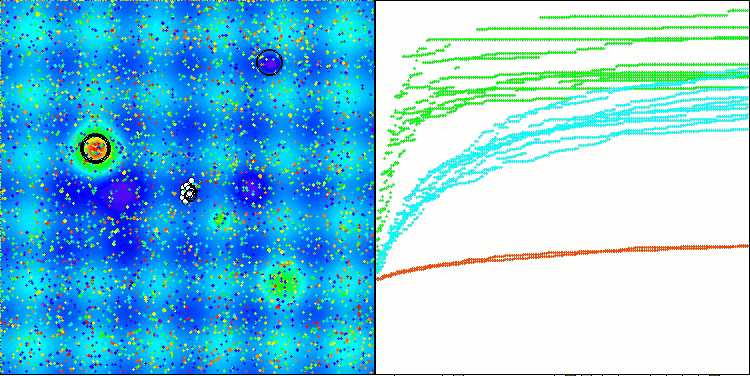
RFO mit die Testfunktion Hilly
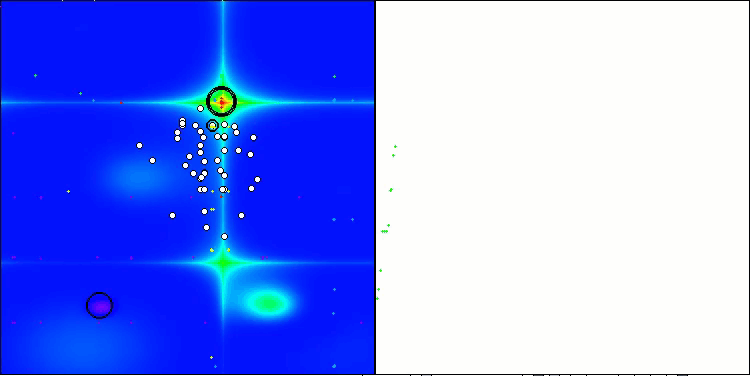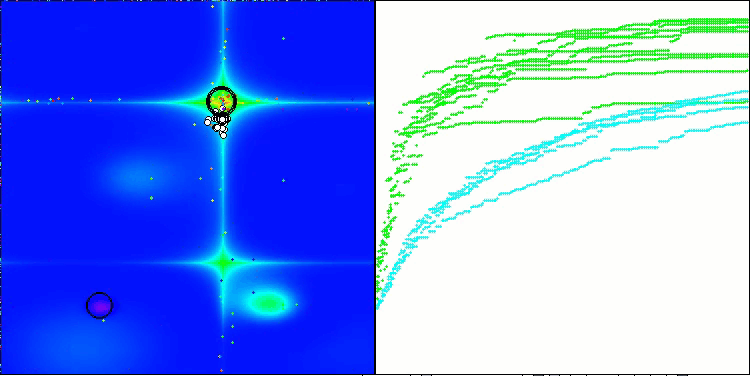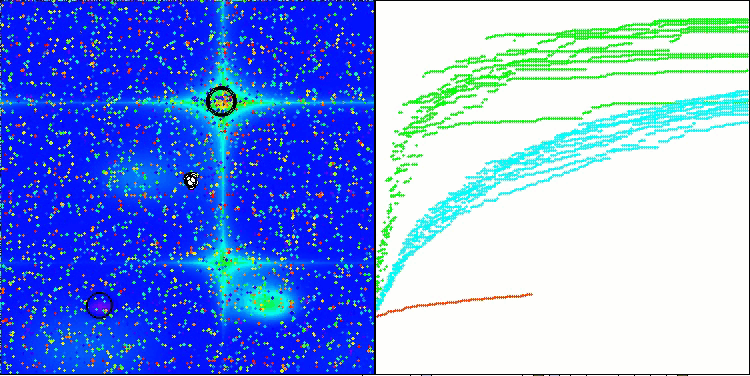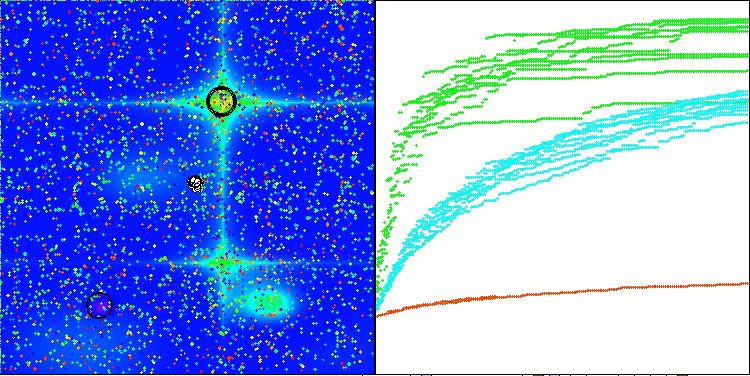
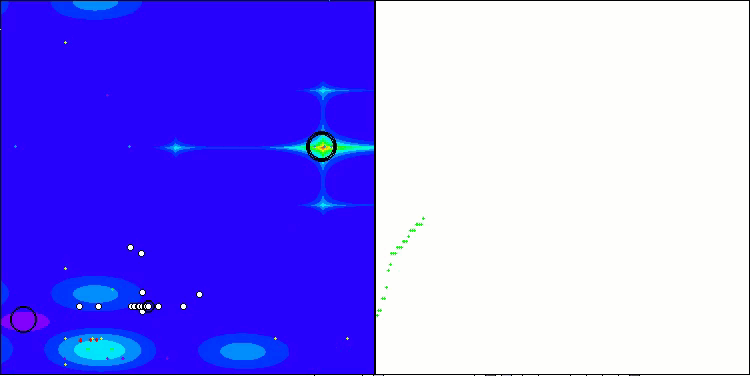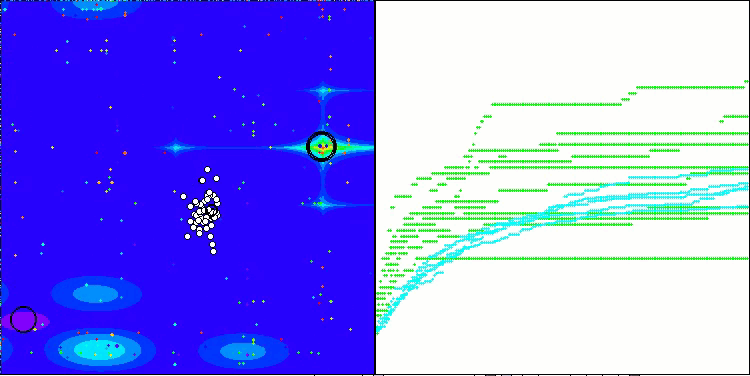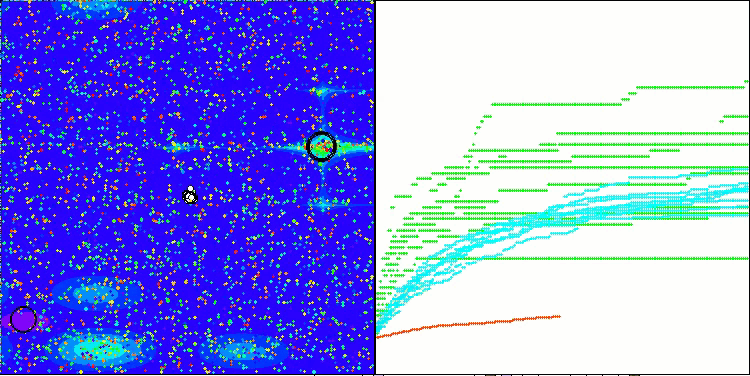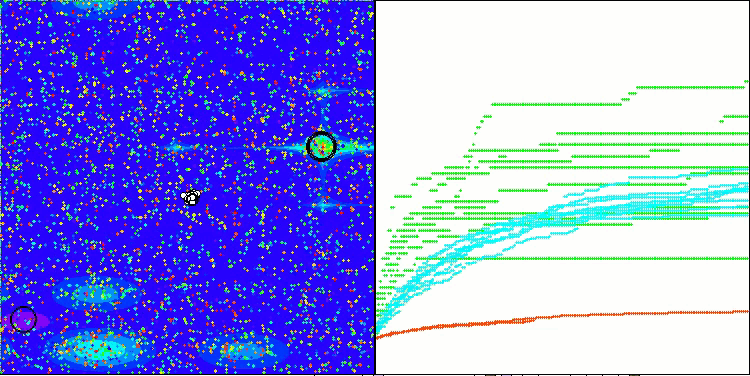
RFO mit die Testfunktion Forest
RFO mit die Testfunktion Megacity
Auf der Grundlage der Testergebnisse belegt der RFO-Optimierungsalgorithmus Platz 15 und reiht sich damit in die Liste der stärksten bekannten Algorithmen ein.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Code-Sperr-Algorithmus (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | TETA | Zeit-Evolutions-Reise-Algorithmus (Joo) | 0.91362 | 0.82349 | 0.31990 | 2.05701 | 0.97096 | 0.89532 | 0.29324 | 2.15952 | 0.73462 | 0.68569 | 0.16021 | 1.58052 | 5.797 | 64.41 |
| 7 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 8 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 9 | ESG | Entwicklung sozialer Gruppen (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 10 | SIA | Simuliertes isotropes Glühen (Joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 11 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 12 | DA | dialektischer Algorithmus | 0.86183 | 0.70033 | 0.33724 | 1.89940 | 0.98163 | 0.72772 | 0.28718 | 1.99653 | 0.70308 | 0.45292 | 0.16367 | 1.31967 | 5.216 | 57.95 |
| 13 | BHAm | Algorithmus für schwarze Löcher M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 14 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 15 | RFO | Optimierung des Royal Flush (joo) | 0.83361 | 0.73742 | 0.34629 | 1.91733 | 0.89424 | 0.73824 | 0.24098 | 1.87346 | 0.63154 | 0.50292 | 0.16421 | 1.29867 | 5.089 | 56.55 |
| 16 | AOSm | Suche nach atomaren Orbitalen M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 17 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 18 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 19 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 20 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 21 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 22 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 23 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 24 | ABO | Optimierung des afrikanischen Büffels | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 25 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 26 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 27 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 28 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 29 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 30 | AEO | Algorithmus zur Optimierung auf der Grundlage künstlicher Ökosysteme | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 31 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 32 | BFO-GA | Optimierung der bakteriellen Futtersuche — ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 33 | SOA | einfacher Optimierungsalgorithmus | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 34 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 35 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 36 | ADAMm | adaptive Momentabschätzung M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 37 | ATAm | Algorithmus für künstliche Stämme M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 38 | ASHA | Algorithmus für künstliches Duschen | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 39 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 40 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 41 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 42 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 43 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 44 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 45 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| RW | Random Walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Zusammenfassung
Bei der Erforschung und Entwicklung neuer Optimierungsmethoden stehen wir oft vor der Notwendigkeit, ein Gleichgewicht zwischen Effizienz und Implementierungskomplexität zu finden. Die Arbeit am Algorithmus der Royal Flush Optimierung (RFO) hat interessante Ergebnisse erbracht, die Fragen über die Natur der Optimierung und Möglichkeiten zu ihrer Verbesserung aufwerfen.
Wenn wir die Leistung des Algorithmus beobachten, wenn er 57 % seines theoretischen Maximums erreicht, sehen wir ein interessantes Phänomen: Manchmal kann Vereinfachung wertvoller sein als Komplikation. RFO zeigt, dass der Verzicht auf eine komplexe binäre Kodierung zugunsten eines einfacheren sektorbasierten Ansatzes zu einer erheblichen Beschleunigung der Algorithmusleistung führen kann, während gleichzeitig eine ausreichend hohe Qualität der Lösungen beibehalten wird. Dies erinnert an die Situation beim Pokern, wo manchmal eine einfachere, aber schnellere Strategie effizienter sein kann als eine komplexere, die langwierige Berechnungen erfordert.
Wenn man über den Platz von RFO in der Familie der Optimierungsalgorithmen nachdenkt, kann man eine Analogie mit der Evolution von Fahrzeugen ziehen. So wie es einen Bedarf an spritsparenden Stadtautos neben leistungsstarken Sportwagen gibt, so gibt es auch in der Welt der Optimierungsalgorithmen Raum für Methoden, die sich auf unterschiedliche Prioritäten konzentrieren. RFO kann als eine „kostengünstige“ Variante des genetischen Algorithmus betrachtet werden, die einen vernünftigen Kompromiss zwischen Leistung und Ressourceneffizienz bietet.
Abschließend ist festzustellen, dass die Entwicklung der RFO interessante Perspektiven für die weitere Forschung eröffnet. Dies könnte nur der erste Schritt zur Entwicklung einer ganzen Familie von Algorithmen sein, die auf einem sektorbasierten Optimierungsansatz basieren. Die Einfachheit und Eleganz der Methode, kombiniert mit ihrer praktischen Wirksamkeit, kann als Inspirationsquelle für die Entwicklung neuer Algorithmen dienen, die ein Gleichgewicht zwischen Leistung und Recheneffizienz herstellen.
Es ist erwähnenswert, dass die Aufteilung in Sektoren virtuell erfolgt, ohne dass Speicher in Form von Arrays zugewiesen wird. Dieser RFO-Rahmen ist ein hervorragender Ausgangspunkt für die weitere Entwicklung verbesserter Versionen des Pokeralgorithmus.
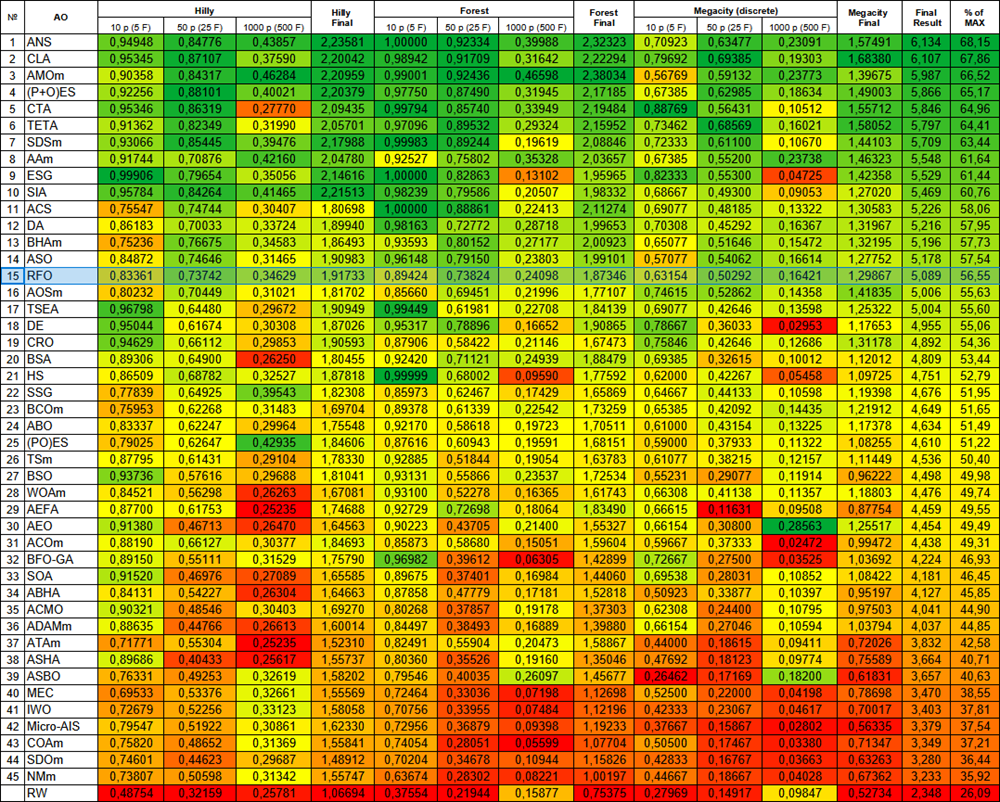
Abbildung 2. Farbabstufung der Algorithmen nach den entsprechenden Tests
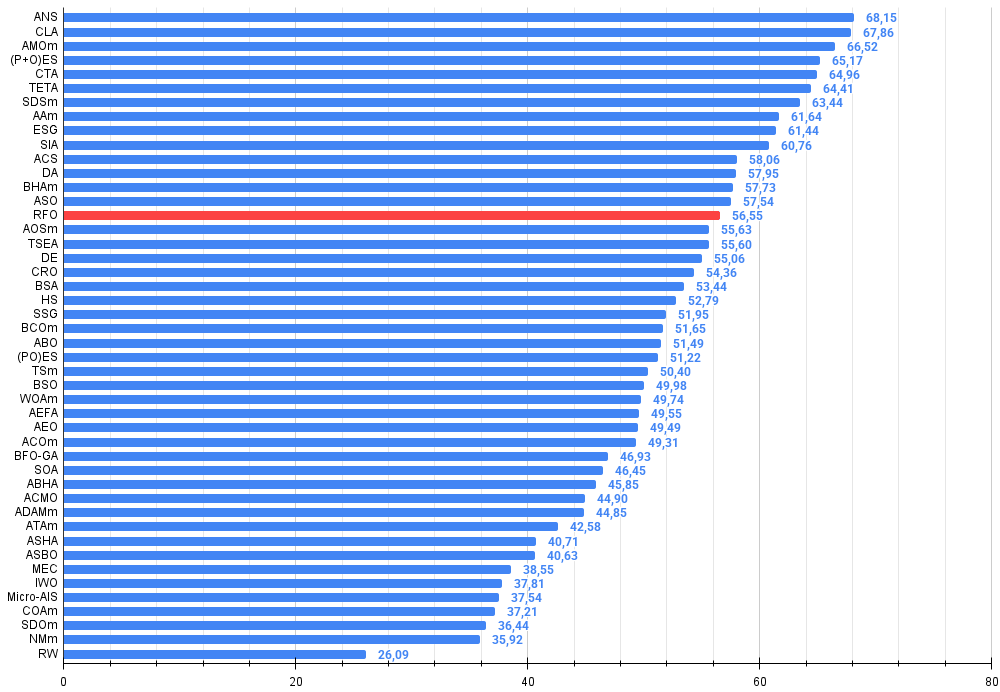
Abbildung 3. Histogramm der Algorithmus-Testergebnisse (Skala von 0 bis 100, je höher, desto besser, wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Bewertungstabelle)
RFO Pro und Kontra:
Vorteile:
- Es gibt nur wenige externe Parameter, nur zwei, wenn man die Populationsgröße nicht mitzählt.
- Einfache Umsetzung.
- Schnell.
- Ausgewogene, gute Leistungen bei Aufgaben verschiedener Dimensionen.
Nachteile:
- Durchschnittliche Konvergenzgenauigkeit.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Übergeordnete Klasse von Populationsoptimierungsalgorithmen |
| 2 | #C_AO_enum.mqh | Include | Enumeration der Algorithmen zur Populationsoptimierung |
| 3 | TestFunctions.mqh | Include | Bibliothek mit Testfunktionen |
| 4 | TestStandFunctions.mqh | Include | Bibliothek mit Funktionen für den Prüfstand |
| 5 | Utilities.mqh | Include | Bibliothek mit Hilfsfunktionen |
| 6 | CalculationTestResults.mqh | Include | Skript zur Berechnung der Ergebnisse in der Vergleichstabelle |
| 7 | Testing AOs.mq5 | Skript | Der einheitliche Prüfstand für alle Algorithmen zur Populationsoptimierung |
| 8 | Simple use of population optimization algorithms.mq5 | Skript | Ein einfaches Beispiel für die Verwendung von Algorithmen zur Populationsoptimierung ohne Visualisierung |
| 9 | Test_AO_RFO.mq5 | Skript | RFO-Teststand |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/17063
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Marktsimulation (Teil 05): Erstellen der Klasse C_Orders (II)
Marktsimulation (Teil 05): Erstellen der Klasse C_Orders (II)
 Neuronale Netze im Handel: Hierarchical Dual-Tower Transforme (letzter Teil)
Neuronale Netze im Handel: Hierarchical Dual-Tower Transforme (letzter Teil)
 Biologisches Neuron zur Vorhersage von Finanzzeitreihen
Biologisches Neuron zur Vorhersage von Finanzzeitreihen
 Von der Grundstufe bis zur Mittelstufe: Struct (I)
Von der Grundstufe bis zur Mittelstufe: Struct (I)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
In allen Fällen, in denen es darum geht, die beste Lösung unter vielen möglichen zu finden. Zum Beispiel, Berater mit Selbst-Optimierung.