Algoritmo de otimização Royal Flush — Royal Flush Optimization (RFO)
113
2
Conteúdo
Introdução
Existem diversas abordagens para resolver problemas de otimização, e entre elas os algoritmos genéticos ocupam um lugar especial, devido à sua capacidade de explorar com eficiência o espaço de busca por meio da simulação dos processos da evolução natural. O algoritmo genético clássico utiliza a codificação binária das soluções, o que exige a conversão de números reais para o formato binário. Essa conversão não apenas adiciona uma complexidade extra, como também torna o algoritmo significativamente mais pesado. No mundo atual, minimizar os custos computacionais é fundamental, e a produtividade de um método tende a ser diretamente proporcional à sua velocidade. Ao lidar com essa questão, ocorreu-me como seria possível preservar os operadores genéticos e, ao mesmo tempo, substituir os cálculos mais pesados da conversão de números reais por operações mais simples e menos exigentes em termos de recursos.
O algoritmo que proponho, "Royal Flush Optimization" (RFO), representa uma nova abordagem para resolver problemas de otimização, mantendo as principais vantagens dos algoritmos genéticos, mas utilizando uma forma mais direta de representar as soluções. A ideia central consiste em dividir cada coordenada do espaço de busca em setores, assim como uma combinação de pôquer é composta por cartas individuais de determinados postos. Em vez de trabalhar com cadeias de bits, o algoritmo opera com os postos das cartas (números dos setores), o que permite preservar de forma natural a topologia do espaço de busca.
Na minha opinião, as principais vantagens da abordagem proposta são tanto a simplicidade de implementação e a clareza intuitiva (trabalhar com "cartas" é mais visual do que com cadeias de bits), quanto a eliminação da necessidade de codificar e decodificar números reais, mantendo as propriedades combinatórias do algoritmo genético. No artigo apresentado, analisaremos em detalhes a implementação do algoritmo e as particularidades dos operadores de modificação das soluções.
A metáfora do pôquer não apenas dá nome ao algoritmo, como também descreve bem sua essência: assim como no pôquer o jogador busca montar a melhor combinação de cartas, o algoritmo combina setores de diferentes soluções, formando gradualmente "mãos" otimizadas. Como no pôquer, cada carta tem seu posto e naipe, no algoritmo cada setor tem seu valor e posição no espaço de busca. Além disso, assim como no jogo real, não importa apenas o valor de cada carta individualmente, mas também como elas interagem na combinação geral.
É importante destacar que essa abordagem pode ser considerada uma generalização das ideias da otimização discreta para o caso de espaços contínuos, o que abre perspectivas interessantes tanto para análise teórica quanto para aplicação prática. Assim como o pôquer combina elementos de acaso e estratégia, o RFO une a busca aleatória com a otimização orientada, tornando-o eficaz para problemas complexos e multidimensionais.
Implementação do algoritmo
O princípio de funcionamento do algoritmo Royal Flush Optimization (RFO) é baseado na ideia de representar o espaço de busca como setores discretos, da mesma forma que, no pôquer, as cartas têm determinados postos. No algoritmo genético clássico, os valores (parâmetros a serem otimizados) em todas as coordenadas são convertidos em código binário e reunidos em uma sequência que forma o cromossomo, o que exige um custo computacional adicional. No RFO, abandonamos essa abordagem em favor de uma representação mais simples e intuitiva.
Em vez da codificação binária, dividimos cada coordenada do espaço de busca em setores, atribuindo-lhes valores semelhantes aos das cartas de pôquer, de valete até ás (J, Q, K, A). O número de postos (setores) é definido por um parâmetro externo do algoritmo e pode ser qualquer valor inteiro. Assim, qualquer ponto do espaço de busca pode ser representado como uma combinação de cartas, onde cada carta corresponde a um determinado setor de uma coordenada. Essa abordagem não apenas simplifica os cálculos, como também preserva as propriedades combinatórias do algoritmo genético.
Durante a otimização, o algoritmo trabalha com "mãos", isto é, conjuntos de cartas que representam diferentes soluções. Os operadores de crossover e mutação são aplicados diretamente às "mãos" (conjuntos de cartas), onde cada mão é análoga a um cromossomo, o que permite explorar o espaço de busca sem a necessidade de conversões para código binário e vice-versa.
A ilustração abaixo (figura 1) demonstra visualmente esse princípio. Na ela mostrado um espaço de busca tridimensional com coordenadas X, Y e Z, onde cada coordenada é dividida em setores correspondentes aos postos das cartas. À direita, são apresentados exemplos de "mãos", quer dizer, diferentes combinações de cartas que o algoritmo forma no processo de busca pela solução ideal.
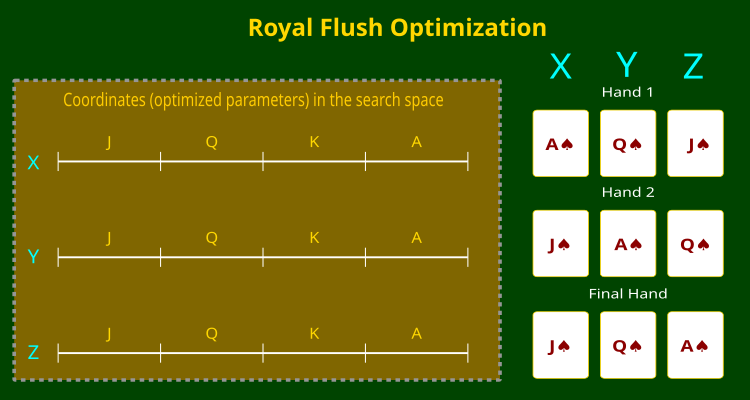
Figura 1. Algoritmo RFO e divisão das coordenadas em postos do baralho
Vamos agora à escrita do pseudocódigo do algoritmo Royal Flush Optimization (RFO):
- Definimos o número de jogadores na "mesa de pôquer" (tamanho da população)
- Determinamos o tamanho do "baralho" (quantidade de setores para cada dimensão)
- Estabelecemos a probabilidade de "blefe" (mutação)
- Criamos a "mão" inicial, isto é, geramos aleatoriamente os postos das cartas para cada coordenada
- Convertemos os postos em valores reais com deslocamento aleatório dentro do setor
- Para cada posição na mesa:
- Selecionamos um "oponente" usando seleção quadrática (as "mãos" mais fortes têm maior chance de serem escolhidas)
- Copiamos a "mão" atual (solução)
- Executamos uma troca de cartas em três pontos:
- Selecionamos aleatoriamente três pontos de "corte"
- Ordenamos os pontos de corte
- Escolhemos aleatoriamente o ponto inicial (0 ou 1)
- Trocamos cartas entre a mão atual e a mão do oponente
- Pode ocorrer "blefe" (probabilidade de mutação) — alteração aleatória do posto de uma carta com a probabilidade definida
- Convertamos os postos obtidos das cartas em valores reais para as coordenadas
- Calculamos o valor de cada "mão" (valor da função objetivo)
- Memorizamos a melhor combinação encontrada (melhor solução global)
- Unimos as mãos atuais com o baralho anterior
- Classificamos todas as "mãos" pelo seu valor
- As melhores "mãos" passam para a próxima geração
Vamos agora escrever o código do algoritmo. Escrevemos a estrutura "S_RFO_Agent", representando o objeto contendo a informação da "mão" no contexto do jogo.
Campos da estrutura:
- card [] — vetor para armazenar o valor real da carta.
- f — valor da mão (valor da função de adaptabilidade).
- cardRanks [] — vetor de inteiros representando os "postos das cartas" (números dos setores).
Método Init () — inicializa a estrutura, recebe como parâmetro "coords", que indica a quantidade de cartas na "mão".
//—————————————————————————————————————————————————————————————————————————————— // Структура для представления отдельной "руки" struct S_RFO_Agent { double card []; // карты double f; // значение функции пригодности ("ценность руки") int cardRanks []; // номера секторов ("ранги карт") void Init (int coords) { ArrayResize (cardRanks, coords); ArrayResize (card, coords); f = -DBL_MAX; // инициализация минимальным значением } }; //——————————————————————————————————————————————————————————————————————————————
A classe "C_AO_RFO" implementa o algoritmo e herda as propriedades e métodos da classe base "C_AO". Vamos analisá-la com mais detalhes.
Construtor C_AO_RFO () — define os valores das variáveis da classe, inicializando os parâmetros:- popSize — o tamanho da população (mesa de pôquer) é definido como 50.
- deckSize — o número de cartas no baralho (ou setores) é 1000.
- dealerBluff — a probabilidade de blefe (mutação) é definida em 3% (0,03).
- O vetor params — serve para armazenar os parâmetros, é redimensionado para tamanho 3 e preenchido com os valores correspondentes a "popSize", "deckSize" e "dealerBluff".
Método SetParams ()— extrai os valores do vetor "params" e os atribui às variáveis correspondentes da classe.
Método Init ()— é destinado à inicialização da classe com os parâmetros fornecidos, como os valores mínimo e máximo dos parâmetros a serem otimizados e seus respectivos passos.
Métodos Moving() e Revision() — servem para realizar operações relacionadas ao embaralhamento das cartas nas "mãos" e à revisão da melhor combinação entre elas.
Campos da classe:- deckSize — quantidade de setores por dimensão.
- dealerBluff — probabilidade de mutação.
- deck[], tempDeck[], hand[] — vetores do tipo "S_RFO_Agent", representando o baralho principal, um baralho temporário para ordenação e a mão atual (descendentes), respectivamente.
- cutPoints — quantidade de pontos de "corte" no conjunto de cartas das mãos, usados para combinar diferentes conjuntos de cartas.
- tempCuts[] e finalCuts[] — vetores para armazenar os índices temporários e finais dos pontos de "corte".
- Métodos utilizados em Evolution () — responsável pela execução da evolução principal das permutações de cartas, enquanto DealCard() realiza a conversão de um setor para seu valor real. O método "ShuffleRanks()" é responsável pela mutação dos postos (seleção aleatória entre os postos disponíveis).
//—————————————————————————————————————————————————————————————————————————————— class C_AO_RFO : public C_AO { public: C_AO_RFO () { ao_name = "RFO"; ao_desc = "Royal Flush Optimization"; ao_link = "https://www.mql5.com/ru/articles/17063"; popSize = 50; // размер "покерного стола" (популяции) deckSize = 1000; // количество "карт" в колоде (секторов) dealerBluff = 0.03; // вероятность "блефа" (мутации) ArrayResize (params, 3); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "deckSize"; params [1].val = deckSize; params [2].name = "dealerBluff"; params [2].val = dealerBluff; } void SetParams () { popSize = (int)params [0].val; deckSize = (int)params [1].val; dealerBluff = params [2].val; } bool Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0); // количество эпох void Moving (); void Revision (); //---------------------------------------------------------------------------- int deckSize; // количество секторов в измерении double dealerBluff; // вероятность мутации S_RFO_Agent deck []; // основная колода (популяция) S_RFO_Agent tempDeck []; // временная колода для сортировки S_RFO_Agent hand []; // текущая рука (потомки) private: //------------------------------------------------------------------- int cutPoints; // количество точек разрезания int tempCuts []; // временные индексы точек разрезания int finalCuts []; // финальные индексы с учетом начала и конца void Evolution (); // основной процесс эволюции double DealCard (int rank, int suit); // преобразование сектора в реальное значение void ShuffleRanks (int &ranks []); // мутация рангов }; //——————————————————————————————————————————————————————————————————————————————
O método "Init" é responsável por inicializar o objeto da classe "C_AO_RFO".
O método começa chamando uma função que executa a inicialização padrão dos parâmetros definidos, como os valores mínimo e máximo, além dos passos de variação. Caso essa inicialização não seja concluída com sucesso, o método encerra sua execução e retorna o valor "false". Após a inicialização bem-sucedida dos parâmetros, o método começa a preparar as estruturas de dados para armazenar informações sobre as "mãos" e os "baralhos". Isso inclui redimensionar os vetores destinados ao armazenamento das "mãos" e dos "baralhos", de modo que estejam alinhados com a quantidade da população.
Em seguida, o método inicializa cada elemento do vetor de "mãos" usando um método específico, que os configura considerando as coordenadas definidas. De maneira semelhante, os vetores do "baralho" e do "baralho temporário" também são preparados e inicializados. O método define a quantidade de pontos de corte necessária para o algoritmo de crossover. Neste caso, são definidos três pontos de corte (este foi o valor ideal encontrado após os testes realizados). Depois disso, os vetores para armazenar os pontos de corte temporários e finais são configurados. Por fim, o método retorna o valor "true", o que confirma que a inicialização foi concluída com sucesso.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_RFO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- // Инициализация структур для хранения "рук" и "колод" ArrayResize (hand, popSize); for (int i = 0; i < popSize; i++) hand [i].Init (coords); ArrayResize (deck, popSize * 2); ArrayResize (tempDeck, popSize * 2); for (int i = 0; i < popSize * 2; i++) { deck [i].Init (coords); tempDeck [i].Init (coords); } // Инициализация массивов для точек разрезания cutPoints = 3; // три точки разрезания для "трехкарточного" кроссовера ArrayResize (tempCuts, cutPoints); ArrayResize (finalCuts, cutPoints + 2); return true; } //——————————————————————————————————————————————————————————————————————————————
O método "Moving" é responsável pelo processo de "movimentação" ou atualização do estado da população dentro do algoritmo RFO.
Verificação de estado — o método começa verificando a condição que determina se a "distribuição" inicial das cartas já foi concluída. Caso contrário (revision == false), o método realiza a inicialização.
Inicialização da distribuição inicial — o método percorre todos os elementos da população, e para cada elemento (cada "mão") é criado um conjunto de cartas. O laço interno percorre a quantidade necessária de cartas e realiza as seguintes ações:
- Um posto de carta é escolhido aleatoriamente a partir do baralho.
- Em seguida, é chamado um método que realiza a distribuição da carta com base no posto gerado.
- A carta obtida é ajustada por meio de uma função que verifica se ela está dentro do intervalo especificado e realiza as modificações necessárias, de acordo com os parâmetros definidos.
- Por fim, o valor da carta obtida é gravado no vetor "a".
Atualização de estado — após concluir a inicialização, "revision" é definido como "true", indicando que a distribuição inicial foi concluída e não precisa mais ser repetida.
Chamada do método Evolution() — se a distribuição inicial já foi realizada, o método prossegue com a execução do processo evolutivo de embaralhamento e redistribuição das cartas para as "mãos".
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RFO::Moving () { //---------------------------------------------------------------------------- if (!revision) { // Инициализация начальной "раздачи" for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { hand [i].cardRanks [c] = u.RNDminusOne (deckSize); hand [i].card [c] = DealCard (hand [i].cardRanks [c], c); hand [i].card [c] = u.SeInDiSp (hand [i].card [c], rangeMin [c], rangeMax [c], rangeStep [c]); a [i].c [c] = hand [i].card [c]; } } revision = true; return; } //---------------------------------------------------------------------------- Evolution (); } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" é responsável por buscar a melhor "combinação" nas "mãos", avaliar sua adaptabilidade e atualizar o baralho geral.
Busca pela melhor combinação:
- O método começa inicializando a variável "bestHand", que armazenará o índice da melhor mão entre todos os membros da população.
- Em seguida, executa-se um laço que percorre todos os elementos da população (de 0 até popSize). Dentro do laço, o método compara o valor de adaptabilidade de cada mão "a" com o valor atual considerado o melhor, "fB".
- Se o valor de adaptabilidade da mão atual for maior que "fB", ocorre a atualização com o novo melhor valor, e a variável "bestHand" recebe o índice dessa mão.
Se uma melhor mão tiver sido encontrada, suas cartas são copiadas para o vetor "cB", o que permite manter o estado da melhor combinação (melhor solução global). O método então atualiza os valores de adaptabilidade de cada mão no vetor "hand", definindo-os iguais aos valores correspondentes no vetor "a". Isso é necessário para garantir que os dados sobre a adaptabilidade de cada mão estejam atualizados. Após a atualização dos valores de adaptabilidade, as mãos atuais do vetor "hand" são adicionadas ao vetor geral "deck", a partir da posição "popSize" (ou seja, ao final da população, na sua segunda metade).
Por fim, o método realiza a ordenação do vetor "deck", utilizando um vetor temporário separado "tempDeck" para organizar o baralho de acordo com o valor das combinações. Isso permite aumentar a probabilidade de seleção das combinações mais valiosas de cartas durante a seleção, antes de combiná-las.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RFO::Revision () { // Поиск лучшей "комбинации" int bestHand = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; bestHand = i; } } if (bestHand != -1) ArrayCopy (cB, a [bestHand].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- // Обновление значений пригодности for (int i = 0; i < popSize; i++) { hand [i].f = a [i].f; } // Добавление текущих рук в общую колоду for (int i = 0; i < popSize; i++) { deck [popSize + i] = hand [i]; } // Сортировка колоды по ценности комбинаций u.Sorting (deck, tempDeck, popSize * 2); } //——————————————————————————————————————————————————————————————————————————————
O método "Evolution" é responsável pela lógica principal do algoritmo, onde ocorre a troca de cartas entre as "mãos" dos jogadores na mesa, o "blefe" e a atualização dos valores reais das cartas.
O método inicia com um laço que percorre todos os elementos da população. Para cada elemento, são executadas as seguintes etapas:
Seleção do oponente:
- Para escolher o oponente, é gerado um número aleatório, que é então elevado ao quadrado para reforçar o efeito da seleção (a chance de escolha do oponente se relaciona com seu desempenho). Isso favorece a seleção de combinações de mãos superiores.
- O número aleatório é escalado usando a função "u.Scale", para obter o índice do oponente.
A mão atual (do vetor "deck") é copiada para o vetor "hand". O método então gera aleatoriamente os pontos de "corte" do conjunto de cartas nas mãos. Esses pontos definem quais cartas serão trocadas entre duas mãos. Os pontos de corte são ordenados e complementados com os limites; o primeiro limite é fixado em "0" e o último em "coords - 1". O método escolhe aleatoriamente o ponto inicial da troca de cartas usando "u.RNDbool()". Após a troca de cartas, há uma chance de ocorrer "blefe".
Conversão de postos em valores reais:- No laço final, os postos das cartas são convertidos em seus respectivos valores reais, usando o método "DealCard", e é feita uma verificação para garantir que os valores estejam dentro dos limites estabelecidos.
- Depois disso, os valores são atualizados no vetor "a", que contém as cartas finais.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RFO::Evolution () { // Для каждой позиции за столом for (int i = 0; i < popSize; i++) { // Выбор оппонента с учетом его рейтинга (квадрат вероятности для усиления селекции) double rnd = u.RNDprobab (); rnd *= rnd; int opponent = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1); // Копирование текущей руки hand [i] = deck [i]; // Определение точек разрезания для обмена картами for (int j = 0; j < cutPoints; j++) { tempCuts [j] = u.RNDminusOne (coords); } // Сортировка точек разрезания и добавление границ ArraySort (tempCuts); ArrayCopy (finalCuts, tempCuts, 1, 0, WHOLE_ARRAY); finalCuts [0] = 0; finalCuts [cutPoints + 1] = coords - 1; // Случайный выбор начальной точки для обмена int startPoint = u.RNDbool (); // Обмен картами между руками for (int j = startPoint; j < cutPoints + 2; j += 2) { if (j < cutPoints + 1) { for (int len = finalCuts [j]; len < finalCuts [j + 1]; len++) hand [i].cardRanks [len] = deck [opponent].cardRanks [len]; } } // Возможность "блефа" (мутации) ShuffleRanks (hand [i].cardRanks); // Преобразование рангов в реальные значения for (int c = 0; c < coords; c++) { hand [i].card [c] = DealCard (hand [i].cardRanks [c], c); hand [i].card [c] = u.SeInDiSp (hand [i].card [c], rangeMin [c], rangeMax [c], rangeStep [c]); a [i].c [c] = hand [i].card [c]; } } } //——————————————————————————————————————————————————————————————————————————————
O método "DealCard" é um elemento-chave do algoritmo Royal Flush Optimization, encarregado de converter os setores discretos do espaço de busca em valores contínuos das coordenadas. O método recebe dois parâmetros: "rank" — o posto da carta, e "suit" — o índice da coordenada (naipe).
O processo de conversão ocorre em duas etapas. Primeiro, calcula-se o tamanho de um setor (suitRange), dividindo-se toda a faixa de busca pela quantidade de setores. Em seguida, é gerado um valor específico dentro do setor selecionado. O deslocamento aleatório "u.RNDprobab()" garante a exploração uniforme do espaço dentro de cada setor, enquanto o "rank" define a posição base no espaço de busca.
Essa abordagem permite combinar a representação discreta das soluções por meio de setores com o espaço de busca contínuo, proporcionando um equilíbrio entre a busca global e a busca local.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_RFO::DealCard (int rank, int suit) { // Преобразование ранга карты в реальное значение с случайным смещением внутри сектора double suitRange = (rangeMax [suit] - rangeMin [suit]) / deckSize; return rangeMin [suit] + (u.RNDprobab () + rank) * suitRange; } //——————————————————————————————————————————————————————————————————————————————
O método "ShuffleRanks" implementa o mecanismo de mutação no algoritmo Royal Flush Optimization, funcionando como um "blefe" ao lidar com os postos das cartas. Recebendo um vetor de postos por referência, o método percorre cada coordenada e, com a probabilidade definida em "dealerBluff", substitui o posto atual por um valor aleatório dentro do intervalo permitido de postos do baralho. Esse processo pode ser comparado a uma situação no pôquer em que o jogador inesperadamente troca uma carta da mão, introduzindo um elemento de imprevisibilidade no jogo. Esse mecanismo de mutação tem como objetivo ajudar o algoritmo a evitar ficar preso em ótimos locais e manter a diversidade de soluções possíveis durante o processo de otimização.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RFO::ShuffleRanks (int &ranks []) { // Перетасовка рангов (мутация) for (int i = 0; i < coords; i++) { if (u.RNDprobab () < dealerBluff) ranks [i] = (int)MathRand () % deckSize; } } //——————————————————————————————————————————————————————————————————————————————
Resultados dos testes
Impressão dos resultados dos testes do algoritmo RFO:
RFO|Royal Flush Optimization|50.0|1000.0|0.03|
=============================
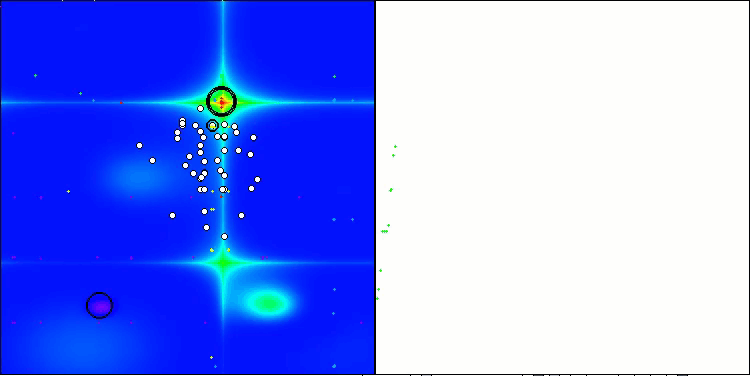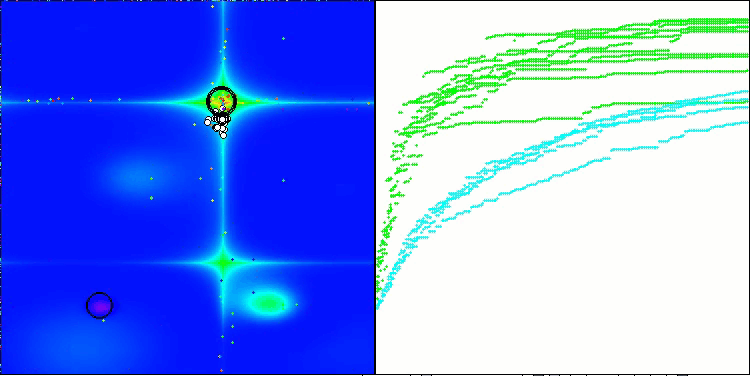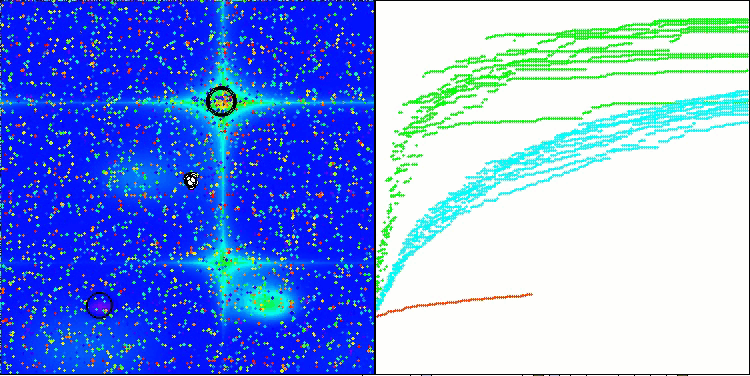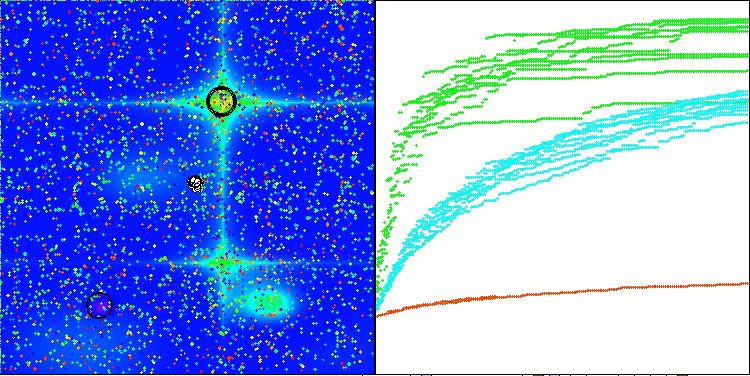
5 Hilly's; Func runs: 10000; result: 0.8336125672709654
25 Hilly's; Func runs: 10000; result: 0.7374210861383783
500 Hilly's; Func runs: 10000; result: 0.34629436610445113
=============================
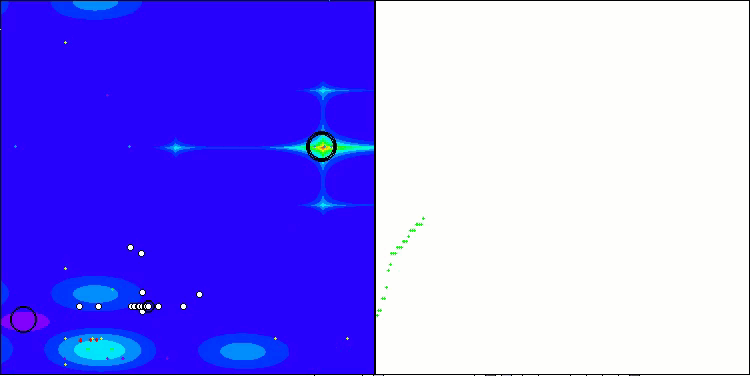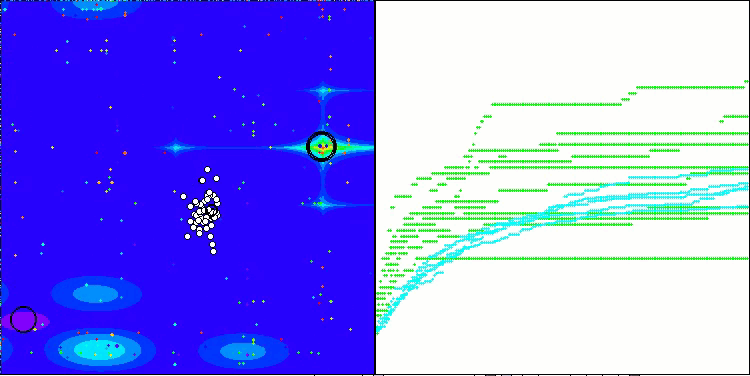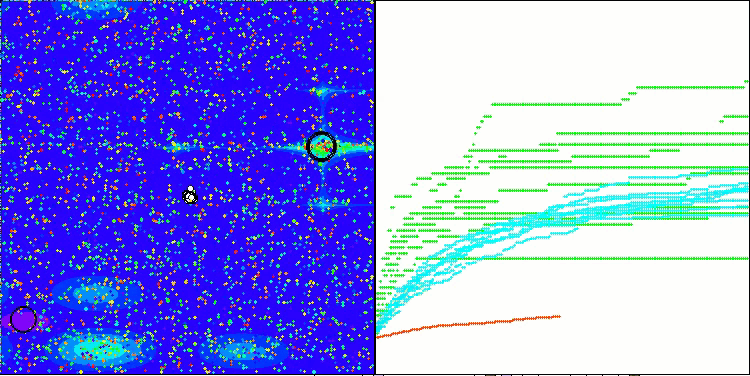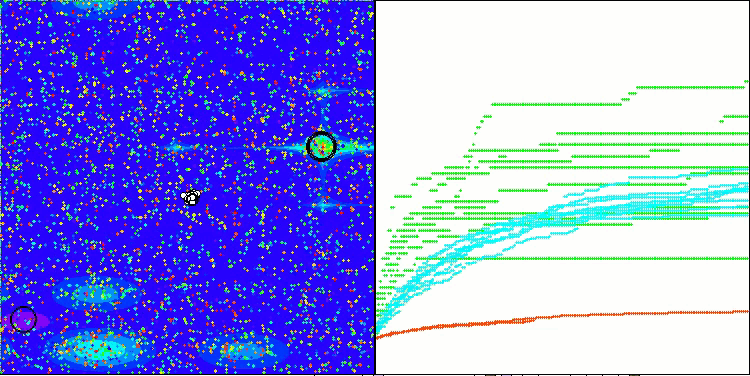
5 Forest's; Func runs: 10000; result: 0.8942431024645086
25 Forest's; Func runs: 10000; result: 0.7382367793268382
500 Forest's; Func runs: 10000; result: 0.24097956383750824
=============================
5 Megacity's; Func runs: 10000; result: 0.6315384615384616
25 Megacity's; Func runs: 10000; result: 0.5029230769230771
500 Megacity's; Func runs: 10000; result: 0.16420769230769366
=============================
All score: 5.08946 (56.55%)
Avaliação final em 56,55% — um resultado bastante respeitável. Na visualização, o algoritmo não apresenta nenhum comportamento específico, parecendo um passeio caótico de pontos individuais.
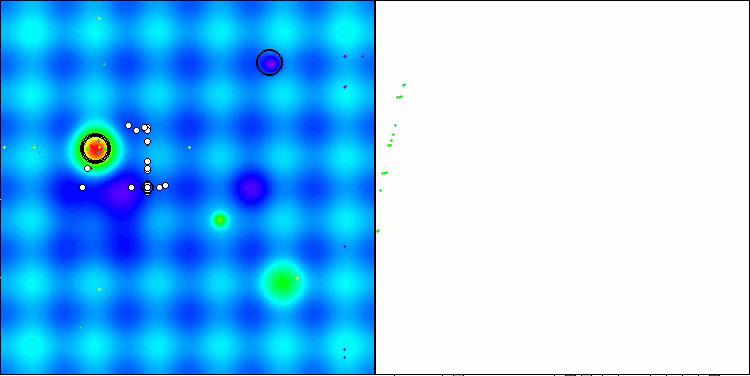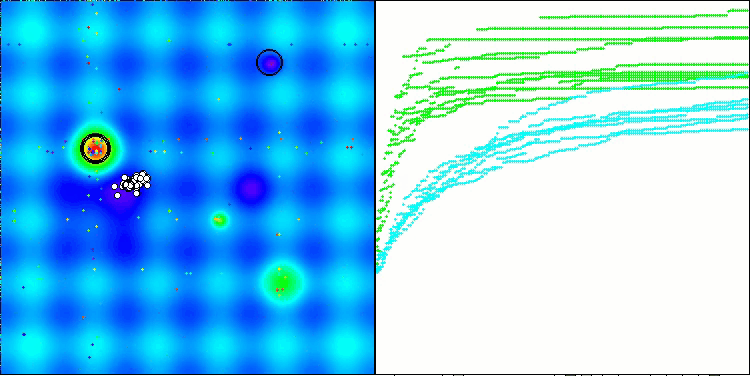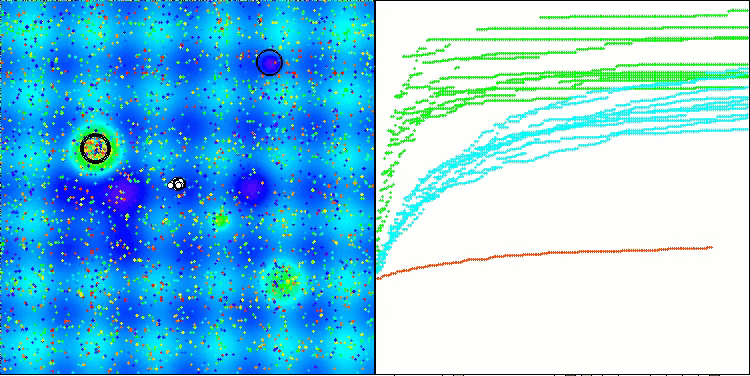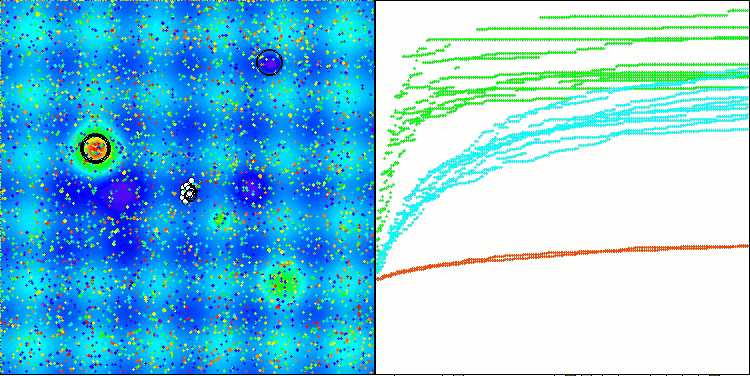
RFO na função de teste Hilly
RFO na função de teste Forest
RFO na função de teste Megacity
Com base nos testes realizados, o algoritmo de otimização RFO ocupa a 15ª posição, somando-se à lista dos algoritmos mais eficazes já conhecidos.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 9 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 10 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 11 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 12 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 13 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 14 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 15 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 16 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 17 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 18 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 19 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 20 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 21 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 22 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 23 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 24 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 25 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 26 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 27 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 28 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 29 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 30 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 31 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 32 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 33 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 34 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 35 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 36 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 37 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 38 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 39 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 40 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 41 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 42 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 43 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 44 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 45 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Considerações finais
Durante a pesquisa e o desenvolvimento de novos métodos de otimização, frequentemente nos deparamos com a necessidade de encontrar um equilíbrio entre eficiência e complexidade de implementação. O trabalho no algoritmo Royal Flush Optimization (RFO) levou a resultados interessantes que nos fazem refletir sobre a natureza dos processos de otimização e as formas de aprimorá-los.
Observando o funcionamento do algoritmo, que alcança 57% da performance teoricamente máxima possível, vemos um fenômeno curioso: às vezes, simplificar pode ser mais valioso do que complicar. O RFO mostra que abandonar a codificação binária complexa em favor de uma abordagem setorial mais direta pode resultar em uma aceleração significativa do algoritmo, mantendo uma qualidade de solução suficientemente alta. Isso lembra uma situação no pôquer, em que uma estratégia mais simples e rápida pode ser mais eficaz do que outra complexa e cheia de cálculos.
Ao refletir sobre o lugar do RFO no universo dos algoritmos de otimização, pode-se fazer uma analogia com a evolução dos meios de transporte. Assim como, além dos carros esportivos potentes, há uma necessidade por modelos urbanos econômicos, também no mundo dos algoritmos de otimização há espaço para métodos com diferentes prioridades. O RFO pode ser visto como uma versão "econômica" do algoritmo genético, oferecendo um compromisso razoável entre desempenho e eficiência no uso de recursos.
Para concluir, vale destacar que o desenvolvimento do RFO abre perspectivas interessantes para pesquisas futuras. É possível que este seja apenas o primeiro passo na criação de toda uma família de algoritmos baseados na abordagem setorial para otimização. A simplicidade e elegância do método, aliadas à sua eficácia prática, podem servir de inspiração para o surgimento de novos algoritmos que equilibrem desempenho com eficiência computacional.
É importante mencionar que a divisão em setores ocorre de forma virtual, sem a alocação de memória específica para isso na forma de vetores. Essa base do RFO é um excelente ponto de partida para o desenvolvimento de versões aprimoradas do algoritmo de pôquer.
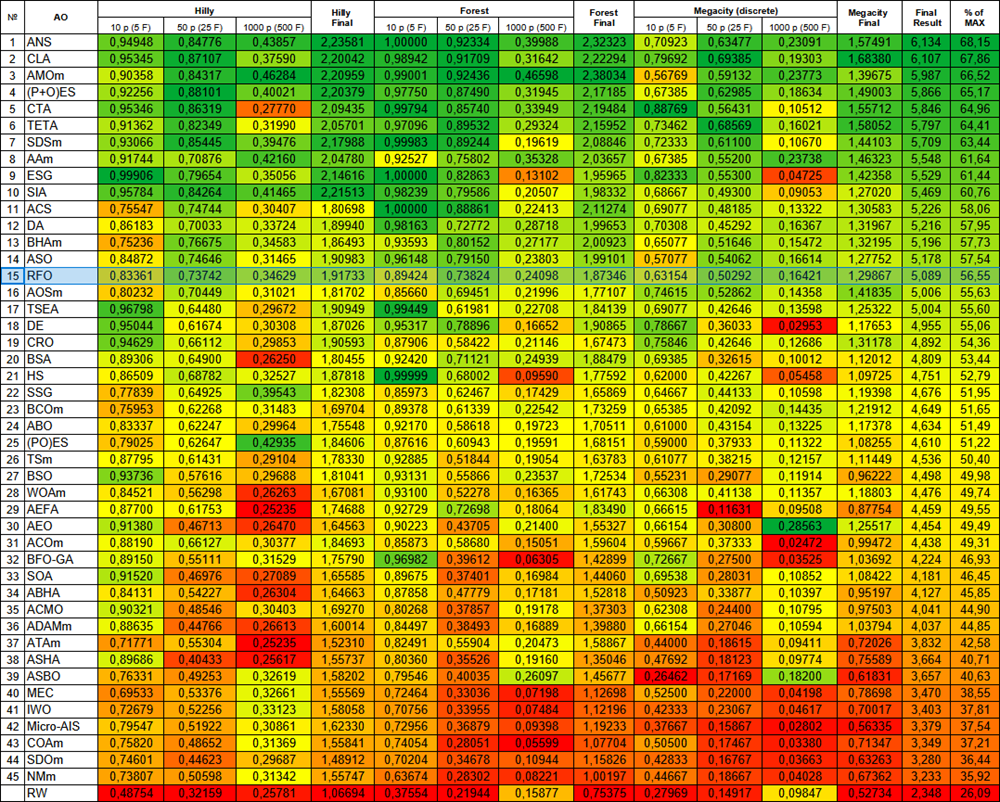
Figura 2. Graduação de cores dos algoritmos nos respectivos testes
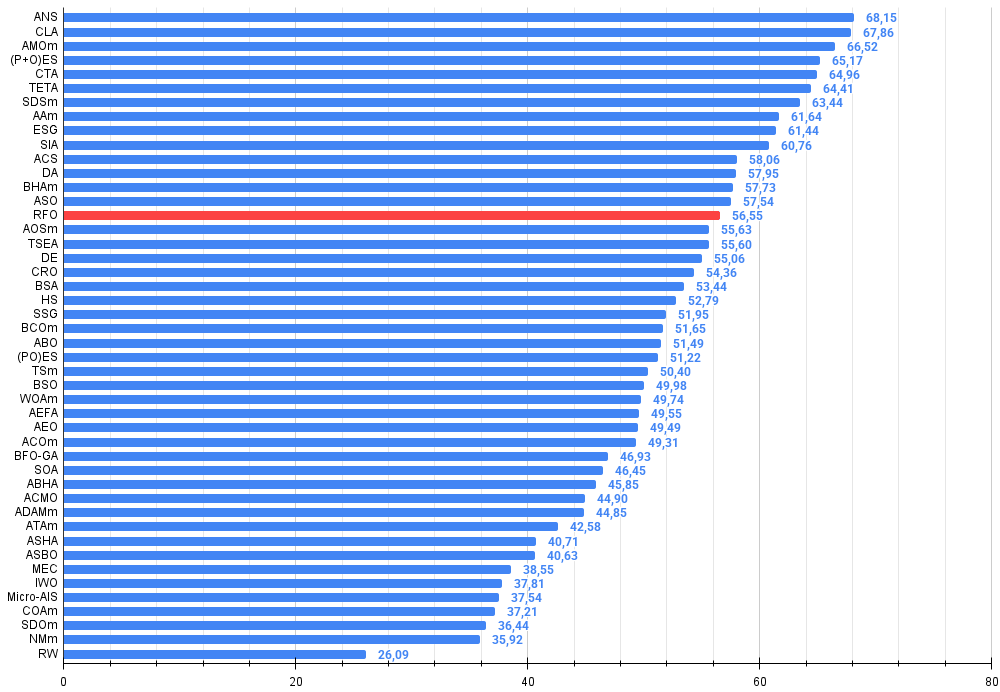
Figura 3. Histograma dos resultados dos testes dos algoritmos (na escala de 0 a 100, quanto maior, melhor, onde 100 é o resultado teórico máximo possível, no arquivo há um script para calcular a tabela de classificação)
Vantagens e desvantagens do algoritmo RFO:
Vantagens:
- Poucos parâmetros externos, apenas dois, sem contar o tamanho da população.
- Implementação simples.
- Rápido.
- Resultados equilibrados e satisfatórios em tarefas com diferentes dimensionalidades.
Desvantagens:
- Precisão média de convergência.
Um arquivo compactado com as versões atualizadas dos códigos dos algoritmos está anexado ao artigo. O autor não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar suas capacidades de busca. As conclusões e interpretações apresentadas nos artigos são baseadas nos resultados dos experimentos realizados.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | C_AO.mqh | Arquivo incluído | Classe pai dos algoritmos populacionais de otimização |
| 2 | C_AO_enum.mqh | Arquivo incluído | Enumeração dos algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo incluído | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo incluído | Biblioteca de funções da plataforma de testes |
| 5 | Utilities.mqh | Arquivo incluído | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo incluído | Script para cálculo dos resultados na tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Plataforma de testes unificada para todos os algoritmos populacionais de otimização |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Exemplo simples de uso dos algoritmos populacionais de otimização sem visualização |
| 9 | Test_AO_RFO.mq5 | Script | Plataforma de testes para o RFO |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/17063
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
Redes neurais em trading: Aprendizado multitarefa baseado no modelo ResNeXt
Redes neurais em trading: Transformador hierárquico com duas torres (Conclusão)
Analisando o código binário dos preços no mercado (Parte II): Convertendo para BIP39 e criando um modelo GPT
Redes neurais em trading: Transformador hierárquico de duas torres (Hidformer)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Em todos os casos em que é necessário encontrar a melhor solução entre muitas possíveis. Por exemplo, consultores com auto-otimização.