皇冠同花顺优化（RFO）

MetaTrader 5 — 交易系统 | 12 一月 2026, 09:43

109

Andrey Dik

概述

有多种方式可解决优化问题，其中遗传算法占据了特殊的地位，因其能够模拟自然演化过程，从而有效探索搜索空间。传统的遗传算法使用解的二进制编码，这需要将真实数字转换为二进制格式。这种变换不仅增加了复杂度，也显著拉低了算法的权重。在现代社会，最小化计算成本扮演着决定性角色，方法的生产率往往直接与其速度成正比。而为了解决这个问题，我迸发出一个思路，如何在保留遗传算子的同时，用更简单、更低能耗的运算替代最难的真实数字转换计算。

我的算法，皇冠同花顺优化（RFO），是一种新的优化问题解决方法，保留了遗传算法的主要优势，但采用了解的更直接表述方式。关键思路是将搜索空间的每个坐标划分为扇区，类似于一手扑克牌是由确定排位的单张卡牌组成。取代比特位字符串操作，算法管理排位映射（扇区编号），这令搜索空间的拓扑结构得以自然预留。

以我观点，该方式的主要优点在于实现简单、且直观明了（处置“映射”更直观，远超比特位字符串），并且无需真实数字编码和解码，同时保留遗传算法的组合属性。在本文中，我们将详细探讨该算法的实现，以及决策修改算子的特性。

扑克牌比喻不仅赋予了算法的名字，也很好地描述了其本质：正如在牌局中玩家努力收集最佳牌面组合，算法将不同解的扇区结合起来，逐渐形成最优的“牌面”。正如扑克牌中每张卡牌都有自己的排位和花色，算法中每个扇区也有其数值和搜索空间中的位置。在这种情况下，正如真实游戏一样，不仅单张卡牌的价值重要，还要看它们在整体组合中的互动。

值得注意的是，该方式能视作把离散优化思路推广到连续空间的情况，这为理论分析和实际应用开创出有趣的前景。正如扑克牌结合了机遇和策略元素，RFO 将随机搜索与有向优化结合起来，令其有效应对复杂的多变量问题。

算法的实现

皇冠同花顺优化（RFO）算法基于将搜索空间表示为离散扇区的理念，类似于扑克牌中如何排位。在传统的遗传算法中，所有坐标的数值（优化的参数）都被转换为二进制代码，并折叠成类似染色体的序列，这需要额外的计算成本。在 RFO 中，我们放弃了该方式，转而采用更简单、更直观的表述。

取代二进制编码，我们而是将搜索空间的每个坐标拆分为扇区，赋予类似扑克牌的数值 — 从 J 到 A（J、Q、K、A）。排位的数量（扇区数）在算法的外部参数中指定，可以是任意整数值。因此，搜索空间中的任意点都能表示为一组映射，每个映射根据坐标对应一个特定的扇区。该方式不仅简化了计算，还保留了遗传算法的组合属性。

在优化期间，算法遵照“牌型”工作 — 代表不同解的一组卡牌。交叉和突变算子直接应用于“牌型”（一组卡牌），每副牌型模拟一条染色体，允许探索搜索空间，而无需二进制来回转换。

下面的示意图（图例 1）清晰展示了这一原理。它展示了一个三维搜索空间，坐标为 X、Y 和 Z，每个坐标被划分到与排位映射对应的扇区。右侧是“牌型”的示例 — 算法在寻找最优解时形成的各种卡牌组合。

RFO

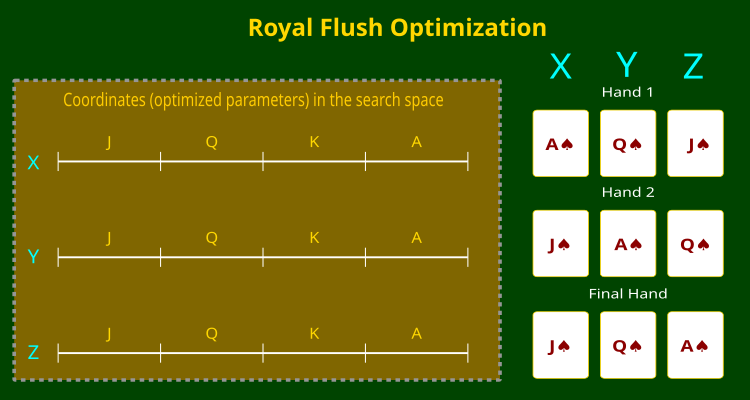
图例 1. RFO 算法及坐标分区到卡牌底牌排位

我们转至编写皇冠同花顺优化（RFO）算法的伪代码：

初始化：

设定“牌桌”上的玩家人数（种群规模）
判定“底牌”的大小（每个维度的扇区数量）
设定“叫注”（突变）的概率
创建初始“牌型” — 随机生成每个坐标的卡牌排位
将排位变换为扇区内随机偏移的真实数值

主游戏环路：

对于牌桌上的每个位置：
- 使用二次选择法选择“对手”（较强的“牌型”拥有更高的选中机会）
- 复制当前的“牌型”（解）
- 执行三次换牌：
  - 随机选择三个“切割”点
  - 排序切割点
  - 随机选择一个起始点（0 或 1）
  - 当前牌型与对手牌型互换
  - “叫注”（变异概率）是可能的 — 卡牌排位按给定概率随机变化
- 将获得的映射排位转换为真实坐标值

排位与更新：

计算每副“牌型”（目标函数的值）的数值
记住发现的最佳组合（全局最佳解）
将当前牌型与之前的底牌合并
按它们的分值排序所有“牌型”
最好的“牌型”会传给下一代

达到停止准则时算法终止

接下来是编写算法代码。编写 S_RFO_Agent 结构，代表游戏过程中包含“牌型”信息的对象。

结构字段：

card [] — 存储卡牌真实数值的数组。
f — 牌型值（适应度函数值）。
cardRanks [] — 表示“卡牌排位”（扇区编号）的整数数组。

init ()方法初始化结构，取单个“坐标”参数，指定“牌型”中的卡牌数量。

//——————————————————————————————————————————————————————————————————————————————
// Structure for representing a single "hand"
struct S_RFO_Agent
{
    double card [];       // cards
    double f;             // value of the fitness function ("hand value")
    int    cardRanks [];  // sector numbers ("map ranks") 

    void Init (int coords)
    {
      ArrayResize (cardRanks, coords);
      ArrayResize (card,      coords);
      f = -DBL_MAX;       // initialization with minimum value
    }
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_RFO 类实现该算法，并继承来自 C_AO 基类的属性和方法。我们来更详细地考察。

C_AO_RFO () 构造器为类变量设置数值，初始化参数：

popSize — 种群规模（扑克牌桌）设置为 50。
deckSize — 底牌（或扇区）中的卡牌数量 - 1000。
dealerBluff — 叫注（突变）概率设定为 3%（0.03）。
'params' 数组存储参数，大小调整为 3，并填充对应于 popSize、deckSize 和 dealerBluff 的数值。

SetParams () 方法 — 该方法从 “params” 数组中提取数值，并将其分配给对应的类变量。

init () 方法设计用来按照传递的参数初始化类，譬如待优化参数的最小值和最大值、及其步长。

Moving() 和 Revision() 方法执行与洗牌和修改最佳组合相关的操作。

类字段：

deckSize — 维度中的扇区数量。
dealerBluff — 突变概率。
deck [], tempDeck [], hand [] — S_RFO_Agent 类型的数组，分别代表主要底牌、排序用的临时底牌、及当前牌型（后代）。

私密类成员：

cutPoints — 牌型中用来组合卡牌组变体的“切”点数量。
tempCuts [] 和 finalCuts [] — 存储临时和最终“切”点索引的数组。
所用的方法包括 Evolution() — 负责执行卡牌排列的基本演化，以及 DealCard() — 负责将扇区转换为其真实数值。ShuffleRanks () 方法负责突变排位（从可用排排位中随机选择）。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_RFO : public C_AO
{
  public:
  C_AO_RFO ()
  {
    ao_name = "RFO";
    ao_desc = "Royal Flush Optimization";
    ao_link = "https://www.mql5.com/en/articles/17063";

    popSize      = 50;      // "poker table" (population) size
    deckSize     = 1000;    // number of "cards" in the deck (sectors)
    dealerBluff  = 0.03;    // "bluff" (mutation) probability

    ArrayResize (params, 3);

    params [0].name = "popSize";      params [0].val = popSize;
    params [1].name = "deckSize";     params [1].val = deckSize;
    params [2].name = "dealerBluff";  params [2].val = dealerBluff;
  }

  void SetParams ()
  {
    popSize     = (int)params [0].val;
    deckSize    = (int)params [1].val;
    dealerBluff = params      [2].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum values
             const double &rangeMaxP  [],  // maximum values
             const double &rangeStepP [],  // step change
             const int     epochsP = 0);   // number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    deckSize;         // number of sectors in the dimension
  double dealerBluff;      // mutation probability

  S_RFO_Agent deck [];     // main deck (population)
  S_RFO_Agent tempDeck []; // temporary deck for sorting
  S_RFO_Agent hand [];     // current hand (descendants)

  private: //-------------------------------------------------------------------
  int cutPoints;           // number of cutting points
  int tempCuts  [];        // temporary indices of cutting points
  int finalCuts [];        // final indices taking the beginning and end into account

  void   Evolution ();     // main process of evolution
  double DealCard (int rank, int suit);  // convert sector to real value
  void   ShuffleRanks (int &ranks []);   // rank mutation
};
//——————————————————————————————————————————————————————————————————————————————

Init 方法旨在初始化 C_AO_RFO 类对象。

该方法首先调用一个函数，按给定参数执行标准初始化，如最小值和最大值、以及参数变化步长。如果初始化失败，方法终止，并返回 “false”。初始化参数成功之后，方法继续准备存储“牌型”和“底牌”信息的数据结构。这涉及调整存储“牌型”和“底牌”的数组大小，以便匹配种群规模。

该方法随后使用一种特殊方法初始化“牌型”数组中的每个元素，其基于指定的坐标进行配置。类似地，还会准备和初始化 “deck” 和 “temp deck” 数组。该方法设定交叉算法所需的切点数量。在该情况下，设定三个切点（这是实验后找到的最佳值）。然后，设置数组来存储临时和最终的切点。在结尾处，方法返回 “true” 值，确认初始化已成功完成。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_RFO::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  // Initialize structures for storing "hands" and "decks"
  ArrayResize (hand, popSize);
  for (int i = 0; i < popSize; i++) hand [i].Init (coords);

  ArrayResize (deck,     popSize * 2);
  ArrayResize (tempDeck, popSize * 2);
  for (int i = 0; i < popSize * 2; i++)
  {
    deck     [i].Init (coords);
    tempDeck [i].Init (coords);
  }

  // Initialize arrays for cutting points
  cutPoints = 3;  // three cutting points for a "three-card" crossover
  ArrayResize (tempCuts,  cutPoints);
  ArrayResize (finalCuts, cutPoints + 2);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Moving 方法负责在 RFO 算法中“移动”、或更新种群状态的过程。

检查状态 — 方法首先执行条件检查，判定初始化“发牌”是否完成。如果情况并非如此（revision == false），该方法会执行初始化。

初始化初始分布 — 方法迭代遍历种群的所有元素，为种群的每个元素（每副"牌型"）创建一组卡牌。内环路会迭代遍历每个所需数量的卡牌，并执行以下动作：

从底牌随机抽取一张卡牌排位。
然后调用该方法，基于生成的排位发牌。
生成的映射由一个函数进行调整，其检查是否在给定范围内，并根据指定参数进行必要改变。
最后，接收到的映射值被设置到 “a” 数组。

更新状态 — 初始化完成后，“revision” 被设置为 “true”，表示初始分布已完成，无需再次初始化。

调用 Evolution () 方法 — 如果初始发牌已经完成，该方法将继续执行牌型的洗牌和发牌的演化过程。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_RFO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    // Initialize the initial "distribution"
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        hand [i].cardRanks [c] = u.RNDminusOne (deckSize);
        hand [i].card      [c] = DealCard (hand [i].cardRanks [c], c);
        hand [i].card      [c] = u.SeInDiSp (hand [i].card [c], rangeMin [c], rangeMax [c], rangeStep [c]);

        a [i].c [c] = hand [i].card [c];
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  Evolution ();
}
//——————————————————————————————————————————————————————————————————————————————

Revision 方法负责寻找“牌型”的最佳“组合”，评估其适用性，并更新整体底牌。

寻找最佳组合：

该方法首先初始化 bestHand 变量，其存储所有种群成员的最佳牌型索引。
然后执行一个环路，迭代遍历种群中的所有元素（从 0 到 popSize）。在环路内，该方法取每副 “a” 牌型的适应度值，并与当前最佳 fB 值比较。
如果当前牌型的适应度值大于 fB，则会更新最佳值，并将该“牌型”的索引赋予 bestHand 变量。

如果找到最佳牌型，其卡牌会复制到 cB 数组之中，这样最佳组合状态（全局最佳解）就得以保存。该方法随后将 “hand” 数组中每副牌型的适应度值更新为等于 “a” 数组对应数值。这是确保每副牌型的适用性数据都会如期最新的必要步骤。更新适应度值之后，“hand” 数组中的当前牌型会从 popSize 位置（即种群的末端）开始添加普通 “deck” 数组。

最后，该方法用一个独立的 tempDeck 临时数组，为 “deck” 数组进行排序，以便按组合值布置底牌。在据后续组合选择期间，选择有价值的卡牌组合来提升概率，这令我们能从中受益。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_RFO::Revision ()
{
  // Search for the best "combination"
  int bestHand = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      bestHand = i;
    }
  }

  if (bestHand != -1) ArrayCopy (cB, a [bestHand].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  // Update fitness values
  for (int i = 0; i < popSize; i++)
  {
    hand [i].f = a [i].f;
  }

  // Add current hands to the general deck
  for (int i = 0; i < popSize; i++)
  {
    deck [popSize + i] = hand [i];
  }

  // Sort the deck by combination value
  u.Sorting (deck, tempDeck, popSize * 2);
}
//——————————————————————————————————————————————————————————————————————————————

Evolution 方法负责该算法的主要逻辑，即在牌桌上玩家的“牌型”之间换牌，“叫注”取位，并更新卡牌的真实数值。

该方法从一个环路开始，迭代遍历种群中的所有元素。执行以下动作：

选择一名对手：

选择对手时，会生成一个随机数字，然后将其平方，以提升选择范围（选中对手的概率与其排名相交）。这令您更有可能选择最佳的牌型组合。
随机数由 u.Scale 函数进行缩放，以获得对手的索引。

当前的牌型（来自 “deck” 数组）会被复制到 “hand” 数组当中。该方法为牌型生成随机的“切”点。这些切点判定了两副牌型之间哪些卡牌要交换。切点会被排序，并为它们添加边界；第一个边界设置为 “0”，最后一个边界设置为 “coords - 1”。该方法选择一个随机起点，调用 u.RNDbool () 开始换牌。换牌之后，有机会“叫注”。

将排位转换为真实数值：

在最后的环路中，调用 DealCard 方法将卡牌排位转换为其数值，并检查是否遵从既定界限。
之后，包含最终卡牌数值的 “a” 数组会被更新。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_RFO::Evolution ()
{
  // For each position at the table
  for (int i = 0; i < popSize; i++)
  {
    // Select an opponent based on their rating (probability squared to enhance selection)
    double rnd = u.RNDprobab ();
    rnd *= rnd;
    int opponent = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1);

    // Copy the current hand
    hand [i] = deck [i];

    // Define cutting points for card exchange
    for (int j = 0; j < cutPoints; j++)
    {
      tempCuts [j] = u.RNDminusOne (coords);
    }

    // Sort cutting points and add borders
    ArraySort (tempCuts);
    ArrayCopy (finalCuts, tempCuts, 1, 0, WHOLE_ARRAY);
    finalCuts [0] = 0;
    finalCuts [cutPoints + 1] = coords - 1;

    // Random selection of a starting point for exchange
    int startPoint = u.RNDbool ();

    // Exchange cards between hands
    for (int j = startPoint; j < cutPoints + 2; j += 2)
    {
      if (j < cutPoints + 1)
      {
        for (int len = finalCuts [j]; len < finalCuts [j + 1]; len++) hand [i].cardRanks [len] = deck [opponent].cardRanks [len];
      }
    }

    // Possibility of "bluffing" (mutation)
    ShuffleRanks (hand [i].cardRanks);

    // Convert ranks to real values
    for (int c = 0; c < coords; c++)
    {
      hand [i].card [c] = DealCard (hand [i].cardRanks [c], c);
      hand [i].card [c] = u.SeInDiSp (hand [i].card [c], rangeMin [c], rangeMax [c], rangeStep [c]);

      a [i].c [c] = hand [i].card [c];
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

DealCard 方法是皇冠同花顺优化算法的关键元素，将搜索空间中的离散扇区变换为连续坐标值。该方法取两个参数作为输入：“rank” — 卡牌的排位，及 “suit” — 坐标索引（花色）。

变换由两个阶段组成。首先，计算一个扇区（suitRange）的大小，即整个搜索范围除以扇区数量。然后在所选扇区内生成特定值。u.RNDprobab() 随机偏移量确保每个扇区内空间的均匀探索，“rank” 定义搜索空间中的基准位置。

该方式能够把解的离散表示、与连续搜索空间的扇区结合，提供全局与局部搜索之间的平衡。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_RFO::DealCard (int rank, int suit)
{
  // Convert the map rank to a real value with a random offset within the sector
  double suitRange = (rangeMax [suit] - rangeMin [suit]) / deckSize;
  return rangeMin [suit] + (u.RNDprobab () + rank) * suitRange;
}
//——————————————————————————————————————————————————————————————————————————————

ShuffleRanks方法实现了皇冠同花顺优化算法中的突变机制，权当处置卡牌排位时的“叫注”。给定一个排位数组的引用，方法迭代遍历每个坐标，并按 dealerBluff 概率，将当前排位替换为底牌中有效排位范围中的随机值。这一过程能够比作扑克牌中玩家意外更换了牌型中的卡牌，这为游戏引入了不可预测性。这种突变机制旨在帮助算法避免陷入局部最优，并在优化期间维持可能解的多样性。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_RFO::ShuffleRanks (int &ranks [])
{
  // Rank shuffle (mutation)
  for (int i = 0; i < coords; i++)
  {
    if (u.RNDprobab () < dealerBluff) ranks [i] = (int)MathRand () % deckSize;
  }
}
//——————————————————————————————————————————————————————————————————————————————

测试结果

RFO 算法测试结果：

RFO|Royal Flush Optimization|50.0|1000.0|0.03|
=============================
5 Hilly's; Func runs: 10000; result: 0.8336125672709654
25 Hilly's; Func runs: 10000; result: 0.7374210861383783
500 Hilly's; Func runs: 10000; result: 0.34629436610445113
=============================
5 Forest's; Func runs: 10000; result: 0.8942431024645086
25 Forest's; Func runs: 10000; result: 0.7382367793268382
500 Forest's; Func runs: 10000; result: 0.24097956383750824
=============================
5 Megacity's; Func runs: 10000; result: 0.6315384615384616
25 Megacity's; Func runs: 10000; result: 0.5029230769230771
500 Megacity's; Func runs: 10000; result: 0.16420769230769366
=============================
All score: 5.08946 (56.55%)

最终得分 56.55% 是一个非常值得尊敬的结果。在可视化中，算法并未表现出任何特殊行为；看起来像是独立点的散落。

Hilly

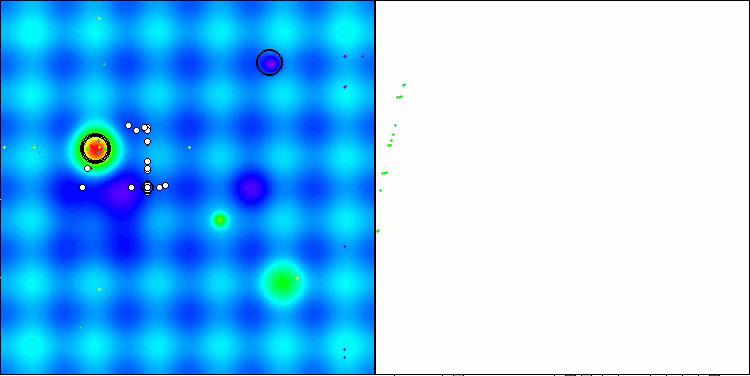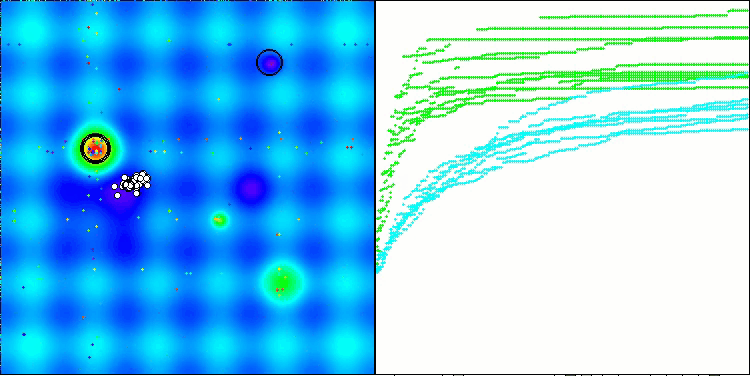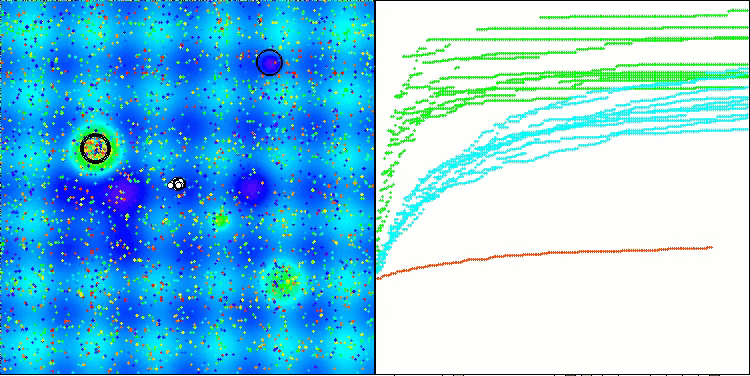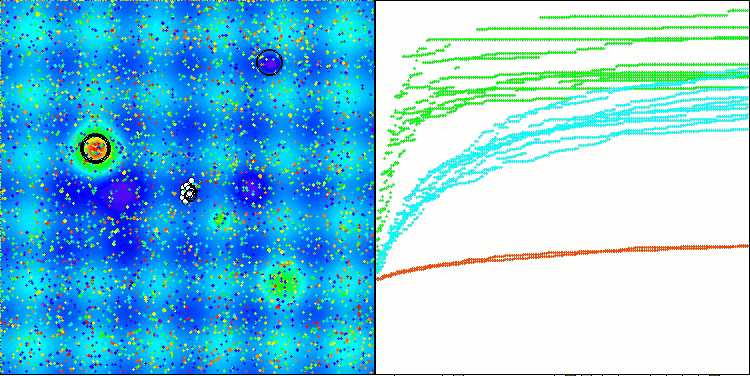
Hilly 测试函数得出的 RFO

Forest

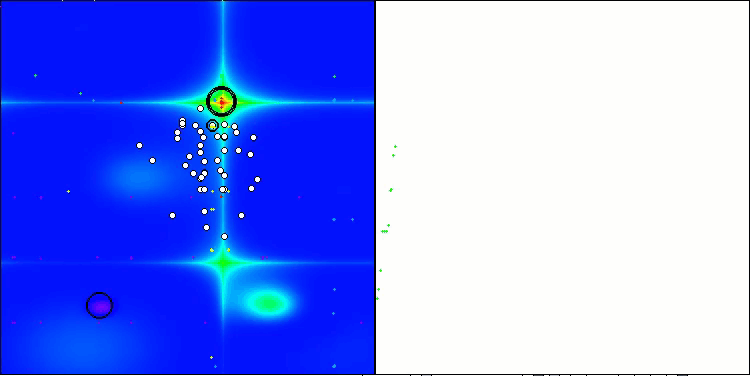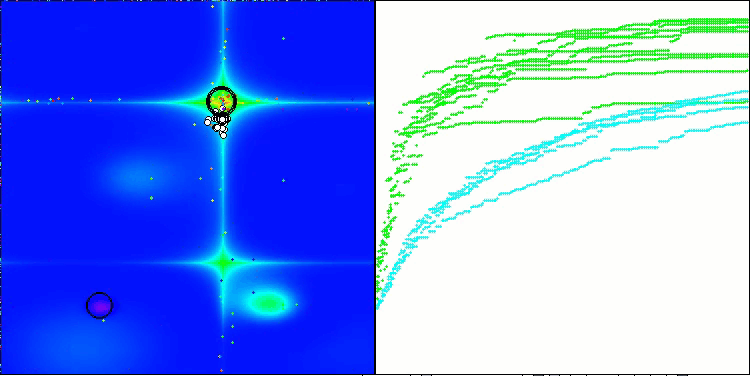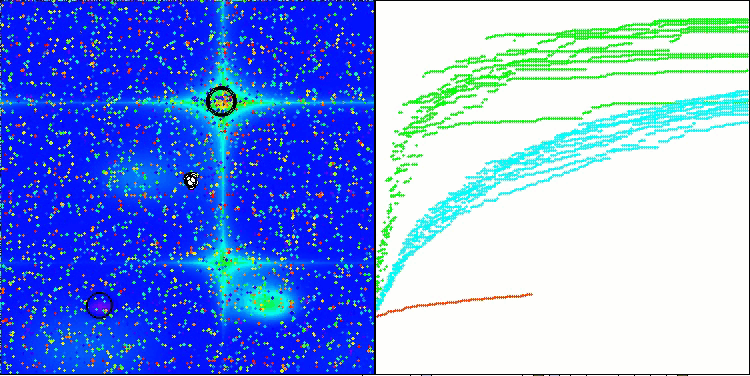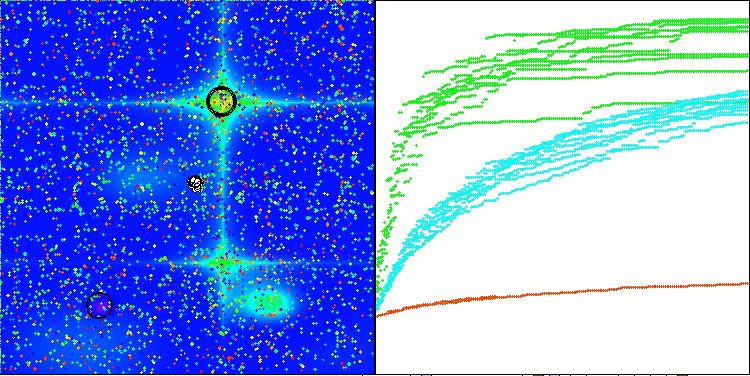
Forest 测试函数得出的 RFO

Megacity

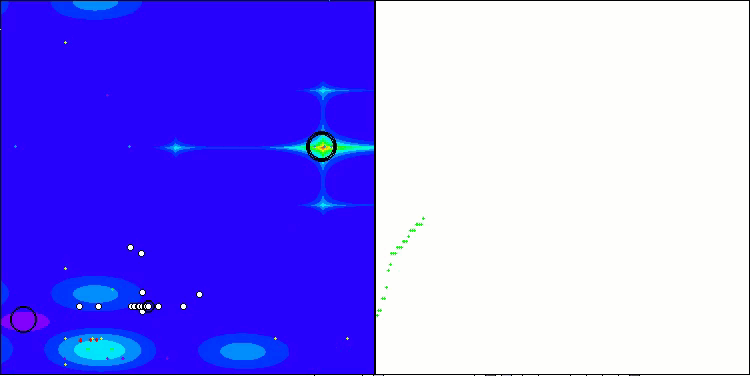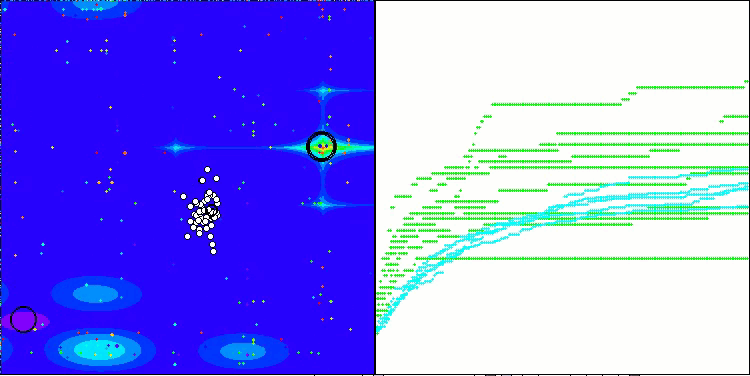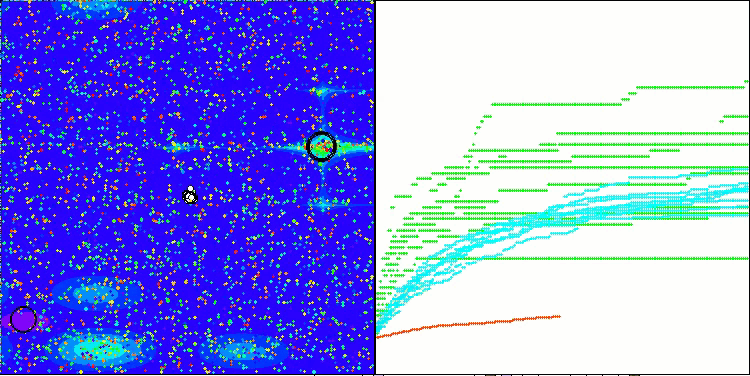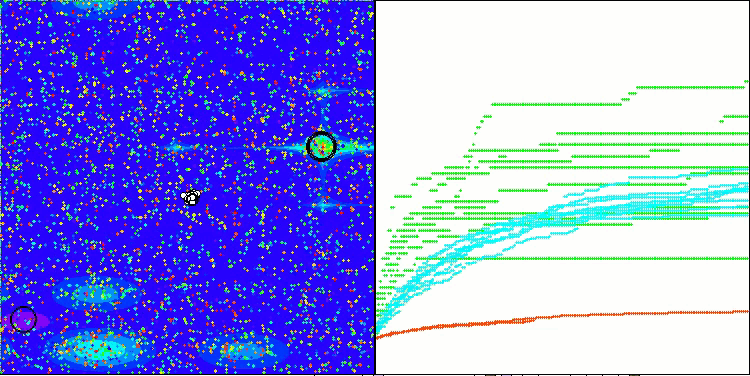
Megacity 测试函数得出的 RFO

基于测试结果，RFO 优化算法排位第 15，入选最强已知算法的行列。

#	AO	说明	Hilly			Hilly 最终	Forest			Forest 最终	Megacity (离散)			Megacity 最终	最终结果	最大 %
#	AO	说明	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Hilly 最终	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Forest 最终	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Megacity 最终	最终结果	最大 %
1	ANS	跨邻域搜索	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	密码锁算法（joo）	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	动物迁徙优化 M	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	（P+O）进化策略	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	彗尾算法（joo）	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	TETA	时间演化旅行算法（joo）	0.91362	0.82349	0.31990	2.05701	0.97096	0.89532	0.29324	2.15952	0.73462	0.68569	0.16021	1.58052	5.797	64.41
7	SDSm	随机扩散搜索 M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
8	AAm	射箭算法 M	0.91744	0.70876	0.42160	2.04780	0.92527	0.75802	0.35328	2.03657	0.67385	0.55200	0.23738	1.46323	5.548	61.64
9	ESG	社会群体演变（joo）	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
10	SIA	模拟各向同性退火（joo）	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
11	ACS	人工协同搜索	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
12	DA	辩证算法	0.86183	0.70033	0.33724	1.89940	0.98163	0.72772	0.28718	1.99653	0.70308	0.45292	0.16367	1.31967	5.216	57.95
13	BHAm	黑洞算法 M	0.75236	0.76675	0.34583	1.86493	0.93593	0.80152	0.27177	2.00923	0.65077	0.51646	0.15472	1.32195	5.196	57.73
14	ASO	无政府社会优化	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
15	RFO	皇冠同花顺优化（joo）	0.83361	0.73742	0.34629	1.91733	0.89424	0.73824	0.24098	1.87346	0.63154	0.50292	0.16421	1.29867	5.089	56.55
16	AOSm	原子轨道搜索 M	0.80232	0.70449	0.31021	1.81702	0.85660	0.69451	0.21996	1.77107	0.74615	0.52862	0.14358	1.41835	5.006	55.63
17	TSEA	龟壳进化算法（joo）	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
18	DE	差别演化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
19	CRO	化学反应优化	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
20	BSA	鸟群算法	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
21	HS	和声搜索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
22	SSG	树苗播种和生长	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
23	BCOm	细菌趋化性优化 M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
24	ABO	非洲水牛优化	0.83337	0.62247	0.29964	1.75548	0.92170	0.58618	0.19723	1.70511	0.61000	0.43154	0.13225	1.17378	4.634	51.49
25	(PO)ES	（PO）进化策略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
26	TSm	禁忌搜索 M	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
27	BSO	头脑风暴优化	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
28	WOAm	wale 优化算法 M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
29	AEFA	人工电场算法	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
30	AEO	基于人工生态系统的优化算法	0.91380	0.46713	0.26470	1.64563	0.90223	0.43705	0.21400	1.55327	0.66154	0.30800	0.28563	1.25517	4.454	49.49
31	ACOm	蚁群优化 M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
32	BFO-GA	细菌觅食优化 - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
33	SOA	简单优化算法	0.91520	0.46976	0.27089	1.65585	0.89675	0.37401	0.16984	1.44060	0.69538	0.28031	0.10852	1.08422	4.181	46.45
34	ABHA	人工蜂巢算法	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
35	ACMO	大气云团模型优化	0.90321	0.48546	0.30403	1.69270	0.80268	0.37857	0.19178	1.37303	0.62308	0.24400	0.10795	0.97503	4.041	44.90
36	ADAMm	自适应动量估算 M	0.88635	0.44766	0.26613	1.60014	0.84497	0.38493	0.16889	1.39880	0.66154	0.27046	0.10594	1.03794	4.037	44.85
37	ATAm	人工部落算法 M	0.71771	0.55304	0.25235	1.52310	0.82491	0.55904	0.20473	1.58867	0.44000	0.18615	0.09411	0.72026	3.832	42.58
38	ASHA	人工洒水算法	0.89686	0.40433	0.25617	1.55737	0.80360	0.35526	0.19160	1.35046	0.47692	0.18123	0.09774	0.75589	3.664	40.71
39	ASBO	自适应社会行为优化	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
40	MEC	思维进化计算	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
41	IWO	入侵性杂草优化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
42	Micro-AIS	微型人工免疫系统	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
43	COAm	布谷鸟优化算法 M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
44	SDOm	螺旋动力学优化 M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
45	NMm	Nelder-Mead 方法 M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
	RW	随机游走	0.48754	0.32159	0.25781	1.06694	0.37554	0.21944	0.15877	0.75375	0.27969	0.14917	0.09847	0.52734	2.348	26.09

摘要

在研究和开发新的优化方法时，我们往往面临在效率与实现复度性之间寻求平衡的需求。皇冠同花顺优化（RFO）算法的研究成果亦引发了关于优化本质及改进方法的有趣问题。

通过观察算法的性能表现，其已达到理论最大值的 57%，我们见识到一个有趣的现象：有时简化比复杂化更有价值。RFO 证明，放弃复杂的二进制编码，转而采用更直接的基于扇区的方法，能够在维持足够高品质解的同时，显著提升算法性能。这令人联想到扑克牌中的状况，有时简单但更快的策略，比需要长时间计算的复杂策略更有效。

在思考 RFO 在优化算法家族中的地位时，可将其比作车辆的演变。正如节能城市车与强劲跑车的需求一样，优化算法领域同样存在专注不同优先级的方法空间。RFO 可被视为遗传算法的“低成本”变体，在性能与资源效率之间提供了合理的权衡。

总之，值得注意的是，RFO 的发展为进一步研究打开了有趣的前景。这或许只是基于扇区优化方法开发整一系列算法的第一步。该方法简洁优雅，结合其实用性，能成为创造平衡性能与计算效率新算法的灵感来源。

值得注意的是，扇区的划分是虚拟的，并未以数组形式分配内存。该 RFO 框架是进一步开发扑克牌算法改进版本的绝佳起点。

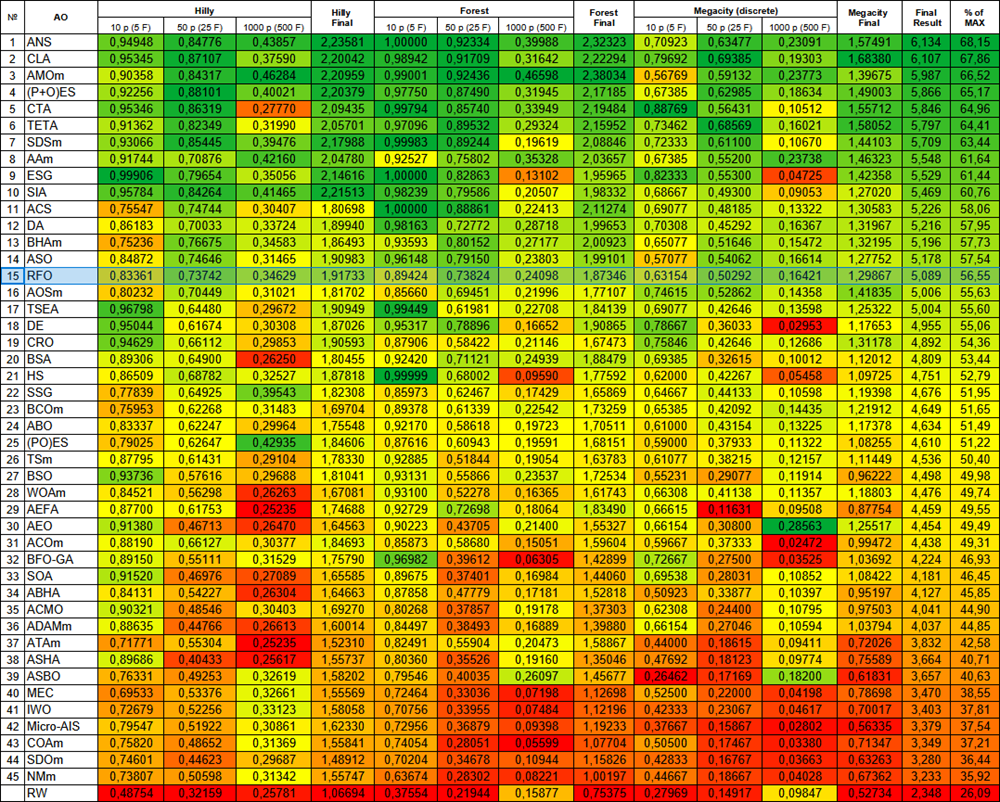
图例 2. 算法的颜色渐变根据相应测试

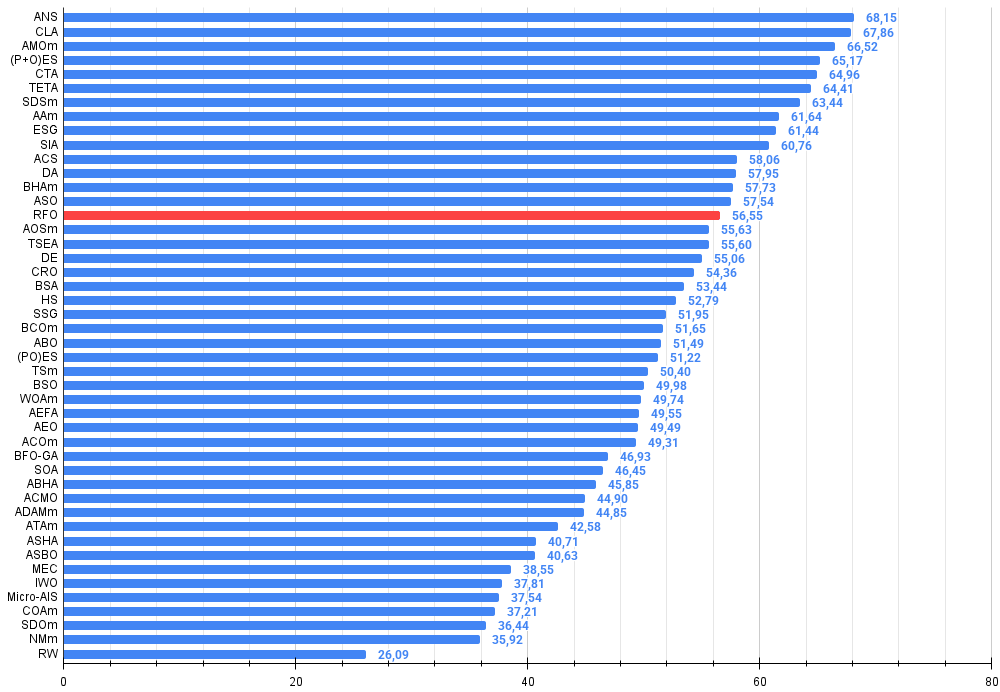
图例 3. 算法测试结果的直方图（从 0 到 100 刻度，越高越好，100 是理论上的最大可能结果，存档中有计算评分表的脚本）

RFO 优缺点：

优点：

外部参数很少，仅有两个，不包括种群规模。
简单的实现。
快速。
平衡良好，在多个维度的任务中表现出色。

缺点：

收敛准确率平均。

文章附有当前版本算法代码的存档。本文作者不对规范算法描述的绝对准确性负责。许多部分都进行了修改，以变提升搜索能力。文章中所给出的结论和判断基于实验结果。

GitHub：https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

文章中用到的程序

#	名称	类型	说明
1	#C_AO.mqh	包含	种群优化算法的父类
2	#C_AO_enum.mqh	包含	种群优化算法的枚举
3	TestFunctions.mqh	包含	测试函数库
4	TestStandFunctions.mqh	包含	测试台函数库
5	Utilities.mqh	包含	辅助函数库
6	CalculationTestResults.mqh	包含	比较表格中计算结果的脚本
7	Testing AOs.mq5	脚本	所有种群优化算法的统一测试台
8	Simple use of population optimization algorithms.mq5	脚本	一个简单的示例，用无可视化的群体优化算法
9	Test_AO_RFO.mq5	脚本	RFO 测试台