
Algoritmo de optimización de la fuerza central — Central Force Optimization (CFO)
Contenido
Introducción
La naturaleza, que ha evolucionado a lo largo de miles de millones de años, ha creado numerosos mecanismos de optimización eficaces que inspiran a los investigadores para crear nuevos algoritmos. Uno de esos fenómenos naturales inspiradores es la gravedad , la fuerza fundamental que rige el movimiento de los cuerpos celestes. Ya hemos analizado muchas veces este tipo de algoritmos....
El algoritmo de Optimización de la Fuerza Central (CFO) es un intento de trasladar los principios de la cinemática gravitatoria al campo de la optimización numérica. Este algoritmo metaheurístico, basado en leyes de movimiento deterministas, modela la interacción de partículas virtuales en un espacio de soluciones multidimensional, donde cada partícula tiende a las regiones con los mejores valores de la función objetivo bajo la acción de una fuerza gravitatoria análoga.
La CFO se basa en una metáfora sencilla e intuitiva: imagine un conjunto de puntos de prueba (ensayos) distribuidos en el espacio de las posibles soluciones. Cada muestra tiene una "masa" proporcional a la calidad de la solución que representa: el valor de la función objetivo. Al igual que los cuerpos celestes masivos atraen a otros menos masivos, las muestras con mejores soluciones crean un campo gravitatorio virtual que atrae a otras muestras.
El movimiento de cada muestra obedece a leyes similares a las de Newton; la aceleración viene determinada por la fuerza total de atracción de las otras muestras y el desplazamiento se produce según las ecuaciones cinemáticas del movimiento. Una característica importante del algoritmo es su naturaleza determinista: a diferencia de muchos otros métodos metaheurísticos, el CFO no utiliza variables aleatorias en su ciclo de trabajo principal.
Implementación del algoritmo
La historia del algoritmo CFO comenzó cuando los investigadores pensaron: ¿y si aplicáramos las leyes de la física a la búsqueda de soluciones óptimas? Imagine un vasto terreno accidentado en el que la altura de cada punto corresponde a la calidad de una solución. Cuanto más alta sea la colina, mejor será la solución. Nuestro objetivo consiste en encontrar el punto más alto, pero el problema es que no podemos ver todo el paisaje a la vez. En su lugar, tenemos un grupo de exploradores (que llamaremos sondas) que pueden navegar por este terreno e informar de la altitud de su posición actual.
Al principio, nuestras muestras se distribuyen aleatoriamente por toda la zona. Algunas se encuentran en tierras bajas, otras en laderas, y algunas pueden tener la suerte de llegar directamente a las cimas de pequeñas elevaciones. Cada muestra tiene un "peso" diferente, proporcional a la altura del punto en el que se encuentra. Cuanto más alto sea el punto, más "pesada" será la muestra. Y aquí empieza lo más interesante: nuestras muestras no vagan al azar, sino que obedecen a las leyes de la gravedad. Imagínese que las muestras "más pesadas" (aquellas que se encuentran en las mejores posiciones) atraen hacia sí a las muestras "más ligeras" (las que se hallan en las peores posiciones). Esta atracción, además, solo funciona en un sentido: las buenas soluciones atraen a las malas, pero no al revés.
La fuerza de atracción se calcula usando reglas similares a la ley de gravitación universal de Newton. Esta depende de la diferencia de "peso" entre las muestras (diferencia de calidad de las soluciones) y de la distancia entre ellas. Una muestra con un valor alto de la función de aptitud atrae fuertemente a las muestras cercanas con valores bajos, pero influye débilmente en las muestras distantes. Bajo la acción de estas fuerzas, cada muestra recibe una aceleración y comienza a moverse. Las muestras más pequeñas y "ligeras" se precipitan hacia las más pesadas, como si las bolas rodaran ladera arriba hacia las cumbres. A cada paso del algoritmo, las muestras recalculan las fuerzas de atracción y ajustan su movimiento. Si una muestra intenta salir de la zona de búsqueda, se activará un mecanismo de reflexión: imagine que hay un muro en el borde de la zona y la muestra rebota y vuelve a la zona permitida.
Con el tiempo, las muestras empiezan a acumularse alrededor de los puntos altos del paisaje. La mayoría de ellos se concentran alrededor de las zonas más prometedoras y, con cada iteración, son cada vez más precisas a la hora de determinar la posición de los cimas. En el mejor de los casos, si se da tiempo suficiente al algoritmo, todas las muestras deberían reunirse en torno a un máximo global, es decir, el punto más alto de todo el paisaje.
La peculiaridad del CFO es que se trata fundamentalmente de un algoritmo determinista: si se ejecuta dos veces con la misma distribución inicial de muestras, dará el mismo resultado. Esto lo distingue de muchos otros algoritmos metaheurísticos que se basan en la aleatoriedad.
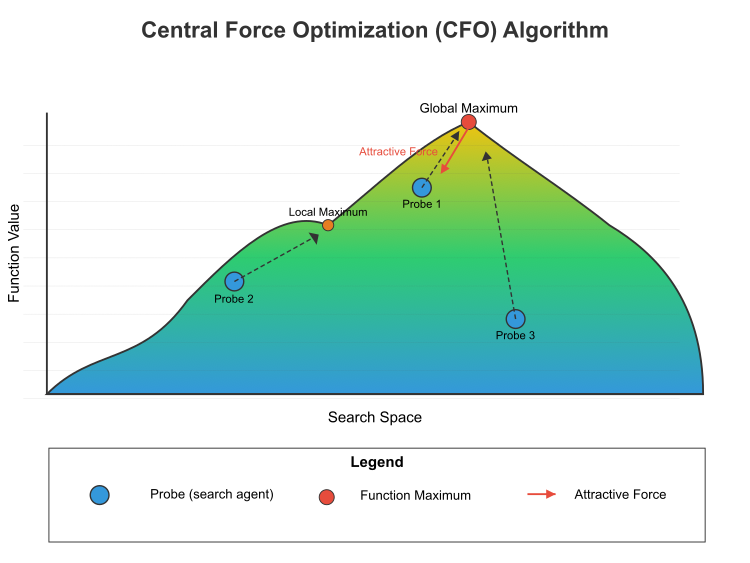
Figura 1. Esquema del algoritmo de CFO
La figura 1 muestra el principio de funcionamiento del algoritmo de optimización de la fuerza central (CFO) en el espacio de búsqueda. Se presenta el paisaje de la función objetivo, con un gradiente de color que va del azul (valores bajos) al amarillo (valores altos). Máximo global (punto más elevado) y máximo local (pico más bajo). Tres muestras (agentes de búsqueda) etiquetadas como Muestra 1, Muestra 2 y Muestra 3. Las fuerzas de atracción (flecha roja), muestra cómo los puntos más altos atraen las muestras. Este es un concepto central del CFO: las mejores soluciones atraen a las peores, pero no al revés. Las líneas punteadas indican la trayectoria de las muestras hasta los máximos. La fórmula matemática de este proceso incluye:
El cálculo de la fuerza: para dos muestras cualesquiera i y j, si el valor de la función (masa) de j es mayor que el de i, entonces j ejercerá una fuerza sobre i según: F = g × [(m_j - m_i)^α / d^β] × dirección, donde:- g — constante gravitatoria
- m_j y m_i — valores de la función (masa) de las muestras j e i
- α — índice de masa (normalmente 2)
- d — distancia entre muestras
- β — indicador de distancia (normalmente 2)
- dirección — vector unitario dirigido de la muestra i a la muestra j
La actualización de la posición: la posición de cada sonda se actualiza según x_new = x_old + 0,5 × a, donde:
- x_new — nueva posición
- x_old — posición actual
- a — aceleración
El algoritmo aplicará iterativamente estos cálculos a todas las muestras, desplazándolas gradualmente hacia los óptimos en el espacio de búsqueda. Con el tiempo, las muestras tienden a agruparse en torno a los máximos globales y locales, y la mayor concentración suele darse en torno al óptimo global.
La peculiaridad del CFO está condicionada porsu naturaleza determinista y su mecanismo de atracción unidireccional, que orienta la investigación hacia mejores soluciones sin que intervenga el azar en su forma básica. Pseudocódigo del algoritmo CFO:
- Inicialización:
- Definimos los límites del espacio de búsqueda.
- Fijamos los parámetros: el número de muestras, la constante gravitatoria, los índices de grado para la masa y la distancia, y el factor de reposicionamiento.
- Creamos un número determinado de muestras y las colocamos en el espacio de búsqueda aleatoriamente.
- Para cada muestra, calculamos el valor inicial de la función objetivo.
- Ciclo principal (repetimos un número determinado de épocas):
- Para cada muestra:
- Ponemos a cero el vector de aceleración.
- Considerando el impacto de otras muestras:
- Si la otra muestra tiene un valor de función objetivo mejor (más "masa"), se creará una fuerza de atracción.
- Calculamos la distancia entre las muestras.
- La fuerza de atracción es proporcional a la diferencia de "masas" en el grado alfa e inversamente proporcional a la distancia en el grado beta.
- La dirección de la fuerza es de la muestra actual respecto a la muestra más "pesada".
- Resumimos los efectos de todas las muestras con los mejores valores de función.
- Tras calcular todas las aceleraciones, actualizamos las posiciones de las muestras:
- Nueva posición = antigua posición + la mitad de la aceleración.
- Si la muestra se extiende más allá de los límites del espacio de búsqueda, aplicaremos el reposicionamiento:
- Si se sobrepasa el límite inferior: reflejamos la muestra en el interior del espacio teniendo en cuenta el factor de reposicionamiento.
- Si se supera el límite superior: de forma similar, pero en el otro lado.
- Recalculamos los valores de la función objetivo para todas las muestras en sus nuevas posiciones.
- Actualizaciones sobre la mejor solución encontrada.
- Para cada muestra:
- Finalización:
- Retorna la mejor solución encontrada (las coordenadas de la muestra con el valor máximo de la función objetivo).
Vamos a escribir el código del algoritmo; así, definiremos la estructura "S_CFO_Agent", que hereda de "S_AO_Agent" y implica que "S_CFO_Agent" obtiene todas las propiedades y métodos definidos en "S_AO_Agent".
Campos de estructura: a[] es un array dinámico que se utiliza para almacenar valores de aceleración. El método "Init()" se usa para inicializar la estructura, redimensionar el array "c" según el parámetro pasado "coords" y redimensionar el array de aceleración "a" según "coords". Esto permite establecer dinámicamente el tamaño del array según el número de coordenadas; inicializa todos los elementos del array de aceleración "a" con un valor de "0.0", poniendo a cero los valores antes de utilizarlos; establece el valor de la variable "f" al valor mínimo posible para el tipo "double", para inicializar la función de aptitud para asegurar que cualquier otro valor calculado será mayor que este.
//—————————————————————————————————————————————————————————————————————————————— //--- CFO probe structure struct S_CFO_Agent : public S_AO_Agent { double a []; // acceleration vector void Init (int coords) { ArrayResize (c, coords); // coordinates ArrayResize (a, coords); // acceleration ArrayInitialize (a, 0.0); // reset accelerations f = -DBL_MAX; // fitness function value } }; //——————————————————————————————————————————————————————————————————————————————
La clase "C_AO_CFO" hereda de la clase "C_AO" y define el algoritmo CFO. Constructor y destructor. En este caso, el destructor no lleva a cabo ninguna acción específica. C_AO_CFO () es un constructor que inicializa los parámetros del algoritmo. Este establece los valores de diversas variables como:
- popSize, g, alpha, beta, initialFrep, finalFrep, noiseFactor son parámetros relacionados con el algoritmo y las funciones de optimización de este.
- frep — factor de reposicionamiento actual, inicializado con el valor "initialFrep".
- inicializa la array "params", que contendrá los parámetros del algoritmo, tras lo cual sus valores se copiarán en un array con los nombres apropiados.
Métodos de clase:
- SetParams () — establece los parámetros del algoritmo, tomando valores de la array "params". También establece el factor de reposicionamiento actual en "initialFrep".
- Init () — se encarga de inicializar el algoritmo con los valores mínimo y máximo de los parámetros, así como los pasos utilizados para cambiarlos. El parámetro "epochsP" indica el número de épocas para ejecutar el algoritmo.
- Moving () — se encarga del proceso de desplazamiento de muestras (agentes) en el algoritmo.
- Revision () — se puede utilizar para realizar una revisión o actualizar el estado de los agentes.
Campos de clase:
- S_CFO_Agent probe [] — array de muestras (agentes) que se utilizarán en el proceso de optimización.
- epochs, epochNow — campos privados, número total de épocas y época actual.
Métodos privados adicionales:
- InitialDistribution () — se utiliza para inicializar la distribución de los agentes en el espacio de búsqueda.
- UpdateRepFactor () — se encarga de actualizar el factor de reposicionamiento según el estado actual del sistema.
- CalculateAccelerations () — se utiliza para calcular las aceleraciones de los agentes según sus posiciones e interacciones.
- UpdatePositions () — se utiliza para actualizar las posiciones de los agentes según sus aceleraciones.
- CalculateDistanceSquared () — método para calcular la distancia entre dos puntos en el espacio; se utiliza para evaluar la interacción entre agentes.
//—————————————————————————————————————————————————————————————————————————————— //--- Main class of the CFO algorithm class C_AO_CFO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_CFO () { } C_AO_CFO () { ao_name = "CFO"; ao_desc = "Central Force Optimization"; ao_link = "https://www.mql5.com/es/articles/17167"; popSize = 30; // number of probes g = 1.0; // gravitational constant alpha = 0.1; // mass power beta = 0.1; // degree for distance initialFrep = 0.9; // initial repositioning factor finalFrep = 0.1; // final repositioning factor noiseFactor = 1.0; // random noise factor frep = initialFrep; // current repositioning factor ArrayResize (params, 7); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "g"; params [1].val = g; params [2].name = "alpha"; params [2].val = alpha; params [3].name = "beta"; params [3].val = beta; params [4].name = "initialFrep"; params [4].val = initialFrep; params [5].name = "finalFrep"; params [5].val = finalFrep; params [6].name = "noiseFactor"; params [6].val = noiseFactor; } void SetParams () { popSize = (int)MathMax (1, params [0].val); g = params [1].val; alpha = params [2].val; beta = params [3].val; initialFrep = params [4].val; finalFrep = params [5].val; noiseFactor = params [6].val; frep = initialFrep; } bool Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0); // number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double g; // gravitational constant double alpha; // power for mass double beta; // degree for distance double initialFrep; // initial repositioning factor double finalFrep; // final repositioning factor double noiseFactor; // random noise factor S_CFO_Agent probe []; // array of probes private: //------------------------------------------------------------------- int epochs; // total number of epochs int epochNow; // current epoch double frep; // repositioning factor void InitialDistribution (); void UpdateRepFactor (); void CalculateAccelerations (); void UpdatePositions (); double CalculateDistanceSquared (const double &x1 [], const double &x2 []); }; //——————————————————————————————————————————————————————————————————————————————
El método "Init ()" de la clase "C_AO_CFO" es responsable de la inicialización del algoritmo CFO, acepta los arrays de valores mínimo y máximo de los parámetros, el paso de cambio de estos valores y el número de épocas (0 por defecto). Llama al método "StandardInit" para comprobar si los rangos de valores transmitidos son correctos. Si falla la comprobación, el método retornará "false". Establece el número total de épocas y la época actual (0). Cambia el tamaño del array de muestras (agentes) al tamaño de la población (popSize). Inicializa cada agente en el array "probe" llamando al método "Init" para cada uno de ellos con las coordenadas pasadas. Si la inicialización se ha realizado correctamente, el método retornará "true". Así, el método "Init" establece los parámetros y condiciones iniciales para que el algoritmo sea ejecutado.
//—————————————————————————————————————————————————————————————————————————————— //--- Initialization bool C_AO_CFO::Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; // Initialization of probes ArrayResize (probe, popSize); for (int i = 0; i < popSize; i++) probe [i].Init (coords); return true; } //——————————————————————————————————————————————————————————————————————————————
El método "Moving ()" de la clase "C_AO_CFO" es responsable del paso principal del algoritmo CFO; el método comienza a ejecutarse incrementando el contador de épocas actual, indicando el siguiente paso del algoritmo si el método es llamado por primera vez; cuando "revision" es igual a "false", realiza una inicialización inicial, después de lo cual termina la ejecución. Esto es necesario para establecer los valores iniciales y el estado. A continuación, los valores de la función de aptitud se copian del array del agente a un array temporal para mantenerlos relevantes para cálculos posteriores.
El método actualiza el parámetro responsable del reposicionamiento de los agentes en el espacio de búsqueda, lo cual resulta importante para la adaptabilidad del algoritmo; a continuación, el método calcula la aceleración de los agentes según el estado actual y actualiza sus posiciones, lo que garantiza que los agentes se muevan en el espacio de búsqueda. Al final, el método sincroniza las nuevas posiciones de los agentes con el array principal, capturando los cambios y garantizando la coherencia de los datos. El método "Moving ()" ofrece una actualización sistemática del estado de los agentes basada en sus funciones de aptitud y sus posiciones actuales, a medida que se ejecuta el algoritmo.
//—————————————————————————————————————————————————————————————————————————————— //--- The main step of the algorithm void C_AO_CFO::Moving () { epochNow++; // Initial initialization if (!revision) { InitialDistribution (); revision = true; return; } //---------------------------------------------------------------------------- // Copy the fitness function values from the base class for (int p = 0; p < popSize; p++) { probe [p].f = a [p].f; } // Update the repositioning parameter UpdateRepFactor (); // Main CFO loop CalculateAccelerations (); UpdatePositions (); // Synchronize positions with the base class for (int p = 0; p < popSize; p++) { ArrayCopy (a [p].c, probe [p].c); } } //——————————————————————————————————————————————————————————————————————————————
El método "InitialDistribution" de la clase "C_AO_CFO" se encarga de la distribución inicial de las muestras (agentes) en el espacio de búsqueda. El método itera cada agente de la población "popSize". Para cada agente, los valores se inicializan poniendo el array "a" a cero y fijando la función de aptitud "f" en un valor mínimo. Para cada coordenada del agente, se lleva a cabo una distribución aleatoria de valores dentro de los límites dados (rangeMin y rangeMax). Una vez generado el valor aleatorio, se procesa usando el método "SeInDiSp", que lleva el valor a un rango determinado y un paso "rangeStep". Por último, las coordenadas de los agentes se copian desde el array temporal "c" al array principal "a", fijando el estado inicial de cada agente.
//—————————————————————————————————————————————————————————————————————————————— //--- Initial probe distribution void C_AO_CFO::InitialDistribution () { for (int p = 0; p < popSize; p++) { ArrayInitialize (probe [p].a, 0.0); probe [p].f = -DBL_MAX; // Random distribution for (int c = 0; c < coords; c++) { probe [p].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); probe [p].c [c] = u.SeInDiSp (probe [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } ArrayCopy (a [p].c, probe [p].c); } } //——————————————————————————————————————————————————————————————————————————————
El método "UpdateRepFactor" de la clase "C_AO_CFO" se encarga de actualizar el factor de reposicionamiento (o factor represivo) durante el algoritmo. El método comienza comprobando si el número de épocas "epochs" es superior a cero, a continuación se calcula un nuevo valor del factor de reposicionamiento "frep" decreciendo linealmente desde el valor inicial "initialFrep" hasta el valor final "finalFrep". Se basa en la época actual "epochNow" dentro del número de épocas total. Si el número de épocas es cero, el valor de "frep" seguirá siendo igual al valor inicial de "initialFrep". Esto garantizará la estabilidad del factor si el algoritmo se encuentra en su fase inicial. Al final del método, el valor "frep" se limitará entre 0 y 1 mediante las funciones "MathMax" y "MathMin". Esto garantiza que el factor de reposicionamiento no supere los límites establecidos, lo que resulta importante para la estabilidad y la corrección del algoritmo.
//—————————————————————————————————————————————————————————————————————————————— //--- Update the repositioning factor void C_AO_CFO::UpdateRepFactor () { // Linearly decrease frep from the initial to the final value if (epochs > 0) frep = initialFrep - (initialFrep - finalFrep) * epochNow / epochs; else frep = initialFrep; // Value constraint frep = MathMax (0.0, MathMin (1.0, frep)); } //——————————————————————————————————————————————————————————————————————————————
El método "CalculateAccelerations" de la clase "C_AO_CFO" está diseñado para calcular las aceleraciones de cada agente (o muestra) de la población basándose en la influencia de todos los demás agentes. A continuación le describimos los pasos básicos y la lógica del método. Para cada agente de la población (de 0 a popSize), los valores de aceleración "probe[p].a" se ponen a cero. Esto se hace para comenzar el cálculo desde cero y acumular aceleraciones basadas en interacciones con otros agentes. Para cada agente, el ciclo interno enumera todos los demás agentes (de 0 a popSize). Si el índice del agente actual "p" coincide con el índice de otro agente "k", se saltará la iteración mediante el comando "continue". Luego se calcula la diferencia entre los valores de aptitud de los dos agentes (massDiff = probe[k].f - probe[p].f). Este valor se usa para determinar cuánto más "pesado" (o mejor) es un agente en comparación con otro. Si "massDiff" es superior a cero, significará que el segundo agente con índice "k" tiene mayor aptitud que el agente actual con índice "p". Al hacerlo, se cumplirá lo siguiente:
-
Cálculo de la distancia: se calculará el cuadrado de la distancia entre las coordenadas actuales de los dos agentes mediante la función "CalculateDistanceSquared". Si esta distancia es demasiado pequeña (menor que el valor positivo más pequeño), se saltará la iteración.
-
Generación de la dirección de la fuerza: si la distancia es mayor que "DBL_EPSILON", se calculará la distancia real y, para cada coordenada "c", se determinará la dirección de la fuerza dirigida desde el agente actual al agente con mayor aptitud.
-
Fórmula de aceleración: la aceleración para el agente actual se actualiza usando como base la fórmula probe[p].a[c] += g * MathPow (massDiff, alpha) * direction / MathPow (distance, beta), donde se tienen en cuenta la diferencia de masas (valores de aptitud), la distancia entre muestras y ciertos coeficientes (g, alpha, beta) que afectan a la fuerza de interacción.
El método permite a cada agente considerar la influencia de otros agentes en su aceleración, lo que constituye un elemento clave en el proceso de optimización. Las aceleraciones calculadas de este modo se usarán posteriormente para actualizar las posiciones de los agentes en el espacio de soluciones.
//—————————————————————————————————————————————————————————————————————————————— //--- Calculate accelerations void C_AO_CFO::CalculateAccelerations () { for (int p = 0; p < popSize; p++) { // Reset the acceleration for the current probe ArrayInitialize (probe [p].a, 0.0); // Summarize the influence of all other probes for (int k = 0; k < popSize; k++) { if (k == p) continue; // Difference in masses (fitness values) double massDiff = probe [k].f - probe [p].f; // Check the condition of the U(...) unit function if (massDiff > 0) // Strict condition for the unit function { // Calculate the distance between probes double distSquared = CalculateDistanceSquared (probe [k].c, probe [p].c); if (distSquared < DBL_EPSILON) continue; double distance = MathSqrt (distSquared); for (int c = 0; c < coords; c++) { // Force direction double direction = (probe [k].c [c] - probe [p].c [c]) / distance; // Acceleration equation probe [p].a [c] += g * MathPow (massDiff, alpha) * direction / MathPow (distance, beta); } } } } } //——————————————————————————————————————————————————————————————————————————————
El método "UpdatePositions" de la clase "C_AO_CFO" se utiliza para actualizar las posiciones de los agentes (o muestras) en el espacio de decisiones, teniendo en cuenta sus aceleraciones, los factores aleatorios y las restricciones de contorno. En este método se ejecutan varios pasos:
Reducción del nivel de ruido aleatorio:- Se analiza el valor actual del factor de ruido aleatorio "currentNoiseFactor" y se inicializa con un valor igual a "noiseFactor".
- Si el número de épocas "epochs" es mayor que cero, el coeficiente disminuye proporcionalmente a la época actual "epochNow"; esto significa que a medida que aumente el número de épocas, el ruido disminuirá, permitiendo al algoritmo encontrar gradualmente la solución óptima con mayor precisión.
El método itera todos los agentes de la población (de 0 a popSize) y para cada agente, el método itera todas sus coordenadas (de 0 a coords). La posición del agente se actualiza usando una fórmula que utiliza la aceleración actual "probe[p].a[c]". En este caso, se usa una fórmula sencilla en la que la nueva posición es igual a la posición anterior más la mitad de la aceleración actual.
Además, se añade un pequeño desplazamiento aleatorio a la posición actualizada, que depende de la cifra de ruido actual, el valor de gravedad "g" y un número aleatorio entre -1 y 1. El algoritmo original es estrictamente determinista, así que decidimos añadir un elemento de aleatoriedad. Hablaremos de ello más adelante. Este desplazamiento añade un elemento de aleatoriedad y ayuda a evitar quedarse atascado en mínimos localizados. Si la nueva posición supera los límites especificados (valores mínimo y máximo almacenados en rangeMin y rangeMax), la posición se ajusta para que permanezca dentro del rango aceptable y, si se especifica un paso de muestreo, la posición del agente se ajusta aún más usando el método "SeInDiSp" que lleva la posición al valor más cercano múltiplo del paso.
//—————————————————————————————————————————————————————————————————————————————— //--- Update positions void C_AO_CFO::UpdatePositions () { // Random noise ratio decreases with increasing epoch number double currentNoiseFactor = noiseFactor; if (epochs > 0) currentNoiseFactor *= (1.0 - (double)epochNow / epochs); for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { // Update the position by equation probe [p].c [c] += 0.5 * probe [p].a [c]; // Add a small random offset directly to the position probe [p].c [c] += currentNoiseFactor * g * u.RNDfromCI (-1.0, 1.0); // Reposition when going out of bounds if (probe [p].c [c] < rangeMin [c]) probe [p].c [c] = rangeMin [c]; if (probe [p].c [c] > rangeMax [c]) probe [p].c [c] = rangeMax [c]; // Discretization if step is specified probe [p].c [c] = u.SeInDiSp (probe [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
El método "CalculateDistanceSquared" de la clase "C_AO_CFO" se encarga de calcular el cuadrado de la distancia entre dos puntos en un espacio multidimensional. El método se usa para la optimización porque al retornar el valor del cuadrado de la distancia se elimina la necesidad de calcular la raíz cuadrada, lo que reduce significativamente el coste computacional. El método toma dos parámetros: x1 y x2. Se trata de arrays (const double &x1[] y const double &x2[]) que representan las coordenadas de dos puntos en el espacio cuya dimensionalidad es igual al número de coordenadas "coords". Al principio del método, se crea una variable "suma" inicializada con cero. Esta variable se usa para acumular la suma de cuadrados de las diferencias de coordenadas. El método itera todas las coordenadas (de 0 a coords-1) y para cada coordenada:
- Se calcula la diferencia entre los elementos correspondientes de los arrays x1 y x2 (diff = x1[i] - x2[i]).
- Se calcula el cuadrado de esta diferencia (diff * diff).
- El cuadrado de la diferencia se añade a la variable "sum".
//—————————————————————————————————————————————————————————————————————————————— //--- Calculate distance (returns squared distance for optimization) double C_AO_CFO::CalculateDistanceSquared (const double &x1 [], const double &x2 []) { double sum = 0.0; for (int i = 0; i < coords; i++) { double diff = x1 [i] - x2 [i]; sum += diff * diff; } return sum; } //——————————————————————————————————————————————————————————————————————————————
El método "Revision ()" de la clase "C_AO_CFO" se encarga de actualizar la mejor solución encontrada durante el proceso de optimización. El método itera todos los agentes (o muestras) de la población "popSize". Para cada agente, se comprueba si su función de aptitud "a[p].f" es mayor que el mejor valor actual "fB". De ser así, se actualiza el valor de "fB", haciéndolo igual a la función de aptitud de este agente; luego se copian las coordenadas de "cB" del agente si su solución es la mejor. Así, el método Revision encuentra y almacena la mejor solución entre todos los agentes, actualizando los parámetros globales en cuanto se observa que un agente ha mejorado el resultado.
//—————————————————————————————————————————————————————————————————————————————— //--- Update the best solution void C_AO_CFO::Revision () { for (int p = 0; p < popSize; p++) { if (a [p].f > fB) { fB = a [p].f; ArrayCopy (cB, a [p].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Resultados de las pruebas
El algoritmo original, estrictamente determinista, muestra en su versión básica los siguientes resultados:
CFO|Central Force Optimization|30.0|1.0|0.1|0.1|0.9|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.34508431921321436
25 Hilly's; Func runs: 10000; result: 0.2826594689557952
500 Hilly's; Func runs: 10000; result: 0.25174636412054047
=============================
5 Forest's; Func runs: 10000; result: 0.26234538930351947
25 Forest's; Func runs: 10000; result: 0.1852230195779629
500 Forest's; Func runs: 10000; result: 0.15353213276989314
=============================
5 Megacity's; Func runs: 10000; result: 0.24923076923076923
25 Megacity's; Func runs: 10000; result: 0.1261538461538462
500 Megacity's; Func runs: 10000; result: 0.09492307692307768
=============================
All score: 1.95090 (21.68%)
Con estos resultados, el algoritmo lamentablemente no puede entrar en nuestra tabla de clasificación. Se necesitan mejoras. Por eso, como hemos dicho antes, hemos añadido el elemento de aleatoriedad a esta línea; sin él, la naturaleza determinista de la búsqueda carecía de diversidad de soluciones.
// Add a small random offset directly to the position probe [p].c [c] += currentNoiseFactor * g * u.RNDfromCI (-1.0, 1.0);
Tras añadir un ligero elemento de aleatoriedad (un pequeño desplazamiento aleatorio al movimiento de cada muestra), el algoritmo ha podido comenzar a explorar direcciones inesperadas. Volvamos a probar de nuevo. Ahora podemos observar resultados completamente diferentes, que ya podemos registrar en nuestra tabla de clasificación.
CFO|Central Force Optimization|30.0|1.0|0.1|0.1|0.9|0.1|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6096110105488222
25 Hilly's; Func runs: 10000; result: 0.5495761567207647
500 Hilly's; Func runs: 10000; result: 0.27830861578120414
=============================
5 Forest's; Func runs: 10000; result: 0.6341793648294705
25 Forest's; Func runs: 10000; result: 0.4683296629644541
500 Forest's; Func runs: 10000; result: 0.22540930020804817
=============================
5 Megacity's; Func runs: 10000; result: 0.5723076923076923
25 Megacity's; Func runs: 10000; result: 0.2347692307692307
500 Megacity's; Func runs: 10000; result: 0.09586153846153929
=============================
All score: 3.66835 (40.76%)
Ahora podemos ver cómo funciona el algoritmo. Como ve, el algoritmo funciona bien en funciones de dimensión media, pero no lo suficientemente bien en funciones de dimensión pequeña y alta.

CFO en la función de prueba de Hilly

CFO en la función de prueba Forest

CFO en la función de prueba Megacity
Según los resultados, el algoritmo se encuentra entre los mejores algoritmos de optimización de poblaciones y ocupa el puesto 42.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration optimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0.91362 | 0.82349 | 0.31990 | 2.05701 | 0.97096 | 0.89532 | 0.29324 | 2.15952 | 0.73462 | 0.68569 | 0.16021 | 1.58052 | 5.797 | 64.41 |
| 7 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 8 | BOAm | billiards optimization algorithm M | 0.95757 | 0.82599 | 0.25235 | 2.03590 | 1.00000 | 0.90036 | 0.30502 | 2.20538 | 0.73538 | 0.52523 | 0.09563 | 1.35625 | 5.598 | 62.19 |
| 9 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 10 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 12 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 13 | DA | dialectical algorithm | 0.86183 | 0.70033 | 0.33724 | 1.89940 | 0.98163 | 0.72772 | 0.28718 | 1.99653 | 0.70308 | 0.45292 | 0.16367 | 1.31967 | 5.216 | 57.95 |
| 14 | BHAm | black hole algorithm M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 15 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 16 | RFO | royal flush optimization (joo) | 0.83361 | 0.73742 | 0.34629 | 1.91733 | 0.89424 | 0.73824 | 0.24098 | 1.87346 | 0.63154 | 0.50292 | 0.16421 | 1.29867 | 5.089 | 56.55 |
| 17 | AOSm | búsqueda de orbitales atómicos M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 18 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 19 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 20 | SRA | successful restaurateur algorithm (joo) | 0.96883 | 0.63455 | 0.29217 | 1.89555 | 0.94637 | 0.55506 | 0.19124 | 1.69267 | 0.74923 | 0.44031 | 0.12526 | 1.31480 | 4.903 | 54.48 |
| 21 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 22 | BIO | blood inheritance optimization (joo) | 0.81568 | 0.65336 | 0.30877 | 1.77781 | 0.89937 | 0.65319 | 0.21760 | 1.77016 | 0.67846 | 0.47631 | 0.13902 | 1.29378 | 4.842 | 53.80 |
| 23 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 24 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 25 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 26 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 27 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 28 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 29 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 30 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 31 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 32 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 33 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 34 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 35 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 36 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 37 | ABH | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 38 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 39 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 40 | CGO | chaos game optimization | 0.57256 | 0.37158 | 0.32018 | 1.26432 | 0.61176 | 0.61931 | 0.62161 | 1.85267 | 0.37538 | 0.21923 | 0.19028 | 0.78490 | 3.902 | 43.35 |
| 41 | ATAm | artificial tribe algorithm M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 42 | CFO | central force optimization | 0.60961 | 0.54958 | 0.27831 | 1.43750 | 0.63418 | 0.46833 | 0.22541 | 1.32792 | 0.57231 | 0.23477 | 0.09586 | 0.90294 | 3.668 | 40.76 |
| 43 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 44 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 45 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| R.W. | random walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Conclusiones
El algoritmo CFO, basado en los principios de la atracción gravitatoria entre objetos, supone un interesante intento de aplicar las leyes de la física a problemas complejos de optimización. Tras rigurosas pruebas con nuestro conjunto de características estándar, el CFO ha demostrado una eficacia ligeramente superior al 40% del máximo teóricamente posible, lo cual lo sitúa en el puesto 42 de los 45 mejores algoritmos de optimización de poblaciones. Hay que señalar que incluso este modesto resultado solo se ha logrado modificando el algoritmo original introduciendo un componente aleatorio a su naturaleza originalmente determinista.
A pesar de su rendimiento relativamente bajo, el CFO tiene una serie de características atractivas. En primer lugar, es un algoritmo con una interpretación física muy clara, lo que lo hace intuitivo. La sencillez del concepto básico (las muestras que representan soluciones potenciales son atraídas hacia soluciones mejores de forma similar a como los cuerpos materiales son atraídos hacia objetos más masivos) garantiza que el algoritmo funcione de forma transparente y sea fácil de aplicar.
Sin embargo, las pruebas también han revelado importantes limitaciones del CFO que deben revisarse o mejorarse. El exceso de confianza en la distribución inicial de las muestras es uno de los principales problemas: debido al mecanismo determinista del movimiento, las posiciones iniciales de las muestras predeterminan en gran medida el resultado final de la búsqueda.
El mecanismo de atracción unidireccional, por el que solo las mejores soluciones influyen en las peores y no a la inversa, aunque tiene una justificación lógica, puede limitar considerablemente la capacidad del algoritmo para explorar el espacio de búsqueda. Introducir un mecanismo adaptativo que permita también cierta influencia de soluciones peores, especialmente en las primeras fases de la búsqueda, podría mejorar la capacidad del algoritmo para detectar regiones prometedoras del espacio de soluciones.

Figura 2. Clasificación por colores de los algoritmos según las pruebas respectivas

Figura 3. Histograma de los resultados de las pruebas de algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de puntuación está en el archivo)
Ventajas y desventajas del algoritmo CFO:
Ventajas:
- Funciona bien en funciones de dimensionalidad media.
Desventajas:
- No funciona bien con funciones de baja y alta dimensionalidad.
- La capacidad de búsqueda en funciones discretas es bastante floja.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | #C_AO.mqh | Archivo de inclusión | Clase padre de algoritmos de población optimizaciones |
| 2 | #C_AO_enum.mqh | Archivo de inclusión | Enumeración de los algoritmos de optimización basados en la población |
| 3 | TestFunctions.mqh | Archivo de inclusión | Biblioteca de funciones de prueba |
| 4 | TestStandFunctions.mqh | Archivo de inclusión | Biblioteca de funciones del banco de pruebas |
| 5 | Utilities.mqh | Archivo de inclusión | Biblioteca de funciones auxiliares |
| 6 | CalculationTestResults.mqh | Archivo de inclusión | Script para calcular los resultados en una tabla comparativa |
| 7 | Testing AOs.mq5 | Script | Banco de pruebas único para todos los algoritmos de optimización basados en la población |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización |
| 9 | Test_AO_CFO.mq5 | Script | Banco de pruebas CFO |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/17167
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Desarrollo de estrategias comerciales de tendencia basadas en el aprendizaje automático
Desarrollo de estrategias comerciales de tendencia basadas en el aprendizaje automático
 Técnicas de remuestreo para la evaluación de predicciones y clasificaciones en MQL5
Técnicas de remuestreo para la evaluación de predicciones y clasificaciones en MQL5
 Automatización de estrategias de trading en MQL5 (Parte 12): Implementación de la estrategia Mitigation Order Blocks (MOB)
Automatización de estrategias de trading en MQL5 (Parte 12): Implementación de la estrategia Mitigation Order Blocks (MOB)
 Ondas triangulares y de sierra: herramientas para el tráder
Ondas triangulares y de sierra: herramientas para el tráder
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso