Modelos ocultos de Márkov en sistemas comerciales de aprendizaje automático

MetaTrader 5 — Trading | 17 febrero 2026, 14:38

[Eliminado]

Contenido

Introducción

Los modelos de Márkov ocultos (HMM) son una potente clase de modelos probabilísticos diseñados para analizar datos secuenciales, donde los eventos observados dependen de alguna secuencia de estados no observados (ocultos) que forman un proceso de Márkov. Los HMM son procesos estocásticos duales caracterizados por un conjunto finito de estados ocultos y una secuencia de eventos observables cuya probabilidad depende del estado oculto actual. Los principales supuestos del HMM incluyen la propiedad de Márkov para estados ocultos, lo que significa que la probabilidad de transición al siguiente estado depende solo del estado actual y la independencia de las observaciones dado el conocimiento del estado oculto actual.

Los modelos de Márkov ocultos han encontrado una amplia aplicación en varios campos, incluido el reconocimiento de voz e imágenes, el procesamiento del lenguaje natural (por ejemplo, el etiquetado gramatical), la bioinformática (análisis de secuencias de ADN y proteínas) y el análisis de series temporales (predicciones, detección de anomalías). La capacidad de modelar sistemas cuya estructura interna no resulta directamente observable pero que influye en resultados observables hace de los HMM una herramienta valiosa para analizar relaciones complejas dependientes del tiempo. Las observaciones en dichos modelos suponen solo reflejos indirectos de procesos ocultos, y comprender estos procesos puede proporcionar información importante sobre la dinámica del sistema.

La biblioteca hmmlearn es un conjunto de algoritmos en Python para el aprendizaje no supervisado (modelos de Márkov ocultos). Está diseñado para proporcionar herramientas simples y eficientes para trabajar con SMM, siguiendo la API de la biblioteca scikit-learn, lo cual facilita la integración en proyectos de aprendizaje automático existentes y simplifica el proceso de aprendizaje para los usuarios familiarizados con scikit-learn. Hmmlearn está construido sobre bibliotecas científicas fundamentales de Python como NumPy, SciPy y Matplotlib.

Las principales capacidades de hmmlearn incluyen la implementación de varios modelos HMM con diferentes tipos de distribuciones de emisión, entrenamiento de parámetros del modelo a partir de los datos observados, inferencia de las secuencias más probables de los estados ocultos, generación de muestras a partir de los modelos entrenados y capacidad de guardar y cargar modelos entrenados. La variedad de modelos implementados permite a los usuarios elegir el tipo de distribución de emisiones más apropiado, dependiendo de la naturaleza de sus datos. El tipo de datos (continuos, discretos, contadores) determina qué distribución de probabilidad describe mejor el proceso de generación de observaciones en cada estado oculto.

Algoritmos presentados en la biblioteca hmmlearn

La biblioteca hmmlearn implementa los siguientes modelos HMM básicos:

hmm.CategoricalHMM: para modelar secuencias de observaciones categóricas (discretas).
hmm.GaussianHMM: para modelar secuencias de observaciones continuas asumiendo una distribución gaussiana en cada estado oculto.
hmm.GMMHMM: para modelar secuencias de observaciones continuas donde las emisiones de cada estado oculto se describen usando una mezcla de distribuciones gaussianas.
hmm.MultinomialHMM: para modelar secuencias de observaciones discretas, donde cada estado tiene una distribución de probabilidad sobre un conjunto fijo de símbolos.
hmm.PoissonHMM: para modelar secuencias de datos que representan contadores de eventos, donde las emisiones de cada estado oculto siguen una distribución de Poisson.
vhmm.VariationalCategoricalHMM: una versión variacional de CategoricalHMM que usa métodos de inferencia variacional para el aprendizaje.
vhmm.VariationalGaussianHMM: una versión variacional de GaussianHMM diseñada para observaciones continuas distribuidas de acuerdo con una ley normal multivariada y entrenada con la ayuda de inferencia variacional.

Nos interesan los algoritmos que trabajan con datos continuos, por lo que solo consideraremos estos.

Descripción detallada de la clase hmm.GaussianHMM

La clase hmm.GaussianHMM de la biblioteca hmmlearn implementa un modelo de Márkov oculto con emisiones gaussianas. Este modelo se aplica cuando las variables observadas son continuas y se supone que siguen una distribución normal multivariada (gaussiana) en cada estado oculto.

El HMM gaussiano se usa ampliamente para modelar diversas series temporales, como datos financieros (por ejemplo, precios de acciones), lecturas de varios sensores y otros procesos continuos donde los valores observados pueden describirse mediante una distribución gaussiana en cada uno de los estados ocultos.

El constructor de la clase hmm.GaussianHMM toma los siguientes parámetros:

n_components (int, por defecto 1): define la cantidad de estados ocultos en el modelo. Cada estado estará asociado a su propia distribución gaussiana.
covariance_type ({"spherical", "diag", "full", "tied"}, por defecto "diag"): especifica el tipo de matriz de covarianza utilizada para cada estado. La elección del tipo de covarianza afecta directamente la complejidad del modelo y el número de parámetros estimados.

"spherical": cada estado utiliza la misma varianza para todas las características. La matriz de covarianza es un múltiplo de la matriz identidad.
"diag": cada estado utiliza una matriz de covarianza diagonal, asumiendo que las características dentro de un estado son estadísticamente independientes pero pueden tener varianzas distintas.
"full": cada estado utiliza una matriz de covarianza completa (sin restricciones), lo que nos permite modelar correlaciones entre características dentro de cada estado. Esta opción es la más flexible, pero requiere más datos para su evaluación y puede ser propensa a sobreajuste.
"tied": todos los estados ocultos comparten la misma matriz de covarianza completa. Esto permite considerar las correlaciones entre las características, pero supone que la estructura de estas correlaciones es la misma en todas las condiciones.

min_covar (flotante, por defecto 1e-3): establece el valor mínimo para los elementos diagonales de la matriz de covarianza para evitar que se degenere (por ejemplo, varianza cero) durante el entrenamiento y para evitar el sobreajuste.
startprob_prior (array, forma(n_components,), opcional): parámetros a priori de Dirichlet para las probabilidades iniciales startprob_, que determinan la probabilidad de iniciar la secuencia de observación en cada uno de los estados ocultos.
transmat_prior (array, forma(n_components, n_components), opcional): los parámetros del prior de Dirichlet para cada fila de la matriz de transición transmat_, que determina la probabilidad de transición entre estados ocultos.
means_prior(array, shape(n_components,), opcional): la media de la distribución normal previa para las medias (means_) de cada estado oculto.
means_weight(array, shape(n_components,), opcional): el peso (o precisión, varianza inversa) de la distribución normal previa para las medias (means_) de cada estado oculto.
covars_prior(array, shape(n_components,), opcional): parámetros de la distribución previa para la matriz de covarianza covars_. El tipo de esta distribución depende del parámetro covariance_type. Para "spherical" y "diag", estos son parámetros de la distribución gamma inversa, y para "full" y "tied", estos son parámetros asociados con la distribución Wishart inversa.
covars_weight(array, shape(n_components,), opcional): pesos de los parámetros de distribución anteriores para la matriz de covarianza covars_. De forma similar a covars_prior, la interpretación depende de covariance_type (parámetros de escala para distribuciones gamma inversa o Wishart inversa).
algorithm ({"viterbi", "map"}, opcional): el algoritmo utilizado para decodificar, es decir, para encontrar la secuencia más probable de estados ocultos correspondientes a la secuencia observada. "viterbi" implementa el algoritmo de Viterbi, y "map" (maximum a posteriori estimation) realiza un suavizado (forward-backward) para encontrar el estado más probable en cada instante.
random_state (RandomState o int, opcional): un objeto generador de números aleatorios o una seed entera para inicializar los parámetros del modelo de forma aleatoria, lo que garantiza resultados reproducibles.
n_iter (int, opcional): el número máximo de iteraciones realizadas por el algoritmo Expectation-Maximization (EM) al entrenar el modelo. El valor por defecto es 10.
tol (flotante, opcional): umbral de convergencia del algoritmo EM. Si el cambio en la verosimilitud logarítmica entre dos iteraciones consecutivas se vuelve inferior a este valor, se detiene el entrenamiento. El valor por defecto es 0,01.
verbose (bool, opcional): si se establece en True, la información de convergencia se escribirá en el error estándar en cada iteración. La convergencia también se puede monitorizar a través del atributo monitor_.
params (cadena, opcional): una cadena que especifica qué parámetros del modelo se actualizarán durante el entrenamiento. Puede contener una combinación de símbolos: 's' para probabilidades iniciales (startprob_), 't' para probabilidades de transición (transmat_), 'm' para medias (means_) y 'c' para covarianzas (covars_). El valor por defecto es 'stmc' (todos los parámetros se actualizan).
init_params (cadena, opcional): una cadena que indica qué parámetros del modelo se inicializarán antes de que comience el entrenamiento. Los símbolos tienen el mismo significado que en el parámetro params. El valor por defecto es 'stmc' (todos los parámetros están inicializados).
implementación (string, opcional): especifica si se utilizará la implementación logarítmica ("log") o de escala del algoritmo de avance-retroceso. De forma predeterminada, se usa "log" para compatibilidad con versiones anteriores, sin embargo, la implementación de "scaling" suele ser más rápida.

La inicialización de los parámetros GaussianHMM ocurre antes de entrenar el modelo usando el algoritmo EM. Los parámetros de inicialización definen el estado inicial del modelo. El parámetro init_params controla qué parámetros se inicializarán. Si algún parámetro no está incluido en init_params, se asume que su valor ya ha sido establecido manualmente.

Los valores iniciales de los parámetros se pueden establecer de forma aleatoria o calcularse según los datos proporcionados. La inicialización correcta de los parámetros puede afectar sustancialmente la tasa de convergencia del algoritmo EM y la calidad del modelo final, ya que el algoritmo EM puede quedar estancado en óptimos locales.

La optimización de los parámetros GaussianHMM se realiza usando el algoritmo iterativo Expectation-Maximization (EM). Este algoritmo consta de dos pasos principales que se realizan de forma iterativa hasta lograr la convergencia:

Paso E (Expectation): en este paso, dadas las estimaciones actuales de los parámetros del modelo y la secuencia de datos observada, se calculan las probabilidades posteriores de que el sistema estuviera en un determinado estado oculto en cada punto del tiempo. Generalmente esto se hace usando un algoritmo forward-backward.
Paso M (Maximization): En este paso, los parámetros del modelo (probabilidades iniciales, probabilidades de transición entre estados, medias y covarianzas para cada estado) se actualizan de manera de maximizar la verosimilitud logarítmica esperada de los datos observados, sujeto a las probabilidades posteriores calculadas en el paso E.

El proceso se repite hasta que se logra la convergencia, lo que se determina al alcanzar el número máximo de iteraciones indicado por el parámetro n_iter o cuando el cambio en la verosimilitud logarítmica entre iteraciones sucesivas se vuelve menor que el umbral tol especificado. El algoritmo EM aumenta de forma garantizada (o mantiene sin cambios) la verosimilitud logarítmica en cada iteración, sin embargo, no garantiza encontrar el máximo global y el resultado puede depender de la inicialización inicial de los parámetros.

La elección del parámetro covariance_type tiene un impacto directo en la estructura de la matriz de covarianza usada para modelar las emisiones en cada estado oculto.

Al elegir "spherical", se supone una covarianza isótropa, es decir, la varianza de todas las características en un estado dado es la misma y la matriz de covarianza es proporcional a la unidad.
"diag" indica el uso de una matriz de covarianza diagonal, lo cual significa que las características en cada condición se consideran estadísticamente independientes, aunque puedan tener varianzas diferentes.
"full" permite utilizar la matriz de covarianza completa, teniendo en cuenta las correlaciones entre diferentes características dentro de cada estado oculto.
"tied" significa que todos los estados ocultos comparten la misma matriz de covarianza completa. La elección del tipo de covarianza debe basarse en supuestos sobre la estructura de los datos en cada estado oculto. Los tipos de covarianza más complejos, como "full", pueden ajustarse mejor a los datos con dependencias complejas entre características, pero requieren más parámetros para estimarlos, lo que puede generar sobreajuste cuando los datos son insuficientes.

La flexibilidad que ofrecen los distintos parámetros de hmm.GaussianHMM permite a los investigadores adaptar el modelo a las características específicas de las series temporales financieras. En particular, el parámetro `covariance_type` nos permite realizar diferentes suposiciones sobre las relaciones entre las características en cada estado oculto.

Al ajustar los parámetros hmm.GaussianHMM para series temporales financieras, se deben tener en cuenta sus características específicas, como la volatilidad, los saltos de precio y las posibles desviaciones de las distribuciones respecto a la ley normal. El número de estados ocultos (n_components) debe elegirse según el número esperado de modos de mercado. Esto se puede determinar basándose en el conocimiento de expertos o usando criterios de selección de modelos como AIC o BIC.

Se recomienda comenzar con una cantidad pequeña de estados (por ejemplo, 2 o 3) y aumentarla según resulte necesario, controlando al mismo tiempo el riesgo de sobreajuste. Para series temporales financieras univariadas (por ejemplo, retornos), los tipos de covarianza "diag" o "spheric" pueden ser suficientes. Para series multivariadas (por ejemplo, retornos de múltiples activos o características como precio y volumen), "full" permite modelar correlaciones, pero aumenta la complejidad del modelo. El tipo de covarianza "tied" asume la misma estructura de correlación para todas las condiciones.

El parámetro min_covar ayuda a prevenir el sobreajuste garantizando que las variaciones no sean demasiado pequeñas. El valor por defecto de 1e-3 suele ser un buen punto de partida. La configuración de distribuciones a priori informativas (por ejemplo, utilizando startprob_prior y transmat_prior para reflejar ideas previas sobre las probabilidades del estado inicial y las tendencias de transición) puede resultar útil, especialmente cuando los datos son limitados. Por ejemplo, se podría esperar estabilidad en los modos de mercado, lo cual puede codificarse en la distribución previa de la matriz de transición.

Los parámetros n_iter y tol controlan el número máximo de iteraciones y el umbral de convergencia del algoritmo EM. Un valor mayor de n_iter puede provocar una mejor convergencia, pero también aumentará el tiempo de entrenamiento. Un valor menor de tol da como resultado criterios de convergencia más estrictos.

El preprocesamiento de datos financieros resulta crucial. Se recomienda usar retornos (cambios porcentuales) en lugar de precios y posiblemente incluir indicadores técnicos como medias móviles, medidas de volatilidad (por ejemplo, ATR) e indicadores de volumen como métricas. También se recomienda la normalización o estandarización de características. Las series temporales financieras con frecuencia no son estacionarias. Se debería considerar la diferenciación de los datos o el uso de una ventana deslizante para la estimación de parámetros para adaptarse a la dinámica cambiante del mercado.

Para encontrar la combinación óptima de hiperparámetros para un conjunto de datos financieros particular, se deben usar métodos como la búsqueda en cuadrícula o la optimización bayesiana (por ejemplo, utilizando Optuna). La naturaleza no estacionaria de las series temporales financieras requiere un preprocesamiento cuidadoso y posiblemente el uso de métodos adaptativos como el aprendizaje de ventana deslizante. El ajuste de los hiperparámetros también resulta crucial para garantizar que el modelo GaussianHMM capture eficazmente la dinámica subyacente del mercado sin sobreajustarse a los datos históricos.

Descripción detallada de la clase hmm.GMMHMM

La clase hmm.GMMHMM está diseñada para trabajar con emisiones continuas que se representan mejor mediante una mezcla de varias distribuciones gaussianas. Esto permite modelar patrones de emisión más complejos que usando una única distribución gaussiana, lo que resulta particularmente útil para datos con clústeres pronunciados dentro de cada estado oculto.

hmm.GMMHMM puede ser útil cuando la distribución de datos financieros dentro de un modo dado es multimodal o significativamente diferente de la gaussiana. Por ejemplo, los retornos en un modo de alta volatilidad pueden mostrar características diferentes dependiendo de la dirección del movimiento del precio. hmm.GMMHMM extiende las capacidades de hmm.GaussianHMM al permitir que cada estado oculto se asocie con una mezcla de distribuciones gaussianas. Esto resulta particularmente beneficioso para las series temporales financieras que pueden exhibir un comportamiento más complejo y no distribuido normalmente bajo diferentes modos de mercado.

El constructor de la clase hmm.GMMHMM incluye todos los parámetros de la clase hmm.GaussianHMM y también añade el parámetro n_mix (entero, por defecto 1) que especifica la cantidad de componentes de la mezcla en cada estado y los valores anteriores asociados con los pesos de la mezcla.
El parámetro covariance_type en GMMHMM tiene una opción "tied" ligeramente distinta: todos los componentes de la mezcla de cada estado comparten la misma matriz de covarianza completa.
Los parámetros params e init_params también incluyen el símbolo 'w' para controlar los pesos de la mezcla GMM.
La diferencia clave en los parámetros está en n_mix y los valores anteriores asociados para los pesos de la mezcla, lo cual permite un modelado más flexible de las probabilidades de emisión en cada estado oculto. La opción "tied" más sutil para la covarianza en GMMHMM también ofrece una forma adicional de restringir el modelo.

Al configurar los parámetros hmm.GMMHMM para series temporales financieras, seleccionar la cantidad de componentes de mezcla (n_mix) es un paso fundamental. El número de componentes de la mezcla debería representar mejor la distribución de datos financieros en cada estado oculto. Y esto puede requerir de experimentación. Resulta recomendable comenzar con una pequeña cantidad de componentes (por ejemplo, 2 o 3) y aumentarla si el modelo no se ajusta lo suficiente, pero evitando el sobreajuste.

Se pueden usar criterios de información como AIC o BIC para determinar el valor óptimo de n_mix. Otros parámetros se pueden ajustar de forma similar a los parámetros hmm.GaussianHMM, considerando las características específicas de los datos financieros. Por ejemplo, la elección de covariance_type influirá en cómo se modela la varianza dentro de cada componente de la mezcla. Seleccionar el número óptimo de componentes de la mezcla (n_mix) es un paso importante en el uso efectivo de hmm.GMMHMM para series temporales financieras. Esto implica equilibrar la capacidad del modelo para captar distribuciones de datos complejas con el riesgo de sobreajuste y puede requerir el uso de métodos como la validación cruzada o criterios de información para obtener estimaciones sólidas.

Descripción detallada de la clase vhmm.VariationalGaussianHMM

La clase vhmm.VariationalGaussianHMM es un modelo de Márkov oculto con emisiones gaussianas multivariadas que se entrena usando inferencia variacional en lugar del algoritmo de expectativa-maximización (EM) utilizado en hmm.GaussianHMM.

La inferencia variacional tiene como objetivo encontrar los parámetros de una distribución que estarían más cerca de la verdadera distribución posterior de las variables latentes y los parámetros del modelo. A diferencia del EM, que proporciona estimaciones puntuales de los parámetros, la inferencia variacional ofrece distribuciones posteriores para los parámetros del modelo, que pueden ser útiles para estimar la incertidumbre.

La principal diferencia de vhmm.VariationalGaussianHMM reside en el uso de inferencia variacional para el entrenamiento. Este enfoque bayesiano tiene ventajas sobre la estimación de máxima verosimilitud en hmm.GaussianHMM, especialmente al proporcionar una medida de incertidumbre a través de las distribuciones posteriores de los parámetros del modelo.

El constructor de la clase vhmm.VariationalGaussianHMM incluye parámetros n_components, covariance_type, algorithm, random_state, n_iter, tol, verbose, params, init_params e implementation similares a los de hmm.GaussianHMM.
Los parámetros adicionales clave relacionados con las distribuciones a priori son startprob_prior, transmat_prior, means_prior, beta_prior, dof_prior, scale_prior. Si estos parámetros se establecen en None, se utilizan distribuciones a priori predeterminadas. El parámetro beta_prior está relacionado con la precisión de la distribución previa normal para las medias. Los parámetros dof_prior y scale_prior determinan la distribución previa de la matriz de covarianza (distribución de Wishart inversa o gamma inversa según el tipo de covarianza).
La inicialización de vhmm.VariationalGaussianHMM requiere la especificación de distribuciones a priori para todos los parámetros del modelo. Estas distribuciones a priori juegan un papel importante en el proceso de aprendizaje, sobre todo cuando los datos son limitados y permiten incorporar conocimientos o creencias previas sobre los parámetros.

Al ajustar los parámetros de vhmm.VariationalGaussianHMM para series temporales financieras, la selección de distribuciones a priori es importante. Las distribuciones a priori actúan como una forma de regularización, evitando que el modelo se sobreajuste a los datos de entrenamiento. También permiten la inclusión de conocimientos o creencias existentes respecto a los parámetros del modelo.

Por ejemplo, si existen motivos para creer que la distribución inicial de estados (startprob_) debería ser relativamente uniforme, se puede usar una distribución previa de Dirichlet con parámetros simétricos cercanos a 1. De forma similar, las creencias sobre las probabilidades de transición (transmat_), los valores medios (means_prior) o las covarianzas (scale_prior, dof_prior) se pueden codificar a través de elecciones correspondientes de distribuciones a priori.

La elección de distribuciones a priori influye en las distribuciones posteriores resultantes de los parámetros del modelo después de entrenar con los datos. Las distribuciones a priori informativas (por ejemplo, con baja varianza alrededor de un valor dado) tendrán una influencia más fuerte, sesgando la distribución posterior hacia la previa. Las distribuciones a priori débiles o no informativas (por ejemplo, aquellas con grandes variaciones o distribuciones uniformes) tendrán menos influencia, lo cual permitirá que los datos dominen la distribución posterior.

Comparación del desempeño de los modelos para series temporales financieras

El modelo hmm.GaussianHMM es un modelo básico que supone que los datos financieros observados en cada estado oculto tienen una distribución gaussiana. Sus puntos fuertes son la simplicidad y la eficiencia computacional, lo cual lo hace adecuado para grandes conjuntos de datos y casos en los que no hay motivos para creer que las distribuciones se desvían significativamente de lo normal.

Sin embargo, su debilidad es el supuesto de distribuciones normales, que puede no ser válido para muchas series temporales financieras caracterizadas por la asimetría, la curtosis y las colas pesadas. En escenarios donde los datos financieros de cada modo están relativamente bien aproximados por una distribución normal, hmm.GaussianHMM puede funcionar bien, por ejemplo, al modelar modos de mercado importantes en datos diarios o semanales. También puede mostrar un peor rendimiento al modelar datos de alta frecuencia o datos sujetos a picos y distribuciones no normales.

El modelo hmm.GMMHMM amplía las capacidades de hmm.GaussianHMM al permitir utilizar una combinación de distribuciones gaussianas para modelar las emisiones en cada estado oculto. Su fortaleza reside en su capacidad para modelar distribuciones multimodales más complejas, lo que lo hace más adecuado para datos financieros que pueden exhibir diferentes subpatrones dentro de un modo de mercado único. Por ejemplo, durante períodos de alta volatilidad, los rendimientos pueden comportarse de forma diferente dependiendo de la dirección del mercado.

La debilidad de hmm.GMMHMM reside en el aumento en el número de parámetros, lo que puede provocar un sobreajuste, especialmente con datos limitados. Además, el entrenamiento puede resultar computacionalmente más costoso en comparación con hmm.GaussianHMM.

hmm.GMMHMM puede funcionar mejor al modelar series temporales financieras donde las distribuciones dentro de los modos no son normales o multimodales, como cuando se analizan datos intradiarios o de volatilidad. Puede tener un peor rendimiento al modelar modos simples con distribuciones aproximadamente normales o con conjuntos de datos muy pequeños donde el riesgo de sobreajuste resulta elevado.

El modelo vhmm.VariationalGaussianHMM utiliza inferencia variacional para el entrenamiento, que supone un enfoque bayesiano. Su fortaleza se muestra en la capacidad de ofrecer distribuciones posteriores de parámetros, lo que permite evaluar la incertidumbre del modelo. El enfoque bayesiano también puede resultar útil cuando los datos son limitados, gracias al uso de distribuciones a priori que pueden regularizar el modelo e incorporar conocimiento previo.

Una debilidad de vhmm.VariationalGaussianHMM es la dificultad de ajustar las distribuciones a priori, lo cual puede afectar significativamente los resultados. Además, la inferencia variacional supone un método de aproximación, y la distribución posterior resultante puede diferir de la distribución posterior verdadera.

vhmm.VariationalGaussianHMM puede funcionar mejor al modelar series temporales financieras donde la incertidumbre de los parámetros resulta importante o cuando hay datos limitados disponibles y se debe utilizar conocimiento previo. Puede tener un peor desempeño si las distribuciones a priori están mal elegidas o si se necesita una precisión muy alta en las estimaciones de los parámetros, que el método de máxima verosimilitud puede proporcionar en el que caso de que haya datos suficientes.

La elección del modelo está influenciada por factores como la cantidad de datos disponibles, la complejidad de la dinámica del mercado y los requisitos de interpretabilidad del modelo. Para conjuntos de datos grandes y dinámicas de mercado relativamente simples, hmm.GaussianHMM puede resultar suficiente y preferible debido a su simplicidad y eficiencia computacional. Para dinámicas más complejas o distribuciones no normales, podría ser necesario hmm.GMMHMM. Si la evaluación de la incertidumbre es importante o hay pocos datos disponibles, entonces se debe considerar vhmm.VariationalGaussianHMM.

Conclusión y recomendaciones

Para las series temporales financieras, un modelo potencialmente mejor o peor depende del problema específico y de las características de los datos.

En general, si los datos financieros dentro de los modos de mercado pueden aproximarse razonablemente mediante una distribución gaussiana, hmm.GaussianHMM es una opción simple y eficiente. Si las distribuciones son más complejas o multimodales, hmm.GMMHMM puede ofrecer un mejor ajuste, pero requiere una configuración más cuidadosa y puede ser más propenso al sobreajuste. vhmm.VariationalGaussianHMM ofrece un enfoque bayesiano con la capacidad de estimar la incertidumbre, lo que puede ser útil en ciertos escenarios, pero requiere comprensión y selección adecuada de las distribuciones a priori.

Debemos destacar que la elección del modelo no puede hacerse únicamente sobre bases teóricas. La validación empírica y las pruebas retrospectivas sobre datos financieros reales son pasos necesarios a la hora de determinar qué modelo es el más adecuado para un problema particular. Para comparar el desempeño de los modelos y seleccionar el más adecuado para resolver un problema particular de análisis de series temporales financieras, se deben usar varias métricas de desempeño, como la verosimilitud logarítmica, la precisión de las previsiones y métricas financieras específicas (por ejemplo, MAPE, R^2).

Métodos para determinar matrices de covarianza a priori para series temporales en la biblioteca hmmlearn

Un tipo común de HMM es el modelo de emisión gaussiana, donde se supone que los datos observados en cada estado oculto se distribuyen según una ley normal multivariada. Los parámetros de esta distribución son el vector de valores medios y la matriz de covarianza, que determina la forma, orientación y grado de dependencia entre los componentes de los datos observados.

Al entrenar HMM gaussianos, especialmente cuando se usan enfoques bayesianos como la inferencia variacional, la definición de matrices de covarianza previa juega un papel importante. El conocimiento a priori sobre la estructura de covarianza de una serie temporal puede ayudar sustancialmente durante el entrenamiento del modelo, especialmente en situaciones donde la cantidad de datos disponibles es limitada. Los valores anteriores a priori especificados incorrectamente pueden conducir a resultados subóptimos, problemas de convergencia en los algoritmos de aprendizaje o sobreajuste del modelo.

La biblioteca Python hmmlearn ofrece las clases hmm.GaussianHMM (y hmm.GMMHMM) y vhmm.VariationalGaussianHMM para trabajar con HMM con emisiones gaussianas. La clase hmm.GaussianHMM implementa el entrenamiento del modelo usando el algoritmo clásico Expectation-Maximization (EM), mientras que vhmm.VariationalGaussianHMM ofrece un enfoque bayesiano basado en inferencia variacional.

Ambas clases ofrecen parámetros para influir en el proceso de entrenamiento y la inicialización del modelo, incluida la capacidad de especificar distribuciones a priori en las matrices de covarianza. En particular, el parámetro covariance_type permite seleccionar el tipo de matriz de covarianza (esférica, diagonal, completa o vinculada), y los parámetros covars_prior y covars_weight en hmm.GaussianHMM, así como scale_prior y dof_prior en vhmm.VariationalGaussianHMM, permiten indicar distribuciones a priori en las covarianzas. El uso correcto de estos parámetros requiere una comprensión de los distintos métodos para determinar matrices de covarianza previa para series temporales.

Métodos para determinar matrices de covarianza a priori para series temporales

Existen varios enfoques para determinar matrices de covarianza a priori para series temporales, cada uno basado en distintos supuestos sobre los datos y la información previa disponible.

Evaluación empírica. Una de las formas más directas es estimar la matriz de covarianza directamente a partir de datos de series temporales previamente recopilados. La matriz de covarianza muestral refleja la covarianza entre diferentes componentes de una serie temporales, donde cada elemento (i, j) de la matriz representa la covarianza muestral entre los componentes i-ésimo y j-ésimo, mientras que los elementos diagonales representan las varianzas muestrales.

Para una serie temporal X de longitud T y dimensionalidad p, la matriz de covarianza muestral Σ̂ se puede calcular utilizando la fórmula estándar. Sin embargo, la aplicación de la estimación empírica a series temporales tiene sus limitaciones.

En primer lugar, se supone que la serie temporal es estacionaria, es decir, sus propiedades estadísticas, como la media y la covarianza, no cambian con el paso del tiempo.

En segundo lugar, para obtener una estimación fiable, se requiere una cantidad de datos suficiente en comparación con la dimensionalidad de la serie temporal.

En tercer lugar, cuando el tamaño de la muestra es pequeño en comparación con la dimensionalidad, puede surgir el problema de la singularidad de la matriz de covarianza, lo cual la hace inadecuada para su uso en algunos algoritmos.

A pesar de estas limitaciones, la estimación empírica puede servir como un punto de partida razonable si disponemos de suficientes datos estacionarios.

Métodos de compresión (Shrinkage). En situaciones donde la estimación empírica de la matriz de covarianza puede no ser fiable debido al volumen limitado de datos o a la alta dimensionalidad, se pueden utilizar métodos de compresión. Estos métodos combinan una matriz de covarianza muestral con una matriz objetivo, usando un factor de compresión para determinar el peso de cada matriz.

La matriz objetivo puede ser, por ejemplo, una matriz unitaria (asumiendo la independencia de los componentes), una matriz diagonal (asumiendo que no haya correlación entre componentes) o una matriz de varianza constante. La fórmula para la compresión lineal es Rα = (1 − α)S + αT, donde S es la matriz de covarianza muestral, T es la matriz objetivo y α ∈ es el coeficiente de compresión.

Los métodos de compresión resultan especialmente útiles cuando la cantidad de datos es limitada, ya que permiten reducir el error en la estimación de la matriz de covarianza, mejorar su estabilidad y evitar el sobreajuste del modelo. La elección de la estructura de destino supone la presencia de cierta información a priori sobre la naturaleza de las dependencias en los datos.

Utilizando distribuciones a priori informativas. Si existe conocimiento previo sobre el dominio del tema o la estructura de covarianza de la serie temporal, este conocimiento puede incorporarse formalmente al modelo usando distribuciones a priori informativas.

Para las matrices de covarianza, a menudo se usa la distribución Wishart inversa, que es la distribución previa conjugada para las matrices de covarianza en la distribución normal multivariada. Los parámetros de la distribución Wishart inversa son la matriz de escala (scale matrix) y los grados de libertad (degrees of freedom).

La elección de los parámetros de la distribución a priori debe reflejar las creencias a priori existentes sobre la estructura de covarianza. Podemos formar distribuciones a priori informativas basándonos en los resultados de investigaciones previas, el conocimiento de expertos o el análisis de series temporales similares. El uso de dichos antecedentes puede mejorar sustancialmente la calidad del entrenamiento del modelo, sobre todo cuando se dispone de un conocimiento previo razonable.

Distribuciones a priori no informativas. En los casos en que no existen creencias previas fuertes sobre la estructura de covarianza de la serie temporal, se pueden utilizar distribuciones a priori no informativas. El propósito de estos datos previos es minimizar su influencia en la distribución posterior, permitiendo que los datos determinen en gran medida los resultados del aprendizaje.

Un ejemplo de una distribución a priori no informativa para la matriz de covarianza es la distribución de Jeffreys. Para las matrices de correlación, a menudo se usa la prior LKJ, que garantiza una distribución uniforme en el espacio de matrices de correlación o permite especificar diferentes niveles de concentración alrededor de la correlación cero. Sin embargo, debe considerarse que la identificación de un prior verdaderamente no informativo puede ser un desafío, e incluso los priores débilmente informativos pueden influir en los resultados, sobre todo cuando los datos son limitados.

Supuestos estructurales sobre series temporales. Si una serie temporal exhibe propiedades de autocorrelación conocidas, este conocimiento puede usarse para formar una matriz de covarianza a priori. Por ejemplo, analizar la función de autocorrelación (ACF) y la función de autocorrelación parcial (PACF) puede ayudar a revelar el orden de los procesos autorregresivos (AR) o de media móvil (MA) que pueden describir una serie temporal.

A partir de los parámetros de estos modelos, podemos construir una matriz de covarianza a priori que refleje dependencias temporales conocidas. Por ejemplo, para un proceso AR(1), la estructura de la matriz de covarianza dependerá del parámetro de autocorrelación. Este enfoque supone que las series temporales pueden describirse adecuadamente usando algún modelo de series temporales y que los parámetros de este modelo pueden estimarse a partir de datos previos.

Aplicación de métodos para determinar matrices de covarianza a priori en hmmlearn

La biblioteca hmmlearn ofrece varias opciones para definir matrices de covarianza previa utilizando las clases hmm.GaussianHMM y vhmm.VariationalGaussianHMM.

La estimación empírica de la matriz de covarianza obtenida a partir de los datos preliminares se puede usar para inicializar directamente el atributo covars_ tanto en la clase hmm.GaussianHMM como en la clase vhmm.VariationalGaussianHMM. De forma similar, los resultados de la aplicación de los métodos de compresión a la matriz de covarianza empírica se pueden utilizar para inicializar covars_.

Para especificar distribuciones a priori informativas, la clase hmm.GaussianHMM ofrece los parámetros covars_prior y covars_weight. Estos parámetros controlan los parámetros de la distribución previa para la matriz de covarianza covars_. El tipo de distribución previa depende del valor del parámetro covariance_type. Si covariance_type se establece en "spheric" o "diag", se utiliza la distribución gamma inversa. Si covariance_type se establece en "full" o "tied", se utiliza la distribución Wishart inversa.

El parámetro covars_prior se interpreta como un parámetro de forma para la distribución gamma inversa y se relaciona con los grados de libertad de la distribución Wishart inversa. El parámetro covars_weight es un parámetro de escala para la distribución gamma inversa y se relaciona con la matriz de escala para la distribución Wishart inversa.

La clase vhmm.VariationalGaussianHMM también permite especificar distribuciones a priori informativas en matrices de covarianza utilizando los parámetros scale_prior y dof_prior. El parámetro dof_prior indica los grados de libertad para la distribución Wishart (para "full" y "tied") o la distribución gamma inversa (para "spheric" y "diag"). El parámetro scale_prior especifica la matriz de escala para la distribución Wishart (para "full" y "tied") o el parámetro de escala para la distribución gamma inversa (para "spheric" y "diag"). Estos parámetros determinan las creencias a priori sobre la estructura de covarianza en un modelo bayesiano implementado usando inferencia variacional.

Para especificar distribuciones a priori no informativas, se pueden utilizar los parámetros correspondientes covars_prior, covars_weight, scale_prior y dof_prior, estableciendo sus valores de manera que la distribución previa sea débil o difusa. Por ejemplo, podemos especificar valores muy pequeños para parámetros relacionados con la precisión o la escala inversa, o valores muy grandes para parámetros relacionados con la escala.

Finalmente, las suposiciones estructurales sobre la serie temporal se pueden considerar construyendo la matriz de covarianza correspondiente basada en el análisis de autocorrelación y utilizando esta matriz para inicializar el atributo covars_ en ambas clases hmmlearn.

Identificación de modos de mercado con HMM: pasamos a la práctica

Antes de leer esta sección, le recomiendo leer los dos artículos anteriores:

Estos artículos describen el principio básico de creación de los sistemas comerciales utilizados. Pero en lugar de inferencia causal o clusterización de modos de mercado, se usarán modelos ocultos de Márkov para identificar modos de mercado. De esta manera, podrá probar y comparar estos enfoques entre sí y formarse su propia opinión sobre su eficacia.

Antes de comenzar, asegúrese de tener instalados los paquetes necesarios:

import math
import pandas as pd
from datetime import datetime
from catboost import CatBoostClassifier

from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans
from hmmlearn import hmm, vhmm

from bots.botlibs.labeling_lib import *
from bots.botlibs.tester_lib import tester_one_direction
from bots.botlibs.export_lib import export_model_to_ONNX

El algoritmo identificará los modos de mercado entrenando modelos de Márkov ocultos usando el mismo principio descrito en los artículos sobre clusterización de modos de mercado. Por consiguiente, los cambios al código solo afectarán el proceso de determinación de los modos de mercado.

A continuación le mostramos la función que define los modos de mercado:

def markov_regime_switching(dataset, n_regimes: int, model_type="GMMHMM") -> pd.DataFrame:
    data = dataset[(dataset.index < hyper_params['forward']) & (dataset.index > hyper_params['backward'])].copy()
    
    # Extract meta features
    meta_X = data.loc[:, data.columns.str.contains('meta_feature')]
    
    if meta_X.shape[1] > 0:
        # Format data for HMM (requires 2D array)
        X = meta_X.values
        
        # Features normalization before training
        from sklearn.preprocessing import StandardScaler
        scaler = StandardScaler()
        X_scaled = scaler.fit_transform(X)
        
        # Create and train the HMM model
        if model_type == "HMM":
            model = hmm.GaussianHMM(
                n_components=n_regimes,
                covariance_type="spherical",
                n_iter=10,
            )
        elif model_type == "GMMHMM":
            model = hmm.GMMHMM(
                n_components=n_regimes,
                covariance_type="spherical",
                n_iter=10,
                n_mix=3,
            )
        elif model_type == "VARHMM":
            model = vhmm.VariationalGaussianHMM(
                n_components=n_regimes,
                covariance_type="spherical",
                n_iter=10,
            )
           
        # Fit the model
        model.fit(X_scaled)     
        # Predict the hidden states (regimes)
        hidden_states = model.predict(X_scaled)
        # Assign states to clusters
        data['clusters'] = hidden_states
        
    return data

El código presenta 3 modelos descritos en la parte teórica, los cuales tienen los parámetros por defecto. Primero debe asegurarse de que funcionen y luego pasar a configurar los parámetros. Puede seleccionar uno de los modelos al llamar a la función y probar directamente la calidad de la clusterización.

El ciclo de entrenamiento sigue siendo el mismo, salvo la función de identificación de los modos de mercado:

for i in range(1):
    data = markov_regime_switching(dataset, n_regimes=hyper_params['n_clusters'], model_type="HMM")
    sorted_clusters = data['clusters'].unique()
    sorted_clusters.sort()
    for clust in sorted_clusters:
        clustered_data = data[data['clusters'] == clust].copy()
        if len(clustered_data) < 500:
            print('too few samples: {}'.format(len(clustered_data)))
            continue
    
        clustered_data = get_labels_one_direction(clustered_data,
                                       markup=hyper_params['markup'],
                                       min=1,
                                       max=15,
                                       direction=hyper_params['direction'])
        
        print(f'Iteration: {i}, Cluster: {clust}')
        clustered_data = clustered_data.drop(['close', 'clusters'], axis=1)

        meta_data = data.copy()
        meta_data['clusters'] = meta_data['clusters'].apply(lambda x: 1 if x == clust else 0)
        models.append(fit_final_models(clustered_data, meta_data.drop(['close'], axis=1)))

Los hiperparámetros de entrenamiento se establecen de la forma siguiente:

hyper_params = {
    'symbol': 'XAUUSD_H1',
    'export_path': '/drive_c/Program Files/MetaTrader 5/MQL5/Include/Trend following/',
    'model_number': 0,
    'markup': 0.2,
    'stop_loss':  10.000,
    'take_profit': 5.000,
    'periods': [i for i in range(5, 300, 30)],
    'periods_meta': [5],
    'backward': datetime(2000, 1, 1),
    'forward': datetime(2024, 1, 1),
    'full forward': datetime(2026, 1, 1),
    'direction': 'buy',
    'n_clusters': 5,
}

El periodo de características en el que se realizará el entrenamiento de los modelos ocultos de Márkov es igual a 5.
Dirección de compra de oro.
El número estimado de modos es 5.

Todos los modelos se probarán en desviaciones estándar en una ventana móvil (volatilidad) como características:

def get_features(data: pd.DataFrame) -> pd.DataFrame:
    pFixed = data.copy()
    pFixedC = data.copy()
    count = 0

    for i in hyper_params['periods']:
        pFixed[str(count)] = pFixedC.rolling(i).std()
        count += 1
    
    for i in hyper_params['periods_meta']:
        pFixed[str(count)+'meta_feature'] = pFixedC.rolling(i).std()
        count += 1

    return pFixed.dropna()

Resultados del entrenamiento con los parámetros por defecto

El algoritmo GaussianHMM con parámetros por defecto ha demostrado la capacidad de encontrar eficazmente estados (modos) ocultos, lo que ha redundado en una curva de balance aceptable en los datos de prueba.

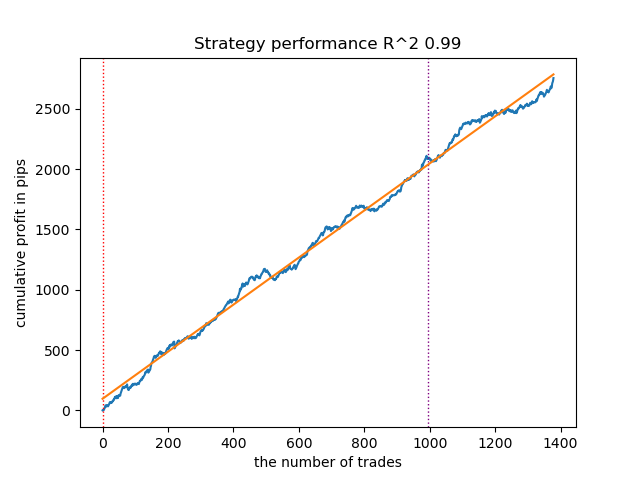
Fig. 1. Prueba de GaussianHMM con la configuración predeterminada

El algoritmo GMMHMM también ha tenido un buen desempeño, sin cambios notables en la calidad de los modelos observados.

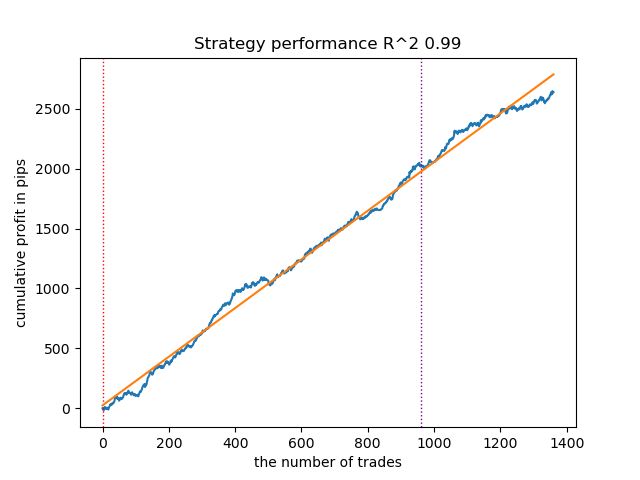
Fig. 2. Prueba de GMMHMM con la configuración predeterminada

El algoritmo VariationalGaussianHMM puede parecer un caso atípico, pero después de unos cuantos reentrenamientos, puede producir curvas de mejor aspecto.

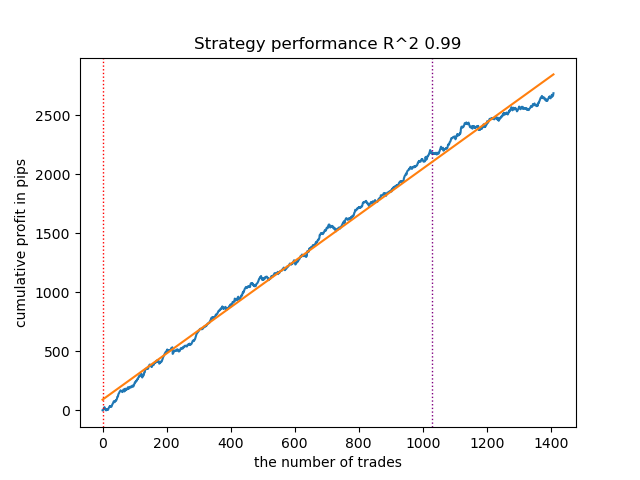
Fig. 3. Prueba de VariationalGaussianHMM con configuración predeterminada

En general, todos los algoritmos han demostrado su eficacia, lo cual significa que podemos pasar a ajustar sus parámetros.

Aumento del número de iteraciones de inicio (n_iter = 100)

Con un aumento en el número de iteraciones de entrenamiento de los modelos de Márkov, los resultados con los nuevos datos han mejorado algo para todas las modificaciones del algoritmo. Aparentemente, esto se debe al hecho de que los algoritmos han encontrado óptimos locales más rentables. En general, en esta etapa, no se han observado diferencias significativas en la calidad de los modelos resultantes para los diferentes algoritmos. Pero GaussianHMM se ha entrenado algo más rápido debido a su simplicidad.

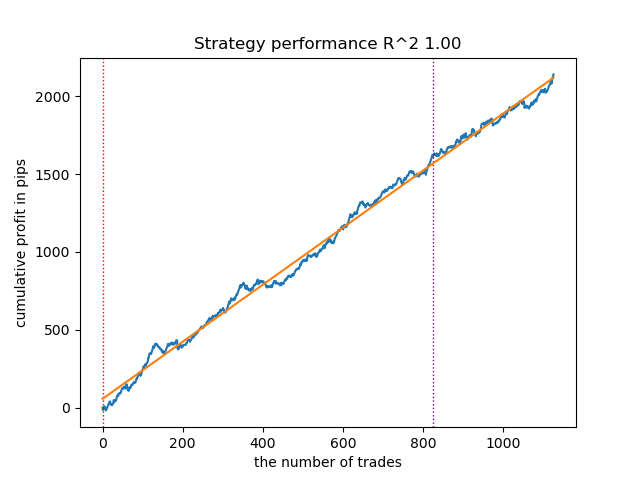
Figura 4. Prueba de GaussianHMM con n_iter = 100

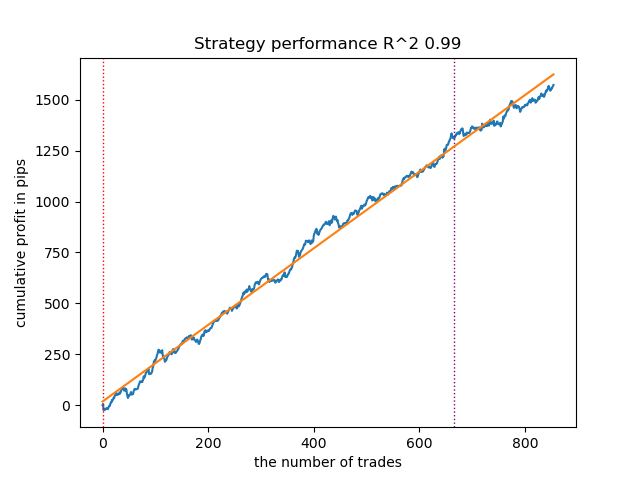
Figura 5. Prueba de GMMHMM con n_iter = 100

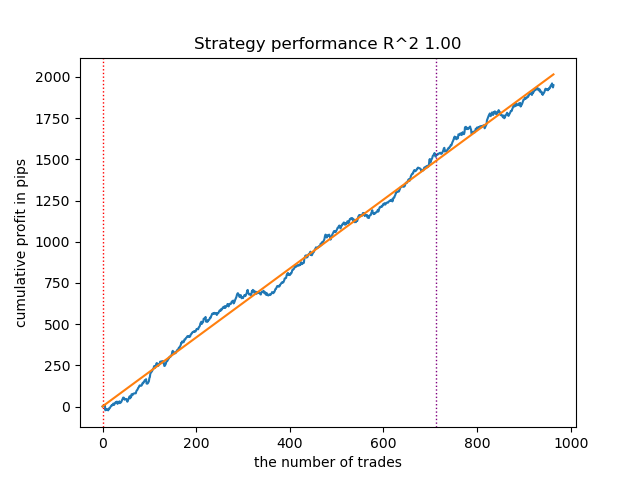
Figura 6. Prueba de HMM gaussiano variacional con n_iter = 100

Reducción de número de modos de mercado a tres

El número de iteraciones influye en la calidad de los modelos; dejaremos este parámetro igual a 100 iteraciones. Intentaremos reducir el número de modos (estados ocultos de los modelos) a tres y a observaremos los resultados.

hyper_params = {
    'symbol': 'XAUUSD_H1',
    'export_path': '/drive_c/Program Files/MetaTrader 5/MQL5/Include/Trend following/',
    'model_number': 0,
    'markup': 0.2,
    'stop_loss':  10.000,
    'take_profit': 5.000,
    'periods': [i for i in range(5, 300, 30)],
    'periods_meta': [5],
    'backward': datetime(2000, 1, 1),
    'forward': datetime(2024, 1, 1),
    'full forward': datetime(2026, 1, 1),
    'direction': 'buy',
    'n_clusters': 3,
}

GaussianHMM, GMMHMM y VariationalGaussianHMM han tenido un buen desempeño al identificar los tres modos de mercado, pero el último ha requerido varios reinicios de entrenamiento.

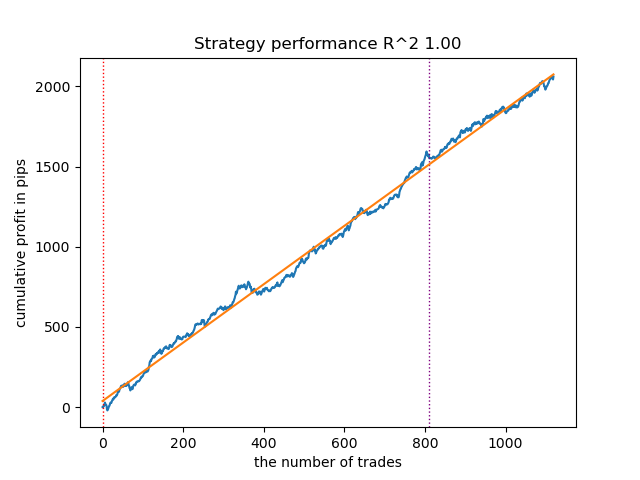
Figura 7. Prueba de VariationalHMM con n_iter = 100 y tres modos

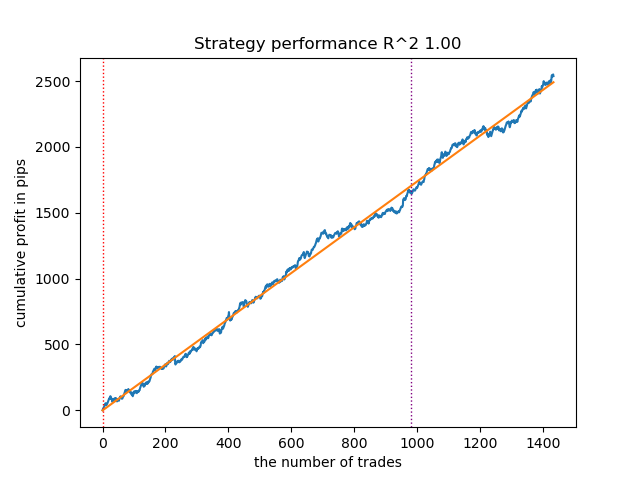
Figura 8. Prueba de GMMHMM con n_iter = 100 y tres modos

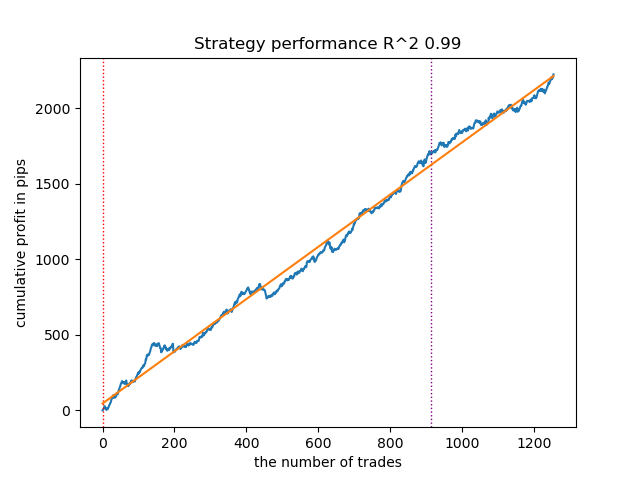
Figura 9. Prueba de HMM gaussiano variacional con n_iter = 100 y tres modos

Creación de matrices de covarianza a priori para modelos ocultos de Márkov

En la parte teórica del artículo analizamos 5 métodos para determinar las matrices de covarianza a priori para las series temporales. El primer y último método son los más adecuados para nosotros, vamos a recordarlos:

Evaluación empírica. Una de las formas más directas es estimar la matriz de covarianza directamente a partir de datos de series temporales previamente recopilados. La matriz de covarianza muestral refleja la covarianza entre los diferentes componentes de la serie temporal, donde cada elemento (i, j) de la matriz representa la covarianza muestral entre los componentes i-ésimo y j-ésimo, mientras que los elementos diagonales son las varianzas muestrales. Para una serie temporal X de longitud T y dimensionalidad p, la matriz de covarianza muestral Σ̂ se puede calcular utilizando la fórmula estándar. Sin embargo, la aplicación de la estimación empírica a series temporales tiene sus limitaciones. En primer lugar, se supone que la serie temporal es estacionaria, es decir, sus propiedades estadísticas, como la media y la covarianza, no cambian a lo largo del tiempo. En segundo lugar, para obtener una estimación fiable se requiere una cantidad de datos suficiente en comparación con la dimensionalidad de la serie temporal. En tercer lugar, cuando el tamaño de la muestra es pequeño en comparación con la dimensionalidad, puede surgir el problema de la singularidad de la matriz de covarianza, lo cual la hace inadecuada para su uso en algunos algoritmos. A pesar de estas limitaciones, la estimación empírica puede servir como un punto de partida razonable si disponemos de suficientes datos estacionarios.
Supuestos estructurales sobre las series temporales. Si una serie temporal exhibe propiedades de autocorrelación conocidas, este conocimiento puede usarse para formar una matriz de covarianza a priori. Por ejemplo, analizar la función de autocorrelación (ACF) y la función de autocorrelación parcial (PACF) puede ayudar a revelar el orden de los procesos autorregresivos (AR) o de media móvil (MA) que pueden describir una serie temporal. A partir de los parámetros de estos modelos, podemos construir una matriz de covarianza a priori que refleje dependencias temporales conocidas. Por ejemplo, para un proceso AR(1), la estructura de la matriz de covarianza dependerá del parámetro de autocorrelación. Este enfoque supone que las series temporales pueden describirse adecuadamente usando algún modelo de series temporales y que los parámetros de este modelo pueden estimarse a partir de datos previos.

Sin embargo, no podemos decir con certeza que las series temporales financieras puedan describirse adecuadamente usando modelos tan simples. Los experimentos han demostrado que dichos priores no siempre mejoran los resultados de la determinación de los estados ocultos de Márkov. Asimismo, hemos experimentado con la clusterización previa utilizando k-means para inicializar las matrices de transición con los valores obtenidos. Esto ha dado como resultado que los modelos de Márkov ocultos provocan resultados similares a los del artículo anterior, donde se producía una clusterización del modo de mercado con poca o ninguna mejora en la curva de balance en los nuevos datos.

Creación de valores anteriores basados en clusterización

El script de entrenamiento presenta una función experimental para precalcular priores mediante clusterización y luego entrenar modelos de Márkov ocultos.

def markov_regime_switching_prior(dataset, n_regimes: int, model_type="HMM", n_iter=100) -> pd.DataFrame:
    data = dataset[(dataset.index < hyper_params['forward']) & (dataset.index > hyper_params['backward'])].copy()
    
    # Extract meta features
    meta_X = data.loc[:, data.columns.str.contains('meta_feature')]
    
    if meta_X.shape[1] > 0:
        # Format data for HMM (requires 2D array)
        X = meta_X.values
        
        # Features normalization before training
        scaler = StandardScaler()
        X_scaled = scaler.fit_transform(X)
        
        # Calculate priors from meta_features using k-means clustering
        from sklearn.cluster import KMeans
        
        # Use k-means to cluster the data into n_regimes groups
        kmeans = KMeans(n_clusters=n_regimes, n_init=10)
        cluster_labels = kmeans.fit_predict(X_scaled)
        
        # Calculate cluster-specific means and covariances to use as priors
        prior_means = kmeans.cluster_centers_  # Shape: (n_regimes, n_features)
        
        # Calculate empirical covariance for each cluster
        from sklearn.covariance import empirical_covariance
        prior_covs = []
        
        for i in range(n_regimes):
            cluster_data = X_scaled[cluster_labels == i]
            if len(cluster_data) > 1:  # Need at least 2 points for covariance
                cluster_cov = empirical_covariance(cluster_data)
                prior_covs.append(cluster_cov)
            else:
                # Fallback to overall covariance if cluster is too small
                prior_covs.append(empirical_covariance(X_scaled))
        
        prior_covs = np.array(prior_covs)  # Shape: (n_regimes, n_features, n_features)
        
        # Calculate initial state distribution from cluster proportions
        initial_probs = np.bincount(cluster_labels, minlength=n_regimes) / len(cluster_labels)
        
        # Calculate transition matrix based on cluster sequences
        trans_mat = np.zeros((n_regimes, n_regimes))
        for t in range(1, len(cluster_labels)):
            trans_mat[cluster_labels[t-1], cluster_labels[t]] += 1
            
        # Normalize rows to get probabilities
        row_sums = trans_mat.sum(axis=1, keepdims=True)
        # Avoid division by zero
        row_sums[row_sums == 0] = 1
        trans_mat = trans_mat / row_sums
    
        # Initialize model parameters based on model type
        if model_type == "HMM":
            model_params = {
                'n_components': n_regimes,
                'covariance_type': "full",
                'n_iter': n_iter,
                'init_params': ''  # Don't use default initialization
            }
            
            from hmmlearn import hmm
            model = hmm.GaussianHMM(**model_params)
            
            # Set the model parameters directly with our k-means derived priors
            model.startprob_ = initial_probs
            model.transmat_ = trans_mat
            model.means_ = prior_means
            model.covars_ = prior_covs
            
                
        # Fit the model
        model.fit(X_scaled)
        
        # Predict the hidden states (regimes)
        hidden_states = model.predict(X_scaled)
        
        # Assign states to clusters
        data['clusters'] = hidden_states    
        return data
    
    return data

La preparación de distribuciones a priori, utilizando el modelo GaussianHMM como ejemplo, se ve así:

Normalización de datos. Las metacaracterísticas se escalan utilizando StandardScaler para eliminar la influencia de la escala en los resultados de la clusterización.
Clusterización de k-means. Define los parámetros iniciales para estados (modos) ocultos. Los datos se agrupan en clústeres n_regimes. Las etiquetas de clúster obtenidas cluster_labels se utilizan para calcular las medias prior_means (centros de los clústeres) y las matrices de covarianza proir_covs suponen la covarianza empírica dentro de los clústeres o la covarianza total si el clúster es demasiado pequeño.
Cálculo de probabilidades iniciales. La distribución inicial initial_probs es la proporción de puntos en cada clúster. Por ejemplo, si el 30% de los datos pertenecen al clúster 0, entonces initial_probs[0] = 0,3.
Matriz de transición. Calcula con qué frecuencia un clúster sigue a otro en el tiempo.
Luego, el modelo de marzo oculto se inicializa con estos priores y se entrena.

Los métodos restantes hacen suposiciones aún más débiles sobre las dependencias y, por consiguiente, no se han considerado en absoluto. Probablemente esta no sea una lista completa de posibles métodos para determinar valores anteriores. Podemos utilizar otros métodos, pero deben basarse en el criterio de expertos.

Prueba de modelos ocultos de Márkov con distribuciones a priori

Podemos observar que la dispersión de los resultados ha disminuido. Los modelos han comenzado a estancarse menos en los mínimos locales, pero su diversidad ha disminuido. Además, la identificación de modos de mercado utilizando modelos de Márkov ocultos normalmente requiere un número menor de modos (clústeres), a diferencia de k-means.

A continuación le mostramos los resultados de la prueba de tres modelos con valores anteriores dados:

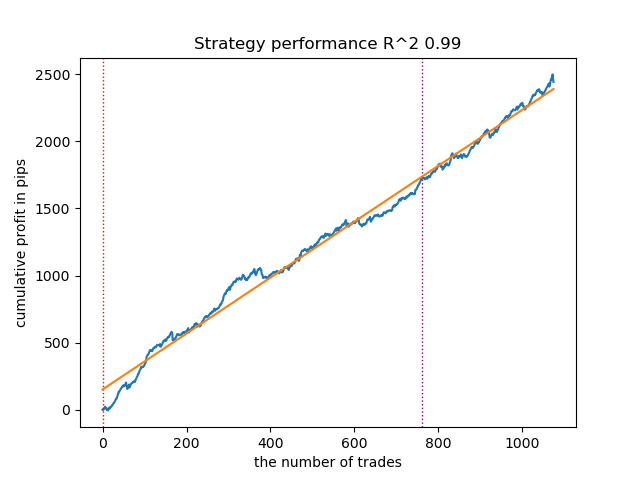
Figura 10. Prueba del HMM gaussiano con distribuciones a priori

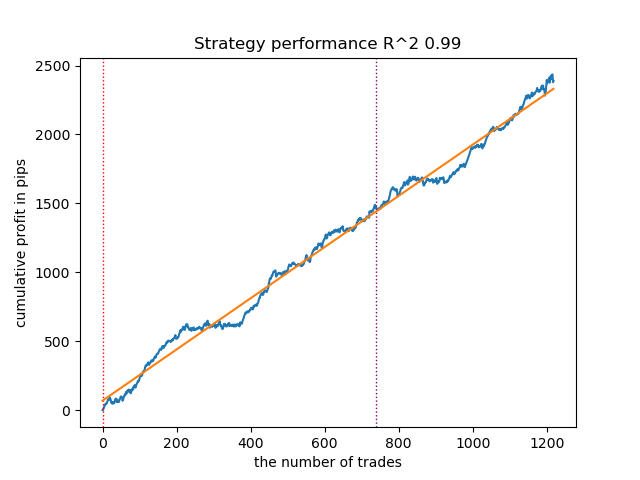
Figura 11. Prueba de GMMHMM con distribuciones anteriores

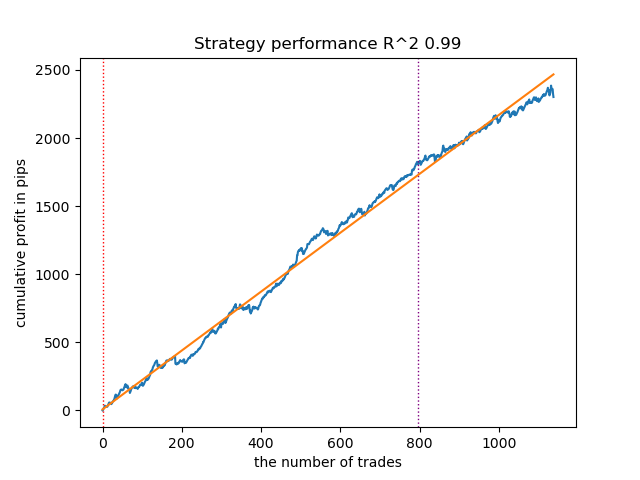
Figura 12. Prueba del HMM gaussiano variacional con distribuciones a priori

Exportación de modelos y compilación de un bot para la plataforma Meta Trader 5

La exportación de modelos se produce exactamente de la misma manera que sugerimos en artículos anteriores. El módulo con exportación está incluido en el archivo adjunto.

Supongamos que hemos seleccionado un modelo utilizando un simulador de estrategias personalizado.

# TESTING & EXPORT
models.sort(key=lambda x: x[0])
test_model_one_direction(models[-1][1:],
                        hyper_params['stop_loss'],
                        hyper_params['take_profit'],
                        hyper_params['forward'],
                        hyper_params['backward'],
                        hyper_params['markup'],
                        hyper_params['direction'],
                        plt=True)

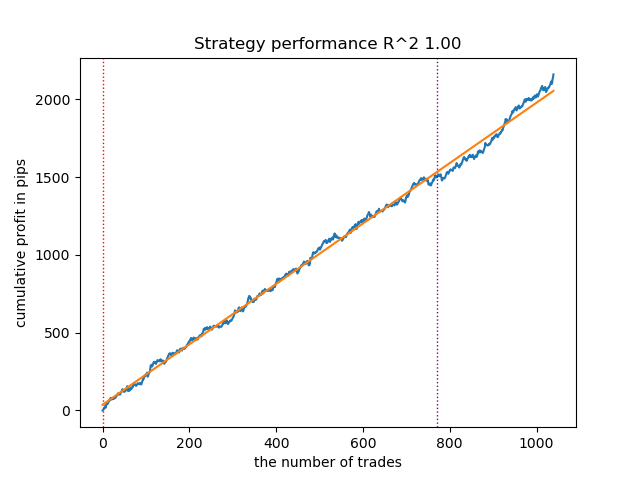
Figura 13. Prueba del mejor modelo usando un simulador de estrategias personalizado

Ahora deberemos llamar a la función de exportación, que guardará los modelos en la carpeta del terminal.

export_model_to_ONNX(model = models[-1],
                     symbol = hyper_params['symbol'],
                     periods = hyper_params['periods'],
                     periods_meta = hyper_params['periods_meta'],
                     model_number = hyper_params['model_number'],
                     export_path = hyper_params['export_path'])

Luego, deberemos compilar el bot adjunto al final del artículo y probarlo en el simulador de MetaTrader 5.

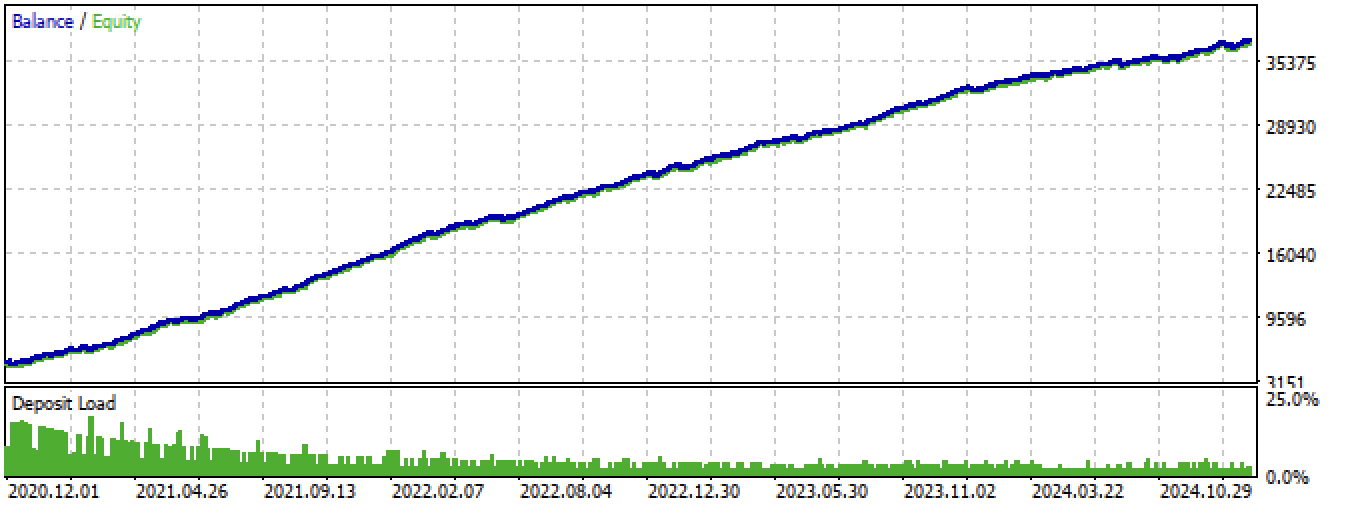
Fig. 14. Prueba del mejor modelo en el terminal Meta Trader 5 durante todo el periodo

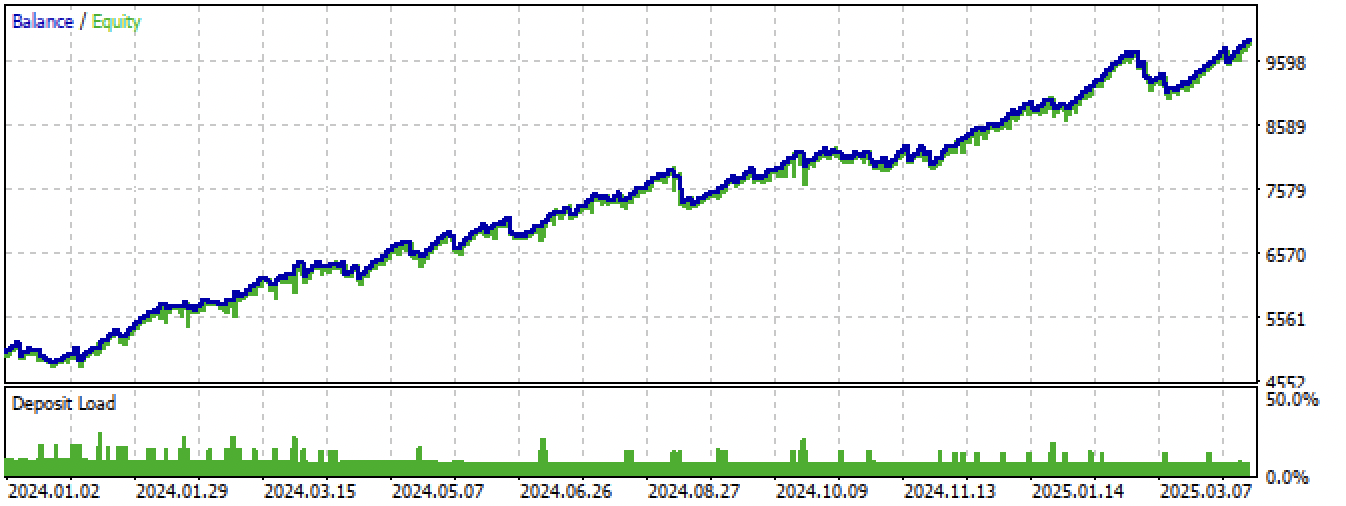
Figura 15. Prueba del mejor modelo en el terminal Meta Trader 5 con nuevos datos

Conclusión

Los modelos de Márkov ocultos son un método interesante para identificar modos de mercado. Pero, como todos los modelos de aprendizaje automático, son propensos a sobreajustarse en series temporales no estacionarias.

Una tarea de alta calidad de matrices a priori nos permite encontrar modos de mercado más estables que continúan trabajando con nuevos datos. Por lo general, se requieren menos modos de mercado que en el caso de la clusterización. Si en el primer caso se necesitan 10 clústeres, en el segundo a veces basta con establecer entre 3 y 5 estados ocultos.

No hemos encontrado mucha diferencia en el rendimiento de los tres algoritmos, todos muestran aproximadamente los mismos resultados. Por consiguiente, puede utilizar GaussianHMM, ya que es el más simple y rápido. GMMHMM teóricamente produce curvas de balance más suaves debido a la presencia de una mezcla de distribuciones, lo que ayuda a encontrar subpatrones en cada modo de mercado, pero puede sufrir un mayor sobreajuste debido precisamente a esto. El HMM gaussiano variacional requiere una especificación de priores más minuciosa, mientras que sus parámetros son más difíciles de especificar e interpretar.

Otro enfoque útil podría ser la validación cruzada de modelos usando la estimación de los parámetros de las distribuciones modales en diferentes niveles, pero este enfoque no se ha considerado en este artículo.

El archivo Python files.zip contiene los siguientes archivos para desarrollar en el entorno Python:

Nombre del archivo	Descripción
one direction HMM.py	Script básico para el entrenamiento de modelos
labeling_lib.py	Módulo actualizado con marcadores de transacciones
tester_lib.py	Simulador personalizado actualizado para estrategias basadas en aprendizaje automático
export_lib.py	Módulo de exportación de modelos al terminal
XAUUSD_H1.csv	Archivo con las cotizaciones exportadas desde el terminal MetaTrader 5

El archivo MQL5 files.zip contiene archivos para el terminal MetaTrader 5:

Nombre del archivo	Descripción
one direction HMM.ex5	Bot recopilado de este artículo
one direction HMM.mq5	Bot fuente del artículo
carpeta Include//Trend following	Asimismo, encontrará los modelos ONNX y el archivo de encabezado para conectarse al bot

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/17917

Archivos adjuntos |

Descargar ZIP

Python_files.zip (549.18 KB)

MQL5_files.zip (360.22 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.

Otros artículos del autor

Últimos comentarios | Pasar a la discusión en el foro de los operadores (2)

fxsaber | 12 may 2025 en 10:01

Затем, следует скомпилировать приложенного в конце статьи бота и протестировать его в тестере MetaTrader 5.

Fig. 14. Prueba del mejor modelo en el terminal MetaTrader 5 para todo el período

El archivo MQL5 files.zip contiene archivos para el terminal MetaTrader 5

Por favor, haga un estándar para publicar los correspondientes tst-files de backtest resultados publicados en los artículos. Muchas gracias.

[Eliminado] | 12 may 2025 en 10:17

fxsaber #:

Por favor, que sea norma publicar también los correspondientes archivos tst de los resultados de backtest publicados en los artículos. Muchas gracias.

Por desgracia, no escribo tan a menudo. Intentaré recordarlo para el futuro.

Utilizando redes neuronales en MetaTrader

En el artículo se muestra la aplicación de las redes neuronales en los programas de MQL, usando la biblioteca de libre difusión FANN. Usando como ejemplo una estrategia que utiliza el indicador MACD se ha construido un experto que usa el filtrado con red neuronal de las operaciones. Dicho filtrado ha mejorado las características del sistema comercial.

Automatización de estrategias de trading en MQL5 (Parte 17): Dominar la estrategia de scalping Grid-Mart con un panel de control dinámico

En este artículo, exploramos la estrategia de scalping Grid-Mart, automatizándola en MQL5 con un panel de control dinámico para obtener información comercial en tiempo real. Detallamos su lógica martingala basada en cuadrículas y sus características de gestión de riesgos. También guiamos en las pruebas retrospectivas y la implementación para obtener un rendimiento sólido.

Particularidades del trabajo con números del tipo double en MQL4

En estos apuntes hemos reunido consejos para resolver los errores más frecuentes al trabajar con números del tipo double en los programas en MQL4.

$Algoritmo basado en fractales — Fractal-Based Algorithm (FBA)$ Algoritmo basado en fractales — Fractal-Based Algorithm (FBA)

Hoy veremos un nuevo método metaheurístico basado en un enfoque fractal que permite particionar el espacio de búsqueda para resolver problemas de optimización. El algoritmo identifica y separa secuencialmente las áreas prometedoras, creando una estructura fractal autosimilar que concentra los recursos computacionales en las áreas más prometedoras. El mecanismo de mutación único orientado a las mejores soluciones garantiza un equilibrio óptimo entre la exploración y la explotación del espacio de búsqueda, aumentando significativamente la eficiencia del algoritmo.