Algoritmo de Otimização de Força Central (Central Force Optimization, CFO)
98
0
Conteúdo
Introdução
A natureza, evoluindo por bilhões de anos, criou inúmeros mecanismos de otimização eficientes que inspiram pesquisadores a desenvolver novos algoritmos. Um desses fenômenos naturais inspiradores é a gravidade a força fundamental que governa o movimento dos corpos celestes. Já analisamos anteriormente algoritmos de natureza semelhante.
O algoritmo de otimização de força central (Central Force Optimization, CFO) representa uma tentativa de transferir os princípios da cinemática gravitacional para o campo da otimização numérica. Este algoritmo meta-heurístico, baseado em leis de movimento determinísticas, modela a interação de partículas virtuais em um espaço multidimensional de soluções, onde cada partícula busca regiões com melhores valores da função objetivo sob a ação de um análogo da força gravitacional.
A base do CFO é uma metáfora simples e intuitiva: imagine um conjunto de pontos de teste (probes) distribuídos no espaço de soluções possíveis. Cada probe possui uma massa proporcional à qualidade da solução que represent ao valor da função objetivo. Assim como corpos celestes massivos atraem os menos massivos, os probes com melhores soluções criam um campo gravitacional virtual que atrai os demais.
O movimento de cada probe obedece a leis análogas às leis de Newton: a aceleração é determinada pela força total de atração proveniente dos outros probes, e o deslocamento ocorre de acordo com as equações cinemáticas do movimento. Uma característica importante do algoritmo é sua natureza determinística diferentemente de muitos outros métodos meta-heurísticos, o CFO não utiliza variáveis aleatórias em seu ciclo principal de operação.
Implementação do algoritmo
A história do algoritmo CFO começou quando pesquisadores se perguntaram: e se aplicássemos as leis da física à busca por soluções ótimas? Imagine uma vasta paisagem montanhosa, onde a altura de cada ponto corresponde à qualidade da solução. Quanto mais alto o pico, melhor a solução. Nosso objetivo é encontrar o ponto mais alto, mas o problema é que não conseguimos ver toda a paisagem de uma só vez. Em vez disso, temos um grupo de exploradores, chamemo-los de probes, que podem se mover por essa paisagem e relatar a altura de sua posição atual.
No início, nossos probes estão distribuídos aleatoriamente pelo território. Alguns acabam em vales, outros em encostas de colinas, e alguns podem ter sorte e cair diretamente no topo de pequenas elevações. Cada probe possui seu próprio peso, proporcional à altura do ponto em que se encontra. Quanto mais alto o ponto, mais pesado o probe. É aqui que começa a parte mais interessante: nossos probes não se movem de forma aleatória, eles seguem as leis da gravidade. Imagine que os probes mais pesados (aqueles que encontraram pontos melhores) atraem os probes mais leves (aqueles que estão em posições piores). Essa atração, porém, funciona apenas em uma direção: boas soluções atraem as ruins, mas não o contrário.
A força de atração é calculada segundo regras semelhantes à lei da gravitação universal de Newton. Ela depende da diferença de peso entre os probes (diferença na qualidade das soluções) e da distância entre eles. Um probe com alto valor de função de fitness exerce forte atração sobre probes próximos com valores mais baixos, mas tem pouca influência sobre probes distantes. Sob a ação dessas forças, cada probe adquire aceleração e começa a se mover. Os probes pequenos e leves se dirigem em direção aos mais pesados, como se esferas rolassem pelas encostas das colinas rumo aos picos. A cada passo do algoritmo, os probes recalculam as forças de atração e ajustam seus movimentos. Caso um probe tente sair dos limites definidos da área de busca, entra em ação o mecanismo de reflexão: imagine uma parede na borda do território, contra a qual o probe rebate e retorna à área permitida.
Com o passar do tempo, os probes começam a se agrupar em torno das regiões mais altas do terreno. A maioria deles se concentra nas áreas mais promissoras e, a cada iteração, localiza com maior precisão as posições dos picos. No cenário ideal, se o algoritmo tiver tempo suficiente para operar, todos os probes acabam se reunindo em torno do máximo global, o ponto mais alto de todo o terreno.
A característica distintiva do CFO é que, em sua essência, ele é um algoritmo determinístico. Se for executado duas vezes com a mesma distribuição inicial de probes, o resultado será exatamente o mesmo. Essa propriedade o diferencia de muitos outros algoritmos meta-heurísticos que dependem de elementos aleatórios.
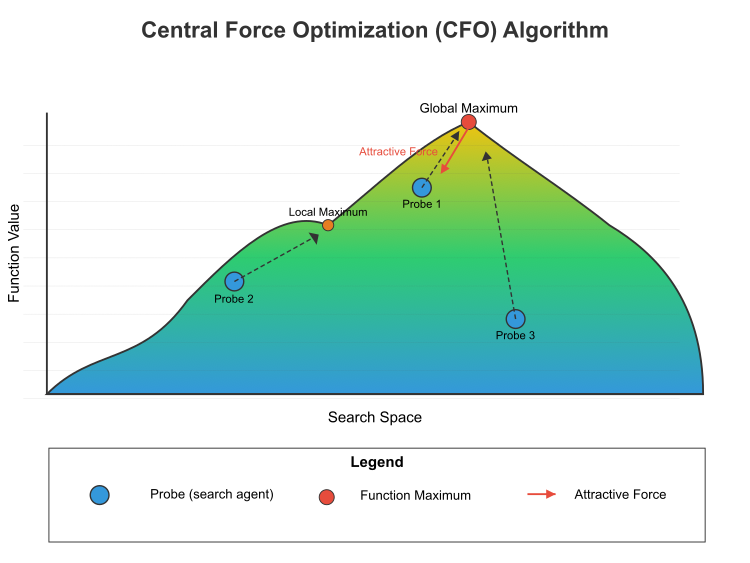
Figura 1. Esquema de funcionamento do algoritmo de otimização de força central
Na figura 1 é mostrado o princípio de funcionamento do algoritmo de otimização de força central (CFO) no espaço de busca. É apresentado o relevo da função objetivo, com um gradiente de cores do azul (valores baixos) ao amarelo (valores altos). Máximo global (ponto mais alto) e máximo local (pico mais baixo). Três probes (agentes de busca), identificados como Probe 1, Probe 2 e Probe 3. Forças de atração (seta vermelha) mostram como pontos mais altos atraem os probes. Isso é a ideia central do CFO, melhores soluções atraem as piores, mas não o contrário. Linhas pontilhadas mostram a trajetória dos probes rumo aos máximos. A fórmula matemática desse processo inclui:
Cálculo da força: para quaisquer dois probes i e j, se o valor da função (massa) de j for maior que o de i, então j exerce força sobre i de acordo com: F = g × [(m_j - m_i)^α / d^β] × direção, onde:- g — constante gravitacional
- m_j e m_i — valores da função (massas) dos probes j e i
- α — expoente de massa (geralmente 2)
- d — distância entre os probes
- β — expoente de distância (geralmente 2)
- direção — vetor unitário apontando do probe i para o probe j
Atualização de posição: a posição de cada probe é atualizada de acordo com: x_new = x_old + 0,5 × a, onde:
- x_new — nova posição
- x_old — posição atual
- a — aceleração
O algoritmo aplica iterativamente esses cálculos a todos os probes, movendo-os gradualmente em direção aos ótimos no espaço de busca. Com o tempo, os probes tendem a se agrupar em torno dos máximos globais e locais, sendo que a maior concentração geralmente é observada ao redor do ótimo global.
A particularidade do CFOdecorre de sua natureza determinística e do mecanismo de atração unidirecional, que direciona a busca para as melhores soluções sem envolver aleatoriedade em sua forma básica. Pseudocódigo do algoritmo CFO:
- Inicialização:
- Definimos os limites do espaço de busca.
- Definimos os parâmetros: número de probes, constante gravitacional, expoentes para massa e distância, fator de reposicionamento.
- Criamos o número especificado de probes e os posicionamos aleatoriamente no espaço de busca.
- Para cada probe, calculamos o valor inicial da função objetivo.
- Ciclo principal (repetimos por um número definido de épocas):
- Para cada probe:
- Zeramos o vetor de aceleração.
- Consideramos a influência de outros probes:
- Se outro probe tiver melhor valor de função objetivo (maior "massa"), ele cria uma força de atração.
- Calculamos a distância entre os probes.
- A força de atração é proporcional à diferença de "massas" elevada à potência alpha e inversamente proporcional à distância elevada à potência beta.
- Direção da força: do probe atual para o mais "pesado".
- Somamos as influências de todos os probes com melhores valores de função.
- Após calcular todas as acelerações, atualizamos as posições dos probes:
- Nova posição = posição antiga + metade da aceleração.
- Se um probe ultrapassar os limites do espaço de busca, aplicamos reposicionamento:
- Ao ultrapassar o limite inferior: refletimos o probe para dentro do espaço considerando o fator de reposicionamento.
- Ao ultrapassar o limite superior: de forma análoga, mas do outro lado.
- Recalculamos os valores da função objetivo para todos os probes em suas novas posições.
- Atualizamos a informação sobre a melhor solução encontrada.
- Para cada probe:
- Encerramento:
- Devolvemos a melhor solução encontrada (coordenadas do probe com o valor máximo da função objetivo).
Passemos à implementação do código do algoritmo, definindo a estrutura "S_CFO_Agent", que herda de "S_AO_Agent" e indica que "S_CFO_Agent" recebe todas as propriedades e métodos definidos em "S_AO_Agent".
Os campos da estrutura: a[] — é um array dinâmico destinado a armazenar os valores de aceleração. O método "Init()" é usado para inicializar a estrutura, redimensionando o array "c" de acordo com o parâmetro "coords" recebido e redimensionando o array de aceleração "a" conforme "coords". Isso permite definir dinamicamente o tamanho do array com base no número de coordenadas. Todos os elementos do array de aceleração "a" são inicializados com o valor "0.0", zerando os valores antes de seu uso. O valor da variável "f" é definido como o menor valor possível do tipo "double" para inicializar a função de fitness, garantindo que qualquer valor calculado posteriormente seja maior que esse valor.
//—————————————————————————————————————————————————————————————————————————————— //--- Структура для пробы CFO struct S_CFO_Agent : public S_AO_Agent { double a []; // вектор ускорения void Init (int coords) { ArrayResize (c, coords); // координаты ArrayResize (a, coords); // ускорение ArrayInitialize (a, 0.0); // обнуляем ускорения f = -DBL_MAX; // значение фитнес-функции } }; //——————————————————————————————————————————————————————————————————————————————
A classe "C_AO_CFO" herda da classe "C_AO" e define o algoritmo CFO. Construtor e destrutor. Neste caso, o destrutor não executa nenhuma ação específica. "C_AO_CFO()" é o construtor, responsável por inicializar os parâmetros do algoritmo. Ele define os valores de várias variáveis, tais como:
- popSize, g, alpha, beta, initialFrep, finalFrep, noiseFactor são parâmetros relacionados ao algoritmo e às suas funções de otimização.
- frep — o fator de reposicionamento atual, inicializado com o valor de "initialFrep".
- inicializa o array "params", que conterá os parâmetros do algoritmo, e em seguida copia seus valores para o array com os nomes correspondentes.
Métodos da classe:
- SetParams() — define os parâmetros do algoritmo com base nos valores do array "params". Também define o fator de reposicionamento atual para "initialFrep".
- Init() — responsável pela inicialização do algoritmo, configurando os valores mínimos e máximos dos parâmetros, bem como os passos utilizados para suas variações. O parâmetro "epochsP" define o número de épocas em que o algoritmo será executado.
- Moving() — responsável pelo processo de movimentação dos probes (agentes) dentro do algoritmo.
- Revision() — pode ser utilizado para realizar uma revisão ou atualização do estado dos agentes.
Campos da classe:
- S_CFO_Agent probe[] — array de probes (agentes) que serão utilizados no processo de otimização.
- epochs, epochNow — campos privados, representando respectivamente o número total de épocas e a época atual.
Métodos privados adicionais:
- InitialDistribution() — utilizado para inicializar a distribuição dos agentes no espaço de busca.
- UpdateRepFactor() — responsável por atualizar o fator de reposicionamento conforme o estado atual do sistema.
- CalculateAccelerations() — usado para calcular as acelerações dos agentes com base em suas posições e interações.
- UpdatePositions() — utilizado para atualizar as posições dos agentes de acordo com suas acelerações.
- CalculateDistanceSquared() — método usado para calcular a distância entre dois pontos no espaço, servindo para estimar a interação entre os agentes.
//—————————————————————————————————————————————————————————————————————————————— //--- Основной класс алгоритма CFO class C_AO_CFO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_CFO () { } C_AO_CFO () { ao_name = "CFO"; ao_desc = "Central Force Optimization"; ao_link = "https://www.mql5.com/ru/articles/17167"; popSize = 30; // число проб g = 1.0; // гравитационная постоянная alpha = 0.1; // степень для массы beta = 0.1; // степень для расстояния initialFrep = 0.9; // начальный фактор репозиционирования finalFrep = 0.1; // конечный фактор репозиционирования noiseFactor = 1.0; // фактор случайного шума frep = initialFrep; // текущий фактор репозиционирования ArrayResize (params, 7); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "g"; params [1].val = g; params [2].name = "alpha"; params [2].val = alpha; params [3].name = "beta"; params [3].val = beta; params [4].name = "initialFrep"; params [4].val = initialFrep; params [5].name = "finalFrep"; params [5].val = finalFrep; params [6].name = "noiseFactor"; params [6].val = noiseFactor; } void SetParams () { popSize = (int)MathMax (1, params [0].val); g = params [1].val; alpha = params [2].val; beta = params [3].val; initialFrep = params [4].val; finalFrep = params [5].val; noiseFactor = params [6].val; frep = initialFrep; } bool Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0); // количество эпох void Moving (); void Revision (); //---------------------------------------------------------------------------- double g; // гравитационная постоянная double alpha; // степень для массы double beta; // степень для расстояния double initialFrep; // начальный фактор репозиционирования double finalFrep; // конечный фактор репозиционирования double noiseFactor; // фактор случайного шума S_CFO_Agent probe []; // массив проб private: //------------------------------------------------------------------- int epochs; // общее число эпох int epochNow; // текущая эпоха double frep; // фактор репозиционирования void InitialDistribution (); void UpdateRepFactor (); void CalculateAccelerations (); void UpdatePositions (); double CalculateDistanceSquared (const double &x1 [], const double &x2 []); }; //——————————————————————————————————————————————————————————————————————————————
O método "Init()" da classe "C_AO_CFO" é responsável pela inicialização do algoritmo CFO, recebendo arrays com os valores mínimos e máximos dos parâmetros, o passo de variação desses valores e o número de épocas (por padrão, 0). Ele chama o método "StandardInit" para verificar a validade dos intervalos de valores fornecidos. Caso a verificação falhe, o método retorna "false". Define o número total de épocas e a época atual (0). Redimensiona o array de probes (agentes) para corresponder ao tamanho da população (popSize). Inicializa cada agente no array "probe", chamando o método "Init" para cada um deles e passando as coordenadas correspondentes. Se a inicialização for bem-sucedida, o método retorna "true". Assim, o método "Init" define os parâmetros e as condições iniciais necessárias para o funcionamento do algoritmo.
//—————————————————————————————————————————————————————————————————————————————— //--- Инициализация bool C_AO_CFO::Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; // Инициализация проб ArrayResize (probe, popSize); for (int i = 0; i < popSize; i++) probe [i].Init (coords); return true; } //——————————————————————————————————————————————————————————————————————————————
O método "Moving()" da classe "C_AO_CFO" é responsável pela etapa principal do algoritmo CFO. O método começa incrementando o contador da época atual, indicando o próximo passo da execução. Se o método for chamado pela primeira vez, quando "revision" é igual a "false", ele realiza a inicialização inicial e encerra em seguida. Isso é necessário para configurar os valores e estados iniciais. Em seguida, ocorre a cópia dos valores da função de fitness do array de agentes para um array temporário, garantindo que os dados permaneçam atualizados para os cálculos subsequentes.
O método atualiza o parâmetro responsável pelo reposicionamento dos agentes no espaço de busca, algo essencial para a adaptabilidade do algoritmo, em seguida, o método calcula as acelerações dos agentes com base em seu estado atual e atualiza suas posições, garantindo o movimento dos agentes dentro do espaço de busca. Ao final, o método sincroniza as novas posições dos agentes com o array principal, registrando as mudanças e assegurando a consistência dos dados. O método "Moving()" realiza uma atualização sistemática do estado dos agentes, baseada em suas funções de fitness e posições atuais durante a execução do algoritmo.
//—————————————————————————————————————————————————————————————————————————————— //--- Основной шаг алгоритма void C_AO_CFO::Moving () { epochNow++; // Начальная инициализация if (!revision) { InitialDistribution (); revision = true; return; } //---------------------------------------------------------------------------- // Копируем значения фитнес-функции из базового класса for (int p = 0; p < popSize; p++) { probe [p].f = a [p].f; } // Обновляем параметр репозиционирования UpdateRepFactor (); // Основной цикл CFO CalculateAccelerations (); UpdatePositions (); // Синхронизируем позиции с базовым классом for (int p = 0; p < popSize; p++) { ArrayCopy (a [p].c, probe [p].c); } } //——————————————————————————————————————————————————————————————————————————————
O método "InitialDistribution" da classe "C_AO_CFO" é responsável pela distribuição inicial dos probes (agentes) no espaço de busca. O método percorre cada agente da população "popSize". Para cada agente, os valores são inicializados, atribuindo o array "a" com zeros e configurando a função de fitness "f" para o menor valor possível. Para cada coordenada do agente, é realizado um sorteio aleatório de valores dentro dos limites especificados (rangeMin e rangeMax). Após gerar o valor aleatório, ele é processado pelo método "SeInDiSp", que ajusta o valor para o intervalo permitido e o passo "rangeStep". Por fim, as coordenadas do agente são copiadas do array temporário "c" para o array principal "a", registrando o estado inicial de cada agente.
//—————————————————————————————————————————————————————————————————————————————— //--- Начальное распределение проб void C_AO_CFO::InitialDistribution () { for (int p = 0; p < popSize; p++) { ArrayInitialize (probe [p].a, 0.0); probe [p].f = -DBL_MAX; // Случайное распределение for (int c = 0; c < coords; c++) { probe [p].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); probe [p].c [c] = u.SeInDiSp (probe [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } ArrayCopy (a [p].c, probe [p].c); } } //——————————————————————————————————————————————————————————————————————————————
O método "UpdateRepFactor" da classe "C_AO_CFO" é responsável por atualizar o fator de reposicionamento (ou fator de ajuste) durante a execução do algoritmo. O método começa verificando se o número de épocas "epochs" é maior que zero, caso positivo, calcula-se um novo valor para o fator de reposicionamento "frep" através de uma redução linear entre o valor inicial "initialFrep" e o valor final "finalFrep". Esse cálculo é baseado na época atual "epochNow" dentro do total de épocas definido. Se o número de épocas for igual a zero, o valor de "frep" permanece igual ao valor inicial "initialFrep". Isso garante estabilidade do fator quando o algoritmo ainda está na fase inicial. No final do método, o valor de "frep" é limitado ao intervalo entre 0 e 1 utilizando as funções "MathMax" e "MathMin". Essa limitação garante que o fator de reposicionamento não ultrapasse os limites definidos, o que é essencial para a estabilidade e a precisão do funcionamento do algoritmo.
//—————————————————————————————————————————————————————————————————————————————— //--- Обновление фактора репозиционирования void C_AO_CFO::UpdateRepFactor () { // Линейное уменьшение frep от начального к конечному значению if (epochs > 0) frep = initialFrep - (initialFrep - finalFrep) * epochNow / epochs; else frep = initialFrep; // Ограничение значения frep = MathMax (0.0, MathMin (1.0, frep)); } //——————————————————————————————————————————————————————————————————————————————
O método "CalculateAccelerations" da classe "C_AO_CFO" é projetado para calcular as acelerações de cada agente (ou probe) da população com base na influência de todos os outros agentes. A seguir, são descritos os principais passos e a lógica de funcionamento do método. Para cada agente da população (de 0 até popSize), os valores de aceleração "probe[p].a" são zerados. Isso é feito para garantir que o cálculo comece do zero e que as acelerações sejam acumuladas apenas com base nas interações com os outros agentes. Para cada agente, um laço interno percorre todos os demais agentes (de 0 até popSize). Se o índice do agente atual "p" for igual ao índice de outro agente "k", a iteração é ignorada com o comando "continue". Em seguida, é calculada a diferença entre os valores de fitness dos dois agentes (massDiff = probe[k].f - probe[p].f). Esse valor é usado para determinar o quanto um agente é "mais pesado" (ou melhor) em comparação ao outro. Se "massDiff" for maior que zero, isso significa que o agente com índice "k" possui um valor de fitness superior ao do agente com índice "p". Nesse caso, executam-se as seguintes operações:
-
Cálculo da distância: é calculado o quadrado da distância entre as coordenadas atuais de dois agentes utilizando a função "CalculateDistanceSquared". Se essa distância for muito pequena (menor que o menor valor positivo possível), a iteração é ignorada.
-
Formação da direção da força: se a distância for maior que "DBL_EPSILON", calcula-se a distância real e, para cada coordenada "c", é determinado o vetor de direção da força, apontando do agente atual para o agente com maior valor de fitness.
-
Fórmula de aceleração: a aceleração do agente atual é atualizada de acordo com a fórmula: probe[p].a[c] += g * MathPow(massDiff, alpha) * direction / MathPow(distance, beta), onde são considerados a diferença de massa (valores de fitness), a distância entre os probes e os coeficientes definidos (g, alpha, beta), que influenciam a intensidade da interação.
O método permite que cada agente leve em consideração a influência dos demais sobre sua aceleração, o que constitui um elemento essencial do processo de otimização. As acelerações calculadas dessa forma serão posteriormente utilizadas para atualizar as posições dos agentes no espaço de soluções.
//—————————————————————————————————————————————————————————————————————————————— //--- Вычисление ускорений void C_AO_CFO::CalculateAccelerations () { for (int p = 0; p < popSize; p++) { // Обнуляем ускорение для текущей пробы ArrayInitialize (probe [p].a, 0.0); // Суммируем влияние всех других проб for (int k = 0; k < popSize; k++) { if (k == p) continue; // Разница масс (фитнес-значений) double massDiff = probe [k].f - probe [p].f; // Проверяем условие единичной функции U(...) if (massDiff > 0) // Строгое условие для единичной функции { // Вычисляем расстояние между пробами double distSquared = CalculateDistanceSquared (probe [k].c, probe [p].c); if (distSquared < DBL_EPSILON) continue; double distance = MathSqrt (distSquared); for (int c = 0; c < coords; c++) { // Направление силы double direction = (probe [k].c [c] - probe [p].c [c]) / distance; // Формула ускорения probe [p].a [c] += g * MathPow (massDiff, alpha) * direction / MathPow (distance, beta); } } } } } //——————————————————————————————————————————————————————————————————————————————
O método "UpdatePositions" da classe "C_AO_CFO" tem a função de atualizar as posições dos agentes (ou probes) no espaço de soluções, levando em conta suas acelerações, fatores aleatórios e as restrições das fronteiras. Dentro desse método, são realizadas diversas etapas:
Redução do coeficiente de ruído aleatório:- É analisado o valor atual do coeficiente de ruído "currentNoiseFactor", inicialmente definido como igual a "noiseFactor".
- Se o número de épocas "epochs" for maior que zero, o coeficiente é reduzido proporcionalmente à época atual "epochNow". Isso significa que, conforme o número de épocas aumenta, o ruído diminui, permitindo que o algoritmo encontre soluções cada vez mais precisas à medida que se aproxima do ótimo.
O método percorre todos os agentes da população (de 0 até popSize) e, para cada agente, percorre todas as suas coordenadas (de 0 até coords). A posição do agente é atualizada pela fórmula que utiliza a aceleração atual "probe[p].a[c]". Nesse caso, é usada uma fórmula simples em que a nova posição é igual à posição antiga somada à metade da aceleração atual.
Na nova posição é adicionado um pequeno desvio aleatório, que depende do valor atual do coeficiente de ruído, da constante gravitacional "g" e de um número aleatório dentro do intervalo de -1 a 1. O algoritmo original é estritamente determinístico, mas decidi acrescentar esse elemento de aleatoriedade, sobre isso falarei mais adiante. Esse desvio introduz um componente estocástico que ajuda a evitar o travamento em mínimos locais. Caso a nova posição ultrapasse os limites definidos (valores mínimos e máximos armazenados em rangeMin e rangeMax), a posição é ajustada de modo que permaneça dentro do intervalo permitido. Se existir um passo de discretização definido, a posição do agente é ainda ajustada usando o método "SeInDiSp", que adapta a posição ao valor mais próximo múltiplo do passo.
//—————————————————————————————————————————————————————————————————————————————— //--- Обновление позиций void C_AO_CFO::UpdatePositions () { // Коэффициент случайного шума, уменьшается с ростом номера эпохи double currentNoiseFactor = noiseFactor; if (epochs > 0) currentNoiseFactor *= (1.0 - (double)epochNow / epochs); for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { // Обновление позиции по формуле probe [p].c [c] += 0.5 * probe [p].a [c]; // Добавление небольшого случайного смещения непосредственно к позиции probe [p].c [c] += currentNoiseFactor * g * u.RNDfromCI (-1.0, 1.0); // Репозиционирование при выходе за границы if (probe [p].c [c] < rangeMin [c]) probe [p].c [c] = rangeMin [c]; if (probe [p].c [c] > rangeMax [c]) probe [p].c [c] = rangeMax [c]; // Дискретизация если задан шаг probe [p].c [c] = u.SeInDiSp (probe [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
O método "CalculateDistanceSquared" da classe "C_AO_CFO" é responsável por calcular o quadrado da distância entre dois pontos em um espaço multidimensional. O método é utilizado por razões de eficiência, já que retornar o quadrado da distância elimina a necessidade de calcular a raiz quadrada, reduzindo significativamente o custo computacional. O método recebe dois parâmetros: x1 e x2. Esses parâmetros são arrays (const double &x1[] e const double &x2[]), que representam as coordenadas de dois pontos no espaço, cuja dimensionalidade é igual ao número de coordenadas "coords". No início do método é criada a variável "sum", inicializada com zero. Essa variável serve para acumular a soma dos quadrados das diferenças entre as coordenadas. O método percorre todas as coordenadas (de 0 até coords-1) e, para cada uma delas:
- Calcula-se a diferença entre os elementos correspondentes dos arrays x1 e x2 (diff = x1[i] - x2[i]).
- Calcula-se o quadrado dessa diferença (diff * diff).
- O valor obtido é somado à variável "sum".
//—————————————————————————————————————————————————————————————————————————————— //--- Вычисление расстояния (возвращает квадрат расстояния для оптимизации) double C_AO_CFO::CalculateDistanceSquared (const double &x1 [], const double &x2 []) { double sum = 0.0; for (int i = 0; i < coords; i++) { double diff = x1 [i] - x2 [i]; sum += diff * diff; } return sum; } //——————————————————————————————————————————————————————————————————————————————
O método "Revision()" da classe "C_AO_CFO" é responsável por atualizar a melhor solução encontrada durante o processo de otimização. O método percorre todos os agentes (ou probes) da população "popSize". Para cada agente, verifica se o valor da sua função de adaptabilidade "a[p].f" é maior que o valor atual do melhor fitness "fB". Caso essa condição seja verdadeira, o valor de "fB" é atualizado para o fitness do agente, e as coordenadas "cB" do agente são copiadas, registrando a nova melhor posição encontrada. Dessa forma, o método "Revision" identifica e armazena a melhor solução entre todos os agentes, atualizando os parâmetros globais sempre que um agente apresenta um resultado superior.
//—————————————————————————————————————————————————————————————————————————————— //--- Обновление лучшего решения void C_AO_CFO::Revision () { for (int p = 0; p < popSize; p++) { if (a [p].f > fB) { fB = a [p].f; ArrayCopy (cB, a [p].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Resultados dos testes
A versão original, estritamente determinística do algoritmo, em sua forma básica, apresentou os seguintes resultados:
CFO|Central Force Optimization|30.0|1.0|0.1|0.1|0.9|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.34508431921321436
25 Hilly's; Func runs: 10000; result: 0.2826594689557952
500 Hilly's; Func runs: 10000; result: 0.25174636412054047
=============================
5 Forest's; Func runs: 10000; result: 0.26234538930351947
25 Forest's; Func runs: 10000; result: 0.1852230195779629
500 Forest's; Func runs: 10000; result: 0.15353213276989314
=============================
5 Megacity's; Func runs: 10000; result: 0.24923076923076923
25 Megacity's; Func runs: 10000; result: 0.1261538461538462
500 Megacity's; Func runs: 10000; result: 0.09492307692307768
=============================
All score: 1.95090 (21.68%)
Com esses resultados, infelizmente, o algoritmo não pôde ser incluído em nossa tabela de classificação. Melhorias eram necessárias. Por isso, como mencionei anteriormente, foi adicionado um elemento de aleatoriedade ao código. Sem esse componente, a natureza determinística do processo de busca não possuía diversidade suficiente nas soluções.
// Добавление небольшого случайного смещения непосредственно к позиции probe [p].c [c] += currentNoiseFactor * g * u.RNDfromCI (-1.0, 1.0);
Após a introdução de um leve elemento aleatório, um pequeno desvio estocástico adicionado ao movimento de cada probe, o algoritmo passou a explorar direções inesperadas. Realizamos então um novo conjunto de testes. Agora podemos observar resultados completamente diferentes, já dignos de serem registrados em nossa tabela de desempenho.
CFO|Central Force Optimization|30.0|1.0|0.1|0.1|0.9|0.1|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6096110105488222
25 Hilly's; Func runs: 10000; result: 0.5495761567207647
500 Hilly's; Func runs: 10000; result: 0.27830861578120414
=============================
5 Forest's; Func runs: 10000; result: 0.6341793648294705
25 Forest's; Func runs: 10000; result: 0.4683296629644541
500 Forest's; Func runs: 10000; result: 0.22540930020804817
=============================
5 Megacity's; Func runs: 10000; result: 0.5723076923076923
25 Megacity's; Func runs: 10000; result: 0.2347692307692307
500 Megacity's; Func runs: 10000; result: 0.09586153846153929
=============================
All score: 3.66835 (40.76%)
Podemos também observar a visualização do funcionamento do algoritmo. Nota-se que o método apresenta bom desempenho em funções de dimensão média, mas não é suficientemente eficaz em funções de baixa ou alta dimensionalidade.
CFO na função de teste Hilly
CFO na função de teste Forest
CFO na função de teste Megacity
Com base nos testes realizados, o algoritmo entrou para o grupo dos melhores algoritmos populacionais de otimização, ocupando a 42ª posição.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 13 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 14 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 15 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 16 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 17 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 18 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 19 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 20 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 21 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 22 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 23 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 24 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 25 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 26 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 27 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 28 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 29 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 30 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 31 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 32 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 33 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 34 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 35 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 36 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 37 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 38 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 39 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 40 | CGO | chaos game optimization | 0,57256 | 0,37158 | 0,32018 | 1,26432 | 0,61176 | 0,61931 | 0,62161 | 1,85267 | 0,37538 | 0,21923 | 0,19028 | 0,78490 | 3,902 | 43,35 |
| 41 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 42 | CFO | central force optimization | 0,60961 | 0,54958 | 0,27831 | 1,43750 | 0,63418 | 0,46833 | 0,22541 | 1,32792 | 0,57231 | 0,23477 | 0,09586 | 0,90294 | 3,668 | 40,76 |
| 43 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 44 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 45 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Considerações finais
O algoritmo CFO, baseado nos princípios da atração gravitacional entre objetos, representa uma tentativa interessante de aplicar as leis da física à resolução de problemas complexos de otimização. Após testes detalhados em nosso conjunto padrão de funções, o CFO demonstrou uma eficiência de aproximadamente 40% do máximo teórico possível, o que lhe garantiu o 42º lugar entre os 45 melhores algoritmos populacionais de otimização. Vale destacar que até mesmo esse resultado modesto só foi alcançado após a modificação do algoritmo original, com a introdução de um componente aleatório em sua estrutura inicialmente determinística.
Apesar do desempenho relativamente baixo, o CFO possui diversas características atrativas. Em primeiro lugar, é um algoritmo com uma interpretação física extremamente clara, o que o torna intuitivo e fácil de compreender. A simplicidade de sua ideia central, as probes, representando possíveis soluções, sendo atraídas pelas melhores soluções assim como corpos materiais são atraídos por objetos mais massivos, confere transparência ao funcionamento do algoritmo e facilita sua implementação.
Entretanto, os testes também revelaram limitações significativas do CFO, que exigem revisão ou aprimoramento. A excessiva dependência da distribuição inicial das probes é uma das principais fragilidades, já que, devido ao mecanismo determinístico de movimento, as posições iniciais dos probes acabam influenciando fortemente o resultado final da busca.
O mecanismo de atração unidirecional, no qual apenas as melhores soluções influenciam as piores, mas não o contrário, embora tenha uma justificativa lógica, pode limitar significativamente a capacidade do algoritmo de explorar o espaço de busca. A introdução de um mecanismo adaptativo, que permitisse certa influência também das piores soluções, especialmente nas fases iniciais da busca, poderia ampliar o potencial do algoritmo na identificação de regiões promissoras dentro do espaço de soluções.
Figura 2. Gradação de cores dos algoritmos de acordo com os testes correspondentes
Figura 3. Histograma dos resultados de testes dos algoritmos (em escala de 0 a 100, quanto maior melhor, onde 100 é o resultado teórico máximo possível, no arquivo compactado há um script para calcular a tabela de classificação)
Vantagens e desvantagens do algoritmo CFO:
Vantagens:
- Desempenho satisfatório em funções de média dimensionalidade.
Desvantagens:
- Desempenho insatisfatório em funções de baixa e alta dimensionalidade.
- Baixa capacidade de exploração em funções discretas.
O artigo inclui um arquivo compactado com as versões mais recentes dos códigos dos algoritmos. O autor não se responsabiliza pela precisão absoluta na descrição das versões canônicas dos algoritmos, pois diversas modificações foram implementadas para melhorar suas capacidades de busca. As conclusões e considerações apresentadas neste material baseiam-se exclusivamente nos resultados dos experimentos realizados.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | #C_AO.mqh | Arquivo incluído | Classe base dos algoritmos populacionais de otimização |
| 2 | #C_AO_enum.mqh | Arquivo incluído | Enumeração dos algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo incluído | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo incluído | Biblioteca de funções da plataforma de testes |
| 5 | Utilities.mqh | Arquivo incluído | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo incluído | Script para cálculo dos resultados e geração da tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Plataforma unificada de testes para todos os algoritmos populacionais de otimização |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Exemplo simples de uso dos algoritmos populacionais de otimização sem visualização |
| 9 | Test_AO_CFO.mq5 | Script | Plataforma de testes para o CFO |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/17167
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
Reimaginando Estratégias Clássicas (Parte 12): Estratégia de Breakout EURUSD
Ondas triangulares e em forma de serra: ferramentas para o trader
Desenvolvimento de estratégias de trading de tendência baseadas em aprendizado de máquina
Do básico ao intermediário: Classes (II)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso