Técnicas de remuestreo para la evaluación de predicciones y clasificaciones en MQL5

Introducción

El rendimiento de los modelos de aprendizaje automático se evalúa normalmente en dos fases distintas: el entrenamiento con un conjunto de datos y la prueba con otro. Sin embargo, en situaciones en las que la recopilación de múltiples conjuntos de datos puede resultar poco práctica debido a restricciones de recursos o limitaciones logísticas, es necesario emplear enfoques alternativos.

Uno de estos métodos consiste en utilizar técnicas de remuestreo para evaluar el rendimiento de los modelos de predicción o clasificación. Se ha demostrado que este enfoque proporciona resultados fiables a pesar de sus posibles inconvenientes. En este artículo, exploraremos una metodología novedosa para evaluar la calidad de los modelos que utiliza un único conjunto de datos como conjuntos de entrenamiento y validación. La razón principal para aplicar estos métodos es la disponibilidad limitada de datos para realizar pruebas.

Por lo tanto, los profesionales deben emplear sofisticados algoritmos de remuestreo para producir métricas de rendimiento comparables a las generadas por enfoques más sencillos. Estas técnicas requieren importantes recursos computacionales y pueden introducir complejidad en los procesos de desarrollo de modelos. A pesar de esta compensación, el empleo de estrategias de evaluación basadas en el remuestreo puede resultar valioso en determinados contextos en los que los beneficios superan a los costes.

Descomposición de errores

Para facilitar la exposición de los conceptos algorítmicos presentados en este texto, se introduce un sistema de notación. Este marco notacional aborda principalmente la descomposición del error del modelo en elementos constitutivos. Consideremos un conjunto de datos, denominado T, derivado de una población caracterizada por una distribución desconocida, F. Este conjunto de datos comprende n observaciones, cada una de las cuales consta de una variable predictora, x, que puede ser escalar o vectorial, y una variable predicha, y, que es escalar. Para enfatizar la interdependencia inherente de las variables predictoras y predichas, se emplea el término compuesto t (para entrenamiento) para representar el par (x, y). Por lo tanto, la observación «i» del conjunto de datos se representa como t_i = (x_i, y_i). Si bien esta notación sugiere un marco de predicción numérica. Los problemas de clasificación pueden resolverse interpretando y_i como la pertenencia a la clase de la observación i-ésima.

El conjunto de datos completo se denomina T. Cuando se entrena un modelo utilizando T como conjunto de entrenamiento, el modelo entrenado resultante se designa como M_T. La aplicación de este modelo entrenado, M_T, a un valor específico de la variable predictora, x, para generar una estimación de la variable predicha correspondiente, da como resultado la predicción del modelo, denotada como M_T(x). En aras de la brevedad, una predicción de modelo genérico puede abreviarse como M. Al evaluar la eficacia de un modelo predictivo, a menudo es necesario cuantificar la discrepancia entre la predicción del modelo, M, y el valor observado, y, de la variable predicha. Esta discrepancia se define formalmente como una medida de error, denotada como Ef[y, M]. Una medida de error común empleada en contextos de regresión es el error cuadrático medio, que utiliza la diferencia al cuadrado, tal y como se muestra en la ecuación siguiente. En los problemas de clasificación, Ef[y, M] puede definirse como una función binaria, que asigna un valor de cero si y es igual a M y uno en caso contrario.

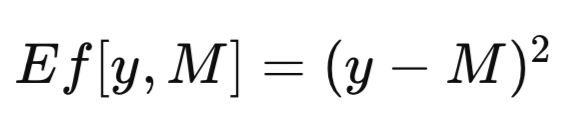
Cuando el modelo entrenado se aplica al mismo conjunto de datos utilizado para su entrenamiento, el error medio, en todas las instancias de entrenamiento, se designa como error aparente. Mientras que el enfoque convencional consiste en entrenar el modelo minimizando este error aparente, la metodología aquí presentada no impone tal restricción. Se permite la optimización de cualquier medida arbitraria, seguida de la evaluación de la calidad del modelo entrenado utilizando un criterio distinto. El error aparente, definido a continuación, es únicamente una función del rendimiento del modelo en los datos de entrenamiento y de la aplicación de la función Ef[] a cada predicción; la metodología de entrenamiento es irrelevante.

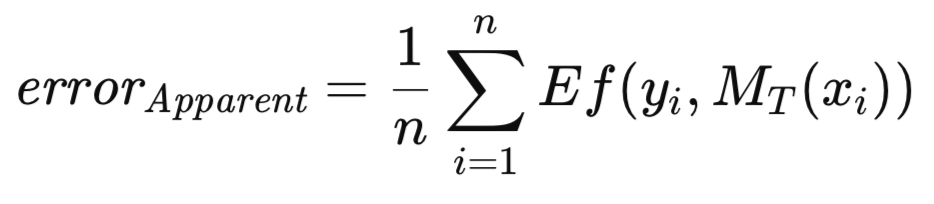
Está bien establecido que el error aparente muestra un sesgo optimista, un fenómeno que a veces se denomina sesgo de entrenamiento, debido a la evaluación del modelo sobre los mismos datos utilizados para su entrenamiento. Para mitigar este sesgo, cuando se dispone de datos suficientes, el modelo entrenado se evalúa con un conjunto de datos independiente. Este procedimiento facilita la estimación del error esperado del modelo entrenado cuando se aplica a la población general. Este error esperado, condicionado al modelo que ha sido entrenado en el conjunto de entrenamiento, se denomina error de predicción. Aquí se hace hincapié en la evaluación del rendimiento futuro previsto de un modelo específico entrenado. El error de predicción se expresa formalmente en la siguiente ecuación.

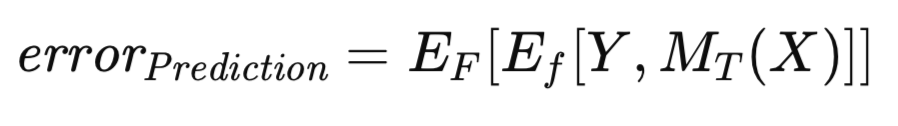
Una medida del error relacionada, aunque conceptualmente distinta, merece ser tenida en cuenta. El error de predicción, tal y como se ha definido anteriormente, depende de un modelo específico entrenado con un conjunto de datos concreto. Sin embargo, es posible ampliar la expectativa para abarcar el conjunto de todos los conjuntos de entrenamiento posibles. Concretamente, dado que el conjunto de entrenamiento comprende n observaciones muestreadas a partir de una distribución desconocida, se puede evaluar el error de predicción asociado al modelo entrenado en este conjunto de datos de entrenamiento concreto, aproximándolo potencialmente mediante un conjunto de validación independiente. Ahora, consideremos el escenario en el que se extrae un nuevo conjunto de entrenamiento y se repite el procedimiento de entrenamiento. Inevitablemente, se obtendría un error de predicción ligeramente divergente. Por consiguiente, resulta necesario formular una medida que capte el error de predicción esperado en todo el espectro de posibles conjuntos de entrenamiento. Esta medida, denominada error de población, se define formalmente a continuación.

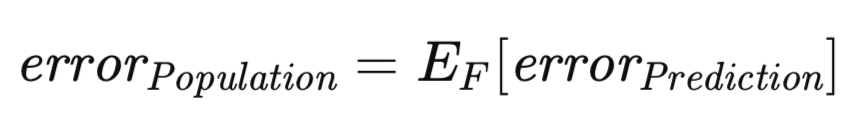
Es un principio bien establecido que, para cualquier conjunto de entrenamiento dado, el error aparente, con alta probabilidad, subestimará el error de predicción. Esta discrepancia surge de la tendencia del modelo a ajustarse excesivamente a las características específicas de los datos de entrenamiento, lo que compromete su generalización a la población en general. La magnitud de la diferencia entre el error de predicción y el error aparente se define como el error excesivo.

En este contexto, el error excesivo esperado tiene una importancia especial. Reconociendo que tanto el error de predicción como el error aparente dependen de un conjunto de entrenamiento específico, es necesario considerar el valor esperado del exceso de error en el conjunto de todos los posibles conjuntos de entrenamiento, de forma análoga a la derivación del error de población. Esto se representa formalmente en la siguiente ecuación.

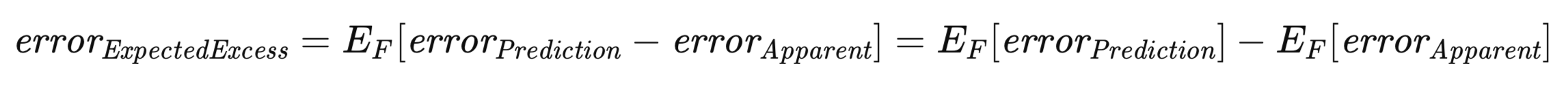
La ecuación anterior subraya la dualidad en la conceptualización del error excesivo esperado. Se puede considerar como la expectativa, en todos los conjuntos de entrenamiento posibles, de la diferencia entre el error de predicción y el error aparente para cada conjunto de entrenamiento individual. Esta interpretación concuerda con una comprensión intuitiva del concepto. Alternativamente, se puede expresar como la diferencia entre el error de población y el error aparente esperado.

Validación cruzada: Metodología y limitaciones

La validación cruzada es una técnica bien establecida dentro de la comunidad investigadora. Entre los algoritmos analizados en este texto, la validación cruzada destaca por su simplicidad conceptual y facilidad de implementación, y a menudo muestra una gran eficiencia computacional. Posee la ventaja de ofrecer una estimación casi imparcial del rendimiento futuro esperado de un modelo.

Además, su amplia aplicabilidad se extiende a una gran variedad de algoritmos de entrenamiento de modelos, una característica que no comparten otros métodos. Sin embargo, la validación cruzada está sujeta a una limitación significativa: su varianza inherente suele ser considerable, posiblemente hasta un grado inaceptable. Esto implica una mayor sensibilidad a las variaciones estocásticas introducidas por el muestreo aleatorio del conjunto de datos original.

En concreto, un investigador que recopila una muestra, entrena un modelo y posteriormente emplea la validación cruzada para evaluar el rendimiento futuro esperado del modelo puede observar un resultado notablemente diferente al repetir el procedimiento con una muestra independiente. Si bien la naturaleza casi imparcial de la estimación es una propiedad deseable, a menudo se ve eclipsada por la magnitud de la varianza. Es importante destacar que los profesionales suelen subestimar esta variabilidad.

A pesar de la existencia de metodologías superiores para tareas análogas, la validación cruzada sigue siendo ampliamente utilizada, a menudo debido a su simplicidad y su aplicabilidad en escenarios en los que los enfoques alternativos son inviables. No obstante, dada su prevalencia y su ocasional necesidad, se justifica una exposición detallada del procedimiento de validación cruzada.

El principio fundamental que subyace a la validación cruzada es conceptualmente sencillo. Implica dividir el conjunto de datos en dos subconjuntos distintos: un conjunto de entrenamiento, utilizado para la estimación de los parámetros del modelo, y un conjunto de validación, empleado para la evaluación independiente del modelo, reflejando el procedimiento adoptado cuando la abundancia de datos no es una limitación.

Sin embargo, a diferencia de la asignación de una parte sustancial de los datos al conjunto de validación para obtener una estimación robusta del rendimiento, la validación cruzada utiliza un conjunto de validación mínimo, asignando la mayoría de las observaciones al conjunto de entrenamiento. En concreto, es habitual emplear una única observación como conjunto de validación.

Tras el entrenamiento y la evaluación del modelo con esta partición, el conjunto de validación se reintegra en el conjunto de datos y se designa una observación diferente como conjunto de validación. Este proceso se repite hasta que cada observación haya servido como punto de validación una vez. El error medio de la prueba en todas las iteraciones constituye la estimación del error de validación cruzada.

La variante más frecuente de la validación cruzada consiste en la exclusión secuencial de observaciones individuales. La adaptación de estos algoritmos para la exclusión de observaciones múltiples debería ser bastante sencilla. Dado que M_T representa el modelo entrenado en el conjunto de datos completo, T, sea M_T(i) el modelo entrenado en el conjunto de datos T excluyendo la observación i-ésima. La estimación de validación cruzada del error futuro esperado del modelo se expresa formalmente de la siguiente manera.

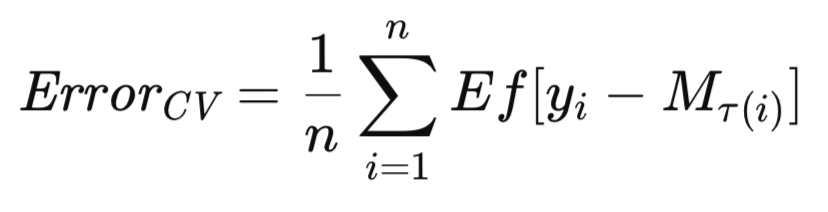
En esta sección se presenta el algoritmo de validación cruzada, acompañado de notas explicativas. Al final de este artículo se incluyen evaluaciones comparativas del rendimiento. Todos los algoritmos utilizados para estimar los errores esperados se presentan en el archivo de encabezado error_variance_estimation.mqh. El algoritmo de validación cruzada se implementa como el método cross_validation(). Esta rutina y las utilizadas para implementar otros algoritmos de estimación de errores tienen una estructura y parámetros de función similares. Estos parámetros son:

• Los dos primeros argumentos obligatorios del método son matrices del conjunto de datos de entrenamiento. La primera matriz contiene los predictores y la segunda, los objetivos correspondientes.
  
• El tercer argumento de la rutina es una instancia de un modelo que implementa la interfaz IModel. Esto representa el modelo de predicción que se está evaluando.
• El último argumento pasado a cross_validation() contiene la medida de error final obtenida del cálculo. Si se produce un error, el método devolverá el valor booleano «false» (falso).

//+------------------------------------------------------------------+
//| estimate error variance using cross validation testing           |
//+------------------------------------------------------------------+
bool CErrorVar::cross_validation(matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   out_err = 0.0;
   vector test;
   double test_target;
   matrix preds,targs;

   for(ulong i = 0; i<predictors.Rows(); i++)
     {
      test = predictors.Row(i);
      test_target = targets[i][0];
      
      predictors.SwapRows(i,(predictors.Rows()-1));
      targets.SwapRows(i,(targets.Rows()-1));
      
      preds = np::sliceMatrixRows(predictors,0,long(predictors.Rows()-1));
      targs = np::sliceMatrixRows(targets,0,long(targets.Rows()-1));

      if(!model.train(preds,targs))
        {
         Print(__FUNCTION__," failed to train model ");
         return false;
        }

      out_err += error_fun(test_target,model.forecast(test));
      
      predictors.SwapRows(i,(predictors.Rows()-1));
      targets.SwapRows(i,(targets.Rows()-1));
     }

   out_err/=double(predictors.Rows());

   return true;
  }

La invocación de cross_validation() activa el inicio de un bucle que recorre el conjunto de datos de entrenamiento. La última posición en el conjunto de datos de entrenamiento siempre se utiliza como punto de prueba. El bucle intercambia otras muestras en esta posición en las matrices predictora y objetivo, una por una. Una vez que los datos están divididos, se entrena el modelo y luego se prueba en la única muestra que no se usó para entrenarlo. Su error se acumula y finalmente se devuelve como resultado de pasar por todo el bucle.

Estimación bootstrap (inicialización) del error de población

Esta sección describe un algoritmo básico de bootstrap para la estimación del error de población. Se reconoce que este algoritmo no se recomienda generalmente para aplicaciones prácticas, ya que los algoritmos E0 y E632, que se detallan en secciones posteriores, suelen ofrecer un rendimiento superior. No obstante, el método bootstrap directo que aquí se presenta sirve como principio fundamental sobre el que se construyen algoritmos más sofisticados. Por lo tanto, es indispensable comprender a fondo su mecánica operativa para entender a sus sucesores.

En el escenario actual, postulamos una población, F, de la que se extraen aleatoriamente las observaciones que componen nuestro conjunto de entrenamiento. El modelo se entrena y evalúa en T, lo que da como resultado el error aparente. Este error es intrínsecamente optimista, y se espera que el error poblacional supere el error aparente por el exceso de error. Sin embargo, en ausencia de un conjunto de validación independiente, ni el error por exceso ni el error de población, las cantidades de interés principal, son directamente observables. Nos limitamos al optimista error aparente. No obstante, la metodología bootstrap puede emplearse para estimar el error excesivo, que luego puede añadirse al error aparente para proporcionar una estimación aproximada del error de población.

El uso del bootstrap para la estimación del error excesivo refleja el procedimiento para estimar el sesgo de los parámetros. Se sustituye la distribución empírica por la distribución poblacional desconocida y se extraen numerosas muestras bootstrap. Para cada muestra de bootstrap, se entrena el modelo. El error del modelo en la muestra bootstrap representa el error aparente para esa muestra. El error del modelo en el conjunto de datos completo representa el error de predicción, ya que la distribución empírica funciona efectivamente como la población completa. La diferencia entre estos dos errores da como resultado el error excesivo para esa muestra de bootstrap. El promedio de este error excesivo en numerosas réplicas de bootstrap proporciona una estimación del error excesivo esperado.

Para mejorar el rigor del algoritmo mencionado anteriormente, se introducen una serie de definiciones y ecuaciones. Denotemos por B un conjunto de entrenamiento generado mediante muestreo bootstrap a partir del conjunto de datos original. Concretamente, B se construye seleccionando aleatoriamente n observaciones de T con reemplazo. Posteriormente, el modelo se entrena utilizando B. El error de predicción de este modelo se determina promediando su error en todas las observaciones de la población de la que se extrajo la muestra bootstrap, que, en este contexto, es el conjunto de datos original. Esto se representa formalmente en la siguiente ecuación.

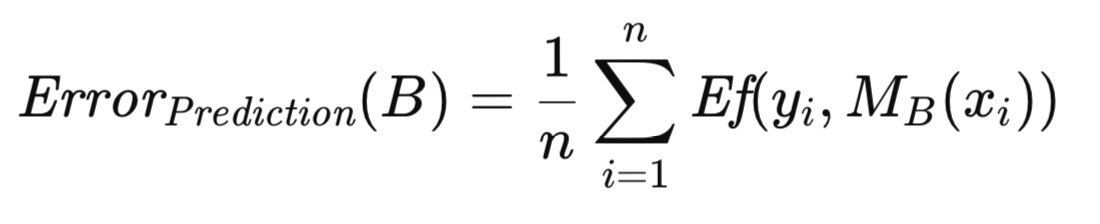
Sea k_i la frecuencia con la que la i-ésima observación de T aparece en B. El error aparente asociado a B se calcula promediando el error del modelo entre las observaciones que componen B, como se muestra en la ecuación siguiente.

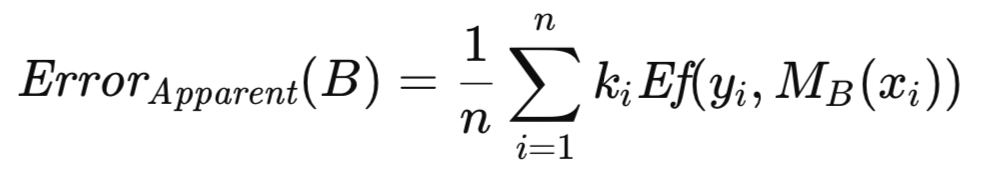
El error excesivo asociado con B se define como la diferencia entre su error de predicción y su error aparente. En lugar de calcularlos por separado y luego restarlos, lo que sería computacionalmente redundante debido a la presencia de términos de error compartidos, se obtiene una formulación más eficiente al factorizar la cantidad común. Esto da como resultado una expresión que debe evaluarse para cada una de las numerosas réplicas de bootstrap (del orden de cientos a miles). El error excesivo medio en estas réplicas proporciona una estimación del error excesivo esperado, que luego se suma al error aparente de la muestra completa para obtener una aproximación del error de población.

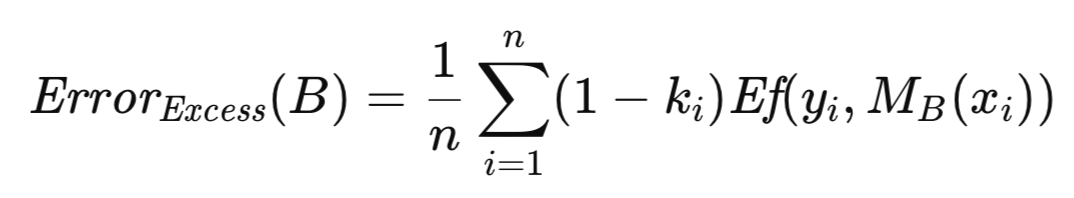
La técnica bootstrap para la estimación de errores se implementa como el método boot_strap(). Además de los parámetros enumerados para la implementación de la validación cruzada, este método incluye un parámetro adicional que especifica el número de réplicas de bootstrap. La rutina comienza inicializando una instancia de un generador de números aleatorios, cortesía de la implementación MQL5 de la librería Alglib. El generador de números aleatorios se utiliza para seleccionar un índice de fila aleatorio como muestra de bootstrap que se coloca en las variables matriciales «preds» y «targs» del conjunto de entrenamiento original. El conjunto de muestras bootstrap se utiliza para entrenar el modelo y, posteriormente, probarlo, con el fin de acumular el exceso de error.

//+------------------------------------------------------------------+
//| estimate error variance using ordinary bootstrap                 |
//+------------------------------------------------------------------+
bool CErrorVar::boot_strap(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   double err,apparent,excess;
   excess = 0.0;
   ulong nsize = predictors.Rows();
   ulong count[];
   ulong k;

   ArrayResize(count,int(nsize));

   vector predicted(nsize);

   CHighQualityRandStateShell rstate;
   CHighQualityRand::HQRndRandomize(rstate.GetInnerObj());

   matrix preds = predictors;
   matrix targs = targets;

   for(ulong boot = 0; boot<nboot; boot++)
     {
      ArrayInitialize(count,0);
      //---
      for(ulong i=0; i<nsize; i++)
        {
         k=(int)(CAlglib::HQRndUniformR(rstate)*nsize);
         //---
         if(k>=nsize)
            k=nsize-1;
         //---
         preds.Row(predictors.Row(k),i);
         targs.Row(targets.Row(k),i);
         ++count[k];
        }

      if(!model.train(preds,targs))
        {
         Print(__FUNCTION__," failed to train model ", boot);
         return false;
        }

      for(ulong i=0; i<nsize; i++)
        {
         predicted[i] = model.forecast(predictors.Row(i));
         err = error_fun(targets[i][0],predicted[i]);
         excess+=(1.0 - double(count[i]))*err;
        }
     }

   excess/=double(nsize*nboot);

Una vez completada la operación de bootstrap, se utiliza el conjunto de datos de entrenamiento original para calcular el error aparente. La estimación final del error se convierte en el valor combinado del exceso y los errores aparentes.

if(!model.train(predictors,targets))
     {
      Print(__FUNCTION__," failed to train model ");
      return false;
     }
   apparent = 0.0;
   for(ulong i=0; i<nsize; i++)
     {
      predicted[i] = model.forecast(predictors.Row(i));
      err = error_fun(targets[i][0],predicted[i]);
      apparent+=err;
     }
   apparent/=double(nsize);
   out_err = apparent+excess;
   return true;
  }

Estimador E0 de Efron para el error de población

Un reto notable que surge de la duplicación de casos de entrenamiento dentro de las muestras bootstrap es la posibilidad de que ciertas clases de modelos dejen de funcionar. En concreto, las redes neuronales probabilísticas y de regresión generalizada son especialmente susceptibles. A menos que la constante de suavizado sea lo suficientemente grande, un caso de prueba idéntico a un caso de entrenamiento producirá una predicción casi perfecta, lo que agravará el problema del sesgo optimista. Para mitigar este problema, Bradley Efron propuso una solución sencilla; la prevención de los artefactos de duplicación. Esto implica generar conjuntos de entrenamiento bootstrap mediante procedimientos de remuestreo estándar. Sin embargo, para cada replicación bootstrap, el modelo se evalúa únicamente sobre aquellas observaciones originales que están ausentes del conjunto de entrenamiento. El error medio entre estas observaciones excluidas se emplea entonces como estimación del error de población. Esta metodología se denomina estimador E0 del error de población.

La literatura académica presenta dos enfoques distintos para calcular E0. El método original consiste en sumar todos los errores y dividirlos por el número total de casos evaluados. Este enfoque se adopta en el presente artículo. Investigaciones teóricas posteriores sobre las propiedades de E0 proponen un algoritmo alternativo que descompone el proceso de promediado en dos etapas. En primer lugar, para cada observación original, se suman los errores de todas las réplicas de bootstrap que carecen de esa observación y se dividen por el número de dichas réplicas, lo que da como resultado un error medio para esa observación. Posteriormente, estos errores medios se suman en todas las observaciones y se dividen por el número total de observaciones para obtener una media general. Aunque este último método presenta una mayor complejidad computacional, es asintóticamente equivalente al primero, y las evaluaciones empíricas demuestran que las diferencias de rendimiento son insignificantes. Por consiguiente, se selecciona el método original por su simplicidad.

Para proporcionar una mejor descripción del algoritmo, se introduce una anotación adicional. Como antes, T denota el conjunto de datos original y B representa una muestra bootstrap. Sea C el conjunto de observaciones en T que no están incluidas en B. Sea count(C) la cardinalidad (número de observaciones) de C. Entonces, la estimación original E0 de Efron del error poblacional se expresa formalmente a continuación.

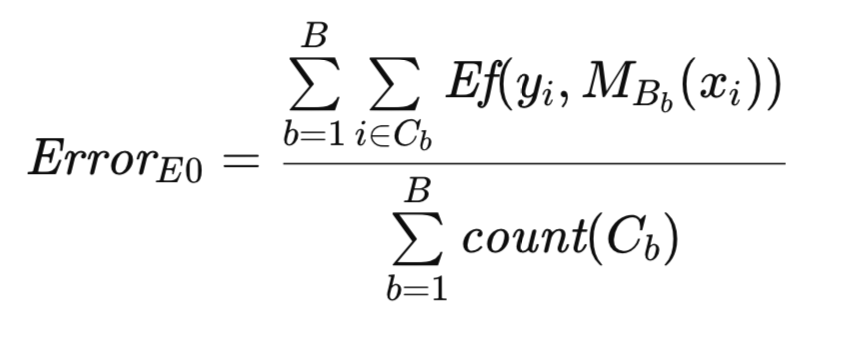
La implementación algorítmica del estimador E0 se asemeja a la rutina bootstrap descrita anteriormente. La generación y utilización de muestras bootstrap para el entrenamiento del modelo son consistentes en ambos métodos. Sin embargo, en este contexto, la matriz de recuento sirve como indicador binario, representando la presencia o ausencia de una observación, en lugar de como contador de frecuencia como en la rutina anterior. El algoritmo se implementa como el método efrons_0(). 

//+------------------------------------------------------------------+
//| estimate error variance using efron's E0 bootstrap               |
//+------------------------------------------------------------------+
bool CErrorVar::efrons_0(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   out_err = 0.0;
   ulong tot = 0;
   ulong nsize = predictors.Rows();
   ulong count[];
   ulong k;

   ArrayResize(count,int(nsize));

   vector predicted(nsize);

   CHighQualityRandStateShell rstate;
   CHighQualityRand::HQRndRandomize(rstate.GetInnerObj());

   matrix preds = predictors;
   matrix targs = targets;

   for(ulong boot = 0; boot<nboot; boot++)
     {
      ArrayInitialize(count,0);
      //---
      for(ulong i=0; i<nsize; i++)
        {
         k=(int)(CAlglib::HQRndUniformR(rstate)*nsize);
         //---
         if(k>=nsize)
            k=nsize-1;
         //---
         preds.Row(predictors.Row(k),i);
         targs.Row(targets.Row(k),i);
         ++count[k];
        }

      if(!model.train(preds,targs))
        {
         Print(__FUNCTION__," failed to train model ", boot);
         continue;//return false;
        }

      for(ulong i=0; i<nsize; i++)
        {
         if(count[i])
            continue;
         predicted[i] = model.forecast(predictors.Row(i));
         out_err+= error_fun(targets[i][0],predicted[i]);
         ++tot;
        }
     }

   if(tot)
      out_err/=double(tot);
   else
     {
      Print(__FUNCTION__, " zero denominator ");
      return false;
     }
   return true;
  }

Estimador E632 de Efron para el error de población

El estimador E0, tal y como se ha descrito anteriormente, presenta propiedades deseables y, por lo general, se recomienda para aplicaciones prácticas. El hecho de evitar evaluar las observaciones presentes en el conjunto de entrenamiento garantiza su compatibilidad con diversas clases de modelos. Además, su varianza está razonablemente limitada, lo que refleja el estado actual del desarrollo metodológico.

Sin embargo, el estimador E0 se caracteriza por un sesgo conservador moderado, que tiende a sobreestimar el error real de la población. Es importante señalar que, siempre que este sesgo no sea excesivo, generalmente se considera menos problemático que la subestimación. La subestimación, tal y como se observa con el bootstrap ordinario, es más perjudicial debido a su propensión a fomentar un optimismo injustificado. El uso del método E0 suele garantizar que el error real de la población sea más probable que sea inferior al valor calculado. Este conservadurismo inherente, aunque generalmente ventajoso, puede llevar al rechazo erróneo de un modelo debido a un pesimismo indebido. El estimador E632 está diseñado para abordar este problema mitigando el sesgo conservador inherente al E0.

Tenga en cuenta las limitaciones inherentes al empleo del error aparente (el error obtenido al evaluar el conjunto de entrenamiento) como estimación del error de población. El procedimiento de evaluación es intrínsecamente sesgado, ya que solo se someten a evaluación las observaciones utilizadas en la formación. Este subconjunto no es representativo de toda la población, ya que muestra una similitud excesiva con el conjunto de entrenamiento, lo que da lugar a un sesgo optimista.

Por el contrario, el estimador E0 presenta el sesgo opuesto. Al excluir deliberadamente las observaciones de entrenamiento de la evaluación, el conjunto de pruebas deja de ser representativo de la población y muestra una diferencia excesiva con respecto al conjunto de entrenamiento. En situaciones reales, inevitablemente surgirán observaciones idénticas o casi idénticas a las observaciones de entrenamiento. La exclusión de estas observaciones por parte de E0 conduce a un sesgo pesimista.

El algoritmo E632 busca establecer un equilibrio entre estos dos extremos. Un enfoque más equitativo podría consistir en evaluar el modelo mediante el muestreo tanto dentro como fuera del conjunto de entrenamiento, con probabilidades que reflejen su ocurrencia en el mundo real. Alternativamente, se pueden realizar ajustes para tener en cuenta las discrepancias en el muestreo. A medida que aumenta el tamaño de la muestra, la probabilidad de que una observación determinada aparezca en una muestra bootstrap converge a 1 − 1/e ≈ 0,632. La heurística de Efron propone estimar el error poblacional como una suma ponderada de E0 y el error aparente, con ponderaciones determinadas por estas probabilidades de muestreo. Su estimador, denominado E632, se representa formalmente en la ecuación siguiente.

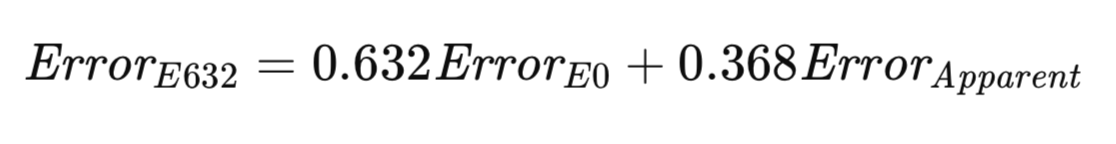
La implementación del algoritmo E632 se proporciona como el método efrons_632(), que se muestra a continuación.

//+------------------------------------------------------------------+
//| estimate error variance using efron's E632 bootstrap             |
//+------------------------------------------------------------------+
bool CErrorVar::efrons_632(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   double apparent;

   if(!efrons_0(nboot,predictors,targets,model,out_err))
      return false;


   if(!model.train(predictors,targets))
     {
      Print(__FUNCTION__," failed to train model ");
      return false;
     }

   apparent = 0.0;
   
   vector predicted(predictors.Rows());

   for(ulong i=0; i<predictors.Rows(); i++)
     {
      predicted[i] = model.forecast(predictors.Row(i));
      apparent+= error_fun(targets[i][0],predicted[i]);
     }

   apparent/=double(predictors.Rows());

   out_err = 0.632*out_err + 0.368*apparent;

   return true;
  }

Todos los algoritmos discutidos en este texto hasta ahora se implementan como miembros de la clase CErrorVar. Esta clase también define el método error_fun() utilizado para calcular el error entre un valor predicho, proporcionado como segundo parámetro, y el valor objetivo correspondiente, proporcionado como primer parámetro del método.

//+------------------------------------------------------------------+
//|  class for estimating error variance                             |
//+------------------------------------------------------------------+
class CErrorVar
  {
public:
                     CErrorVar(void);
                    ~CErrorVar(void);

   virtual double    error_fun(const double truevalue,const double predictedvalue);
   virtual bool      cross_validation(matrix &predictors, matrix &targets, IModel & model,double &out_err);
   virtual bool      boot_strap(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err);
   virtual bool      efrons_0(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err);
   virtual bool      efrons_632(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err);
  };
//+------------------------------------------------------------------+
//| constructor                                                      |
//+------------------------------------------------------------------+
CErrorVar::CErrorVar(void)
  {
  }
//+------------------------------------------------------------------+
//| destructor                                                       |
//+------------------------------------------------------------------+
CErrorVar::~CErrorVar(void)
  {
  }
//+------------------------------------------------------------------+
//| calculate the error                                              |
//+------------------------------------------------------------------+
double CErrorVar::error_fun(const double truevalue,const double predictedvalue)
  {
   return pow(truevalue-predictedvalue,2.0);
  }

La siguiente sección ofrece una demostración del uso de estos algoritmos para estimar el error de un modelo entrenado utilizando únicamente el conjunto de datos de entrenamiento.

Análisis comparativo de estimadores de error de predicción

Este texto ha presentado un conjunto de metodologías para estimar el error poblacional de un modelo predictivo. Se deben tener en cuenta las siguientes consideraciones clave:

• Validación cruzada: esta técnica se caracteriza por su facilidad de implementación y eficiencia computacional. Muestra una amplia aplicabilidad en diversas clases de modelos y proporciona una estimación prácticamente imparcial. Sin embargo, es susceptible a una alta varianza, especialmente en escenarios que implican procedimientos de entrenamiento inestables. Por consiguiente, la validación cruzada no suele recomendarse como método principal, salvo que no existan otros enfoques alternativos. Aunque es eficaz, no se considera óptimo.
• Bootstrap directo: este método se considera generalmente la opción menos deseable. Es incompatible con modelos que no pueden acomodar observaciones de entrenamiento duplicadas o aquellas comprometidas por la presencia de observaciones de prueba dentro del conjunto de entrenamiento. Además, muestra un sesgo significativo hacia la subestimación del error real de la población. Por lo tanto, carece de ventajas convincentes.
• Estimador E0: En escenarios en los que el proceso de entrenamiento permite observaciones duplicadas, el estimador E0 suele ser la opción preferida. Su aplicabilidad se extiende a una amplia gama de modelos, ya que evita evaluar las observaciones de entrenamiento. Demuestra solidez en presencia de condiciones de aprendizaje inestables, como las que implican modelos con procedimientos de entrenamiento estocásticos. Empíricamente, su varianza se aproxima a la de la validación cruzada en entornos de aprendizaje estables, y muestra una varianza significativamente reducida en entornos inestables. Además, es computacionalmente eficiente, dado que el error aparente, necesario para el estimador E632, puede calcularse simultáneamente con la estimación E0. Sin embargo, es importante reconocer que los profesionales pueden dar prioridad al sesgo conservador de E0 sobre la varianza potencialmente mayor asociada con el estimador E632, menos sesgado.

Para evaluar empíricamente estos estimadores, se llevó a cabo un estudio de simulación utilizando datos artificiales generados según el modelo especificado como y = x_1 - x_2 + error. En este modelo, las variables predictoras, x_1 y x_2, siguen una distribución normal estándar, y el término de error se distribuye normalmente con una media de cero y una varianza especificada por el usuario. Se ajustó un modelo lineal ordinario al conjunto de datos y se estimó el error cuadrático medio de la población utilizando los algoritmos presentados en este artículo. El modelo ajustado también se evaluó con datos de prueba independientes para determinar su error real. Este proceso se repitió para un número de ensayos especificado por el usuario, y se calcularon la media y la desviación estándar de las estimaciones de error. Esto se implementa en el script ErrorVarianceEstimation_NumericalPredictionDemo.mq5.

//+------------------------------------------------------------------+
//|              ErrorVarianceEstimation_NumericalPredictionDemo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<error_variance_estimation.mqh>
#include<OLS.mqh>
//--- input parameters
input ulong      NumSamples=15;
input ulong      NumBootStraps = 1000;
input ulong      NumReplications = 100;
input double     Variance = 1.0;
//---
//+------------------------------------------------------------------+
//|  normal(rngstate)                                                |
//+------------------------------------------------------------------+
double normal(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndNormal(state);
  }
//+------------------------------------------------------------------+
//|   unifrand(rngstate)                                             |
//+------------------------------------------------------------------+
double unifrand(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndUniformR(state);
  }
//+------------------------------------------------------------------+
//| ordinary least squares class                                     |
//+------------------------------------------------------------------+
class COrdReg:public IModel
  {
private:
   OLS*              m_ols;
public:
                     COrdReg(void)
     {
      m_ols = new OLS();
     }
                    ~COrdReg(void)
     {
      if(CheckPointer(m_ols) == POINTER_DYNAMIC)
         delete m_ols;
     }
   bool              train(matrix &predictors,matrix& targets)
     {
      return m_ols.Fit(targets.Col(0),predictors);
     }
   double            forecast(vector &predictors)
     {
      return m_ols.Predict(predictors);
     }
  };
//---
ulong nreplications, itry, nsamps, nboots, divisor, ndone;
vector computed_err_cv, computed_err_boot, predictions;
vector computed_err_E0, computed_err_E632 ;
double temperr,sum_observed_error, mean_computed_err, var_computed_err,dfactor,dif;
matrix xdata, testdata,trainpreds,traintargs,testpreds,testtargs;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndRandomize(rngstate.GetInnerObj());
//---
   nboots = NumBootStraps;
   nsamps = NumSamples ;
   nreplications = NumReplications ;
   dfactor = Variance ;

   if((nsamps <= 3)  || (nreplications <= 0) || (dfactor < 0.0) || nboots<=0)
     {
      Alert(" Invalid inputs ");
      return;
     }

   double std = sqrt(dfactor) ;

   divisor = 1000000 / (nsamps * nboots) ;  // This is for progress reports only
   if(divisor < 2)
      divisor = 2 ;

   xdata = matrix::Zeros(nsamps,3);

   sum_observed_error = mean_computed_err = var_computed_err = 0.0;
   computed_err_cv = vector::Zeros(nreplications);
   computed_err_E0 = vector::Zeros(nreplications);
   computed_err_E632 = vector::Zeros(nreplications);
   computed_err_boot = vector::Zeros(nreplications);

   testdata = matrix::Zeros(nsamps*10,3);
   predictions = vector::Zeros(nsamps*10);

   CErrorVar errorvar;
   COrdReg regmodel;

   for(ulong irep = 0; irep<nreplications; irep++)
     {
      ndone = irep + 1 ;

      for(ulong i =0; i<nsamps; i++)
        {
         xdata[i][0] = normal(rngstate);
         xdata[i][1] = normal(rngstate);
         xdata[i][2] = xdata[i][0] - xdata[i][1] + std * normal(rngstate);
        }


      for(ulong j =0; j<testdata.Rows(); j++)
        {
         testdata[j][0] = normal(rngstate);
         testdata[j][1] = normal(rngstate);
         testdata[j][2] = testdata[j][0] - testdata[j][1] + std *normal(rngstate);
        }

      trainpreds = np::sliceMatrixCols(xdata,0,2);
      traintargs = np::sliceMatrixCols(xdata,2);

      if(!regmodel.train(trainpreds,traintargs))
        {
         Print(" fitting first model failed ");
         return;
        }

      testpreds=np::sliceMatrixCols(testdata,0,2);
      testtargs=np::sliceMatrixCols(testdata,2);
      temperr = 0.0;
      for(ulong i = 0;i<testpreds.Rows(); i++)
        {
         predictions[i] = regmodel.forecast(testpreds.Row(i));
         temperr += errorvar.error_fun(testtargs[i][0],predictions[i]);
        }

      sum_observed_error += temperr/double(10*nsamps);

      if(!errorvar.cross_validation(trainpreds,traintargs,regmodel,computed_err_cv[irep]) ||
         !errorvar.boot_strap(nboots,trainpreds,traintargs,regmodel,computed_err_boot[irep]) ||
         !errorvar.efrons_0(nboots,trainpreds,traintargs,regmodel,computed_err_E0[irep]) ||
         !errorvar.efrons_632(nboots,trainpreds,traintargs,regmodel,computed_err_E632[irep])
        )
        {
         Print(" error variance calculation failed ");
         return;
        }
      //---
     }
//---
   PrintFormat("Number of Iterations %d   Observed error = %.5lf",ndone, sum_observed_error / double(ndone)) ;
//---
   PrintFormat("CV: computed error  mean=%10.5lf      std=%10.5lf",computed_err_cv.Mean(), computed_err_cv.Std()) ;
//---
   PrintFormat("BOOT: computed error  mean=%10.5lf      std=%10.5lf",computed_err_boot.Mean(), computed_err_boot.Std()) ;
//---
   PrintFormat("E0: computed error  mean=%10.5lf      std=%10.5lf",computed_err_E0.Mean(), computed_err_E0.Std()) ;
//---
   PrintFormat("E632: computed error  mean=%10.5lf      std=%10.5lf",computed_err_E632.Mean(), computed_err_E632.Std()) ;
  }
//+------------------------------------------------------------------+

Utilizando una varianza de 1,0, un tamaño de muestra de 15 observaciones y 1000 iteraciones de bootstrap. Los resultados fueron los siguientes:

MJ      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    Number of Iterations 100   Observed error = 1.18380
RF      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    CV: computed error  mean=   1.18825      std=   0.53117
PK      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    BOOT: computed error  mean=   1.12521      std=   0.48780
IR      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E0: computed error  mean=   1.38168      std=   0.63579
NO      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E632: computed error  mean=   1.18647      std=   0.52380

Como se preveía, el método bootstrap estándar mostró una subestimación del error real. Por el contrario, el estimador E0 sobreestimó significativamente el error. Aunque esta sobreestimación puede percibirse como una limitación, es importante señalar que el estimador E0 también presentó la desviación estándar más alta. Este grado de sobreestimación se atribuye principalmente al reducido tamaño de la muestra. Sin embargo, la decisión sobre su aceptabilidad sigue siendo subjetiva. Para evaluar más a fondo el rendimiento de los estimadores de error, se repitió el estudio de simulación con un tamaño de muestra mayor, de 100 observaciones, un escenario más representativo para muchas aplicaciones prácticas. Estos son los resultados:

KG      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    CV: computed error  mean=   1.01810      std=   0.24132
LH      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    BOOT: computed error  mean=   1.01672      std=   0.14194
PS      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E0: computed error  mean=   1.01989      std=   0.14441
IP      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E632: computed error  mean=   1.01855      std=   0.14099

Los resultados de este experimento demuestran un rendimiento satisfactorio en las cuatro metodologías. Cabe destacar que el estimador E0 mostró una ligera sobreestimación del error. Los tres algoritmos restantes mostraron una subestimación insignificante. Aunque el estimador E0 mantuvo la desviación estándar más alta, la diferencia fue mínima. En escenarios caracterizados por una alta calidad general de la estimación, es probable que se prefiera la sobreestimación menor del error producida por el estimador E0 a la subestimación trivial observada en los demás métodos, especialmente teniendo en cuenta las implicaciones de la subestimación para la selección y evaluación de modelos.

El ejemplo anterior ilustraba ciertas distinciones entre los distintos métodos para estimar el error poblacional. Sin embargo, puede haber transmitido inadvertidamente la impresión de que la validación cruzada es sistemáticamente comparable a otros métodos en términos de eficacia. Esta percepción se debe al empleo de una función de error suave, concretamente el error cuadrático medio de un modelo simple, que fomenta un entorno de aprendizaje estable.

Las tareas de clasificación, por el contrario, se caracterizan generalmente por una inestabilidad inherente. Las perturbaciones menores en los datos pueden provocar fluctuaciones abruptas y sustanciales en la tasa de error. En esta sección se presenta un ejemplo que explora este fenómeno. Los algoritmos empleados para estimar el error de población siguen siendo coherentes con los analizados anteriormente. Las principales modificaciones se refieren a la definición de la función de error de predicción y a la estructura del programa principal utilizado para la evaluación comparativa.

El código de prueba, ErrorVarianceEstimation_ClassificationDemo.mq5, genera datos bivariados que muestran una correlación positiva moderada.

//+------------------------------------------------------------------+
//|                   ErrorVarianceEstimation_ClassificationDemo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<error_variance_estimation.mqh>
#include<OLS.mqh>
//--- input parameters
input ulong      NumSamples=15;
input ulong      NumBootStraps = 1000;
input ulong      NumReplications = 100;
input double     PredictionDifficultyLevel = 0.0;
//---
//+------------------------------------------------------------------+
//|  normal(rngstate)                                                |
//+------------------------------------------------------------------+
double normal(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndNormal(state);
  }
//+------------------------------------------------------------------+
//|   unifrand(rngstate)                                             |
//+------------------------------------------------------------------+
double unifrand(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndUniformR(state);
  }
//+------------------------------------------------------------------+
//| ordinary least squares class                                     |
//+------------------------------------------------------------------+
class COrdReg:public IModel
  {
private:
   OLS*              m_ols;
public:
                     COrdReg(void)
     {
      m_ols = new OLS();
     }
                    ~COrdReg(void)
     {
      if(CheckPointer(m_ols) == POINTER_DYNAMIC)
         delete m_ols;
     }
   bool              train(matrix &predictors,matrix& targets)
     {
      return m_ols.Fit(targets.Col(0),predictors);
     }
   double            forecast(vector &predictors)
     {
      return m_ols.Predict(predictors);
     }
  };
//+------------------------------------------------------------------+
//| error variance for classification models                         |
//+------------------------------------------------------------------+
class CErrorVarC:public CErrorVar
  {
public:
                     CErrorVarC(void)
     {
     }
                    ~CErrorVarC(void)
     {
     }

   virtual double    error_fun(const double truevalue,const double predictedvalue)
     {
      if(truevalue*predictedvalue>0.0)
         return 0.0;
      else
         return 1.0;
     }


  };
//---
ulong nreplications, itry, nsamps, nboots, divisor, ndone;
vector computed_err_cv, computed_err_boot, predictions;
vector computed_err_E0, computed_err_E632 ;
double temperr,sum_observed_error, mean_computed_err, var_computed_err,dfactor,dif;
matrix xdata, testdata,trainpreds,traintargs,testpreds,testtargs;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndRandomize(rngstate.GetInnerObj());
//---
   nboots = NumBootStraps;
   nsamps = NumSamples ;
   nreplications = NumReplications ;
   dfactor = PredictionDifficultyLevel ;

   if((nsamps <= 3)  || (nreplications <= 0) || (dfactor < 0.0) || nboots<=0)
     {
      Alert(" Invalid inputs ");
      return;
     }

   double std = sqrt(dfactor) ;

   divisor = 1000000 / (nsamps * nboots) ;  // This is for progress reports only
   if(divisor < 2)
      divisor = 2 ;

   xdata = matrix::Zeros(nsamps,3);

   sum_observed_error = mean_computed_err = var_computed_err = 0.0;
   computed_err_cv = vector::Zeros(nreplications);
   computed_err_E0 = vector::Zeros(nreplications);
   computed_err_E632 = vector::Zeros(nreplications);
   computed_err_boot = vector::Zeros(nreplications);

   testdata = matrix::Zeros(nsamps*10,3);
   predictions = vector::Zeros(nsamps*10);

   CErrorVarC errorvar;
   COrdReg olsmodel;

   for(ulong irep = 0; irep<nreplications; irep++)
     {
      ndone = irep + 1 ;

      for(ulong i =0; i<nsamps; i++)
        {
         xdata[i][0] = normal(rngstate);
         xdata[i][1] = 0.7071 * xdata[i][0]  +  0.7071 * normal(rngstate);
         if(CAlglib::HQRndUniformR(rngstate)>0.5)
           {
            xdata[i][0] -=dfactor;
            xdata[i][1] +=dfactor;
            xdata[i][2] = 1.0;
           }
         else
           {
            xdata[i][0] +=dfactor;
            xdata[i][1] -=dfactor;
            xdata[i][2] = -1.0;
           }
        }


      for(ulong j =0; j<testdata.Rows(); j++)
        {
         testdata[j][0] = normal(rngstate);
         testdata[j][1] = 0.7071 * testdata[j][0]  +  0.7071 * normal(rngstate);
         if(CAlglib::HQRndUniformR(rngstate)>0.5)
           {
            testdata[j][0] -=dfactor;
            testdata[j][1] +=dfactor;
            testdata[j][2] = 1.0;
           }
         else
           {
            testdata[j][0] +=dfactor;
            testdata[j][1] -=dfactor;
            testdata[j][2] = -1.0;
           }
        }

      trainpreds = np::sliceMatrixCols(xdata,0,2);
      traintargs = np::sliceMatrixCols(xdata,2);

      if(!olsmodel.train(trainpreds,traintargs))
        {
         Print(" fitting first model failed ");
         return;
        }

      testpreds=np::sliceMatrixCols(testdata,0,2);
      testtargs=np::sliceMatrixCols(testdata,2);
      temperr = 0.0;
      for(ulong i = 0;i<testpreds.Rows(); i++)
        {
         predictions[i] = olsmodel.forecast(testpreds.Row(i));
         temperr += errorvar.error_fun(testtargs[i][0],predictions[i]);
        }

      sum_observed_error += temperr/double(10*nsamps);

      if(!errorvar.cross_validation(trainpreds,traintargs,olsmodel,computed_err_cv[irep]) ||
         !errorvar.boot_strap(nboots,trainpreds,traintargs,olsmodel,computed_err_boot[irep]) ||
         !errorvar.efrons_0(nboots,trainpreds,traintargs,olsmodel,computed_err_E0[irep]) ||
         !errorvar.efrons_632(nboots,trainpreds,traintargs,olsmodel,computed_err_E632[irep])
        )
        {
         Print(" error variance calculation failed ");
         return;
        }
     }

   PrintFormat("Number of Iterations %d   Observed error = %.5lf",ndone, sum_observed_error / double(ndone)) ;
//---
   PrintFormat("CV: computed error  mean=%10.5lf      std=%10.5lf",computed_err_cv.Mean(), computed_err_cv.Std()) ;
//---
   PrintFormat("BOOT: computed error  mean=%10.5lf    std=%10.5lf",computed_err_boot.Mean(), computed_err_boot.Std()) ;
//---
   PrintFormat("E0: computed error  mean=%10.5lf      std=%10.5lf",computed_err_E0.Mean(), computed_err_E0.Std()) ;
//---
   PrintFormat("E632: computed error  mean=%10.5lf    std=%10.5lf",computed_err_E632.Mean(), computed_err_E632.Std()) ;
  }
//+--------------------------------------------------------------------+

Un diagrama de dispersión de los datos para un «PredictionDifficultyLevel» (nivel de dificultad de predicción) dado de 1,0 revelaría una distribución elíptica con su eje mayor orientado diagonalmente hacia arriba y hacia la derecha. El parámetro «PredictionDifficultyLevel» del script controla el grado de separación entre los clústeres, lo que facilita la identificación de clases. Cuanto más bajo sea este parámetro, más difícil será para el modelo inferir la pertenencia a una clase.

Se generan dos clases distintas, con sus respectivas distribuciones de datos desplazadas aproximadamente perpendicularmente al eje principal por una magnitud especificada por el usuario. Se ajusta un modelo lineal a los datos, asignando a la variable predicha un valor de −1,0 para una clase y +1,0 para la otra. El error de predicción se define como 0,0 si los valores reales y los valores previstos comparten el mismo signo, y como 1,0 si presentan signos opuestos. Esta métrica de error binario refleja la naturaleza inherente de los problemas de clasificación.

Se llevaron a cabo dos evaluaciones experimentales distintas. El primer experimento utilizó una muestra de 15 observaciones, 1000 repeticiones de bootstrap, 100 ensayos y una separación de cero. Esta configuración simuló eficazmente un escenario sin información discriminativa, ya que las dos clases mostraban distribuciones idénticas. Como se había previsto, el error medio observado fue de alrededor de 0,5. A continuación se presentan los resultados de este experimento:

OO      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) Number of Iterations 100   Observed error = 0.50267
PS      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) CV: computed error  mean=   0.50267      std=   0.18389
KM      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) BOOT: computed error  mean=   0.45214    std=   0.11748
EQ      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E0: computed error  mean=   0.50517      std=   0.10845
RF      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E632: computed error  mean=   0.45196    std=   0.09941

La validación cruzada demostró una vez más su naturaleza casi imparcial. Este resultado es previsible en este escenario, ya que la falta de capacidad predictiva del modelo da lugar a una probabilidad del 50% de clasificación errónea para cualquier observación dada. El mismo razonamiento se aplica al estimador E0. Aunque normalmente se espera que E0 muestre un sesgo pesimista, esta característica solo se manifiesta cuando el modelo posee cierto grado de eficacia. En este caso, la exclusión forzada de las observaciones de prueba del conjunto de entrenamiento por parte de E0 tiene un impacto neutro.

Sin embargo, esta neutralidad no se extiende al estimador E632. Debido a la combinación de un componente verdaderamente imparcial y un componente fuertemente sesgado hacia el optimismo, E632 muestra un sesgo optimista significativo. Este posible sesgo merece una cuidadosa consideración. Este experimento también pone de relieve la principal crítica a la validación cruzada: su elevada varianza. La desviación estándar del estimador de validación cruzada es sustancialmente mayor que la del estimador E0. Como se observa con frecuencia, el estimador E632 presenta la desviación estándar más baja. Sin embargo, esta ventaja se ve mermada por el fuerte sesgo optimista inherente al E632.

También se realizó un segundo experimento, en el que el modelo poseía cierta capacidad predictiva (el parámetro PredictionDifficultyLevel se incrementó a 1,0). A continuación se presentan los resultados de este experimento:

GM      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) Number of Iterations 100   Observed error = 0.00747
NM      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) CV: computed error  mean=   0.00533      std=   0.01909
RO      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) BOOT: computed error  mean=   0.00716    std=   0.01766
OG      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E0: computed error  mean=   0.01012      std=   0.01878
FD      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E632: computed error  mean=   0.00820    std=   0.01869

Este experimento demuestra que el estimador E632 es el más eficaz. Presenta un sesgo bajo y la desviación estándar más baja. Sin embargo, el estimador E0 mantiene una desviación estándar moderadamente más alta y muestra su sesgo pesimista característico, que a menudo resulta deseable. Teniendo en cuenta los resultados del experimento anterior, este factor debe evaluarse cuidadosamente al elegir entre los estimadores E0 y E632. Una vez más, la validación cruzada muestra la desviación estándar más alta, y el bootstrap directo muestra un sesgo optimista potencialmente peligroso.

Nota sobre el uso de los algoritmos presentados para estimar el rendimiento de la clasificación. Existe una limitación significativa relacionada con la generación de conjuntos de datos de clasificación bootstrap. A veces, un conjunto de muestras bootstrap puede acabar conteniendo ejemplos de una sola clase, lo que provoca problemas en el algoritmo de clasificación o, en algunos casos, su fallo total. Los lectores que deseen emplear las técnicas descritas deben ser conscientes de estos posibles inconvenientes.

Conclusión

Un examen superficial del contenido de este artículo puede llevar a la percepción de que las técnicas de remuestreo para estimar el error poblacional de un modelo son conceptualmente interesantes, pero excesivamente complejas y de utilidad práctica limitada. Tal conclusión sería lamentable, ya que las metodologías de remuestreo aquí presentadas ofrecen ventajas sustanciales y merecen una consideración seria.

En concreto, estos métodos abordan un reto fundamental en la evaluación de modelos: la necesidad de disponer de un conjunto de datos independiente. El enfoque convencional requiere la adquisición de un conjunto de datos independiente, un proceso que a menudo resulta logísticamente oneroso y, en algunos casos, inviable.

Las técnicas de remuestreo que se analizan en este texto evitan este requisito. El conjunto de datos completo se puede utilizar tanto para el entrenamiento del modelo como para la estimación de su rendimiento futuro, maximizando así la utilización de los datos. Esta capacidad representa un avance metodológico significativo y no debe descartarse a la ligera.

Nombre	Descripción
MQL5/include/error_variance_estimation.mqh	Archivo de encabezado que contiene las definiciones de los algoritmos de estimación de errores descritos en el artículo.
MQL5/include/imodel.mqh	Archivo de encabezado incluye la definición de las interfaces utilizadas para interactuar con los modelos de aprendizaje automático.
MQL5/include/np.mqh	Archivo de encabezado con diversas funciones utilitarias de vectores y matrices.
MQL5/include/OLS.mqh	Archivo de inclusión define la clase OLS que implementa modelos de mínimos cuadrados ordinarios.
MQL5/scripts/ErrorVarianceEstimation_NumericalPredictionDemo.mq5	Archivo de demostración que muestra la utilidad de los algoritmos de estimación de errores en la predicción numérica.
MQL5/scripts/ErrorVarianceEstimation_ClassificationDemo.mq5	Archivo de demostración que muestra la utilidad de los algoritmos de estimación de errores en la clasificación de datos.