
Алгоритм оптимизации центральной силы — Central Force Optimization (CFO)
Содержание
Введение
Природа, эволюционирующая миллиарды лет, создала множество эффективных механизмов оптимизации, которые вдохновляют исследователей на создание новых алгоритмов. Одним из таких вдохновляющих природных явлений стала гравитация — фундаментальная сила, управляющая движением космических тел. Мы неоднократно уже разбирали подобные алгоритмы...
Алгоритм оптимизации центральной силы (Central Force Optimization, CFO) представляет собой попытку перенести принципы гравитационной кинематики в область численной оптимизации. Этот метаэвристический алгоритм, основанный на детерминированных законах движения, моделирует взаимодействие виртуальных частиц в многомерном пространстве решений, где каждая частица стремится к областям с лучшими значениями целевой функции под действием аналога гравитационной силы.
В основе CFO лежит простая и интуитивно понятная метафора: представьте себе множество пробных точек (проб), распределенных в пространстве возможных решений. Каждая проба обладает "массой", пропорциональной качеству представляемого ею решения — значению целевой функции. Подобно тому, как массивные небесные тела притягивают менее массивные, пробы с лучшими решениями создают виртуальное гравитационное поле, притягивающее другие пробы.
Движение каждой пробы подчиняется законам, аналогичным законам Ньютона, ускорение определяется суммарной силой притяжения со стороны других проб, а перемещение происходит согласно кинематическим уравнениям движения. Важной особенностью алгоритма является его детерминированная природа — в отличие от многих других метаэвристических методов, CFO не использует случайные величины в своем основном цикле работы.
Реализация алгоритма
История алгоритма CFO началась с того момента, когда исследователи задумались: что если применить законы физики к поиску оптимальных решений? Представьте себе обширную холмистую местность, где высота каждой точки соответствует качеству решения. Чем выше холм, тем лучше решение. Наша цель — найти самую высокую точку, но проблема в том, что мы не видим весь ландшафт сразу. Вместо этого у нас есть группа исследователей — назовем их пробами — которые могут перемещаться по этой местности и сообщать о высоте своего текущего положения.
В начале наши пробы случайно распределены по территории. Одни оказываются в низинах, другие — на склонах холмов, а некоторым может повезти сразу попасть на вершины небольших возвышенностей. Каждая проба имеет свой "вес", пропорциональный высоте точки, где она находится. Чем выше точка, тем "тяжелее" проба. И вот начинается самое интересное — наши пробы не просто бродят наугад, а подчиняются законам гравитации. Представьте, что более "тяжелые" пробы (те, что нашли лучшие точки) притягивают к себе "легкие" пробы (те, что находятся в худших позициях). Причем это притяжение работает только в одну сторону: хорошие решения притягивают плохие, но не наоборот.
Сила притяжения рассчитывается по правилам, похожим на закон всемирного тяготения Ньютона. Она зависит от разницы в "весе" между пробами (разницы в качестве решений) и расстояния между ними. Проба с высоким значением фитнес-функции сильно притягивает близлежащие пробы с низкими значениями, но слабо влияет на далекие пробы. Под действием этих сил каждая проба получает ускорение и начинает двигаться. Маленькие, "легкие" пробы устремляются в сторону более "тяжелых", как если бы шарики катились по склонам холмов к вершинам. С каждым шагом алгоритма пробы пересчитывают силы притяжения и корректируют свое движение. Если проба пытается выйти за установленные границы области поиска, срабатывает механизм отражения – представьте, что на краю территории стоит стена, от которой проба отскакивает обратно в допустимую область.
Со временем пробы начинают собираться вокруг высоких точек ландшафта. Большинство из них концентрируется вокруг наиболее перспективных областей, и с каждой итерацией они всё точнее определяют положение вершин. В идеале, если дать алгоритму достаточно времени, все пробы должны собраться вокруг глобального максимума — самой высокой точки во всем ландшафте.
Особенность CFO в том, что он в своей основе является детерминированным алгоритмом – если запустить его дважды с одинаковым начальным распределением проб, он даст одинаковый результат. Это отличает его от многих других метаэвристических алгоритмов, которые полагаются на случайность.
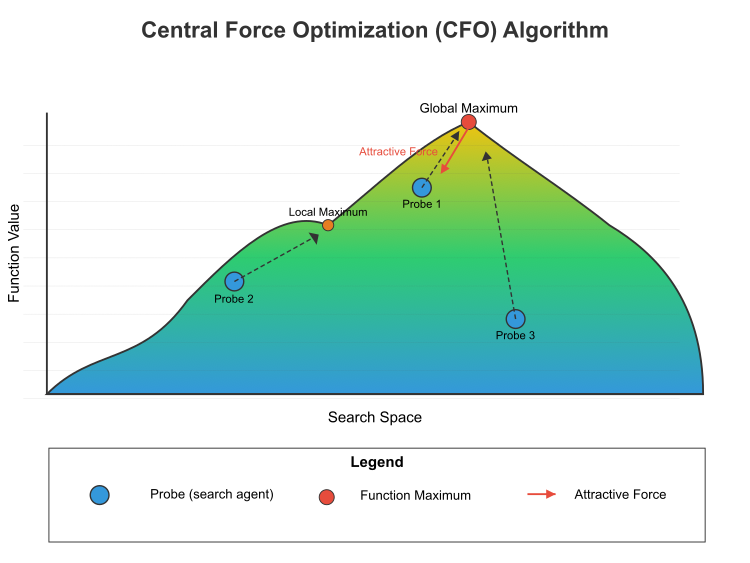
Рисунок 1. Схема работы алгоритма оптимизации центральной силы
На рисунке 1 показан принцип работы алгоритма оптимизации центральной силы (CFO) в пространстве поиска. Представлен ландшафт целевой функции, с цветовым градиентом от синего (низкие значения) до желтого (высокие значения). Глобальный максимум (высшая точка) и локальный максимум (низшая вершина). Три пробы (поисковые агенты), обозначенные как Проба 1, Проба 2 и Проба 3. Силы притяжения (красная стрелка), показывает, как более высокие точки притягивают пробы. Это центральная концепция CFO — лучшие решения притягивают худшие, но не наоборот. Пунктирные линии показывают траекторию проб к максимумам. Математическая формула этого процесса включает:
Расчет силы: для любых двух проб i и j, если значение функции (масса) j больше, чем у i, то j оказывает силу на i в соответствии с: F = g × [(m_j - m_i)^α / d^β] × направление, где:- g — гравитационная постоянная
- m_j и m_i — значения функций (массы) проб j и i
- α — массовый показатель (обычно 2)
- d — расстояние между пробами
- β — показатель расстояния (обычно 2)
- направление — единичный вектор, направленный от пробы i к пробе j
Обновление позиции: позиция каждого зонда обновляется в соответствии с: x_new = x_old + 0,5 × a, где:
- x_new — это новая позиция
- x_old — текущая позиция
- а — ускорение
Алгоритм итеративно применяет эти вычисления ко всем пробам, постепенно перемещая их к оптимумам в пространстве поиска. Со временем пробы имеют тенденцию группироваться вокруг глобальных и локальных максимумов, причем наибольшая концентрация обычно наблюдается вокруг глобального оптимума.
Особенность CFO обусловлена его детерминированной природой и односторонним механизмом притяжения, который направляет исследования на лучшие решения без участия случайности в его базовой форме. Псевдокод алгоритма CFO:
- Инициализация:
- Определяем границы пространства поиска.
- Устанавливаем параметры: число проб, гравитационную постоянную, показатели степени для массы и расстояния, фактор репозиционирования.
- Создаем заданное число проб и случайно размещаем их в пространстве поиска.
- Для каждой пробы вычисляем начальное значение целевой функции.
- Основной цикл (повторяем заданное число эпох):
- Для каждой пробы:
- Обнуляем вектор ускорения.
- Рассматриваем влияние других проб:
- Если другая проба имеет лучшее значение целевой функции (большую "массу"), она создает силу притяжения.
- Вычисляем расстояние между пробами.
- Сила притяжения пропорциональна разнице "масс" в степени alpha и обратно пропорциональна расстоянию в степени beta.
- Направление силы - от текущей пробы к более "тяжелой".
- Суммируем влияния всех проб с лучшими значениями функции.
- После расчета всех ускорений, обновляем позиции проб:
- Новая позиция = старая позиция + половина ускорения.
- Если проба выходит за границы пространства поиска, применяем репозиционирование:
- При выходе за нижнюю границу: отражаем пробу внутрь пространства с учетом фактора репозиционирования.
- При выходе за верхнюю границу: аналогично, но с другой стороны.
- Пересчитываем значения целевой функции для всех проб в их новых позициях.
- Обновляем информацию о лучшем найденном решении.
- Для каждой пробы:
- Завершение:
- Возвращаем лучшее найденное решение (координаты пробы с максимальным значением целевой функции).
Перейдем к написанию кода алгоритма, определим структуру "S_CFO_Agent", которая наследует от "S_AO_Agent" и означает, что "S_CFO_Agent" получает все свойства и методы, определенные в "S_AO_Agent".
Поля структуры: a[] — это динамический массив, который предназначен для хранения значений ускорения. Метод "Init()" используется для инициализации структуры, изменяет размер массива "c" в зависимости от переданного параметра "coords" и изменяет размер массива ускорения "a" в зависимости от "coords". Это позволяет динамически задавать размер массива в зависимости от количества координат, инициализирует все элементы массива ускорения "a" значением "0.0", обнулением значений перед их использованием, устанавливает значение переменной "f" в минимально возможное значение для типа "double", для инициализации фитнес-функции, чтобы обеспечить, что любое другое рассчитанное значение будет больше этого.
//—————————————————————————————————————————————————————————————————————————————— //--- Структура для пробы CFO struct S_CFO_Agent : public S_AO_Agent { double a []; // вектор ускорения void Init (int coords) { ArrayResize (c, coords); // координаты ArrayResize (a, coords); // ускорение ArrayInitialize (a, 0.0); // обнуляем ускорения f = -DBL_MAX; // значение фитнес-функции } }; //——————————————————————————————————————————————————————————————————————————————
Класс "C_AO_CFO" наследуется от класса "C_AO" и определяет алгоритм CFO. Конструктор и деструктор. В данном случае деструктор не выполняет никаких специфических действий. C_AO_CFO () это конструктор, который инициализирует параметры алгоритма. Он задает значения различных переменных, таких как:
- popSize, g, alpha, beta, initialFrep, finalFrep, noiseFactor - это параметры, которые связаны с алгоритмом и его функциями оптимизации.
- frep — текущий фактор репозиционирования, инициализируется значением "initialFrep".
- инициализирует массив "params", который будет содержать параметры алгоритма, после чего их значения копируются в массив с соответствующими именами.
Методы класса:
- SetParams () — устанавливает параметры алгоритма, беря значения из массива "params". Он также устанавливает текущий фактор репозиционирования в "initialFrep".
- Init () — отвечает за инициализацию алгоритма с минимальными и максимальными значениями параметров, а также шагами, которые используются для их изменения. Параметр "epochsP" задает количество эпох для выполнения алгоритма.
- Moving () — отвечает за процесс перемещения проб (агентов) в алгоритме.
- Revision () — может использоваться для проведения ревизии или обновления состояния агентов.
Поля класса:
- S_CFO_Agent probe [] — это массив проб (агентов), которые будут использоваться в процессе оптимизации.
- epochs, epochNow — приватные поля, общее количество эпох и текущая эпоха.
Дополнительные приватные методы:
- InitialDistribution () — используется для инициализации распределения агентов в пространстве поиска.
- UpdateRepFactor () — отвечает за обновление фактора репозиционирования в зависимости от текущего состояния системы.
- CalculateAccelerations () — используется для вычисления ускорений агентов на основе их положений и взаимодействий.
- UpdatePositions () — используется для обновления позиций агентов на основе их ускорений.
- CalculateDistanceSquared () — метод для вычисления расстояния между двумя точками в пространстве и используется для оценки взаимодействия между агентами.
//—————————————————————————————————————————————————————————————————————————————— //--- Основной класс алгоритма CFO class C_AO_CFO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_CFO () { } C_AO_CFO () { ao_name = "CFO"; ao_desc = "Central Force Optimization"; ao_link = "https://www.mql5.com/ru/articles/17167"; popSize = 30; // число проб g = 1.0; // гравитационная постоянная alpha = 0.1; // степень для массы beta = 0.1; // степень для расстояния initialFrep = 0.9; // начальный фактор репозиционирования finalFrep = 0.1; // конечный фактор репозиционирования noiseFactor = 1.0; // фактор случайного шума frep = initialFrep; // текущий фактор репозиционирования ArrayResize (params, 7); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "g"; params [1].val = g; params [2].name = "alpha"; params [2].val = alpha; params [3].name = "beta"; params [3].val = beta; params [4].name = "initialFrep"; params [4].val = initialFrep; params [5].name = "finalFrep"; params [5].val = finalFrep; params [6].name = "noiseFactor"; params [6].val = noiseFactor; } void SetParams () { popSize = (int)MathMax (1, params [0].val); g = params [1].val; alpha = params [2].val; beta = params [3].val; initialFrep = params [4].val; finalFrep = params [5].val; noiseFactor = params [6].val; frep = initialFrep; } bool Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0); // количество эпох void Moving (); void Revision (); //---------------------------------------------------------------------------- double g; // гравитационная постоянная double alpha; // степень для массы double beta; // степень для расстояния double initialFrep; // начальный фактор репозиционирования double finalFrep; // конечный фактор репозиционирования double noiseFactor; // фактор случайного шума S_CFO_Agent probe []; // массив проб private: //------------------------------------------------------------------- int epochs; // общее число эпох int epochNow; // текущая эпоха double frep; // фактор репозиционирования void InitialDistribution (); void UpdateRepFactor (); void CalculateAccelerations (); void UpdatePositions (); double CalculateDistanceSquared (const double &x1 [], const double &x2 []); }; //——————————————————————————————————————————————————————————————————————————————
Метод "Init ()" класса "C_AO_CFO" отвечает за инициализацию алгоритма CFO, принимает массивы минимальных и максимальных значений параметров, шаг изменения этих значений и количество эпох (по умолчанию 0). Вызывает метод "StandardInit" для проверки корректности переданных диапазонов значений. Если он не проходит проверку, метод возвращает "false". Устанавливает общее число эпох и текущую эпоху (0). Изменяет размер массива проб (агентов) на размер популяции (popSize). Инициализирует каждого агент в массиве "probe", вызывая метод "Init" для каждого из них с передачей координат. Если инициализация прошла успешно, метод возвращает "true". Таким образом, метод "Init" настраивает начальные параметры и условия для работы алгоритма.
//—————————————————————————————————————————————————————————————————————————————— //--- Инициализация bool C_AO_CFO::Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; // Инициализация проб ArrayResize (probe, popSize); for (int i = 0; i < popSize; i++) probe [i].Init (coords); return true; } //——————————————————————————————————————————————————————————————————————————————
Метод "Moving ()" класса "C_AO_CFO" отвечает за основной шаг алгоритма CFO, метод начинает работать с увеличения счётчика текущей эпохи, указывая на очередной шаг алгоритма, если метод вызывается впервые, когда "revision" равен "false", он выполняет начальную инициализацию, после чего завершает выполнение. Это необходимо для установки начальных значений и состояния. Далее происходит копирование значений фитнес-функций из массива агентов во временный массив, чтобы сохранить их актуальность для дальнейших вычислений.
Метод обновляет параметр, отвечающий за репозиционирование агентов в пространстве поиска, что важно для адаптивности алгоритма, затем метод рассчитывает ускорения агентов на основе текущего состояния и обновляет их позиции, что обеспечивает движение агентов в поисковом пространстве. В конце метод синхронизирует новые позиции агентов с основным массивом, фиксируя изменения и обеспечивая согласованность данных. Метод "Moving ()" обеспечивает систематическое обновление состояния агентов, основанное на их фитнес-функциях и текущих позициях, в процессе работы алгоритма.
//—————————————————————————————————————————————————————————————————————————————— //--- Основной шаг алгоритма void C_AO_CFO::Moving () { epochNow++; // Начальная инициализация if (!revision) { InitialDistribution (); revision = true; return; } //---------------------------------------------------------------------------- // Копируем значения фитнес-функции из базового класса for (int p = 0; p < popSize; p++) { probe [p].f = a [p].f; } // Обновляем параметр репозиционирования UpdateRepFactor (); // Основной цикл CFO CalculateAccelerations (); UpdatePositions (); // Синхронизируем позиции с базовым классом for (int p = 0; p < popSize; p++) { ArrayCopy (a [p].c, probe [p].c); } } //——————————————————————————————————————————————————————————————————————————————
Метод "InitialDistribution" класса "C_AO_CFO" отвечает за начальное распределение проб (агентов) в пространстве поиска. Метод проходит по каждому агенту в популяции "popSize". Для каждого агента инициализируются значения, задавая массив "a" равным нулю и устанавливая фитнес-функцию "f" в минимальное значение. Для каждой координаты агента выполняется случайное распределение значений в заданных границах (rangeMin и rangeMax). После генерации случайного значения происходит его обработка с использованием метода "SeInDiSp", который приводит значение к определённому диапазону и шагу "rangeStep". Наконец, координаты агента копируются из временного массива "c" в основной массив "a", фиксируя начальное состояние для каждого агента.
//—————————————————————————————————————————————————————————————————————————————— //--- Начальное распределение проб void C_AO_CFO::InitialDistribution () { for (int p = 0; p < popSize; p++) { ArrayInitialize (probe [p].a, 0.0); probe [p].f = -DBL_MAX; // Случайное распределение for (int c = 0; c < coords; c++) { probe [p].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); probe [p].c [c] = u.SeInDiSp (probe [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } ArrayCopy (a [p].c, probe [p].c); } } //——————————————————————————————————————————————————————————————————————————————
Метод "UpdateRepFactor" класса "C_AO_CFO" отвечает за обновление фактора репозиционирования (или репрессивного фактора) в процессе работы алгоритма. Метод начинается с проверки, если количество эпох "epochs" больше нуля, то вычисляется новое значение фактора репозиционирования "frep" путем линейного уменьшения от начального "initialFrep" к конечному значению "finalFrep". Это происходит на основе текущей эпохи "epochNow" в пределах общего числа эпох. Если количество эпох равно нулю, значение "frep" остается равным начальному значению "initialFrep". Это обеспечивает стабильность фактора, если алгоритм находится на начальном этапе. В конце метода происходит ограничение значения "frep" в диапазоне от 0 до 1 с помощью функций "MathMax" и "MathMin". Это гарантирует, что фактор репозиционирования не выйдет за установленные пределы, что имеет важное значение для стабильности и корректности работы алгоритма.
//—————————————————————————————————————————————————————————————————————————————— //--- Обновление фактора репозиционирования void C_AO_CFO::UpdateRepFactor () { // Линейное уменьшение frep от начального к конечному значению if (epochs > 0) frep = initialFrep - (initialFrep - finalFrep) * epochNow / epochs; else frep = initialFrep; // Ограничение значения frep = MathMax (0.0, MathMin (1.0, frep)); } //——————————————————————————————————————————————————————————————————————————————
Метод "CalculateAccelerations" класса "C_AO_CFO" предназначен для вычисления ускорений для каждого агента (или пробы) в популяции на основе влияния всех других агентов. Ниже описаны основные шаги и логика работы метода. Для каждого агента в популяции (от 0 до popSize) значения ускорения "probe[p].a" обнуляются. Это делается для того, чтобы начать вычисление с нуля и накопить ускорения на основе взаимодействия с другими агентами. Для каждого агента внутренний цикл перебирает всех других агентов (от 0 до popSize). Если индекс текущего агента "p" совпадает с индексом другого агента "k", итерация пропускается через команду "continue". Вычисляется разница между фитнес-значениями двух агентов (massDiff = probe[k].f - probe[p].f). Это значение используется для определения, насколько "тяжелее" (или лучше) один агент в сравнении с другим. Если "massDiff" больше нуля, это значит, что второй агент с индексом "k" имеет больший фитнес, чем текущий агент с индексом "p". При этом выполняется следующее:
-
Расчет расстояния: вычисляется квадрат расстояния между текущими координатами двух агентов с помощью функции "CalculateDistanceSquared". Если это расстояние слишком мало (меньше самой малой положительной величины), итерация пропускается.
-
Формирование направления силы: если расстояние больше "DBL_EPSILON", рассчитывается фактическое расстояние, и для каждой координаты "c" определяется направление силы, направленной от текущего агента к агенту с большим фитнесом.
-
Формула ускорения: ускорение для текущего агента обновляется на основе формулы: probe [p].a [c] += g * MathPow (massDiff, alpha) * direction / MathPow (distance, beta), где учитываются разница масс (фитнес-значений), расстояние между пробами и определённые коэффициенты (g, alpha, beta), влияющие на силу взаимодействия.
Метод позволяет каждому агенту учитывать влияние других агентов на его ускорение, что является ключевым элементом в процессе оптимизации. Ускорения, вычисленные таким образом, будут использоваться в дальнейшем для обновления положений агентов в пространстве решения.
//—————————————————————————————————————————————————————————————————————————————— //--- Вычисление ускорений void C_AO_CFO::CalculateAccelerations () { for (int p = 0; p < popSize; p++) { // Обнуляем ускорение для текущей пробы ArrayInitialize (probe [p].a, 0.0); // Суммируем влияние всех других проб for (int k = 0; k < popSize; k++) { if (k == p) continue; // Разница масс (фитнес-значений) double massDiff = probe [k].f - probe [p].f; // Проверяем условие единичной функции U(...) if (massDiff > 0) // Строгое условие для единичной функции { // Вычисляем расстояние между пробами double distSquared = CalculateDistanceSquared (probe [k].c, probe [p].c); if (distSquared < DBL_EPSILON) continue; double distance = MathSqrt (distSquared); for (int c = 0; c < coords; c++) { // Направление силы double direction = (probe [k].c [c] - probe [p].c [c]) / distance; // Формула ускорения probe [p].a [c] += g * MathPow (massDiff, alpha) * direction / MathPow (distance, beta); } } } } } //——————————————————————————————————————————————————————————————————————————————
Метод "UpdatePositions" класса "C_AO_CFO" служит для обновления позиций агентов (или проб) в пространстве решений с учетом их ускорений, случайных факторов и ограничений на границы. В этом методе выполняются несколько шагов:
Уменьшение коэффициента случайного шума:- Анализируется текущее значение коэффициента случайного шума "currentNoiseFactor", который инициализируется равным "noiseFactor".
- Если количество эпох "epochs" больше нуля, коэффициент уменьшается пропорционально текущей эпохе "epochNow", это значит, что при увеличении числа эпох шум будет уменьшаться, что позволяет алгоритму постепенно более точно находить оптимальное решение.
Метод проходит по всем агентам в популяции (от 0 до popSize) и для каждого агента метод проходит по всем его координатам (от 0 до coords). Позиция агента обновляется по формуле, используя текущее ускорение "probe[p].a[c]". В этом случае используется простая формула, в которой новая позиция равняется старой позиции плюс половина текущего ускорения.
В обновленную позицию добавляется небольшое случайное смещение, которое зависит от текущего коэффициента шума, значения гравитации "g" и случайного числа в диапазоне от -1 до 1. Оригинальный алгоритм строго детерминирован и я решил добавить элемент случайности, об этом расскажу ниже. Это смещение добавляет элемент случайности и помогает избегать застревания в локальных минимумах. Если новая позиция превышает заданные границы (минимальные и максимальные значения, хранящиеся в rangeMin и rangeMax), позиция корректируется так, чтобы она оставалась в допустимом диапазоне и если задан шаг дискретизации, позиция агента дополнительно корректируется с использованием метода "SeInDiSp", который приводит позицию к ближайшему значению, кратному шагу.
//—————————————————————————————————————————————————————————————————————————————— //--- Обновление позиций void C_AO_CFO::UpdatePositions () { // Коэффициент случайного шума, уменьшается с ростом номера эпохи double currentNoiseFactor = noiseFactor; if (epochs > 0) currentNoiseFactor *= (1.0 - (double)epochNow / epochs); for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { // Обновление позиции по формуле probe [p].c [c] += 0.5 * probe [p].a [c]; // Добавление небольшого случайного смещения непосредственно к позиции probe [p].c [c] += currentNoiseFactor * g * u.RNDfromCI (-1.0, 1.0); // Репозиционирование при выходе за границы if (probe [p].c [c] < rangeMin [c]) probe [p].c [c] = rangeMin [c]; if (probe [p].c [c] > rangeMax [c]) probe [p].c [c] = rangeMax [c]; // Дискретизация если задан шаг probe [p].c [c] = u.SeInDiSp (probe [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Метод "CalculateDistanceSquared" класса "C_AO_CFO" отвечает за вычисление квадрата расстояния между двумя точками в многомерном пространстве. Метод используется для оптимизации, поскольку возвращение значения квадрата расстояния устраняет необходимость в вычислении квадратного корня, что позволяет существенно сократить вычислительные затраты. Метод принимает два параметра: x1 и x2. Это массивы (const double &x1[] и const double &x2[]), представляющие координаты двух точек в пространстве, размерность которых равна количеству координат "coords". В начале метода создается переменная "sum", инициализированная нулем. Эта переменная используется для накопления суммы квадратов разностей координат. Метод проходит в цикле по всем координатам (от 0 до coords-1) и для каждой координаты:
- Вычисляется разность между соответствующими элементами массивов x1 и x2 (diff = x1[i] - x2[i]).
- Рассчитывается квадрат этой разности (diff * diff).
- Квадрат разности добавляется к переменной "sum".
//—————————————————————————————————————————————————————————————————————————————— //--- Вычисление расстояния (возвращает квадрат расстояния для оптимизации) double C_AO_CFO::CalculateDistanceSquared (const double &x1 [], const double &x2 []) { double sum = 0.0; for (int i = 0; i < coords; i++) { double diff = x1 [i] - x2 [i]; sum += diff * diff; } return sum; } //——————————————————————————————————————————————————————————————————————————————
Метод "Revision ()" класса "C_AO_CFO" отвечает за обновление лучшего найденного решения в процессе оптимизации. Метод проходит по всем агентам (или пробам) в популяции "popSize". Для каждого агента проверяется, если его функция приспособленности "a[p].f" больше текущего лучшего значения "fB". Если это так, обновляется значение "fB", устанавливая его равным функции приспособленности данного агента, далее происходит копирование координат "cB" агента, если его решение является лучшим. Таким образом, метод Revision находит и сохраняет наилучшее решение среди всех агентов, обновляя глобальные параметры, как только оказывается, что агент улучшил результат.
//—————————————————————————————————————————————————————————————————————————————— //--- Обновление лучшего решения void C_AO_CFO::Revision () { for (int p = 0; p < popSize; p++) { if (a [p].f > fB) { fB = a [p].f; ArrayCopy (cB, a [p].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Результаты тестов
Оригинальный, строго детерминированный алгоритм в его базовой версии показывает следующие результаты:
CFO|Central Force Optimization|30.0|1.0|0.1|0.1|0.9|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.34508431921321436
25 Hilly's; Func runs: 10000; result: 0.2826594689557952
500 Hilly's; Func runs: 10000; result: 0.25174636412054047
=============================
5 Forest's; Func runs: 10000; result: 0.26234538930351947
25 Forest's; Func runs: 10000; result: 0.1852230195779629
500 Forest's; Func runs: 10000; result: 0.15353213276989314
=============================
5 Megacity's; Func runs: 10000; result: 0.24923076923076923
25 Megacity's; Func runs: 10000; result: 0.1261538461538462
500 Megacity's; Func runs: 10000; result: 0.09492307692307768
=============================
All score: 1.95090 (21.68%)
С такими результатами алгоритм, к сожалению не может попасть в нашу рейтинговую таблицу. Необходимы улучшения. Поэтому, как я говорил выше, в эту строчку был добавлен элемент случайности, без него детерминированной природе поиска не хватало разнообразия решений.
// Добавление небольшого случайного смещения непосредственно к позиции probe [p].c [c] += currentNoiseFactor * g * u.RNDfromCI (-1.0, 1.0);
После добавления легкого элемента случайности — небольшого случайного смещения к движению каждой пробы, алгоритм смог начать исследовать неожиданные направления. Проведем повторное тестирование. Теперь можем наблюдать совершенно другие результаты, которые уже можно записать в нашу рейтинговую таблицу.
CFO|Central Force Optimization|30.0|1.0|0.1|0.1|0.9|0.1|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6096110105488222
25 Hilly's; Func runs: 10000; result: 0.5495761567207647
500 Hilly's; Func runs: 10000; result: 0.27830861578120414
=============================
5 Forest's; Func runs: 10000; result: 0.6341793648294705
25 Forest's; Func runs: 10000; result: 0.4683296629644541
500 Forest's; Func runs: 10000; result: 0.22540930020804817
=============================
5 Megacity's; Func runs: 10000; result: 0.5723076923076923
25 Megacity's; Func runs: 10000; result: 0.2347692307692307
500 Megacity's; Func runs: 10000; result: 0.09586153846153929
=============================
All score: 3.66835 (40.76%)
Теперь можем посмотреть визуализацию работы алгоритма. Как можно заметить, алгоритм хорошо работает на функциях средней размерности, однако недостаточно хорошо на функциях малой и высокой размерности.

CFO на тестовой функции Hilly

CFO на тестовой функции Forest

CFO на тестовой функции Megacity
По результатам тестирования, алгоритм входит в топ самых лучших популяционных алгоритмов оптимизации и занимает 42 место.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 13 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 14 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 15 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 16 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 17 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 18 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 19 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 20 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 21 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 22 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 23 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 24 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 25 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 26 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 27 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 28 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 29 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 30 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 31 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 32 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 33 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 34 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 35 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 36 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 37 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 38 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 39 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 40 | CGO | chaos game optimization | 0,57256 | 0,37158 | 0,32018 | 1,26432 | 0,61176 | 0,61931 | 0,62161 | 1,85267 | 0,37538 | 0,21923 | 0,19028 | 0,78490 | 3,902 | 43,35 |
| 41 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 42 | CFO | central force optimization | 0,60961 | 0,54958 | 0,27831 | 1,43750 | 0,63418 | 0,46833 | 0,22541 | 1,32792 | 0,57231 | 0,23477 | 0,09586 | 0,90294 | 3,668 | 40,76 |
| 43 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 44 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 45 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Алгоритм CFO, основанный на принципах гравитационного притяжения между объектами, представляет собой интересную попытку применить законы физики к решению сложных оптимизационных задач. После тщательного тестирования на нашем стандартном наборе функций, CFO продемонстрировал эффективность чуть более 40% от теоретически возможного максимума, что позволило ему занять 42-е место среди 45 лучших популяционных алгоритмов оптимизации. Необходимо отметить, что даже этот скромный результат был достигнут только благодаря модификации оригинального алгоритма путем введения случайного компонента в его изначально детерминированную природу.
Несмотря на относительно невысокие показатели эффективности, CFO обладает рядом привлекательных особенностей. Прежде всего, это алгоритм с чрезвычайно ясной физической интерпретацией, что делает его интуитивно понятным. Простота основной концепции – пробы, представляющие потенциальные решения, притягиваются к лучшим решениям подобно тому, как материальные тела притягиваются к более массивным объектам – обеспечивает прозрачность работы алгоритма и легкость его реализации.
Однако тестирование выявило и существенные ограничения CFO, которые требуют пересмотра или улучшения. Чрезмерная зависимость от начального распределения проб является одной из ключевых проблем – из-за детерминированного механизма движения, начальные позиции проб во многом предопределяют конечный результат поиска.
Механизм одностороннего притяжения, при котором только лучшие решения влияют на худшие, но не наоборот, хотя и имеет логическое обоснование, может существенно ограничивать возможности алгоритма по исследованию пространства поиска. Внедрение адаптивного механизма, который допускал бы некоторое влияние и от худших решений, особенно на ранних стадиях поиска, могло бы расширить возможности алгоритма по обнаружению перспективных областей пространства решений.

Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам

Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма CFO:
Плюсы:
- Хорошо работает на функциях средней размерности.
Минусы:
- Недостаточно хорошо работает на функциях малой и высокой размерности.
- Слабые поисковые способности на дискретных функциях.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_CFO.mq5 | Скрипт | Испытательный стенд для CFO |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Арбитражный трейдинг Forex: Анализ движений синтетических валют и их возврат к среднему
Арбитражный трейдинг Forex: Анализ движений синтетических валют и их возврат к среднему
 Нейросети в трейдинге: Адаптивное обнаружение рыночных аномалий (Окончание)
Нейросети в трейдинге: Адаптивное обнаружение рыночных аномалий (Окончание)
 Разработка системы репликации (Часть 73): Неожиданный способ оповещений (II)
Разработка системы репликации (Часть 73): Неожиданный способ оповещений (II)
 Возможности Мастера MQL5, которые вам нужно знать (Часть 37): Регрессия гауссовских процессов с линейными ядрами и ядрами Матерна
Возможности Мастера MQL5, которые вам нужно знать (Часть 37): Регрессия гауссовских процессов с линейными ядрами и ядрами Матерна
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования