
Central Force Optimization (CFO) algorithm
Contents
Introduction
Nature, evolving over billions of years, has created many efficient optimization mechanisms that inspire researchers to create new algorithms. One of these inspiring natural phenomena is gravity — the fundamental force that governs the motion of cosmic bodies. We have already analyzed similar algorithms many times...
The Central Force Optimization (CFO) algorithm is an attempt to transfer the principles of gravitational kinematics to the field of numerical optimization. This metaheuristic algorithm, based on deterministic laws of motion, simulates the interaction of virtual particles in a multidimensional solution space, where each particle tends to regions with better values of the objective function under the influence of the gravitational force analogue.
CFO is based on a simple and intuitive metaphor: imagine a set of trial points (probes) distributed across a space of possible solutions. Each probe has a "mass" proportional to the quality of the solution it represents — the value of the objective function. Just as massive celestial bodies attract less massive ones, probes with the best solutions create a virtual gravitational field that attracts other probes.
The movement of each probe is subject to laws similar to Newton's laws, acceleration is determined by the total force of attraction from other probes, and displacement occurs according to the kinematic equations of motion. An important feature of the algorithm is its deterministic nature — unlike many other metaheuristic methods, CFO does not use random variables in its core operating loop.
Implementation of the algorithm
The history of the CFO algorithm began when researchers wondered: what if the laws of physics were applied to finding optimal solutions? Imagine a vast hilly area where the height of each point corresponds to the quality of the solution. The higher the hill, the better the solution. Our goal is find the highest point, but the problem is that we do not see the whole landscape at once. Instead, we have a group of researchers (samples) that are able to move around the area and report the altitude of their current position.
At the beginning, our probes are randomly distributed across the area. Some end up in the lowlands, others on the slopes of hills, and some may be lucky enough to get straight to the tops of small hills. Each probe has its own "weight", proportional to the height of the point where it is located. The higher the dot, the "heavier" the probe. And now the most interesting part begins — our probes do not just wander around at random, but obey the laws of gravity. Imagine that the "heavier" probes (those that found the best points) attract the "lighter" probes (those that are in the worst positions). Moreover, this attraction works only in one direction: good decisions attract bad ones, but not vice versa.
The force of attraction is calculated according to rules similar to Newton's law of universal gravitation. It depends on the difference in "weight" between the probes (the difference in the quality of solutions) and the distance between them. A probe with a high fitness function value strongly attracts nearby probes with low values, but has little effect on distant samples. Under the influence of these forces, each probe is accelerated and begins to move. Small, "light" probes rush towards the "heavier" ones, as if balls were rolling down the slopes of hills to the top. With each step of the algorithm, the probes recalculate the forces of attraction and adjust their movement. If a probe attempts to move beyond the established boundaries of the search area, a reflection mechanism is triggered – imagine that there is a wall at the edge of the area, from which the probe bounces back into the allowed area.
Over time, the probes begin to collect around high points in the landscape. Most of them are concentrated around the most promising areas, and with each iteration they determine the position of the peaks more accurately. Ideally, if you give the algorithm enough time, all the probes should converge around the global maximum — the highest point in the entire landscape.
The peculiarity of CFO is that it is essentially a deterministic algorithm - if you run it twice with the same initial distribution of probes, it will give the same result. This distinguishes it from many other metaheuristic algorithms that rely on randomness.
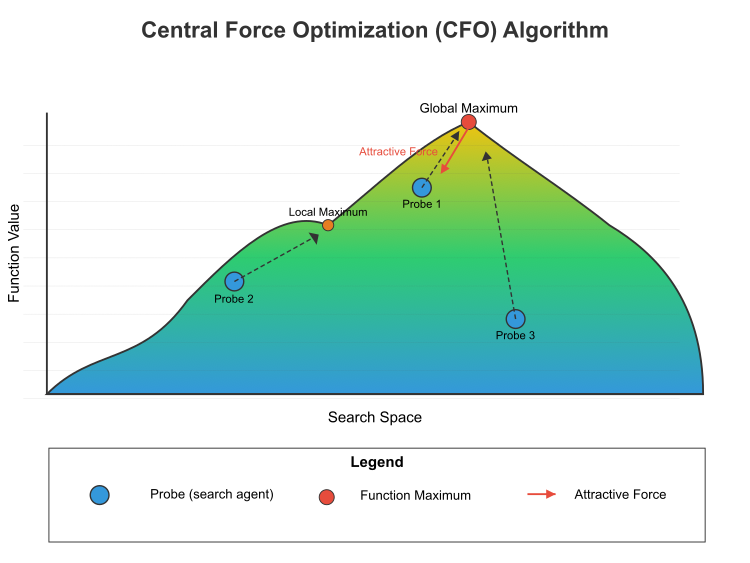
Figure 1. The flow chart of the central force optimization algorithm
Figure 1 shows the operating principle of the central force optimization (CFO) algorithm in the search space. The objective function landscape is shown, with a color gradient from blue (low values) to yellow (high values). Global maximum (highest point) and local maximum (lowest peak). Three probes (search agents) are designated as Probe 1, Probe 2 and Probe 3. The force of attraction (red arrow) shows how higher points attract the probes. This is a central concept of CFO — the best decisions attract the worst, but not vice versa. The dotted lines show the trajectory of the samples to the maxima. The mathematical equation for this process includes:
Force calculation: for any two i and j probes, if the function value (mass) of j is greater than that of i, then j exerts a force on i according to: F = g × [(m_j - m_i)^α / d^β] × direction, where:- g — gravitational constant
- m_j and m_i — values of the functions (masses) of j and i probes
- α — mass index (usually 2)
- d — distance between probes
- β — distance exponent (usually 2)
- direction is a unit vector directed from probe i to probe j
Position update: the position of each probe is updated according to с: x_new = x_old + 0,5 × a, where:
- x_new — new position
- x_old — current position
- a — acceleration
The algorithm iteratively applies these calculations to all samples, gradually moving them towards optima in the search space. Over time, samples tend to cluster around global and local maxima, with the highest concentration typically observed around the global optimum.
The uniqueness of CFO lies in its deterministic nature and one-way attraction mechanism, which directs research toward the best solutions without the involvement of randomness in its basic form. Pseudocode for the CFO algorithm:
- Initialization:
- Define the boundaries of the search space.
- We set the parameters: number of samples, gravitational constant, exponents for mass and distance, repositioning factor.
- Create a given number of samples and randomly place them in the search space.
- For each sample, calculate the initial value of the objective function.
- Main loop (repeat the specified number of epochs):
- For each probe:
- Reset the acceleration vector to zero.
- Consider the influence of other probes:
- If another sample has a better objective function value (larger "mass"), it creates a force of attraction.
- Calculate the distance between probes.
- The force of attraction is proportional to the difference in "masses" to the 'alpha' power and inversely proportional to the distance to the 'beta' power.
- The direction of force is from the current probe to the "heavier" one.
- Sum up the influences of all probes with the best function values.
- Update the positions of the probes after calculating all accelerations:
- New position = old position + half acceleration.
- If the probe falls outside the search space, apply repositioning:
- When going beyond the lower boundary: we reflect the probe into the space taking into account the repositioning factor.
- When going beyond the upper limit: similarly, but on the other side.
- Recalculate the values of the objective function for all probes in their new positions.
- Update information about the best solution found.
- For each probe:
- Completion:
- Return the best solution found (the coordinates of the probe with the maximum value of the objective function).
Let's move on to writing the algorithm code, define the S_CFO_Agent structure, which inherits from S_AO_Agent and means that S_CFO_Agent receives all the properties and methods defined in S_AO_Agent.
Structure fields: a[] — dynamic array designed to store acceleration values. The Init() method is used to initialize the structure, resize the c array based on the passed coords parameter, and resize the a acceleration array based on coords. This allows the array size to be dynamically set based on the number of coordinates, initializes all elements of the a acceleration array to 0.0 by clearing the values before using them, and sets the value of the f variable to the minimum possible value for the double type to initialize the fitness function to ensure that any other value calculated will be greater than the current one.
//—————————————————————————————————————————————————————————————————————————————— //--- CFO probe structure struct S_CFO_Agent : public S_AO_Agent { double a []; // acceleration vector void Init (int coords) { ArrayResize (c, coords); // coordinates ArrayResize (a, coords); // acceleration ArrayInitialize (a, 0.0); // reset accelerations f = -DBL_MAX; // fitness function value } }; //——————————————————————————————————————————————————————————————————————————————
The C_AO_CFO class inherits from the C_AO class and defines the CFO algorithm. Constructor and destructor. In this case, the destructor does not perform any specific actions. C_AO_CFO () is a constructor that initializes the algorithm parameters. It sets the values of various variables, such as:
- popSize, g, alpha, beta, initialFrep, finalFrep, noiseFactor are parameters related to the algorithm and its optimization functions.
- frep — current repositioning factor, initialized by initialFrep.
- The params array is initialized. It will contain the algorithm parameters. After that their values are copied into an array with the corresponding names.
Class methods:
- SetParams () sets the algorithm parameters by taking values from the params array. It also sets the current repositioning factor to initialFrep.
- Init () is responsible for initializing the algorithm with minimum and maximum parameter values, as well as the steps used to change them. The epochsP parameter specifies the number of epochs to execute the algorithm.
- Moving () is responsible for moving the probes (agents) within the algorithm.
- Revision () can be used to audit or update the status of agents.
Class fields:
- S_CFO_Agent probe [] — array of probes (agents) to be used in optimization.
- epochs, epochNow — private fields, total number of epochs and current epoch.
Additional private methods:
- InitialDistribution () - initialize the distribution of agents in the search space.
- UpdateRepFactor () — update the repositioning factor depending on the current state of the system.
- CalculateAccelerations () — calculate the accelerations of agents based on their positions and interactions.
- UpdatePositions () — used to update agents' positions based on their accelerations.
- CalculateDistanceSquared () — method for calculating the distance between two points in space and evaluating the interaction between agents.
//—————————————————————————————————————————————————————————————————————————————— //--- Main class of the CFO algorithm class C_AO_CFO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_CFO () { } C_AO_CFO () { ao_name = "CFO"; ao_desc = "Central Force Optimization"; ao_link = "https://www.mql5.com/en/articles/17167"; popSize = 30; // number of probes g = 1.0; // gravitational constant alpha = 0.1; // mass power beta = 0.1; // degree for distance initialFrep = 0.9; // initial repositioning factor finalFrep = 0.1; // final repositioning factor noiseFactor = 1.0; // random noise factor frep = initialFrep; // current repositioning factor ArrayResize (params, 7); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "g"; params [1].val = g; params [2].name = "alpha"; params [2].val = alpha; params [3].name = "beta"; params [3].val = beta; params [4].name = "initialFrep"; params [4].val = initialFrep; params [5].name = "finalFrep"; params [5].val = finalFrep; params [6].name = "noiseFactor"; params [6].val = noiseFactor; } void SetParams () { popSize = (int)MathMax (1, params [0].val); g = params [1].val; alpha = params [2].val; beta = params [3].val; initialFrep = params [4].val; finalFrep = params [5].val; noiseFactor = params [6].val; frep = initialFrep; } bool Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0); // number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double g; // gravitational constant double alpha; // power for mass double beta; // degree for distance double initialFrep; // initial repositioning factor double finalFrep; // final repositioning factor double noiseFactor; // random noise factor S_CFO_Agent probe []; // array of probes private: //------------------------------------------------------------------- int epochs; // total number of epochs int epochNow; // current epoch double frep; // repositioning factor void InitialDistribution (); void UpdateRepFactor (); void CalculateAccelerations (); void UpdatePositions (); double CalculateDistanceSquared (const double &x1 [], const double &x2 []); }; //——————————————————————————————————————————————————————————————————————————————
The Init () method of the C_AO_CFO class is responsible for initializing the CFO algorithm, accepts arrays of minimum and maximum parameter values, the step for changing these values, and the number of epochs (the default is 0). It calls the StandardInit method to check the validity of the passed value ranges. If it fails the check, the method returns 'false'. It sets the total number of epochs and the current epoch (0). The size of the probes (agents) array is changed to the population size (popSize). The method initializes each agent in the "probe" array by calling the Init method for each of them while passing the coordinates. If initialization is successful, the method returns 'true'. Thus, the Init method sets up the initial parameters and conditions for the algorithm to operate.
//—————————————————————————————————————————————————————————————————————————————— //--- Initialization bool C_AO_CFO::Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; // Initialization of probes ArrayResize (probe, popSize); for (int i = 0; i < popSize; i++) probe [i].Init (coords); return true; } //——————————————————————————————————————————————————————————————————————————————
The Moving () method of the C_AO_CFO class is responsible for the main step of the CFO algorithm. The method starts by increasing the current epoch counter, indicating the next step of the algorithm. If the method is called for the first time, when "revision" is equal to 'false', it performs the initial initialization, after which it completes execution. This is necessary to set the initial values and state. Next, the values of the fitness functions are copied from the array of agents to a temporary array to keep them relevant for further calculations.
The method updates the parameter responsible for the repositioning of agents in the search space, which is important for the adaptability of the algorithm, then the method calculates the acceleration of agents based on the current state and updates their positions, which ensures the movement of agents in the search space. Finally, the method synchronizes the new agent positions with the main array, recording the changes and ensuring data consistency. The Moving() method provides systematic updating of the agents' state based on their fitness functions and current positions during the algorithm execution.
//—————————————————————————————————————————————————————————————————————————————— //--- The main step of the algorithm void C_AO_CFO::Moving () { epochNow++; // Initial initialization if (!revision) { InitialDistribution (); revision = true; return; } //---------------------------------------------------------------------------- // Copy the fitness function values from the base class for (int p = 0; p < popSize; p++) { probe [p].f = a [p].f; } // Update the repositioning parameter UpdateRepFactor (); // Main CFO loop CalculateAccelerations (); UpdatePositions (); // Synchronize positions with the base class for (int p = 0; p < popSize; p++) { ArrayCopy (a [p].c, probe [p].c); } } //——————————————————————————————————————————————————————————————————————————————
The InitialDistribution method of the C_AO_CFO class is responsible for the initial distribution of probes (agents) in the search space. The method iterates over each agent in the popSize population. For each agent, the values are initialized by setting the a array to zero and setting the f fitness function to the minimum value. For each agent coordinate, a random distribution of values is performed within the specified boundaries (rangeMin and rangeMax). After generating a random value, it is processed using the SeInDiSp method, which brings the value to a specific range and rangeStep step. Finally, the agent coordinates are copied from the temporary c array to the a main array, fixing the initial state for each agent.
//—————————————————————————————————————————————————————————————————————————————— //--- Initial probe distribution void C_AO_CFO::InitialDistribution () { for (int p = 0; p < popSize; p++) { ArrayInitialize (probe [p].a, 0.0); probe [p].f = -DBL_MAX; // Random distribution for (int c = 0; c < coords; c++) { probe [p].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); probe [p].c [c] = u.SeInDiSp (probe [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } ArrayCopy (a [p].c, probe [p].c); } } //——————————————————————————————————————————————————————————————————————————————
The UpdateRepFactor method of the C_AO_CFO class is responsible for updating the repositioning factor (or repressive factor) during the algorithm operation. The method starts with a check. If the number of epochs is greater than zero, then a new value of the "frep" repositioning factor is calculated by linearly decreasing from the initialFrep to finalFrep. This is done based on the current epochNow within the total number of epochs. If the number of epochs is zero, frep remains equal to initialFrep. This ensures the stability of the factor if the algorithm is at the initial stage. At the end of the method, frep is limited in the range from 0 to 1 using the MathMax and MathMin functions. This ensures that the repositioning factor does not go beyond the established limits, which is important for the stability and correct operation of the algorithm.
//—————————————————————————————————————————————————————————————————————————————— //--- Update the repositioning factor void C_AO_CFO::UpdateRepFactor () { // Linearly decrease frep from the initial to the final value if (epochs > 0) frep = initialFrep - (initialFrep - finalFrep) * epochNow / epochs; else frep = initialFrep; // Value constraint frep = MathMax (0.0, MathMin (1.0, frep)); } //——————————————————————————————————————————————————————————————————————————————
The CalculateAccelerations method of the C_AO_CFO class is designed to calculate accelerations for each agent (or sample) in the population based on the influence of all other agents. The main steps and logic of the method are described below. For each agent in the population (from 0 to popSize), the probe[p].a acceleration values are reset to zero. This is done in order to start the computation from scratch and accumulate speedups based on interactions with other agents. For each agent, the inner loop iterates over all other agents (from 0 to popSize). If the index of the current p agent matches the index of another k agent, the iteration is skipped through the "continue" command. The difference between the fitness values of two agents is calculated (massDiff = probe[k].f - probe[p].f). This value is used to determine how much "harder" (or better) one agent is compared to another. If massDiff is greater than zero, it means that the second agent with k index has greater fitness than the current agent with p index. In this case, the following is done:
-
Distance calculation: the square of the distance between the current coordinates of two agents is calculated using the CalculateDistanceSquared function. If this distance is too small (less than the smallest positive value), the iteration is skipped.
-
Forming the force direction: if the distance is greater than DBL_EPSILON, the actual distance is calculated. The direction of the force directed from the current agent to the agent with greater fitness is determined for each c coordinate.
-
Acceleration equations: The acceleration for the current agent is updated based on the equation: probe [p].a [c] += g * MathPow (massDiff, alpha) * direction / MathPow (distance, beta), which takes into account the difference in masses (fitness values), the distance between probes, and certain ratios (g, alpha, beta) that affect the interaction strength.
The method allows each agent to take into account the influence of other agents on its acceleration, which is a key element in the optimization. The accelerations calculated in this way will be used later to update the positions of agents in the solution space.
//—————————————————————————————————————————————————————————————————————————————— //--- Calculate accelerations void C_AO_CFO::CalculateAccelerations () { for (int p = 0; p < popSize; p++) { // Reset the acceleration for the current probe ArrayInitialize (probe [p].a, 0.0); // Summarize the influence of all other probes for (int k = 0; k < popSize; k++) { if (k == p) continue; // Difference in masses (fitness values) double massDiff = probe [k].f - probe [p].f; // Check the condition of the U(...) unit function if (massDiff > 0) // Strict condition for the unit function { // Calculate the distance between probes double distSquared = CalculateDistanceSquared (probe [k].c, probe [p].c); if (distSquared < DBL_EPSILON) continue; double distance = MathSqrt (distSquared); for (int c = 0; c < coords; c++) { // Force direction double direction = (probe [k].c [c] - probe [p].c [c]) / distance; // Acceleration equation probe [p].a [c] += g * MathPow (massDiff, alpha) * direction / MathPow (distance, beta); } } } } } //——————————————————————————————————————————————————————————————————————————————
The UpdatePositions method of the C_AO_CFO class is used to update the positions of agents (or samples) in the solution space taking into account their accelerations, random factors, and boundary constraints. This method involves several steps:
Reducing the random noise factor:- The current value of the currentNoiseFactor random noise ratio is analyzed. The ratio is initialized equal to noiseFactor.
- If the number of epochs is greater than zero, the ratio decreases proportionally to the epochNow current epoch. This means that as the number of epochs increases, the noise will decrease, which allows the algorithm to gradually find the optimal solution more accurately.
The method goes through all agents in the population (from 0 to popSize) and for each agent the method goes through all its coordinates (from 0 to coords). The agent position is updated using the formula using the current acceleration probe[p].a[c]. In this case, a simple equation is used, in which the new position is equal to the old position plus half the current acceleration.
A small random offset is added to the updated position, which depends on the current noise factor, the g gravity value and a random number within the range from -1 to 1. The original algorithm is strictly deterministic, so I decided to add an element of randomness I am going to discuss below. This offset adds an element of randomness and helps avoid getting stuck in local minima. If the new position exceeds the specified limits (minimum and maximum values stored in rangeMin and rangeMax), the position is adjusted so that it remains within the allowed range and if a sampling step is specified, the agent's position is further adjusted using the SeInDiSp method, which brings the position to the nearest multiple of the step.
//—————————————————————————————————————————————————————————————————————————————— //--- Update positions void C_AO_CFO::UpdatePositions () { // Random noise ratio decreases with increasing epoch number double currentNoiseFactor = noiseFactor; if (epochs > 0) currentNoiseFactor *= (1.0 - (double)epochNow / epochs); for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { // Update the position by equation probe [p].c [c] += 0.5 * probe [p].a [c]; // Add a small random offset directly to the position probe [p].c [c] += currentNoiseFactor * g * u.RNDfromCI (-1.0, 1.0); // Reposition when going out of bounds if (probe [p].c [c] < rangeMin [c]) probe [p].c [c] = rangeMin [c]; if (probe [p].c [c] > rangeMax [c]) probe [p].c [c] = rangeMax [c]; // Discretization if step is specified probe [p].c [c] = u.SeInDiSp (probe [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
The CalculateDistanceSquared method of the C_AO_CFO class is responsible for calculating the square of the distance between two points in multidimensional space. The method is used for optimization because returning the squared distance value eliminates the need to calculate the square root, which significantly reduces computational costs. The method takes two parameters: x1 and x2. These are arrays (const double &x1[] and const double &x2[]), representing the coordinates of two points in space, the dimensions of which are equal to the number of 'coord' coordinates. At the beginning of the method, a variable "sum" is created, initialized to zero. This variable is used to accumulate the sum of squared differences of coordinates. The method loops through all coordinates (from 0 to coords-1) and for each coordinate:
- Calculate the difference between the corresponding elements of x1 and x2 arrays (diff = x1[i] - x2[i]).
- Calculate the square of the difference (diff * diff).
- The square of the difference is added to the 'sum' variable.
//—————————————————————————————————————————————————————————————————————————————— //--- Calculate distance (returns squared distance for optimization) double C_AO_CFO::CalculateDistanceSquared (const double &x1 [], const double &x2 []) { double sum = 0.0; for (int i = 0; i < coords; i++) { double diff = x1 [i] - x2 [i]; sum += diff * diff; } return sum; } //——————————————————————————————————————————————————————————————————————————————
The Revision () method of the C_AO_CFO class is responsible for updating the best solution found during optimization. The method runs through all agents (or samples) in the popSize population. For each agent, it is checked if its a[p].f fitness function is greater than the current best fB value. If so, the value of fB is updated to be equal to the fitness function of the agent, and then the agent's cB coordinates are copied if its solution is the best. Thus, the Revision method finds and stores the best solution among all agents, updating the global parameters as soon as it turns out that the agent has improved the result.
//—————————————————————————————————————————————————————————————————————————————— //--- Update the best solution void C_AO_CFO::Revision () { for (int p = 0; p < popSize; p++) { if (a [p].f > fB) { fB = a [p].f; ArrayCopy (cB, a [p].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Test results
The original, strictly deterministic algorithm in its basic version shows the following results:
CFO|Central Force Optimization|30.0|1.0|0.1|0.1|0.9|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.34508431921321436
25 Hilly's; Func runs: 10000; result: 0.2826594689557952
500 Hilly's; Func runs: 10000; result: 0.25174636412054047
=============================
5 Forest's; Func runs: 10000; result: 0.26234538930351947
25 Forest's; Func runs: 10000; result: 0.1852230195779629
500 Forest's; Func runs: 10000; result: 0.15353213276989314
=============================
5 Megacity's; Func runs: 10000; result: 0.24923076923076923
25 Megacity's; Func runs: 10000; result: 0.1261538461538462
500 Megacity's; Func runs: 10000; result: 0.09492307692307768
=============================
All score: 1.95090 (21.68%)
With such results, the algorithm cannot be included in our rating table. We need improvements. Therefore, as I said above, an element of randomness was added to this string. Without it, the deterministic nature of the search lacks a variety of solutions.
// Add a small random offset directly to the position probe [p].c [c] += currentNoiseFactor * g * u.RNDfromCI (-1.0, 1.0);
After adding a slight element of randomness (a small random bias into the movement of each probe), the algorithm was able to begin exploring unexpected directions. Let's perform another test. Now we can observe completely different results, which can already be recorded in our rating table.
CFO|Central Force Optimization|30.0|1.0|0.1|0.1|0.9|0.1|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6096110105488222
25 Hilly's; Func runs: 10000; result: 0.5495761567207647
500 Hilly's; Func runs: 10000; result: 0.27830861578120414
=============================
5 Forest's; Func runs: 10000; result: 0.6341793648294705
25 Forest's; Func runs: 10000; result: 0.4683296629644541
500 Forest's; Func runs: 10000; result: 0.22540930020804817
=============================
5 Megacity's; Func runs: 10000; result: 0.5723076923076923
25 Megacity's; Func runs: 10000; result: 0.2347692307692307
500 Megacity's; Func runs: 10000; result: 0.09586153846153929
=============================
All score: 3.66835 (40.76%)
Now we can look at the visualization of the algorithm operation. As can be seen, the algorithm works well on medium-dimensional functions, but not well enough on low- and high-dimensional functions.

CFO on the Hilly test function

CFO on the Forest test function

CFO on the Megacity test function
Based on the test results, the algorithm is among the top best population optimization algorithms and ranks 42nd.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration ptimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0.91362 | 0.82349 | 0.31990 | 2.05701 | 0.97096 | 0.89532 | 0.29324 | 2.15952 | 0.73462 | 0.68569 | 0.16021 | 1.58052 | 5.797 | 64.41 |
| 7 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 8 | BOAm | billiards optimization algorithm M | 0.95757 | 0.82599 | 0.25235 | 2.03590 | 1.00000 | 0.90036 | 0.30502 | 2.20538 | 0.73538 | 0.52523 | 0.09563 | 1.35625 | 5.598 | 62.19 |
| 9 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 10 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 12 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 13 | DA | dialectical algorithm | 0.86183 | 0.70033 | 0.33724 | 1.89940 | 0.98163 | 0.72772 | 0.28718 | 1.99653 | 0.70308 | 0.45292 | 0.16367 | 1.31967 | 5.216 | 57.95 |
| 14 | BHAm | black hole algorithm M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 15 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 16 | RFO | royal flush optimization (joo) | 0.83361 | 0.73742 | 0.34629 | 1.91733 | 0.89424 | 0.73824 | 0.24098 | 1.87346 | 0.63154 | 0.50292 | 0.16421 | 1.29867 | 5.089 | 56.55 |
| 17 | AOSm | atomic orbital search M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 18 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 19 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 20 | SRA | successful restaurateur algorithm (joo) | 0.96883 | 0.63455 | 0.29217 | 1.89555 | 0.94637 | 0.55506 | 0.19124 | 1.69267 | 0.74923 | 0.44031 | 0.12526 | 1.31480 | 4.903 | 54.48 |
| 21 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 22 | BIO | blood inheritance optimization (joo) | 0.81568 | 0.65336 | 0.30877 | 1.77781 | 0.89937 | 0.65319 | 0.21760 | 1.77016 | 0.67846 | 0.47631 | 0.13902 | 1.29378 | 4.842 | 53.80 |
| 23 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 24 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 25 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 26 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 27 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 28 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 29 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 30 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 31 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 32 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 33 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 34 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 35 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 36 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 37 | ABHA | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 38 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 39 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 40 | CGO | chaos game optimization | 0.57256 | 0.37158 | 0.32018 | 1.26432 | 0.61176 | 0.61931 | 0.62161 | 1.85267 | 0.37538 | 0.21923 | 0.19028 | 0.78490 | 3.902 | 43.35 |
| 41 | ATAm | artificial tribe algorithm M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 42 | CFO | central force optimization | 0.60961 | 0.54958 | 0.27831 | 1.43750 | 0.63418 | 0.46833 | 0.22541 | 1.32792 | 0.57231 | 0.23477 | 0.09586 | 0.90294 | 3.668 | 40.76 |
| 43 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 44 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 45 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| RW | random walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Summary
The CFO algorithm, based on the principles of gravitational attraction between objects, is an interesting attempt to apply the laws of physics to solving complex optimization problems. After extensive testing on our standard feature set, CFO demonstrated an efficiency of just over 40% of the theoretical maximum, ranking 42nd among the top 45 population-based optimization algorithms. It should be noted that even this modest result was achieved only by modifying the original algorithm by introducing a random component into its initially deterministic nature.
Despite relatively low performance indicators, the CFO has a number of attractive features. First of all, it has an extremely clear physical interpretation, which makes it intuitive. The simplicity of the basic concept (probes representing potential solutions are attracted to better solutions, just as material bodies are attracted to more massive objects) ensures the transparency of the algorithm operation and the ease of its implementation.
However, the testing also revealed significant limitations of the CFO that require revision or improvement. Over-reliance on the initial distribution of probes is one of the key problems – due to the deterministic movement mechanism, the initial positions of probes largely predetermine the final search result.
The one-way attraction mechanism, in which only the best solutions influence the worst ones, but not vice versa, although it has a logical justification, can significantly limit the algorithm ability to explore the search space. Introducing an adaptive mechanism that would allow some influence from worse solutions, especially in the early stages of the search, could enhance the algorithm ability to detect promising areas of the solution space.

Figure 2. Color gradation of algorithms according to the corresponding tests

Figure 3. Histogram of algorithm testing results (scale from 0 to 100, the higher the better, where 100 is the maximum possible theoretical result, in the archive there is a script for calculating the rating table)
CFO pros and cons:
Pros:
- Works well on medium dimensional functions.
Cons:
- Does not work well enough for low and high dimensional functions.
- Weak search capabilities on discrete functions.
The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.
Programs used in the article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Parent class of population optimization algorithms |
| 2 | #C_AO_enum.mqh | Include | Enumeration of population optimization algorithms |
| 3 | TestFunctions.mqh | Include | Library of test functions |
| 4 | TestStandFunctions.mqh | Include | Test stand function library |
| 5 | Utilities.mqh | Include | Library of auxiliary functions |
| 6 | CalculationTestResults.mqh | Include | Script for calculating results in the comparison table |
| 7 | Testing AOs.mq5 | Script | The unified test stand for all population optimization algorithms |
| 8 | Simple use of population optimization algorithms.mq5 | Script | A simple example of using population optimization algorithms without visualization |
| 9 | Test_AO_CFO.mq5 | Script | CFO test stand |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/17167
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Forex Arbitrage Trading: Relationship Assessment Panel
Forex Arbitrage Trading: Relationship Assessment Panel
 Introduction to MQL5 (Part 36): Mastering API and WebRequest Function in MQL5 (X)
Introduction to MQL5 (Part 36): Mastering API and WebRequest Function in MQL5 (X)
 Python-MetaTrader 5 Strategy Tester (Part 04): Tester 101
Python-MetaTrader 5 Strategy Tester (Part 04): Tester 101
 MQL5 Trading Tools (Part 12): Enhancing the Correlation Matrix Dashboard with Interactivity
MQL5 Trading Tools (Part 12): Enhancing the Correlation Matrix Dashboard with Interactivity
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use