
Der Algorithmus Central Force Optimization (CFO)
Inhalt
Einführung
Die Natur, die sich über Milliarden von Jahren entwickelt hat, hat viele effiziente Optimierungsmechanismen geschaffen, die Forscher zur Entwicklung neuer Algorithmen inspirieren. Eines dieser inspirierenden Naturphänomene ist die Schwerkraft – die fundamentale Kraft, die die Bewegung der kosmischen Körper bestimmt. Wir haben ähnliche Algorithmen bereits mehrfach analysiert...
Der Algorithmus der Optimierung der zentralen Kraft (Central Force Optimization, CFO) ist ein Versuch, die Prinzipien der Schwerkraft bedingten Bewegungen auf den Bereich der numerischen Optimierung zu übertragen. Dieser metaheuristische Algorithmus, der auf deterministischen Bewegungsgesetzen beruht, simuliert die Interaktion virtueller Teilchen in einem mehrdimensionalen Lösungsraum, wobei jedes Teilchen unter dem Einfluss der analogen Gravitationskraft zu Regionen mit besseren Werten der Zielfunktion tendiert.
CFO basiert auf einer einfachen und intuitiven Metapher: Stellen Sie sich eine Reihe von Versuchspunkten (Sonden) vor, die über einen Raum von möglichen Lösungen verteilt sind. Jede Sonde hat eine „Masse“, die proportional zur Qualität der Lösung ist, die sie darstellt – dem Wert der Zielfunktion. So wie massive Himmelskörper weniger massive anziehen, erzeugen die Sonden mit den besten Lösungen ein virtuelles Gravitationsfeld, das andere Sonden anzieht.
Die Bewegung jeder Sonde unterliegt ähnlichen Gesetzen wie den Newtonschen Gesetzen, die Beschleunigung wird durch die Gesamtanziehungskraft der anderen Sonden bestimmt, und die Verschiebung erfolgt gemäß den kinematischen Bewegungsgleichungen. Ein wichtiges Merkmal des Algorithmus ist seine deterministische Natur – im Gegensatz zu vielen anderen metaheuristischen Methoden verwendet CFO keine Zufallsvariablen in seiner Kernarbeitsschleife.
Implementierung des Algorithmus
Die Geschichte des CFO-Algorithmus begann, als Forscher sich fragten: Was wäre, wenn die Gesetze der Physik auf die Suche nach optimalen Lösungen angewendet würden? Stellen Sie sich ein weitläufiges hügeliges Gebiet vor, in dem die Höhe der einzelnen Punkte der Qualität der Lösung entspricht. Je höher der Hügel, desto besser die Lösung. Unser Ziel ist es, den höchsten Punkt zu finden, aber das Problem ist, dass wir nicht die ganze Landschaft auf einmal sehen können. Stattdessen haben wir eine Gruppe von Forschern (samples), die in der Lage sind, sich in der Gegend zu bewegen und die Höhe ihrer aktuellen Position zu melden.
Zu Beginn werden unsere Sonden zufällig über das Gebiet verteilt. Einige landen im Flachland, andere an den Hängen von Hügeln, und einige haben das Glück, direkt auf die Gipfel kleiner Hügel zu gelangen. Jede Sonde hat ihr eigenes „Gewicht“, das proportional zur Höhe des Punktes ist, an dem sie sich befindet. Je höher der Punkt, desto „schwerer“ ist die Sonde. Und nun beginnt der interessanteste Teil – unsere Sonden wandern nicht einfach nur wahllos umher, sondern gehorchen den Gesetzen der Schwerkraft. Stellen Sie sich vor, dass die „schwereren“ Sonden (die, die die besten Punkte gefunden haben) die „leichteren“ Sonden (die, die sich an den schlechtesten Stellen befinden) anziehen. Außerdem wirkt diese Anziehungskraft nur in eine Richtung: Gute Entscheidungen ziehen schlechte an, aber nicht umgekehrt.
Die Anziehungskraft wird nach ähnlichen Regeln berechnet wie das Newtonsche Gesetz der universellen Gravitation. Sie hängt von der unterschiedlichen Gewichtung“ der Sonden (der unterschiedlichen Qualität der Lösungen) und dem Abstand zwischen ihnen ab. Eine Sonde mit einem hohen Fitnessfunktionswert zieht nahegelegene Sonden mit niedrigen Werten stark an, hat aber kaum Auswirkungen auf weiter entfernte Proben. Unter dem Einfluss dieser Kräfte wird jede Sonde beschleunigt und beginnt sich zu bewegen. Kleine, „leichte“ Sonden eilen auf die „schwereren“ zu, als würden Kugeln die Hänge von Hügeln hinunterrollen. Mit jedem Schritt des Algorithmus berechnen die Sonden die Anziehungskräfte neu und passen ihre Bewegung an. Wenn eine Sonde versucht, sich über die festgelegten Grenzen des Suchbereichs hinaus zu bewegen, wird ein Reflexionsmechanismus ausgelöst – stellen Sie sich vor, dass sich am Rand des Bereichs eine Wand befindet, an der die Sonde in den erlaubten Bereich zurückprallt.
Mit der Zeit sammeln sich die Sonden um hohe Punkte in der Landschaft. Die meisten von ihnen konzentrieren sich auf die vielversprechendsten Bereiche, und mit jeder Iteration bestimmen sie die Position der Spitzenwerte genauer. Wenn Sie dem Algorithmus genügend Zeit geben, sollten im Idealfall alle Sonden um das globale Maximum konvergieren – den höchsten Punkt der gesamten Landschaft.
Die Besonderheit des CFO ist, dass es sich im Wesentlichen um einen deterministischen Algorithmus handelt – wenn man ihn zweimal mit der gleichen Anfangsverteilung der Sonden durchführt, wird er das gleiche Ergebnis liefern. Dies unterscheidet ihn von vielen anderen metaheuristischen Algorithmen, die auf Zufälligkeit beruhen.
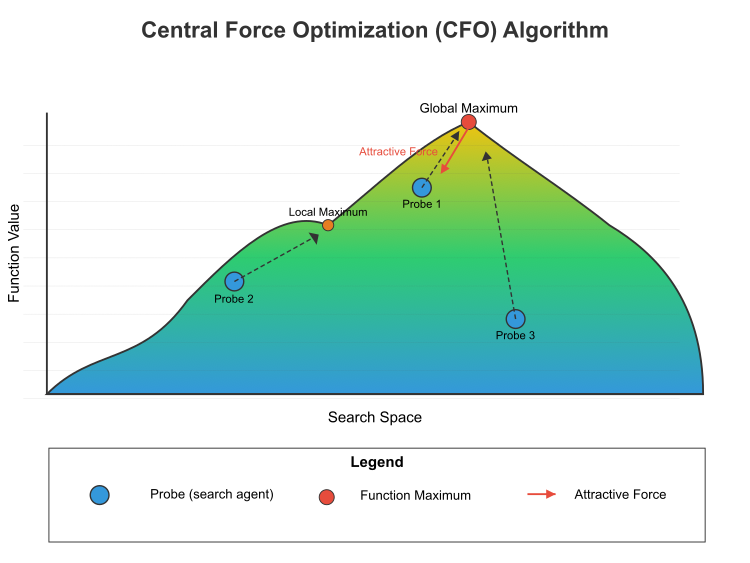
Abbildung 1. Das Flussdiagramm des Algorithmus zur Optimierung der zentralen Kraft
Abbildung 1 zeigt das Funktionsprinzip des Algorithmus der zentralen Kraftoptimierung (CFO) im Suchraum. Die Zielfunktionslandschaft ist mit einem Farbverlauf von blau (niedrige Werte) nach gelb (hohe Werte) dargestellt. Globales Maximum (höchster Punkt) und lokales Maximum (niedrigste Spitze). Drei Sonden (Suchagenten) werden als Probe 1, Probe 2 und Probe 3 bezeichnet. Die Anziehungskraft (roter Pfeil) zeigt, wie höhere Punkte die Sonden anziehen. Dies ist ein zentrales Konzept des CFO – die besten Entscheidungen ziehen die schlechtesten an, aber nicht umgekehrt. Die gestrichelten Linien zeigen den Weg der Proben zu den Maxima. Die mathematische Gleichung für diesen Prozess lautet:
Kraftberechnung: Für zwei beliebige Sonden i und j gilt: Wenn der Funktionswert (Masse) von j größer ist als der von i, dann übt j eine Kraft auf i aus gemäß: F = g × [(m_j – m_i)^α / d^β] × direction, wobei:- g – Gravitationskonstante
- m_j und m_i – Werte der Funktionen (Massen) der j- und i-Sonden
- α – Massenindex (normalerweise 2)
- d – Abstand zwischen den Sonden
- β – Abstandsexponent (normalerweise 2)
- direction ist ein Einheitsvektor, der von Sonde i zu Sonde j gerichtet ist
Positionsaktualisierung: Die Position jeder Sonde wird gemäß с aktualisiert: x_new = x_old + 0,5 × a, wobei:
- x_new – neue Position
- x_old – aktuelle Position
- a – Beschleunigung
Der Algorithmus wendet diese Berechnungen iterativ auf alle Proben an und bewegt sie schrittweise in Richtung der Optima im Suchraum. Im Laufe der Zeit neigen die Proben dazu, sich um globale und lokale Maxima zu gruppieren, wobei die höchste Konzentration in der Regel um das globale Optimum herum beobachtet wird.
Die Einzigartigkeit des CFO liegt in seiner deterministischen Natur und seinem einseitigen Anziehungsmechanismus, der die Forschung auf die besten Lösungen lenkt, ohne dass der Zufall in seiner Grundform beteiligt ist. Pseudocode für den CFO-Algorithmus:
- Initialisierung:
- Definiere die Grenzen des Suchraums.
- Lege die Parameter fest: Anzahl der Proben, Gravitationskonstante, Exponenten für Masse und Abstand, Repositionierungsfaktor.
- Erstelle eine bestimmte Anzahl von Stichproben und platziere diese zufällig im Suchraum.
- Berechne für jede Probe den Anfangswert der Zielfunktion.
- Hauptschleife (Wiederholung der angegebenen Anzahl von Epochen):
- Für jede Sonde:
- Setzte den Beschleunigungsvektor zurück auf Null.
- Berücksichtige den Einfluss von anderen Sonden:
- Wenn eine andere Probe einen besseren Zielfunktionswert (größere „Masse“) hat, erzeugt sie eine Anziehungskraft.
- Berechne den Abstand zwischen den Sonden.
- Die Anziehungskraft ist proportional zur Differenz der „Massen“ in der Potenz „alpha“ und umgekehrt proportional zum Abstand in der Potenz „beta“.
- Die Richtung der Kraft (direction) ist von der aktuellen Sonde zur „schwereren“ Sonde.
- Summiere die Einflüsse aller Sonden mit den besten Funktionswerten.
- Nach der Berechnung der Beschleunigungen aktualisiere die Positionen der Sonden:
- Neue Position = alte Position + halbe Beschleunigung.
- Wenn die Sonde aus dem Suchraum herausfällt, muss sie neu positioniert werden:
- Beim Überschreiten der unteren Grenze: Wir reflektieren die Sonde in den Raum und berücksichtigen dabei den Repositionierungsfaktor.
- Bei Überschreitung der Obergrenze: Ähnlich, aber auf der anderen Seite.
- Berechne die Werte der Zielfunktion für alle Sonden an ihren neuen Positionen neu.
- Aktualisiere die Informationen über die beste gefundene Lösung.
- Für jede Sonde:
- Fertigstellung:
- Rückgabe der besten gefundenen Lösung (die Koordinaten der Sonde mit dem maximalen Wert der Zielfunktion).
Gehen wir nun zum Schreiben des Algorithmuscodes über, definieren wir die Struktur S_CFO_Agent, die von S_AO_Agent erbt und bedeutet, dass S_CFO_Agent alle in S_AO_Agent definierten Eigenschaften und Methoden erhält.
Strukturfelder: a[] – dynamisches Array zur Speicherung von Beschleunigungswerten. Die Methode Init() wird verwendet, um die Struktur zu initialisieren, die Größe des Arrays c anhand des übergebenen Parameters coords zu ändern und die Größe des Beschleunigungs-Arrays a anhand der coords zu ändern. Dadurch kann die Größe des Arrays dynamisch auf der Grundlage der Anzahl der Koordinaten festgelegt werden, alle Elemente des Arrays der Beschleunigungen a werden auf 0,0 initialisiert, indem die Werte vor ihrer Verwendung gelöscht werden, und der Wert der Variablen f wird auf den kleinstmöglichen Wert für den Typ double festgelegt, um die Fitnessfunktion zu initialisieren und sicherzustellen, dass jeder andere berechnete Wert größer als der aktuelle Wert ist.
//—————————————————————————————————————————————————————————————————————————————— //--- CFO probe structure struct S_CFO_Agent : public S_AO_Agent { double a []; // acceleration vector void Init (int coords) { ArrayResize (c, coords); // coordinates ArrayResize (a, coords); // acceleration ArrayInitialize (a, 0.0); // reset accelerations f = -DBL_MAX; // fitness function value } }; //——————————————————————————————————————————————————————————————————————————————
Die Klasse C_AO_CFO wird von der Klasse C_AO abgeleitet und definiert den CFO-Algorithmus. Konstruktor und Destruktor. In diesem Fall führt der Destruktor keine spezifischen Aktionen aus. C_AO_CFO () ist ein Konstruktor, der die Algorithmusparameter initialisiert. Sie setzt die Werte verschiedener Variablen, wie z. B.:
- popSize, g, alpha, beta, initialFrep, finalFrep, noiseFactor sind Parameter, die sich auf den Algorithmus und seine Optimierungsfunktionen beziehen.
- frep – aktueller Repositionierungsfaktor, initialisiert durch initialFrep.
- Das Array params wird initialisiert. Es enthält die Parameter des Algorithmus. Danach werden ihre Werte in ein Array mit den entsprechenden Namen kopiert.
Methoden der Klasse:
- SetParams () setzt die Algorithmusparameter, indem es Werte aus dem Array params übernimmt. Es setzt auch den aktuellen Repositionierungsfaktor auf initialFrep.
- Init () ist verantwortlich für die Initialisierung des Algorithmus mit den minimalen und maximalen Parameterwerten sowie den Schritten, die zu deren Änderung verwendet werden. Der Parameter epochsP gibt die Anzahl der Epochen an, in denen der Algorithmus ausgeführt wird.
- Moving () ist für die Bewegung der Sonden (Agenten) innerhalb des Algorithmus verantwortlich.
- Revision () kann verwendet werden, um den Status von Agenten zu überprüfen oder zu aktualisieren.
Felder der Klasse:
- S_CFO_Agent probe [] – Array von Sonden (Agenten), die bei der Optimierung verwendet werden sollen.
- epochs, epochNow – private Felder, Gesamtzahl der Epochen und aktuelle Epoche.
Zusätzliche private Methoden:
- InitialDistribution () – initialisiert die Verteilung der Agenten im Suchraum.
- UpdateRepFactor () – aktualisiert den Repositionierungsfaktor in Abhängigkeit vom aktuellen Zustand des Systems.
- CalculateAccelerations () – berechnet die Beschleunigungen der Agenten auf der Grundlage ihrer Positionen und Interaktionen.
- UpdatePositions () – dient zur Aktualisierung der Positionen der Agenten auf der Grundlage ihrer Beschleunigungen.
- CalculateDistanceSquared () – ist die Methode zur Berechnung des Abstands zwischen zwei Punkten im Raum und zur Bewertung der Interaktion zwischen Agenten.
//—————————————————————————————————————————————————————————————————————————————— //--- Main class of the CFO algorithm class C_AO_CFO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_CFO () { } C_AO_CFO () { ao_name = "CFO"; ao_desc = "Central Force Optimization"; ao_link = "https://www.mql5.com/en/articles/17167"; popSize = 30; // number of probes g = 1.0; // gravitational constant alpha = 0.1; // mass power beta = 0.1; // degree for distance initialFrep = 0.9; // initial repositioning factor finalFrep = 0.1; // final repositioning factor noiseFactor = 1.0; // random noise factor frep = initialFrep; // current repositioning factor ArrayResize (params, 7); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "g"; params [1].val = g; params [2].name = "alpha"; params [2].val = alpha; params [3].name = "beta"; params [3].val = beta; params [4].name = "initialFrep"; params [4].val = initialFrep; params [5].name = "finalFrep"; params [5].val = finalFrep; params [6].name = "noiseFactor"; params [6].val = noiseFactor; } void SetParams () { popSize = (int)MathMax (1, params [0].val); g = params [1].val; alpha = params [2].val; beta = params [3].val; initialFrep = params [4].val; finalFrep = params [5].val; noiseFactor = params [6].val; frep = initialFrep; } bool Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0); // number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double g; // gravitational constant double alpha; // power for mass double beta; // degree for distance double initialFrep; // initial repositioning factor double finalFrep; // final repositioning factor double noiseFactor; // random noise factor S_CFO_Agent probe []; // array of probes private: //------------------------------------------------------------------- int epochs; // total number of epochs int epochNow; // current epoch double frep; // repositioning factor void InitialDistribution (); void UpdateRepFactor (); void CalculateAccelerations (); void UpdatePositions (); double CalculateDistanceSquared (const double &x1 [], const double &x2 []); }; //——————————————————————————————————————————————————————————————————————————————
Die Methode Init () der Klasse C_AO_CFO ist für die Initialisierung des CFO-Algorithmus zuständig und akzeptiert Arrays mit den minimalen und maximalen Parameterwerten, den Schritt für die Änderung dieser Werte und die Anzahl der Epochen (die Vorgabe ist 0). Sie ruft die Methode StandardInit auf, um die Gültigkeit der übergebenen Wertebereiche zu prüfen. Schlägt die Prüfung fehl, gibt die Methode „false“ zurück. Sie stellt die Gesamtzahl der Epochen und die aktuelle Epoche (0) ein. Die Größe des Sondenfeldes (Agenten) wird auf die Populationsgröße (popSize) geändert. Die Methode initialisiert jeden Agenten im Array „probe“, indem sie die Init-Methode für jeden von ihnen aufruft und die Koordinaten übergibt. Wenn die Initialisierung erfolgreich war, gibt die Methode „true“ zurück. Mit der Init-Methode werden also die Anfangsparameter und -bedingungen für die Arbeit des Algorithmus festgelegt.
//—————————————————————————————————————————————————————————————————————————————— //--- Initialization bool C_AO_CFO::Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; // Initialization of probes ArrayResize (probe, popSize); for (int i = 0; i < popSize; i++) probe [i].Init (coords); return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode Moving () der Klasse C_AO_CFO ist für den Hauptschritt des CFO-Algorithmus verantwortlich. Die Methode beginnt mit der Erhöhung des aktuellen Epochenzählers, was den nächsten Schritt des Algorithmus anzeigt. Wird die Methode zum ersten Mal aufgerufen, wenn „revision“ gleich „false“ ist, führt sie die anfängliche Initialisierung durch und beendet danach die Ausführung. Dies ist notwendig, um die Anfangswerte und den Status festzulegen. Anschließend werden die Werte der Fitnessfunktionen aus dem Array der Agenten in ein temporäres Array kopiert, damit sie für weitere Berechnungen relevant bleiben.
Die Methode aktualisiert den Parameter, der für die Neupositionierung der Agenten im Suchraum verantwortlich ist, was für die Anpassungsfähigkeit des Algorithmus wichtig ist, dann berechnet die Methode die Beschleunigung der Agenten auf der Grundlage des aktuellen Zustands und aktualisiert ihre Positionen, was die Bewegung der Agenten im Suchraum gewährleistet. Schließlich synchronisiert die Methode die neuen Agentenpositionen mit dem Hauptfeld, wobei die Änderungen aufgezeichnet werden und die Datenkonsistenz gewährleistet wird. Die Methode Moving() sorgt für eine systematische Aktualisierung des Zustands der Agenten auf der Grundlage ihrer Fitnessfunktionen und aktuellen Positionen während der Ausführung des Algorithmus.
//—————————————————————————————————————————————————————————————————————————————— //--- The main step of the algorithm void C_AO_CFO::Moving () { epochNow++; // Initial initialization if (!revision) { InitialDistribution (); revision = true; return; } //---------------------------------------------------------------------------- // Copy the fitness function values from the base class for (int p = 0; p < popSize; p++) { probe [p].f = a [p].f; } // Update the repositioning parameter UpdateRepFactor (); // Main CFO loop CalculateAccelerations (); UpdatePositions (); // Synchronize positions with the base class for (int p = 0; p < popSize; p++) { ArrayCopy (a [p].c, probe [p].c); } } //——————————————————————————————————————————————————————————————————————————————
Die Methode InitialDistribution der Klasse C_AO_CFO ist für die Anfangsverteilung der Sonden (Agenten) im Suchraum zuständig. Die Methode iteriert über jeden Agenten in der Population popSize. Für jeden Agenten werden die Werte initialisiert, indem das Array a auf Null und die Fitnessfunktion f auf den Minimalwert gesetzt wird. Für jede Agentenkoordinate wird eine Zufallsverteilung der Werte innerhalb der festgelegten Grenzen (rangeMin und rangeMax) durchgeführt. Nach der Erzeugung eines Zufallswertes wird dieser mit der Methode SeInDiSp verarbeitet, die den Wert in einen bestimmten Bereich und einen rangeStep-Schritt bringt. Schließlich werden die Koordinaten der Agenten aus dem temporären Array c in das Hauptarray a kopiert, wodurch der Anfangszustand für jeden Agenten festgelegt wird.
//—————————————————————————————————————————————————————————————————————————————— //--- Initial probe distribution void C_AO_CFO::InitialDistribution () { for (int p = 0; p < popSize; p++) { ArrayInitialize (probe [p].a, 0.0); probe [p].f = -DBL_MAX; // Random distribution for (int c = 0; c < coords; c++) { probe [p].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); probe [p].c [c] = u.SeInDiSp (probe [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } ArrayCopy (a [p].c, probe [p].c); } } //——————————————————————————————————————————————————————————————————————————————
Die Methode UpdateRepFactor der Klasse C_AO_CFO ist für die Aktualisierung des Repositionierungsfaktors (oder Repressionsfaktors) während der Durchführung des Algorithmus zuständig. Die Methode beginnt mit einer Prüfung. Wenn die Anzahl der Epochen größer als Null ist, wird ein neuer Wert des Repositionierungsfaktors „frep“ berechnet, indem er linear von initialFrep bis finalFrep abnimmt. Dies geschieht auf der Grundlage der aktuellen EpocheNow innerhalb der Gesamtzahl der Epochen. Ist die Anzahl der Epochen gleich Null, bleibt frep gleich initialFrep. Dies gewährleistet die Stabilität des Faktors, wenn sich der Algorithmus in der Anfangsphase befindet. Am Ende der Methode wird frep mit Hilfe der Funktionen MathMax und MathMin im Bereich von 0 bis 1 begrenzt. Dadurch wird sichergestellt, dass der Repositionierungsfaktor die festgelegten Grenzen nicht überschreitet, was für die Stabilität und den korrekten Betrieb des Algorithmus wichtig ist.
//—————————————————————————————————————————————————————————————————————————————— //--- Update the repositioning factor void C_AO_CFO::UpdateRepFactor () { // Linearly decrease frep from the initial to the final value if (epochs > 0) frep = initialFrep - (initialFrep - finalFrep) * epochNow / epochs; else frep = initialFrep; // Value constraint frep = MathMax (0.0, MathMin (1.0, frep)); } //——————————————————————————————————————————————————————————————————————————————
Die Methode CalculateAccelerations der Klasse C_AO_CFO dient der Berechnung von Beschleunigungen für jede Belastung (oder Stichprobe) in der Grundgesamtheit unter Berücksichtigung des Einflusses aller anderen Belastungen. Die wichtigsten Schritte und die Logik der Methode werden im Folgenden beschrieben. Für jeden Agenten in der Population (von 0 bis popSize) werden die Beschleunigungswerte von probe[p].a auf Null zurückgesetzt. Dies geschieht, um die Berechnung von Grund auf neu zu beginnen und durch die Interaktion mit anderen Agenten eine Beschleunigung zu erreichen. Für jeden Agenten durchläuft die innere Schleife alle anderen Agenten (von 0 bis popSize). Wenn der Index des aktuellen Agenten p mit dem Index eines anderen k-Agenten übereinstimmt, wird die Iteration durch den Befehl „Weiter“ übersprungen. Die Differenz zwischen den Fitnesswerten zweier Agenten wird berechnet (massDiff = probe[k].f – probe[p].f). Dieser Wert wird verwendet, um festzustellen, wie viel „härter“ (oder besser) ein Agent im Vergleich zu einem anderen ist. Wenn massDiff größer als Null ist, bedeutet dies, dass der zweite Agent mit dem Index k eine größere Fitness hat als der aktuelle Agent mit dem Index p. In diesem Fall wird wie folgt vorgegangen:
-
Abstandsberechnung: Das Quadrat des Abstands zwischen den aktuellen Koordinaten zweier Agenten wird mit der Funktion CalculateDistanceSquared berechnet. Wenn dieser Abstand zu klein ist (kleiner als der kleinste positive Wert), wird die Iteration übersprungen.
-
Bildung der Kraftrichtung: Wenn der Abstand größer als DBL_EPSILON ist, wird der tatsächliche Abstand berechnet. Für jede c-Koordinate wird die Richtung der Kraft bestimmt, die von dem aktuellen Agenten zu dem Agenten mit der größeren Fitness führt.
-
Beschleunigungsgleichungen: Die Beschleunigung für den aktuellen Agenten wird auf der Grundlage der folgenden Gleichung aktualisiert: probe [p].a [c] += g * MathPow (massDiff, alpha) * direction / MathPow (distance, beta), die den Unterschied in den Massen (Fitnesswerte), den Abstand zwischen den Sonden und bestimmte Verhältnisse (g, alpha, beta) berücksichtigt, die die Interaktionsstärke beeinflussen.
Die Methode ermöglicht es jedem Agenten, den Einfluss der anderen Agenten auf seine Beschleunigung zu berücksichtigen, was ein Schlüsselelement bei der Optimierung ist. Die auf diese Weise berechneten Beschleunigungen werden später zur Aktualisierung der Positionen der Agenten im Lösungsraum verwendet.
//—————————————————————————————————————————————————————————————————————————————— //--- Calculate accelerations void C_AO_CFO::CalculateAccelerations () { for (int p = 0; p < popSize; p++) { // Reset the acceleration for the current probe ArrayInitialize (probe [p].a, 0.0); // Summarize the influence of all other probes for (int k = 0; k < popSize; k++) { if (k == p) continue; // Difference in masses (fitness values) double massDiff = probe [k].f - probe [p].f; // Check the condition of the U(...) unit function if (massDiff > 0) // Strict condition for the unit function { // Calculate the distance between probes double distSquared = CalculateDistanceSquared (probe [k].c, probe [p].c); if (distSquared < DBL_EPSILON) continue; double distance = MathSqrt (distSquared); for (int c = 0; c < coords; c++) { // Force direction double direction = (probe [k].c [c] - probe [p].c [c]) / distance; // Acceleration equation probe [p].a [c] += g * MathPow (massDiff, alpha) * direction / MathPow (distance, beta); } } } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode UpdatePositions der Klasse C_AO_CFO dient zur Aktualisierung der Positionen von Agenten (oder Proben) im Lösungsraum unter Berücksichtigung ihrer Beschleunigungen, Zufallsfaktoren und Randbedingungen. Diese Methode umfasst mehrere Schritte:
Verringerung des Faktors Rauschen:- Der aktuelle Wert des Zufallsrauschverhältnisses currentNoiseFactor wird ausgewertet. Das Verhältnis wird gleich dem NoiseFactor initialisiert.
- Wenn die Anzahl der Epochen größer als Null ist, verringert sich das Verhältnis proportional zur aktuellen Epoche epochNow. Das bedeutet, dass mit zunehmender Anzahl von Epochen das Rauschen abnimmt, wodurch der Algorithmus schrittweise die optimale Lösung genauer finden kann.
Die Methode geht durch alle Agenten in der Population (von 0 bis popSize) und für jeden Agenten geht die Methode durch alle seine Koordinaten (von 0 bis coords). Die Position des Agenten wird anhand der Formel mit der aktuellen Beschleunigung probe[p].a[c] aktualisiert. In diesem Fall wird eine einfache Gleichung verwendet, bei der die neue Position gleich der alten Position plus der Hälfte der aktuellen Beschleunigung ist.
Zur aktualisierten Position wird ein kleiner zufälliger Offset hinzugefügt, der vom aktuellen Rauschfaktor, dem g-Schwerkraftwert und einer Zufallszahl im Bereich von -1 bis 1 abhängt. Der ursprüngliche Algorithmus ist streng deterministisch, daher habe ich beschlossen, ein Zufallselement hinzuzufügen, das ich weiter unten erläutern werde. Dieser Offset fügt ein Element der Zufälligkeit hinzu und hilft zu vermeiden, dass man in lokalen Minima stecken bleibt. Überschreitet die neue Position die angegebenen Grenzen (Mindest- und Höchstwerte, die in rangeMin und rangeMax gespeichert sind), wird die Position so angepasst, dass sie innerhalb des zulässigen Bereichs bleibt, und wenn ein Abtastschritt angegeben ist, wird die Position des Agenten mit der Methode SeInDiSp weiter angepasst, wodurch die Position auf das nächste Vielfache des Schritts gebracht wird.
//—————————————————————————————————————————————————————————————————————————————— //--- Update positions void C_AO_CFO::UpdatePositions () { // Random noise ratio decreases with increasing epoch number double currentNoiseFactor = noiseFactor; if (epochs > 0) currentNoiseFactor *= (1.0 - (double)epochNow / epochs); for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { // Update the position by equation probe [p].c [c] += 0.5 * probe [p].a [c]; // Add a small random offset directly to the position probe [p].c [c] += currentNoiseFactor * g * u.RNDfromCI (-1.0, 1.0); // Reposition when going out of bounds if (probe [p].c [c] < rangeMin [c]) probe [p].c [c] = rangeMin [c]; if (probe [p].c [c] > rangeMax [c]) probe [p].c [c] = rangeMax [c]; // Discretization if step is specified probe [p].c [c] = u.SeInDiSp (probe [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode CalculateDistanceSquared der Klasse C_AO_CFO ist für die Berechnung des Quadrats des Abstands zwischen zwei Punkten im mehrdimensionalen Raum zuständig. Die Methode wird für die Optimierung verwendet, da die Rückgabe des quadrierten Abstandswertes die Berechnung der Quadratwurzel überflüssig macht, was die Rechenaufwand erheblich reduziert. Die Methode benötigt zwei Parameter: x1 und x2. Es handelt sich um Felder (const double &x1[] und const double &x2[]), die die Koordinaten von zwei Punkten im Raum darstellen und deren Größe der Anzahl der Koordinaten „coord“ entspricht. Zu Beginn der Methode wird eine Variable „sum“ erstellt, die mit Null initialisiert wird. Diese Variable wird zur Akkumulation der Summe der quadrierten Differenzen der Koordinaten verwendet. Die Methode führt eine Schleife durch alle Koordinaten (von 0 bis coords-1) und für jede Koordinate:
- Berechne die Differenz zwischen den entsprechenden Elementen der Arrays x1 und x2 (diff = x1[i] – x2[i]).
- Berechne das Quadrat der Differenz (diff * diff).
- Addiere das Quadrat der Differenz zu der Variablen „sum“.
//—————————————————————————————————————————————————————————————————————————————— //--- Calculate distance (returns squared distance for optimization) double C_AO_CFO::CalculateDistanceSquared (const double &x1 [], const double &x2 []) { double sum = 0.0; for (int i = 0; i < coords; i++) { double diff = x1 [i] - x2 [i]; sum += diff * diff; } return sum; } //——————————————————————————————————————————————————————————————————————————————
Die Methode Revision () der Klasse C_AO_CFO ist für die Aktualisierung der bei der Optimierung gefundenen besten Lösung zuständig. Die Methode durchläuft alle Bearbeiter (oder Stichproben) in der Population popSize. Für jeden Agenten wird geprüft, ob seine Fitnessfunktion a[p].f größer ist als der aktuell beste fB-Wert. Wenn dies der Fall ist, wird der Wert von fB so aktualisiert, dass er gleich der Fitnessfunktion des Agenten ist, und dann werden die cB-Koordinaten des Agenten kopiert, wenn seine Lösung die beste ist. So findet und speichert die Revisionsmethode die beste Lösung unter allen Agenten und aktualisiert die globalen Parameter, sobald sich herausstellt, dass der Agent das Ergebnis verbessert hat.
//—————————————————————————————————————————————————————————————————————————————— //--- Update the best solution void C_AO_CFO::Revision () { for (int p = 0; p < popSize; p++) { if (a [p].f > fB) { fB = a [p].f; ArrayCopy (cB, a [p].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Testergebnisse
Der ursprüngliche, streng deterministische Algorithmus in seiner Grundversion zeigt folgende Ergebnisse:
CFO|Central Force Optimization|30.0|1.0|0.1|0.1|0.9|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.34508431921321436
25 Hilly's; Func runs: 10000; result: 0.2826594689557952
500 Hilly's; Func runs: 10000; result: 0.25174636412054047
=============================
5 Forest's; Func runs: 10000; result: 0.26234538930351947
25 Forest's; Func runs: 10000; result: 0.1852230195779629
500 Forest's; Func runs: 10000; result: 0.15353213276989314
=============================
5 Megacity's; Func runs: 10000; result: 0.24923076923076923
25 Megacity's; Func runs: 10000; result: 0.1261538461538462
500 Megacity's; Func runs: 10000; result: 0.09492307692307768
=============================
All score: 1.95090 (21.68%)
Mit solchen Ergebnissen kann der Algorithmus nicht in unsere Bewertungstabelle aufgenommen werden. Wir brauchen Verbesserungen. Daher wurde, wie ich bereits sagte, ein Element des Zufalls in diese Zeichenfolge eingefügt. Ohne sie fehlt es dem deterministischen Charakter der Suche an einer Vielfalt von Lösungen.
// Add a small random offset directly to the position probe [p].c [c] += currentNoiseFactor * g * u.RNDfromCI (-1.0, 1.0);
Nach dem Hinzufügen eines kleinen Zufallselements (eine kleine zufällige Verzerrung in der Bewegung jeder Sonde) war der Algorithmus in der Lage, unerwartete Richtungen zu erkunden. Führen wir einen weiteren Test durch. Jetzt können wir ganz andere Ergebnisse beobachten, die bereits in unserer Bewertungstabelle festgehalten werden können.
CFO|Central Force Optimization|30.0|1.0|0.1|0.1|0.9|0.1|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6096110105488222
25 Hilly's; Func runs: 10000; result: 0.5495761567207647
500 Hilly's; Func runs: 10000; result: 0.27830861578120414
=============================
5 Forest's; Func runs: 10000; result: 0.6341793648294705
25 Forest's; Func runs: 10000; result: 0.4683296629644541
500 Forest's; Func runs: 10000; result: 0.22540930020804817
=============================
5 Megacity's; Func runs: 10000; result: 0.5723076923076923
25 Megacity's; Func runs: 10000; result: 0.2347692307692307
500 Megacity's; Func runs: 10000; result: 0.09586153846153929
=============================
All score: 3.66835 (40.76%)
Nun können wir uns die Visualisierung der Algorithmusoperation ansehen. Wie man sieht, funktioniert der Algorithmus gut bei mittelgroßen Funktionen, aber nicht gut genug bei niedrig- und hochdimensionalen Funktionen.

CFO mit der Testfunktion Hilly

CFO mit der Testfunktion Forest

CFO mit der Testfunktion Megacity
Auf der Grundlage der Testergebnisse gehört der Algorithmus zu den besten Algorithmen für die Bevölkerungsoptimierung und liegt auf Platz 42.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Code-Sperr-Algorithmus (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | TETA | Zeit-Evolutions-Reise-Algorithmus (Joo) | 0.91362 | 0.82349 | 0.31990 | 2.05701 | 0.97096 | 0.89532 | 0.29324 | 2.15952 | 0.73462 | 0.68569 | 0.16021 | 1.58052 | 5.797 | 64.41 |
| 7 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 8 | BOAm | Billard-Optimierungsalgorithmus M | 0.95757 | 0.82599 | 0.25235 | 2.03590 | 1.00000 | 0.90036 | 0.30502 | 2.20538 | 0.73538 | 0.52523 | 0.09563 | 1.35625 | 5.598 | 62.19 |
| 9 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 10 | ESG | Entwicklung sozialer Gruppen (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 11 | SIA | Simuliertes isotropes Glühen (Joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 12 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 13 | DA | dialektischer Algorithmus | 0.86183 | 0.70033 | 0.33724 | 1.89940 | 0.98163 | 0.72772 | 0.28718 | 1.99653 | 0.70308 | 0.45292 | 0.16367 | 1.31967 | 5.216 | 57.95 |
| 14 | BHAm | Algorithmus für schwarze Löcher M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 15 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 16 | RFO | Optimierung des Royal Flush (joo) | 0.83361 | 0.73742 | 0.34629 | 1.91733 | 0.89424 | 0.73824 | 0.24098 | 1.87346 | 0.63154 | 0.50292 | 0.16421 | 1.29867 | 5.089 | 56.55 |
| 17 | AOSm | Suche nach atomaren Orbitalen M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 18 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 19 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 20 | SRA | Algorithmus für erfolgreiche Gastronomen (joo) | 0.96883 | 0.63455 | 0.29217 | 1.89555 | 0.94637 | 0.55506 | 0.19124 | 1.69267 | 0.74923 | 0.44031 | 0.12526 | 1.31480 | 4.903 | 54.48 |
| 21 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 22 | BIO | Optimierung der Blutvererbung (joo) | 0.81568 | 0.65336 | 0.30877 | 1.77781 | 0.89937 | 0.65319 | 0.21760 | 1.77016 | 0.67846 | 0.47631 | 0.13902 | 1.29378 | 4.842 | 53.80 |
| 23 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 24 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 25 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 26 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 27 | ABO | Optimierung des afrikanischen Büffels | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 28 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 29 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 30 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 31 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 32 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 33 | AEO | Algorithmus zur Optimierung auf der Grundlage künstlicher Ökosysteme | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 34 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 35 | BFO-GA | Optimierung der bakteriellen Futtersuche — ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 36 | SOA | einfacher Optimierungsalgorithmus | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 37 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 38 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 39 | ADAMm | adaptive Momentabschätzung M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 40 | CGO | Chaos Game Optimization | 0.57256 | 0.37158 | 0.32018 | 1.26432 | 0.61176 | 0.61931 | 0.62161 | 1.85267 | 0.37538 | 0.21923 | 0.19028 | 0.78490 | 3.902 | 43.35 |
| 41 | ATAm | Algorithmus für künstliche Stämme M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 42 | CFO | Schwerkraftoptimierung | 0.60961 | 0.54958 | 0.27831 | 1.43750 | 0.63418 | 0.46833 | 0.22541 | 1.32792 | 0.57231 | 0.23477 | 0.09586 | 0.90294 | 3.668 | 40.76 |
| 43 | ASHA | Algorithmus für künstliches Duschen | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 44 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 45 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| RW | Random Walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Zusammenfassung
Der CFO-Algorithmus, der auf den Prinzipien der Anziehungskraft zwischen Objekten beruht, ist ein interessanter Versuch, die Gesetze der Physik auf die Lösung komplexer Optimierungsprobleme anzuwenden. Nach umfangreichen Tests mit unseren Standardmerkmalen zeigte CFO eine Effizienz von knapp über 40 % des theoretischen Maximums und belegte damit Platz 42 unter den 45 besten populationsbasierten Optimierungsalgorithmen. Es sei darauf hingewiesen, dass selbst dieses bescheidene Ergebnis nur durch eine Änderung des ursprünglichen Algorithmus erreicht wurde, indem eine Zufallskomponente in seinen ursprünglich deterministischen Charakter eingeführt wurde.
Trotz der relativ niedrigen Leistungsindikatoren weist das CFO eine Reihe attraktiver Merkmale auf. Zunächst einmal hat sie eine sehr klare physikalische Interpretation, die sie intuitiv macht. Die Einfachheit des Grundkonzepts (Sonden, die potenzielle Lösungen repräsentieren, werden von besseren Lösungen angezogen, so wie materielle Körper von massiveren Objekten angezogen werden) gewährleistet die Transparenz der Funktionsweise des Algorithmus und die Leichtigkeit seiner Umsetzung.
Die Prüfung ergab jedoch auch erhebliche Einschränkungen des CFO, die eine Überarbeitung oder Verbesserung erfordern. Die übermäßige Abhängigkeit von der anfänglichen Verteilung der Sonden ist eines der Hauptprobleme – aufgrund des deterministischen Bewegungsmechanismus bestimmen die Anfangspositionen der Sonden weitgehend das endgültige Suchergebnis.
Der Mechanismus der einseitigen Anziehung, bei dem nur die besten Lösungen die schlechtesten beeinflussen, aber nicht umgekehrt, hat zwar eine logische Begründung, kann aber die Fähigkeit des Algorithmus, den Suchraum zu erkunden, erheblich einschränken. Die Einführung eines adaptiven Mechanismus, der einen gewissen Einfluss von schlechteren Lösungen zulässt, insbesondere in den frühen Phasen der Suche, könnte die Fähigkeit des Algorithmus verbessern, vielversprechende Bereiche des Lösungsraums zu erkennen.

Abbildung 2. Farbabstufung der Algorithmen nach den entsprechenden Tests

Abbildung 3. Das Histogramm der Algorithmus-Testergebnisse (Skala von 0 bis 100, je höher, desto besser, wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Bewertungstabelle)
Vor- und Nachteile des CFO:
Vorteile:
- Gut geeignet für mittelgroße Funktionen.
Nachteile
- Funktioniert nicht gut genug für niedrig- und hochdimensionale Funktionen.
- Schwache Suchmöglichkeiten bei diskreten Funktionen.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Elternklasse der Populationsoptimierung Algorithmen |
| 2 | #C_AO_enum.mqh | Include | Enumeration der Algorithmen zur Populationsoptimierung |
| 3 | TestFunctions.mqh | Include | Bibliothek mit Testfunktionen |
| 4 | TestStandFunctions.mqh | Include | Bibliothek mit Funktionen für den Prüfstand |
| 5 | Utilities.mqh | Include | Bibliothek mit Hilfsfunktionen |
| 6 | CalculationTestResults.mqh | Include | Skript zur Berechnung der Ergebnisse in der Vergleichstabelle |
| 7 | Testing AOs.mq5 | Skript | Der einheitliche Prüfstand für alle Algorithmen zur Populationsoptimierung |
| 8 | Simple use of population optimization algorithms.mq5 | Skript | Ein einfaches Beispiel für die Verwendung von Algorithmen zur Populationsoptimierung ohne Visualisierung |
| 9 | Test_AO_CFO.mq5 | Skript | CFO-Prüfstand |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/17167
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Vom Neuling zum Experten: Forex Markt Perioden
Vom Neuling zum Experten: Forex Markt Perioden
 Vom Neuling zum Experten: Die Schatten der Kerzen enthüllen (Dochte)
Vom Neuling zum Experten: Die Schatten der Kerzen enthüllen (Dochte)
 Aufbau eines Remote-Forex-Risikomanagementsystems in Python
Aufbau eines Remote-Forex-Risikomanagementsystems in Python
 Indikator für die Stärke eines Währungspaares in reinem MQL5
Indikator für die Stärke eines Währungspaares in reinem MQL5
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.